由于具有可单位功率因数运行、交流侧电流谐波含量低等优点, 三相电压源型脉宽调制(pulse width modulation, PWM)逆变器被广泛应用于电气传动、不间断电源、有源滤波等领域.随着电力电子器件开关频率的不断升高, 逆变器输出的电能质量得到了很大改善, 然而它所产生的高频共模电压将带来更严重的负面影响[1].当逆变器驱动电机时, 高频共模电压会通过电机内部的耦合电容在电机转轴上产生轴电压和轴电流, 给电机轴承带来严重的电腐蚀[2-4], 降低整个系统的可靠性.因此, 如何抑制因使用PWM调制算法而产生的共模电压是当前国内外的研究热点.
目前, 共模电压的抑制主要分为2类:一类是被动抑制:通过在电路中加入共模电感、共模变压器[5]或无源滤波器[6-8]等无源器件[9]来减小共模电流;另一类是主动抑制:通过在电路中接入有源滤波器[10-11]或者采用三电平变流器[12]或三相四桥臂变流器[13]来降低系统的共模电压输出;或是在不增加硬件成本的条件下, 通过改变传统空间电压矢量调制(space vector PWM, SVPWM)的开关模式来降低逆变器的共模电压输出.
Lai等[14]揭示了传统SVPWM中不同电压矢量对应的共模电压输出, 提出用2个非零电压矢量来等效零矢量作用的调制算法(active zero state PWM1, 2, 3, AZSPWM1, 2, 3), 从而将共模电压限制在±udc/6范围内, 其中udc为直流母线电压.Cacciato等[15]采用3个非零奇电压矢量或者3个非零偶电压矢量(remote state PWM, RSPWM1, 2)来合成参考电压矢量, 该方案最大的缺陷是线性调制范围比较低,最大线性调制范围为
上述方法都是基于理想条件, 并未考虑逆变器的死区时间.周娟等[19]分析了逆变器死区对AZSPWM1输出共模电压的影响, 并做了简单修正;但并未分析共模电压尖峰出现时需满足的负载功率因数、所在扇区中的位置以及修正后的AZSPWM1适用调制范围等问题.Hava等[20]将NSPWM和AZSPWM1相结合, 以获得输出电流性能最优的共模电压抑制算法, 但未考虑死区对二者的影响.
可见, 到目前为止, 还没有文献对死区条件下PWM共模电压抑制算法的输出进行详细地分析, 也没有一种既考虑死区影响又能在全功率因数条件下宽调制范围内将逆变器输出的共模电压一直限制在±udc/6范围内的PWM调制算法.鉴此, 本文提出了一种混合调制算法.实现对共模电压尖峰的有效抑制.
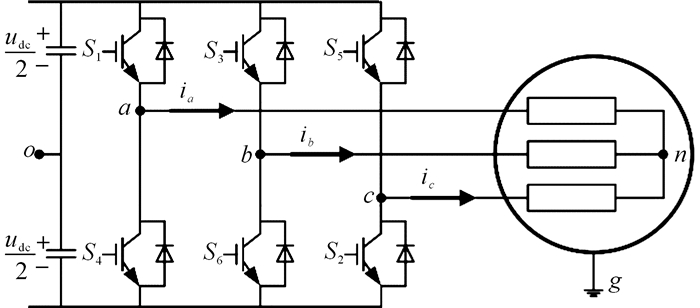
1 NSPWM和AZSPWM1技术 1.1 共模电压一个典型的两电平三相电压源型逆变器结构如图 1所示, 图中udc为直流母线电压, ia, ib, ic为三相电流, 其正方向如箭头所示.根据共模电压的定义, 共模电压ung为负载中性点n与接地点g之间的电势差, uno为负载中性点n与电容中性点o之间的电势差, uog为电容中性点o与接地点g之间的电势差.由于ung=uno+uog, 考虑到uog比较小, 且与uno相比, 变化非常慢, 因此可以将uog忽略, 用uno来表示系统的共模电压输出:
|
图 1 三相电压源型逆变器结构图 Fig. 1 Schematic diagram of three-phase voltage sourceinverter |
| $ {u_{no}} = \frac{{\left( {{u_{ao}} + {u_{bo}} + {u_{co}}} \right)}}{3}. $ | (1) |
式中:uao, ubo和uco分别为三相桥臂输出点a, b, c与电容中性点o之间的电势差.
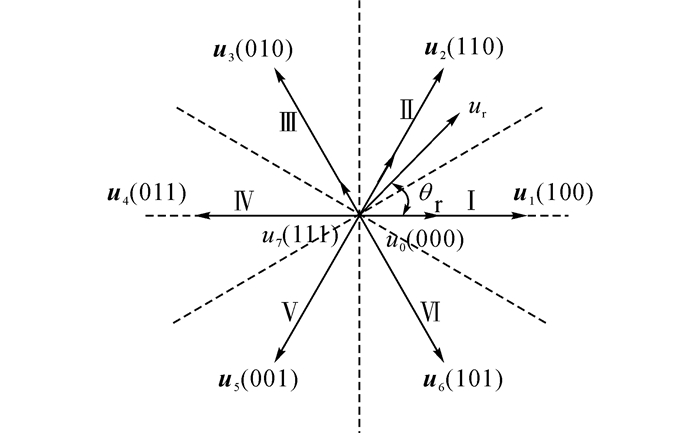
1.2 NSPWM技术在NSPWM中, 3个非零矢量被用来合成参考电压矢量:一个离参考电压矢量最近的非零矢量和与它相邻的2个非零矢量, 没有零矢量.其合成原理和扇区划分如图 2所示.图中, ur为参考电压矢量, θr为ur的位置角, urm为ur的幅值.在扇区Ⅱ(π/6~π/2)中, 参考电压矢量ur由u1、u2和u3合成.将调制度m定义为
|
图 2 NSPWM调制技术 Fig. 2 NSPWM modulation algorithm |
| $ m = \frac{{\sqrt 3 {u_{{\rm{rm}}}}}}{{{u_{{\rm{dc}}}}}}. $ | (2) |
在不考虑死区的条件下, NSPWM适用的线性调制范围为2/3~1.
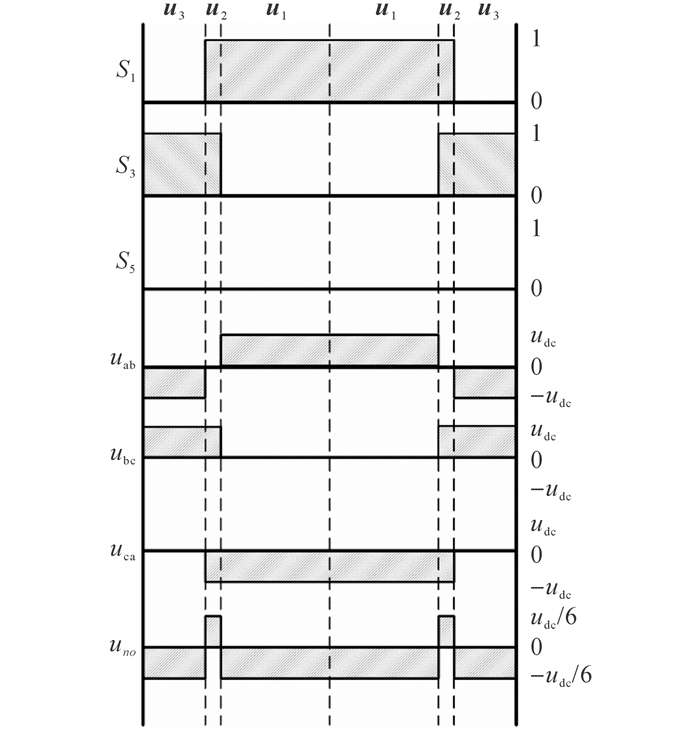
在扇区Ⅱ中, 所用电压矢量的排列顺序为u3→u2→u1→u2→u3.在一个开关周期内, 若不考虑死区的影响, NSPWM各相上管开关信号、输出线电压和共模电压波形如图 3所示.从图中可以看出:3个线电压中仅有uab存在极性翻转, 正负电平之间的零电压间隔时间由u2的作用时间决定;系统的共模电压输出uno被限制在±udc/6范围内.
|
图 3 NSPWM开关信号、输出线电压和共模电压波形图 Fig. 3 Output for gate pulses, line-to-line voltages and common-mode voltage for NSPWM |
AZSPWM1调制算法的扇区定义和矢量合成原理如图 4所示.图中, 参考电压矢量ur位于扇区Ⅰ(0~π/3)内, 其位置角为θr.非零矢量u1和u2用来合成参考电压矢量, u3和u6分别作用相同的时间来等效零矢量的作用.在不考虑死区的前提下, AZSPWM1调制算法适用的线性调制范围为0~1.

|
图 4 AZSPWM1调制技术 Fig. 4 AZSPWM1 modulation algorithm |
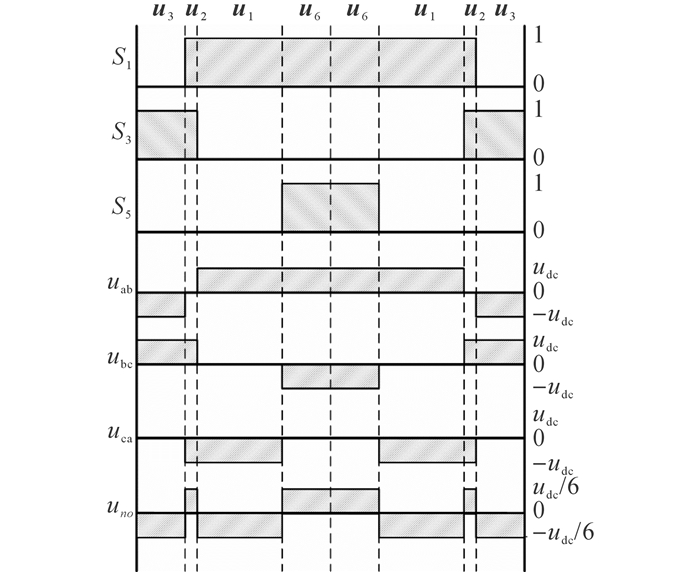
以扇区Ⅰ为例, 在一个开关周期内, 其电压矢量作用顺序为u3→u2→u1→u6→u1→u2→u3.若不考虑死区的影响, 各相上管开关信号、输出线电压和共模电压波形如图 5所示.
|
图 5 AZSPWM1开关信号、输出线电压和共模电压波形图 Fig. 5 Output of gate pulses, line-to-line voltages and common-mode voltage for AZSPWM1 |
如图 5所示, 在一个开关周期内, AZSPWM1输出的线电压中uab和ubc发生了极性翻转.线电压uab中零电平的时间间隔为u2作用时间的一半;线电压ubc中零电平的时间间隔为u1作用时间的一半.AZSPWM1的共模电压输出uno在不考虑死区影响的条件下被限制在±udc/6范围内.
2 死区对系统共模电压输出的影响 2.1 参考电压矢量的合成假设参考电压矢量ur位于图 4所示的位置, 由u6、u1、u2和u3合成, 根据伏秒平衡原理, 需满足如下关系:
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{u}}_1}{t_1} + {\mathit{\boldsymbol{u}}_2}{t_2} + {\mathit{\boldsymbol{u}}_3}{t_3} + {\mathit{\boldsymbol{u}}_6}{t_6} = {\mathit{\boldsymbol{u}}_{\rm{r}}}{T_{\rm{s}}},\\ {t_1} + {t_2} + {t_3} + {t_6} = {T_{\rm{s}}}. \end{array} \right\} $ | (3) |
式中:Ts代表一个开关周期, t1、t2、t3和t6分别代表各电压矢量的作用时间.对式(3)中各个变量进行归一化处理(此后表达式中各时间分量和电压分量均经过归一化处理), 即令tx=tx/Ts, 其中x=1, 2, 3, 6;ux=ux/udc, 其中x=1, 2, 3, 6, r.对式(3)进行求解可得
| $ \left. \begin{array}{l} {t_1} = 1 - 2{t_6} - m\sin {\theta _{\rm{r}}},\\ {t_2} = - 1 + 2{t_6} + \sqrt 3 m\sin \left( {{\theta _{\rm{r}}} + \frac{{\rm{ \mathsf{ π} }}}{6}} \right),\\ {t_3} = 1 - {t_6} - m\sin \left( {{\theta _{\rm{r}}} + \frac{{\rm{ \mathsf{ π} }}}{3}} \right). \end{array} \right\} $ | (4) |
式中:若令t3=t6, 即可求得AZSPWM1在扇区Ⅰ中各电压矢量的作用时间;若令t6=0, 则可以求出NSPWM在扇区Ⅱ中各电压矢量的作用时间.
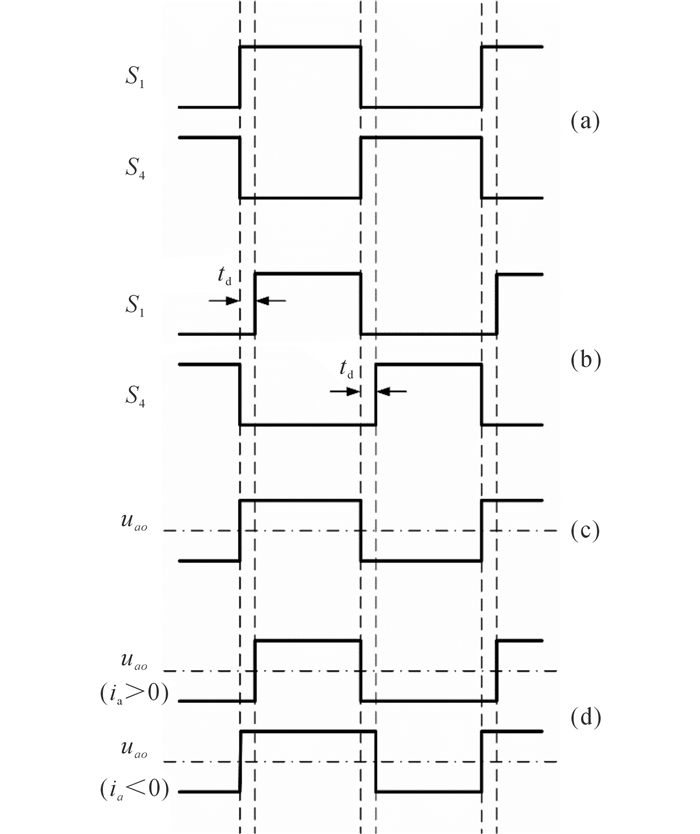
2.2 死区效应在死区条件下, 逆变器的输出如图 6所示.以图 1中逆变器的A相桥臂为例, 其上下开关管在无死区的条件下的开关信号如图 6(a)所示, 上下开关管的脉冲为互补信号.在实际应用中, 由于开关管的关断时间大于其开通时间, 为避免该桥臂上下管同时导通, 需在其开关信号的上升沿加入适当的时间延迟, 也即死区时间td, 该时间须大于开关管的关断延迟时间.对死区时间td进行归一化处理, 即td=td/Ts.添加死区后的驱动信号如图 6(b)所示.图 6(c)给出了无死区时, 逆变器A相输出的电压波形uao.在死区时间内, 开关管中的反并联二极管导通, 进行续流, 输出电压的极性由线路an上流过电流的极性决定, 如图 6(d)所示:若此时电流ia>0, 电流则通过逆变器A相桥臂下管中的反并联二极管进行续流, 将逆变器的输出电压uao钳制在直流母线的负极上;若此时电流ia < 0, 电流则通过逆变器A相桥臂上管中的反并联二极管进行续流, 将逆变器的输出电压uao钳制在直流母线的正极上.
|
图 6 死区对逆变器输出的影响 Fig. 6 Voltage output of inverter with dead-band |
假设参考电压矢量ur位于图 2所示的扇区Ⅱ中.在式(4)中, 令t6=0, 则各电压矢量的作用时间为
| $ \left. \begin{array}{l} {t_1} = 1 - m\sin {\theta _{\rm{r}}},\\ {t_2} = - 1 + \sqrt 3 m\sin \left( {{\theta _{\rm{r}}} + \frac{{\rm{ \mathsf{ π} }}}{6}} \right),\\ {t_3} = 1 - m\sin \left( {{\theta _{\rm{r}}} + \frac{{\rm{ \mathsf{ π} }}}{3}} \right). \end{array} \right\} $ | (5) |
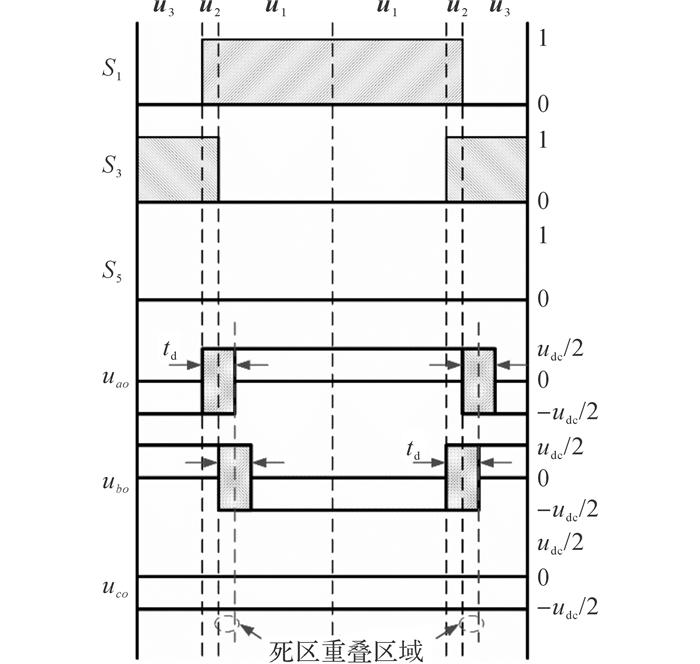
死区对NSPWM调制算法的影响如图 7所示:在一个开关周期内若u2的作用时间t2 < 2td, 逆变器的电压输出uao和ubo之间存在死区重叠的部分, 若在此区间内相电流ia和ib同时大于零, 则uao和ubo将被钳制在直流母线的负极上, 再加上当前uco的状态, 在逆变器输出的共模电压中将出现-udc/2的窄脉冲, 导致共模电压抑制算法失效.
|
图 7 死区对NSPWM电压输出的影响 Fig. 7 Voltage output of NSPWM with dead-band |
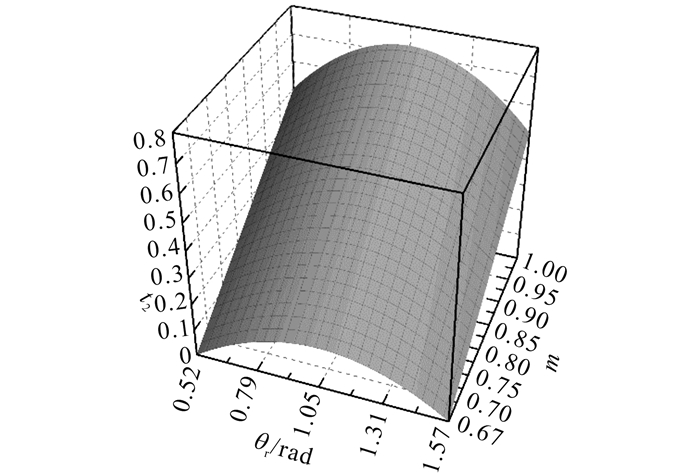
如图 8所示描述了电压矢量u2的作用时间t2与调制度m和参考电压矢量位置角θr之间的关系.从图中可以看出, 在调制度m较低且距离2/3较近的情况下, 当参考电压矢量ur位于扇区Ⅱ(π/6~π/2)的起始位置附近或结束位置附近时, t2的值会比较小, 在一些区域会出现t2 < 2td的情况.
|
图 8 NSPWM中有关电压矢量的作用时间 Fig. 8 Time duration of voltage vector related for NSPWM |
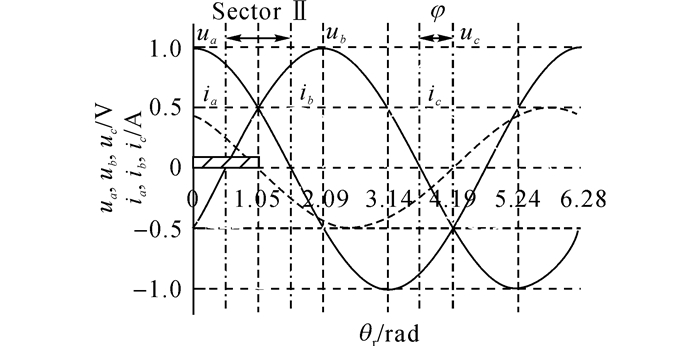
图 9给出了当负载功率因数角φ=-π/6时三相电压电流之间的相位关系.图中矩形阴影部分代表ia、ib同时大于零的区间, 改变负载的功率因数角φ即可移动矩形阴影部分.根据前面的分析, 只要矩形阴影部分与扇区Ⅱ之间有交集, 也即功率因数角φ在-π/3~π/3范围内, 若同时满足u2的作用时间t2 < 2td, 逆变器输出的共模电压中就存在-udc/2的窄脉冲, 导致共模电压抑制算法失效.
|
图 9 功率因数角为-π/6时NSPWM三相电压电流之间的相位关系 Fig. 9 Phase relationship between three-phase voltage and current for NSPWM when power factor angle is-π/6 |
假设参考电压矢量ur位于图 4所示的扇区Ⅰ中, 令t3=t6, 根据式(4)即可求得AZSPWM1调制算法中各电压矢量的作用时间.
| $ \left. \begin{array}{l} {t_1} = m\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{3} - {\theta _{\rm{r}}}} \right),\\ {t_2} = m\sin {\theta _{\rm{r}}},\\ {t_3} = {t_6},\\ {t_6} = \frac{1}{2} - \frac{1}{2}m\sin \left( {{\theta _{\rm{r}}} + \frac{{\rm{ \mathsf{ π} }}}{3}} \right). \end{array} \right\} $ | (6) |
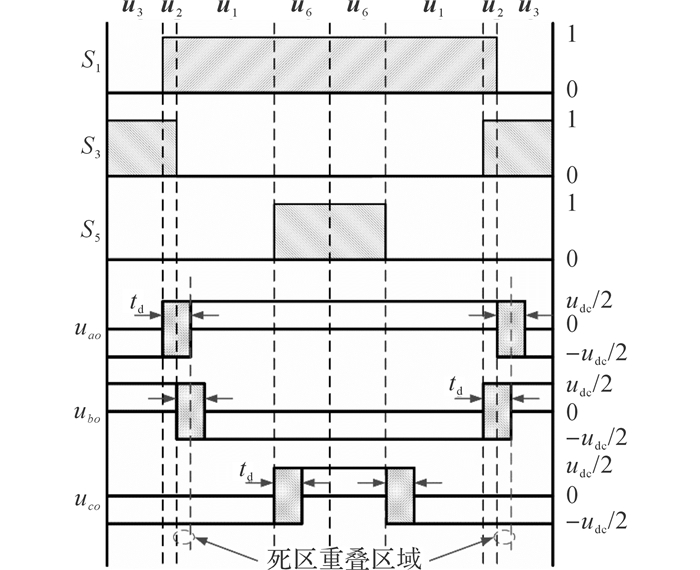
当θr在0~π/6之间时, 若t2 < 2td且t1>2td, 死区对AZSPWM1的影响如图 10所示.从图中可以看出, 由于t2 < 2td, 逆变器输出电压uao和ubo之间存在死区重叠部分.在此区域内, 若ia和ib同时大于零, 则uao和ubo将被钳制在直流母线的负极上, 此时uco刚好也处在直流母线负极上, 因此, 在AZSPWM1输出的共模电压中就会出现-udc/2的窄脉冲, 共模电压抑制算法失效.
|
图 10 前半扇区中死区对AZSPWM1输出电压的影响 Fig. 10 Voltage output of AZSPWM1 with dead-band in former half sector |
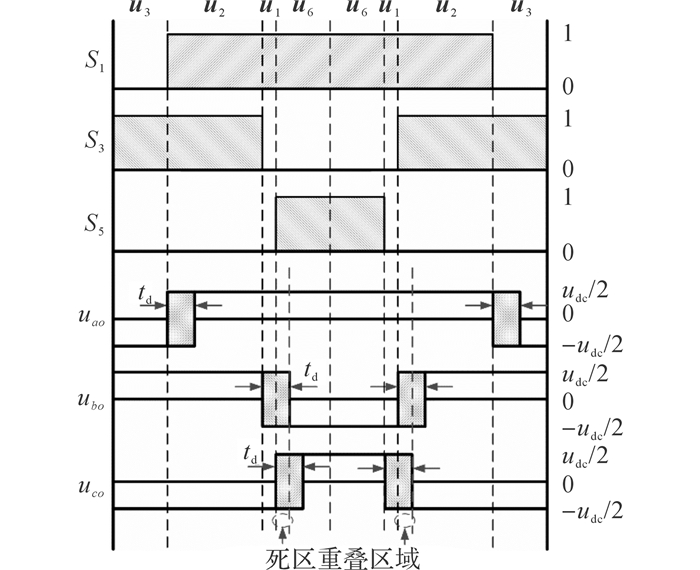
当θr在π/6~π/3的范围内时, 若t1 < 2td且t2>2td, 死区对AZSPWM1调制算法的影响如图 11所示.图中显示:由于t1 < 2td, 逆变器输出电压ubo和uco之间存在死区重叠部分.在此区域内, 如果ib、ic同时小于零, 则ubo和uco将被钳制在直流母线的正极上, 此时由于uao也处于直流母线的正极上, 在AZSPWM1输出的共模电压中将出现udc/2的窄脉冲, 此时共模电压抑制算法失效.
|
图 11 后半扇区中死区对AZSPWM1输出电压的影响 Fig. 11 Voltage output of AZSPWM1 with dead-band in latter half sector |
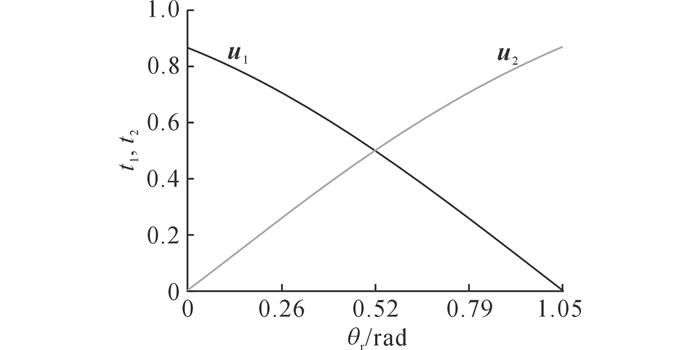
根据式(6), 2个非零矢量u1和u2的作用时间t1和t2与θr之间的关系如图 12所示.从图中可以看出:无论调制度m为0~1之间任何值, 当ur位于扇区Ⅰ(0~π/3)的起始位置附近时, u2的作用时间t2很小, 会出现t2 < 2td的区间;同样当ur位于扇区Ⅰ的结束位置附近时, u1的作用时间t1很小, 会出现t1 < 2td的区间.
|
图 12 非零矢量作用时间与参考电压矢量位置角之间关系 Fig. 12 Relationship between time durations of active voltage vectors and angular position of reference voltage vector |
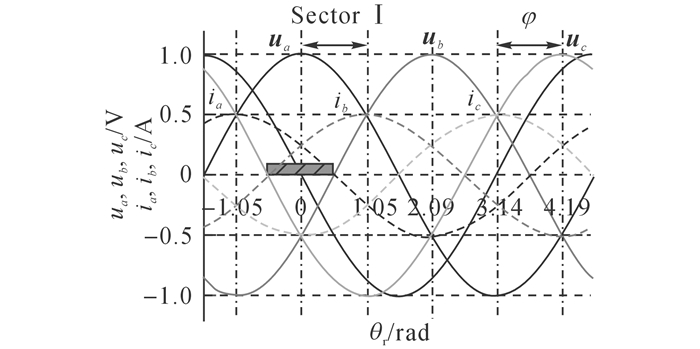
图 13显示了功率因数角φ=-π/3时, 三相电压电流之间的相位关系.图中矩形阴影部分代表ia、ib同时大于零的区域, 改变功率因数角φ的大小即可移动矩形阴影区域的位置.只要矩形区域与扇区Ⅰ的起始部分有交集, 也即功率因数角φ在-π/2~-π/6范围内, 若同时满足t2 < 2td, 逆变器输出的共模电压中就有-udc/2的窄脉冲.当φ在-π/6~0之间变化时, 若此时调制度m满足式(7)限定的条件, 也即在矩形阴影部分与扇区Ⅰ前半部分(0~π/6)交集的区域内出现t2 < 2td的情况, 逆变器也会输出共模电压尖峰.
|
图 13 功率因数角为-π/3时AZSPWM1三相电压电流之间的相位关系 Fig. 13 Phase relationship between three-phase voltage and current for AZSPWM1 when power factor angle is-π/3 |
| $ m < \frac{{2{t_{\rm{d}}}}}{{\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{6} + \varphi } \right)}}. $ | (7) |
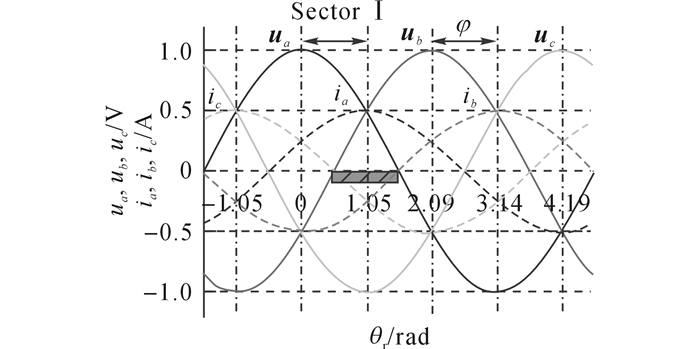
如图 14所示显示了功率因数角φ=π/3时, 三相电压电流之间的相位关系.图中矩形阴影部分表示电流ib、ic同时小于零的区域, 改变功率因数角φ的大小将移动矩形阴影部分的位置.只要矩形区域与扇区Ⅰ的结束部分有交集, 也即功率因数角φ在π/6~π/2范围内, 若同时满足t1 < 2td, 在逆变器输出的共模电压中就会出现udc/2的窄脉冲, 导致AZSPWM1共模电压抑制算法失效.当功率因数角φ在0~π/6范围内, 若此时调制度m满足式(8)限定的条件, 也即在矩形阴影部分与扇区Ⅰ的后半部分(π/6~π/3)交集的区域内出现t1 < 2td时, 逆变器也会输出共模电压尖峰.
|
图 14 功率因数角为π时AZSPWM1三相电压电流之间相位关系 Fig. 14 hase relationship between three-phase voltage and current for AZSPWM1 when power factor angle is π/3 |
| $ m < \frac{{2{t_{\rm{d}}}}}{{\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{6} - \varphi } \right)}}. $ | (8) |
综上所述, 当考虑死区时, 无论是NSPWM调制算法还是AZSPWM1调制算法, 在一定条件下, 均存在调制算法失效的工作区间, 出现共模电压尖峰.因此, 为保证共模电压抑制算法一直有效, 需对这2种调制算法分别进行修正.
3 混合调制技术 3.1 修正NSPWM调制技术根据第1节分析, 在NSPWM调制算法中, 有一个线电压存在极性翻转.为防止正负电平翻转在电机端产生很高的过电压, 需限制该线电压中零电平间隔的最小时间, 在扇区Ⅱ中, 即限制非零矢量u2的最小作用时间tzmin[21].同样, 在死区存在的条件下, 当u2的作用时间t2 < 2td时, 将产生共模电压尖峰.此外, 功率器件工作时存在的开通延时td(on)和关断延时td(off), 会使t2在2td(off)~2[td+td(on)]的范围内, 产生共模电压尖峰.为避免共模电压尖峰的出现, 也需限制u2的最小作用时间2tdmin, 使其大于2[td+td(on)][19].假设tmin=max (tdmin, tzmin), 将u2的最小作用时间限制为2tmin.对tmin进行归一化处理, 可得tmin=tmin/Ts.在扇区Ⅱ(π/6~π/2)中:
| $ {t_2} = - 1 + \sqrt 3 m\sin \left( {{\theta _r} + \frac{{\rm{ \mathsf{ π} }}}{6}} \right) \ge 2{t_{\min }}. $ | (9) |
若已知tmin的值, 调制度m需满足如下限制条件:
| $ m \ge \frac{2}{3}\left( {1 + 2{t_{\min }}} \right). $ | (10) |
由式(10)可知, 由于限制了u2的最小作用时间, NSPWM的线性调制范围由2/3~1缩小为2(1+2tmin)/3~1, tmin的取值越大, NSPWM适用的线性调制范围将越小.
3.2 修正AZSPWM1调制技术如第1节所述, 在扇区Ⅰ中, AZSPWM1输出的线电压中有2个发生了极性翻转, 其零电平的间隔时间分别由u1、u2的作用时间t1、t2来决定.因此, 为避免线电压极性翻转在电机端产生过电压, 需限制u1、u2的最小作用时间2tzmin.同样, 在死区存在的条件下, 当t2 < 2td或t1 < 2td时, 且满足一定的负载功率因数条件, 在逆变器输出的共模电压中就会出现尖峰毛刺.考虑功率器件工作时存在的开通延时td(on)和关断延时td(off)时, 当t1或t2在2td(off)~2[td+td(on)]的范围内变化, 且满足相应的负载功率因数条件, 就会产生共模电压尖峰.为消除共模电压中的尖峰毛刺, 也需限制u1、u2的最小作用时间2tdmin, 使其大于2[td+td(on)].与修正NSPWM调制算法一样, 取tmin=max (tdmin, tzmin), 将u1、u2的最小作用时间均限制为2tmin.
在扇区Ⅰ的前半部分(0~π/6), 非零矢量的作用时间t2≤t1.根据式(6), 假设
| $ \left. \begin{array}{l} {t_1} \ge 2{t_{\min }},\\ {t_2} \le 2{t_{\min }}. \end{array} \right\} $ | (11) |
上式成立时, 调制度m需满足m≥4tmin.
在t2 < 2tmin的区域内, 令t2=2tmin, 根据式(4), 可分别求出其余各个矢量的作用时间:
| $ \left. \begin{array}{l} {t_1} = - 2{t_{\min }} + m\sin \left( {{\theta _{\rm{r}}} + \frac{{\rm{ \mathsf{ π} }}}{3}} \right),\\ {t_3} = \frac{1}{2} - {t_{\min }} + \frac{1}{2}m\sin \left( {{\theta _{\rm{r}}} - \frac{{\rm{ \mathsf{ π} }}}{3}} \right),\\ {t_6} = \frac{1}{2} + {t_{\min }} - \frac{{\sqrt 3 }}{2}m\sin \left( {{\theta _r} + \frac{{\rm{ \mathsf{ π} }}}{6}} \right). \end{array} \right\} $ | (12) |
要求在修正后t1≥2tmin, t3≥0且t6≥0, 则调制度m需满足:m≥8tmin/3且m≤2(1+2tmin)/3.
在扇区Ⅰ的后半部分(π/6~π/3), 非零矢量的作用时间t1≤t2.根据式(6), 假设
| $ \left. \begin{array}{l} {t_2} \ge 2{t_{\min }},\\ {t_1} \le 2{t_{\min }}. \end{array} \right\} $ | (13) |
上式成立时, 调制度m需满足m≥4tmin.
在t1 < 2tmin的区域内, 令t1=2tmin, 根据式(4), 可分别求出其余各个矢量的作用时间
| $ \left. \begin{array}{l} {t_2} = - 2{t_{\min }} + m\sin \left( {{\theta _{\rm{r}}} + \frac{{\rm{ \mathsf{ π} }}}{3}} \right),\\ {t_3} = \frac{1}{2} + {t_{\min }} - \frac{{\sqrt 3 }}{2}m\cos {\theta _{\rm{r}}},\\ {t_6} = \frac{1}{2} - {t_{\min }} - \frac{1}{2}m\sin {\theta _r}. \end{array} \right\} $ | (14) |
要求在修正后t2≥2tmin, t3≥0且t6≥0, 则调制度m需满足:m≥8tmin/
对于t1≥2tmin且t2≥2tmin的区域, 可直接使用AZSPWM1调制算法, 无需修正.
根据以上分析, 若将调制度m限制在8tmin/3~2(1+2tmin)/3的范围内, 则可将AZSPWM1中参与参考电压矢量合成的2个非零矢量的最小作用时间限制在2tmin以上, 2个等效零矢量作用的非零矢量的作用时间限制在零以上, 也即修正AZSPWM1(modified AZSPWM1, MAZSPWM1)调制技术适用于调制度m位于8tmin/
在AZSPWM1调制算法中, 对于调制度m < 8tmin/
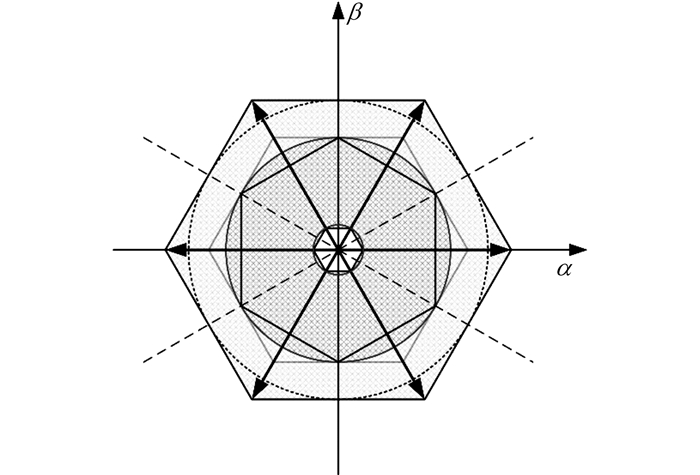
根据前面的分析, 修正后的NSPWM调制算法适用的线性调制范围为2(1+2tmin)/3~1, 而MAZSPWM1调制算法的线性调制范围为8tmin/
|
图 15 混合调制算法的适用范围 Fig. 15 Linear modulation range of hybrid modulation |
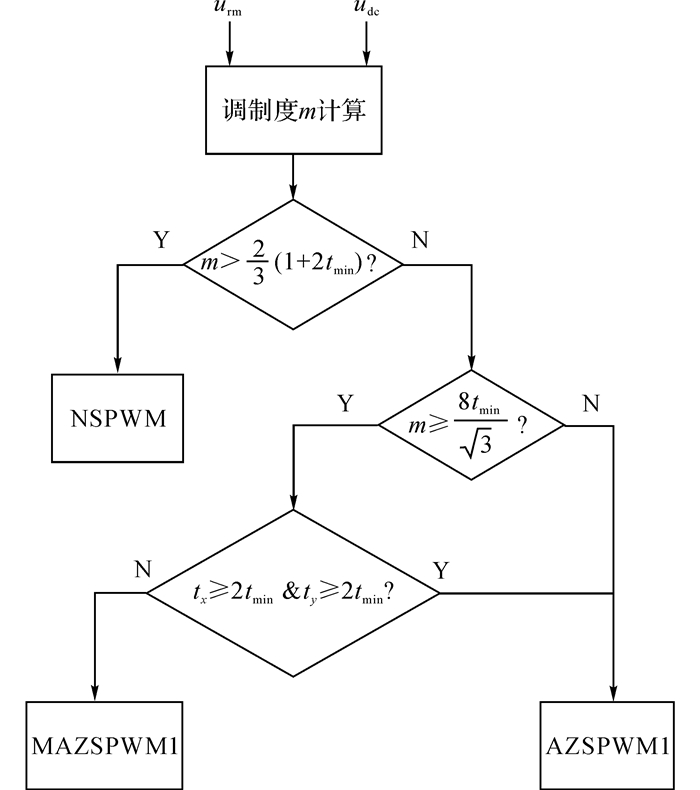
混合调制算法的流程图如图 16所示, 根据逆变器的调制度m来选择相应的调制算法模块, 并根据有关电压矢量的作用时间tx和ty在MAZSPWM1模块和AZSPWM1模块之间进行切换.
|
图 16 混合调制算法 Fig. 16 Hybrid modulation algorithm |
为检验本文分析的有效性, 需使逆变器运行在不同负载功率因数条件下.鉴于在永磁同步电机的矢量控制中, 可通过调节电机d轴和q轴电流分量改变电机的功率因数, 因此, 本文用一台7.5 kW凸极式永磁同步电机(IPMSM)充当逆变器的负载.一台5.0 kW的凸极式永磁同步发电机IPMSG与IPMSM通过联轴器连接构成对拖系统.在测试中, 整个IPMSM+IPMSG对拖系统的运行转速由一台安川A1000逆变器通过控制IPMSG调节, 将其固定在37.5 r/min.相关共模电压抑制算法都通过一个型号为TMS320F2808的DSP产生逆变器所需的开关信号.
在所有测试中, 将IPMSM定子电流幅值的给定值设置为6 A, 根据不同的功率因数条件, 期望的d轴电流isd*和q轴电流isq*的分配情况如表 1所示.其中φ*为功率因数角给定值.此外, 鉴于逆变器IGBT的驱动板上自带3.3 μs的死区时间, 功率器件工作时的开通延时td(on)为320 ns, 关断延时td(off)为550 ns, 综合考虑逆变器输出的共模电压尖峰抑制和减小电机侧的电压过冲, 本文将共模电压抑制算法中的电压矢量最小作用时间tmin设置为5 μs.根据式(10), NSPWM调制算法在调制度m处于2/3~0.711的范围内将有可能出现共模电压尖峰;在混合调制算法中, NSPWM工作在调制度m大于0.733的区间内, MAZSPWM1工作在调制度m处于0.231~0.733的范围内, AZSPWM1工作在调制度m小于0.231的区间内以及调制度m处于0.231~0.733中且不需要修正的区域内.
| 表 1 不同功率因数角对应的定子电流dq轴分量 Table 1 Assignment of desired d-axis and q-axis currents under different load power factor conditions |
本文利用高压隔离探头直接测量图 1所示的负载中性点n和电容中性点o之间的电势差uno, 也即逆变器输出的共模电压;利用电流探头按图 1规定的电流正方向, 直接测量逆变器输出的A相电流isa.此外, 将同时刻参考电压矢量所处的扇区位置sector经DSP计算后, 直接传输出来.
在共模电压测试中, 保持IPMSM的工作状态不变, 然后分别在直流母线电压udc为350、400和600 V的条件下, 也即在不同调制度m的条件下, 测量系统的共模电压输出.为了便于对比不同udc下逆变器输出的共模电压, 本文将测量到的共模电压uno统一进行归一化处理, 也即令CMV=uno/udc, 并在实验结果中用黑色线条表示.为将同时刻的负载A相电流isa和扇区sector与共模电压在相同的纵横坐标下表示, 本文分别对其进行了处理:实验结果中横坐标为时间t, 单位为s;正弦曲线表示0.2isa, 阶梯波代表(sector×0.1+0.5);其中, 共模电压CMV和扇区sector为无量纲变量, 电流isa的刻度单位为安培(A).
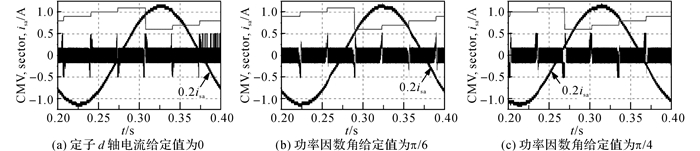
4.1 NSPWM调制技术鉴于NSPWM调制技术工作在调制度m>2/3的区域内, 针对当前IPMSM的运行状态, 分别在udc=350和400 V的条件下测量系统的共模电压输出.根据前面的分析结果, 当功率因数角φ在-π/3~π/3的范围内时, 采用NSPWM调制技术时会出现共模电压尖峰, 因此, 分别在表 1所罗列的前3种功率因数下测量系统的共模电压输出情况, 其结果如图 17和18所示.
|
图 17 NSPWM调制技术在直流母线电压为400 V时的共模电压输出 Fig. 17 CMV outputs for the NSPWM when DC-link voltage is 400 V |
|
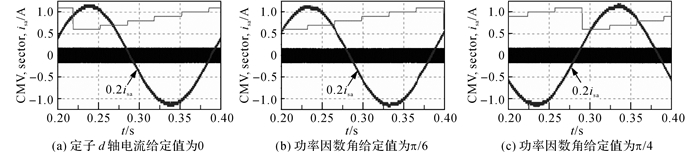
图 18 NSPWM调制技术在直流母线电压为350 V时的共模电压输出 Fig. 18 CMV outputs for the NSPWM when DC-link voltage is 350 V |
当udc=400 V且isd*=0时, φ>0且在零附近变化, 此时在扇区的两端均会出现共模电压尖峰, 如图 17(a)所示.另外, 当udc=400 V时, 调制度m会在2/3附近波动, 当m < 2/3时, NSPWM调制算法会达到适用调制范围的下限, 出现共模电压尖峰.当φ分别为π/6和π/4时, 均会在扇区的结束位置出现共模电压尖峰.当udc=350 V时, 无论负载功率因数为何值, NSPWM调制算法输出的共模电压中没有共模电压尖峰, 其结果如图 18所示.
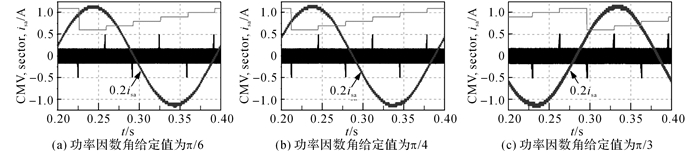
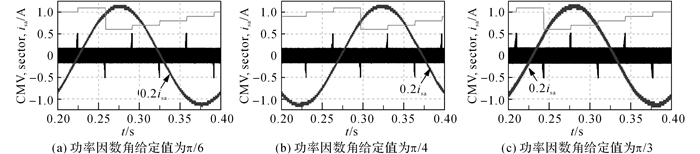
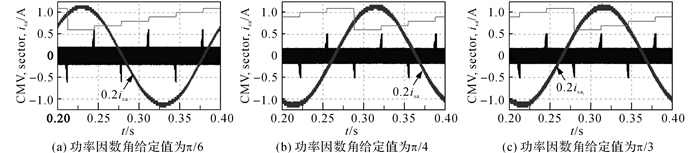
4.2 AZSPWM1调制技术鉴于负载功率因数角φ在π/6~π/2或-π/2~-π/6的范围内变化时, AZSPWM1输出的共模电压中会有尖峰毛刺出现, 分别在表 1所罗列后3种负载功率因数条件下来测试逆变器输出的共模电压, 其结果如图 19~21所示.从图中可以看出, 无论调制度m以及负载功率因数角φ为何值, 在扇区结束的位置附近, AZSPWM1调制算法输出的共模电压中一直存在尖峰毛刺.另外, 对比不同udc下的共模电压尖峰输出情况, 可见, 随着调制度m的降低, 出现共模电压尖峰的区域变宽了, 这与前面的分析保持一致.
|
图 19 AZSPWM1调制在直流母线电压为350 V时的共模电压输出 Fig. 19 CMV outputs for AZSPWM1 when DC-link voltage is 350 V |
|
图 20 AZSPWM1调制在直流母线电压为400 V时的共模电压输出 Fig. 20 CMV outputs for AZSPWM1 when DC-link voltage is 400 V |
|
图 21 AZSPWM1调制在直流母线电压为600 V时的共模电压输出 Fig. 21 CMV outputs for AZSPWM1 when DC-link voltage is 600 V |
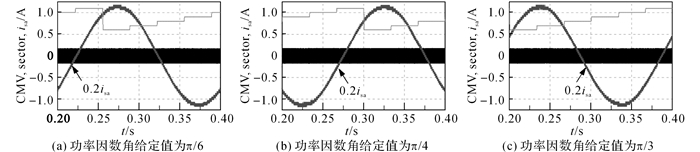
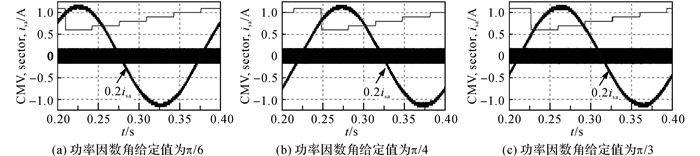
在混合调制技术中, 当udc=350 V时, NSPWM调制算法作用, 其输出的结果如图 18所示;当udc分别为400和600 V时, MAZSPWM1调制算法作用, 其共模电压输出情况如图 22和23所示.从图中可以发现, 采用MAZSPWM1调制算法时, 逆变器输出的共模电压中没有尖峰毛刺出现.由此可见, 本文所提出的混合调制算法在相应的测试条件下, 逆变器输出的共模电压均在±udc/6的范围内变化, 没有共模电压尖峰出现.
|
图 22 MAZSPWM1调制在直流母线电压为400 V时共模电压输出 Fig. 22 CMV outputs for MAZSPWM1 when DC-link voltage is 400 V |
|
图 23 MAZSPWM1调制在直流母线电压为600 V时共模电压输出 Fig. 23 CMV outputs for MAZSPWM1 when DC-link voltage is 600 V |
本文提出了一种混合调制算法, 该算法通过对传统算法进行简单修正并结合, 在全功率因数条件下宽调制范围内实现了对PWM逆变器输出的共模电压尖峰的有效抑制.该算法可在不增加系统硬件成本的条件下, 减轻共模电压尖峰对系统可靠性的影响, 提高系统的使用寿面.实验结果验证了本文理论分析的正确性和所提混合调制算法的有效性.
| [1] |
姜艳姝. 现代变频调速系统负面效应研究及其对策[D]. 哈尔滨: 哈尔滨理工大学, 2007.
JIANG Yan-shu. Research on adverse effects of modern pwm adjustable speed drive system and the associated countermeasures[D]. Harbin:Harbin University of Science and Technology, 2007. http://doi.wanfangdata.com.cn/10.7666/d.y1195088 |
| [2] | ERDMAN J M, KERKMAN R J, SCHLEGEL D W, et al. Effect of PWM inverters on AC motor bearing currents and shaft voltages[J]. IEEE Transactions on Industry Applications, 1996, 32(2): 250–259. DOI:10.1109/28.491472 |
| [3] | COSTELLO M J. Shaft voltages and rotating machinery[J]. IEEE Transactions on Industry Applications, 1993, 29(2): 419–426. DOI:10.1109/28.216553 |
| [4] | MACDONALD D, GRAY W. PWM drive related bearing failures[J]. IEEE Industry Applications Magazine, 1999, 5(4): 41–47. DOI:10.1109/2943.771365 |
| [5] |
裴雪军, 张凯, 康勇, 等. PWM逆变器共模干扰电流的衰减和抑制[J].
中国电机工程学报, 2004, 24(11): 80–84.
PEI Xue-jun, ZHANG Kai, KANG Yong, et al. Damping and suppression of common mode interference currents in PWM inverter[J]. Proceedings of the CSEE, 2004, 24(11): 80–84. DOI:10.3321/j.issn:0258-8013.2004.11.016 |
| [6] |
高强, 徐殿国. PWM逆变器输出端共模与差模电压dv/dt滤波器设计[J].
电工技术学报, 2007, 22(1): 79–84.
GAO Qiang, XU Dian-guo. Design of common-mode and differential-mode voltage dv/dt filter at PWM inverter output terminals[J]. Transactions of China Electrotechnical Society, 2007, 22(1): 79–84. |
| [7] |
陈希有, 徐殿国, 马洪飞, 等. 兼有共模电压抑制作用的逆变器输出无源滤波器[J].
电工技术学报, 2002, 17(06): 38–42.
CHEN Xi-you, XU Dian-guo, MA Hong-fei, et al. The inverter output passive filter with the suppressing of common-mode voltage[J]. Transactions of China Electrotechnical Society, 2002, 17(06): 38–42. DOI:10.3321/j.issn:1000-6753.2002.06.009 |
| [8] |
姜艳姝, 徐殿国, 刘宇, 等. 一种新颖的逆变器输出无源滤波器的研究(英文)[J].
中国电机工程学报, 2004, 24(11): 134–138.
JIANG Yan-shu, XU Dian-guo, LIU Yu, et al. Research on a novel inverter output passive filter[J]. Proceedings of the CSEE, 2004, 24(11): 134–138. DOI:10.3321/j.issn:0258-8013.2004.11.027 |
| [9] | VON J A, HAORAN Z, WALLACE A K. An evaluation of mitigation techniques for bearing currents, EMI and overvoltages in ASD applications[J]. IEEE Transactions on Industry Applications, 1998, 34(5): 1113–1122. DOI:10.1109/28.720452 |
| [10] |
姜艳姝, 刘宇, 徐殿国, 等. PWM变频器输出共模电压及其抑制技术的研究[J].
中国电机工程学报, 2005, 25(9): 47–53.
JIANG Yan-shu, LIU Yu, XU Dian-guo, et al. Research on common-mode voltage generated by a PWM inverter and its cancellation technology[J]. Proceedings of the CSEE, 2005, 25(9): 47–53. |
| [11] |
姜艳姝, 陈希有, 徐殿国, 等. 一种消除PWM逆变器驱动系统中电动机端轴电压和轴承电流的前馈有源滤波器[J].
中国电机工程学报, 2003, 23(7): 134–138.
JIANG Yan-shu, CHEN Xi-you, XU Dian-guo, et al. A novel feed-forward-type active filter to eliminate shaft voltage and bearing current at motor terminal in a PWM inverter drives[J]. Proceedings of the CSEE, 2003, 23(7): 134–138. |
| [12] |
钟玉林, 赵争鸣, 袁立强. 逆变器驱动电机的共模电压和轴电压的抑制[J].
清华大学学报:自然科学版, 2009, 49(1): 25–28.
ZHONG Yu-lin, ZHAO Zheng-ming, YUAN Li-qiang. Suppression of common-mode and shaft voltages in inverter-driven induction motor[J]. Journal of Tsinghua University:Science and Technology, 2009, 49(1): 25–28. |
| [13] | ORITI G, JULIAN A L, LIPO T A. A new space vector modulation strategy for common mode voltage reduction[C]//PESC'97 Record. 28th Annual IEEE Power Electronics Specialists Conference. Saint Louis, MO:IEEE 1997. https://es.scribd.com/doc/229974655/Switching-Power-Converters |
| [14] | LAI Y S. New random technique of inverter control for common mode voltage reduction of inverter-fed induction motor drives[J]. IEEE Transactions on Energy Conversion, 1999, 14(4): 1139–1146. DOI:10.1109/60.815039 |
| [15] | CACCIATO M, CONSOLI A, SCARCELLA G, et al. Reduction of common-mode currents in PWM inverter motor drives[J]. IEEE Transactions on Industry Applications, 1999, 35(2): 469–476. DOI:10.1109/28.753643 |
| [16] | UN E, HAVA A M. A near-state PWM method with reduced switching losses and reduced common-mode voltage for three-phase voltage source inverters[J]. IEEE Transactions on Industry Applications, 2009, 45(2): 782–793. DOI:10.1109/TIA.2009.2013580 |
| [17] | HAVA A M, UN E. Performance analysis of reduced common-mode voltage PWM methods and comparison with standard PWM methods for three-phase voltage-source inverters[J]. IEEE Transactions on Power Electronics, 2009, 24(1): 241–252. DOI:10.1109/TPEL.2008.2005719 |
| [18] |
陆海峰, 瞿文龙, 张星, 等. 抑制共模电压的不对称NZPWM技术[J].
清华大学学报:自然科学版, 2007, 47(7): 1122–1125.
LU Hai-feng, QU Wen-long, ZHANG Xing, et al. Asymmetrical NZPWM technique for reducing the common-mode voltage[J]. Journal of Tsinghua University:Science and Technology, 2007, 47(7): 1122–1125. |
| [19] |
周娟, 魏琛, 杨宇, 等. 逆变器简化PWM算法及抑制共模电压策略[J].
电工技术学报, 2014, 29(8): 158–165.
ZHOU Juan, WEI Chen, YANG Yu, et al. Inverter simplified algorithm of PWM and inhibit common-mode voltage strategy[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 158–165. |
| [20] | HAVA A M, U X, N E. A high-performance PWM algorithm for common-mode voltage reduction in three-phase voltage source inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(7): 1998–2008. DOI:10.1109/TPEL.2010.2100100 |



