2. 中国舰船设计研究中心, 湖北 武汉 430064;
3. 武汉大学 水资源与水电科学国家重点实验室, 湖北 武汉 430072
2. China Ship Development and Design Center, wuhan 430064, China;
3. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
可再生能源的迅猛发展使现代抽水蓄能电站对负荷变化需要有更快的响应能力、调节稳定性和更宽的稳定运行范围.然而, 水泵水轮机在泵工况部分负荷运行时, 水轮机内流动结构复杂, 特性曲线易出现驼峰特性, 使压力脉动和机组振动剧烈, 威胁机组运行安全[1].因此, 揭示水轮机内的流动变化规律对驼峰特性的影响, 对转轮优化设计和安全运行控制具有十分重要的意义.
目前, 对于水泵水轮机部分负荷工况产生驼峰区内流机理的开展了大量的研究.冉红娟等[2-4]对高水头水泵水轮机驼峰区转轮内部流态进行数值分析, 发现转轮及活动导叶内复杂的流动分离与驼峰区的形成有着密切的关系, 并在此基础上对转轮的出口角及包角进行了优化, 改善了驼峰特性.王茂焕等[5]对水泵水轮机的驼峰特性进行数值模拟, 发现转轮进口及导叶区域的回流与驼峰的形成有密切的联系.陶然等[6]对某可逆式水泵水轮机进行了全流道非定常数值模拟, 认为转轮与扩散段之间的不良流态使过流部件水力损失增大, 导致驼峰区.Xiao等[7]对驼峰区的压力脉动和转轮内部流态进行了数值模拟分析, 认为驼峰特性是由于导叶、转轮和尾水管内的流动损失共同产生的.李德友等[8-10]通过实验和数值模拟的方法对水泵水轮机3个不同开度下的驼峰特性进行了研究, 同样认为驼峰特性与转轮流道内和固定导叶部分流道内的流动分离及旋涡有关.也有部分学者认为旋转失速对驼峰特性的影响.Mark等[11]和JeŠe等[12]分别通过数值模拟和模型试验发现旋转失速与驼峰特性的形成时刻近乎一致.然而, Braun等[13-14]和Pacot等[15]对某模型水泵水轮机在部分负荷工况下的内部流态进行了模型试验和数值模拟研究, 发现旋转失速发生起始流量大于驼峰特性产生时的流量.张春泽等[16-17]对某模型水泵水轮机在泵工况下的旋转失速现象进行的数值研究, 发现旋转失速发生时并未出现驼峰特性.Yin等[18]和Yang等[19]的数值模拟和模型试验结果显示, 驼峰特性发生于65%最优流量工况点, 早于旋转失速发生点.前述工作对部分负荷下的流态及与水泵驼峰特性的关系做了大量研究, 但并没有得到驼峰特性内流机理的一致结论.并且, 由于分析工况点较少, 并未清晰地得到转轮内部流动特性演变规律.
本文对某低比转速水泵水轮机泵工况进行了全流道三维非恒定数值模拟, 对不同工况下的流态演变规律进行分析, 建立起导叶、转轮和尾水管内部流动结构演变的联系, 揭示转轮进口回流涡导致尾水管和导叶区流态突变的作用机理, 并探讨其对驼峰特性的影响.
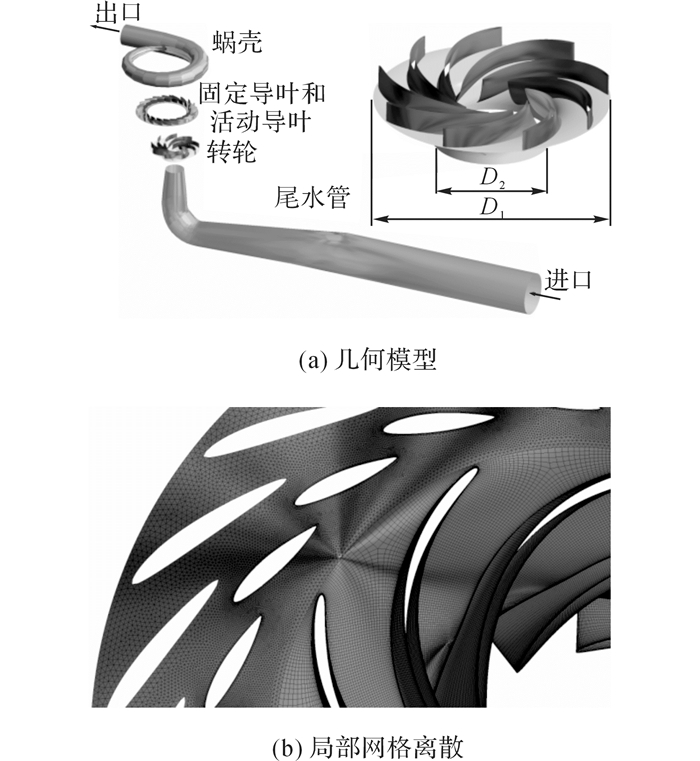
1 数值模型和条件 1.1 计算体型参数计算采用全流道三维非恒定数值模拟方法, 模拟体型如图 1(a)所示, 部分包括蜗壳, 导叶, 水轮机及尾水管.为了避免小流量工况下, 转轮进口的形成的回流对计算边界条件恒定值给定产生影响, 尾水管出口管道延长了6倍管径的长度.转轮高压侧直径D1=0.28 m, 低压侧直径D2=0.14 m, 转轮叶片数zb=9, 固定导叶nsv=9, 活动导叶数ngv=9, 水泵转速np=1 200 r/min, 计算所用活动导叶开度α=15°.
|
图 1 水泵水轮机转轮体型及网格划分示意图 Fig. 1 Geometry and mesh of simulation domain |
计算采用商业软件Ansys fluent 14.5, 选用SAS-SST湍流模型.该模型在标准SST湍流模型的ω输运方程的产生项中增加了QSAS项, 改项把von Karman尺度引入湍流尺度方程, 在流动分离区具有大涡模拟特性, 在非稳态计算中通过尺度方程动态适应流动结构[20].
| $ \begin{array}{l} {Q_{SAS}} = {\rm{max}}[\rho \zeta \kappa {S^2}{\left( {\frac{L}{{{L_{vk}}}}} \right)^2}-\\ \;\;\;\;\;\;\;\;\;C\frac{{2\rho k}}{{{\sigma _\varphi }}}{\rm{max}}\left( {\frac{{{{\left| {\nabla \omega } \right|}^2}}}{{{\omega ^2}}}, \frac{{{{\left| {\nabla k} \right|}^2}}}{{{k^2}}}} \right), 0]. \end{array} $ | (1) |
式中:
边界条件:尾水管进口为流量边界, 蜗壳出口为压力边界, 固体壁面为无滑移边界.
1.3 网格及时间步长采用混合网格划分方式, 由于蜗壳体型复杂, 采用四面体网格;导叶区采用楔形网格;转轮和尾水管采用六面体网格.为了更好地捕捉近壁流态, 对活动导叶和转轮叶片边界层加密(图 1(b)), 保证y+ < 10 (见图 2), 满足湍流模型要求[21-22].为消除因网格数量引起的求解误差, 对不同尺度的网格做无关性分析.通过恒定流计算所得设计工况下的扬程随网格数量的变化确定计算网格, 结算结果如图 3所示, N为网格单元数.当网格数量大于450万时, 计算所得扬程差异小于1%.考虑到部分负荷工况复杂流动结构需要精细的网格捕捉, 最终选取网格单元总数为882万的划分方式.蜗壳, 导叶, 转轮和尾水管区域的网格单元数量分别为101万, 242万, 245万和234万.

|
图 2 转轮叶片和导叶壁面Y+值分布 Fig. 2 Y+ value on surfaces of runner blades and guide vanes |

|
图 3 网格敏感性分析 Fig. 3 Grid dependence analysis |
在数值计算过程中, 首先进行稳态计算, 稳态计算的结果作为非稳态计算的初始条件.为了准确模拟活动转轮与导叶之间的动静干涉对流态的影响, 非稳态计算时间步长设为1.562 5×10-4 s, 相当于转轮旋转1.125°为一个时间步长.每个时间步长最大迭代40步, 收敛残差目标值为1.0×10-4.计算采用至强20核双线程工作站, 每个工况计算一个旋转周期根据收敛情况需要10~16 h, 计算时长不少于10个转动周期.
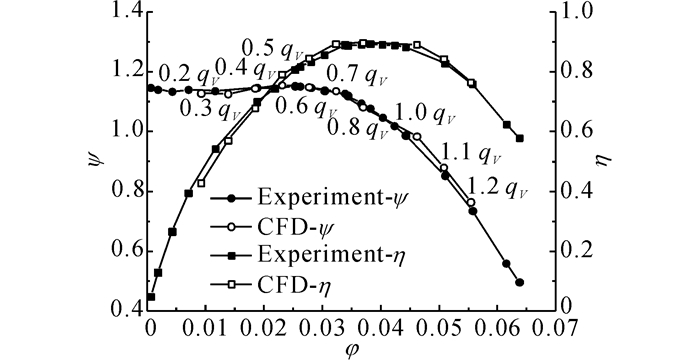
2 结果及分析本文选取15°开度下10个工况点进行数值计算, 所得能量特性结果与模型试验结果(试验数据采用哈尔滨电机厂提供的数据)吻合良好, 如图 4所示, 图中Ψ为扬程系数, Ψ=2gH/(ω2R22), φ为流量系数, φ=qV/(πωR23), η为效率, qV为设计工况点流量.从图中可以看出, 转轮驼峰特性在此开度下并不十分明显, 在当流量小于0.5qV时, 扬程有小幅下降, 呈现轻微的驼峰特性.
|
图 4 转速流量特性曲线 Fig. 4 Comparison between experimental and numerical performance |
尾水管内的流态随流量减少存在有规律的变化.当流量大于0.5qV时, 水轮从尾水管平顺流入转轮.随着流量的减少, 流入尾水管流速逐渐降低, 见图 5(a)~(d).图中,Vm为水流速度大小.然而, 当流量减小到0.5qV时, 部分流入转轮的水流开始沿着尾水管边壁反向流动(图 5(e)).随着流量的进一步减小, 尾水管边壁的回流加剧, 流速增大, 见图 5(f)~(i).

|
图 5 不同流量下尾水管内部流态 Fig. 5 Flow patterns in draft tube at different flow rate |
轮叶片进口边且靠近下环侧发生流动分离是尾水管回流产生的主要原因.如图 6(a)所示, 当流量较小时, 叶片进口前缘吸力面侧入流攻角较大, 叶道内产生回流涡结构.在此回流涡结构作用下, 流入转轮的部分水体沿着尾水管边壁反向螺旋流回尾水管内.强烈的回流涡结构, 导致在转轮进口形成局部低压区, pA为绝对压力.易导致空化发生.不同转轮叶道进口的回流涡结构发展强度并不相同, 形成的低压不同(图 6(b)), 因而不同叶道进口的空化强弱有别(图 6(c)).本文数值模拟并未考虑空化的影响, 不同空化系数下的空化形态需后续深入分析.

|
图 6 转轮进口流态图(0.4qV) Fig. 6 Flow patterns at runner inlet(0.4qV) |
如图 7所示为不同工况下转轮进口某一截面上的涡量分布随流量的变化过程.图中Vor_z为z方向的涡量.图中可以看到, 转轮叶片进口处涡量在无回流发生时, 几乎为零.当回流涡结构发生时, 正向涡量集中区域随流量减小逐渐增大.由此可见, 转轮叶片进口正向涡量的发展, 是引起尾水管边壁的回流加剧和流速增大的原因.

|
图 7 不同工况下转轮进口截面涡量图 Fig. 7 Distributions of vorticity on planes at runner inlet |
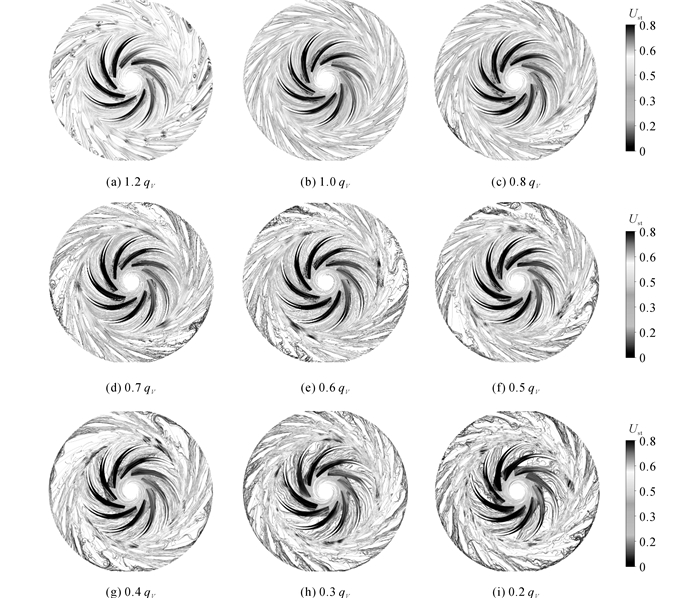
在转轮与导叶区域的叶道内, 流态亦随流量的减小呈现由规律的变化, 如图 8所示.图中Ust为流速系数, 表达式为Ust=V/u, V为瞬时流速, u为叶轮高压侧圆周速度.在大流量区运行时, 转轮内部流态平顺(见图 9(a)), 由于转轮出流流速较大, 相对于活动导叶形成负攻角, 在导叶的吸力面产生流动分离, 且在导叶叶道内产生流速较高的射流.当流量小于1.0qV时, 随着流量的减少, 相对于导叶的入流攻角逐渐增大, 在导叶内逐渐发生流动分离.流量减小到0.8qV时, 固定导叶的流道内首先产生旋转失速结构, 沿周向形成均布的3个旋转失速区域, 但流动分离较弱(图 9(c)).随着流量的进一步减少, 失速流道内的流动分离逐渐增强, 且向活动导叶区域扩展, 所占叶道区域增大.失速叶道内的流动分离涡对转轮出流的阻碍, 使水流流向非失速过流叶道, 局部流速增大, 在对应无叶区位置形成三处高速区(图 3(d)~(f)).然而, 当流量小于0.5qV时, 有规律的旋转失速结构逐渐消失(图 3(g)~(i)).流量小于0.4qV时, 导叶内的所有流道均产生剧烈的流动分离现象, 分离涡结构失去明显分布规律.
|
图 8 不同流量下转轮内部流态 Fig. 8 Flow patterns inside runner and diffuser at different flow rate |
|
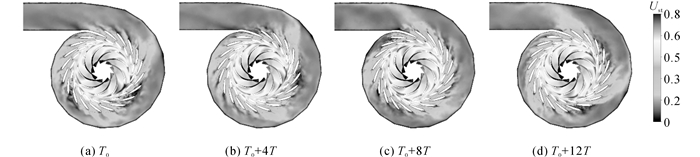
图 9 流量为0.8qV工况下不同时刻绝对速度云图 Fig. 9 Flow evolution inside runner and diffuser on mid-span section (0.8qV) |
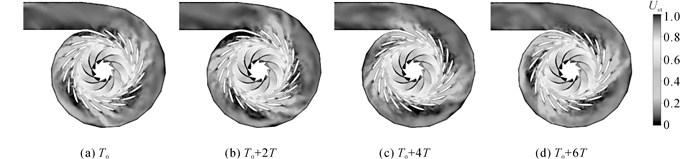
旋转失速在叶道内内随着转轮的转动而缓慢转动.如图 9和10所示分别为0.8 qV和0.6 qV工况下旋转失速发生时叶道内流速分布随时间的变化过程, 图中T0为某一起始时刻, T为转轮转动周期.在0.8qV工况, 旋转失速初生阶段, 周向失速强度并不一致, 而在0.6qV工况, 失速涡充分发展, 周向失速涡强度趋于一致.在0.8qV、0.7qV、0.6qV和0.5qV工况下, 旋转失速涡的转动频率分别为转轮转动频率的8.1%、3.7%、3.3%和4.1%.
|
图 10 流量为0.6qV工况下不同时刻绝对速度云图 Fig. 10 Flow eVolution inside runner and diffuser on mid-span section (0.6qV) |
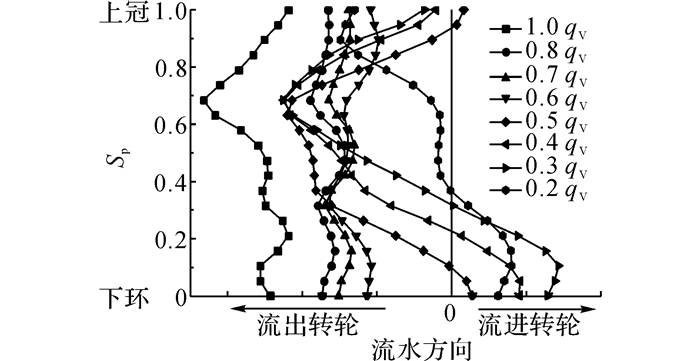
转轮进口下环侧出现的回流涡结构, 不仅改变了尾水管内的流动特性, 而且必然会改变转轮叶道内空间过流能力的分布, 进而影响到转轮出流和导叶内的流态.如图 11所示为转轮出口不同展向位置处周向平均所得的径向流速随流量减小的变化过程, Sp为展向坐标.由图可以看到随着流量的减小, 径向流速度逐渐减小.流量小于0.5qV时, 在转轮入口下环侧发生回流.随着流量的进一步减小, 转轮出口下环侧回流增强.
|
图 11 转轮出口沿高度方向平均流速分布 Fig. 11 Velocity distributions along spanwise at runner outlet at different flow rate |
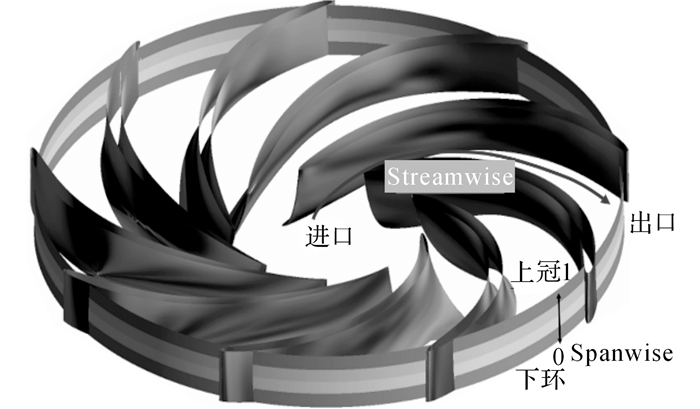
为了进一步分析转轮进口下环处的回流涡结构对转轮过流的影响, 计算了转轮流道内沿展向分布的4个等间距截面在不同工况点过流量的变化, 截面设置如图 12所示, 流量分布如图 13所示.图中St为叶道内的流向坐标, Q*为相对于总过流量的相对值, 为无量纲.从图 13中可以看到, 转轮流道内的过流能力在空间的分布随流量减小呈现有规律的变化.流量较大时, 在入流侧, 水体主要从转轮下环侧进入转轮, 而上冠侧流入量较低;在出流侧, 水流主要从上冠和下环侧流出转轮, 而中部过流能力较低(图 13(a)~(d)).当流量降低到0.5qV时, 转轮进口下环侧入流能力开始迅速降低, 而上冠侧流入量能力上升, 这是由于下环处回流涡结构的出现, 阻碍了此处水流的正常入流, 迫使入流向上冠侧偏移(图 13(e)~(h)).由此导致转轮出口下环侧的径向出流速度降低, 流入导叶的攻角增大, 使导叶流道内下环侧产生剧烈的流动分离, 部分水流反向流入转轮.如图 14所示为典型工况点下转轮出口的径向流速VR分布表明, 下环侧的回流和上冠侧的出流沿周向并不均匀.转轮出流偏向于叶片压力面侧, 而回流偏向叶片吸里面侧.
|
图 12 流量监测面设置 Fig. 12 Schematic of discharge monitoring face |

|
图 13 转轮内部过流量空间分布 Fig. 13 Spatial distribution of discharge capacity inside runner passages |

|
图 14 不同工况下转轮进口径向速度分布图 Fig. 14 Distributions of instantaneous radial velocity around runner inlet |
旋转失速和转轮出口的回流三维分布特性明显, 因而叶道内流态在沿叶片展向差异明显.图 15和16给出了在0.5qV和0.3qV这2个典型工况下, 叶道内不同展向截面上的速度矢量分布.图中Ust为在0.5qV工况(图 15), 导叶叶道内不同展向均存在旋转失速, 但不同截面上的流动分离强度不同, 且周向转播存在轻微的相位差.旋转失速在导叶中间高度较为剧烈, 产生较大的流动阻力, 这与转轮中部出流能力较低一致.而在0.3qV工况(图 16), 导叶上冠侧出流顺畅且流速较高, 而下环侧叶道内同时产生流动分离, 部分水流反向流入转轮, 因而周期性的旋转失速消失.

|
图 15 0.5qV工况下不同展向平面上的速度矢量分布 Fig. 15 Instantaneous flow fields on surfaces at different spanwise (Q=0.5qV) |

|
图 16 0.3qV工况下不同展向平面上的速度矢量分布 Fig. 16 Instantaneous flow fields on surfaces at different spanwise (Q=0.3qV) |
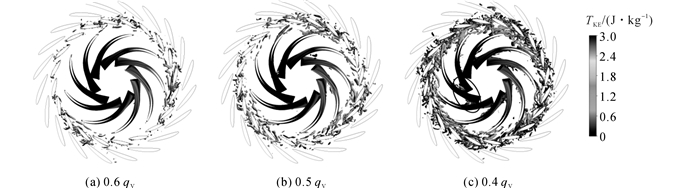
为了更进一步的说明转轮进口的回流涡结构对导叶区域旋转失速涡的影响, 3个典型工况点下转轮内的涡结构以Q准则描述[22], Q=1/2(Ωij Ωij-Sij Sij), Ωij为旋转张量,Sij为应变率张量,其值物理意义为旋转分量与应变分量之差,当Q>0时认为存在涡结构,Q值越大,该处的涡强度越大.如图 17所示.图中TKE为湍动能.在转轮进口无回流涡时(图 17(a)), 导叶区的3个旋转失速涡团均匀分布, 而非失速过流叶道内几乎无流动分离发生;当流量减少到转轮进口开始出现回流涡结构时(图 17(b), 导叶区的旋转失速区域增大, 且非失速叶道产生流动分离;当流量进一步减小, 转轮进口回流涡结构发展增强, 阻塞转轮下环侧入流, 如图 17(c)中圆圈所指, 进而在导叶下滑侧产生剧烈的流动分离, 复杂的涡结构充满整个导叶区域, 旋转失速消失.
|
图 17 水轮机内部涡结构随流量变化 Fig. 17 Instantaneous flow vortex structures identified by Q criterion (Q=700 000 s-2) |
对于水泵水轮机的驼峰特性, 研究者们已经开展了大量实验与数值模拟研究, 主要观点认为转轮与导叶之间的流动分离形成的水头损失对驼峰特性有重要的影响.部分研究认为旋转失速是驼峰特性形成的原因[18, 24], 然而也有试验和数值研究发现旋转失速发生时, 并没有出现驼峰特性[14-16, 27].本文研究的水泵水轮机在发生旋转失速时, 同样未出现驼峰特性.而是在流量小于0.5qV时, 旋转失速逐渐消失, 水泵扬程出现小幅的下降, 呈现轻微的驼峰特性.此时转轮进口出现的回流涡结构, 突然改变了尾水管内的入流流态和导叶与转轮流道内的流动分离特性, 从而突然增加了水轮机内部的流动损失, 导致水轮机出现驼峰特性.Braun[13]认为导叶区流态拓扑结构的突变导致流动损失的突然增加是产生驼峰特性的主要原因.Zhang[14]通过试验发现, 转轮进口回流区突现同样可以导致驼峰特性, 这与本文结果一致.
对于比转速较高的水泵水轮机, 导叶高度较大, 当导叶区域内出现旋转失速时, 旋转失速产生的流动损失比重较大, 对扬程的影响明显;然而转轮内部较高的过流通道使转轮进口的回流涡结构对转轮内部过流量的空间分布影响并不明显, 从而对导叶区流动分离的影响并不明显.对于比转速较低的水泵水轮机, 导叶高度较低, 转轮流道高度偏低, 转轮进口处的回流涡结构对转轮内部过流量的空间分布影响更显著, 导叶与转轮之间的流动分离更易受其影响, 产生的水头损失对扬程的作用更加明显.因此可以推断, 驼峰特性并不与具体的流动分离结构相关, 而是与转轮内流动分离的转捩有关.水轮机内流动特性的突变使流动损失突然增加, 产生驼峰特性.
4 结论本文采用SAS湍流模型对某低比转速模型水泵水轮机进行全流道非定数值模拟.在所得外特性与实验结果吻合的条件下, 分析了水轮机内的流动结构的演变机理及其对驼峰特性的影响, 所得结论如下:
(1) 水泵工况流量小于80%最优流量时, 导叶区发生旋转失速.失速流道的阻塞使水流转移到其他流道, 在其他流道中形成射流.随着流量的降低, 流动分离增强, 失速区域逐渐增大.
(2) 水泵工况流量低于50%最优流量时, 转轮进口出现回流涡结构, 在尾水管内形成螺旋回流.回流结构改变转轮内部过流能力在空间的分布, 使转轮下环侧过流能力迅速降低, 导致导叶区下环侧同时产生严重的流动分离, 导致旋转失速消失.
(3) 水轮机转轮内流动分离的转捩, 使流动特性产生突变, 导致流动损失的突然增加, 产生驼峰特性.
| [1] | ZUO Z, LIU S, SUN Y, et al. Pressure fluctuations in the vaneless space of high-head pump-turbines-A review[J]. Renewable and Sustainable Energy Reviews, 2015, 41: 965–974. DOI:10.1016/j.rser.2014.09.011 |
| [2] |
冉红娟, 张瑶, 罗先武, 等. 可逆式水轮机泵工况下驼峰现象的数值模拟[J].
水力发电学报, 2011, 30(3): 175–179.
RAN Hong-juan, ZHANG Yao, LUO Xian-wu, et al. Numerical simulation of the positive-slope performance curve of a reversible hydro-turbine in pumping mode[J]. Journal of Hydroelectric Engineering, 2011, 30(3): 175–179. |
| [3] | RAN H, LUO X, ZHANG Y, et al. Numerical simulation of the unsteady flow in a high-head pump turbine and the runner improvement[C]//ASME 2008 Fluids Engineering Division Summer Meeting. Jacksonville:American Society of Mechanical Engineers, 2008:1115-1123. https://www.scholarmate.com/pubweb/outside/details?des3Id=lQDmjBVD5JjttSTyBEJr5w%3D%3D¤tDomain=/pubweb&pubFlag=1 |
| [4] | RAN H, LUO X, ZHU L, et al. Experimental study of the pressure fluctuations in a pump turbine at large partial flow conditions[J]. Chinese Journal of Mechanical Engineering, 2012, 25(6): 1205–1209. DOI:10.3901/CJME.2012.06.1205 |
| [5] |
王焕茂, 吴钢, 吴伟章, 等. 混流式水泵水轮机驼峰区数值模拟及分析[J].
水力发电学报, 2012, 31(6): 253–258.
WANG Huan-mao, WU Gang, WU Wei-zhang, et al. Numerical simulation and analysis of the hump district of Francis pump-turbine[J]. Journal of Hydroelectric Engineering, 2012, 31(6): 253–258. |
| [6] |
陶然, 肖若富, 杨魏, 等. 可逆式水泵水轮机泵工况的驼峰特性[J].
排灌机械工程学报, 2014, 32(11): 927–930.
TAO Ran, XIAO Ruo-fu, YANG Wei, et al. Hump characteristic of reversible pump-turbine in pump mode[J]. Journal of Drainage & Irrigation Machinery Engineering, 2014, 32(11): 927–930. DOI:10.3969/j.issn.1674-8530.13.6068 |
| [7] | XIAO Y, YAO Y, WANG Z, et al. Hydrodynamic mechanism analysis of the pump hump district for a pump-turbine[J]. Engineering Computations, 2016, 33(3): 957–976. DOI:10.1108/EC-02-2015-0038 |
| [8] | DEYOU L, HONGJIE W, GAOMING X, et al. Unsteady simulation and analysis for hump characteristics of a pump turbine model[J]. Renewable Energy, 2015, 77: 32–42. DOI:10.1016/j.renene.2014.12.004 |
| [9] | LI D, GONG R, WANG H, et al. Analysis of vorticity dynamics for hump characteristics of a pump turbine model[J]. Journal of Mechanical Science and Technology, 2016, 30(8): 3641–3650. DOI:10.1007/s12206-016-0725-1 |
| [10] |
李德友, 宫汝志, 王洪杰, 等. 水泵水轮机不同导叶开口的驼峰特性[J].
排灌机械工程学报, 2016, 34(1): 1–8.
LI De-you, GONG Ru-zhi, WANG Hong-jie, et al. Unstable head-flow characteristics of pump-turbine under different guide vane openings in pump mode[J]. Journal of Drainage & Irrigation Machinery Engineering, 2016, 34(1): 1–8. DOI:10.3969/j.issn.1674-8530.15.0063 |
| [11] | GUGGENBERGER M, SENN F, JABERG H, et al. Experimental analysis of the flow pattern of a pump turbine model in pump mode[C]//IOP Conference Series:Earth and Environmental Science. Grenoble:IOP Publishing, 2016, 49(4):042001. http://adsabs.harvard.edu/abs/2016E%26ES...49d2001G |
| [12] | JESE U, FORTES-PATELLA R. Unsteady numerical analysis of the rotating stall in pump-turbine geometry[C]//IOP Conference Series:Earth and Environmental Science. Grenoble:IOP Publishing, 2016, 49(4):042005. http://adsabs.harvard.edu/abs/2016E%26ES...49d2005J |
| [13] | BRAUN O, KUUENY J L, AVELLAN F. Numerical analysis of flow phenomena related to the unstable energy-discharge characteristic of a pump-turbine in pump mode[C]//ASME 2005 Fluids Engineering Division Summer Meeting. Houston:American Society of Mechanical Engineers, 2005:1075-1080. http://hal.archives-ouvertes.fr/hal-00262159/en/ |
| [14] | BRAUN O. Part load flow in radial centrifugal pumps[D]. Lausanne:Swiss Federal Institute of Technology, 2009. https://ar.scribd.com/document/332086222/Cavitation-and-dynamic-problems |
| [15] | PACOT O, KATO C, AVELLAN F. High-resolution LES of the rotating stall in a reduced scale model pump-turbine[C]//IOP Conference Series:Earth and Environmental Science. Montreal:IOP Publishing, 2014, 22(2):022018. http://iopscience.iop.org/article/10.1088/1755-1315/22/2/022018/ |
| [16] |
张春泽, 夏林生, 刁伟, 等. 水泵水轮机泵工况旋转失速压力脉动特性及转动机理[J].
水利学报, 2017, 48(7): 837–845.
ZHANG Chun-ze, XIA Lin-sheng, DIAO Wei, et al. Pressure fluctuations characteristics and rotating stall propagation mechanism of a pump-turbine in pump mode[J]. Journal of Hydraulic Engineering, 2017, 48(7): 837–845. |
| [17] | XIA L S, CHENG Y G, ZHANG X X, et al. Numerical analysis of rotating stall instabilities of a pump-turbine in pump mode[C]//IOP Conference Series:Earth and Environmental Science. Montreal:IOP Publishing, 2014, 22(3):032020. http://adsabs.harvard.edu/abs/2014E&ES...22c2020X |
| [18] | YIN J L, LIU J T, WANG L Q, et al. Performance prediction and flow analysis in the vaned distributor of a pump turbine under low flow rate in pump mode[J]. Science China Technological Sciences, 2010, 53(12): 3302–3309. DOI:10.1007/s11431-010-4175-1 |
| [19] | YANG J, PAVESI G, YUAN S, et al. Experimental characterization of a pump-turbine in pump mode at hump instability region[J]. Journal of Fluids Engineering, 2015, 137(5): 051109. DOI:10.1115/1.4029572 |
| [20] | LUCIUS A, BRENNER G. Unsteady CFD simulations of a pump in part load conditions using scale-adaptive simulation[J]. International Journal of Heat and Fluid Flow, 2010, 31(6): 1113–1118. DOI:10.1016/j.ijheatfluidflow.2010.06.005 |
| [21] | TRIVEDI, CHIRAG, MICHEL J, et al. Numerical techniques applied to hydraulic turbines:a perspective review[J]. Applied Mechanics Reviews, 2016, 68(1): 010802. DOI:10.1115/1.4032681 |
| [22] | KRAPPEL T, RUPRECHT A, RIEDELBAUCH S. Flow simulation of francis turbines using hybrid rans-les turbulence models[J]. High Performance Computing in Science & Engineering, 2015, 14(0): 417–431. |
| [23] |
夏林生, 程永光, 蔡芳, 等. 水泵水轮机四象限工作区流动特性数值分析[J].
水利学报, 2015, 46(7): 859–868.
XIA Lin-sheng, CHENG Yong-guang, CAI Fang, et al. Numerical analysis of flow characteristics of a model pump-turbine in four operating quadrants[J]. Journal of Hydraulic Engineering, 2015, 46(7): 859–868. |
| [24] |
孙跃昆. 低比转速水泵水轮机驼峰稳定性及其影响因素研究[D]. 北京: 清华大学, 2016.
SUN Yuekun. Instability characteristics and influencing factors of positive slope on pump performance curves of a low-specific-speed pump-turbine[D], Doctoral Thesis, Tsinghua University, 2016. |
| [25] | SINHA M, PINARBASI A, KATZ J. The flow structure during onset and developed states of rotating stall within a vaned diffuser of a centrifugal pump[J]. Journal of Fluids Engineering, 2001, 123(3): 490–499. DOI:10.1115/1.1374213 |
| [26] |
周佩剑, 王福军, 姚志峰. 离心泵叶轮旋转失速团特性分析[J].
水利学报, 2015, 46(9): 1128–1134.
ZHOU Pei-jian, WANG Fu-jun, YAO Zhi-feng. Analysis of rotating stall cells in an impeller of a centrifugal pump[J]. Journal of Hydraulic Engineering, 2015, 46(9): 1128–1134. |
| [27] | ZHANG Z. Rotating stall mechanism and stability control in the pump flows[J]. Proceedings of the Institution of Mechanical Engineers, Part A:Journal of Power and Energy, 2011, 225(6): 779–788. DOI:10.1177/0957650911405106 |



