2. 浙江大学 化工机械研究所, 浙江 杭州 310027;
3. 国网浙江省电力公司电力科学研究院, 浙江 杭州 310014;
4. 浙江科技学院 机械与汽车工程学院, 浙江 杭州 310023
2. Institute of Chemical Machinery, Zhejiang University, Hangzhou 310027, China;
3. State Grid Zhejiang Electric Power Research Institute, Hangzhou 310014, China;
4. Department of Electro-Mechanical Engineering, Zhejiang University of Science and Technology, Hangzhou 310023, China
对于大型汽轮发电机组的转子系统, 轴承的油膜力引起转子运动失稳的现象十分常见[1].为了满足高速转子稳定工作的需要, 可倾瓦滑动轴承被广泛使用, 可倾瓦滑动轴承最突出的优点是本质稳定[2].但随着汽轮机组朝着更加大型化和更高转速的方向发展, 发生在可倾瓦滑动轴承上的异常振动和稳定性事故也有发生[3].近年来, 学者们对可倾瓦滑动轴承的静、动特性进行了全面而深入的理论计算, 综合考虑瓦块支点弹性、瓦块和轴承体热变形以及润滑油热态特性变化等因素的热弹流体动力学(thermo-elasto-hydrodynamic, TEHD)计算模型被广泛使用[4-9].为了综合研究轴承-转子系统的稳定性问题, 许多学者将滑动轴承的润滑流场计算与转子系统的动力学计算耦合起来进行分析[10-14].上述研究中对可倾瓦滑动轴承动力特性的计算大多基于有限差分法求解二维Reynolds方程, 需要对流场特性做出一些简化.随着计算机技术的发展以及计算流体动力学(computational fluid dynamics, CFD)分析软件的普及, 通过直接求解三维N-S方程获得轴承润滑流场特性的方法开始流行, 相关计算在固定瓦滑动轴承的动力性能研究中已经开展的很多[15-18].三维CFD计算方法能够提供更加准确和细节丰富的流场结果, 可以充分考虑润滑流体惯性项和黏性项的影响以及油槽等复杂结构处的流场, 同时扩展性也非常好, 可以方便地对特殊结构的轴承(如在轴瓦和轴颈表面开槽[19-21])进行建模仿真以及建立滑动轴承-转子系统的流固耦合(fluid-structure interaction, FSI)计算分析模型[22-25].
有关可倾瓦滑动轴承三维瞬态流场计算以及流固耦合计算的研究近年来已经有了一些开拓性成果, 如Varela等[26]建立了可倾瓦滑动轴承TEHD分析模型, 采用有限元方法对考虑可控润滑的修正后的Reynolds方程和能量方程、基于傅里叶定律的瓦块内部传热模型以及瓦块支点弹性变形模型进行联立求解, 其中流体域的求解在二维8节点有限元单元上实现.计算得到的油膜温度分布、轴颈和瓦块上的油膜力大小以及轴颈静平衡位置结果与试验值吻合一致.Rindi等[27]提出一种面向工业应用的可倾瓦滑动轴承-转子系统准3D计算模型, 为了兼顾计算精度和效率, 该模型采用了模块化的结构形式, 各模块独立计算并在边界处进行数据交换, 其中的油膜力模型仍基于传统的Reynolds方程.
3D CFD计算理论上适用于任意轴承结构形式, 但对于可倾瓦这类具有复杂结构的轴承形式, 瞬态计算中网格畸变的问题十分突出.针对这一问题, 本文自行开发了一种适用于可倾瓦滑动轴承瞬态流场计算的变流域动网格方法[28], 该方法通过用户自定义程序(user defined function, UDF)加载到FLUENT瞬态计算过程中, 将瞬态流场计算同多圆盘转子系统的动力学计算耦合, 可以得到不同转速下转子系统的轴心轨迹.在考察轴颈涡动过程中可倾瓦轴承瞬态流场的变化, 以及将轴心轨迹同李强、于桂昌等[29-31]的常规固定瓦滑动轴承-转子系统的计算结果进行对比时, 可倾瓦滑动轴承表现出优越的稳定性.最后, 对可倾瓦滑动轴承-多圆盘转子系统进行了不同转速下的振动试验, 转速改变后轴颈振动以及涡动中心的变化与理论计算预测的规律一致, 验证了本文所采用的可倾瓦滑动轴承3D CFD瞬态计算方法的可靠性.
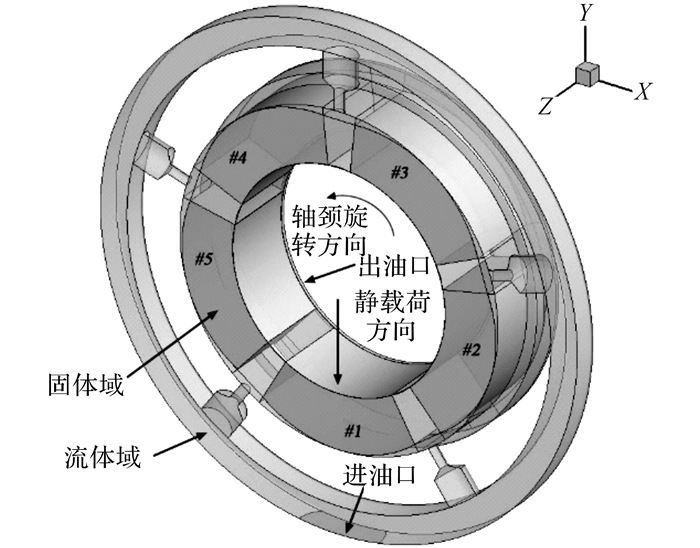
1 计算模型 1.1 轴承模型本文3D CFD计算和实验研究的对象为五瓦可倾瓦滑动轴承, 瓦块支点形式为圆柱面线接触式, 支点偏心0.5, 其他结构参数为:轴承装配直径32.08 mm;瓦块上表面圆弧半径16.09 mm, 装配后半径间隙0.03 mm(预负荷系数0.63);瓦块轴向宽度22 mm(轴承宽径比0.69);轴承承载方式为瓦上承载, 载荷方向竖直向下;瓦块角为60°.轴颈旋转方向、轴承静载荷方向和瓦块编号之间的关系参考如图 1所示.图中#1、#2、#3、#4、#5为瓦块编号.由于计算流场具有轴对称性, 因此采用对称性边界条件将计算模型减半.计算域包含了以下流体域:瓦块间进油间隙的一半、瓦块间进油孔的一半、连接5个进油孔的环形槽的一半、瓦块上下表面油膜间隙的一半以及瓦块轴向一侧的出油间隙;同时还包含了瓦块固体域, 用于辅助油膜与瓦块之间的耦合传热计算.
|
图 1 轴承的3D CFD模型 Fig. 1 3D CFD model of TPJB |
在进行网格敏感性分析时, 瓦块和轴颈之间的小间隙流域处, 周向和轴向的网格尺寸对于计算结果(轴颈表面油膜力)的影响非常小;而径向网格层数达到5层及以上时, 计算偏差减小到5%以内.综合考虑计算精度和效率, 在瓦块表面小间隙处沿径向划分5层网格、轴承的周向和轴向分别划分405层和30层网格, 大间隙流域处尽量保证网格的长宽比近似为1, 最终得到的计算域内网格单元数量为653 275.
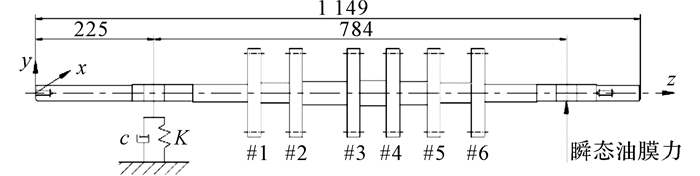
1.2 转子模型及流固耦合计算的实现本文可倾瓦滑动轴承-转子系统流固耦合计算和实验研究采用的多圆盘转子模型与文献[30]一致, 如图 2所示, 转子的主要特征如下:转子两端由试验轴承进行支撑, 轴上分布有6个相同的圆盘, 圆盘直径170 mm, 宽25 mm, 质量4.426 kg.圆盘通过热套的方式固定在转轴上, 转轴设计为阶梯轴, 中间最大直径49 mm, 向两端直径以5 mm梯度递减, 轴颈直径为32.02 mm.转子的总重量为34.6 kg, 其中左侧试验轴承(靠近#1圆盘)的承载为17.073 kg, 右侧试验轴承的承载为17.527 kg.不平衡质量加载在#2圆盘上, 并以圆盘的质量偏心距作为单位.
|
图 2 转子模型示意图 Fig. 2 Diagram of rotor model |
根据达朗伯原理和虚位移原理(约束反力在虚位移上所做的功为零), 可以建立如下刚体运动方程:
| $ {\left( {\frac{{\partial \dot r}}{{\partial \dot s}}} \right)^{\rm{T}}}\left( {\dot P-{f^e}} \right) + {\left( {\frac{{\partial w}}{{\partial \dot s}}} \right)^{\rm{T}}}\left( {\dot L-{M^e}} \right) = 0. $ | (1) |
式中:
在这里, 截面的位移r和转角φ不但是时间t, 而且还是位置z的函数, 直接用它们建立起来的运动方程必定是偏微分方程, 求解困难.为了得到相应于这2个变量的常微分方程, 假设变量r(z, t)和φ(z, t)可以分解成位置函数w(z)和时间函数(即广义坐标)q(t)的乘积:
| $ \left. \begin{array}{l} {r_x}\left( {z, t} \right) = w{\left( z \right)^{\rm{T}}} \cdot {q_x}\left( t \right), \;\;\;w, {q_x}, {q_y} \in {{\bf{R}}^{{n_s}}};\\ {r_y}\left( {z, t} \right) = w{\left( z \right)^{\rm{T}}} \cdot {q_y}\left( t \right)\;\;\;\;\;w, {q_x}, {q_y} \in {{\bf{R}}^{{n_s}}}. \end{array} \right\} $ | (2) |
将轴作为连续梁处理时, φ(z, t)可以通过r(z, t)对z求偏导得到.选择三次多项式作为位置函数, 各多项式之间有一大部分互相重叠, 从而保证整根轴不但位移和速度是连续的, 弯矩和剪力也是连续的.运动方程的维数根据位置函数的个数确定, 选取较多的位置函数时会导致方程的维数很大, 需要对其进行模态降阶以简化运算.选取不考虑阻尼、交叉刚度和陀螺力矩的模态振型作为方程变换的模态矩阵, 而为了进一步降低计算工作量, 在x、y方向选用同一振型函数.最后, 对降阶后的运动方程采用Newmark变步长积分法进行求解.以上仅对运动方程的建立和求解做了简要说明, 详细的推导过程可以参考文献[32].
将转子动力学计算与滑动轴承润滑流场计算进行耦合时, 因为轴承-转子系统中2个滑动轴承的特性差异不大, 为了提高计算效率只进行单可倾瓦滑动轴承-转子系统的耦合计算.图 2中, 左侧试验轴承简化为经典的刚度、阻尼系数模型;仅对右侧轴承进行3D CFD瞬态流场计算.流固耦合计算数据交换的流程为:瞬态流场计算的某时间步开始时, 通过UDF对轴颈表面油膜压力进行积分得到瞬态油膜力的轴向分量Fx和Fy, 将Fx、Fy连同当前瞬态计算时间t和时间步长写入数据文件作为转子动力学程序求解的输入参数, 然后调用转子动力学程序并等待程序计算结束, 等待过程中不断读取轴颈位移文件, 若位移文件生成则表明转子动力学程序求解完成, 通过UDF读取轴颈的轴向位移、删除位移文件并更新网格, 网格更新完成后开始当前时间步内的迭代计算.
2 动网格及边界条件 2.1 动网格更新的实现在瞬态计算过程中, 轴颈的移动和瓦块的转动会引起流体域的变形, 变形的流体域包含:瓦块上下表面的油膜间隙以及瓦块之间的进油间隙, 定义这些变形域为动网格区域.进油孔、环形槽以及出油的侧间隙内网格节点始终保持静止, 动静区域之间采用interface进行连接.动网格区域边界的变形由轴颈的移动和瓦块的转动引起, 变形的复杂加上油膜的小间隙结构特点, 使得动网格的更新变得十分困难.本文作者通过自编程动网格算法成功解决了可倾瓦滑动轴承复杂变形流域内网格更新的问题, 网格节点的移动根据节点距离边界的距离以及边界的变形量插值得到, 更新后的网格始终保持高质量, 保证了瞬态计算的顺利进行.动网格算法的具体推导参见文献[28].
2.2 计算中考虑的热效应因素为了保证结果的准确性, 计算中考虑了润滑油特性随温度的变化.润滑油热特性, 如黏度、密度ρ、比定压热容cp、导热系数κ, 与温度之间存在如下关系[33]:
| $ \log \log \left( {\nu + c'} \right) = a'-b'\log \left( {\theta + 273.15} \right). $ | (3) |
| $ \rho = 850\left[{1-0.00063\left( {\theta-15.6} \right)} \right]. $ | (4) |
| $ {c_p} = 1800\left( {1 + 0.002\theta } \right). $ | (5) |
| $ \kappa = 0.1312\left( {1-6.3 \times {{10}^{-4}}\theta } \right). $ | (6) |
式中:ν为运动黏度(mm2/s), θ为摄氏温度(℃).
式(3) Walther方程中系数c′一般取0.7, a′、b′的取值需要2个温度的润滑油黏度值来确定, 根据#32透平油温度为40和100 ℃时运动黏度值:38.8和4.3 mm2/s计算得到a′和b′的值分别为11.88和4.679.通过UDF的DEFINE_PROPERTY宏可以将温黏关系方程加载到FLUENT材料属性面板的黏度选项下.而式(4)~(6)中润滑油密度、比热容、导热系数随温度升高呈线性变化, 通过材料属性面板中相应选项下的piecewise-linear方式进行设定.
润滑油和瓦块的流固交界壁面采用interface进行连接, 并设置interface类型为“coupled wall”.计算时, 流固交界壁面将自动应用耦合热边界条件, 保证交界面上温度和热通量的连续.
2.3 FLUENT边界条件可倾瓦滑动轴承3D CFD流场计算中求解的控制方程有:连续性方程、动量方程和能量方程.求解时采用基于压力的求解器.进口边界采用压力进口, 压力设置为0.2 MPa, 出口边界采用压力出口, 压力设置为大气压.控制方程离散时, 压力的离散采用PRESTO!算法, 其他项的离散采用QUICK算法, 速度和压力的耦合采用SIMPLE算法.计算中流体的雷诺数在50左右, 故采用层流模型.轴颈偏心后的表面速度通过UDF的DEFINE_PROFILE宏设定.
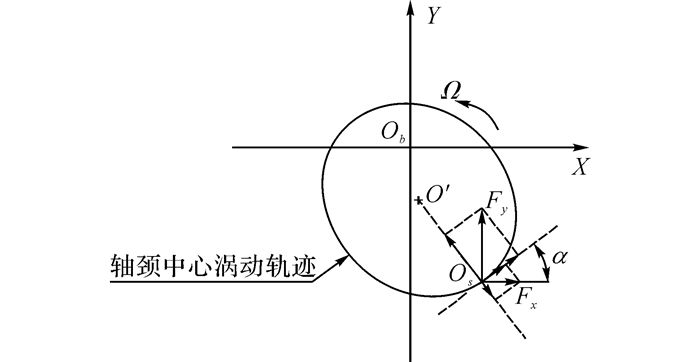
3 可倾瓦滑动轴承瞬态流场分析为了研究可倾瓦滑动轴承优越稳定性的形成机理, 对3D CFD计算得到的瞬态流场结果进行分析.瞬态计算的时间步长为1×10-6 s.在考察轴颈受到的瞬态油膜力随涡动轨迹的变化时, 考虑将油膜力沿涡动轨迹的径向和切向方向进行分解.如图 3所示, Ob、Os和O′分别为轴承中心、轴颈中心和涡动中心, Fr和Fτ分别为轴颈表面油膜力沿涡动轨迹径向和切向的分量, 其中切向角α根据式子α=arctan (Δy/Δx)近似得到.定义Fr由涡动中心指向轴颈中心时为正, Fτ与涡动方向同向时为正;Fr为负值时表征了轴颈受到来自挤压油膜支撑作用的大小, Fτ为负值时对涡动轨迹的增大起阻碍作用, 是使轴颈保持稳定运动的力.
|
图 3 瞬态油膜力分解示意图 Fig. 3 Decomposition diagram of transient oil film force |
考察单一周期内油膜力的变化规律, 如图 4所示为涡动转速ω=1 200 rad/s时轴颈1个涡动周期的轨迹示意图, 图中标示出了轴颈中心的几个关键位置, 其中A为涡动周期的起点, B、D、G为涡动轨迹与坐标轴的交点, C、E点轴颈中心偏位角分别为-36°和36°, 分别对应了轴承下半圆周2个进油间隙的位置, F为油膜力与轴颈偏心距反方向夹角的周期性变化中的一个突变点, β为圆周角,X、Y分别为水平、竖直方向.
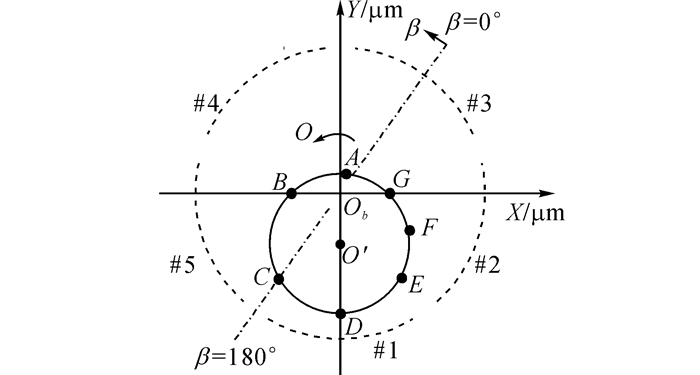
|
图 4 轴颈涡动轨迹示意图 Fig. 4 Orbit diagram of shaft center |
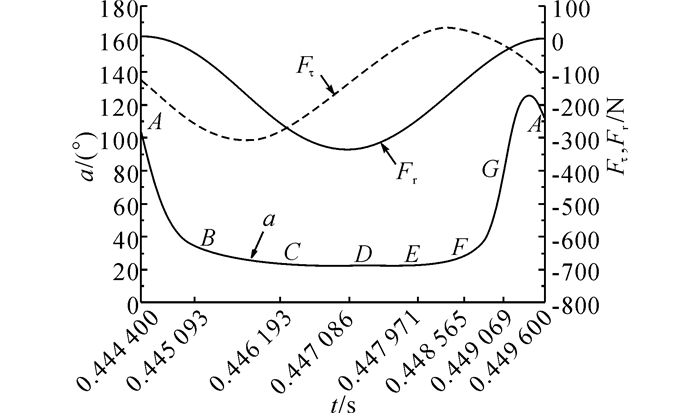
如图 5所示结合油膜力方向与轴颈偏心距反方向的偏差角a对油膜力的分量进行分析, 从图中可以看到:1)轴颈1个涡动周期内的大部分时间(B-C-D-E-F过程), 油膜力的方向由轴颈中心指向轴承中心(即偏心距的反方向), 偏差角保持在23°左右, 表明在轴颈低位涡动的过程中, 承载瓦始终能输出稳定的支撑来抑制轴心轨迹的进一步扩大, 即使到了2个瓦间进油间隙处(C、E两点), 稳定性也不被破坏;2)轴颈中心沿着F-G-A-B运动时, 此时轴颈中心浮的很高, 稳定性变差, 但因为受到重力的作用, 同时油膜力的切向分量朝着负值的方向一直在增大, 轴颈运动失稳的趋势受到抑制.
|
图 5 单一周期内油膜力的径向和切向分量变化 Fig. 5 Radial and tangential components of oil film force in single whirling circle |
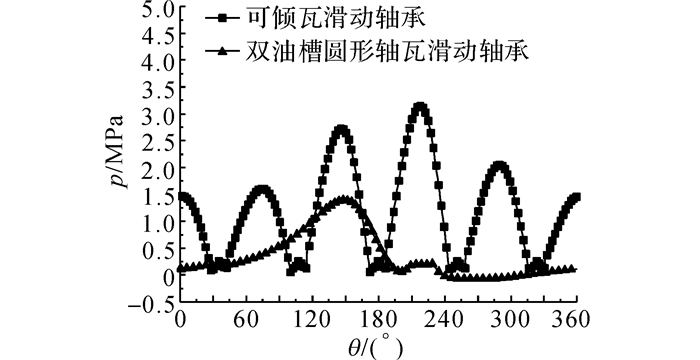
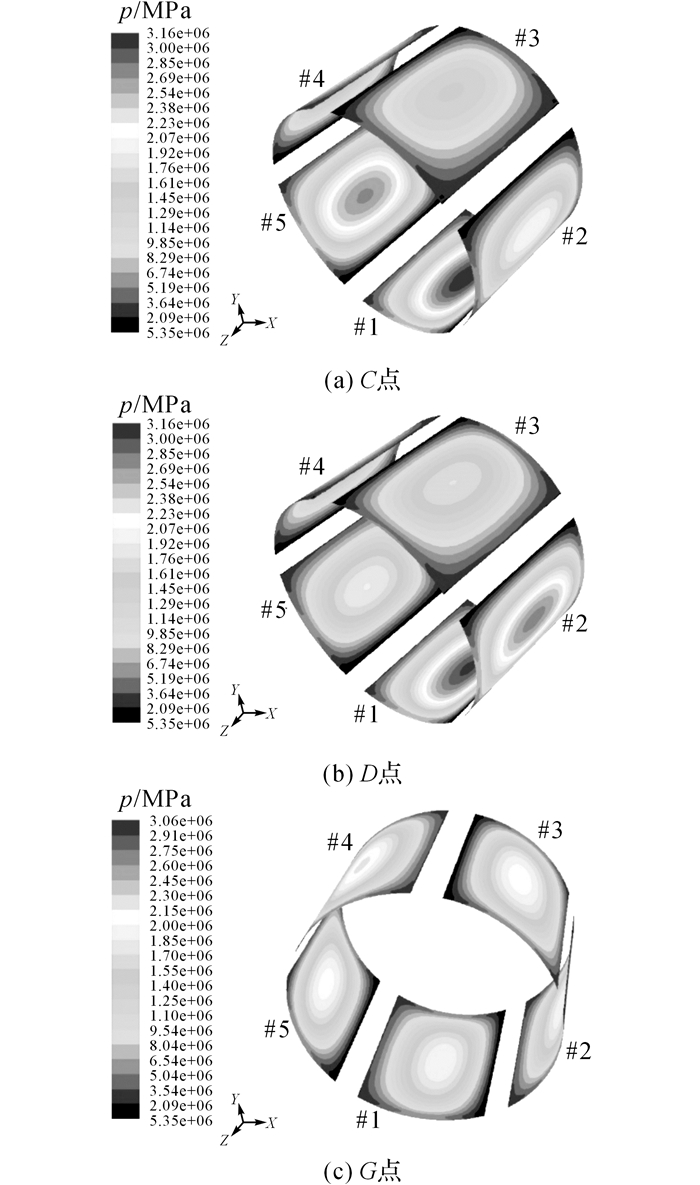
图 6给出了轴颈中心运动到涡动轨迹C点时旋转面上压力p的周向分布, 取的是轴向中间位置网格节点的静压值;同时还参考了某圆柱轴承当轴颈中心处在一偏心位置上工作时旋转面上压力的周向分布[31].在连心线ObC的延长线上取最大间隙一端的圆周角β=0°(见图 4).对于圆柱轴承, 只在略大于180°的间隙内形成了压力分布;而可倾瓦轴承的5个瓦上间隙内均形成了压力分布, 且轴颈前进方向上的#1瓦提供了最大的油膜压力, 有效阻止了涡动轨迹的扩大.轴颈中心位于C、D、G点时, 瓦上压力分布的变化见图 7, 从图 7(a)~(b)可以看出, 当轴颈运动到涡动轨迹的最低点时, #2瓦表面的油膜压力增大, 接替#5瓦输出支撑;而当轴颈上浮到较高的G点时, 五瓦表面油膜压力分布比较接近, 此时位于轴承上半圆周的#3和#4瓦上的油膜压力已经开始明显增大.当轴颈中心运动到不同位置时, 5个瓦上间隙内始终能形成油膜压力, 表明瓦块通过不断调节自身的转动保证了瓦上间隙沿轴颈旋转方向始终保持为由大变小的收敛楔形.
|
图 6 轴颈运动到C点时表面压力分布 Fig. 6 Pressure distribution on shaft surface at location C |
|
图 7 五瓦表面压力分布 Fig. 7 Pressure distributions on pad surfaces |
本节对转子系统不平衡量50 μm时椭圆和可倾瓦轴承支撑下轴心轨迹差异以及转速升高后轴心轨迹变化进行对比.在轴承流场的瞬态计算以及转子模型的动力学计算中, 轴颈中心的起始位置均为轴承中心, 分析中给出的轴心轨迹只保留了计算稳定后的几个涡动周期.椭圆轴承(最小半径间隙32 μm, 预负荷系数0.67, 长径比1)的轴心轨迹数据来自于文献[30]的计算结果.
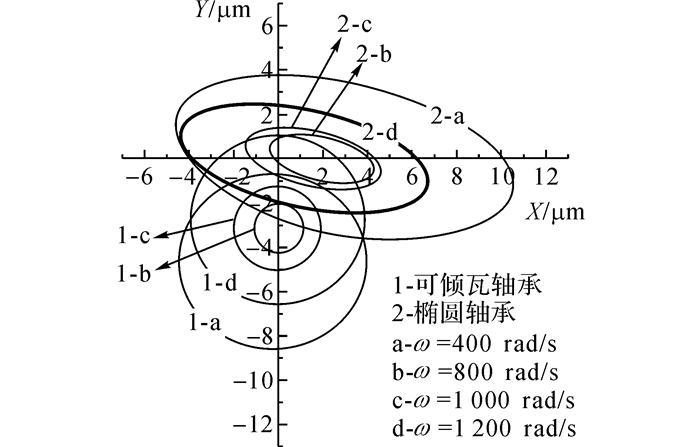
图 8给出了不同转速下椭圆和可倾瓦轴承计算得到的轴心轨迹, 从图中可以看到:1)不同转速时椭圆轴承的轴心轨迹均收敛为椭圆, 水平方向刚度较弱, 这是由于水平方向上轴瓦与轴颈形成开扩形间隙, 间隙内没有建立起油膜压力;而可倾瓦轴承的轴心轨迹具有很好的圆度, 符合瞬态流场分析中观察到的轴颈所受合力的径向分量保持为一个稳定的指向涡动中心的支撑力的规律;2)在相同转速下, 可倾瓦轴承轴心轨迹幅值更小、涡动中心下沉更低且涡动中心偏位角几乎为零, 表现出非常优越的稳定性;3)2种轴承在一阶临界转速(380 rad/s)附近时均具有最大的轴心轨迹幅值, 远离一阶临界转速后随着转速升高, 轴心轨迹的幅值先减小后增大;4)在转速升高后, 轴颈的涡动中心发生偏移, 椭圆轴承的涡动中心沿着椭圆轨迹的长轴进行偏移, 可倾瓦轴承的涡动中心则沿着竖直方向上浮, 偏位角始终为零.轴颈涡动中心位置及轴心轨迹幅值的具体变化见表 1.x0, y0为涡动中心的坐标,X、Y为沿水平、竖直方向峰峰值.
|
图 8 不同转速下椭圆和可倾瓦轴承轴心轨迹对比 Fig. 8 Comparison between shaft center orbit of elliptical and tilting pad journal bearings under different speeds |
| 表 1 涡动中心位置和轴心轨迹幅值统计 Table 1 Center and amplitude of the whirl orbits |
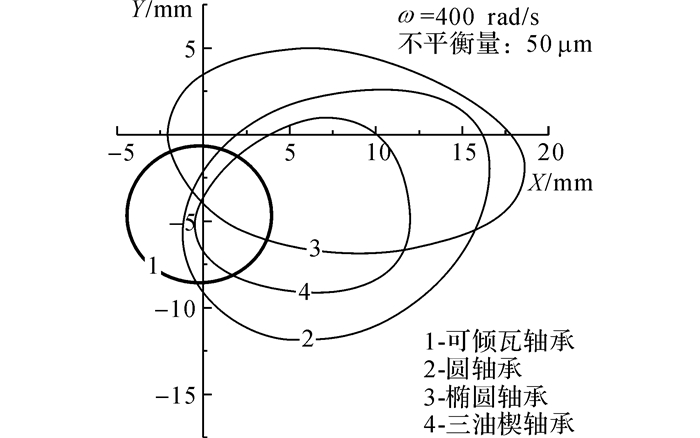
进一步对比不同轴承在相同转速(400 rad/s)和不平衡量(50 μm)条件下计算得到的轴心轨迹差异, 对比的轴承类型有:圆柱轴承(最小半径间隙32 μm, 长径比0.5)、椭圆轴承(最小半径间隙32 μm, 预负荷系数0.67, 长径比0.5)、三油楔轴承(最小半径间隙32 μm, 预负荷系数0.67, 长径比0.5)和可倾瓦轴承.其中, 固定瓦滑动轴承的计算结果均来自于文献[30].
如图 9所示为4种轴承轴心轨迹的对比图, 从图中可以看到:1)椭圆轴承的轴心轨迹结果有2个凸起, 三油楔轴承的有3个凸起, 而可倾瓦轴承的轴心轨迹结果具有最好的圆度;2)可倾瓦轴承具有较低的涡动中心、最小的轴心轨迹幅值且涡动中心偏位角为零, 表现出最优的稳定性, 其次为三油楔轴承.不同轴承的涡动中心位置和轴心轨迹幅值统计见表 2.
|
图 9 不同类型轴承轴心轨迹对比 Fig. 9 Shaft center orbits of different bearing structures |
| 表 2 不同轴承涡动中心位置及轴心轨迹幅值 Table 2 Whirl orbit center and amplitude of different bearing structures |
为了对第4节理论计算总结的规律进行验证, 本节对可倾瓦滑动轴承进行实验研究, 实验基于自行开发的高速转子试验台(见图 10), 试验台的动力装置包括了:45 kW电机、大带轮(速比6:1)、小带轮(过渡轴)等, 其中过渡轴由滚动轴承支撑并通过弹性联轴节与多圆盘转子进行连接;试验台的试验装置包括了:轴承座、工装、多圆盘转子、油路系统和试验轴承等, 其中除试验轴承外, 试验装置的各部件与文献[30]中使用的一致.实验中轴颈振动信号由ENTEK电涡流位移传感器进行测量, 测量信号经数采卡采集和AD转换后输入计算机进行后处理.

|
图 10 高速转子试验台 Fig. 10 High-speed rotor test rig |
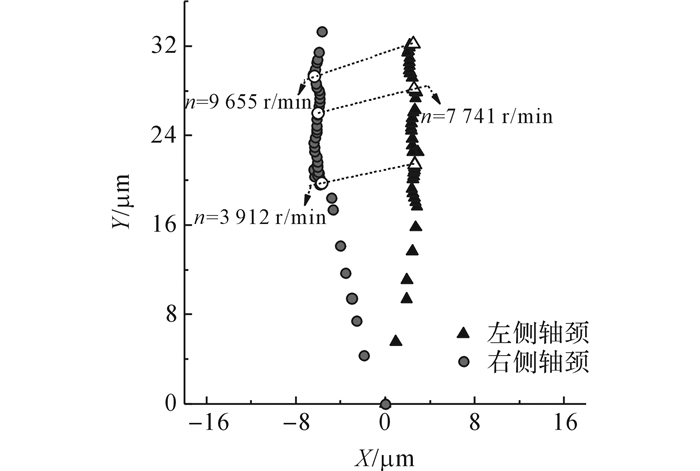
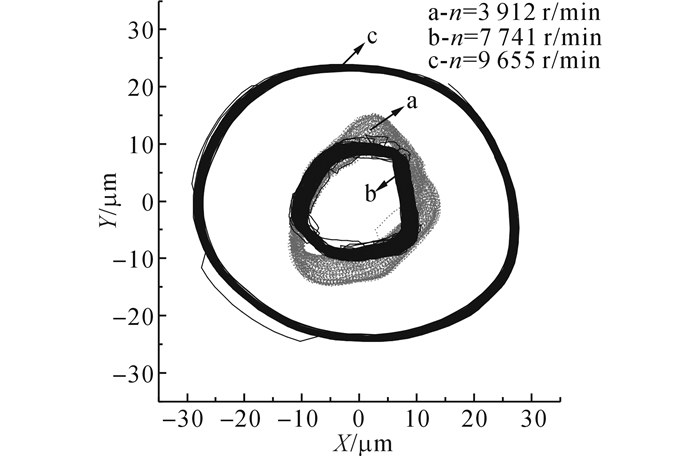
在对可倾瓦滑动轴承进行变转速试验时, 主要采集了两侧轴颈的振动变化以及轴颈涡动中心的偏移情况.图 11给出的是不同转速下两侧轴颈涡动中心的偏移情况, 图中以转速n=500 r/min时的轴颈涡动中心作为参考原点, 并用虚线标示出了n=3 912、7 741和9 655 r/min(分别近似对应理论计算的400、800和1 000 rad/s)时两侧轴颈涡动中心的相对位置.从图 11中可以看到:1)在转速升高过程中, 轴颈涡动中心的水平方向偏移量很小, 与CFD计算中观察到的涡动中心偏位角始终保持在零附近的规律相一致;2)从n=3 912 r/min提高至9 655 r/min的过程中, 轴颈涡动中心沿着竖直方向上浮, 基本不再发生水平偏移, 表现出非常好的稳定性.当n=3 912、7 741和9 655 r/min时右侧轴心轨迹如图 12所示(其中去除了振动信号中的直流分量), 由于这3个转速均在一阶临界转速之上, 轴心轨迹的幅值先减小后增大, 符合滑动轴承支撑时转子不同转速下振幅变化的一般规律.
|
图 11 可倾瓦轴承变转速试验中两侧轴颈涡动中心偏移 Fig. 11 Drift of whirling center under different speeds |
|
图 12 不同转速时右侧可倾瓦试验轴承轴心轨迹 Fig. 12 Whirl orbits of right TPJB under differentspeeds |
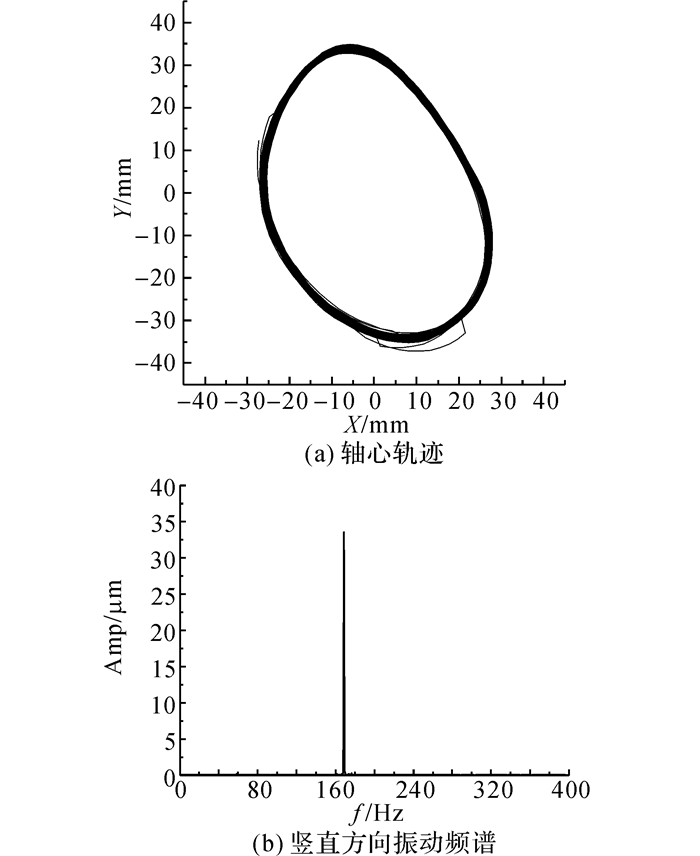
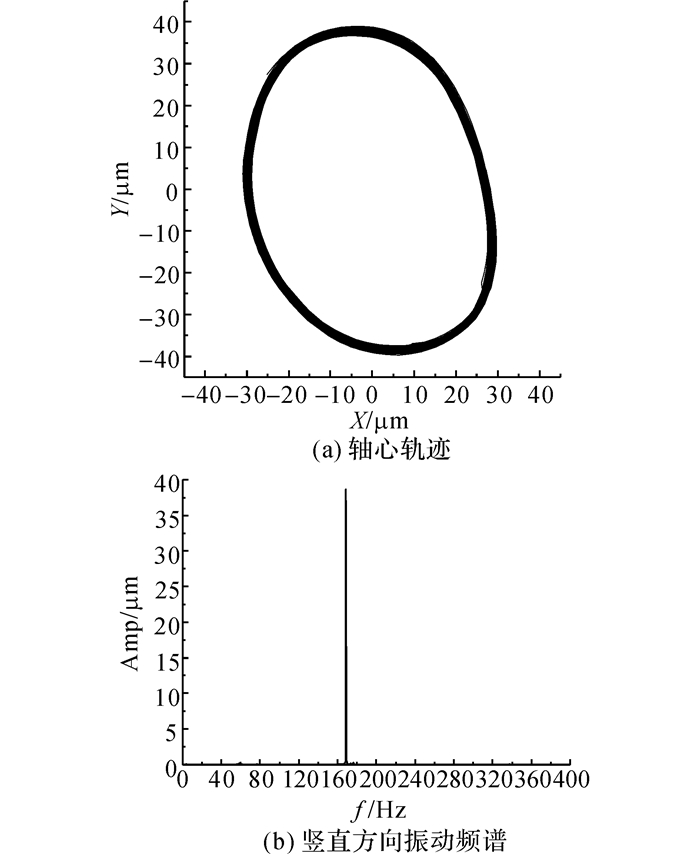
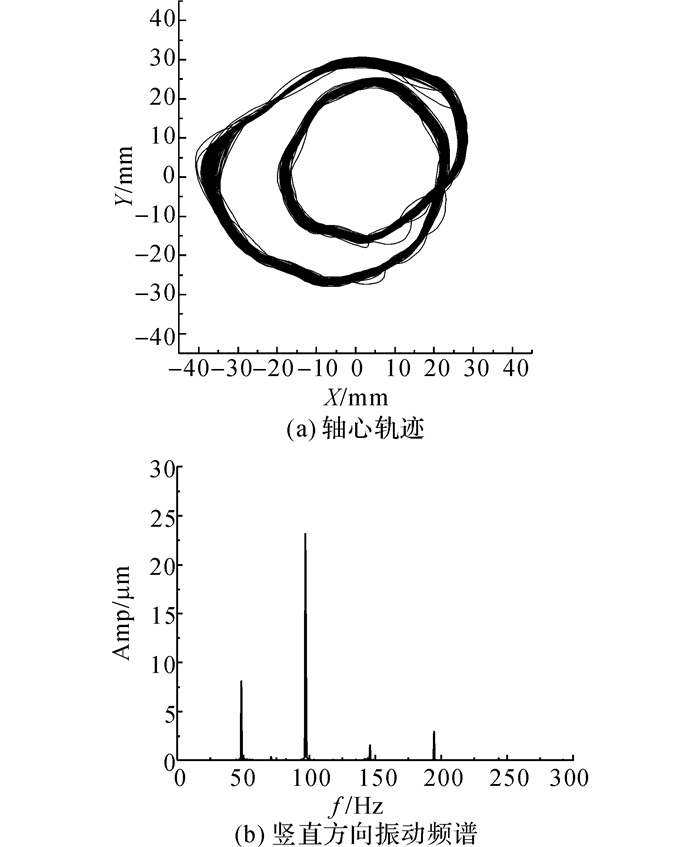
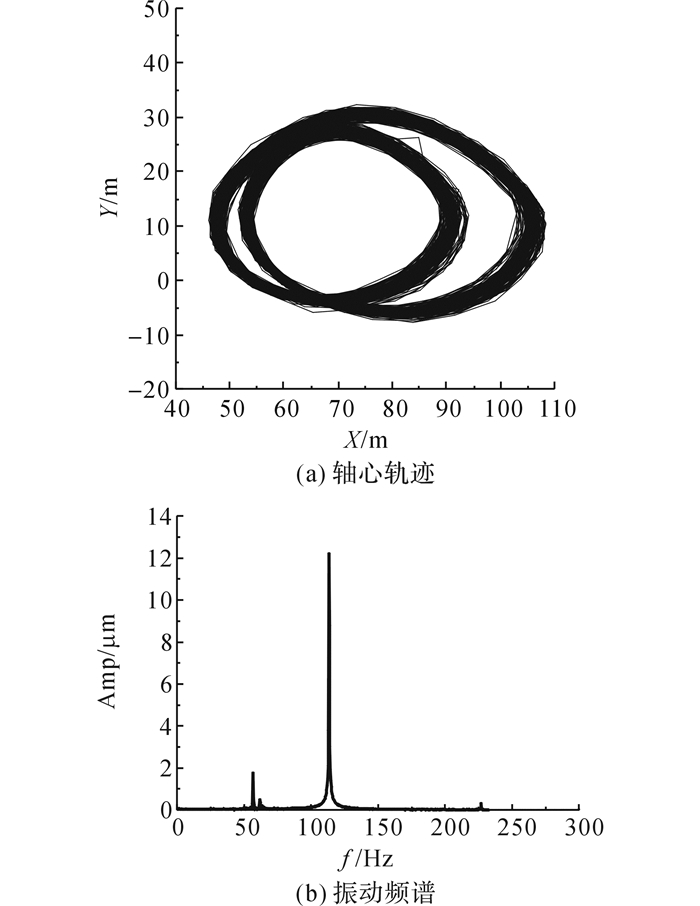
可倾瓦滑动轴承变转速试验达到的最高转速为10 122 r/min.当n=10 122 r/min时, 左侧轴颈水平及竖直方向的振动峰峰值分别为55.5和72.1 μm, 右侧轴颈水平及竖直方向的振动峰峰值分别为60.6和78.6 μm(振动信号换算时采用的是静标灵敏度5 V/mm, 与传感器的动态灵敏度存在偏差, 因而出现了振动峰峰值大于轴承装配间隙的结果),当n=10 122 r/min时两侧轴颈轴心轨迹和竖直方向振动频谱如图 13和14所示, 其中f为频率, 纵坐标(Amp)为频率的幅值, 频谱上只存在明显的工频成分, 轴承的稳定性依然很好, 分析振幅过大的原因主要由转子的不平衡量引起.当试验轴承更换为圆柱轴承时, 转速升至5 847 r/min时, 右侧轴心轨迹出现内“8”形状, 对应振动频谱中出现明显的半频成分(见图 15).而文献[30]中采用椭圆轴承(最小半径间隙35 μm)进行试验时, 当n=6 800 r/min时右侧也出现了上述的半频涡动现象(见图 16), 振动频谱图中出现的半频十分接近系统一阶固有频率, 转子的运动已经变得非常不稳定.
|
图 13 当转速为10 122 r/min时左侧轴颈轴心轨迹和振动频谱 Fig. 13 Whirl orbit and vibration spectrum of TPJB on left side under speed of 10 122 r/min |
|
图 14 当转速为10 122 r/min时右侧轴颈轴心轨迹和振动频谱 Fig. 14 Whirl orbit and vibration spectrum of TPJB on right side under speed of 10 122 r/min |
|
图 15 当圆柱轴承转速为5 847 r/min时右侧轴心轨迹和振动频谱 Fig. 15 Whirl orbit and vibration spectrum of cylindrical bearing on right side under speed of5 847 r/min |
|
图 16 当椭圆轴承转速为6 800 r/min时右侧轴心轨迹和振动频谱[30] Fig. 16 Whirl orbit and vibration spectrum of elliptical bearing on right side under speed of6 800 r/min[30] |
(1) 对可倾瓦滑动轴承-多圆盘转子系统进行了3D CFD瞬态流场和转子动力学耦合计算, 得到了不同转速下的轴心轨迹;随着转速升高, 轴颈涡动中心沿着竖直方向上浮, 始终保持偏位角为零, 表现出优越的稳定性;
(2) 对可倾瓦滑动轴承内部流场进行了分析, 发现在涡动过程中瓦块沿着轴颈中心前进方向接替输出支撑, 有效抑制了涡动轨迹的扩大;且五瓦的瓦上间隙内均能形成油膜压力, 表明瓦块通过不断调节自身的转动确保了瓦上间隙始终保持为收敛楔形;
(3) 对不同轴瓦结构滑动轴承-转子系统在相同转速和不平衡量条件下的轴心轨迹计算结果进行了对比, 可倾瓦轴承得到的结果中轴颈的涡动中心下沉得更低且轴心轨迹的幅值更小, 轴承的稳定裕度更高;同时, 可倾瓦轴承的轴心轨迹收敛为圆形, 在轴颈涡动过程中始终能提供稳定的支撑刚度;
(4) 对可倾瓦滑动轴承-多圆盘转子系统进行了不同转速下的振动试验, 得到了同理论计算预测一致的轴颈振动幅值变化及涡动中心偏移规律, 验证了本文3D CFD方法用于可倾瓦滑动轴承动力性能计算的可靠性.
| [1] | 钟一谔, 何衍宗, 王正, 等. 转子动力学[M]. 北京: 清华大学出版社, 1987: 120-125. |
| [2] | 张直明, 张言羊, 谢友柏. 滑动轴承的流体动力润滑理论[M]. 北京: 高等教育出版社, 1986: 99-100. |
| [3] |
应光耀, 童小忠, 吴文健. 9F燃气机组油膜涡动和油膜振荡的诊断及处理[J].
浙江电力, 2006, 25(1): 10–13.
YING Guang-yao, TONG Xiao-zhong, WU Wen-jian. Diagnosis and treatment of oil whirling and oil whip on 9F combined-cycle power train[J]. Zhejiang Electric Power, 2006, 25(1): 10–13. |
| [4] | BOUARD L, FILLON M, FRENE J. Thermohydrodynamic analysis of tilting-pad journal bearings operating in turbulent flow regime[J]. Journal of Tribology, 1996, 118(1): 225–231. DOI:10.1115/1.2837083 |
| [5] | FILLON M, DESBORDES H, FRENE J, et al. A global approach of thermal effects including pad deformations in tilting-pad journal bearings submitted to unbalance load[J]. Journal of Tribology, 1996, 118(1): 169–174. DOI:10.1115/1.2837074 |
| [6] | MONMOUSSEAU P, FILLON M. Transient thermoelastohydrodynamic analysis for safe operating conditions of a tilting-pad journal bearing during start-up[J]. Tribology International, 2000, 33(3): 225–231. |
| [7] | EL-BUTCH A M, ASHOUR N M. Transient analysis of misaligned elastic tilting-pad journal bearing[J]. Tribology International, 2005, 38(1): 41–48. DOI:10.1016/j.triboint.2004.05.008 |
| [8] | GUO Yong, WANG Xiao-ning, YUAN Xiao-yang, et al. Study on the thermoelastohydrodynamic performance of tilting-pad bearings for large-scale power units[C]//4th IEEE Conference on Industrial Electronics and Applications. Xi'an, China:IEEE, 2009:2070-2075. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&arnumber=5138566 |
| [9] | LI Peng-ju, ZHU Yong-sheng, ZHANG You-yun, et al. The investigation of the temperature of high speed and heavy haul tilting pad journal bearing[J]. Industrial Lubrication and Tribology, 2015, 67(4): 301–307. DOI:10.1108/ILT-07-2013-0081 |
| [10] | PAGANO S, ROCCA E, RUSSO M, et al. Dynamic behaviour of tilting-pad journal bearings[J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology, 1995, 209(4): 275–285. DOI:10.1243/PIME_PROC_1995_209_438_02 |
| [11] |
焦映厚, 陈照波, 刘福利, 等. Jeffcott转子-可倾瓦滑动轴承系统不平衡响应的非线性分析[J].
中国电机工程学报, 2004, 24(12): 227–232.
JIAO Ying-hou, CHEN Zhao-bo, LIU Fu-li, et al. Nonlinear analysis of unbalance response for Jeffcott rotor-tilting pad bearing system[J]. Proceedings of the CSEE, 2004, 24(12): 227–232. DOI:10.3321/j.issn:0258-8013.2004.12.042 |
| [12] | GUO Zeng-lin, HIRANO T, KIRK R G. Application of CFD analysis for rotating machinery-part I:hydrodynamic, hydrostatic bearings and squeeze film damper[J]. Journal of Engineering for Gas Turbines and Power, 2005, 127(2): 445–451. DOI:10.1115/1.1807415 |
| [13] | ABU-MAHFOUZ I, ADAMS M L. Numerical study of some nonlinear dynamics of a rotor supported on a three-pad tilting pad journal bearing (TPJB)[J]. Journal of Vibration and Acoustics, 2005, 127(3): 262–272. DOI:10.1115/1.1888593 |
| [14] | BAI Hui-yu, LIU Xing-xing, LI Hong-guang, et al. Nonlinear dynamic characteristics of a large-scale tilting pad journal bearing-rotor system[J]. Journal of Vibroengineering, 2014, 16(8): 4045–4064. |
| [15] | CHEN P Y P, HAHN E J. Use of computational fluid dynamics in hydrodynamic lubrication[J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology, 1998, 212(6): 427–436. DOI:10.1243/1350650981542236 |
| [16] | CUPILLARD S, GLAVATSKIH S, CERVANTES M J. Computational fluid dynamics analysis of a journal bearing with surface texturing[J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology, 2008, 222(2): 97–107. DOI:10.1243/13506501JET319 |
| [17] | GERTZOS K P, NIKOLAKOPOULOS P G, PAPADOPOULOS C A. CFD analysis of journal bearing hydrodynamic lubrication by Bingham lubricant[J]. Tribology International, 2008, 41(12): 1190–1204. DOI:10.1016/j.triboint.2008.03.002 |
| [18] | SONG Yin, GU Chun-wei. Development and validation of a three-dimensional computational fluid dynamics analysis for journal bearings considering cavitation and conjugate heat transfer[J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(12): 122502. DOI:10.1115/1.4030633 |
| [19] | MENG F M, YANG T. Preliminary study on mechanism of cavitation in lubricant of textured sliding bearing[J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology, 2013, 227(7): 695–708. DOI:10.1177/1350650112468560 |
| [20] | PAPADOPOULOS C I, KAIKTSIS L, FILLON M. CFD thermohydrodynamic analysis of 3-D sector-pad thrust bearings with rectangular dimples[C]//ASME Turbo Expo 2013:Turbine Technical Conference and Exposition. San Antonio, Tx, United states:ASME, 2013:V07BT30A002. http://www.academia.edu/14982522/CFD_Thermohydrodynamic_Analysis_of_3-D_Sector-Pad_Thrust_Bearings_With_Rectangular_Dimples |
| [21] | CUPILLARD S, CERVANTES M J, GLAVATSKIH S. Thermohydrodynamic analysis of a journal bearing with a microgroove on the shaft[J]. Computational Thermal Sciences:An International Journal, 2014, 6(1): 47–57. DOI:10.1615/ComputThermalScien.v6.i1 |
| [22] | MERUANE V, PASCUAL R. Identification of nonlinear dynamic coefficients in plain journal bearings[J]. Tribology International, 2008, 41(8): 743–754. DOI:10.1016/j.triboint.2008.01.002 |
| [23] | LIU Hui-ping, XU Hua, ELLISON P J, et al. Application of computational fluid dynamics and fluid-structure interaction method to the lubrication study of a rotor-bearing system[J]. Tribology Letters, 2010, 38(3): 325–336. DOI:10.1007/s11249-010-9612-6 |
| [24] | LIN Qi-yin, WEI Zheng-ying, WANG Ning, et al. Analysis on the lubrication performances of journal bearing system using computational fluid dynamics and fluid-structure interaction considering thermal influence and cavitation[J]. Tribology International, 2013, 64: 8–15. DOI:10.1016/j.triboint.2013.03.001 |
| [25] | LI Qiang, YU Gui-chang, LIU Shu-lian, et al. Application of computational fluid dynamics and fluid structure interaction techniques for calculating the 3D transient flow of journal bearings coupled with rotor systems[J]. Chinese Journal of Mechanical Engineering, 2012, 25(5): 926–932. DOI:10.3901/CJME.2012.05.926 |
| [26] | VARELA A C, NIELSEN B B, SANTOS I F. Steady state characteristics of a tilting pad journal bearing with controllable lubrication:Comparison between theoretical and experimental results[J]. Tribology International, 2013, 58: 85–97. DOI:10.1016/j.triboint.2012.10.004 |
| [27] | RINDI A, ROSSIN S, CONTI R, et al. Efficient models of three-dimensional tilting pad journal bearings for the study of the interactions between rotor and lubricant supply plant[J]. Journal of Computational and Nonlinear Dynamics, 2016, 11(1): 011011. DOI:10.1115/1.4030509 |
| [28] | LI Meng-xuan, GU Chao-hua, PAN Xiao-hong, et al. A new dynamic mesh algorithm for studying the 3D transient flow field of tilting pad journal bearings[J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribolog, 2016, 230(12): 1470–1482. DOI:10.1177/1350650116638610 |
| [29] |
李强, 刘淑莲, 于桂昌, 等. 非线性转子-轴承耦合系统润滑及稳定性分析[J].
浙江大学学报:工学版, 2012, 46(10): 1729–1736.
LI Qiang, LIU Shu-lian, YU Gui-chang, et al. Lubrication and stability analysis of nonlinear rotor-bearing system[J]. Journal of Zhejiang University (Engineering Science), 2012, 46(10): 1729–1736. |
| [30] |
李强. 滑动轴承动力特性的3D瞬态流场计算和实验研究[D]. 杭州: 浙江大学, 2012.
LI Qiang. 3D transient flow calculation and experimental research on dynamic characteristics of journal bearing[D]. Hangzhou:Zhejiang University, 2012. http://d.g.wanfangdata.com.cn/Thesis_Y2882280.aspx |
| [31] |
于桂昌, 刘淑莲, 郑水英. 扰动情况下双油槽圆形轴瓦滑动轴承性能分析[J].
振动与冲击, 2012, 31(5): 46–49, 54.
YU Gui-chang, LIU Shu-lian, ZHENG Shui-ying. Double oil grooved round sliding bearing performance analysis with disturbance[J]. Journal of Vibration and Shock, 2012, 31(5): 46–49, 54. |
| [32] |
刘淑莲. 转子-轴承系统非线性特性研究及油膜振荡的在线消除[D]. 杭州: 浙江大学, 2004.
LIU Shu-lian. Research on nonlinear dynamics of rotor-bearing system and on-line elimination of the oil film whip[D]. Hangzhou:Zhejiang University, 2004. http://d.wanfangdata.com.cn/Thesis/Y600083 |
| [33] | KHONSARI M M, BOOSER E R. Applied tribology:bearing design and lubrication[M]. Hoboken, New Jersey: John Wiley & Sons, 2008. |



