我国城市发展迅猛, 新旧管道并存, 市政工程、交通碾压导致供水管网异常事件频发, 使整个供水系统运行承受着巨大压力.虽有数据采集与监视控制系统(supervisory control and data acquisition, SCADA)支撑, 但经验式的监控调度已难以承担城市安全供水重任, 城市管网漏失率居高不下.
常规的漏损、爆管检测方法包括负压波分析、瞬态逆分析ITA、频域谱分析、基于管网水力模型分析等.在漏损侦测方面, Chen等[1]引入负压波并使用支持向量机学习方法进行漏失侦测和定位;Stephens等[2], Gong等[3]采用瞬态分析的方法分析管道的损坏情况, 通过实例验证该方法能够估计管道损坏程度及位置;郭新蕾等[4]采用瞬态分析的方法进行漏损侦测, 用拉氏频域变换处理边界条件和实测数据;Wu等[5]通过实例验证表明, 相较于传统侦测方法, 基于压力数据侦测供水管网漏损的方法更适用于各种材料管道的泄露侦测.在爆管侦测方面, 刘书明等[6]基于管网水力学模型和监测点的动态信息, 建立了供水管网爆管定位模型, 依次验证杜鹃算法、遗传算法和粒子群算法, 其中杜鹃算法在爆管定位能力上最为出色;程伟平等[7]建立了基于SCADA和低压供水模型相结合的供水管网爆管定位模型, 通过压差或水力坡降对爆管事件进行初步定位;李稳等[8]利用趋势面定位管网爆管点, 通过分析比较供水管网水压在正常和异常2种情况下水压的趋势面, 以水压差值的形式定位管网爆管点, 实验证明该方法有一定可行性.Ye等[9-10]对水压差值使用卡尔曼滤波侦测和定位爆管, 对突发性爆管和逐渐增强的泄漏侦测效果优于长期稳定的泄漏侦测;Mounce等[11]采用模糊推理系统和人工神经网络结合的方法检测爆管, 在多个独立计量区域(district metering area, DMA)实验中验证了该方法的有效性.
近年随着数据采集与监控系统SCADA应用的普及, 供水管网系统基于数据的异常侦测受到国内外学者重视[12-13].Romano等[14-15]提出了一种数据驱动的近实时异常事件侦测方法, 结合SCADA数据、人工神经网络模型以及统计学方法等, 具有较强自学习能力.在英国, 多个DMA实验表明, 该方法可以快速有效地侦测异常, 具有较高的实用性, 但是该方法更多地依赖于人工神经网络模型的预测精度[16], 需要至少2~3个月的数据训练人工神经网络模型.本文在借鉴Romano M数据驱动思想基础上, 加入外生变量的向量自回归(a Vector Auto-Regressive with eXogenous variables, VARX)[17]模型的压力预测进行差异性分析, 克服了数据缺失问题, 并引入信噪比分析降低了侦测误报率.
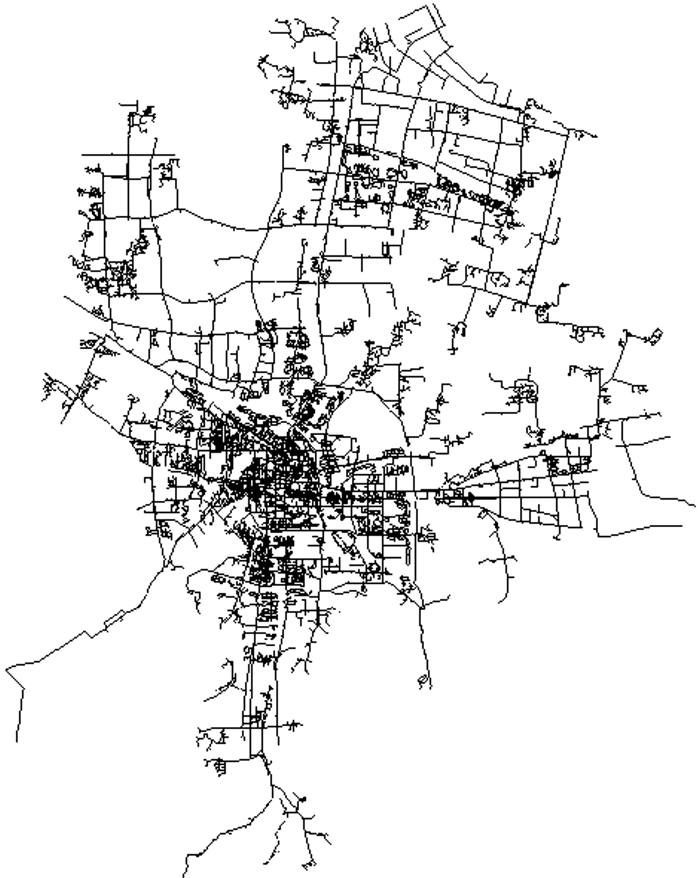
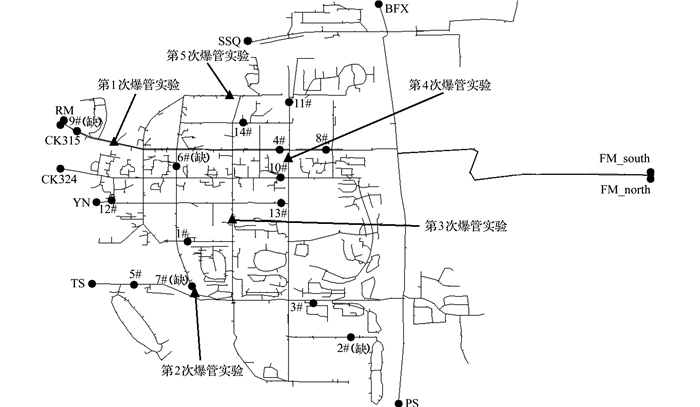
1 爆管模拟实验介绍以某市供水管网系统为研究对象, 该市管网地理信息系统(geographic information system, GIS)系统、SCADA系统以及管理信息系统(management information system, MIS)建设较为完善.该城市供水管网如图 1所示, 已划分了多个DMA区.实验DMA区管网测点及爆管实验点如图 2所示.爆管实验是通过开关消防栓进行模拟, 该DMA区设有3个流量入口(FM_south, FM_north, PS)和7个流量出口(BFX, SSQ, RM, CK315, CK324, YN, TS), 内部包括14个压力测点, 由于2#, 6#, 7#, 9#数据缺失的原因, 本文只使用1#, 3#, 4#, 5#, 8#, 10#, 11#, 12#, 13#, 14#共10个压力监测点, 面积约为15 km2, 主干供水管道长度约10.5 km, 5次爆管实验数据如表 1所示, Px, Py为爆管实验点位置, D为管径, ts为模拟开启时间, te为模拟关闭时间, G为模拟排放量.
|
图 1 城市供水管网图 Fig. 1 Urban water supply network |
|
图 2 某DMA区测点及爆管实验点 Fig. 2 Monitoring points and pipe burst experiment points in DMA |
| 表 1 5次模拟爆管实验数据 Table 1 5 pipe burst simulation experiments data |
在实测数据中, 由于采集或传输问题导致数据缺失现象.当短时缺失时, 采取插值、重采样等方法弥补;当长时缺失时, 只能剔除, 造成数据不连续, 此时采用神经网络模型分析效果不佳.为此, 通过小波降噪[18-19]预处理后, 首先尝试基于VARX模型的差异分析方法.异常侦测思路如下:
1) 计算每个监测点n天内每一时刻预测值和观测值的差异Δy.
2) 计算Δy的平均值X和标准差σ;
3) 单监测点异常判别规则:
a) 任一时间点压力测点差异值低于平均差异值-4σ;
b) 连续2个时间点压力测点差异值低于平均差异值-3σ;
c) 连续4个时间点压力测点差异值低于平均差异值-2σ;
d) 连续8个时间点压力测点差异值低于平均差异值-σ;
4) 多测点异常事件确定规则:
考虑到爆管规模、管网噪声等因素, 测点对异常事件的敏感度不同, 按1/3以上测点同时判别异常定性.即根据步骤3中每个监测点侦测、判别的可能异常, 综合确定异常事件.
2.1 VARX压力预测模型的建立将DMA区10个有效监测点压力作为内生变量, 同时引入3个入水口压力点P1, P2, P3作为外生变量.从SCADA提取从2015年3月20日至2015年4月3日的压力数据, 使用3月20日至4月2日的数据进行模型训练, 对4月3日模拟爆管事件进行侦测.
将压力监测点和入水口压力点通过相关性分析进行分组, 得到压力监测点分组, 如表 2所示.这里, 相关性计算公式如下:
| 表 2 压力监测点分组 Table 2 Group of pressure monitoring point |
| $ \rho \left( {x, y} \right) = \frac{{E\left( {x-E\left( x \right)} \right)E\left( {y-E\left( y \right)} \right)}}{{\sqrt {D\left( x \right)} \times \sqrt {D\left( y \right)} }}. $ | (1) |
式中:ρ(x, y)为相关系数, x, y为2组时间序列数据, E(·)为对时间序列数据求期望值, D(·)为对时间序列数据求方差.
采用赤池信息量准则(akaike information criterion, AIC)定阶准则.其定义如下:
| $ {\rm{AIC = ln}}\left( {\sum\limits_{t = 1}^T {\hat u_t^2/T} } \right) + \frac{{2p}}{T}. $ | (2) |
式中:
VARX模型的表达式[20]为
| $ {y_t} = c + \sum\limits_{i = 1}^P {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i}{y_{t-i}}} + \sum\limits_{j = 0}^q {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_j}{x_{t-j}} + {\xi _t}} . $ | (3) |
| $ {\xi _t} \sim N\left( {0,{\bf{\varepsilon }}} \right). $ | (4) |
式中:xt为d维外生变量, Θj为k×d维待估计的系数矩阵, yt为k维的内生变量, c为k维的常数项, Φi为k×k维待估计的系数矩阵, p, q为滞后阶数, ζt为k维白噪声序列, ε为k×k维协方差矩阵.
VARX模型的参数估计[20]使用极大似然法得到, 设定:
| $ \begin{array}{l} \beta = {\rm{vec}}\left( {\left[{c, {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1}, \cdots, {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_p}, {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}, \cdots, {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_q}} \right]} \right), \\ {W_{t - 1}} = \left[{{1^{\rm{T}}}, y_{t-1}^{\rm{T}}, \cdots, y_{t-p}^{\rm{T}}, x_{t-1}^{\rm{T}}, \cdots, x_{x + 1 - q}^{\rm{T}}} \right] \otimes {I_{k \times k}}, \end{array} $ |
则式(3)可表示为
| $ {y_t} = {W_{t-1}}{\beta _t} + {\xi _t}. $ | (5) |
随后根据极大似然算法有
| $ \begin{array}{l} l\left( \psi \right) = \frac{{Tk}}{2}\ln \left( {2\pi } \right) + \frac{1}{2}\sum\limits_{t = p + 1}^T {\ln \left( {\left| {\varepsilon _{m\left( t \right)}^{-1}} \right|} \right)}-\\ \;\;\;\;\;\;\;\;\;\frac{1}{2}\sum\limits_{t = p + 1}^T {{{\left( {{y_t}-{W_{t - 1}}\beta } \right)}^T}\varepsilon _{m\left( t \right)}^{ - 1}\left( {{y_t} - {W_{t - 1}}\beta } \right)} . \end{array} $ | (6) |
从β和{εm(t)}m(t)=1p方面可以衍生模型参数如下:
| $ \begin{array}{l} {{\hat \varepsilon }_m} = \sum\limits_{t = p|m\left( t \right) = m}^T {\frac{{\left( {{y_t}-{W_{t-1}}\beta } \right){{\left( {{y_t}-{W_{t - 1}}\beta } \right)}^{\rm{T}}}}}{n}}, \\ \forall m = 1, 2, \cdots, p. \end{array} $ | (7) |
| $ \hat \beta = {\left[{\sum\limits_{t = p + 1}^T {W_{t-1}^{\rm{T}}\varepsilon _{m\left( t \right)}^{-1}{W_{t-1}}} } \right]^{ - 1}}\left[{\sum\limits_{t = p + 1}^T {W_{t-1}^{\rm{T}}\varepsilon _{m\left( t \right)}^{-1}{y_t}} } \right]. $ | (8) |
由此建立的VARX模型对2015年4月2日的监测点压力进行预测, 并与目前流行的人工神经网络(artificial neural network, ANN)压力预测模型进行对比, 10个监测点预测误差比较如表 3所示.表 3中, δMRE为平均相对误差, ΔMAE为平均绝对误差, ttotal为耗时.监测点4#, 8#, 10#, 11#预测结果比较如图 3所示.图 3中, p1为压力, t为时刻.通过表 3和图 3可以看出, 2个模型均能达到较好的预测精度, 每个测点压力预测平均相对误差均在5%以内, 且90%的测点预测误差在3%以内.从训练耗时来看, VARX模型耗时更短.ANN模型隐含层层数设定影响了预测精度和训练耗时, 本文通过经验公式及多轮试验优选, 设定了较为合理的ANN模型隐含层层数, 具体的层数为8.同时ANN预测时有时会出现较大的突变, 原因在于本文中仅使用13 d的历史数据作为训练样本, 可能导致模型训练不完善, 不能完全适应各种情况.
| 表 3 VARX、ANN模型压力预测误差表 Table 3 Table of pressure prediction errors of VARX and ANN model |

|
图 3 4#, 8#, 10#, 11#监测点压力预测图 Fig. 3 Picture of Pressure prediction of monitoring points (4#, 8#, 10#, 11#) |
根据历史数据和VARX模型可得到每个监测点的预测值, 并计算每个监测点10 d内每一时间间隔预测值和观测值的差异:设预测值为(y1j′, y2j′, …, yij′), 实测值为(y1j, y2j, …, yij), 时间间隔为5 min.i =1, 2, …, 288, j =1, 2, …, 10, 则差异可表示为
| $ \Delta {y_{ij}} = \left( {{y_{1j}}-{{y'}_{1j}}, {y_{2j}}-{{y'}_{2j}}, \cdots, {y_{ij}}-{{y'}_{ij}}} \right). $ | (9) |
那么9 d差异的平均值
| $ \overline {{X_i}} = \frac{1}{n}\sum\limits_{j = 1}^n {\Delta {y_{ij}}} . $ | (10) |
标准差(σ1, σ2, …, σi)通过下式计算得到
| $ {\sigma _i} = \sqrt {\frac{1}{n}\sum\limits_{j = 1}^n {{{\left( {\Delta {y_{ij}}-{{\bar X}_i}} \right)}^2}} } . $ | (11) |
根据单测点异常判别规则, 得到10个监测点异常判别情况如表 4所示, 部分测点侦测判别情况如图 4所示.图 4中, 实线为测点预测值与实际值差异曲线, 为了便于观察比较, 本文中, 虚线为平均差异值减去2.5σ.
| 表 4 基于差异分析方法的监测点异常判别汇总表 Table 4 Table of anomaly detection of monitoring points based on difference analysis method |

|
图 4 基于差异分析方法的4#, 8#, 10#, 11#监测点异常侦测图 Fig. 4 Picture of anomaly detection of monitoring points (4#, 8#, 10#, 11#) based on difference analysis method |
根据多测点异常事件确定规则, 差异分析方法对2015年4月3日该DMA区一共测定异常事件数为4次, 如表 5所示, 其中包含前3次模拟爆管事件, 因此, 此方法的误报率为25%, 漏报率为40%.
| 表 5 基于差异分析方法的管网异常事件表 Table 5 Table of abnormal events based on difference analysis method |
统计过程控制(statistical process control, SPC)是一种借助数理统计方法的过程控制工具, 通过信息反馈及时发现系统性因素的发生, 采取措施消除其影响, 将整个过程控制在仅受随机性因素扰动的状态下.
对照式(10)和(11), 将式中差异值Δyij换成实测值yij, 计算得到实测值的平均值和标准差.异常侦侧采取类似的单测点异常判别规则和多测点异常确定规则.由此, 采用SPC统计过程分析方法得到监测点异常判别情况如表 6所示, 部分测点侦测判别情况如图 5所示.图 5中, 实线为测点实测值, 虚线为平均实测值减去2.5σ.
| 表 6 基于SPC统计过程分析方法的监测点异常判别汇总表 Table 6 Table of anomaly detection of monitoring points based on SPC method |
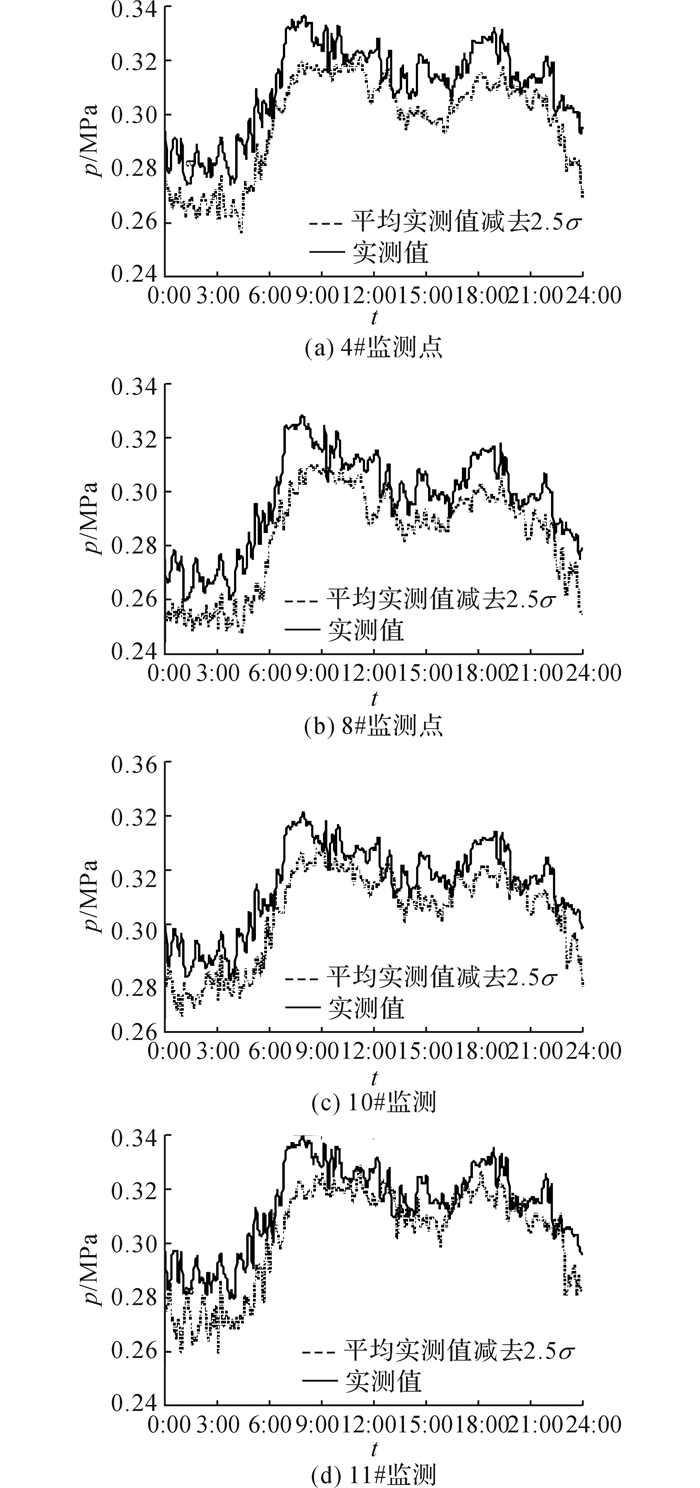
|
图 5 基于SPC统计学分析的4#, 8#, 10#, 11#监测点异常侦测图 Fig. 5 Picture of anomaly detection of monitoring points(4#, 8#, 10#, 11#) based on SPC method |
根据多测点异常事件确定规则, SPC方法对2015年4月3日该DMA区测点的管网异常事件如表 7所示, 一共测得异常事件数为15次, 包含全部5次模拟爆管实验.因此, 此方法的误报率为64.3%, 漏报率为0%.
| 表 7 基于SPC方法的管网异常事件表 Table 7 Table of abnormal events based on SPC method |
贝叶斯网络(Bayesian network)作为一种概率推理方法, 以概率的方式处理条件相关变量间的不确定性问题.贝叶斯网络是一种有向无环图, 它的构成包括模型结构和相关参数2个元素[15].
4.1 贝叶斯网络参数的确定网络参数学习问题可以描述为:在已知观测序列YT的前提下, 模型参数θ未知, 通过相关算法对观测序列进行训练和学习, 得到最符合观测序列的模型参数θ, 使概率P(YT|θ)最大, 即最佳模型参数为
| $ {\theta ^*} = \arg \;\mathop {\max }\limits_\theta P\left( {{Y_t}, {X_t}|\theta } \right). $ | (12) |
最大期望算法(Expectation Maximization, EM)算法是贝叶斯网络学习算法的基础, 其基本思想是用期望的统计值来代替实际的统计值, 依据推导过程来估计P(x1T|y1T).
为方便问题描述, 设Xt, Yt分别表示1:t时刻的状态序列和观测序列, xt, yt分别表示t时刻状态变量和观测变量的值, Xt存在n种状态(即xt∈{1, 2, …, n}), 相对的Yt有m状态(即yt∈{1, 2, …, m}).作为一个迭代算法EM的计算过程可分为2步骤, 简述如下:
1) Expectation过程.假设一个初始模型参数, 进行迭代计算θ, 第k次迭代结果为
| $ \begin{array}{l} E\left[{N\left( {i, j} \right){\rm{|}}{\theta ^k}} \right] = \\ E\left[{\sum\limits_{t = 2}^T {I\left( {{x_{t-1}} = i, {x_t} = j} \right)|{y_{1:T}}} } \right] = \\ \sum\limits_{t = 2}^T {P\left( {\left( {{x_{t -1}} = i, {x_t} = j} \right)|{y_{1:T}}} \right)} = \\ \sum\limits_{t = 2}^T {{\xi _{t -1, t|T}}\left( {i, j} \right)} . \end{array} $ | (13) |
式(13)中:E[N(i, j)|θk]为期望足够统计值(ESS), 可表示为
| $ \sum\limits_{t = 2}^T {{\xi _{t-1, t|T}}\left( {i, j} \right) = \frac{{{\alpha _i}\left( i \right){a_{ij}}{b_j}\left( {{y_{t + 1}}} \right){\beta _t}\left( j \right)}}{{P\left( {Y|\theta } \right)}}} . $ | (14) |
2) Maximization过程.该过程主要目的是通过给定数据, 使网络模型的似然值最大, 即θk+1=argmax Q(θ|θk), 这里的Q表示一个辅助函数:
| $ Q\left( {\theta |{\theta ^k}} \right) = {E_{x\left( {1:T} \right)}}\left[{P\left( {{y_{1:T}}, {x_{1:T}}|\theta } \right)|{\theta ^k}} \right]. $ | (15) |
结合差异分析和SPC统计分析结果, 当Alarm发生的概率值超过一定阈值, 则发出警报提示爆管事件发生.
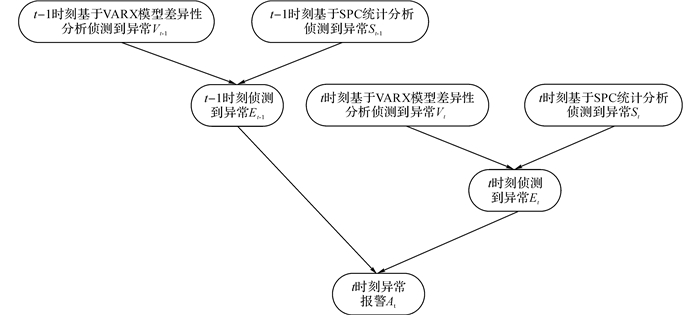
贝叶斯网络模型图如图 6所示.考虑t-1时刻的SPC和VARX状态值得到t-1时刻Event的状态值, 再同样方法得到t时刻Event的状态值, 最后通过前后时刻Event状态值推理得到Alarm状态.根据实验数据训练该贝叶斯网络模型参数, 得到该网络模型条件概率表(conditional probability table, CPT).根据受试者工作特征曲线(receiver operating characteristic curve, ROC)和ROC曲线下面积(area undercurve, AUC)方法[13, 21]得到阈值概率为0.6, 当大于该阈值时判定该事件为爆管, 得到贝叶斯网络下2种分析方法结合的异常侦测结果如表 8所示.对表 8中10个监测点的实验结果做综合推理, 按差异分析方法的异常事件确定规则, 得到管网异常事件表如表 9所示.由此, 异常事件侦测的误报率为42.8%, 漏报率为20%.
|
图 6 贝叶斯网络模型图 Fig. 6 Picture of Bayesian network model |
| 表 8 基于贝叶斯网络的监测点异常侦测汇总表 Table 8 Table of abnormal events detection of monitoring points based on Bayesian network |
| 表 9 基于贝叶斯网络的管网异常事件表 Table 9 Table of events based on Bayesian network |
信噪比(signal-noise ratio, SNR)是信号中有用信号S和噪声N的比值, 信噪比越大, 说明信号中噪声的比例越小, 信号越有代表性.当供水管网中某一时刻发生异常事件时, 产生跳变信号的同时伴随着略大的噪声, 使信噪比变化.信噪比的式为
| $ {N_{{\rm{SNR}}}} = 10 \times \lg \left( {S/N} \right). $ | (15) |
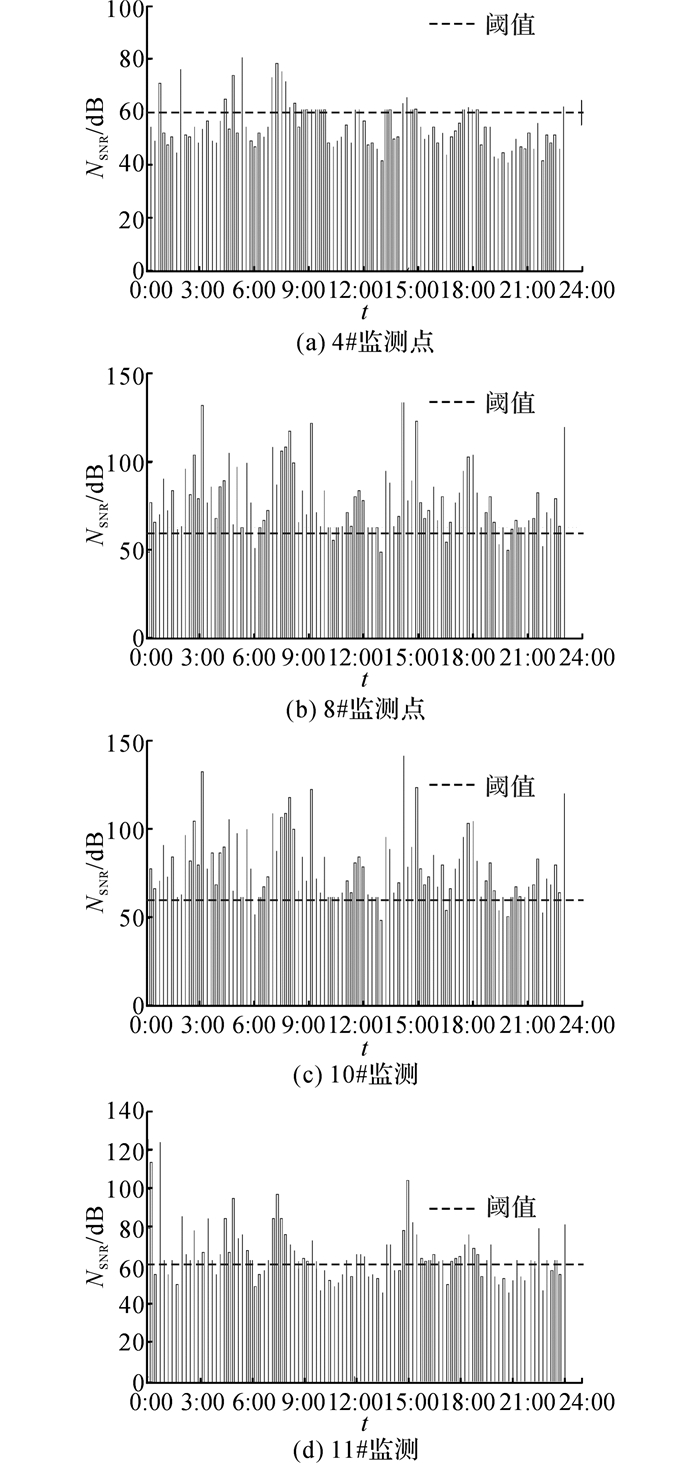
将EPANET[22]离线模拟视为理想模型, 其模拟得到的监测点压力数据可作为监测点理想信号部分.现对DMA区10个监测点在2015年4月2日至4月4日的实测压力数据做小波降噪处理, 得到降噪后的压力数据, 并将其与实测数据做差值视为对应的噪声序列.跳变(有效)信号可通过EPANET模拟值(理想信号)减去降噪后的压力数据得到.由此可以计算得到压力信号的信噪比, 4个监测点情况如图 7所示.图 7中, 横向虚线为阈值.对综合推理的7次异常事件及漏诊的第4次爆管实验, 压力信号信噪比计算结果如表 10所示.
|
图 7 4月3日4#, 8#, 10#, 11#监测点信噪比图 Fig. 7 SNR of monitoring points(4#, 8#, 10#, 11#) on 3rd April |
| 表 10 7次异常事件及第4次爆管实验时的信噪比数据 Table 10 SNR data of 7 abnormal events and 4th Pipe burst experiment |
根据ROC曲线和AUC方法得到压力突变信号的信噪比阈值为60 dB, 当异常事件时间段的信噪比高于该值, 则认为有用信号显著, 肯定此次侦测结果;而当信噪比小于60 dB时, 认为压力信号受噪声污染严重, 可否定该侦测结果.因此, 根据4月3日基于贝叶斯网络的异常事件侦测结果, 可否定第6、7次异常事件, 则该DMA区异常事件侦测误报率为20%, 漏报率为20%, 可见, 利用信噪比分析可进一步降低误报率.此外, 第4次爆管实验由于管径较小, 爆管后对管网压力影响较小, 导致漏报.12:30至12:35为一次误报, 因为午高峰用水时间的用水波动产生了较强的突变信号, 对异常侦测产生了影响.
6 结论供水管网是一个复杂的非线性系统, 机理建模不仅依赖于管网拓扑结构和节点参数, 而且现有检测信息难以满足水力学方程求解的边界条件.同时, 机理模型存在着维数灾难问题.采用数据驱动方法, 可以很好地克服上述问题.
本文基于数据驱动思想对城市供水管网系统异常侦测进行了研究, 结合SCADA实测数据, 采用VARX模型对供水管网监测点压力序列进行预测, 使用基于VARX模型的差异分析方法和SPC统计分析方法, 对供水管网异常事件进行侦测.其中, 基于VARX模型的差异分析方法有较强的抗干扰能力, 可以克服数据缺失问题, 但是没有侦测出小于300DN口径的后两次爆管实验, 说明差异分析方法会受爆管规模影响.基于SPC统计分析方法, 能够侦测出所有爆管实验, 但是因为其敏感性高又极易受噪声干扰而造成误报.通过贝叶斯网络综合推理, 可以降低异常事件侦测的漏报率和误报率.最后通过信噪比分析, 可进一步降低异常事件侦测的误报率.
由于供水管网异常侦测受爆管规模、测点距离、用水波幅等影响, 下一步将针对测点灵敏度、高信噪比信号获取、测点优化布置等开展研究, 进一步完善数据驱动的供水管网异常侦测方法.
| [1] | CHEN H, YE H, CHEN L V, et al.. Application of support vector machine learning to leak detection and location in pipelines[C]//Instrumentation and Measurement Technology Conference. Como, Italy:Proceedings of the IEEE, 2004:2273-2277. http://ieeexplore.ieee.org/xpl/abstractAuthors.jsp?reload=true&arnumber=1351546&sortType%3Dasc_p_Sequence%26filter%3DAND%28p_IS_Number%3A29628%29 |
| [2] | STEPHENS M L, LAMBERT M F, SIMPSON A R. Determining the Internal wall condition of a water pipeline in the field using an inverse transient[J]. Journal of Hydraulic Engineering, 2013, 139(3): 310–324. DOI:10.1061/(ASCE)HY.1943-7900.0000665 |
| [3] | GONG J, SIMPSON A R, LAMBERT M F, et al. Detection of distributed deterioration in single pipes using transient reflections[J]. Journal of Pipeline Systems Engineering & Practice, 2013, 4(1): 32–40. |
| [4] |
郭新蕾, 杨开林. 管道泄漏检测的水力瞬变全频域数学模型[J].
水利学报, 2008, 39(10): 1264–1271.
GUO Xin-lei, YANG Kai-lin. Hydraulic transient model in frequency domain for leak detection in pipeline systems[J]. Journal of Hydraulic Engineering, 2008, 39(10): 1264–1271. DOI:10.3321/j.issn:0559-9350.2008.10.016 |
| [5] | WU Z Y, BURROWS R, MOORCROFT J, et al. Pressure-dependent leakage detection method compared with conventional techniques[C]//Conference on Water Distribution Systems Analysis.[S. l.]:[s. n.] 2011:1083-1092. http://ascelibrary.org/doi/abs/10.1061/41203(425)98 |
| [6] |
刘书明, 王欢欢, 徐锦华, 等. 基于智能优化算法的供水管网漏水点定位[J].
同济大学学报:自然科学版, 2014, 42(5): 740–744.
LIU Shu-ming, WANG Huan-huan, XU Jin-hua, et al. Identification of leakage location based on modern optimization algorithms[J]. Journal of TONGJI University:Natural Science, 2014, 42(5): 740–744. |
| [7] |
程伟平, 赵丹丹, 许刚, 等. 供水管网爆管水力学模型与爆管定位[J].
浙江大学学报:工学版, 2013, 47(6): 1057–1062.
CHENG Wei-ping, ZHAO Dan-dan, XU Gang, et al. Pipe burst hydraulic model of water distribution system and pipe burst location[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(6): 1057–1062. |
| [8] |
李稳, 崔建国, 毛立波. 供水管网压力异常工况下的趋势面分析模型及应用[J].
节水灌溉, 2011(8): 47–50.
LI Wen, CUI Jiun-guo, MAO Li-bo. Study on trend-surface analysis model under abnormal pressure condition in water-supply pipe network and its application[J]. Water Saving Irrigation, 2011(8): 47–50. |
| [9] | YE G, FENNER R A. Kalman Filtering of hydraulic measurements for burst detection in water distribution systems[J]. Journal of Pipeline Systems Engineering & Practice, 2011, 2(1): 14–22. |
| [10] | JUNG D, LANSEY K. Water Distribution System burst detection using a nonlinear kalman filter[J]. Journal of water resources planning and management, 2014, 141(5): 1–13. |
| [11] | MOUNCE S R, BOXALL J B, MACHELL J. Development and verification of an online artificial intelligence system for burst detection in water distribution systems[J]. Journal of Water Resources Planning & Management, 2010, 136(3): 309–318. |
| [12] |
黄廷林, 曹梅花, 张卉. 基于SCADA系统给水管网实时检测爆管位置方法的研究[J].
给水排水, 2007, 33(5): 104–108.
HUANG Ting-lin, CAO Mei-hua, ZHANG Hui. Study on SCADA based real-time detection of pipe bursts location of water supply network[J]. Water & Wastewater Engineering, 2007, 33(5): 104–108. |
| [13] | PALAU C V, ARREGUI F J, CARLOS M. Burst detection in water networks using principal component analysis[J]. Journal of Water Resources Planning & Management, 2011, 138(1): 47–54. |
| [14] | ROMANO M, KAPELAN Z, SAVIC D A. Automated detection of pipe bursts and other events in water distribution systems[J]. Journal of Water Resources Planning & Management, 2012, 140(4): 456–467. |
| [15] | ROMANO M. Near real-time detection and approximate location of pipe bursts and other events in water distribution systems[J]. University of Exeter, 2012. |
| [16] |
李楠楠, 郄志红, 古田均. 供水管网爆管故障诊断的PSO-SVM方法[J].
系统工程理论与实践, 2012, 32(9): 2104–2110.
LI Nan-nan, QIE Zhi-hong, GU Tian-jun. PSO-SVM model for pipe bursting diagnosis of water supply network[J]. Systems Engineering-Theory & Practice, 2012, 32(9): 2104–2110. DOI:10.12011/1000-6788(2012)9-2104 |
| [17] | BOGNER K, PAPPENBERGER F. Multiscale error analysis, correction, and predictive uncertainty estimation in a flood forecasting system[J]. Water Resources Research, 2011, 47(7): 1772–1780. |
| [18] | DONOHO D L, JOHNSTONE I M. Adapting to unknown smoothness via wavelet shrinkage[J]. Journal of the American Statistical Association, 1995, 90(432): 1200–1224. DOI:10.1080/01621459.1995.10476626 |
| [19] |
齐培艳, 段西发, 田铮. 基于小波的非参数回归模型均值变点的Bootstrap监测[J].
系统工程理论与实践, 2014, 34(10): 2650–2655.
QI Pei-yan, DUAN Xi-fu, TIAN Zheng. Bootstrap monitoring for mean change of nonparametric regression models by wavelets[J]. Systems Engineering-Theory & Practice, 2014, 34(10): 2650–2655. DOI:10.12011/1000-6788(2014)10-2650 |
| [20] | SOUTO M, MOREIRA A, VEIGA A, et al. A high-dimensional VARX model to simulate monthly renewable energy supply[C]//Power Systems Computation Conference. Wroclaw Poland:IEEE, 2015:1-7. http://ieeexplore.ieee.org/document/7038460/ |
| [21] | DAN K, KING K. Methods for evaluating water distribution network early warning systems[J]. Journal(American Water Works Association), 2010, 102(1): 79–89. |
| [22] | PANGULURI S, GRAYMAN W M, CLARK R M. Water distribution system and analysis:field studies, modeling and management[EB/OL]. http://www.uky.edu/WDST/PDFs/[53]%20Water%20Distribution%20Systems%20Analysis%20-%20Field%20Studies%20Modeling%20and%20Management.pdf.2005-12-01/2016-09-16. |


