需求-容量分析的概念是使用服务水平(LOS)标准从需求和供给方面来评价系统性能[1].FAA和TRB在1985年联合研究了机场陆侧容量的测量方法, 发现机场陆侧容量评估没有标准的定义和程序[2-4].Parizi等[5]使用时空理论, 提出了动态容量模型, 该模型可以计算机场登机路边区域动态车辆容量. Passos等[6]对2个车道边场景进行建模, 测量了旅客的总等待时间, 以此来评估场景的性能.现有容量模型和通行能力计算方法忽略了送站坪不同车道的速度差异性以及落客车道的车辆行走情况, 使得模型或计算方法会高估送站坪的容量.目前, 我国交通枢纽的送站坪建设往往是依据经验确定[7-9], 随着国内枢纽旅客数量的不断增长, 原有规划和设计的容量不能够满足旅客增长的需求, 许多枢纽接入道路出现严重拥堵, 特别是枢纽送站坪的路边区域出现各种运营问题, 开展送站坪通行能力研究对于解决枢纽接入道路的交通拥堵问题有重要的意义.本文基于车辆轨迹信息, 统计分析送站坪交通特性, 在此基础上研究适用于送站坪的通行能力计算方法, 并对该计算方法进行实例验证.
1 送站坪系统概述在许多大型综合客运枢纽(高铁站、机场等), 为了实现枢纽客流的快速集散, 通常使用高架桥将客运枢纽站房与外围快速路系统衔接起来, 而在高架桥与枢纽站房的结合部, 出发客流下车进入枢纽站房的区域就称为送站坪, 通俗的解释, 送站坪就是枢纽供车辆落客的平台设施[10].
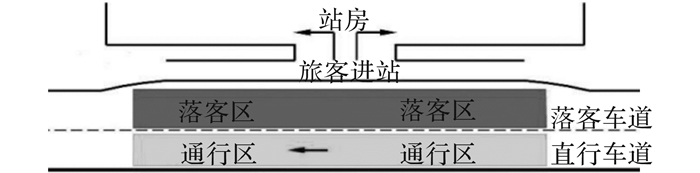
一般枢纽的送站坪都包括若干落客通道, 每个落客通道包含1条落客车道和1条行车道, 并且有的送站坪在不同落客通道之间有安全岛隔离, 安全岛与站房路边有人行横道相连.机场和火车站的送站坪也存在很大的不同, 一般机场送站坪都有4条车道组成, 靠近站房路边的最内侧车道是落客车道, 而外侧的3条车道都是行车道, 这种布局导致了很多2次停车和3次停车情况的发生, 主要原因是很多车辆在外侧车道等待换入内侧车道;由于国外火车站很少有送站坪, 所以国外研究大多集中于机场出发和到达路边, 而火车站送站坪的研究主要集中在国内, 实际调查发现, 火车站和机场的送站坪存在很大的不同, 最主要的区别就是进站入口的设置, 机场的进站口一般根据航空公司进行排列分布, 有多个进站口, 而火车站的进站口一般只有1个, 但会根据实际情况用物理隔离栏进行分流, 比如运用栏杆进行隔离, 人为的制造2个开口.并且火车站的送站坪一般都是有若干落客通道组成的, 1条落客通道包含1条行车道和1条落客车道.2车道的送站坪落客通道如图 1所示, 理论上行车道供车辆行进, 而落客车道则供车辆停车落客.
|
图 1 2车道送站坪示意图 Fig. 1 Schematic diagram of two-lane passenger drop-off area |
受场地的限制, 送站坪路边部分都较为拥挤, 特别是高峰期间, 来往旅客较多, 不便于在路边架设摄像机来进行拍摄.通过实地考察, 考虑利用现有路侧条件, 在尽量不影响车辆和行人的条件下, 采用“伸缩杆件+微型摄像机”的方式来进行拍摄.由于送站坪的交通行为与传统道路存在较大差异, 为了更好的理解送站坪交通流特性和车辆驾驶行为, 需要通过大量的交通流数据和车辆行驶信息来进行统计分析.车辆行驶信息包括了换道行为、停车行为和加减速等, 如果采用一般的统计计数方法很难区分这么细微的车辆操作行为, 为了获取较为精准的统计数据, 采用提取车辆行驶轨迹的方法, 通过轨迹分析开展本文的研究.
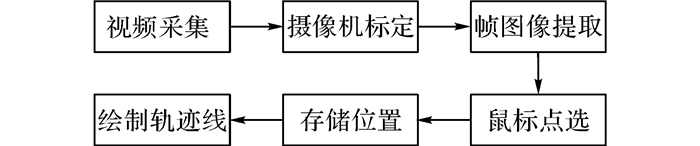
车辆轨迹线是车辆在一段时间内的活动路径, 通常使用的车辆轨迹线采集方法是时间间隔摄影, 视频捕捉和GPS定位等[11], 根据送站坪现场调查的实际情况, 综合效率、精度和成本的考虑, 采用鼠标点选后期处理视频的方案来提取车辆运动轨迹, 数据采集和处理流程见图 2.
|
图 2 数据采集流程图 Fig. 2 Flow chart of data collection |
研究方法是:
1) 根据送站坪实地考察情况, 在尽量不影响的交通的前提下, 充分利用现有路边条件, 在落客通道的路侧栏杆上固定伸缩杆件, 然后架设摄像机, 为了提高点选精准度, 在200 m长度上布设3台摄像机, 通过拍摄获取送站坪原始视频数据;
2) 使用C++编制了车辆轨迹提取软件对视频进行处理, 每1 s提取1帧图像(按照驾驶员反应时间1 s确定的), 根据摄像机标定原理, 建立图像像素点坐标和现实世界坐标的关系.
3) 鼠标点选图像上的目标车辆位置, 存储位置信息, 通过对序列图像的操作, 可以得到一系列点形成的车辆运动轨迹.
4) 通过计算机仿真, 在合适位置设置虚拟线圈, 统计送站坪流量、速度和密度等信息.
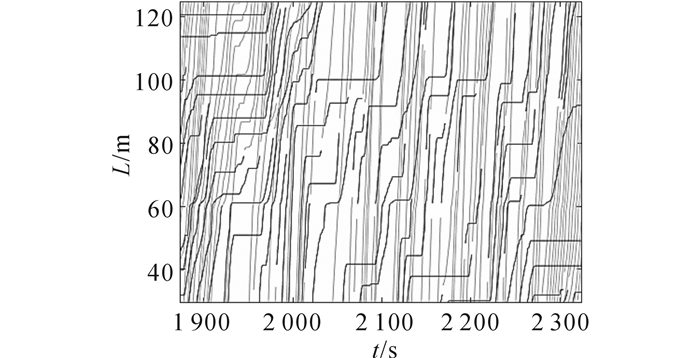
车辆轨迹提取的效果如图 3所示, 横坐标t为示时间轴, 纵坐标L为空间轴, 其中深色轨迹线代表落客车道车辆的行驶轨迹, 而浅色轨迹线代表行车道车辆的行驶轨迹.
|
图 3 车辆时空轨迹图 Fig. 3 Time-space trajectory of vehicles |
对南京火车站、南京南站和南京禄口机场的送站坪进行调查, 发现3个枢纽站点的送站坪在道路交通流较小时能够为旅客提供方便的进站服务, 但在交通量较大时, 车辆的驶入、驶出往往由于小的干扰而引起整个交通流大的波动, 造成交通堵塞.另外, 3个枢纽的送站坪都存在交通组织和管理制度不完善的地方, 很大程度上降低了送站坪的整体服务水平.
本文主要对高峰期间送站坪的交通流进行调查, 分析了送站坪车辆的落客时间分布、车辆车头时距分布以及换道位置和落客位置的偏好, 以及高峰期间送站坪的流量、速度和密度三者之间的关系.
3.1 落客用时分布落客用时以车辆进入停车位停车与车辆完成落客再次启动为计时点, 统计700多辆车的落客时长, 平均落客时长为30 s, 最短落客时长3 s, 短时落客多发生在出租车落客并且乘客没有大量行李的情况下, 最长落客时长775 s, 该情况主要是社会私人车辆落客完成后继续停留在停车位, 车辆未驶离的主要原因是等候旅客上车, 在700多辆车辆中, 停车时间超过100 s的车辆占比不足1%.多人下车与单人下车的人均落客用时差异性不明显, 影响落客时长的主要因素是旅客携带行李的数量, 旅客行李越多, 落客停车时间越长, 反之落客停车时间越短.影响落客时长的另一个主要因素是旅客是否有送行者, 这也是出租车平均落客时长短于私人小汽车的主要原因.
落客时长分布函数的假设检验, 在0.05显著性水平上不能拒绝原假设, 并且测试统计量的值为0.140 8小于接受假设的临界值0.294 1, 因此, 可以认为:车辆落客用时近似服从负指数分布.落客时长的频数直方图如图 4所示, 图中f为频率.

|
图 4 送站坪落客时长的频数直方图 Fig. 4 Frequency of drop-off time histogram |
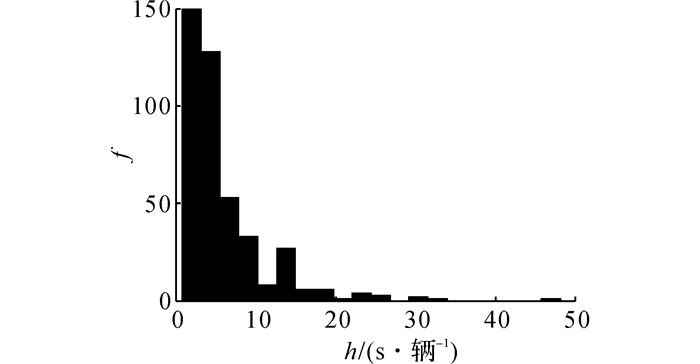
车头时距分布和车辆的到达分布存在一定的对应关系, 车头时距分布为送站坪通行能力分析、交通管理和几何设计等进一步的研究提供分析基础[12].随机抽取南京南站高峰小时送站坪落客区的400多辆车的车头时距数据, 通过假设检验, 送站坪高峰小时的车辆的车头时距近似服从负指数分布.车头时距的频数直方图如图 5所示, 图中h为车头时距.
|
图 5 送站坪入口处车头时距的频数直方图 Fig. 5 Frequency of headway histogram |
车辆到达车头时距分布与客运枢纽时刻表有关, 一般旅客会根据时刻表信息提前到达枢纽, 在列车或飞机出发高峰期, 平均车头时距会小于其他时段.简单的使用不同流量下车头时距分布的历史数据不能准确表示当前车辆到达模式, 收集的车辆到达信息通常是列车或航班运营、送站坪区域交通控制和运营以及一些其他可能因素共同作用的结果, 很难辨别收集到的车辆到达信息是否受特定因素的影响, 并且到达枢纽的交通方式不仅包含车辆, 还包括地铁等大运量交通工具, 这就进一步加大了研究难度, 考虑到技术和预算限制, 到达车头时距分布与列车或飞机调度计划之间的关系在此不做深入研究.
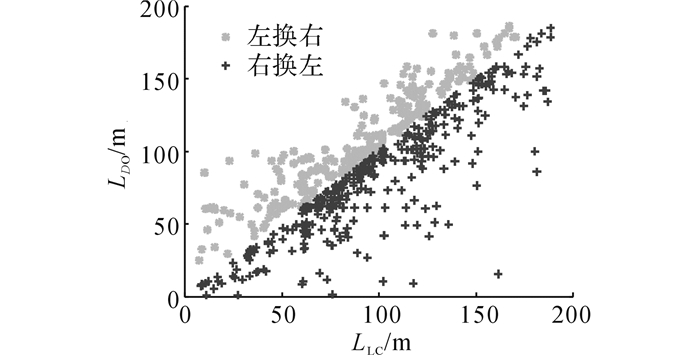
3.3 换道位置和落客位置的差异性调查发现, 有落客需求的车辆在到达理想停车位之前均需要在落客车道上行驶若干距离, 并且完成落客后也会在落客车道上行驶若干距离然后才进行换道, 离开送站坪.图 6显示了换道位置和落客位置的关系, 横坐标LLC表示换道时刻车辆已经行驶的距离长度, 纵坐标LDO表示落客时刻车辆已经行驶的距离长度, 符号“+”和“*”表示换道位置和落客位置的对应点.
|
图 6 换道位置和落客位置的关系 Fig. 6 Relationship between lane-change position and drop-off position |
如果车辆的换道位置就是车辆的落客位置, 说明车辆在换道后立即落客, 未在落客车道上行驶, 则换道位置和落客位置的对应点将落在直线y=x上, 若换道位置和落客位置的对应点落在直线的上方, 说明落客位置要比换道位置靠前;若换道位置和落客位置的对应点落在直线的下方, 说明换道位置比落客位置靠后.图 6中, 车辆从行车道换道至落客车道的换道位置比落客位置提前若干距离, 其平均值为17 m;车辆完成落客后从落客车道换道至行车道的换道位置比落客位置滞后若干距离, 其平均差值为13 m.
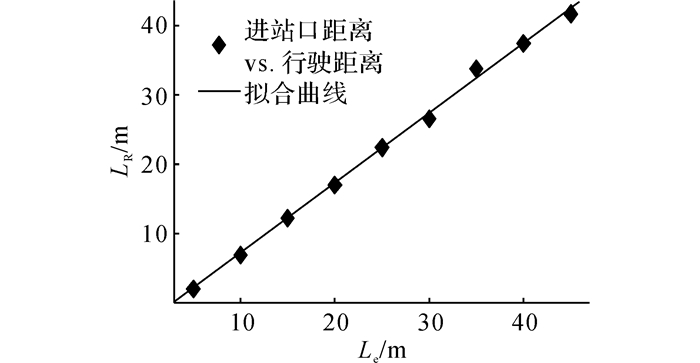
车辆在落客车道的行驶距离和送站坪车流量的大小有关, 当流量较小时, 车辆随流量的增大在落客车道上的行驶距离变长, 流量增大到一定程度后, 车辆在落客车道上的行驶距离会减小.车辆落客前后换道位置距离差值亦同进站口的位置有关, 距离进站口近的位置停车, 平均距离差值较小.车辆落客时距最近进站口的距离Le和落客车道上行驶距离LR的关系图如图 7所示.
|
图 7 落客车道行驶距离和进站口相对位置的关系 Fig. 7 Relationship between driving distance in drop-off lane and the relative position of the entrance |
送站坪行车道的平均行驶速度为15 km/h, 最大速度为33 km/h, 落客车道的平均行驶速度为3 km/h, 最大速度为12 km/h.送站坪2个车道的速度存在较大的差异, 虽然落客车道的速度较低, 但区别于车辆静止, 几乎所有车辆均会在停车位停车落客前行驶若干距离, 直接换道落客并直接换出离开的车辆是不存在的.
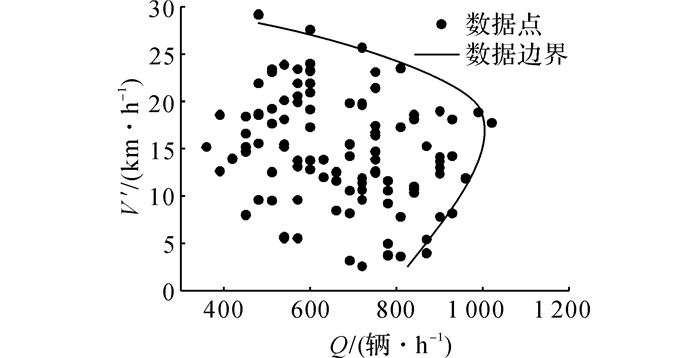
如图 8所示为平均行驶速度V′和流量Q的对应关系, 流量变化在一定范围, 最大流量约为1 020辆/h, 该值反映了送站坪的实际通行能力[13].理论上流量和速度的关系:当流量较少时, 速度较大, 随着流量的增大速度在降低, 当流量增大到一定程度, 流量呈现减少的趋势, 这时速度随流量的减少而减少.图中流量和速度的对应点并非严格按照上述情况进行变化, 只有边界点满足上述变化趋势, 可能是因为送站坪系统是慢速交通系统, 所有车辆的速度均处在一个较低的水平, 车辆进入送站坪需要停车落客, 有寻找停车位的过程, 影响其速度大小的因素是多样的复杂的.可以预见, 送站坪不同部位的速度也存在差异性.
|
图 8 速度和流量的关系 Fig. 8 Relationship between velocity and flow |
通过在送站坪入口处设置虚拟线圈的方法来获得线圈的时间占有率, 时间占有率和密度成正比, 从占有率和流量的关系可得到密度和流量的关系.如图 9所示为占有率和流量的关系, 图中φ为时间占有率, 单位:s/h.随着占有率的增加, 流量增加, 但流量增大到一定程度时, 流量有下降趋势, 这时占有率增加, 流量反而下降.从图 9中可以得到流量的最大值, 即送站坪的实际通行能力.

|
图 9 占有率和流量的关系 Fig. 9 Relationship between occupancy and flow |
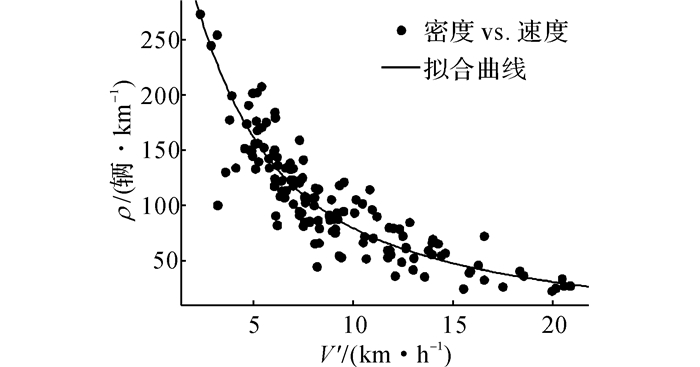
送站坪车辆的速度和密度参数呈现了较好的对应关系:随着速度的增加, 密度呈减小趋势.如10所示为送站坪平均行驶速度和密度ρ的关系.
|
图 10 速度和密度的关系 Fig. 10 Relationship between velocity and density |
本文的研究借鉴了Passos模型的思路, 测量车辆的等待时间和行驶时间, 参照调查情况对Parizi动态容量模型进行了改进, 改进模型考虑了车辆在落客车道上的行驶距离以及行车道和落客车道的速度差异, 使其更加符合实际.
首先做以下假设:
1) 车辆在落客车道上行驶, 并且落客车道上的行驶速度与行车道的车辆行驶速度存在较大差异.
2) 车辆在落客前和完成落客后均要在落客车道上行驶若干距离.
3) 车辆的影响长度和服务时间是固定的.
4) 送站坪是两车道布局.
动态容量的定义为送站坪系统在1个小时周期内能处理的最大车流量.假设1个到达车辆从入口匝道以平均速度vL进入送站坪行车道, 在行车道行走若干时间后换道至落客车道(行驶时间如图 11中的tL1所示), 并在行车道以vR的速度前进, 直到到达停车位(行驶时间如图 11中的tR1所示), 完成停车落客(服务时间tDO), 然后再在落客车道行驶后换道至行车道, 最后离开送站坪.最大流量发生在所有停车位都具有相同使用程度时, 即所有车辆可以在路边的任何部分落客, 并且驾驶员对所有停车位都具有相同的偏好.图 11显示了落客车辆时空轨迹, tR2表示车辆落客完成后在落客车道上的行驶时间, tL2表示车辆从落客车道换道至行车道后在行车道上行驶时间, D则表示延误, 加粗的折线表示车辆在落客车道上的行驶轨迹.
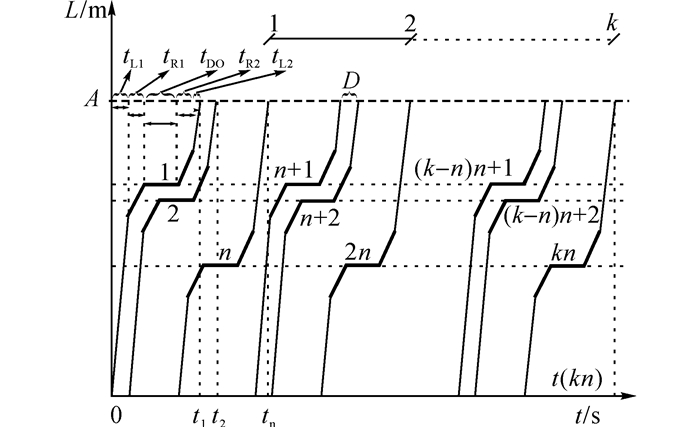
|
图 11 落客车辆时空轨迹示意图 Fig. 11 Time-space trajectory sketch of drop-offvehicles |
车辆在选择车位落客时均会在落客车道上行驶若干车位然后落客, 并不会在最近的停车位落客, 即使进站入口附近的停车位也需要3个车位的移动, 行驶到期望落客车位需要移动2个车位左右的距离, 而在落客完成后则需要行驶1个车位的距离再次换道离开, 送站坪入口处换道进入落客车道的车辆在落客前行驶的距离最长.假设当停车位置固定时, 第1辆落客车辆需要在第1个停车位落客(其他车辆依次进入剩余连续车位进行落客), 这时该车辆落客完成后不会在落客车道上行驶若干距离, 但在落客前该车辆在落客车道上行驶的距离最长.依次类推, 欲占最后1个空车位的车辆, 在落客前不会在落客车道上行驶, 仅在落客完成后在落客车道上行驶较长一段距离.这里假设车辆在落客车道上行驶的距离相同, 该距离为车辆在落客车道上的行驶的期望距离LR(换进17 m, 换出13 m, 共30 m), 包括落客前和落客后在落客车道上的行驶距离.车辆的系统时间为服务时间(即落客时长tDO)加上行驶时间(图 11中的tL1、tR1、tR2和tL2之和), 然后加上延误(图 11中的D), 假设系统中有n个车位, 这时, 车辆从系统中退出时间为
| $ {t_n} = {t_{{\rm{DO}}}} + \frac{{L-{L_{\rm{R}}}}}{{{v_{\rm{L}}}}} + \frac{{{L_{\rm{R}}}}}{{{v_{\rm{R}}}}} + n\frac{{{L_{\rm{V}}}}}{{{v_{\rm{R}}}}}. $ | (1) |
式中:tn为第n辆车退出时间;L为送站坪落客通道长度;LR为落客车道行驶距离;LV为平均车辆影响长度.
式(1)中(L-LR)/vL+LR/vR部分表示行进时间, 而LV/vR则表示图 11中的延误.定义服务周期为系统被占有(装满)和排空的时间次数.故连续到达第2个系列车辆后(继n辆车之后的第2个服务周期, 第2个系列可理解为送站坪所有车位均被占用并排空后, 第2批进入的车辆再次占用车位并排空的过程)和第3个系列车辆到达之前, 车辆的退出时间为
| $ {t_{n + 1}} = {t_n} + {t_{{\rm{DO}}}} + \frac{{{L_{\rm{V}}}}}{{{v_{\rm{R}}}}}. $ | (2) |
| $ {t_{n + 2}} = {t_{n + 1}} + \frac{{{L_{\rm{V}}}}}{{{v_{\rm{R}}}}}. $ | (3) |
| $ {t_{2n}} = 2{t_{{\rm{DO}}}} + \frac{{L-{L_{\rm{R}}}}}{{{v_{\rm{L}}}}} + \frac{{{L_{\rm{R}}}}}{{{v_{\rm{R}}}}} + 2n\frac{{{L_{\rm{V}}}}}{{{v_{\rm{R}}}}}. $ | (4) |
第1个服务周期车辆退出时间与第2个周期车辆退出时间的差值是平均服务时间加上延误的累计值.继续上述过程直到最后1个服务周期结束, 第n辆车在第k个周期退出时间如下:
| $ {t_{kn}} = k{t_{{\rm{DO}}}} + \frac{{L-{L_{\rm{R}}}}}{{{v_{\rm{L}}}}} + \frac{{{L_{\rm{R}}}}}{{{v_{\rm{R}}}}} + kn\frac{{{L_{\rm{V}}}}}{{{v_{\rm{R}}}}}. $ | (5) |
式中:k为在时间周期T内路边占有和排空的周期次数, 则服务周期数k为
| $ k = \frac{{T-\frac{{L-{L_{\rm{R}}}}}{{{v_{\rm{L}}}}}-\frac{{{L_{\rm{R}}}}}{{{v_{\rm{R}}}}}}}{{{t_{{\rm{DO}}}} + n\frac{{{L_{\rm{V}}}}}{{{v_{\rm{R}}}}}}}. $ | (6) |
那么n个车位在时间周期T内可以处理的车辆总数为
| $ C = \frac{{n\left( {T-\frac{{L-{L_{\rm{R}}}}}{{{v_{\rm{L}}}}}-\frac{{{L_{\rm{R}}}}}{{{v_{\rm{R}}}}}} \right)}}{{{t_{{\rm{DO}}}} + n\frac{{{L_{\rm{V}}}}}{{{v_{\rm{R}}}}}}}. $ | (7) |
式中:C为理想情况下(即无车位偏好)在时间周期T内的最大动态容量.
公式(7)假设了车辆落客时对车位没有偏好, 这种假设不符合实际情况, 故称之为理想容量, 如果调整驾驶员行为, 理想容量就是实际容量.为计算实际容量, 考虑车位的选择以及进站口的权重关系, Parizi和Braaksma给出了相应的计算公式[12]为
| $ {f_x} = C_n^x{p^x}{\left( {1-p} \right)^{n-x}}, x = 0, 1, 2, 3, \cdots, n. $ | (8) |
式中:fx为送站坪第x个停车位的交通分配百分比, p表示进站口位置与送站坪总长度的比例.该二项分布表达了进站口附近停车位的利用程度, 越靠近进站口的停车位, 利用率越高.
| $ {w_y} = C_m^y{q^y}{\left( {1-q} \right)^{m-y}} + \frac{{{{\left( {1-q} \right)}^m}}}{m}, y = 1, \cdots, m. $ | (9) |
式中:wy为第y个进站口附近的交通分配百分比, y为进站口编号, m为进站口总数, q表示第1个进站口相对进站口总数的位置, 即q=1/m.该修改的二项分布确保了权重函数是递减的, 即第1个进站口的权重总是最大的, 这与实际情况相符.fx和wy的乘积是所有车位相对于整个送站坪的交通分配比, 若百分比大于0.01, 说明该车位是有效停车位.
根据车位的交通分配比例fx以及入口附近交通分配百分比wy可以计算出有效的车位数量Neff, 用有效车位Neff替换公式(7)中的参数n即可得送站坪的实际通行能力.
公式(7)在实际应用中, 可以根据客运枢纽管理部门提供的速度上限进行计算, 送站坪落客区域的速度限制通常介于15 km/h到40 km/h [14], 行车道速度可以参考速度限制值, 落客车道速度最大值一般为行车道速度的1/3, 对于枢纽送站坪车辆落客时长的统计, 已经有学者对不同枢纽送站坪进行了相关分析研究[1, 15-16], 并且一般落客时长规定不能超过3 min.图 7中, 车辆在落客车道上的行驶距离与进站口的位置呈线性关系, 车辆落客位置与进站口的距离范围是0~LE, 其中LE表示车辆在距离进站口最远的位置落客, 该参数在现实中易获得, 车辆在落客车道上的行驶距离:
| $ {L_{\rm{R}}} = \frac{{1.007{L_{\rm{E}}}-2.959}}{2}. $ | (10) |
运用parizi模型和本文修改的模型分别对南京南站(最外侧两车道)、南京站(最内侧两车道)和禄口机场(最内侧两车道)的送站坪通行能力进行计算, 具体参数和计算结果如表 1所示, 变量R1~R4分别表示实地观测交通量、Parizi模型计算值、本文模型计算值和历史数据, 3个站点的实地观测时间分别为18:00~19:00, 13:00~14:00, 15:00~16:00.结果表明, 本模型计算结果更接近实际通行能力.
| 表 1 3个枢纽调查情况和计算结果 Table 1 Investigation of three hubs and calculated results |
表 1中parizi模型和本文模型对应的计算结果都是基于现场调查数据进行计算的, 例如, 车辆在落客车道上的行驶距离LR采用的是统计数据30 m, 并非式(10)的计算结果.现实应用中, 模型参数往往根据经验数据和政策规定来获得, 其中落客时间tDO可根据文献资料的历史数据, vL和vR则根据枢纽送站坪的速度限制V, 而LR根据公式(10)计算获得.经计算可知, 3个送站坪的历史和经验数据的计算结果(见表 1变量R4)与本文模型计算结果相近似.使用经验数据计算的南京站的通行能力计算结果偏小, 其主要原因是南京站的速度限制较小.
5 结语因为新建或扩大枢纽的交通设施都需要大量的资金支出, 设计这些设施时应该尽可能考虑真实的交通状况, 避免忽略关键的交通行为而造成成本低估或过度规划.本文通过对送站坪交通流调查分析了送站坪落客车道行车行为的普遍性, 对动态容量模型进行了改进, 最后对南京南站送站坪的通行能力进行了估算, 并与实际容量数据进行了对比, 结果表明, 该方法能够较为精确地估计送站坪的通行能力.在实际应用中, 可以根据历史数据、经验数据或枢纽送站坪的政策规定来估计速度、服务时间等数据, 然后根据公式进行计算.本论文的研究可为送站坪的规划设计、组织管理和评价分析提供了理论和数据支撑.
| [1] | TRB. Highway capacity manual (HCM 2010)[R]. Washington, D C:Transportation Research Board, National Research Council, 2010. http://www.trb.org/Main/Blurbs/164718.aspx |
| [2] | TRB. Measuring airport landside capacity[R]. Special Report 215, Washington, D C:Transportation Research Board, National Research Council, 1987. https://trid.trb.org/view.aspx?id=302089 |
| [3] | LEMER A C. Measuring airport landside capacity[C]//Transportation Research Record 1199. Washington, D C:Transportation Research Board, National Research Council, 1988:12-18. https://www.nap.edu/catalog/11361/measuring-airport-landside-capacity-special-report-215 |
| [4] | MUMAYIZ S A. Evaluating Performance and Service Measures for the Airport Landside[C]//Transportation Research Record 1296. Washington, D C:Transportation Research Board, National Research Co-uncil, 1991:23-30. https://trid.trb.org/view/359092 |
| [5] | PARIZI M S, BRAAKSMA J P. Optimum design of airport enplaning curbside areas[J]. Journal of Transportation Engineering-ASCE, 1994, 120(4): 536–551. DOI:10.1061/(ASCE)0733-947X(1994)120:4(536) |
| [6] | PASSOS L S, KOKKINOGENIS Z, ROSSETTI RJ F, et al. Multi-resolution simulation of taxi services on airport terminal's curbside[C]//16th International IEEE Conference on Intelligent Transportation Systems (ITSC). The Hague, Netherlands:Institute of Electrical and Electronics Engineers (IEEE), 2013:2361-2366. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6728580 |
| [7] |
GB 50226-2007. 铁路旅客车站建筑设计规范[S]. 北京: 中国计划出版社, 2012.
GB 50226-2007. The design specification of railway passenger station buildings[S]. Beijing:China Planning Press, 2012. http://www.doc88.com/p-233797435390.html |
| [8] |
GB 50091-2006. 铁路车站及枢纽设计规范[S]. 北京: 中国标准出版社, 2006.
GB 50091-2006. Railway station and terminals design specifications[S]. Beijing:China Standards Press, 2006. http://d.wanfangdata.com.cn/Standard/GB%2050091-2006 |
| [9] |
JG 105-2008. 民用机场工程项目建设标准[S]. 北京: 中国民航出版社, 2008.
JG 105-2008. Civil airport project construction standards[S]. Beijing:China civil aviation Press, 2008. |
| [10] |
李旭宏, 唐怀海, 吴炼, 等. 综合客运枢纽车道边通行能力分析[J].
公路交通科技, 2009, 26(4): 128–132.
LI Xu-hong, TANG Huai-hai, WU Lian, et al. Study on curbside capacity of comprehensive passenger transportation terminal[J]. Journal of Highway and Transportation Research and Development, 2009, 26(4): 128–132. |
| [11] |
吕剑, 史其信, 杨新苗. 基于运动轨迹采集的混合交通特性研究[J].
武汉理工大学学报:交通科学与工程版, 2009, 33(1): 1–4.
LÜ Jian, SHI Qi-xin, YANG Xin-miao. Research of mixed traffic based on trajectories capture[J]. Journal of Wuhan University of Technology:TransportationScience & Engineering, 2009, 33(1): 1–4. |
| [12] |
刘灿齐, 周溪召. 一些常用的车头时距分布所对应的到达分布[J].
公路交通科技, 1995, 12(3): 53–59.
LIU Can-qi, ZHOU Xi-zhao. The arrival distribution corresponded by some common headway distributions[J]. Journal of Highway and Transportation Research and Development, 1995, 12(3): 53–59. |
| [13] |
李秀文, 荣建, 刘小明, 等. 快速路分、合流影响区交通特性及通行能力研究[J].
公路交通科技, 2006, 23(1): 101–104.
LI Xiu-wen, RONG Jian, LIU Xiao-ming, et al. Analysis of traffic flow characteristics and capacities of diverging and merging influence areas[J]. Journal of Highway and Transportation Research and Development, 2006, 23(1): 101–104. |
| [14] | CHANG K Y. A simulation model for analyzing airport terminal roadway and traffic and curbside parking[D]. Colloge Park:University of Maryland, 2001. https://www.scribd.com/document/256049667/Airport-Curbside-and-Terminal-Area-Roadway-Operations-ACRP |
| [15] |
张兰芳, 王知, 防守恩. 机场航站楼路边交通容量需求分析[J].
同济大学学报:自然科学版, 2007, 35(4): 486–490.
ZHANG Lan-fang, WANG Zhi, FANG Shou-en. Study on traffic capacity and demand of airport terminal curbside[J]. Journal of Tongji University:Natural Science, 2007, 35(4): 486–490. |
| [16] |
陆迅, 朱金福, 唐小卫. 航站楼车道边容量评估与优化[J].
哈尔滨工业大学学报, 2009, 41(9): 96–99.
LU Xun, ZHU Jin-fu, TANG Xiao-wei. Capacity assessment and optimization of terminal curbside[J]. Journal of Harbin Institute of Technology, 2009, 41(9): 96–99. |



