丁坝是河流和海岸工程的常见构筑物, 主要用于保护河海岸免遭侵蚀, 改善航道水深条件以维护通航.丁坝会显著改变所处位置附近的水体运动, 引起强三维流动, 造成坝头处较深的局部冲刷坑, 影响坝基稳定和工程安危, 冲刷深度是丁坝设计的重要参数.
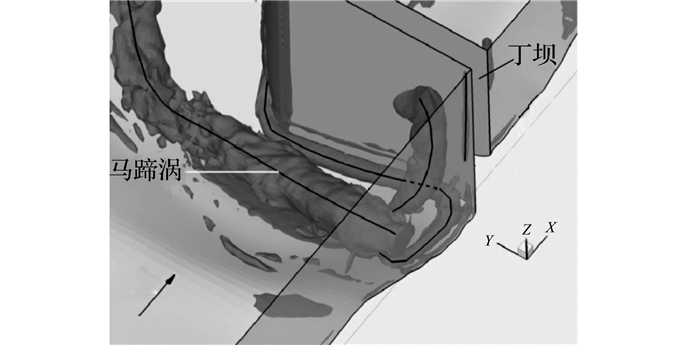
水动力条件和冲刷计算模型是丁坝研究的2个主要方面.水动力条件以丁坝周围马蹄涡系或整体流速场为研究对象.早期马蹄涡系发现于桥墩周围, 后来发现丁坝周围也存在马蹄涡系, 许多在桥墩周围流动研究中的有益成果被借鉴到丁坝周围流动的研究中来.烟气法、染料法、荧光粉法、PIV等[1-3]流动显示方法及数值模拟被用于三维马蹄涡系的视觉呈现.多普勒、ADV等[4-6]仪器广泛用于三维流速测量, 进而分析时均流动状态.
冲刷计算模型可分为经验方法和半经验模型.因不明确丁坝周围流动或因三维流动过于复杂, 直至现在仍有很多研究者采用经验方法[7-9].半经验方法有流量束窄法[10-11], 下降流法[12], 涡量法和切应力法[8]等.
虽然不同学者提出的丁坝局部冲刷模型和计算公式大为不同, 但多数公式最终可归纳为一种形式, 即以正挑矩形丁坝在均匀沙床面清水冲刷情况下的局部冲刷深度为基础值, 其他情况下的局部冲刷深度通过对基础值进行水流强度、岸坡、坝型、含沙浓度、挑角和泥沙级配等方面的修正而得到.
本文通过对各种非淹没直立正挑矩形丁坝三维流场的实验数据和可视化研究成果分析后发现:1)水流遇到丁坝后的流动在时均状态下存在明确的不同流动组成部分, 马蹄涡间存在明显的强弱, 可用于简化流动状态;2)坝头处床面附近流速的3个分量中, 横向(坝根向坝头方向)流速占优, 由于切应力与横向流速的平方成正比, 可知坝头处横向切应力对局部冲刷起着重要作用, 但目前尚无研究者明确指出横向切应力的作用并运用于局部冲刷计算.
本文以非淹没正挑矩形丁坝为对象, 分析丁坝周围流动的马蹄涡系图像, 建立考虑横向流速作用的局部冲刷深度的半经验公式.
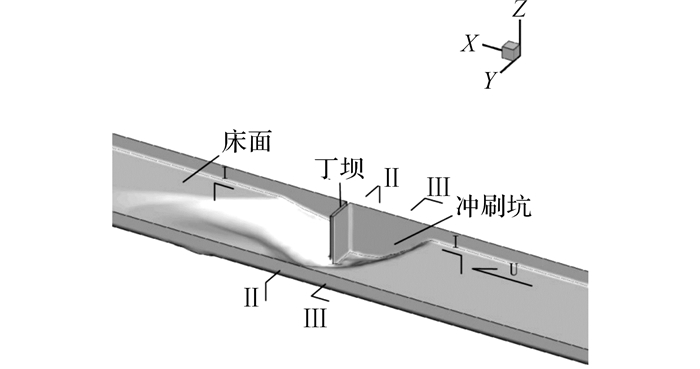
1 物理原型本文以非淹没丁坝周围流动情况作为研究对象:正挑矩形丁坝位于矩形槽内, 槽底铺设均匀沙, 远处行进水流平均流速U, 且U小于槽底泥沙的起动流速(见图 1).行进水流遇到丁坝后, 流动主要分为2个趋势, 表层流体上涌绕过丁坝向下游流动, 另一部分流体向下运动形成马蹄涡系.流动造成坝头处形成较大冲刷坑(见图 2).本文采用统一坐标系, 行进水流方向为x, 即纵向;丁坝坝根指向坝头方向为y, 即横向;按照右手螺旋确定z垂直向上;取未冲刷床面、丁坝及与丁坝相交的侧壁面三平面的交点为坐标原点.
|
图 1 物理模型 Fig. 1 Physical model |
1962年, Schiwind采用烟气法首先研究了层流情况下位于水平底面上的楔形物前的马蹄涡系随雷诺数的变化.随后, Kwan等[1-3, 13-14]采用各种流动显示方法进一步加大加深了对马蹄涡系的探究:从层流扩展到紊流, 从楔形物扩展到圆柱、方体, 障碍物从设置在正中间扩展到位于侧壁, 装置底部由水平面扩展到存在冲刷坑.这一系列的研究结果可以归纳出与本文有关的几点:a)在层流情况下, 随着雷诺数Re的增大, 主涡个数增加, 但目前最多发现为3个, Re数再增大时, 主涡间会出现自我合并;b)在紊流情况下, 床面附近主涡为1~3个, 但在冲刷过程中随冲刷坑的增大, 主涡数量减少;c)当只有2个主涡时, N2明显弱于N1(离障碍物最近的主涡编号为1, 向上游侧主涡编号逐渐增大), 而当有3个涡时, N3明显弱于N1和N2, 即存在明显的强弱之分.
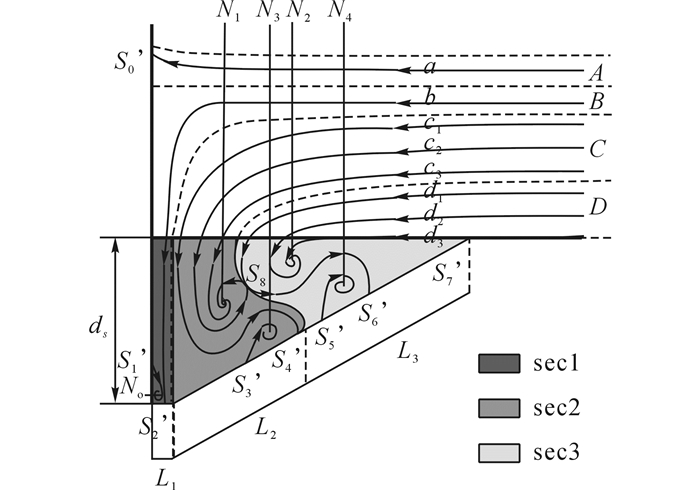
马蹄涡是由源源不断的上部来流、无法穿越的障碍物与足够大的流动动能差转化成的压差造成.当主涡N1形成后, 对于它上游的流体, N1相当于一个新的障碍物.层流在垂向上流速分布为线性, 由于动能与流速的平方成正比, 当Re数增加时, 上游流体能量的增大造成第2个主涡N2形成, 但又由于能量差, N2要弱于N1.等速度再进一步增大时, 主涡N3形成.N2与N3的形成, 分流了一部分原本流向N1的流体, 且由于N2与N3位于上游, 更容易得到流量补给, 造成N2和N3的壮大, N1一定程度的减弱.当流动从层流向紊流过渡, 流速分布由线性向对数分布过渡, N2的能量进一步增大到能够穿透N1的壁垒时, 两涡合并形成新的N1, 如此循环.但为什么目前发现的主涡数量最多只有3个?估计与一个主涡形成所需的能量及一个涡体冲破另一个涡体壁垒所需能量有关, 雷诺数的增大可导致第4个主涡出现, 但同时又使得N1和N2出现合并, 从而造成了主涡个数的稳定.雷诺数越大, N1与N2越容易出现合并, 这就意味着在稳定的紊流条件下, 主涡的个数不多于层流情况下的3个.而存在冲刷坑的情况下, 由于越靠近障碍物冲刷深度越大, 从而相对于其他主涡, N1处于较低位置, 随着冲刷坑深度加大越容易被上游侧的涡体截流合并.从而在考虑存在稳定冲刷坑时的丁坝周围马蹄涡系内的主涡个数时, 本文认为可以采用2个主涡简化(见图 3), N1作用较强, N2相对较弱.图 3中其余3个涡N0为壁涡, N3和N4为副涡, 伴随主涡出现.以此5个涡中心点为结点, 相应流动边界上产生8个半鞍点S0~S7, 流动内部产生1个鞍点S8, 该情况也满足Hunt等[15]提出的结点与鞍点的数量关系要求.
|
图 3 立面I-I拓扑与冲刷坑内流动区域分块 Fig. 3 Topology in vertical profile and flow sections in scour hole |
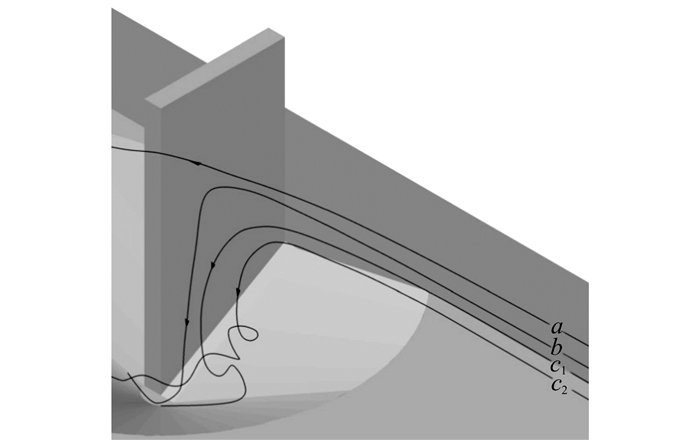
按照马蹄涡系简化流动, 在立面I-I上可将不同高度的行进来流自上而下分成A~D这4个流层, 分别供给马蹄涡系不同部分, 并以a~d表示相应流层的代表迹线.A层流体不参与马蹄涡系, a在流向丁坝过程中上抬, 然后绕过丁坝向下游运动, 在丁坝表面形成半鞍点S0;B层流体主要供给壁涡N0, b在与丁坝作用过程中, 贴壁面斜向下向外运动, 在坝面上和冲刷坑底部形成半鞍点S1和S2;C层流体主要供给主涡N1和副涡N3, c1绕过涡N1向床面运动, 在冲刷坑剖面上形成半鞍点S3和S4, c2和c3缠绕形成主涡N1, 且沿程不断有同层流体加入;D层流体主要供给主涡N2和副涡N4, d1在冲刷坑底部形成半鞍点S5和S6, d2和d3缠绕形成主涡N3, 且在剖面上形成半鞍点S7.由此构成马蹄涡系的三维图像, 图 4给出了三维图像中的部分迹线.
|
图 4 三维流动迹线 Fig. 4 Three dimensional path lines |
B~D层流体分别占据冲刷坑内不同区域sec1~ sec3, 产生了不同的局部冲刷作用.
B层流体因受向外向下的压力梯度作用, 沿丁坝表面斜向下向坝头底部汇聚(见图 5(a)), 流量和流速沿程增大, 在坝头处sec1区域横向流速达到最大, 但因纵向流动区域受限, 纵向流速较小.该层流体在丁坝底部绕过丁坝向下游运动, 从而还存在绕流效应.聚流和绕流作用使坝头处床面最先受到冲刷, 随后受冲刷区域向下游及坝根方向发展.随着冲刷坑加深加大, 因聚流作用增大的横向流速随过水面积的增大而逐渐减小, 降至起动流速时冲刷逐渐停止.绕流作用同样经历逐渐减弱过程, 当冲刷平衡时几可忽略.坝头处B层流体流速尤其是横向流速是影响坝头处冲深的关键因素.
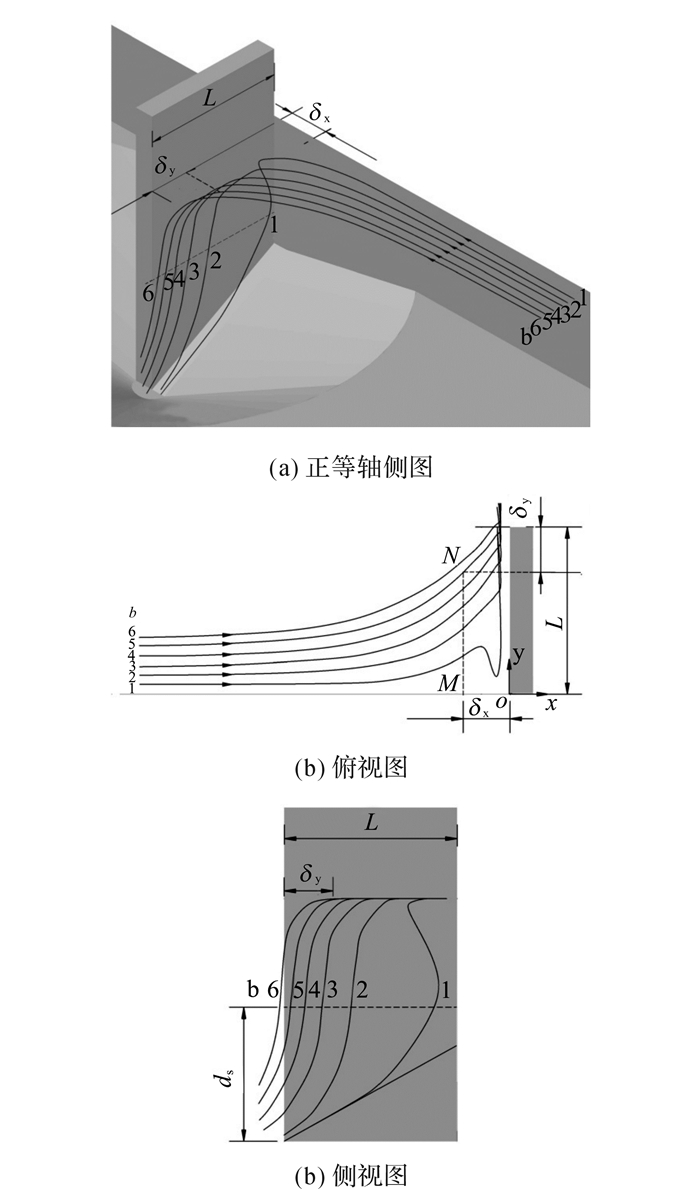
|
图 5 不同视角下的B层流体b1~b6迹线 Fig. 5 Path lines b1~b6 in Layer B viewed from different angles |
C层流体的局部冲刷作用主要体现在冲刷坑坡面上.冲刷初期流速增大, 在sec2区域内近底形成较大的横向和纵向流速.随著冲刷坑进一步增大, 靠近床面的C层流体缓慢减速, 冲刷逐渐停止.
D层流体在sec3区域内近底纵向和横向流速均较小, 冲刷作用较弱.冲刷坑发展过程中, 部分泥沙因水下休止角小于坡面倾角, 沿坡面下滑被水流带走.
各部分流体即是一个整体又有明确分工, 对计算局部冲刷坑深度而言, 下文将重点关注B层流体.
4 最大冲深作用流量由第3部分可知, 坝头最大冲刷深度达到的平衡条件应重点考虑B层流体, 即坝头处B层流体流量可视为最大冲深的作用流量.
B层流体位于流动上层, 除壁面附近外受黏性作用较小, 从而可用势流理论来求解这部分水平面流体的流量.根据镜像理论, 可将丁坝绕流看作是无界流体内的垂直平板绕流(见图 6), 由圆柱绕流的保角变换得到.圆柱绕流的复势函数为
| $ F\left( \xi \right) = {U_0}\left( {\xi + \frac{{r_0^2}}{\xi }} \right) = \phi + {\rm{i}}\varphi . $ | (1) |
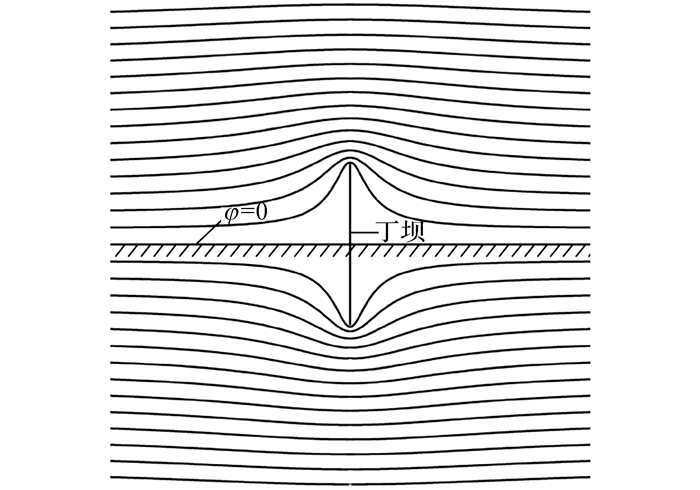
|
图 6 垂直平板绕流流线图 Fig. 6 Flow past vertical flat plate |
式中:ξ为复平面坐标;U0为均匀来流流速;ϕ为势函数;φ为流函数;r0=L/2为圆柱半径;L为坝长.
采用儒可夫斯基变换
| $ Z = \xi + {\left( {{\rm{i}}L/2} \right)^2}/\xi = x + {\rm{i}}y, $ | (2) |
则Z复平面坐标中垂直平板绕流复势为
| $ f\left( Z \right) = \left\{ \begin{array}{l} {U_0}\sqrt {{Z^2} + {L^2}} \;\;\;\;\;\;,x > 0;\\ - {U_0}\sqrt {{Z^2} + {L^2}} \;\;\;\;,x < 0. \end{array} \right. $ | (3) |
从而流函数为
| $ \varphi = {\mathop{\rm Im}\nolimits} \;\;\;\;\left( {f\left( Z \right)} \right). $ | (4) |
式中:Im(*)表示取复函数虚部.取壁面φ=0, 则φ(Z)即为壁面到Z点处的单位厚度过流流量.这种无界流体内的垂直平板绕流是平面流动, 需适当修正才能符合实际三维流动.
B层流体在冲刷坑上部存在很小的垂向流速, 三维迹线b如图 5所示.图 5中第1条迹线b1向右偏转是由于受到指向侧壁的压力梯度的作用.需要指出的是, 由于流体斜向下运动, 通过冲深坑的流体只有b1~b5并不是b1~b6全部(图 5(c)), 对应横向长度为(L-δy).δy是b层进入冲刷坑的流体在考虑向下运动之前能够到达距离丁坝头部最近的y方向距离, 即b5迹线在考虑垂向运动前离坝头部的最近距离.
因丁坝迎流面附近B层流体的垂向流速随与迎流面距离的加大而减小, 设δx为考虑明显垂向作用时该位置与丁坝表面的纵向距离, 即当距离大于δx时流动可视为平面势流, 其流线用公式(4)表示, 从而通过MN段的单位厚度流量为
| $ \varphi \left| {_{x = - {\delta _x},y = L - {\delta _y}}} \right. = {\mathop{\rm Im}\nolimits} \left( { - {U_0}\sqrt {{{\left[ { - {\delta _x} + {\rm{i}}\left( {L - {\delta _y}} \right)} \right]}^2} + {L^2}} } \right). $ | (5) |
δx, δy与L相比为小量, 略去2阶小量δx2、δy2和δxδy得
| $ \begin{array}{*{20}{c}} {\varphi \left| {_{x = {\delta _x},y = L - {\delta _y}}} \right. = \sqrt {2L} {U_0}{\mathop{\rm Im}\nolimits} \left( { - \sqrt {{\delta _y} - {\rm{i}}{\delta _x}} } \right) = }\\ {\sqrt {2L} {U_0}{{\left( {\delta _x^2 + \delta _y^2} \right)}^{1/4}}\sin \left( {0.5\arctan \frac{{{\delta _x}}}{{{\delta _y}}}} \right).} \end{array} $ | (6) |
若设hB为B层流体的垂向厚度, δy=mδx, m为比例系数, 从而B层流体对丁坝局部冲刷起主要作用的流量可表示为
| $ \begin{array}{l} {q_{V,B}} = \varphi \left| {_{x = - {\delta _x},y = L - {\delta _y}}} \right.{h_B} = \\ \sqrt {2L{\delta _x}} {U_B}{h_B}{\left( {1 + {m^2}} \right)^{1/4}}\sin \left( {0.5\arctan {m^{ - 1}}} \right). \end{array} $ | (7) |
式中:UB为B层流体流速.
B层流体对应行进来流中的上层流体, 故UB值与表面流速相当.若采用对数流速分布, 则UB与平均流速U和摩阻流速u*的关系为
| $ {U_B} = U + {u_ * }/\kappa . $ | (8) |
式中:κ为卡门常数.
将式(8)代入(7)可得
| $ \begin{array}{l} {q_{V,B}} = \sqrt 2 {\left( {1 + {m^2}} \right)^{1/4}}\sin \left( {0.5\arctan {m^{ - 1}}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\sqrt {L{\delta _x}} {h_B}\left( {U + {u_ * }/\kappa } \right), \end{array} $ | (9) |
式(9)是本文得到的第一个重要公式, 表示作用于最大冲刷坑深度所在位置的B流层流量, 简称最大冲深作用流量qV, B.
由式(9)可知, qV, B与B层流体流速(U+u*/κ)和厚度hB成正比, 与丁坝长度L和垂向作用距离δx的1/2次方成正比.
5 丁坝局部冲深公式 5.1 函数关系推导qV, B将通过坝头处冲刷坑内断面sec1, 由流量守恒可得
| $ {q_{V,B}} = {k_1}{d_{{\rm{se\_b}}}}{L_1}{v_{{\rm{secl}}}}. $ | (10) |
式中:vsec1为通过sec1的平均横向流速;dse_b为sec1断面最大冲刷深度;k1为sec1形状系数;L1为sec1断面宽度.当冲刷平衡时, vsec1等于起动流速vc, 从而
| $ \begin{array}{l} \sqrt 2 {\left( {1 + {m^2}} \right)^{1/4}}\sin \left( {0.5\arctan {m^{ - 1}}} \right) \times \\ \;\;\;\;\;\;\sqrt {L{\delta _x}} {h_B}\left( {U + {u_ * }/\kappa } \right) = {k_1}{L_1}{d_{{\rm{se\_b}}}}{v_c}. \end{array} $ | (11) |
根据实测数据, 坝头处sec1内横向流速的垂向分布如图 7所示, 床面附近αks处存在最大值vymax, ks为粗糙高度, α为参数.近底区域横向流速的垂向分布近似以下:
| $ \frac{{{v_y}}}{{{v_{y,\max }}}} = {\left( {\frac{{z + {d_{{\rm{se\_b}}}}}}{{\alpha {k_{\rm{s}}}}}} \right)^n},\;\;\;\;\;z \in \left[ { - {d_{{\rm{se\_b}}}}, - {d_{{\rm{se\_b}}}} + \alpha {k_s}} \right], $ | (12) |
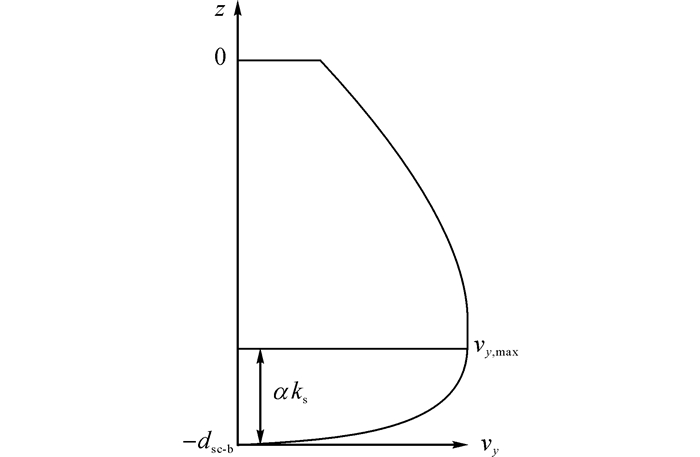
|
图 7 sec1内横向流速分布 Fig. 7 Lateral velocity distribution in section 1 |
式中:vy, max为近底最大横向流速;n为分布指数;z=0为未冲刷床面位置;z=-dse_b+αks为最大横向流速位置.
对近底区域积分得平均横向流速为
| $ \overline {{v_y}} = \frac{1}{{\alpha {k_s}}}\int_{ - {d_{{\rm{se\_b}}}}}^{ - {d_{{\rm{se\_b}}}} + \alpha {k_{\rm{s}}}} {{v_0}{{\left( {\frac{{z + {d_{{\rm{se\_b}}}}}}{{\alpha {k_{\rm{s}}}}}} \right)}^n}dz} = \frac{{{v_{y,\max }}}}{{1 + n}}. $ | (13) |
z=-dse_b +βks时可得床面泥沙作用流速
| $ {v_b} = {v_{y,\max }}{\left( {\frac{{\beta {k_{\rm{s}}}}}{{\alpha {k_{\rm{s}}}}}} \right)^n} = \left( {1 + n} \right)\overline {{v}}_y {\left( {\frac{\beta }{\alpha }} \right)^n}, $ | (14) |
式中:β为常数.
坝头附近冲刷坑三维形状类似倒置圆台, 圆台坡度约等于泥沙休止角.从冲刷坑最深处底部水平的角度及泥沙颗粒受力平衡角度出发, 起动底流速可表示为
| $ {v_{bc}} = {k_2}\sqrt {\left( {{\rho _s}/\rho - 1} \right)gd} , $ | (15) |
式中:ρs为泥沙密度;ρ为清水密度;g为重力加速度;d为泥沙粒径;k2为常数.分析认为sec1内横向流速的垂向平均值与
| $ {v_c} = \frac{{{k_2}{k_3}}}{{\left( {1 + n} \right)}}{\left( {\frac{\alpha }{\beta }} \right)^n}\sqrt {\left( {{\rho _s}/\rho - 1} \right)gd} . $ | (16) |
将式(16)代入式(11)可得
| $ {d_{{\rm{se\_b}}}} = \vartheta \frac{{{h_B}}}{{{L_1}}}\frac{{\sqrt {L{\delta _x}} \left( {U + {u_ * }/\kappa } \right)}}{{\sqrt {\left( {{\rho _s}/\rho - 1} \right)gd} }}. $ | (17) |
其中
| $ \vartheta =\text{ }\sqrt{2}(1+n){{(1+{{m}^{2}})}^{1/4}}\text{sin}\ \text{ }(0.5\text{ arctan }{{\mathit{m}}^{-1}}) $ |
(β/α)n/(k1k2k3)为综合常数.鉴于L1为B流层在冲刷坑内厚度, 与B流层厚度hB直接相关;δx直接影响B层流体在床面上的落点, 与L1成正比, 可知hB、L1和δx均与水深h相关, 从而式(17)可写成
| $ \frac{{{d_{{\rm{se\_b}}}}}}{h} = f\left( h \right)\sqrt {\frac{L}{h}} \frac{{\left( {U + {u_ * }/\kappa } \right)}}{{\sqrt {\left( {{\rho _s}/\rho - 1} \right)gd} }}. $ | (18) |
式(18)是本文得到的第2个重要公式, 表示最大冲刷深度与丁坝尺度及流动参数间的关系.可知最大相对冲刷深度dse_b/h与相对坝长L/h的1/2次方, 和无量纲近表层流速
表 1列出了多位研究者[7-8, 10, 18-22]的直立正挑矩形非淹没丁坝在均匀沙(粒径分布的标准差σg<1.5)床面及清水冲刷情况下的局部冲刷深度实验数据, 各参数变化范围为:中值粒径d50为0.26~18 mm, L/h值为1.0~36.47, 流速U为0.183~1.38 m/s, (ρs-ρ)/ρ=1.65, σg=1~1.46, u*=0.012~0.173 m/s, dse_b/h值0.53~6.75, U/Uc=0.5~1, 这里Uc为与行进流速和水深相对应的起动流速.表中, 文献[7]的u*由对数流速分布公式和(gχJ)0.5计算所得值取几何平均得到(χ为湿周, J为坡度), 其余u*由对数流速分布公式计算得到.
| 表 1 直立正挑矩形丁坝在均匀沙床面及清水冲刷情况下局部冲刷深度实验数据 Table 1 Scourof uniform sediment bed around 90° rectangle spur dikes under clear water situation |
取表 1内冲刷数据对式(18)进行参数率定, 取f(h)=0.402.式(18)可进一步写为
| $ {d_{{\rm{se\_b}}}}/h = 0.402\frac{{\sqrt {L/h} \left( {U + {u_ * }/\kappa } \right)}}{{\sqrt {\left( {{\rho _s}/\rho - 1} \right)gd} }}. $ | (19) |
将表 1中156个实验室实测数据与采用式(19)得到的计算值比较(见图 8), 各点聚集在45°理论线附近, 可见理论与实测符合良好.
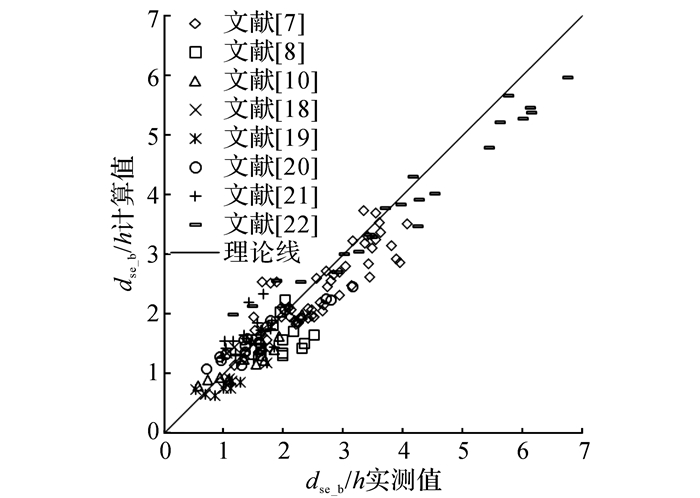
|
图 8 最大相对冲深计算值与实测值比较 Fig. 8 Comparison of calculated and measured relative scour depth |
万艳春等[23]给出了北江一个现场正挑丁坝的实测局部冲深数据, 其中丁坝有效长度L= 25 m, 行进水深h=9.3 m, 行进流速U=1.73 m/s, 边坡M=1:2.5, 非均匀沙中值粒径d50=1 mm, 平均粒径dm=2.36 mm, (ρs-ρ)/ρ=1.65, 局部冲刷深度dse=8.3 m.由对数流速分布公式可得u*=0.064 m/s, 由沙莫夫公式可得Uc=0.66 m/s, 可知U/Uc>1.
该情况属于浑水非均匀沙且带边坡的丁坝冲刷情况, 由前言部分可知, 计算此局部冲刷深度需考虑边坡M, 非均匀沙参数σg及水流强度U/Uc>1的影响, 参考常规处理方法, 即
| $ {d_{{\rm{se}}}} = {K_M}{K_I}{K_\sigma }{d_{{\rm{se\_b}}}} $ | (20) |
式中: KM, KI, Kσ分别为岸坡、水流强度、泥沙级配对冲深的修正系数.取d=dm, 并将L, h, U, u*代入式(20), 同时结合常用的边坡对局部冲深dse的影响系数
丁坝作为河流和海岸工程的常见构筑物已有不少研究成果, 但以往计算模型的建立往往基于一、二维流动或经验方法.本文从三维流动出发, 以5个马蹄涡的流动图像刻画非淹没丁坝周围马蹄涡系的流动状态.通过对实验室及数值模拟三维流动数据的分析, 提出了坝头横向流速在冲刷过程中起关键作用这一新结论.在提出的流动图像的基础上, 针对正挑矩形丁坝周围的流动情况, 通过考虑竖向流速, 修正了横向平板绕流的势流解, 导出最大冲深的作用流量公式(9);通过流量守恒和冲刷平衡条件, 建立了最大冲刷深度与坝长、行进流速、水深及床面摩阻流速的函数关系, 表明最大相对冲深dse_b/h与相对坝长L/h的1/2次方和无量纲流速
本文的局部冲深公式基于非淹没正挑矩形丁坝周围的流动图像建立, 而现场丁坝的情况相对复杂, 丁坝挑角、坝型、岸坡等其他参数对水流流动形态有一定影响, 流动图像可能会有所变化, 在后续研究中将进一步考虑由这些因素引起的流动图像变化, 对现有的计算模型进行修正, 以便更符合工程实际.
| [1] | KWAN R T, MELVILLE B W. Local scour and flow measurements at bridge abutments[J]. Journal of Hydraulic Research, 1994, 32(5): 661–673. DOI:10.1080/00221689409498707 |
| [2] | KOKEN M, CONSTANTINESCU G. An investigation of the flow and scour mechanisms around isolated spur dikes in a shallow open channel:2. Conditions corresponding to the final stages of the erosion and deposition process[J]. Water Resources Research, 2008, 44: W08407. DOI:10.1029/2007WR006491 |
| [3] | KOKEN M, GOGUS M. Effect of spur dike length on the horseshoe vortex system and the bed shear stress distribution[J]. Journal of Hydraulic Research, 2015, 53(2): 196–206. DOI:10.1080/00221686.2014.967819 |
| [4] | BARBHUIYA A K, DEY S. Vortex flow field in a scour hole around abutments[J]. International Journal of Sediment Research, 2003, 18(4): 310–325. |
| [5] | DEY S, BARBHUIYA A K. Flow field at a vertical-wall abutment[J]. Journal of Hydraulic Engineering, 2005, 131(12): 1126–1135. DOI:10.1061/(ASCE)0733-9429(2005)131:12(1126) |
| [6] | SAFARZADEH A, SALEHINEYSHABOURI S A A, ZARRATI A R. Experimental investigation on 3d turbulent flow around straight and t-shaped groynes in a flat bed channel[J]. Journal of Hydraulic Engineering, 2016, 142(8): 04016021. DOI:10.1061/(ASCE)HY.1943-7900.0001144 |
| [7] | GILL M A. Erosion of sand beds around spur-dikes[J]. Journal of the Hydraulics Division, American Society of Civil Engineers, 1972, 98: 1587–1602. |
| [8] | DEY S, BARBHUIYA A K. Time variation of scour at abutments[J]. Journal of Hydraulic Engineering, 2005, 131(1): 11–23. DOI:10.1061/(ASCE)0733-9429(2005)131:1(11) |
| [9] | PANDEY M, AHMAD Z, SHARMA P K. Estimation of maximum scour depth near a spur dike[J]. Canadian Journal of Civil Engineering, 2015, 43(3): 270–278. |
| [10] | LIM SY. Equilibrium clear-water scour around an abutment[J]. Journal of Hydraulic Engineering, 1997, 123(3): 237–243. DOI:10.1061/(ASCE)0733-9429(1997)123:3(237) |
| [11] | 张俊华, 许雨新, 张红武, 等. 河道整治及堤防管理[M]. 郑州: 黄河水利出版社, 1998: 78-85. |
| [12] |
沈焕荣, 陈其慧. 丁坝局部冲刷深度计算问题探讨[J].
四川大学学报:工程科学版, 2001, 33(2): 5–8.
Shen Huan-rong, Chen Qi-hui. Preliminary study on the calculation of partial pier scour[J]. Journal of Sichuan University, 2001, 33(2): 5–8. |
| [13] | DARGAHI B. Controlling mechanism of local scouring[J]. Journal of Hydraulic Engineering, 1990, 116(10): 1197–1214. DOI:10.1061/(ASCE)0733-9429(1990)116:10(1197) |
| [14] | UNGER J, HAGER W. The mean characteristics of horseshoe vortex at a cylindrical pier:M. Muzzammil and T. Gangadhariah[J]. Journal of Hydraulic Research, 2003, 41(3): 285–297. DOI:10.1080/00221680309499973 |
| [15] | HUNT J, ABELL C, PETERKA J, et al. Kinematical studies of the flows around free or surface-mounted obstacles; applying topology to flow visualization[J]. Journal of Fluid Mechanics, 1978, 86(1): 179–200. DOI:10.1017/S0022112078001068 |
| [16] |
虞邦义. 丁坝附近局部河床冲刷与防护的实验研究[D]. 合肥: 合肥工业大学, 1986.
Yu Bang-yi. Experimental study of erosion and protection around spur dike[D].HeFei:HeFei University of Technology, 1986. |
| [17] | MELVILLE B W. Pier and abutment scour:integrated approach[J]. Journal of Hydraulic Engineering, 1997, 123(2): 125–136. DOI:10.1061/(ASCE)0733-9429(1997)123:2(125) |
| [18] | GARDE R J, SUBRAMANYA K, NAMBUDRIPAD KD. Closure of 'Study of scour around spur-dikes'[J]. Journal of the Hydraulics Division, American Society of Civil Engineers, 1963, 88: 167–175. |
| [19] | ZAGHLOUL, N A. Analytical and experimental investigations of flow around of a spur-dike[D].:University of Windsor, 1974. http://scholar.uwindsor.ca/etd/1183/ |
| [20] | RAJARATNAM N, NWACHUKWU B A. Flow near groin-like structures[J]. Journal of hydraulic engineering, 1983, 109(3): 463–480. DOI:10.1061/(ASCE)0733-9429(1983)109:3(463) |
| [21] | COLEMAN S E, LAUCHLAN C S, MELVILLE B W. Clear-water scour development at bridge abutments[J]. Journal of Hydraulic Research, 2003, 41(5): 521–531. DOI:10.1080/00221680309499997 |
| [22] | FAEL C M S, SIMARROGRANDE G, MARTNVIDE J P, et al. Local scour at verticalwall abutments under clearwater flow conditions[J]. Water resources research, 2006, 42(10): 277–305. |
| [23] |
万艳春, 黄本胜. 北江下游丁坝坝头最大冲深计算模式探讨[J].
广东水利水电, 2004, 1(1): 16–18.
Wan Yan-chun, Huang Ben-shen. Calculation model of maximum scour depth applying for lower reaches of Beijiang River[J]. Guangdong Water Resources and Hydropower, 2004, 1(1): 16–18. |
| [24] |
LIM S Y, CHIEW Y M. Effect of sediment gradation on scour at spur dikes[C]//国际天然和试验室水力学研究学术会议论文集第2卷. 武汉: . 1992: 112-117.
LIM S Y, CHIEW Y M. Effect of sediment gradation on scour at spur dikes[C]//Proceedings of International. Symposium on Hydraulic Research in Nature and Laboratory vol. 2. Wuhan:. 1992, 112-117. |