2. 浙江大学 软弱土与环境土工教育部重点实验室, 浙江 杭州 310058;
3. 中国电建集团华东勘测设计研究院有限公司, 浙江 杭州 311122
2. Key Laboratory of Soft Soils and Geoenvironmental Engineering, Ministry of Education, Zhejiang University, Hangzhou 310058, China;
3. Power China Huadong Engineering Limited Corporation, Hangzhou 310058, China
基坑抗隆起稳定性验算是基坑支护设计中的关键内容之一, 它不仅关系着基坑的稳定安全问题, 也与基坑的变形密切相关, 因此基坑抗隆起稳定性的分析是学术界和工程界都比较关心的课题.目前常用的基坑抗隆起稳定分析方法主要包括极限平衡法、极限分析法以及数值分析法3大类.
在基坑稳定性数值分析中, 通常是利用数值分析软件在强度折减法的基础上计算分析出安全系数.Zienkiewicz等[1]最早于土坡稳定性分析中提出了强度折减法.此后, Cai等[2]、Feheem等[3]、陈福全等[4]分别采用强度折减法有限元分析了支护结构插入深度、坑底至硬土层厚度、不排水抗剪强度、支护结构条件、基坑尺寸等因素对基坑抗隆起稳定性安全系数的影响.近些年, 以塑性理论为依据的极限分析理论逐渐在岩土工程领域得到应用, Chang[5]以及黄茂松等[6]基于Prandtl破坏机构分析黏土基坑抗隆起稳定性的上限方法.
在我国基坑工程实践分析中主要采用地基承载力模式和圆弧滑动模式2种极限平衡分析方法.Terzaghi[7]法以及Bjerrum和Eide[8]法都是在黏土基坑不排水条件下, 基于地基承载力模式提出的.我国规范[9~12]主要采用考虑土体抗剪强度指标c、φ值的圆弧滑动破坏模式来计算基坑坑底抗隆起稳定性.但对于开挖深度大、平面形状狭长、支护结构插入深度较大的地铁车站基坑, 假定的圆弧滑动面将穿过基坑对侧的支护结构, 显然不合理, 因此传统规范计算方法不再适用.张飞[13]针对软土地基中狭长深基坑开展了抗隆起离心模型试验和有限元数值分析, 结果表明狭长型基坑中坑底隆起破坏仍表现为围护墙绕某点以圆弧或对数螺旋线滑动面向坑内产生转动踢脚破坏.陈孝湘[14]通过强度折减有限元分析指出狭长基坑坑底抗隆起稳定破坏的滑动面依然绕过板桩底部, 但与完整的圆弧滑动的模式不一致.彭孔曙[15]采用数值分析方法对比了地铁车站基坑中支护结构插入深度变化对周边位移场的影响, 指出现行规范的抗隆起稳定计算方法对于狭长型基坑的安全储备偏大.王洪新[16]把基坑开挖引起的隆起失稳问题简化为在坑底位置施加一个负载问题后的塑性区扩展深度问题, 基于Mindlin解提出了考虑尺寸效应的稳定分析方法.王洪新[17]通过移动滑动面圆心位置, 使滑弧经过支护结构底部以及基坑底与对侧支护结构的交点来构造滑动面.
本文首先对4种常用的基于圆弧滑动模式的基坑坑底抗隆起稳定计算方法进行了对比分析;接着提出了考虑基坑宽度影响的基坑抗隆起稳定计算方法, 并对基坑宽度、支护结构插入深度、基坑开挖深度、土体抗剪强度指标和被动区加固等参数的影响进行了分析.
1 常用的坑底抗隆起稳定计算方法及比较分析 1.1 常用的坑底抗隆起稳定计算方法汪炳鉴、夏明耀[18]于1983年在国内首先提出了基于圆弧滑动的基坑坑底抗隆起稳定计算方法(以下简称汪-夏法).目前上海市《基坑工程技术规范》(DG/TJ08-61-2010)[9]、浙江省《基坑工程技术规程》(DB42/T159-2012)[10]、建设部《建筑基坑支护技术规程》(JGJ120-2012)[11]均针对坑底抗隆起稳定验算提出了相应的计算方法.
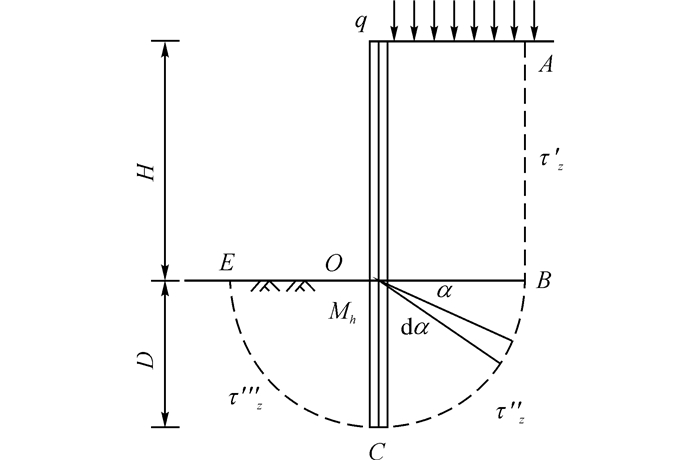
1.1.1 汪-夏法汪炳鉴、夏明耀在1983年分析地下连续墙入土深度时提出了考虑墙体极限弯矩的抗隆起法.该法假设滑动面如图 1所示, 圆弧段的圆心O位于支护结构与坑底的交点.该法抗隆起稳定安全系数计算公式如下:
| $ {K_{\rm{s}}} = \frac{{{M_{\rm{r}}}}}{{{M_{\rm{s}}}}}. $ | (1) |
| $ \begin{array}{l} {M_{\rm{r}}} = \int_o^H {{{\tau '}_z}{\rm{d}}zD} + \int_o^{\frac{{\rm{ \mathsf{ π} }}}{2}} {{{\tau ''}_z}D{\rm{d}}\alpha D} + \\ \;\;\;\;\;\;\;\;\int_o^{\frac{{\rm{ \mathsf{ π} }}}{2}} {{{\tau '''}_z}D{\rm{d}}\alpha D} + {M_{\rm{h}}}. \end{array} $ | (2) |
| $ {M_{\rm{s}}} = \frac{1}{2}\left( {\gamma H + q} \right){D^2}. $ | (3) |
|
图 1 “汪-夏法”计算模型 Fig. 1 Wang-Xia mode |
式中:Mr为抗滑动力矩, Ms为滑动力矩, D为入土深度, H为基坑开挖深度, q为地表超载, γ, c, φ分别为土体容重, 黏聚力及内摩擦角, 有几层不同性质的土时, 可采用加权平均值, Mh为基坑单位宽度上底面处墙体的极限抵抗弯矩, τ′z, τ″z, τ'''z分别为滑动面AB、BC、CE段上的抗剪强度, α为微元体与计算起始面的夹角(见图 1).
滑动面抗剪强度采用τ=σztan φ+c公式计算, 其法向应力σz由土体自重的分力和水平侧压力的分力2部分组成.主动区水平侧压力介于主动土压力与静止土压力之间, 故近似取为σ=γztan2(45°-φ/2), 而不再减去2ctan (45°-φ/2), 其中z为计算点深度.被动区水平侧压力也近似按此公式计算.
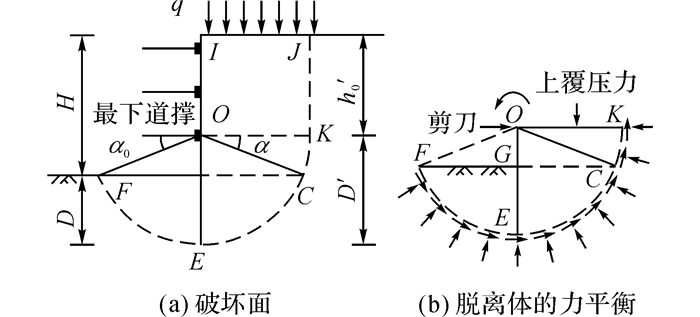
1.1.2 上海市《基坑工程技术规范》法(沪规法)上海市《基坑工程技术规范》(DG/TJ08-61-2010) [9]在汪-夏法基础上进行了改进:假定圆弧段圆心O位于支护结构与最下一道支撑的交点(见图 2), 但滑动面法向应力的计算方法仍同汪-夏法;同时作为安全储备, 忽略滑动面竖直段JK段上抗剪强度产生的抗滑力矩.在第6.3.2条中规定了相应的计算方法如下:
| $ \frac{{{M_{RLk}}}}{{{\gamma _S}{M_{SLk}}}} \ge {\gamma _{RL}}. $ | (4) |
| $ {M_{RLk}} = {M_{sk}} + \sum\limits_{j = 1}^{{n_2}} {{M_{RLkj}}} + \sum\limits_{m = 1}^{{n_3}} {{M_{RLkm}}} . $ | (5) |
| $ {M_{SLk}} = {M_{SLkq}} + \sum\limits_{i = 1}^{{n_1}} {{M_{SLki}}} + \sum\limits_{j = 1}^{{n_4}} {{M_{SLkj}}} . $ | (6) |
|
图 2 沪规法计算模型 Fig. 2 Model of Shanghai technical specification |
式中:MRLk为抗隆起力矩标准值, MSLk为隆起力矩标准值, γS为作用分项系数, γRL为抗隆起分项系数;Msk为围护墙的容许力矩标准值, MRLkj为坑外最下道支撑以下j层土产生的抗隆起力矩标准值, MRLkm为坑内开挖面以下第m层土产生的抗隆起力矩标准值;MSLkq为坑外地面荷载产生的隆起力矩标准值, MSLki为坑外最下道支撑以上第i层土产生的隆起力矩标准值, MSLkj为坑外最下道支撑以下、开挖面以上第j层土的隆起力矩标准值.
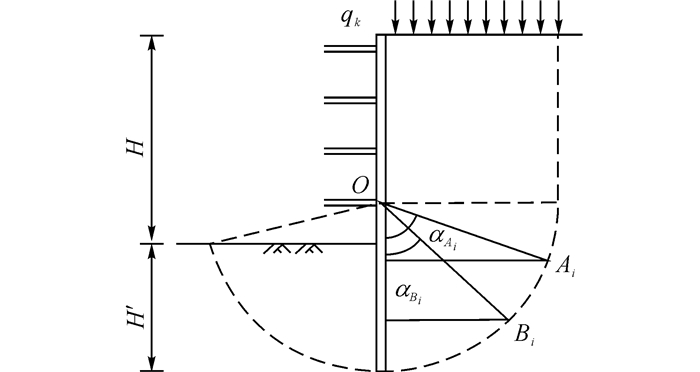
1.1.3 浙江省《基坑工程技术规程》法(浙规法)浙江省《基坑工程技术规程》(DB42/T159-2012)[10]在第6.1.8条中也规定了相应的计算方法(见图 3)如下:
| $ \frac{{2\sum {\left( {{\alpha _{Ai}} - {\alpha _{Bi}}} \right){\tau _i}} }}{{\left( {{q_k} + {\gamma _3}H} \right)}} \ge {K_{\rm{r}}}. $ | (7) |
|
图 3 浙规法计算模型 Fig. 3 Model of Zhejiang technical specification |
式中:Kr为抗隆起稳定安全系数, τi为圆弧AB段范围第i计算土层中间深度点的抗剪强度, αAi、αBi为滑弧面与第i土层的交点Ai、Bi与最下层支点的连线与垂直面的夹角(弧度), γ3为地面至基坑开挖面范围内各土层天然重度的加权平均值, qk为地面超载.
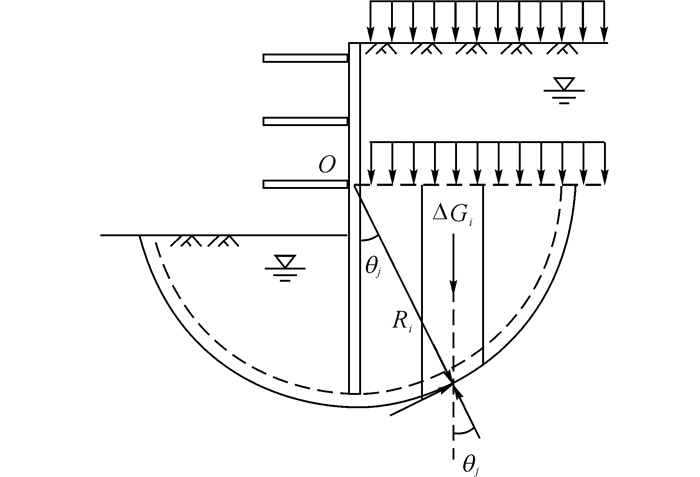
1.1.4 建设部《建筑基坑支护技术规程》法(部规法)建设部《建筑基坑支护技术规程》(JGJ120-2012)[11]在第4.2.5条中也规定了相应的计算方法(见图 4)如下:
| $ \frac{{\sum {\left[ {{c_j}{l_j} + \left( {{q_j}{b_j} + \Delta {G_j}} \right)\cos {\theta _j}\tan {\varphi _j}} \right]} }}{{\sum {\left( {{q_j}{b_j} + \Delta {G_j}} \right)\sin {\theta _j}} }} \ge {K_{\rm{r}}}. $ | (8) |
|
图 4 部规法计算模型 Fig. 4 Model of MOHURD technical specification |
式中:cj、φj分别为第j土条在滑弧面处土的黏聚力、内摩擦角, lj为第j土条的滑弧长度, qj为第j土条顶面上的竖向压力标准值, bj为第j土条的宽度, θj为第j土条滑弧面中点处的法线与垂直面的夹角, ΔGj为第j土条的自重.
在第4.2.5条的条文说明中介绍了该法的滑动面假定源自上海地区的坑底抗隆起稳定计算方法, 并明确安全系数的取值参照沪规法.
各规范要求的基坑抗隆起稳定安全系数见表 1.
| 表 1 各规范要求基坑抗隆起稳定安全系数 Table 1 Basal stability safty factor of each codes |
通过对比1.1.1~1.1.4节所述的4种基坑坑底抗隆起稳定分析方法可见:
1) 4种方法均采用抗滑力矩除以滑动力矩的形式来定义抗隆起稳定安全系数;
2) 4种方法假设的圆弧滑动面基本一致, 但圆心的位置略有差异:汪-夏法滑弧圆心位于支护结构与坑底的交点;而另3种方法则位于支护结构与最下一道支撑的交点, 同时忽略了滑动面竖直段(图 2中AB段)上抗剪强度产生的抗滑力矩;
3) 汪-夏法和沪规法在计算抗滑力矩时均考虑了支护墙体的抗弯能力, 而浙规法和部规法则未予考虑;
4) 4种方法在滑动面的法向应力计算上有较大差异:汪-夏法和沪规法假设滑动面上的法向应力由土体自重的分力与水平侧压力的分力2部分组成, 而浙规法和部规法仅考虑土体自重的分力, 由此导致汪-夏法和沪规法计算得到的滑动面抗剪力和抗隆起稳定安全系数明显大于浙规法和部规法.另外, 浙规法规定还可采用十字板抗剪强度的1.5倍来计算滑动面上的抗剪强度.
5) 部规法在计算滑动面上的法向应力时未考虑水平侧压力的分力, 但要求稳定安全系数达到与沪规法相同的1.7~2.2, 因此其要求最高.
1.2 4种计算方法的算例分析分别选取实际工程中粉土地基和淤泥质土地基的2个工程算例进行对比分析, 其中基坑支护结构的插入比根据当地工程经验分别取为0.75和1.50.
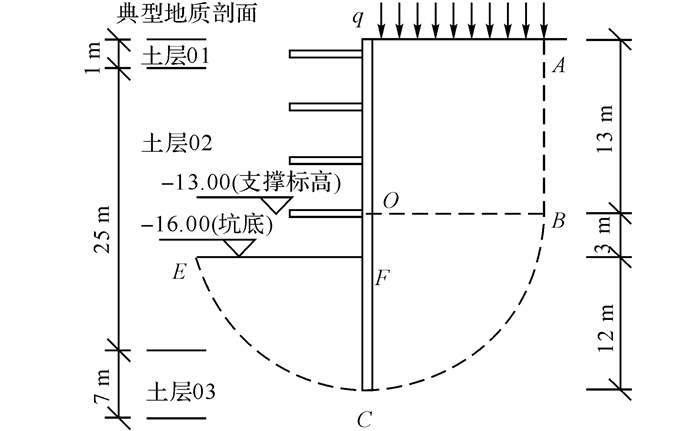
1.2.1 工程算例1工程算例1为杭州城东某粉土地基中基坑, 设计等级为一级.基坑开挖深度为16 m, 支护结构插入深度取12 m, 最下道支撑距离坑底3 m, 计算时考虑地面超载为15 kPa.如图 5所示.基坑所处场地地质条件及计算参数见表 2(本文土的抗剪强度指标皆采用三轴固结不排水剪切试验测定).
|
图 5 算例1基坑剖面图 Fig. 5 Section of foundation pit in model 1 |
| 表 2 算例1各土层计算参数 Table 2 Physico-mechanical parameters of soils in model 1 |
部规法、浙规法、沪规法和汪-夏法计算所得的抗隆起稳定安全系数分别为1.86, 2.03, 2.28和2.99.该基坑已安全开挖到了坑底, 且围护结构的变形小于30 mm.由计算结果可见:1)“汪-夏法”由于考虑了坑外竖直段提供的抗滑动力矩以及水平侧压力的抗滑贡献, 计算所得安全系数最高;2)在土质条件较好的粉土地基中, 以上4种算法都能得到1.6以上的抗隆起稳定安全系数.其中沪规法和浙规法所得安全系数可满足相应规范要求;但部规法所得安全系数为1.86, 仅为该规范要求值的84.5%, 说明该规范中安全系数要求值偏高.
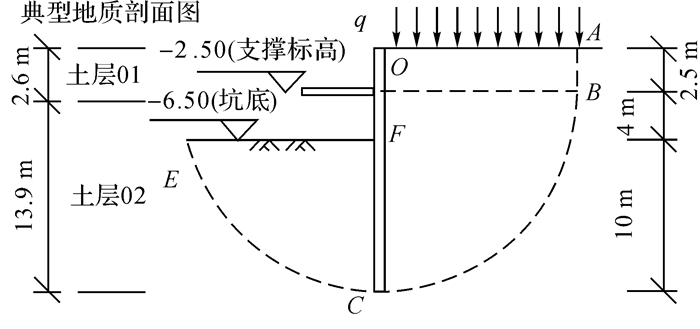
1.2.2 工程算例2工程算例2为杭州城西某淤泥质土地基中基坑, 设计等级为二级.基坑开挖深度为6.5 m, 支护结构插入深度取10 m, 最下道支撑距离坑底4.0 m, 计算时考虑地面超载为20 kPa.如图 6所示.基坑所处场地地质条件及计算参数见表 3.部规法、浙规法、沪规法和汪-夏法计算所得的抗隆起稳定安全系数分别为1.19, 1.36, 1.47和1.81, 但该基坑也已安全顺利地完成了开挖.
|
图 6 算例2基坑剖面图 Fig. 6 Section of foundation pit in model 2 |
| 表 3 算例2各土层计算参数 Table 3 Physico-mechanical parameters of soils in model 2 |
由计算结果可见:在地基土质较差的条件下, 3种规范方法的计算结果都不能满足要求, 即使是安全系数最大的“汪-夏法”也未能达到沪规法的要求值1.9, 而部规法的计算结果仅为要求值的63%.但是该基坑已顺利开挖至基坑底, 并未出现隆起破坏.根据试算分析, 在本算例中如需满足沪规法和部规法的要求值, 支护结构的插入深度需分别达到16.3和24.2 m, 即插入比分别为2.51和3.72, 远大于工程经验值.虽然增大插入深度对于提高基坑稳定性, 减小基坑开挖对周边环境的影响有一定好处, 但过大的插入深度给通常仅作为临时结构的基坑工程带来了沉重的经济负担.
目前浙江温州、宁波、台州等深厚软土地基中在支护结构未能打穿软土层的情况下, 根据实践经验按插入比2.0左右来控制支护结构的插入深度, 取得了较好的效果.由此说明在深厚软弱土地基中, 尤其是在内摩擦角较小的情况下, 各规范给出的抗隆起稳定安全系数要求值普遍偏高.
2 考虑基坑宽度影响的坑底抗隆起稳定计算方法对于狭长型的深基坑, 当采用圆弧滑动模式进行坑底抗隆起稳定验算时常常会出现假设的圆弧滑动面穿过对侧支护结构的不合理情况, 但文献[22]的研究结果表明狭长型基坑中坑底隆起破坏仍表现为围护墙绕某点以圆弧或对数螺旋线滑动面向坑内产生转动踢脚破坏.本文在前人工作的基础上, 提出了考虑基坑宽度影响的坑底隆起稳定计算方法.
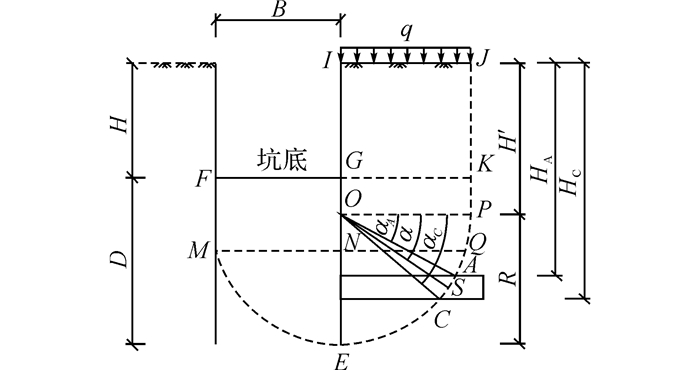
2.1 基本假定1) 对于基坑宽度小于支护结构插入深度的狭长型基坑, 考虑对侧支护结构的抗滑作用, 假定其潜在滑动面由竖直直线段JP、圆弧段PEM和竖直直线段MF组成(见图 7).其中圆弧滑动面PEM经过桩底E以及开挖面与对侧围护结构交点F, 且圆心O位于支护结构上.由几何关系可知, 圆心O位于EF连线的中垂线与支护结构IE的交点.故当基坑宽度等于支护结构的插入深度时, 圆心位于支护结构与坑底交点G, 滑动面即退化成汪-夏法的假定滑动面.
|
图 7 圆弧滑动模式计算简图 Fig. 7 Calculation sketch of circular sliding mode |
2) 土体抗剪强度采用Mohr-Coulomb强度理论, 按τ=σztan φ+c公式计算;
3) 坑外竖向段JP抗剪强度提供的抗滑力矩仅考虑坑底以下部分(即KP段), 坑底以上部分JK段作为安全储备不参与计算[15~17];
4) KPEMF滑动面上的法向应力由2部分组成, 即土体自重的分力和该处的水平侧压力的分力.其中KPE段水平侧压力应介于主动土压力与静止土压力之间, 因此近似地取为
5) 考虑土体分布的成层性;
6) 考虑到基坑产生隆起破坏时, 支护墙体有可能并未产生受弯破坏, 因此在稳定分析时不计入墙体自身的抗弯贡献, 而作为安全储备.
2.2 计算公式推导根据前述假定, NQE区域内土体自重产生的滑动力矩与NEM区域内土体自重产生的抗滑动力矩可相互抵消.因此产生滑动力矩的项包括:1)IJ段作用于地面的均布超载q产生MIJ;2)IJKG区域土体自重产生MIJKG;3)GKQN区域内土体自重产生的滑动力矩与FGNM区域内土体自重产生的抗滑力矩相抵消后剩余的滑动力矩.
产生抗滑动力矩的项有:1)滑动面KP上抗剪强度产生MKP;2)滑动面PE上抗剪强度产生MPE;3)滑动面EM上抗剪强度产生MEM;4)滑动面竖向段MF上抗剪强度产生MMF.
则基坑抗隆起稳定安全系数为
| $ {K_{\rm{s}}} = \frac{{{M_{\rm{R}}}}}{{{M_{\rm{S}}}}}. $ | (9) |
式中:MR、MS分别为
| $ {M_{\rm{R}}} = {M_{KP}} + {M_{PE}} + {M_{EM}} + {M_{MF}}. $ | (10) |
| $ {M_{\rm{s}}} = {M_{IJ}} + {M_{IJKG}} + \left( {{M_{GKPO}} + {M_{OPQN}} - {M_{FGNM}}} \right). $ | (11) |
式中:MIJKG、MGKPO和MOPQN分别为对应区域土体自重产生的滑动力矩;MFGNM为FGNM区域土体自重产生的抗滑动力矩.
1) 滑动圆弧半径
根据前述假定, 滑动圆弧半径为
| $ R = \frac{{{B^2} + {D^2}}}{{2D}}. $ | (12) |
| $ H' = H + D - R. $ | (13) |
式中:B为基坑开挖宽度;H′为滑动圆弧圆心距地表深度.
2) FGNM区域抗滑动力矩
该区域内某层土条重力所产生对圆心O的抗隆起力矩为
| $ M = \int_{{H_A}}^{{H_C}} {\frac{1}{2}{B^2}\gamma {\rm{d}}h} . $ | (14) |
式中:HA为对应土条的层顶埋深;HC为对应土条的层底埋深.
FGNM区域土体自重产生对圆心O的抗隆起力矩为
| $ {M_{FGNM}} = \sum {\frac{1}{2}\gamma {B^2}\left( {{H_C} - {H_A}} \right)} . $ | (15) |
3) 滑动面KP上抗滑动力矩
滑动面KP上任意一点的抗剪强度为
| $ {\tau _{KP}} = {\sigma _{KP}}\tan \varphi + c = {K_a}\left( {q + \gamma h} \right)\tan \varphi + c. $ | (16) |
| $ {K_a} = {\tan ^2}\left( {{{45}^ \circ } - \frac{\varphi }{2}} \right). $ | (17) |
式中:Ka为对应土层的主动土压力系数, σKP为作用在KP段上的有效法向应力.
对圆心O的抗隆起力矩为
| $ {M_{KP}} = \sum {\int_{{H_A}}^{{H_C}} {\left[ {{K_a}\left( {q + \gamma h} \right)\tan \varphi + c} \right] \cdot R{\rm{d}}h} } . $ | (18) |
4) 滑动面PE上抗滑动力矩
对于滑动面PE上的法向应力σn由2部分组成, 即为土体自重在滑面法向上的分力加上该处水平侧压力在滑动面法向上的分力, 则滑动面PE上任意一点的抗剪强度为
| $ \begin{array}{l} {\tau _{PE}} = \left( {{q_1} + \gamma R\sin \alpha - \gamma {H_A} + \gamma H'} \right){\sin ^2}\alpha \tan \varphi + \\ \left( {{q_1} + \gamma R\sin \alpha - \gamma {H_A} + \gamma H'} \right){\cos ^2}\alpha {K_a}\tan \varphi + c. \end{array} $ | (19) |
对圆心O的抗滑动力矩为
| $ \begin{array}{l} {M_{PE}} = \sum {\int_{{\alpha _A}}^{{\alpha _C}} {\left[ {\left( {{q_1} + \gamma R\sin \alpha - \gamma {H_A} + \gamma H'} \right) \times } \right.} } \\ \;\;\;{\sin ^2}\alpha \tan \varphi + \left( {{q_1} + \gamma R\sin \alpha - \gamma {H_A} + \gamma H'} \right) \times \\ \;\;\;\left. {{{\cos }^2}\alpha {K_a}\tan \varphi + c} \right]{R^2}d\alpha . \end{array} $ | (20) |
| $ {\alpha _A} = \arctan \left[ {\frac{{{H_A} - H'}}{{\sqrt {{R^2} - {{\left( {{H_A} - H'} \right)}^2}} }}} \right]. $ | (21) |
| $ {\alpha _C} = \arctan \left[ {\frac{{{H_C} - H'}}{{\sqrt {{R^2} - {{\left( {{H_C} - H'} \right)}^2}} }}} \right]. $ | (22) |
式中:q1为坑外对应土条的上覆竖向应力;αA, αC为对应土条层顶和层底与圆心的水平夹角.
5) 滑动面EM上抗滑动力矩
类比于滑动面PE, 滑动面EM上任意一点的抗剪强度为
| $ \begin{array}{l} {\tau _{EM}} = \left( {{q_1} + \gamma R\sin \alpha - \gamma {H_A} + \gamma H'} \right) \times \\ \;\;\;{\sin ^2}\alpha \tan \varphi + \left( {{q_2} + \gamma R\sin \alpha - \gamma {H_A} + \gamma H'} \right) \times \\ \;\;\;{\cos ^2}\alpha {K_p}\tan \varphi + c. \end{array} $ | (23) |
对圆心O的抗滑动力矩为
| $ \begin{array}{l} {M_{EM}} = \sum {\int_{{\alpha _A}}^{{\alpha _C}} {\left[ {\left( {{q_2} + \gamma R\sin \alpha - \gamma {H_A} + \gamma H'} \right) \times } \right.} } \\ \;\;\;{\sin ^2}\alpha \tan \varphi + \left( {{q_2} + \gamma R\sin \alpha - \gamma {H_A} + \gamma H'} \right) \times \\ \;\;\;\left. {{{\cos }^2}\alpha {K_p}\tan \varphi + c} \right]{R^2}{\rm{d}}\alpha . \end{array} $ | (24) |
式中:q2为坑内对应土条的上覆竖向应力.
6) 滑动面MF上抗滑动力矩
| $ {\tau _{MF}} = {\sigma _{MF}}\mu + c = {K_p}\gamma h\mu + c. $ | (25) |
| $ {K_p} = {\tan ^2}\left( {{{45}^ \circ } + \frac{\varphi }{2}} \right). $ | (26) |
对圆心O的抗滑动力矩为
| $ {M_{MF}} = \sum {\int_{{H_A}}^{{H_C}} {\left( {{K_p}rh\mu + c} \right) \cdot R{\rm{d}}h} } . $ | (27) |
式中:Kp为对应土层的被动土压力系数;μ为桩土摩擦系数.
7) IJ段地面超载的滑动力矩
| $ {M_{IJ}} = \frac{1}{2}q{R^2}. $ | (28) |
8) IJKG、GKPO区域
该区域内某层土重力所产生对圆心O的滑动力矩为
| $ M = \int_{{H_A}}^{{H_C}} {\frac{1}{2}{R^2}\gamma {\rm{d}}h} . $ | (29) |
IJKG、GKPO区域土体自重产生对圆心O的滑动力矩为
| $ M = \sum {\frac{1}{2}\gamma {R^2}\left( {{H_C} - {H_A}} \right)} . $ | (30) |
9) OPQN区域土体自重滑动力矩
该区域内土体自重产生对圆心O的滑动力矩为
| $ \begin{array}{l} {M_{OPQN}} = \\ \sum {\frac{1}{2}\gamma {R^2}\left[ {\left( {\sin {\alpha _C} - \frac{{{{\sin }^3}{\alpha _C}}}{3}} \right) - \left( {\sin {\alpha _A} - \frac{{{{\sin }^3}{\alpha _A}}}{3}} \right)} \right]} . \end{array} $ | (31) |
根据本文提出的考虑基坑宽度的坑底抗隆起稳定性计算方式, 本节就基坑宽度、支护结构插入深度、基坑开挖深度、土体抗剪强度指标和被动区加固等参数对基坑抗隆起稳定性的影响进行探讨, 并与汪-夏法和沪规法的计算结果进行对比分析.由于在淤泥质土和粉土地基中基坑抗隆起稳定安全系数差别较大, 因此本节将就2种土质条件下分别讨论.基本算例均采用均质地基, 土体参数与基坑剖面的几何尺寸见表 4和5, 其中土体参数取自杭州典型的城西软土和城东粉土地基, μ为桩土摩擦系数.
| 表 4 基本算例中土体计算参数 Table 4 Physico-mechanical parameters of basic model |
| 表 5 基本算例中基坑剖面的几何尺寸 Table 5 Geometry size of pit section in model |
1) 开挖宽度
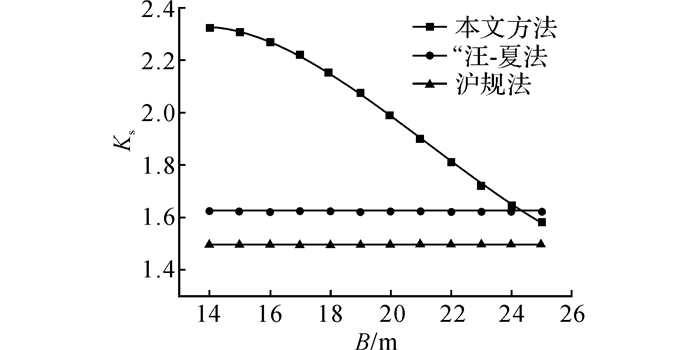
在基本算例的基础上, 保持其他参数不变, 改变基坑宽度B.淤泥质土及粉土地基基坑中基坑宽度B对抗隆起稳定性的影响如图 8和9所示.“汪-夏法”及沪规法由于未考虑基坑宽度的影响, 故计算结果为定值.
|
图 8 基坑宽度对淤泥质土地基基坑抗隆起安全系数的影响 Fig. 8 Influence of foundation pit excavation on safety factor of anti-upheaval at bottom of muddy soil |
|
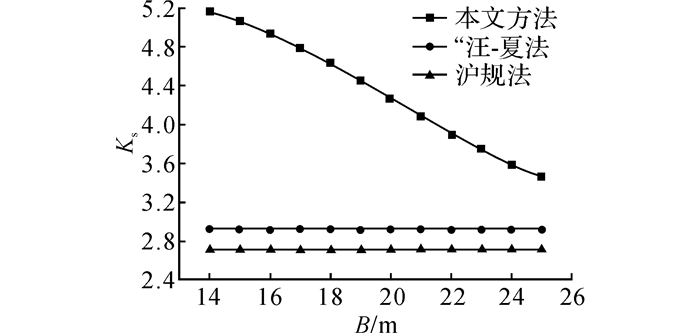
图 9 基坑宽度对粉土地基基坑抗隆起安全系数的影响 Fig. 9 Influence of foundation pit excavation on safety factor of anti-upheaval at bottom of silty soil |
从图 8和9中可以看出:1)对于狭长型基坑, 基坑宽度对基坑抗隆起稳定安全系数有显著影响.由于对侧围护结构的抗滑作用, 随着基坑宽度减小, 抗隆起稳定安全系数显著增大.但增长速率逐步减缓.当基坑宽度由25 m减小至14 m时, 淤泥质土地基中基坑抗隆起安全系数增长了41.0%, 粉土地基中增长了43.4%;2)汪-夏法和沪规法未能考虑对侧支护结构的抗滑作用, 抗隆起稳定安全系数计算值偏小, 偏于保守;3)当基坑宽度为25 m时, 在淤泥质土中虽然本文算法在基坑被动区采用了修正被动土压力, 但是由于淤泥质土体φ值较小, 与“汪-夏法”和沪规法均采用修正主动土压力相比所增加的抗滑力矩不大, 且本文方法未考虑围护墙体自身的抗弯作用;而汪-夏法由于考虑了滑动面竖直段土体提供的抗滑动力矩及围护墙自身的抗弯作用, 同时由于此时基坑宽度与支护结构插入深度相等, 对侧支护结构未产生抗滑作用, 故此时汪-夏法所得安全系数略大于本文算法.但在粉土地基中由于粉土内摩擦角较大, 本文算法在基坑被动区采用的修正被动土压力远大于汪-夏法采用的修正主动土压力, 因此所得的抗隆起稳定安全系数仍要大于汪-夏法.
2) 支护结构插入深度
保持其他参数不变, 改变支护结构插入深度.淤泥质土及粉土地基中支护结构插入深度对基坑中抗隆起稳定性的影响如图 10和11所示.
|
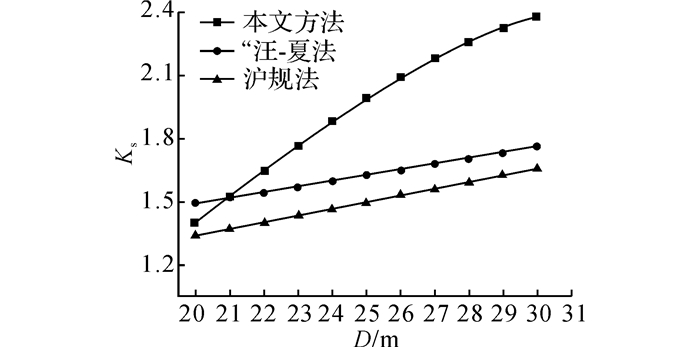
图 10 插入深度对淤泥质土地基基坑抗隆起安全系数的影响 Fig. 10 Influence of embedded depth on safety factor of anti-upheaval at bottom of muddy soil |

|
图 11 插入深度对粉土地基基坑抗隆起安全系数的影响 Fig. 11 Influence of embedded depth on safety factor of anti-upheaval at bottom of silty soil |
图 10和11表明:1)对于狭长型基坑, 支护结构插入深度对基坑抗隆起稳定安全系数有显著影响.由于对侧围护结构的抗滑作用, 随着插入深度增大, 抗隆起稳定安全系数显著增大, 但增长速率逐步减缓.当插入深度由20 m增大至30 m时, 在淤泥质土地基中基坑抗隆起安全系数增长了70.0%, 在粉土地基中增长了74.0%.2)汪-夏法和沪规法未能考虑对侧支护结构的抗滑作用, 基坑抗隆起安全系数呈线性增长, 且增长速率缓慢, 在淤泥质土地基中仅增长18.0%, 在粉土地基中仅增长14.0%.
3)开挖深度
保持其他参数不变, 淤泥质土及粉土地基中基坑开挖深度对基坑中抗隆起稳定性的影响如图 12和13所示.
|
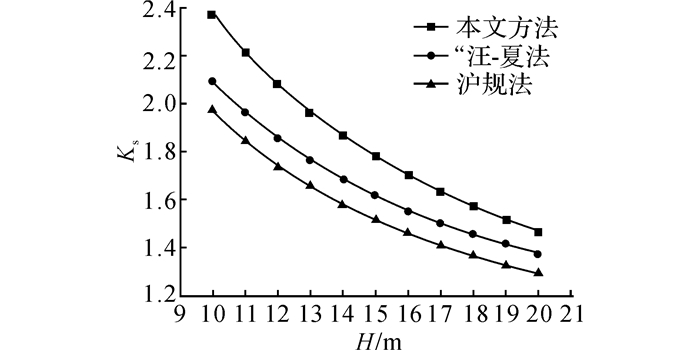
图 12 开挖深度对淤泥质土地基基坑抗隆起安全系数的影响 Fig. 12 Influence of excavation depth on safety factor of anti-upheaval at bottom of muddy soil |
|
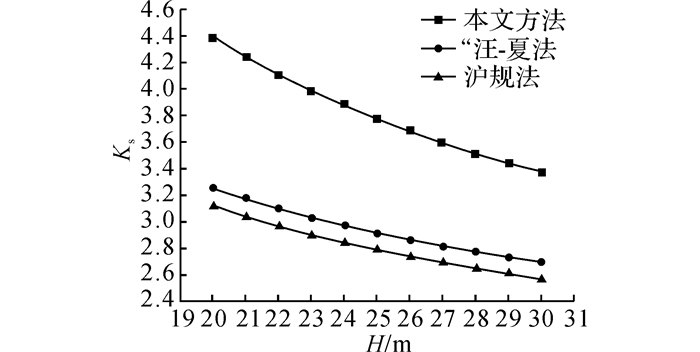
图 13 开挖深度对粉土地基基坑抗隆起安全系数的影响 Fig. 13 Influence of excavation depth on safety factor of anti-upheaval at bottom of silty soil |
从图 12和13中可以看出:在淤泥质土与粉土地基中, 本文方法得到的抗隆起安全稳定系数随开挖深度的变化规律与“汪-夏法”和沪规法一致, 均随着基坑开挖深度的增大而减小, 且变化曲线呈较大的相似性.
4) 土体抗剪强度指标
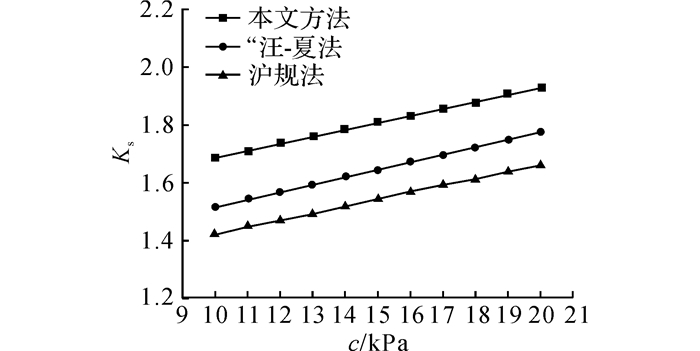
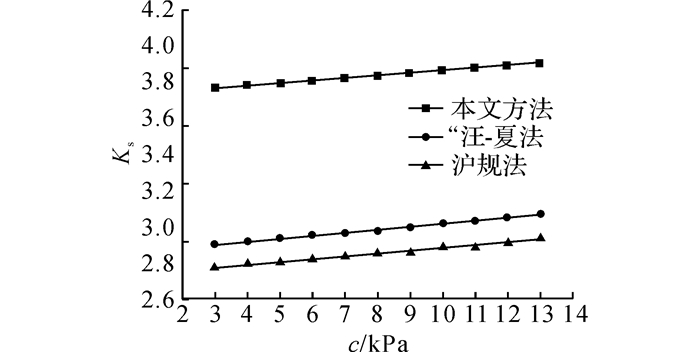
如图 14和15所示分别为淤泥质土及粉土地基基坑中土体黏聚力c对抗隆起稳定安全系数的影响, 分别在基本算例土体黏聚力c的基础上变化±5 kPa, 所得结果如图 14和15所示.从图中可以看出:1)随着土体黏聚力c的增长, 2种土质条件下基坑抗隆起安全系数均发生了近似线性的增长;2)在淤泥质土基坑中, 本文方法得到的抗隆起安全系数从1.68增长至1.93, 增长了14.9%;在粉土基坑中, 抗隆起安全系数从3.76增长至3.90, 增长了3.7%.由此说明对于淤泥质土, 抗隆起安全系数对黏聚力的变化更为敏感.
|
图 14 土体黏聚力对淤泥质土基坑抗隆起安全系数的影响 Fig. 14 Influence of cohesion c on safety factor of anti-upheaval at bottom of muddy soil |
|
图 15 土体黏聚力对粉土地基基坑抗隆起安全系数的影响 Fig. 15 Influence of cohesion c on safety factor of anti-upheaval at bottom of silty soil |
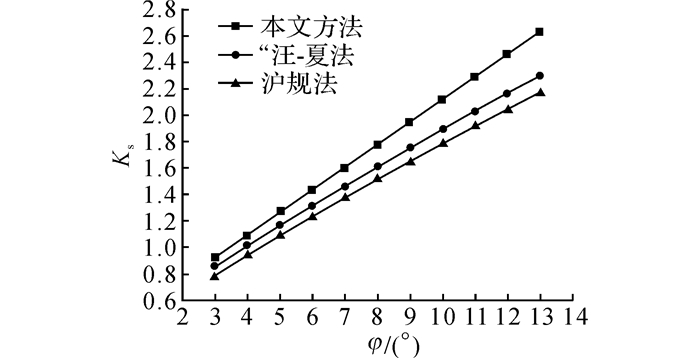
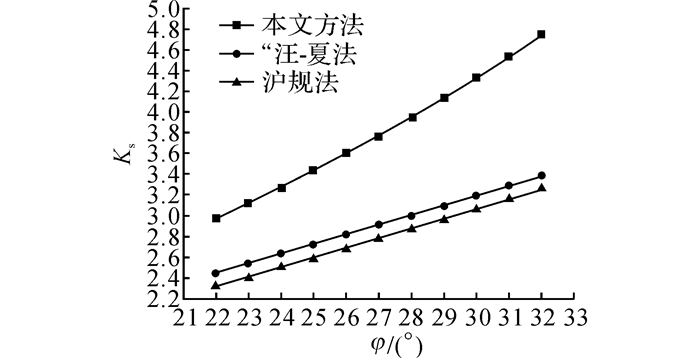
如图 16和17所示分别为淤泥质土及粉土地基基坑中土体内摩擦角φ对抗隆起安全系数的影响.分别在基本算例土体内摩擦角φ的基础上变化±5°, 所得结果如图 16和17所示.从图 16和17可以看出:1)随着土体内摩擦角的增大, 2种土质条件下抗隆起安全系数均发生了较大的增长;2)在淤泥质土基坑中, 本法所得抗隆起安全系数从0.93增长至2.64, 增长了183.9%.在粉土基坑中, 安全系数从2.97增长至4.75, 增长了59.9%.变化范围远远大于调整土体黏聚力后安全系数变化范围, 说明土体内摩擦角对于抗隆起稳定性的影响要大于黏聚力, 同时在淤泥质土地基中的影响也要大于粉土地基.
|
图 16 内摩擦角对淤泥质土地基基坑抗隆起安全系数的影响 Fig. 16 Influence of inner friction angle on safety factor of anti-upheaval at bottom of muddy soil |
|
图 17 内摩擦角对淤泥质土地基基坑抗隆起安全系数的影响 Fig. 17 Influence of inner friction angle on safety factor of anti-upheaval at bottom of silty soil |
5) 被动区加固的影响
当地基地质条件较差时, 往往采用水泥搅拌桩或高压旋喷桩等对基坑被动区土体进行加固.将水泥土与土体视为复合层, 其抗剪强度指标采用Hsieh.H.S(1995)提出的方法确定, 假设复合层内摩擦角与土体相同, 而复合层的黏聚力csp按下式计算:
| $ {{c}_{sp}}=0.25{{\mathit{q}}_{\text{u}}}{{\mathit{I}}_{\text{r}}}+{{\mathit{c}}_{\text{s}}}(1-{{\mathit{I}}_{\text{r}}}). $ | (32) |
式中:qu为水泥土无侧限抗压强度, Ir为加固深度范围水泥土的置换率, cs为土的黏聚力.
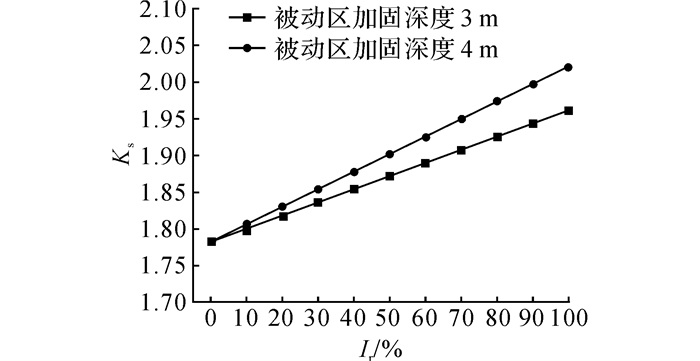
以下从置换率以及加固区深度这2个因素分析被动区加固对抗隆起稳定性的影响, 其余参数与基本算例一致.淤泥质土中被动区加固宽度同基坑宽度, 加固深度分别为3和4 m情况下基坑抗隆起稳定性随置换率变化规律如图 18所示, 水泥土的无侧限抗压强度取为800 kPa.
|
图 18 被动区加固对基坑抗隆起安全系数的影响 Fig. 18 Influence of passive reinforcement on safety factor of anti-upheaval at bottom of muddy soil |
分析结果表明:1)通过对被动区土体加固可以提高基坑抗隆起稳定性, 基坑抗隆起安全系数随着置换率的提高而近似呈线性增加;2)被动区加固深度对基坑抗隆起稳定性同样具有影响, 表现为随着基坑被动区加固深度的增加, 抗隆起稳定安全系数相应提高, 且随置换率增大而增长的速率加快.
3 结论(1) 通过对比常用的4种基坑坑底抗隆起稳定计算方法可见, 建设部《建筑基坑支护技术规程》(JGJ120-2012)要求的安全性最高.另外, 工程经验和算例分析表明:在内摩擦角较小的深厚软土地基中, 现有规范要求的坑底抗隆起稳定安全系数偏高.
(2) 本文提出的考虑基坑宽度影响的抗隆起稳定计算方法具有较好的适应性, 适用于支护结构插入深度大于基坑宽度的狭长型基坑工程.该法避免了狭长型基坑中圆弧滑动面穿过对侧支护结构的问题, 同时其滑动面假定可与汪-夏法实现连续过渡;
(3) 对于狭长型基坑, 随着基坑宽度的减小, 抗隆起稳定安全系数明显增大, 但增长速率逐步放缓;考虑基坑宽度影响后, 随着插入深度的增加抗隆起稳定安全系数的增长速率明显大于常规算法;土体抗剪强度指标中, 内摩擦角对抗隆起稳定安全系数的影响大于黏聚力, 淤泥质土地基中土体抗剪强度指标对抗隆起稳定安全系数的影响大于粉土地基;基坑抗隆起稳定安全系数随着被动加固区置换率的提高近似呈线性增长, 且随着加固区深度的增大, 其增长的速率加快.
| [1] | ZIENKIEWICZ O C, HUMPHESON C, LEWIS R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J]. Géotechnique, 1975, 25(4): 671–689. DOI:10.1680/geot.1975.25.4.671 |
| [2] | CAI F, UGAI K, TOSHIYUKI H. Base stability of circularexcavations in soft clay[J]. Journal of Geotechnical andGeoenvironmental Engineering, ASCE, 2002, 128(8): 702–706. DOI:10.1061/(ASCE)1090-0241(2002)128:8(702) |
| [3] | FEHEEM H, CAI F, UGAI K. Three-dimensional base stability of rectangular excavations in soft soils using FEM[J]. Computers and Geotechnics, 2004, 31(1): 67–74. |
| [4] |
陈福全, 吕艳平, 刘毓氚. 内撑式支护的软土基坑开挖抗隆起稳定性分析[J].
岩土力学, 2008, 29(2): 365–369.
CHEN Fu-quan, LU Yan-ping, LIU Yu-chuan. Base stability of braced excavations in soft clays using FEM[J]. Rock and Soil Mechanics, 2008, 29(2): 365–369. |
| [5] | CHANG M. Basal stability analysis of braced cuts in clay[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2000, 126(3): 276–279. |
| [6] |
黄茂松, 宋晓宇, 秦会来. K0固结黏土基坑抗隆起稳定性上限分析[J].
岩土工程学报, 2008, 30(2): 250–255.
HUANG Mao-song, SONG Xiao-yu, QIN Hui-lai. Basal stability of braced excavations in K0-consolidated soft clay by upper bound method[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 250–255. |
| [7] | TERZAGHI K, PECK R B. Soil mechanics in engineering practice[M]. New York: Wiley, 1948: 235-242. |
| [8] | BJERRUM L, EIDE O. Stability of strutted excavations in clay[J]. Geotechnique, 1956, 6(1): 32–47. DOI:10.1680/geot.1956.6.1.32 |
| [9] |
DG/TJ08-61-2010. 基坑工程技术规范[S]. 上海: 上海市城乡建设和交通委员会, 2010.
DG/TJ08-61-2010. Technical code for design of excavation engineering[S]. Shanghai:Shanghai Municipal Commission of Urban and Rural Construction and Communications, 2010. |
| [10] |
DB33 T1096-2014. 建筑基坑工程技术规程[S]. 杭州: 浙江工商大学出版社, 2014.
DB33 T1096-2014. Technical specification for engineering of foundation excavation[S]. Hangzhou:Zhejiang Gongshang University Press, 2014. http://www.docin.com/p-1012693077.html |
| [11] |
JGJ120-2012. 建筑基坑支护技术规程[S]. 北京: 中国建筑工业出版社, 2012.
JGJ 120-2012. Technical specification for retaining and protection of building foundation excavations[S]. Beijing:China Architecture and Building Press, 2012. http://wenku.baidu.com/view/09a25cb569dc5022aaea0058.html |
| [12] |
. GB50007-2011. 建筑地基基础设计规范[S]. 北京: 中国建筑工业出版社, 2011.
GB 5007-2011. Code for design of building foundation[S]. Beijing:China Architecture and Building Press, 2011. |
| [13] |
张飞, 李静培, 孙长安, 等. 软土狭长深基坑抗隆起破坏模式试验研究[J].
岩土力学, 2016, 37(10): 2748–2754.
ZHANG Fei, LI Jing-pei, SUN Chang-an, et al. Experimental study on casal heave failure mode of narrow-deep excavation in soft clay[J]. Rock and Soil Mechanics, 2016, 37(10): 2748–2754. |
| [14] |
陈孝湘, 赵金飞, 唐自强, 等. 基于强度折减法的狭长基坑坑底抗隆起稳定研究[J].
地下空间与工程学报, 2015, S1: 5–64.
CHEN Xiao-xiang, ZHAO Jin-fei, TANG Zi-qiang, et al. Strength reduction approach for analyzing safety against basal heave of long narrow and deep excavation[J]. Chinese Journal of Underground Space and Engineering, 2015, S1: 5–64. |
| [15] |
彭孔曙, 陈娟, 卢伟平. 窄条形基坑抗隆起稳定问题研究[J].
西部探矿工程, 2015, 12: 160–162.
PENG Kong-shu, CHEN Juan, LU Wei-ping. The study of resistance to uplift stability of narrow foundaton pits[J]. West-China Exploration Engineering, 2015, 12: 160–162. DOI:10.3969/j.issn.1004-5716.2015.05.052 |
| [16] |
王洪新. 考虑二维和三维尺寸效应的基坑抗隆起稳定安全系数[J].
岩土工程学报, 2013, 11: 2144–2152.
WANG Hong-xin. Safety factor of heave-resistant stability considering two-and three-dimensional size effects of foundation pits[J]. Chinese Journal of Geotechnical Engineering, 2013, 11: 2144–2152. |
| [17] |
王洪新. 基坑的尺寸效应及考虑开挖宽度的抗隆起稳定安全系数计算方法[J].
岩土力学, 2016, 10: 433–441.
WANG Hong-xin. Size effect of foundation pits and calculation method of safety factor of heave-resistant stability considering excavation width[J]. Rock and Soil Mechanics, 2016, 10: 433–441. |
| [18] |
汪炳鉴, 夏明耀. 地下连续墙的墙体内力及入土深度问题[J].
岩土工程学报, 1983, 5(3): 103–114.
WANG Bing-jian, XIA Ming-Yao. Embedment depth and internal force of diaphragm wall[J]. Chinese Journal of Geotechnical Engineering, 1983, 5(3): 103–114. |


