2. 浙江大学 岩土工程研究所, 浙江 杭州 310058;
3. 贵州省交通规划勘察设计研究院股份有限公司, 贵州 贵阳 550001;
4. 同济大学 地下建筑与工程系, 上海 200092
2. Institute of Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;
3. Guizhou Transportation Planning Survey and Design Academe Limited Company, Guiyang 550001, China;
4. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
卫生填埋法是目前我国处理城市固体废弃物(municipal solid waste, MSW)的主要方法.为了最大限度地利用空间, 填埋场中的堆体往往越填越高, 边坡也越来越陡, 导致很多地方都相继出现填埋场的稳定破坏现象.同时, 由于MSW的高压缩性和易降解性, 堆体在堆填过程中会发生可观的变形, 从而造成衬垫系统及渗滤液收集和排放系统的破坏, 引起渗滤液的泄漏, 对周围环境和居民造成难以挽回的损失.因此, 稳定和变形问题是填埋场设计的关键.为了解决这些问题, 必须了解MSW的强度与变形特性, 因此对MSW本构关系的研究是非常重要且必要的.
不同于一般土体, MSW具有以下变形特性:
1) 在低轴向应变下MSW具有明显的非线性特性, 当应变较高时会出现硬化趋势[1-2];2)MSW在很高的应变水平(30%以上)下都不易产生明显的破坏面[3-4];3)MSW具有明显的剪缩特性[5];4)MSW的力学和变形特性会受到多方面的影响, 包括组分、降解度、孔隙比、应力历史等[6-7].
针对堆体变形, 一些学者采用或改进传统土力学本构模型, 用于MSW单元体及填埋场工程数值模拟.目前主要分为2类, 一类基于非线性弹性理论, 如双曲线弹性模型[8-11]、复合指数模型等[7];另一类基于弹塑性理论, 如液-生-化多场耦合模型[12]、弹塑性降解蠕变模型[13]、加筋复合材料模型等[14-15].非线性弹性模型具有形式简便, 易于工程应用等特点;由于该类模型建立于增量广义胡克定律基础之上, 较难考虑球张量与偏张量的耦合, 即较难考虑MSW的剪缩特性;弹塑性模型理论较为严密, 且适用于复杂应力路径的模拟, 但模型框架相对复杂, 且模型参数难以获取.
针对当前固废非线性弹性本构的不足, 本文提出了一种可以反映MSW剪缩性和压硬性的非线性弹性模型.基于四参数的模型框架, 采用全量法提出了体积应变和广义剪切应变的具体表达式, 以此获得剪缩模量和压硬模量.并通过其他MSW三轴试验结果的模拟, 对模型进行了验证.
1 MSW的剪缩性土的剪缩性是指土在剪切作用(纯剪或单剪)下也会产生体积变化[16].土体的强度和变形特性会在一定程度上受到剪缩性的影响.试验证明, 在不同的排水条件下, 剪缩性对土体的影响情况是不同的:在不排水条件下, 正常固结黏土在受到不变的剪应力时, 土中的孔隙压力会随着时间而增长, 有效压应力逐渐降低而使土体“软化”, 其变形将很难停滞下来;但如发生排水, 变形可能较快停滞[17].因此对于不同的排水条件, 材料的变形机理和参数指标是不同的.考虑到实际填埋过程中垃圾堆体的渗透性通常为10-3到10-5 cm/s[18-20], 主固结沉降会在较短时间内完成[21], 本文主要研究MSW在排水条件下的力学本构.
对于MSW的剪缩性, 国内外还鲜有相关的试验数据或理论研究.Shi等[5]对MSW试样进行了不同应力路径下的试验, 试验结果表明, MSW在纯剪路径下会产生一定程度上的体积收缩, 即MSW具有剪缩性.
为了进一步验证垃圾的剪缩性, 笔者针对不同龄期和填埋深度的MSW试样, 进行了三轴固结不排水试验.试样均取自成都长安填埋场, 并采用2种方法进行制样:1)对于具有一定填埋龄期和深度的垃圾体, 采用内径为103 mm、高度约240 mm的承模筒进行制样, 试验前先用气缸对垃圾体施加预应力以还原试样原有的应力状态;2)对于新鲜垃圾, 考虑到其无需施加上覆应力, 采取在三轴仪直接固结制样的方式.装样后采取真空和加反压的方式进行饱和, 饱和完成后试样在某个围压下进行24 h左右的固结, 然后以0.4 mm/min的速率进行剪切.试样在以下4种情况下停止剪切:1)随着轴向剪切位移的增加, 轴向荷载不再增加;2)随着轴向剪切位移的增加, 轴向荷载减小;3)试样发生了巨大的变形(如鼓胀);4)达到了三轴仪基座的最大允许变形(该条件是本实验的控制条件).
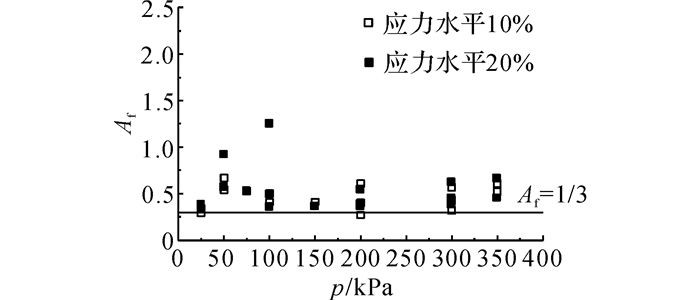
通过对试样应力应变曲线及孔压数据的整理, 可以获得其在不同轴向应变水平下的孔隙水压力系数Af值(剪切破坏时的的孔压系数A, 由于MSW在很高的应变水平下也不易产生明显破坏面, 因此直接取某一特定轴向应变作为MSW的破坏应变), 其结果如图 1所示.图中p为平均正应力,Af亦可用于判断土体的剪缩性, 若Af>1/3, 则认为该土具有剪缩性, 反之若Af<1/3, 则判断该土为剪胀土[22].测试结果表明不同填埋深度与龄期的垃圾Af值绝大多数大于1/3, 大多在0.5左右, 总体上随应力水平的提高而增加, 这初步表明MSW材料剪缩性明显.
|
图 1 部分MSW试样孔隙水压力系数Af值 Fig. 1 Pore water pressure coefficient Af of MSW specimens |
笔者参考中国杭州2000年天子岭填埋场的废弃物成分, 人工配制固废试样以研究固废的强度和变形特性.试样各组分干质量分数wB如表 1所示, 计算得到试样的平均比重为2.06, 尺寸为300 mm× 600 mm, 初始孔隙比为3.试验在经过饱和和固结后, 进行排水剪切试验, 剪切速率取为0.01 mm/s, 围压分别采用100、200、300和400 kPa.
| 表 1 试样各组分干质量分数 Table 1 Physical composition of MSW expressed as dry weight percentage |
试验结果如图 2所示, 其中ε1为轴向应变、εV为体积应变, τ为切应力,从图中可以看到剪应力会随着应变的增大不断发展, 即使应变超过15%试样也没有发生明显的破坏.相比于低围压, 高围压下试样在固结阶段排出的水更多, 而在同样轴向应变条件下由剪切产生的体积应变较小.

|
图 2 三轴固结排水试验结果及拟合效果图 Fig. 2 CD tri-axial tests results and simulating curves |
基于上述的试验结果, 本文提出如式(1)所示的非线性弹性模型框架, 其中K为体变模量, H为剪缩模量, Gp为压硬模量, G为剪切模量;dεV和dγ分别为体积应变增量和广义剪切应变增量.这4个参数一般为应力状态变量的函数.在传统土力学中, 也有考虑剪缩性的非线性弹性本构模型研究, 如Izumi[23]、Graham和Houlsby[24]、Yin.[25]、沈珠江[26]等.这些模型大多如式(1)或式(2)所示, 其中式(1)相对于式(2)能额外考虑压硬性(即平均正应力增量对剪应变增量的影响, 对于MSW, 该项影响较小, 具体见3.3节).
| $ \left. \begin{align} &\rm{d}{{\varepsilon }_{\mathit{V}}}=\rm{ }\!\!~\!\!\rm{ }\frac{\rm{d}\mathit{p}}{\mathit{K}}+\frac{\rm{d}\tau }{\mathit{H}}, \\ &\rm{d}\gamma =\frac{\rm{d}\mathit{p}}{{{\mathit{G}}_{\mathit{p}}}}+\frac{\rm{d}\tau }{3\mathit{G}}. \\ \end{align} \right\} $ | (1) |
| $ \left. \begin{align} &\rm{d}{{\varepsilon }_{\mathit{V}}}=\rm{ }\!\!~\!\!\rm{ }\frac{\rm{d}\mathit{p}}{\mathit{K}}+\frac{\rm{d}\tau }{\mathit{H}}, \\ &\rm{d}\gamma =\frac{\rm{d}\tau }{3\mathit{G}}. \\ \end{align} \right\} $ | (2) |
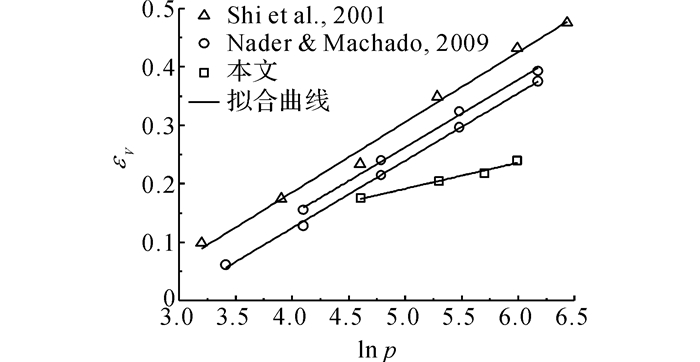
在等压固结试验中, 试样在静水压力作用下压缩固结.参照Domaschuk[27]的做法, 根据试样在试验中孔隙比的变化, 可以求得试样的体积应变和平均正应力的关系.与一般土体类似, MSW试样的体变-自然对数平均正应力曲线也可近似为一条直线, 如图 3所示[28-29].本文采用式(3)描述该线性关系, εV0、λ1为拟合参数, εV0=-0.031 4, λ1=0.044 6, 微分后得式(4), 可求得等向压缩条件下的体变模量.
| $ {{\varepsilon }_{\rm{V}}}={{\varepsilon }_{\mathit{V}0}}+{{\lambda }_{1}}\rm{ln}\mathit{p}. $ | (3) |
| $ K=~\frac{\rm{d}\mathit{p}}{\rm{d}{{\varepsilon }_{\rm{V}}}}=\frac{\mathit{p}}{{{\lambda }_{1}}}. $ | (4) |
|
图 3 等压固结试验体变-自然对数平均正应力曲线 Fig. 3 Volumetric strain-natural logarithm of mean normal stress relationship of MSW on isotropic consolidation conditions |
对于更为一般的应力状态, 加载过程中体变由平均正应力p和切应力τ同时产生.将加载过程中体积应变分为正应力产生和剪切应力产生2部分(体积应变基于固结前试样), 如式(5)所示:
| $ {{\varepsilon }_{\mathit{V}}}={{\varepsilon }_{\mathit{Vp}}}+{{\varepsilon }_{\mathit{V}\tau }}. $ | (5) |
式中:εVp为正应力效应产生的体积应变, εVτ为剪应力效应产生的体积应变.
若假设加载过程中正应力产生的体积应变可由式(3)进行计算, 经试算比选, 剪切应力产生的体积应变可由二次函数描述, 即
| $ {{\varepsilon }_{\mathit{Vp}}}=\mathit{f}\left( \mathit{p}, \tau \right)=\mathit{a}\cdot \rm{ }{{\left( \frac{\tau }{\mathit{p}} \right)}^{\rm{2}}}. $ | (6) |
则总的体积应变可由式(7)表示:
| $ {{\varepsilon }_{\mathit{V}}}={{\varepsilon }_{\mathit{Vp}}}+{{\varepsilon }_{\mathit{Vq}}}={{\varepsilon }_{V0}}+{{\lambda }_{1}}\rm{ln}\mathit{p}+\mathit{a}\cdot \rm{ }{{\left( \frac{\tau }{\mathit{p}} \right)}^{\rm{2}}}. $ | (7) |
式中:a为拟合参数.
图 4给出了分别采用式(3)(不考虑剪缩模量)和式(7)(考虑剪缩模量)计算所得的体积应变曲线.可以看到, 式(3)的拟合结果与试验结果相去甚远.由于未考虑由偏应力产生的体积应变(即剪缩性), 由式(3)(计算所得的体积应变远低于实际值, 两者的差值随着加载的进行而增大, 在轴向应变达到15%时, 误差会超过60%.而采用式(7)对体积应变进行拟合时, 拟合参数a=0.033 62, 拟合效果明显改善, 在轴向应变达到15%时误差小于10%, 这反映了模型考虑剪缩的必要性.对式(7)进行微分, 即可获得体变模量和剪缩模量的具体表达式:
| $ \rm{d}{{\varepsilon }_{\mathit{V}}}=\left( \frac{{{\lambda }_{1}}}{\mathit{p}}-\frac{2\mathit{a}{{\tau }^{2}}}{{{\mathit{p}}^{3}}} \right)\rm{d}\mathit{p}+\frac{2\mathit{a}\tau }{{{\mathit{p}}^{2}}}\rm{d}\tau . $ | (8) |

|
图 4 体积应变拟合效果图 Fig. 4 Experimental and simulating MSW volumetric strain versus mean normal stress curves |
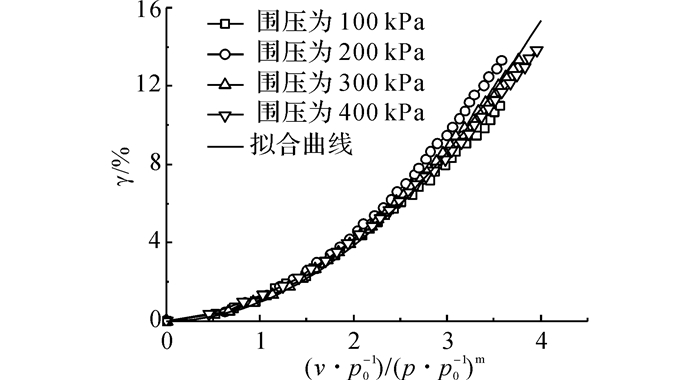
通过对图 2中的试验数据进行处理可以获得广义剪切应变γ=2·(ε1-ε3)/3与偏应力τ的关系, 如图 5所示.不同围压下的多条曲线呈分散化状态, 因此采用式(9)对各条曲线进行归一化, 其中p0=1 kPa使量纲和谐.对归一化后的主干曲线采用二次函数进行拟合, 如图 6所示, c和m为拟合参数, c=0.009 6, m=0.74.从图 5中可以看到式(9)的拟合效果较好(实线), 图 5同时给出了不考虑硬化模量后的拟合效果(虚线), 可见硬化模量会对拟合结果造成一定的影响, 但相比于剪缩模量, 该影响较小.
| $ \gamma =\mathit{c}{{\left[\frac{\tau /{{\mathit{p}}_{0}}~}{{{\left( \mathit{p}/{{\mathit{p}}_{0}} \right)}^{\mathit{m}}}~} \right]}^{2}}. $ | (9) |

|
图 5 广义剪切应变拟合效果图 Fig. 5 Experimental and simulating curves of generalized shear strain |
|
图 6 广义剪切应变归一化及拟合图 Fig. 6 Normalized curves and quadratic fitting curve of generalized shear |
对式(3)进行微分, 即可获得压硬模量和剪切模量的具体表达式:
| $ {\rm{d}}\gamma =\mathit{c}\left( -\frac{2m{{\tau }^{2}}}{{{p}^{2m+1}}}{\rm{d}}\mathit{p}+\frac{2\tau }{{{p}^{2m}}}~{\rm{d}}\tau \right)p_{0}^{2\left( m-1 \right)~}. $ | (10) |
综上, 体积应变与广义剪应变的全量和增量表达式如式(11)、(12)所示:
| $ \left. \begin{align} &{{\varepsilon }_{V}}={{\varepsilon }_{V0}}+{{\lambda }_{1}}{\rm{ln}}\mathit{p}+a{{\left( \frac{\tau }{p} \right)}^{2}}; \\ &\gamma =\mathit{c}{{\left[\frac{\tau /{{\mathit{p}}_{0}}~}{{{\left( \mathit{p}/{{\mathit{p}}_{0}} \right)}^{\mathit{m}}}~} \right]}^{2}}. \\ \end{align} \right\} $ | (11) |
| $ \left. \begin{align} &{\rm{d}}{{\varepsilon }_{\mathit{V}}}=\left( \frac{{{\lambda }_{1}}}{\mathit{p}}-\frac{2a{{\tau }^{2}}}{{{\mathit{p}}^{3}}} \right){\rm{d}}\mathit{p}+\frac{2a\tau }{{{p}^{2}}}{\rm{d}}\tau, \\ &{\rm{d}}\gamma =\mathit{c}\left( -\frac{2m{{\tau }^{2}}}{{{p}^{2m+1}}}{\rm{d}}\tau +\frac{2\tau }{{{p}^{2m}}}~{\rm{d}}\tau \right)p_{0}^{2\left( m-1 \right)~}. \\ \end{align} \right\} $ | (12) |
这样就建立了四参数的非线性弹性模型, 参数εV0和λ1可由等压固结试验获得, 两者分别为体变-自然对数平均正应力曲线的截距和斜率, 参数a、c和m可由三轴固结排水试验获得.利用本模型对图 2的三轴试验数据进行拟合, 由于MSW的高离散性在拟合体变时有一定误差, 但整体上该模型的拟合效果较好, 且能够合理地描述固废的剪缩和硬化特性.
3 模型验证为验证所提出的四参数模型的合理性, 拟采用该模型去拟合Machado(2002)和Vilar(2004)的MSW室内试验结果, 通过体变-剪应变-轴变之间的关系(式(13)), 可由本文提出的模型拟合三轴试验中的应力应变和体变-轴变曲线.
| $ \left. \begin{align} &{{\varepsilon }_{V}}={{\varepsilon }_{1}}+2{{\varepsilon }_{3}}, \\ &\gamma =\frac{2}{3}\left( {{\varepsilon }_{1}}-{{\varepsilon }_{3}} \right).\rm{ } \\ \end{align} \right\} $ | (13) |
式中, ε3为径向应变.
3.1 Machado(2002)Machado等[30]研究的固废样本取自于位于圣保罗郊区的Bandeirantes卫生填埋场的2个钻孔中, 实验室内所用的试验样本龄期为15 a, 其具体配比见表 2, 其中的糊状物包括有机质以及不同比例的土体.
| 表 2 试样各组分干质量分数 Table 2 Physical composition of MSW expressed as dry weight percentage |
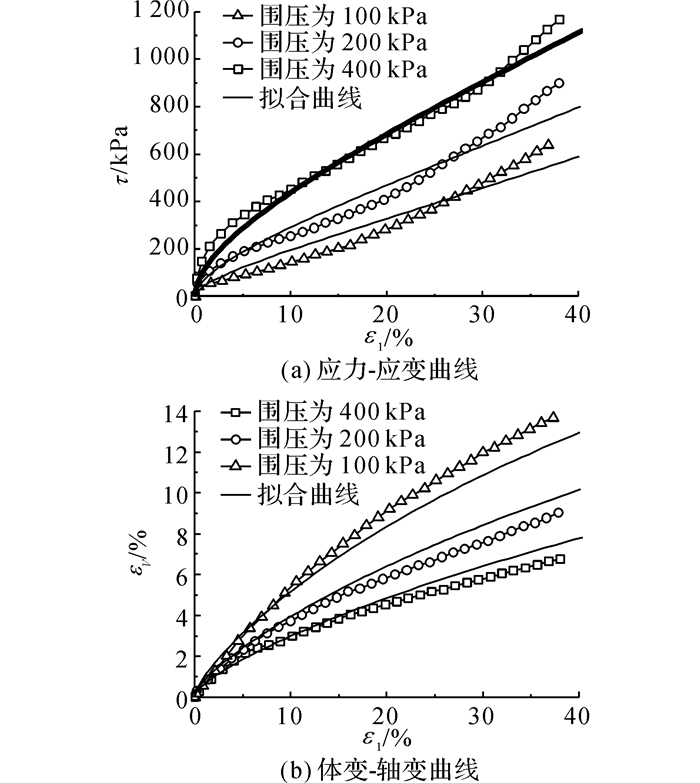
试样通过静态压实成型, 平均容重为10 kN/m3, 试样的直径采用150和200 mm, 高度采用300和400 mm, 对在天然湿度下(67%)的固废试样进行三轴固结排水试验, 加载速率采用0.7 mm/min, 分别对各试样施加100、200、400 kPa的荷载.采用本文所提出的模型对试验结果进行拟合, 拟合效果如图 7所示.
|
图 7 Machado(2002)试验结果及拟合效果图 Fig. 7 Typical results obtained from CD tri-axial tests and simulating curves |
从图 7中可以看到, 该模型对试样应力应变曲线的拟合效果较好, 对于体积应变, 拟合曲线与试验数据有一定误差, 但整体上误差较小, 能够较好地反映试样的变形趋势.
3.2 Vilar and Carvalho(2004)Vilar等[31]采用的固废样本同样取自于Bandeirantes卫生填埋场, 其具体配比同表 2.其中一批样本取自于0~18 m的深度处, 除容重为12 kN/m3外, 试样的尺寸、加载速率、各级荷载大小均与Machado(2002)相同.Vilar和Carvalho分别对在天然湿度下(67%)和饱和条件下的固废试样进行了三轴固结排水试验, 试验结果和模型的拟合效果如图 8和9所示.
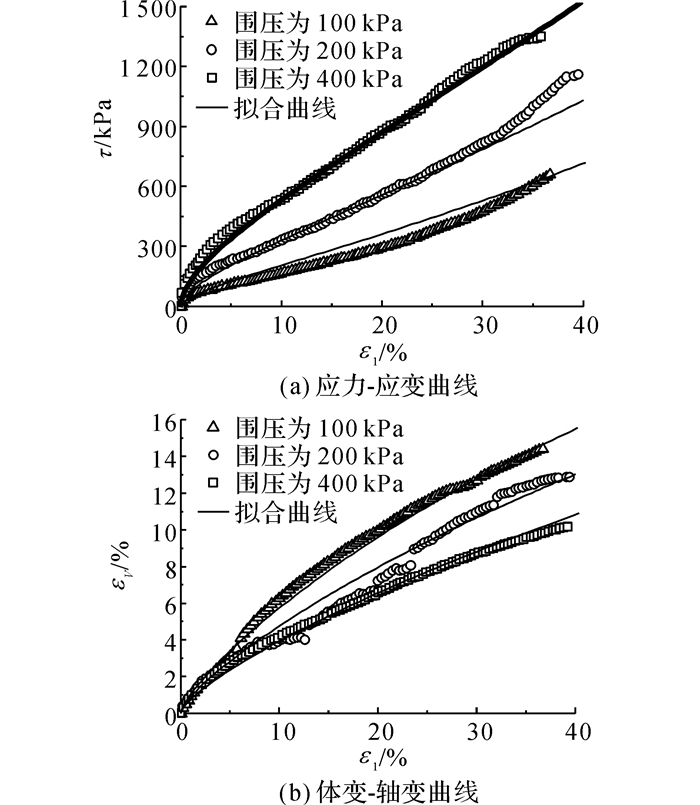
|
图 8 Vilar和Carvalho(2004)天然湿度试样试验结果及拟合效果图 Fig. 8 CD tri-axial tests results and simulating curves on samples molded at natural moisture content |

|
图 9 Vilar和Carvalho(2004)饱和试样试验结果及拟合效果图 Fig. 9 CD tri-axial tests results and simulating curves on saturated samples |
从图 8和9中可以看到, 在低应变水平和高应变水平下, 模型都能很好地拟合试样的体积应变曲线.对于天然湿度下的试样, 应力应变曲线的拟合效果也较好;而对于饱和条件下的试样, 试样在加载后期的硬化效应较大, 拟合曲线与试验结果有所偏离.
表 3给出了上述3个案例中所有拟合参数的具体取值, 这些参数会随着试验条件和固废试样的不同而产生变化, 但离散性较小, 可以认为参数较为稳定.
| 表 3 拟合参数具体取值 Table 3 The values of model parameters |
本文基于等压固结试验和三轴固结排水试验的结果, 提出了一种可以反映MSW剪缩性和压硬性的非线性弹性模型, 并通过拟合其他MSW试验的试验结果, 对模型进行了验证.该模型具有以下特点:
(1) 采用了能够同时考虑剪缩性和压硬性的四参数模型框架, 基于此框架, 通过对已有试验数据的归一化, 建立了体积应变和广义剪切应变的全量表达式, 同时获得了4参数的具体表达式.模型适用于一般加载情况.
(2) 模型的形式简单, 便于工程应用, 拟合参数较少, 且其取值均可从等压固结试验和三轴固结排水试验中获得.
(3) 通过对不同MSW试验结果的模拟表明, 该模型能够合理反映固结围压对试样应力应变关系的影响规律, 以及试样随固结围压的增大而压缩性降低的现象.
| [1] | SINGH M K, FLEMING I R. Application of a hyperbolic model to municipal solid waste[J]. Geotechnique, 2011, 61(7): 533–547. DOI:10.1680/geot.8.P.051 |
| [2] | ZHANG Zhen-ying, WU Da-zhi, YAN Li-jun. Study on the non-linear shear strength properties of municipal solid waste[C]//Geo-Shanghai. Shanghai:2015:90-99. |
| [3] | BRAY J D, ZEKKOS D, KAVAZANJIAN E, et al. Shear strength of municipal solid waste[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2012, 135(6): 709–722. |
| [4] | MACHADO S L, CARVALHO M F, VILAR O M. Constitutive model for municipal solid waste[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2002, 128(11): 940–951. |
| [5] | LI X, SHI J. Stress-strain responses and yielding characteristics of a municipal solid waste (MSW) considering the effect of the stress path[J]. Environmental Earth Sciences, 2015, 73(7): 3901–3912. DOI:10.1007/s12665-014-3674-y |
| [6] | WALL D K, ZEISS C. Municipal Landfill Biodegradation and Settlement[J]. Journal of Environmental Engineering, 1995, 121(121): 214–224. |
| [7] |
陈云敏, 高登, 朱斌. 城市固体废弃物的复合指数应力-应变模型及其应用[J].
岩土工程学报, 2009, 31(7): 1020–1029.
CHEN Yun-min, GAO Deng, ZHU Bin. Composite exponential stress-strain model of municipal solid waste and its application[J]. Yantu Gongcheng Xuebao/chinese Journal of Geotechnical Engineering, 2009, 31(7): 1020–1029. |
| [8] | SINGH M K, SHARMA J S, FLEMING I R. A design chart for estimation of horizontal displacement in municipal landfills[J]. Waste Management, 2009, 29(5): 1577–87. DOI:10.1016/j.wasman.2008.10.003 |
| [9] | SINGH M K, FLEMING I R. Application of a hyperbolic model to municipal solid waste[J]. Geotechnique, 2011, 61(7): 533–547. DOI:10.1680/geot.8.P.051 |
| [10] | REDDY K R, MOTAN E S, KOSGI S. Interface shear behavior of landfill composite liner systems:a finite element analysis[J]. Geosynthetics International, 2014, 3(2): 247–275. |
| [11] | FILZ G M, ESTERHUIZEN J J B, DDUNCAN J M. Progressive failure of lined waste impoundments[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2001, 222(222): 435–480. |
| [12] | MCDOUGALL J. A hydro-bio-mechanical model for settlement and other behaviour in landfilled waste[J]. Computers & Geotechnics, 2007, 34(4): 229–246. |
| [13] | BABU G L S, REDDY K R, CHOUKSEY S K. Constitutive model for municipal solid waste incorporating mechanical creep and biodegradation-induced compression[J]. Waste Management, 2010, 30(1): 11–22. DOI:10.1016/j.wasman.2009.09.005 |
| [14] | ZHANG B. Constitutive modelling of municipal solid waste[J]. Loughborough University, 2007: 0–228. |
| [15] | MACHADO S L, VILAR O M, CARVALHO M F. Constitutive model for long term municipal solid waste mechanical behavior[J]. Computers & Geotechnics, 2008, 35(5): 775–790. |
| [16] | MESCHYAN S R. Dilatancy and contraction of clayey soils under simple shear[J]. Soil Mechanics & Foundation Engineering, 1998, 35(1): 13–16. |
| [17] | BJERRUM L, SIMONS N, TORBLAA I. The Effect of Time on the shear strength of a Soft Marine Clay[C]//Proc. of Brussel Conf. on Earth Pressure Problems. Brussels:. 1958, 1:148-158. |
| [18] | OWEIS I S, SMITH D A, ELLWOOD R B, et al. Hydraulic Characteristics of Municipal Refuse[J]. Journal of Geotechnical Engineering, 1990, 116(4): 539–553. DOI:10.1061/(ASCE)0733-9410(1990)116:4(539) |
| [19] | REDDY K R, HETTIARACHCHI H, PARAKALLA N S, et al. Geotechnical properties of fresh municipal solid waste at Orchard Hills Landfill, USA[J]. Waste Management, 2009, 29(2): 952–9. DOI:10.1016/j.wasman.2008.05.011 |
| [20] | BEAVEN R P, POWRIE W, ZARDAVA K. Hydraulic Properties of MSW[C]//International Symposium on Waste Mechanics. New orleans, Louisiana, United States:2010 American Society of Civil Engineers, 1994:103-104. http://agris.fao.org/agris-search/search.do?recordID=AV2012056422 |
| [21] | WALL D K, ZEISS C. Municipal landfill biodegradation and settlement[J]. Journal of Environmental Engineering, 1995, 121(121): 214–224. |
| [22] | SKEMPTON A W. Mechanical Properties of Soils (ed. M. Reiner)[M]. [S. l.]: Chapter X, Building Materials, 1954. |
| [23] | EDITOR H S G. Finite element analysis of stresses and movements in excavations[J]. Journal of the Society for Information Display, 1978, 15(1): 137. |
| [24] | GRAHAM J, HOULSBY G T. Anisotropic elasticity of a natural clay[J]. Gilbert FlexiVan-Incorporated, 1983, 23(2): 165–180. |
| [25] | YIN J H, SAADAT F, GRAHAM J. Constitutive modelling of a compacted sand-bentonite mixture using three-modulus hypoelasticity[J]. Canadian Geotechnical Journal, 2011, 27(3): 365–372. |
| [26] |
沈珠江. 考虑剪胀性的土和石料的非线性应力应变模式[J].
水利水运工程学报, 1986, 04(4): 3–16.
SHEN Zhu-jiang. A nonlinear dilatant stress-strain model for soils and rock materials[J]. Hydro-Science and Engineering, 1986, 04(4): 3–16. |
| [27] | DOMASCHUK L, VALLIAPPAN P. Nonlinear settlement analysis by finite element[J]. Journal of the Geotechnical Engineering Division, 1975, 101: 601–614. |
| [28] | SHARIATMADARI N, MACHADO S L, NOORZAD A, et al. Municipal solid waste effective stress analysis[J]. Waste Management, 2009, 29(12): 2918–2930. DOI:10.1016/j.wasman.2009.07.009 |
| [29] |
施建勇, 陆晓平. 城市生活垃圾变形性质试验研究[J].
河海大学学报:自然科学版, 2001, B12(B12): 131–134.
SHI Jian-yong, LU Xiao-pin. Experimental study on deformation behavior of solid waste from Xiaping Rubbish-Damping field[J]. Journal of Hohai University:Natural Sciences, 2001, B12(B12): 131–134. |
| [30] | MACHADO S L, CARVALHO M F, VILAR O M. Constitutive model for municipal solid waste[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2002, 128(11): 940–951. |
| [31] | LINK R E, VILAR O M, CARVALHO M. Mechanical properties of municipal solid waste[J]. Journal of Testing & Evaluation, 2004, 32(6): 209–217. |


