给水管网漏损是市政管网普遍遇到的问题[1], 漏损控制也成为研究热点.在众多漏损控制方法中, 给水管网的压力控制被认为是一个有效的手段.在保证输送水压基本要求的基础上, 通过调整给水管网的运行压力, 来减少管网的漏损量[2-4].为了有效地进行压力控制, 需要充分理解压力和渗漏速率的关系.传统的管网渗漏速率和水压的关系根据圆孔出流公式确定[5], 流量和压力的平方根成正比, 即漏损指数为0.5.然而很多现场调查和实验研究表明, 管网的漏损指数往往大于0.5, 甚至大于1[6].由此可见, 管网中的压力控制会比预期的更有效果.
土体的存在对渗流量会产生影响已经被许多研究者证实.Van等[7]漏损实验表明管道的材料、漏损口周围土体的性质、漏损口的大小以及管内水压都对漏损量有影响.杨艳等[8]通过实验证明了管周土对孔口入流的影响.Awad等[9]对漏损口周围土体的稳定进行了研究, 结果显示由于管网的漏损, 使得周围土体的孔隙水压显著增大.Noack等[10]将管道分别埋置在黏性土和砂土中进行管漏实验研究, 发现在这2种不同性质的土体中, 管漏的渗透指数有着极大的不同, 在砂土中接近于0.5, 而在黏性土中接近于1, 管道周围土体对管网漏损影响不可忽视.Walski等[11]提出可将管道漏损的水头损失h, 分为漏损口的水头损失h1和土体中的水头损失h2.郭帅等[12]在假设破损口为长线性破损口的基础上, 将管内水渗入周围土中的运动简化为二维模型, 得到漏损率和压力成线性关系, 分析了土体性质对渗漏量的影响, 为长线性漏损量的计算提供了可靠的依据.
从上述可知, 在埋地管道中, 漏损口周围土体对漏损系数有重要影响, 而且管网渗漏是往往一个三维的问题, 尚未得出合理的渗漏量计算方法.鉴此,本文通过将管道漏损口周围土体中的复杂渗流简化为以破损口为点源的球形渗漏模型, 结合孔口出流推导了考虑土体影响的三维渗漏量计算公式并设计实验进行验证.
1 渗漏计算的理论推导给水管网渗漏量受到许多因素的影响, 本文主要考虑漏损口周围土体性质对渗漏量的影响.为了公式推导的方便, 提出了如下的假设条件:
1) 考虑到多数管网漏损研究以圆孔为基础, 因此本文假设漏损口为圆形的孔口;
2) 随着给水管道的漏损, 管道周围的土体已经达到完全饱和;
3) 孔隙水不可以压缩, 渗流符合达西渗流定律;
4) 土体不发生变形, 并且各向同性, 均质.
Zoueshtiagh等[13]对土体中的孔口出流进行了实验研究, 通过表面流速的测定发现漏损口周围土体中的流场的分布可以近似为漏损口为点源的渗流场.Collins等[14]CFD模型结果显示漏损口的水流方向包括管道周围的各个方向.Van等[15]对漏损口土体中的压力进行测量, 发现水头的损失主要集中在漏损口附近的土体.一些学者也通过有限元分析以及实验测量发现管道漏损点周围会形成以漏损点为中心的渗流场[16-17].杨艳[18]在管道破损口污染物入侵计算时, 假定了渗流影响区.研究表明只需对破损口一定距离范围为R0的球体进行计算, 在R0外流速较慢, 水头损失可以忽略, 在并且可以将圆形破损孔口面积简化为半径为r0的球体, 该模型有效的预测了污染物入侵量.因此, 本文在点源模型的基础上, 建立了理想状态下考虑土体影响的管道三维的渗漏简化计算方法.
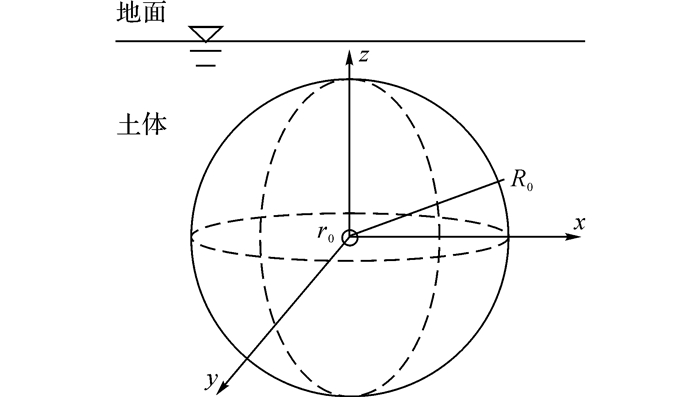
简化模型如图 1所示, 其中r0为漏损孔口等效半径, R0为渗流计算边界, 漏损口的等效半径r0由面积等效的方式进行计算得
| $ 4\pi \mathit{r}_{0}^{2}=\pi \mathit{d}_{0}^{2}/4. $ | (1) |
|
图 1 简化的渗漏模型 Fig. 1 Simplified leakage model |
式中:d0为管道圆形漏损口的直径(mm).由式(1)可知r0=0.25d0.
管道漏损处孔口压力损失由孔口的水头损失h1和土体水头h2组成.其中孔口处的水头损失可以由孔口出流公式得到
| $ {{\mathit{h}}_{1}}=\frac{8\mathit{q}_{\mathit{V}}^{2}~}{{{\pi }^{2}}\mathit{d}_{0}^{2}\mathit{g}}\frac{1}{\mathit{C}_{\text{d}}^{2}}. $ | (2) |
式中:qV为孔口流量(m3/s), g为重力加速度(m2/s), Cd为流量系数.
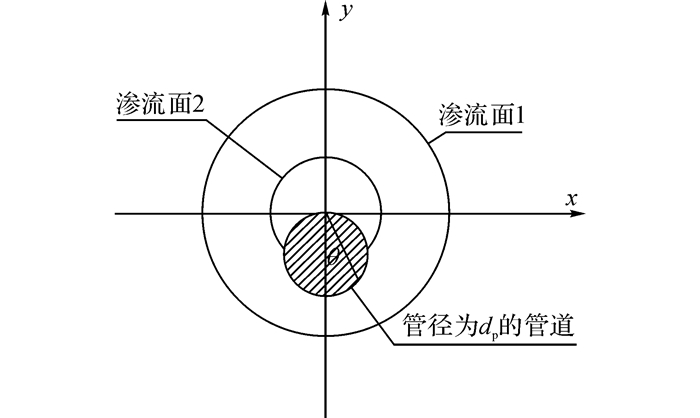
如图 2所示, 以管道漏损处圆孔中心为参考系原点, 建立三维的笛卡尔直角坐标系.管道的直径为dp, 饱和土层中的水的运动符合达西定律[19], 则土体中的流速可表示为
| $ \mathit{v}=\mathit{ki}=\mathit{k}\Delta {{\mathit{h}}_{2}}/\Delta \mathit{r}.~ $ | (3) |
|
图 2 给水管影响下渗漏面计算示意图 Fig. 2 Calculation scheme of the seepage area considering the pipe |
式中:v为土体中水的流速(m/s), i为土体水的压力梯度, r为渗流区域内的到原点的距离(m), k为土体的渗透系数(m/s), Δh2为土体水头差值, Δr为距离差值.
由渗流区流场为球形的假设条件可知, 在距离原点为r的流速为
| $ \mathit{v}={{\mathit{q}}_{\mathit{V}\rm{s}}}/{{\mathit{A}}_{\rm{s}}}={{\mathit{q}}_{\mathit{V}\rm{s}}}/(4\pi {{\mathit{r}}^{2}}).\rm{ } $ | (4) |
式中:As为渗流面积(m2), qVs为通过土体的流量(m3/s)把式(4)代入到式(3)中并且积分可得
| $ {{\mathit{h}}_{2}}=\int_{{{r}_{0}}}^{{{\mathit{R}}_{0}}}{\left( \frac{{{\mathit{q}}_{\mathit{V}\text{s}}}}{\mathit{k}{{\mathit{A}}_{\text{s}}}}~ \right)\text{d}\mathit{r}\text{=}\frac{{{\mathit{q}}_{\mathit{V}\text{s}}}~}{\text{4}\pi \mathit{k}}(\frac{\text{1}}{{{r}_{\text{0}}}}-\frac{\text{1}}{{{R}_{\text{0}}}}).} $ | (5) |
在实际运行的给水管网的中, 埋深埋置深度远远大于管径和漏损孔径, 即R0≫r0所以式(5)可以简化为
| $ {{\mathit{h}}_{2}}=\frac{{{\mathit{q}}_{\mathit{V}\rm{s}}}}{\pi \mathit{k}{{\mathit{d}}_{0}}}. $ | (6) |
但是管道本身的存在会占据渗流区域[16], 从而对土体中的渗流产生影响, 由此对h2的计算引入管道影响的几何系数G进行调整, 由此得到
| $ {{\mathit{h}}_{2}}=\rm{ }\frac{\mathit{G}{{\mathit{q}}_{\mathit{V}\rm{s}}}}{\mathit{k}{{\mathit{d}}_{0}}}. $ | (7) |
对渗流面积As的计算实际上是一个分段函数, 如图(2)所示.
当r≤dp时, 对于渗流面2进行积分, 当r>dp时对于渗流面1进行积分.于是As的面积可以表示为
当r>dp时
| $ {{\mathit{A}}_{\rm{s}}}=2\pi {{r}^{2}}+4\mathit{r}\int_{0}^{\pi /2}{\sqrt{{{\mathit{r}}^{2}}-\mathit{d}_{\rm{p}}^{2}\rm{co}{{\rm{s}}^{2}}\theta }~\rm{d}\theta .} $ | (8) |
当r≤dp时
| $ {{\mathit{A}}_{\rm{s}}}=2\pi {{r}^{2}}+4\mathit{r}\int_{\rm{arcos}\frac{\mathit{r}}{{{\mathit{d}}_{\rm{p}}}}}^{\pi /2}{\sqrt{{{\mathit{r}}^{2}}-\mathit{d}_{\rm{p}}^{2}\rm{co}{{\rm{s}}^{2}}\theta }~\rm{d}\theta .} $ | (9) |
与式(6)类似, 可得到实际的土体水头损失h2为
| $ {{\mathit{h}}_{2}}=\mathit{M}{{\mathit{q}}_{\mathit{V}\rm{s}}}/\left( \pi \mathit{k}{{\mathit{d}}_{0}} \right).\rm{ } $ | (10) |
式中:参数
| $ \mathit{M}=\mathit{G}/{{\mathit{d}}_{0}}. $ | (11) |
用matlab程序用二分法对参数M在不同管径和破损口直径进行了计算, 其计算结果如表 1所示.
将表中的数据代入式(11)中, G的值是随着dp而变化, 将G和dp的关系的进行拟合得到
| $ \mathit{G}=0.58\mathit{d}_{\rm{p}}^{0.02}. $ | (12) |
| 表 1 不同管径和破损直径下M的结果 Table 1 Result of M at different diameters of the pipe and leakage orifice |
由于土体中的渗透流量qVs=qV将式(12)代入(7), 结合式(2)于是得到渗漏流量计算的的三维近似解:
| $ \mathit{h}=\frac{8\mathit{q}V_{\rm{s}}^{2}}{~{{\pi }^{2}}\mathit{d}_{0}^{2}\mathit{g}}\frac{1}{\mathit{C}_{\rm{d}}^{2}}+\frac{0.58\mathit{d}_{\rm{p}}^{0.02}\mathit{q}{{\mathit{V}}_{\rm{s}}}}{\mathit{k}{{\mathit{d}}_{0}}}~. $ | (13) |
由式(13)可知渗漏处孔口水头压力损失有2部分组成, 即右边第1项的孔口水头损失和第2项的土体中的水头损失.从公式中可以看出渗漏量与土体的渗透性、管径、管内压力、孔洞大小有着密切的关系.该公式很好地解释了渗漏指数大于0.5理论值的事实.
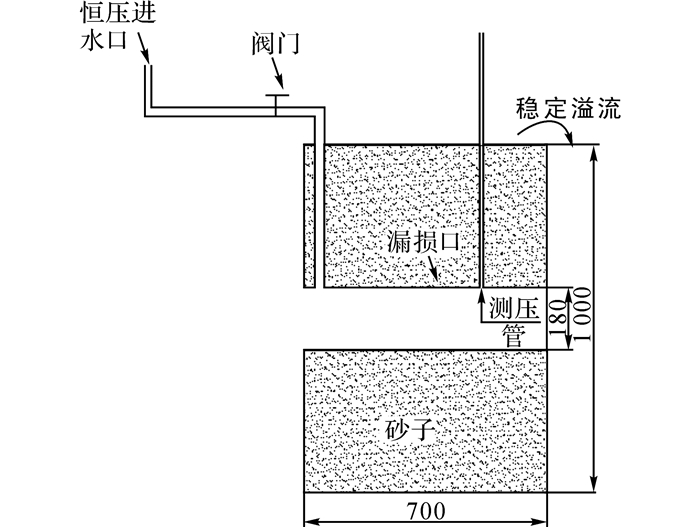
2 实验验证 2.1 实验装置和方法实验模拟地下管道的渗漏, 实验装置由有机玻璃制作.实验简图如图 3所示, 模型箱的长700 mm, 宽700 mm, 高为1 000 mm, 采用的圆管外径为180 mm, 漏损口为圆孔, 为了防止漏损口中有砂子流入, 在孔洞处设置纱网, 孔口采用的直径d0分别为5、10、20 mm进行实验.在漏损圆孔附近管壁设置一个测压管, 用于测量渗漏时漏损口的水压力.
|
图 3 漏损实验装置图 Fig. 3 Schematics of the leakage experiments |
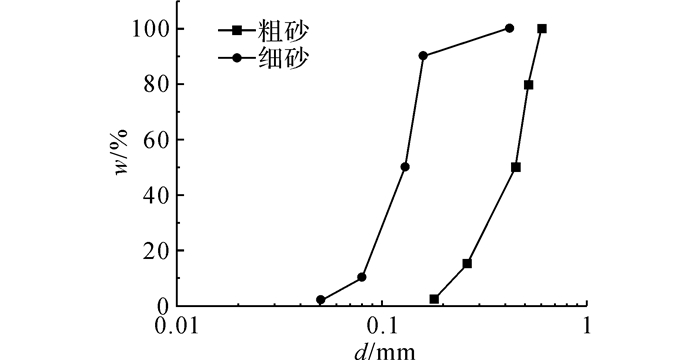
实验采用2种砂样:细砂, 粗砂.细砂和粗砂的不均匀系数d60/d10分别为1.41, 1.6, 砂样级配均匀[20].砂样的颗粒级配曲线如图 4所示, 其中w为小于某粒径的含量, d为颗粒粒径.砂子颗粒密度测得为2.65 g/cm3, 2种砂样平均粒径ds =0.13和0.45 mm, 实验中采用控制砂样空隙率n=0.5.
|
图 4 砂颗粒级配曲线 Fig. 4 Cumulative size distribution of sand |
实验前先测量砂样在孔隙率n=0.5时的渗透系数, 采用的方法为常水头试验进行测试, 具体测量步骤可见参考文献[20].实验测得到细砂和粗砂的渗透系数k分别为5.77×10-2和3.16×10-1cm/s.
实验用水来实验大厅的溢流水箱, 使得实验时能够得到恒定的水压力.流量大小用阀门进行控制.实验过程中逐渐加大阀门来改变流量, 并记录稳定后测压管高度.模型箱中通过溢流保持恒定的水位, 通过测量一定时间内的溢流水的重量, 换算成体积来计算渗流量.在流量较大时, 可以通过管路中的流量计测流量.
2.2 实验程序1) 每组实验分层装砂, 采用控制孔隙率n称量计算所需的砂子重量和水的体积.然后放入模型箱, 压实到计算高度.装载和压实到400 mm后, 放入实验管道, 管道用铁架进行固定, 以防止在填砂时发生位移.然后继续填砂, 直到砂子高度达到孔口高度400 mm.在装完砂子后静置一段时间, 使得实验砂子充分饱和.
2) 展开实验, 打开阀门, 等到模型箱中慢慢有水溢出, 观察测压管读数.当测验管读数稳定后测量流量, 连续测3次并取平均值.
3) 一组实验完成后, 调节阀门, 改变流量, 重复步骤2).完成当前漏损口管道和砂样后, 更换管道和砂样, 直到完成所有实验.
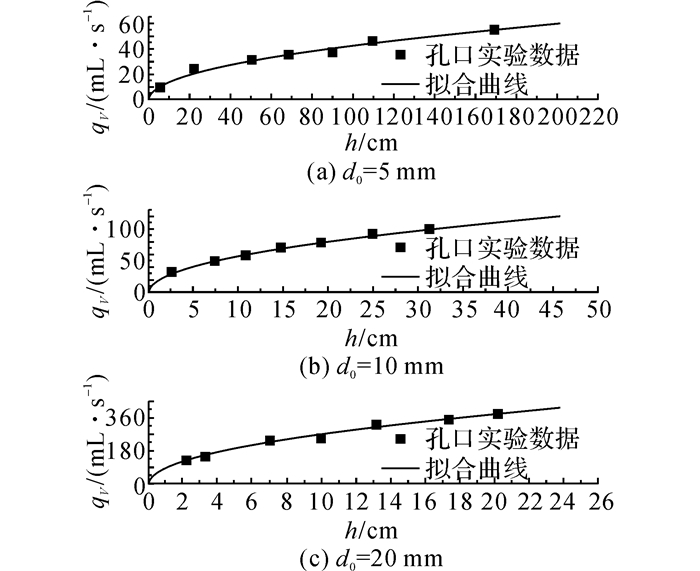
3 实验结果和讨论 3.1 孔口的漏损系数实验先测量覆盖纱网的漏损口在周围没有埋砂时, 流量和水头压力之间的关系.实验结果如图 5所示.实验数据可以证明当没孔介质条件下, 孔口漏损量qV和水头高度h符合传统的孔口公式.因此用孔口出流式(1)对实验数据进行拟合.从图中可以看到, 用孔口公式拟合曲线和实验数据吻合较好.拟合得到3组不同孔径的Cd如表 2所示.
|
图 5 管道周围无状态下, 各孔口流量和水头高度关系图 Fig. 5 Plot of orifice flow rate versus water head height for each of three orifices without sand |
| 表 2 实验测得的孔口系数Cd Table 2 Measured Cd for different orifices in experiments |
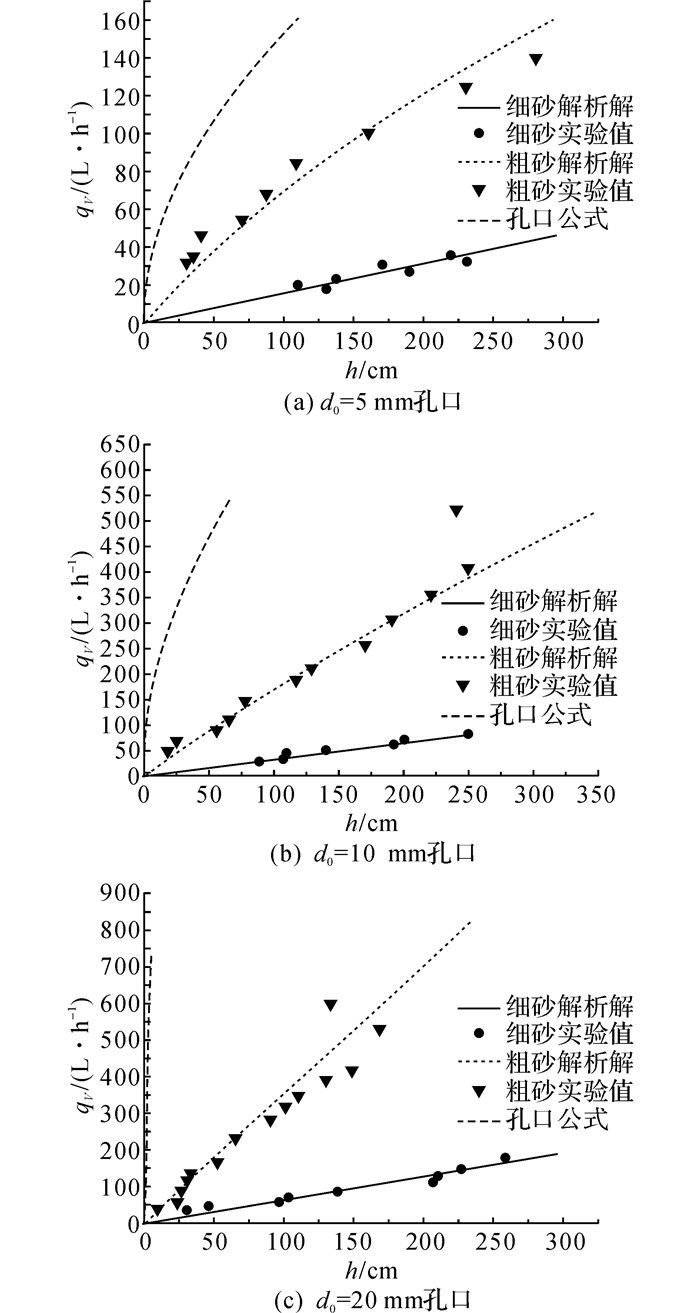
用本文推导的渗漏量式(13)对实验中的几种工况进行了预测, 并且与实验结果进行了对比, 得到不同工况下漏损量qV和水头h的关系, 结果如图 6所示.尽管图中实验结果存在一些离散性, 特别是小流量下更容易产生测量误差, 但实验值和模型结果基本一致.
|
图 6 漏损口实验结果和解析模型比较 Fig. 6 Comparison of experimental data and analytical results |
图 6(a)显示了当漏损口d0=5 mm时的实验结果和解析模型比较.从图中可以看到, 在相同水头压力下, 漏损口周围土体的存在, 使得漏损量大大减少.在介质为细砂时, 漏损量qV和水头高度h1表现出线性关系;当介质粗砂时则表现出曲线关系.这是由于介质是粗砂时, 孔口水头损失占据重要部分.当为细砂时, 实验中的水头损失则主要由土体引起, 孔口水头损失比重较小.
图 6(b), (c)是孔口直径d0=10和20 mm的实验结果比较图.结合图 6(a)比较可知, 在相同水头压力下, 随着孔口的增大, 渗漏量也相应增大.从图 6(b)和(c)中可以发现实验和拟合的结果几乎都为直线, 根据公式(13)可知土体部分引起的水头损失和流量成线性关系, 由此推断, 对于这2组实验, 在实验流量范围内, 漏损处的水头损失主要由于周围土体引起.需要注意的是在图 6(b)和(c)中, 粗砂介质的最后一个实验结果都发生了突变.在水压不变甚至减小的情况下, 流量突然的增大, 在实验中发现此时上部砂体移动, 土体部分流化, 这与模型假定不符.在实际管网中, 当土体发生流化, 往往是发生爆管, 此时的漏损往往可见并且能及时修复, 然而大多数的漏损往往是在地下不可见的暗漏.
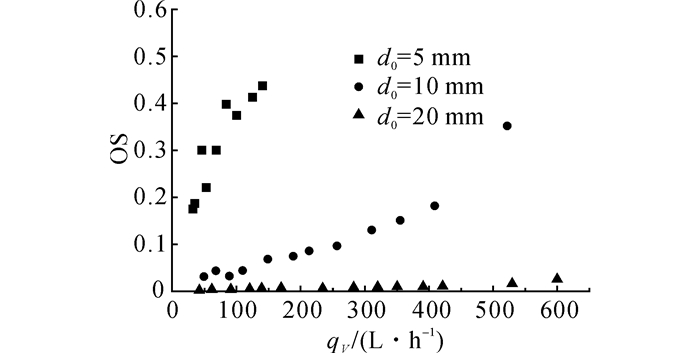
引用参考文献[11]对OS数的定义:OS = h1/h2.如图 7所示为本次实验中3种不同孔径的漏损口在细砂时OS随着流量的变化曲线.从图中可以看出, 相同的土体, 在同一流量情况下, 漏损口孔径越小, OS系数越大.这是由于孔径小时, 孔口水头损失增大.3种漏损口的的OS值都是随着流量的增大而逐渐增大, 这说明随着流量的增大, 孔口水头损失在总水头损失中所占的比例逐渐变高.孔口比例越高, 非线性就越明显.本实验流量范围内中, d0=10 mm的OS基本小于0.1, d0=20 mm的OS甚至小于0.05, 这也再一次解释了实验中这2组漏损口拟合的qV-h趋于线性的原因.
|
图 7 细砂条件下, 不同漏损口OS的变化 Fig. 7 Relationship between qV and OS for different orifices for fine sands |
(1) 本文通过将管道漏损口周围土体中的复杂渗流简化为以破损口为点源的球形渗流模型并考虑了管道对渗流场的影响, 推导了考虑土体影响的管道稳定渗漏模型, 结合实验数据, 得到的结果吻合较好.为管网压力控制管理提供了理论依据, 具有一定的实用价值.
(2) 过去的研究主要集中在管内水压对渗漏量的影响, 本文揭示了土体对渗漏量的影响, 正是由于漏损口周围土体的存在, 使得渗漏的压力指数往往大于传统孔口公式的0.5.管网漏损处水头损失主要有2部分组成, 当土体中的水头损失占据比例越大, 压力指数越偏向1, 因此土体对管道渗漏量的影响不可忽略.
(3) 本文推导的渗漏公式, 有效地解释了水头压力、土体性质、破损口孔径以及管径对漏损量的影响.然而该公式仅仅局限于土体未被冲刷, 当水压较高时, 漏损口周围土体形成冲刷侵蚀, 这一过程有待进一步研究.为了更好地了解漏损口周围的渗流情况, 数值模拟也将进一步展开.
| [1] |
朱东海, 张土乔, 毛根海. 城市供水管网爆管点动态定位的神经网络模型研究[J].
水利学报, 2000, 5(1): 1–6.
ZHU Dong-hai, ZHANG Tu-qiao, MAO Gen-hai. The dynamic location of the water distribution by neural network model[J]. Journal of Hydraulic Engineering, 2000, 5(1): 1–6. |
| [2] | ARAUJO L S, RAMOS H, COELHO S T. Pressure control for leakage minimisation in water distribution systems management[J]. Water Resources Management, 2006, 20(1): 133–149. DOI:10.1007/s11269-006-4635-3 |
| [3] | ORAZIO G, DANIELE L. Water distribution network pressure-driven analysis using the ehanced dlobal gradient algorithm(EGGA)[J]. Journal of Water Resources Planning and Management, 2011, 137(6): 498–510. DOI:10.1061/(ASCE)WR.1943-5452.0000140 |
| [4] | ORAZIO G, DRAGAN S, ZORAN K. Pressure-driven dmand and leakage simuation for water distribution networks[J]. Journal of Hydraulic Engineering, 2008, 134(5): 626–635. DOI:10.1061/(ASCE)0733-9429(2008)134:5(626) |
| [5] |
郭帅. 城市排水系统地下水入渗及土壤侵蚀问题研究[D]. 杭州: 浙江大学, 2011.
GUO Shuai. Study on infiltration and soil erosion due to cracks in sewer pipes[D]. Hang Zhou:Zhejiang University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013147751.htm |
| [6] | LAMBERT A. What do we know about pressure:leakage relationships in distribution systems[C]//System Approach to Leakage Control and Water Distribution Systems Management. Czech Republic, Brno:water management, 2000:255-260. http://www.mendeley.com/research/we-know-about-pressureleakage-relationships-distribution-systems/ |
| [7] | VAN ZYL J E, ClAYTON C R I. The effect of pressure on leakage in water distribution systems[C]//The Institution of Civil Engineers-Water Management.Cincinnati:AWWA-Water Quality, 2007, 160(2):109-114. http://www.mendeley.com/catalog/effect-pressure-leakage-water-distribution-systems/ |
| [8] |
杨艳, 张土乔, 刘伟超. 给水管网负压引起污染物入侵的流量计算方法[J].
浙江大学学报:工学版, 2015, 49(7): 1262–1267.
YANG Yan, ZHANG Tu-qiao, LIU Wei-chao. Calculation method of contaminant intrusion flow rate induced by negative pressure events in water distribution system[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(7): 1262–1267. |
| [9] | KAMI A, AWAD A S. Stability of saturated cohesionless soil layer due to water flowing from a broken underground pipline[J]. Journal of King Saud University, 2000, 12(1): 27–44. |
| [10] | NOACK C, ULANICKI B. Modelling of soil diffusibility on leakage characteristics of buried pipes[C]//Water Distribution Systems Analysis Symposium. Cincinnati, Ohio, USA:Journal of Hydraulic Engineering, 2006:11-20. http://www.mendeley.com/research/modelling-soil-diffusibility-leakage-characteristics-burried-pipes/ |
| [11] | WALSK T, BEZTS W, POSLUSZNY E T, et al. Modeling leakage reduction through pressure control[J]. American Water Works Association Journal, 2006, 94(4): 147–155. |
| [12] | GUO S, ZHANG T Q, SHAO W Y, et al. Two-dimensional pipe leakage through a line crack in water distribution systems[J]. Journal of Zhejiang University Science A, 2013, 14(5): 371–376. DOI:10.1631/jzus.A1200227 |
| [13] | ZOUESHTIAGH F, MERLEN A. Effect of a vertically flowing water jet underneath a granular bed[J]. Physical Review E, 2007, 75(5): 1–12. |
| [14] | COLLINS R, BERNER M, BECK S. Intrusion modelling and effect of groundwater conditions[C]//Water Distribution System Analysis.Tucson, AZ, US:Springer, 2010:585-594. |
| [15] | GREYVENSTEIN B, VAN ZYL J E. An experimental investigation into the pressure-leakage relationship of some failed water pipes[J]. Journal of Water Supply:Research and Technology-AQUA, 2007, 56(2): 117–124. DOI:10.2166/aqua.2007.065 |
| [16] |
陈川.
地下排水管道泄漏对地面塌陷的影响研究[M]. 北京: 首都经济贸易大学, 2015.
CHEN Chuan. The influence of pipe leakage on the ground collapse[M]. Beijing: Capital University of Economics and Business, 2015. |
| [17] | RICHARD C, JOBY B. Influence of ground conditions on intrusion flows through apertures in distribution pipes[J]. Journal of Hydraulic Engineering, 2013, 139(10): 1052–1061. DOI:10.1061/(ASCE)HY.1943-7900.0000719 |
| [18] |
杨艳. 给水管网的污染物入侵模型研究[D]. 杭州: 浙江大学. 2015.
YANG Yan. Modelling of Contaminant intrusion flow rate into water distribution Systems. Hang Zhou:Zhejiang University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10335-1015596461.htm |
| [19] | TERZAGHI K, PECK R B, MESRI G. Soil Mechanics in Engineering Practice[M]. 3th Ed. John Wiley & Sons, Inc, 1996. |
| [20] | 龚晓南. 土力学[M]. 北京: 中国建筑工业出版社, 2002: 38. |



