地震滑坡常见于地震灾害链中, 不仅会带来生命财产损失, 还严重影响震后救援.Keeper[1]总结世界上40次历史地震的数据后发现地震滑坡是造成生命财产损失的主要原因;2013年庐山地震诱发了数万处滑坡, 造成了巨大的人员财产损失[2];汶川地震诱发了近20万处滑坡, 造成约2万人死亡[3].因此, 进行地震滑坡易发性评价具有重要意义.
通过监测斜坡岩土体应力、应变以及孔隙水压力等关键信息, 可实现从滑坡机理层面对单个坡体进行稳定性分析.然而, 对于大范围区域的滑坡易发性评价, 获取全空间范围内所有坡体的上述参数几乎不可能实现.因此, 国内外学者提出基于地形、地貌和地层岩性等容易获取的参数进行滑坡易发性评价的统计分析方法[4-7], 从而规避了采用物理模型法存在的物理参数和监测数据获取困难的问题.
借助3S技术可以快速提取地震滑坡编目和影响因子, 并初步分析滑坡与相关影响因子之间的关系[8].选取典型影响因子, 通过建立数学模型对地震滑坡易发性进行评估, 获得影响因子与地震滑坡之间的定量关系, 得到地震滑坡易发性评价图[9].
地震滑坡易发性评价典型影响因子通常包括地质、地形和地震相关因素.地震相关因素包括地震动、震源距离等.地震动数据通常由于地震测量站数量和密度不够而难以用于较小范围内的地震滑坡易发性评价.既有研究表明, 对于有地表破裂带的地震, 地震诱发的滑坡分布与破裂带的距离具有明显的相关性[10], 可用与破碎带的距离进行滑坡易发性评价;但对于无地表破裂带型地震诱发的滑坡, 则无明显空间分布规律[11], 易发性评价效果不够理想.因此, 无地表破裂带地震滑坡的易发性评价需要增加影响因子以提升评价效果.
同震地表变形表征着地震前后地表的绝对永久变形量, 与地震滑坡有一定相关性, 可以考虑作为地震滑坡易发性评价影响因子.同震地表变形可通过地震前后的高分辨率数字高程模型(Digtal elevation model, DEM)解耦计算获得, 研究表明水平向变形与深层滑坡分布具有明显相关性[12].因此, 可以将同震地表变形作为影响因子加入模型, 尤其对于无地表破裂带地震能在一定程度上弥补地表破裂带缺失对地震滑坡易发性评价的影响, 提高模型效果.
本文以2004年日本新泻中越地震为例, 除选取常规影响因子之外, 增加同震地表变形这一影响因子, 并基于地理信息系统(Geographical information system, GIS)平台采用神经网络法开展了无地表破裂带型地震的滑坡易发性评价研究.
1 研究区域本文以2004年日本新泻中越地震所引发的滑坡为研究对象.这次地震发生于2004年10月23日, 主震矩震级Mw=6.6(37.30°N, 138.84°E), 震源深度10 km, 共有4次较大的余震, 引发了总计1 353处滑坡, 带来巨大的损失[13].本次地震没有明显的地表破裂带.如图 1所示, 研究区域大体位于日本长冈市和小千谷市接壤区域, 为低山丘陵地带, 东西长约9 km, 南北长约7 km, 总面积约为56 km2.研究区域处于本次地震的震中地带, 发现地震诱发滑坡400余处.

|
图 1 研究区域滑坡编目 Fig. 1 Landslides inventory of study area |
地震滑坡易发性评价需选取与地震无关的影响因子, 如地层岩性、地形要素、植被及土地利用类型、水系道路距离等[14], 通常还包括与地震相关的影响因子, 例如地震动、与地表破裂带的距离等.根据本次地震特点和滑坡分布特征选取了地层岩性、高程、坡度、坡向、地表曲率、地震加速度峰值、距道路的距离以及同震地表变形作为影响因子.文中地层岩性资料来源于日本通商产业省工业技术院地质调查所绘制的长冈和小千谷两市的1: 50 000地质图;用于震前通过立体像对分析得到, 并使用大地测量的三角点进行校对.DEM数据原始分辨率为2 m, 但由于高分辨率DEM表现了过多的地表细节, 对分析结果不利, 因此使用通过重采样获得的分辨率为10 m的DEM;同震地表变形计算主要依据使用机载激光雷达测得的地震发生后的高精度DEM数据, 分辨率为2 m.
2.1 地层岩性地层岩性类别决定了斜坡岩土体的密度、强度和剪切模量等物理力学特性, 对坡体稳定性有直接影响.如图 2(a)所示, 研究区域共划分为11类地层岩性类型, 以砂岩和泥岩为主, 划分结果如表 1所示.其中, Ai为第i类区域的面积, A(pi)为第i中区域的面积占研究面的百分比;Li为第i类区域中滑坡的面积, L(pi)为第i类区域中滑坡的面积占第i类区域面积的百分比.

|
图 2 地震滑坡影响因子 Fig. 2 Impact factors for earthquake triggered landslides |
| 表 1 研究区域地层岩性详表 Table 1 Detailed geology table of study area |
高程影响了山体对地震的响应[15], 高处山体较易发生滑坡.高程与滑坡势能有关[9], 关系到滑坡的滑动距离和影响范围.如图 2(b)所示, 研究区域内海拔为35~520 m, 最高处为521.08 m, 大部分地区海拔为160~280 m.
2.3 坡度坡度是直接影响坡体稳定性的因素.研究区域内的坡度信息通过地震发生前获得的DEM计算获得, 如图 2(c)所示, 大部分区域坡度为10°~40°, 坡度最大处超过60°.
2.4 坡向由于地震波在垂直于断层走向的方向传播能量较大, 导致滑坡在坡向上分布不均匀[10].在季风区, 坡向还会导致山体坡面水分分布不均匀, 对坡体稳定有一定的影响.图 2(d)为坡向分布图, 由地震发生前获得的DEM计算获得, 研究区域内各个坡向面积比例接近.
2.5 曲率地表曲率决定了地表水的汇集和分散, 影响了岩土体的强度和稳定性[10].曲率较大的凸起处可以视作较小的结构物, 在鞭梢效应的影响下更易发生破坏.另外, 土壤厚度与地表曲率存在很强的相关性[16].图 2(e)为地表曲率分布图, 可通过地震发生前获得的DEM计算获得, 统计结果表明研究区域内区域的曲率值在0附近呈近似对称的单峰状分布.
2.6 地震加速度峰值地震加速度峰值是地表质点在地震中加速度的最大绝对值, 而地震产生的惯性力对坡体结构的扰动和破坏是地震滑坡的重要原因之一.因此, 地震加速度峰值被普遍选取为地震本身对地震滑坡的影响因子.研究区域地震加速度峰值数据取自日本文部科学省关于中越地震的调查资料, 通过地震测站数据反演分析获得[17], 反演后获得的地震动栅格数据分辨率为350 m.由于研究区域位于震中地区, 如图 2(g)所示, 地震加速度峰值普遍偏高, 最大加速度峰值为15.15 m/s2.
2.7 道路人类活动极大的改变了地形地貌特征, 交通系统的影响尤其重要.道路修建不仅产生了新的较为陡峭的路堑边坡, 同时也对原始坡体产生了极大的扰动, 为地震滑坡埋下了隐患.因此, 距道路的距离通常作为人类活动对滑坡的影响因子考虑到易发性评价中.如图 2(h)所示, 本文中道路信息由研究区域航拍影像解译获得, 航拍影像取自日本文部科学省关于中越地震的研究资料[17], 分辨率为0.2 m.如图 2(g)所示, 研究区域道路多为崎岖的乡间田野的低等级公路, 并按50、100、200、300、500 m以及>500 m划分缓冲区.
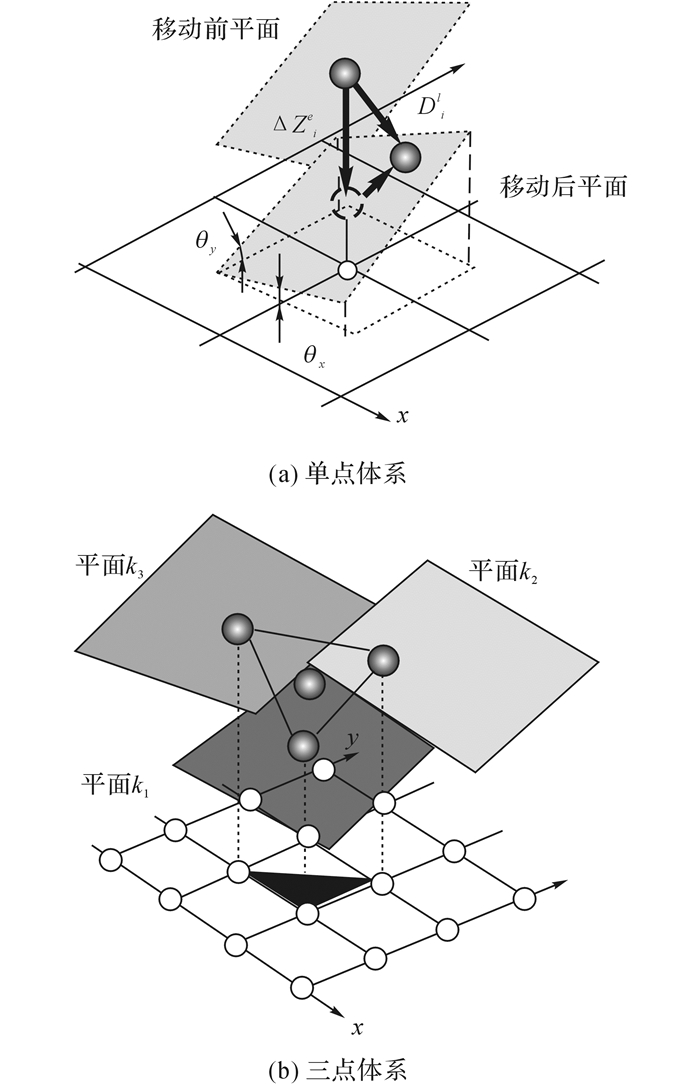
2.8 同震地表变形同震地表变形通过解耦地震前后DEM数据分析同震形变获得.如图 3(a)所示, 空间中编号为i的微平面与欧拉坐标系x、y轴的夹角分别为θx、θy, 其中心点的欧拉位移Δzie和拉格郎日位移矢量Dil=[Δxil, Δyil, Δzil]T之间可以建立式(1).
| $ \Delta z_i^e = \left[{{t_{x, i}}, {t_{y, i}}, 1} \right]\;\;{\left[{\Delta x_i^l, \Delta y_i^l, \Delta z_i^l} \right]^{\rm{T}}}. $ | (1) |
|
图 3 拉格朗日与欧拉方法求解同震地表变形 Fig. 3 Description of landform changes in Lagrangian and Eularian manners |
式中:tx, i和ty, i分别为所选取的平面x和y的上的正切值.
如图 3(b)所示,假设空间中第k组相邻三平面k1、k2、k3在地震中经历刚体平动, 可以求解式(2)的三维线形方程从而解耦变形.
| $ \left[\begin{array}{l} \Delta z_{{k_1}}^e\\ \Delta z_{{k_2}}^e\\ \Delta z_{{k_3}}^e \end{array} \right] = \left[{\begin{array}{*{20}{l}} {{t_{x, {k_1}}}}&{{t_{y, {k_1}}}}&1\\ {{t_{x, {k_2}}}}&{{t_{y, {k_2}}}}&1\\ {{t_{x, {k_3}}}}&{{t_{y, {k_1}}}}&1 \end{array}} \right]\left[\begin{array}{l} \Delta x_k^l\\ \Delta y_k^l\\ \Delta z_k^l \end{array} \right] $ | (2) |
式中:Δzk1e、Δzk2e、Δzk3e分别为平面k1、k2、k3中心点的欧拉位移,tx, k1、ty, k1, tx, k2、ty, k2,tx, k3、ty, k3分别为平面k1,k2,k3与欧拉坐标系的x、y轴的正切值,[Δxlk, Δylk, Δzlk]T为第k组相邻三平面的中心点构成用三角形的形心发生的拉格郎日位移矢量.赵宇[12]提供了一种更加严密的求解方法, 包括名义平面的定义, DEM可比性的改进和矩阵条件数检验等.其研究表明, 地壳形变场中2个横向变形较大地区均发现了大量的滑坡, 而局部形变可用来探讨目标区域内是否有隐藏滑坡存在.
同震地表变形表征着地震前后地表的绝对永久变形矢量值, 其中水平向变形与深层滑坡分布具有明显相关性[12].本文中采用其标量值, 图 2(f)为水平向同震地表变形图.
3 分析方法基于GIS平台的滑坡易发性评价常用的分析方法有逻辑回归法、判别分析法[14]、支持向量机[9]等.神经网络法由于在高度非线性、非数值和逻辑关系并不明确的模拟分析中具有出色的适用性, 在滑坡易发性评价中已有广泛运用, 陈晓利等[18]利用径向基神经网络法对云南龙陵地震滑坡做了易发性评价, 准确度达到89%以上;谭龙等[19]利用误差反向传播算法(Back Propagation, BP)神经网络对白龙江地震滑坡进行了易发性评价, 受试者工作曲线(Receiver operating characteristic curve, ROC)下面积为0.833;刘艺梁等[20]的研究结果表明三峡附近区域滑坡易发性评价效果中神经网络法比逻辑回归法要好;柯福阳等[21]利用BP神经网络对汶川地震滑坡进行了易发性评价, 模型结果和实际滑坡吻合度达到80%以上.因此本文采用神经网络法进行分析.
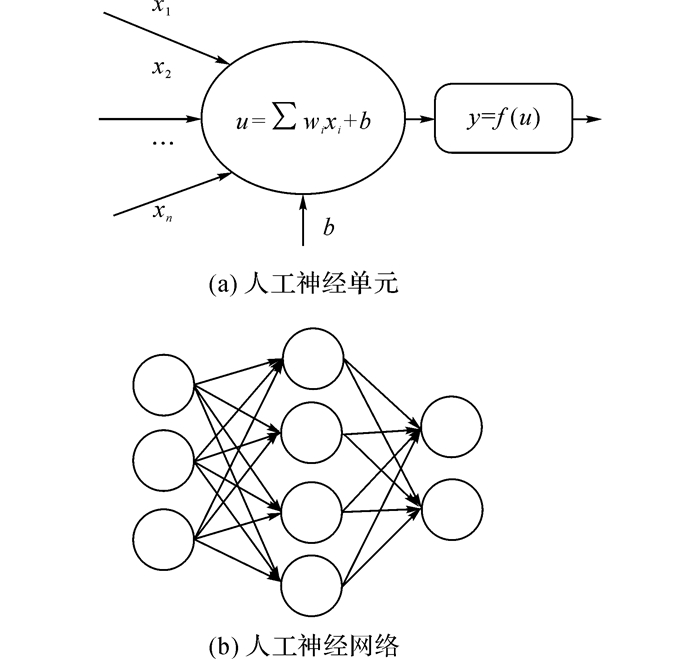
神经网络法模仿生物神经信号传递反式, 建立如图 4(a)所示的数学神经单元, 变量输入后进行加权求和, 通过激活函数得到输出值.将多个神经单元组合成如图 4(b)所示的神经网络, 输入训练样本通过错误函数进行自我学习, 最终将参数优化后的网络用于检验样本模拟.本文采用多层感知机神经网络法(MLP).其处理过程是一层层向前进行, 层与层之间具有高度的连接性, 采用最普遍的误差反向传播算法(BP), 在监控条件下训练神经网络.
|
图 4 人工神经网络算法原理 Fig. 4 Artificial neural network |
样本点数据通过DEM的每个栅格像素单元中心位置对影响因子地图和滑坡编目地图采样获得, 并通过SPSS软件中的多层神经网络感知机程序分析计算出采样点发生滑坡的概率.分析中的因变量为是否为滑坡单元, 自变量因子为地层岩性、海拔、坡度、坡向、曲率、地震加速度峰值、距道路的距离和同震地表变形, 并进行标准正态分布归一化处理, 模型的基本信息如表 2所示.其中, 因变量1表示“滑坡单元”, 0表示“非滑坡单元”.
| 表 2 神经网络模型信息 Table 2 Information of neural network model |
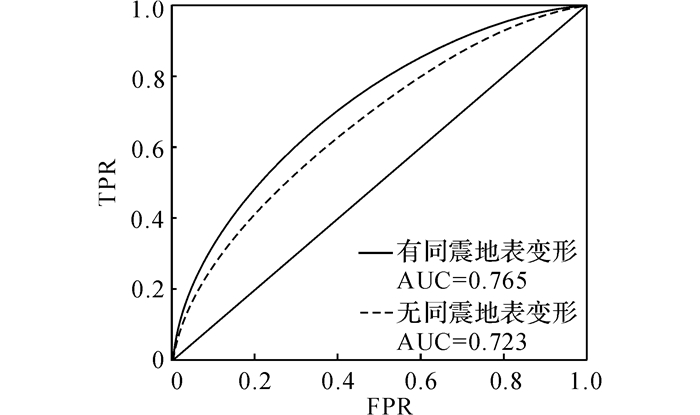
ROC曲线通常用于衡量预测模型的准确程度, 如图 5所示, 图中FPR为假正类比例,TPR为真正类比例.AUC为ROC曲线下面积, 考虑同震地表变形的神经网络法模型得到的ROC曲线下的面积为0.765, 说明了模型具有了较好的评估效果.而不考虑同震地表变形的ROC曲线下的面积为0.723, 说明选取同震地表变形作为影响因子具有一定的合理性, 对模型评估具有一定贡献.
|
图 5 ROC曲线 Fig. 5 ROC Curve |
输入变量的重要性可以通过方差分析方法计算获得.通过分析输出变量的方差随输入变量的变化, 计算两者相关的显著性.相关性越强, 可以认为输入变量对输出变量越重要.SPSS中因子重要性表如表 3所示, 列出了各因子重要性之间的相对值, 其中, sig.值代表该因子对模型的重要性, NS为归一化后的sig.值, 是各因子重要性相对最重要因子重要性的比值.地层岩性对地震滑坡的影响最大, 依次为坡度、曲率、地震加速度峰值、同震地表变形、高程、坡向和距道路的距离.值得注意的是, 同震地表变形的重要性高于被普遍选取为影响因子的高程、坡向和距道路的距离.虽然地震并没有产生明显可见的地裂缝, 但是同震地表变形较大的区域表征着岩土体裂缝可能进一步发育, 降低了岩土体的整体性, 不仅容易在地震时发生滑坡, 而且对以后的稳定性也有深远的影响.因此, 尤其在无地表破裂带的地震中, 同震地表变形可以作为重要影响因子考虑到地震滑坡易发性评价中.
| 表 3 影响因子重要性 Table 3 Importance of impact factors |
如图 6所示, 依据滑坡易发性评价结果将研究区域划分为4个等级.滑坡易发性最高的区域主要分布在研究区域东部图中椭圆区域, 该区域发生了大体量的深层滑坡.西北部区域也存在一定面积的极高易发性区, 总体看来, 极高易发性区分布较为集中.研究区域中部的滑坡易发性相对较低, 西南沿河平地大部分地区为低易发性区域, 基本不会对河道安全产生影响.

|
图 6 滑坡易发性评价 Fig. 6 Landslides hazard |
滑坡易发性分区的统计结果如表 4所示, 其中, B(pi)为分区滑坡面积占总滑坡面积比例, 结果显示, 极高易发性区占研究区域总面积的8.60%, 分区滑坡面积占总滑坡面积的28.38%, 该区域内发生滑坡的面积比例为27.09%, 在所有分区中滑坡面积占分区面积比例最高.随着滑坡易发性等级的提高, 分区总面积逐渐减少, 分区内滑坡面积占比逐渐增加, 说明滑坡命中率提高.同时, 随着易发性等级的提高, 分区总面积减少, 这有利于对高易发性区域的重点防控.说明滑坡易发性分区图具有很好的评估效果, 具有实际的应用价值.
| 表 4 滑坡易发性评价统计 Table 4 Statistics of landslides hazard |
(1) 本文以2004年日本新泻中越地震为研究对象, 基于GIS平台搭建神经网络法模型, 除地层岩性、高程等常规影响因子之外, 针对无地表破裂带地震, 新增了同震地表变形作为影响因子, 开展了地震滑坡易发性评价研究.ROC曲线的AUC值为0.765, 说明运用神经网络法进行地震滑坡易发性评价具有良好的效果.
(2) 地震滑坡的影响因子按贡献排序依次为地层岩性、坡度、地震加速度峰值、曲率、同震地表变形、高程、坡向和距道路的距离.同震地表变形重要性高于常见的高程、坡度等影响因子.
(3) 通过增加同震地表变形作为影响因子, ROC曲线下面积由0.723提高到0.765.说明同震地表变形是十分重要的地震滑坡影响因子, 尤其对于无地表破裂带的地震, 考虑同震地表变形可以较好的提高模型评估的准确性.
(4) 滑坡易发性评价图对研究区域滑坡易发性分划比较合理, 随着易发性等级升高, 分区面积减少, 滑坡面积占分区面积比例显著提高.本文提出的研究方法对类似地震的震后救灾及重建具有重要的指导意义.
| [1] | KEEFER D K. Landslides caused by earthquakes[J]. Geological Society of America Bulletin, 1984, 95(4): 406–421. DOI:10.1130/0016-7606(1984)95<406:LCBE>2.0.CO;2 |
| [2] | XU C. Assessment of earthquake-triggered landslide susceptibility based on expert knowledge and information value methods:a case study of the 20 April 2013 Lushan, China Mw6. 6 earthquake[J]. Disaster Advances, 2013, 6(13): 119–130. |
| [3] |
许冲, 徐锡伟, 吴熙彦, 等. 2008年汶川地震滑坡详细编目及其空间分布规律分析[J].
工程地质学报, 2013(1): 25–44.
XU Chong, XU Xi-wei, WU Xi-yan, et al. Response rate of seismic slope mass movements related to 2008 WenChuan earthquake and its spatial distribution analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2013(1): 25–44. |
| [4] | POURGHASEMI H R, JIRANDEH A G, PRADHAN B, et al. Landslide susceptibility mapping using support vector machine and GIS at the Golestan Province, Iran[J]. Journal of Earth System Science, 2013, 122(2): 349–369. DOI:10.1007/s12040-013-0282-2 |
| [5] | NANDI A, SHAKOOR A. A GIS-based landslide susceptibility evaluation using bivariate and multivariate statistical analyses[J]. Engineering Geology, 2010, 110(1/2): 11–20. |
| [6] | YILMAZ I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison:A case study from Kat landslides (Tokat-Turkey)[J]. Computers & Geosciences, 2009, 35(6): 1125–1138. |
| [7] | YESILNACAR E, TOPAL T. Landslide susceptibility mapping:A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey)[J]. Engineering Geology, 2005, 79(3/4): 251–266. |
| [8] | SATO H P, SEKIGUCHI T, KOJIROI R, et al. Overlaying landslides distribution on the earthquake source, geological and topographical data:the Mid Niigata prefecture earthquake in 2004, Japan[J]. Landslides, 2005, 2(2): 143–152. DOI:10.1007/s10346-005-0053-5 |
| [9] | XU C, DAI F, XU X, et al. GIS-based support vector machine modeling of earthquake-triggered landslide susceptibility in the Jianjiang River watershed, China[J]. Geomorphology, 2012, 145-146: 70–80. DOI:10.1016/j.geomorph.2011.12.040 |
| [10] |
许冲, 戴福初, 姚鑫, 等. 基于GIS的汶川地震滑坡灾害影响因子确定性系数分析[J].
岩石力学与工程学报, 2010, 29(S1): 2972–2981.
XU Chong, DAI Fu-chu, YAO Xiao-li, et al. GIS based certainty factor analysis of landslide triggering factors in WenChuan earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 2972–2981. |
| [11] |
许冲. 利用同震滑坡分析2014年鲁甸地震震源性质与破裂过程[J].
工程地质学报, 2015, 23(4): 755–759.
XU Chong. Utilizing coseismic landslides to analyze the source and rupturing process of the 2014 LuDian earthquake[J]. Journal of Engineering Geology, 2015, 23(4): 755–759. |
| [12] | YU Z, KAZUO K, TOMOHIRO F. Multi-scale decomposition of co-seismic deformation from high resolution dems:a case study of the 2004 mid-niigata earthquake[J]. Acta Geologica Sinica-English Edition, 2012, 86(4): 1013–1021. DOI:10.1111/j.1755-6724.2012.00725.x |
| [13] | MORI J, SOMERVILLE P. Seismology and strong ground motions in the 2004 niigata ken chuetsu, japan, earthquake[J]. Earthquake Spectra, 2006, 22(S1): 9–21. DOI:10.1193/1.2172914 |
| [14] | GUZZETTI F, CARRARA A, CARDINALI M, et al. Landslide hazard evaluation:a review of current techniques and their application in a multi-scale study, Central Italy[J]. Geomorphology, 1999, 31(1/4): 181–216. |
| [15] | HASEGAWA S, DAHAL R K, NISHIMURA T, et al. DEM-Based analysis of earthquake-induced shallow landslide susceptibility[J]. Geotechnical and Geological Engineering, 2009, 27(3): 419–430. DOI:10.1007/s10706-008-9242-z |
| [16] |
许冲, 徐锡伟, 于贵华, 等. 玉树地震滑坡影响因子敏感性分析[J].
科技导报, 2012, 30(01): 18–24.
XU Chong, XU Xi-wei, YU Gui-hua, et al. Susceptibility analysis of impact factors of landslides triggered by Yushu earthquake[J]. Science and Technology Review, 2012, 30(01): 18–24. DOI:10.3969/j.issn.1008-0864.2012.01.03 |
| [17] |
土木学会, 東京大学, 京都大学等. 活褶曲地帯における地震被害データアーカイブスの構築と社会基盤施設の防災対策への活用法の提案[R]. 日本: 文部科学省, 2008.
Japan Society of Civil Engineers, Tokyo University, Kyoto University, et al. The flexible method of seismic damage data archive building and social infrastructure disaster prevention in active fault region[R]. Japan:Ministry of Education, Culture, Sports, Science and Technology, 2008. |
| [18] |
陈晓利, 赵健, 叶洪. 应用径向基概率神经网络研究地震滑坡[J].
地震地质, 2006, 28(3): 430–440.
CHEN Xiao-li, ZHAO Jian, YE Hong. application of RBPNN in the research of earthquake-induced landslide[J]. Seismology and Geology, 2006, 28(3): 430–440. |
| [19] |
谭龙, 陈冠, 曾润强, 等. 人工神经网络在滑坡敏感性评价中的应用[J].
兰州大学学报:自然科学版, 2014, 50(01): 15–20.
TAN Long, CHEN Guan, ZENG Run-qiang, et al. Application of artificial neural network in landslide susceptibility assessment[J]. Journal of Lanzhou University:Natural Sciences, 2014, 50(01): 15–20. |
| [20] |
刘艺梁, 殷坤龙, 刘斌. 逻辑回归和人工神经网络模型在滑坡灾害空间预测中的应用[J].
水文地质工程地质, 2010, 37(05): 92–96.
LIU Yi-liang, YIN Kun-long, LIU Bin. Application of logistic regression and artificial neural networks in spatial assessment of landslide hazard[J]. Hydrogeology and Engineering Geology, 2010, 37(05): 92–96. DOI:10.3969/j.issn.1000-3665.2010.05.017 |
| [21] |
柯福阳, 李亚云. 基于BP神经网络的滑坡地质灾害预测方法[J].
工程勘察, 2014, 42(8): 55–60.
KE Fu-yang, LI Ya-yun. The forecasting method of landslides based on improved BP neural network[J]. Geotechnical Investigation and Surveying, 2014, 42(8): 55–60. |



