2. 福建省建筑设计研究院 林颖孜结构工作室, 福州 福建 350001
2. Lin Yingzi Structure Studio, Architectural Design and Research Institute of Fujian Province, Fuzhou, China
随着经济的发展与城市的现代化建设, 人行桥梁在市政建设与旅游产业中的重要性日益显著.人行桥梁不仅具有提供交通便利的一般功能, 而且往往兼有提升城市形象的作用.旅游区的景观人行桥本身就是重要的景点.因此人行桥梁的设计中对建筑外形有较高的要求, 通常比一般桥梁更为轻盈.景观人行桥梁往往建在地形地貌复杂的景区(如陡峭悬崖边沿).人行桥梁的这些特点使得风致结构响应问题比较突出[1], 难以采用规范计算方法予以准确把握.
经典的大跨度桥梁风振理论一般不适用于人行桥梁.大跨度桥梁风振理论建立在片条假定基础上[2-6], 而许多人行桥梁的风效应则具有复杂的三维流动特点, 往往使得片条假定不满足[7].大跨度桥梁风振理论中对湍流风场的描述针对开阔水面上的桥梁[8-11], 相对比较简单.但人行桥梁(城市人行桥或景观人行桥)的周边地形与地貌通常都很复杂, 难以给出简单的归纳与描述.
迄今为止, 桥梁的全气动弹性模型试验方法主要应用于验证大跨度桥梁节段模型与风振理论的分析结果.本文提出了可以拓展这一方法, 直接应用于求算复杂三维流场下三维空间桥梁结构的风振响应, 以解决这类问题在计算与分析方面的困难.
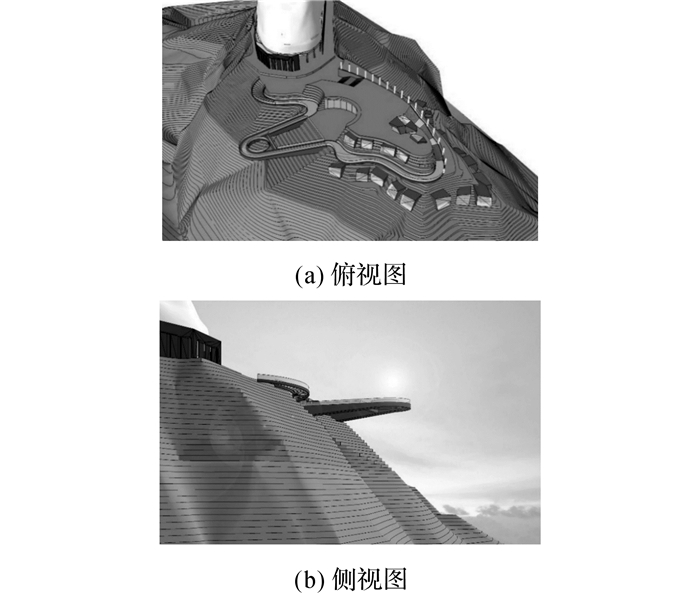
1 廊桥风效应的研究目的与方法本文以一座位于海拔1 800 m的山顶上双悬挑主梁(外侧宽度3.4 m)的悬挑玻璃廊桥为例, 研究了其复杂的风致结构响应.该桥的悬挑长度达33.33 m, 远远超过著名的美国科罗拉多大峡谷玻璃廊桥的21 m悬挑[12], 是目前世界上在建的最大悬挑玻璃廊桥(见图 1).
|
图 1 环形悬挑玻璃景观廊桥效果图 Fig. 1 Images of cantilever skywalk bridge |
初步分析表明, 由于该桥自重较轻、阻尼较低, 加之山顶风速很大, 使得风荷载成为结构设计的主要控制荷载.此外作为观光桥梁, 风致振动评估也是结构设计中需要重点考虑的内容.
廊桥外形与结构都比较独特, 没有现成的规范条款或工程实例提供设计参考.周围山地地貌产生的复杂风场进一步增加了准确估计风振响应与风荷载的技术难度.
目前桥梁空气动力学研究主要有3类方法:
1) 气动弹性模型的风洞试验研究方法.这类方法采用能模拟实际桥梁的空气动力学特性和结构动力学特性的桥梁气动弹性模型, 在大气边界层风洞中直接测试不同风速下桥梁模型的风振响应与风荷载, 然后通过模型相似律推导实际桥梁上的相应数值.气动弹性模型风洞试验研究方法的优点是其适用性较广, 而且被认为是比较最可靠的方法.但缺点是气动弹性模型的设计与加工都很复杂, 难度较高, 相应的费用投入也较多.所以目前主要用于验证大跨度桥梁节段模型试验与风振理论分析的结果.
2) 风洞试验与理论分析结合的方法.这类方法采用桥梁节段模型的风洞试验确定桥梁的空气动力学特性, 然后将其结合理论分析求解结构动力学方程, 最后确定实际桥梁的风振响应与风荷载.这一方法在模型设计与加工方面都相对简单, 费用也低于气动弹性模型方法, 但这一方法必须假定片条理论成立, 因此在应用上有一定的局限性.
3) 数值模拟与理论分析结合的方法.这类方法采用计算流体力学(CFD)的方法求算桥梁的空气动力学特性以取代风洞试验方法.但这一方法目前尚不成熟, 不能作为工程设计的依据.
本文研究的环形悬挑廊桥的风效应具有复杂的三维流动特点, 不满足片条理论的基本假定, 因此决定采用气动弹性模型的风洞试验研究方法准确把握其风振响应与风荷载.国内的桥梁气动弹性模型研究主要针对大跨度公路或铁路桥梁[13-15], 对复杂的三维空间结构行人桥的气动弹性模型研究则鲜有报道.
在实施气动弹性模型试验研究之前, 首先需要对当地的风气候进行了研究.根据桥址周围3个独立气象站近30多年来的逐时风速风向记录(近25万条记录), 对廊桥所在区域建立了风气候的统计模型(Weibull模型), 用于描述强风时的风速风向联合概率分布.
在此基础上, 采用1: 1 500缩尺的山体地貌模型试验对桥址的风环境进行详细研究, 进一步确定在当地风气候的大环境下廊桥位置处详细的局部风环境, 其中包括风速、风向、风攻角、风偏角、紊流度等参数.结果发现桥址处的风攻角变化范围达到-15°至+20°, 这对于悬挑结构是非常不利的, 对气动弹性模型的设计也带来了新的难度.此外桥址处的来流紊流度可达30%, 这对模型试验中风洞风场的模拟也造成一定困难.
本文着重讨论了针对上述难点的廊桥气动弹性模型的理论设计、构造设计、以及试验方法.并给出气动弹性模型的主要试验结果, 以揭示这类桥梁的风致结构响应特点.
虽然本文的研究是针对某一特定的结构系统, 但所给出研究方法与技术路线对研究人行桥梁与空间结构的风效应具有一定的普适性与参考价值.
2 气动弹性模型的设计与制作 2.1 气动弹性模型的相似准则气动弹性模型的设计目标是满足与实际结构之间的动力相似性.为此需要依据所研究桥梁结构风致响应的物理过程, 罗列与此有关的独立物理参数, 得到包括结构尺度、结构刚度、风速等在内共计16个参数.由于基本物理量纲只有3个(长度l、时间t、质量m), 根据Buckingham定理, 可以得到13个独立的无量纲参数.只要气动弹性模型与实际桥梁之间满足这些无量纲参数(相似参数)的一致性, 则气动弹性模型与实际桥梁的风致响应之间就存在动力相似性, 即由模型试验得到的测试数据可以通过相似关系换算成实际桥梁的风致响应.
这些相似参数可以归纳为以下各项.弗劳德数(Froude数), 代表流体惯性力与重力之比, 表示为U2/gB; 柯西数(Cauchy数), 代表弹性力与流体惯性力之比, 包括EA/ρB2U2;EIx/ρB4U2;EIy/ρB4U2;GK/ρB4U2; 雷诺数(Reynolds数), 代表流体惯性力与流体黏滞力之比, 表示为ρBU/μ; 密度比, 代表结构惯性力与流体惯性力之比, 包括m/ρB2和Im/ρB4; 阻尼比ζ, 为结构阻尼与其临界阻尼值之比; 质量与刚度中心相对坐标, 代表质量与刚度的中心位置, 包括zm/B和zs/B; 约化频率, 代表湍流尺度与结构尺度之比, 表示为fB/U; 无量纲湍流功率谱, 代表湍流能量在各频段的分布, 表示为fS(f)/U2.
式中16个独立物理参数分别为:U为平均风速;g为重力加速度;B为桥梁特征宽度;EA为桥梁断面的轴向刚度;Elx、Ely为桥梁断面关于x与y轴的弯曲刚度;GK为桥梁断面的扭转刚度;m为桥梁断面的单位长度质量;lm为桥梁断面的单位长度质量矩;zm、zs分别为桥梁断面质量中心与刚度中心的位置坐标;f为频率;S为风湍流谱;ρ为空气密度;μ为空气的黏性系数;ζ为结构阻尼比.
这些动力相似参数也可以通过对空气动力学基本方程(Navier-Stokes方程)和结构动力学基本方程(运动方程)进行量纲分析得出.
事实上, 上述的动力相似参数是无法全部满足的.大气边界层风洞内与实际桥梁所在地的重力加速度与黏性系数是几乎相同的, 因此弗劳德数与雷诺数相似要求之间是相悖的.按照弗劳德数相似, 模型与足尺之间的风速比应该等于几何缩尺比的平方根;而按照雷诺数相似, 模型与足尺之间的风速比应该反比于几何缩尺比.因此需要根据研究对象对相似参数进行一定的取舍.
国内外研究表明, 对于如本文桥梁这类钝体断面, 气流的分离点是固定的, 黏性参数条件并不显著影响其绕流形态, 所以适当放松对雷诺数的相似性要求并不会影响气动弹性模型试验的精度.
由此得出如表 1所示的气动弹性模型设计的相似比, 其中长度相似比λL(即模型几何缩尺比)可根据风洞试验段尺寸与风场模拟尺度独立选取, 而其他物理量的相似比则由几何缩尺比决定.
| 表 1 气动弹性模型的相似比 Table 1 Similarity factors of aeroelastic model |
考虑到对所研究的悬挑廊桥, 其结构重力作用对结构振动模态的影响很小, 所以弗劳德数的模拟也可以放松.这样在表 1所示的相似比中, 风速比λV也能成为一个可以独立选取的相似比.一般来说对悬吊结构(如悬索桥)弗劳德数的相似性才比较重要.在气动弹性模型设计中, 增加可独立选取的相似比个数, 能够显著降低模型设计与加工的难度.
2.2 气动弹性模型的设计与制作根据大气边界层风洞内湍流尺度与风洞试验段尺寸, 取气动弹性模型的几何缩尺为1: 40.风速比取值中略微放松对弗劳德数的模拟要求, 取为1: 6.由此确定气动弹性模型设计中对刚度与质量的要求.
由于材料特性的原因, 外形相似的缩尺模型本身无法同时提供符合相似性要求的刚度特性, 所以采用骨架+外壳的方式, 分别模拟缩尺模型的气动外形与刚度特性.骨架隐藏在外壳内, 模拟桥梁的刚度系统, 而外壳模拟桥梁的气动外形.骨架与外壳通过连接构件相连, 以确保外壳受到的风力能够有效传递到骨架上.由外壳与骨架构成的系统质量约为目标质量的80%左右, 剩余的20%则采用在指定位置附加配重的方式达到, 以精确模拟满足相似性要求的质量及其分布.
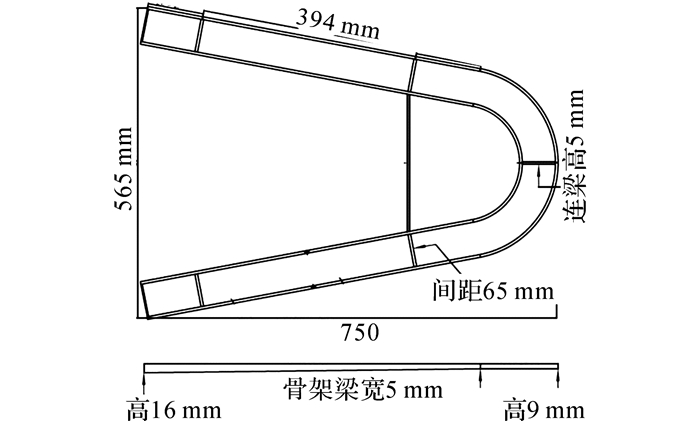
根据相似性要求设计的模型骨架尺寸如图 2所示,骨架选用Q235钢材, 在一块完整的钢板上利用铣床加工完成.如图 3所示为安装在模型主梁内的骨架.模型的外壳按照几何缩尺比采用轻质航空模型板制作.为避免外壳对骨架提供附加刚度, 外壳按一定间隔进行隔断处理.整个外壳分成10段, 相邻段之间留有约1 mm的空隙(见图 4).在各段的中心位置采用连接构件将外壳固定在骨架上, 并确保外壳受到的风力能有效传递到骨架上(见图 5).
|
图 2 廊桥气动弹性模型的骨架设计 Fig. 2 Spine design of aeroelastic model |

|
图 3 实际模型中的气动弹性模型骨架 Fig. 3 Spine shown in completed model |

|
图 4 廊桥气动弹性模型的外壳 Fig. 4 Shell of completed model |

|
图 5 廊桥气动弹性模型的骨架与外壳的连接 Fig. 5 Connections between spine and shell |
为了模拟山坡效应产生的平均风攻角, 将廊桥模型的支座部分设计成可以整体转动+/-20°的机构.通过转动模型以模拟来流风与桥梁之间的相对攻角.如图 6所示为支座实物图.

|
图 6 气动弹性模型变攻角支座实物图 Fig. 6 Adjustment system for model angle of attack |
在气动弹性模型制作完成后, 需要对模型进行动力特性测试, 以把握模型制作中的材料特性与加工误差对实际模型的动力特性可能带来的差异.动力特性测试的目的一方面用于检验这一差异的程度;另一方面, 根据可能存在的差异对测试中的相似参数作必要调整, 以修正由这些差异产生的测试误差.
气动弹性模型动力特性的测试与验证主要包括3方面:固有频率与振型的测试与验证;广义质量的测试与验证;结构阻尼比的测试与调整.
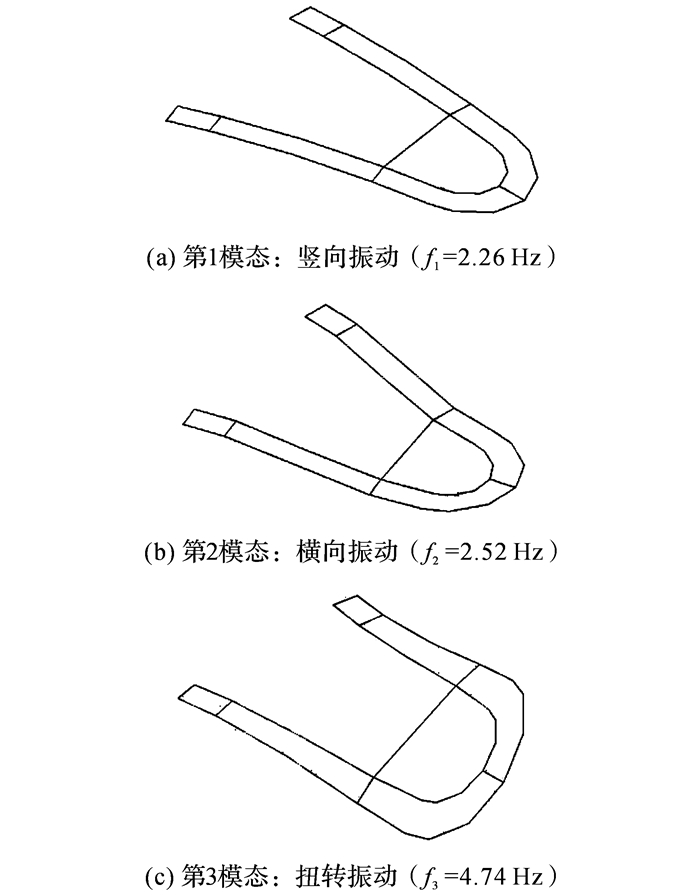
根据结构工程师提供的资料, 影响风致振动和风荷载的结构模态主要是前三阶, 分别是竖向平动、横向平动和绕对称轴扭转(见图 7).高于第三阶的固有频率已达到10 Hz, 因此其相应模态的风振响应可忽略不计.
|
图 7 足尺廊桥结构固有振动模态 Fig. 7 Modes of vibrations of full-scale bridge |
固有频率与振型的测试采用自由振动方法.通过同步测试安装在模型上各点的加速度与位移时程, 由谱分析得到各阶模态的固有频率及其振型.结果表明竖向与扭转模态的频率与设计目标值非常接近, 竖向频率的误差仅为0.1%, 扭转频率的误差也仅为2.2%, 与气动稳定性关系密切的扭弯频率比误差为1.9%.但实测得到的横向频率误差较大, 实测模型频率明显小于设计目标值.这可能由2方面原因造成:其一是模型主梁之间的横向连接与计算模型之间可能存在一定差异;其二是变攻角支座可能削弱了模型的横向刚度.考虑到廊桥的横向振动与其他振动分量之间没有模态耦合, 可以通过试验数据处理中调整对横向振动响应的风速比的方法予以修正.表 2给出模型设计目标频率和模型实测频率的比较以及相应的风速比调整.表中, fF为足尺频率;fM为模型频率
| 表 2 设计目标频率和模型实测频率的比较及调整 Table 2 Comparison between design frequencies and measured frequencies and corresponding adjustment |
气动弹性模型的广义质量测试验证采用同步测试模型加速度与根部弯矩的方法.在自由振动情况下, 桥梁根部弯矩与悬挑端加速度之间满足下列关系:
| $ {r_{\rm{F}}} = \frac{{\int\limits_0^L {m\left( x \right)\varphi \left( x \right)x{\rm{d}}x} }}{{{a_F}}}. $ | (1) |
式中:rF则为足尺结构上桥梁根部弯矩与悬挑端加速度之比, m(x)为沿桥梁的分布质量,φ(x)为按悬挑端归一后的振型,L为悬挑端至根部弯矩测试点的距离,aF为悬挑端加速度.
如果气动弹性模型的质量分布满足广义质量的相似性要求, 则由表 2所列相似关系, 气动弹性模型自由振动中根部测试弯矩与端部测试加速度之间应满足下列比例关系:
| $ {r_{\rm{M}}} = {r_{\rm{F}}}\lambda _L^4. $ | (2) |
其中:rM为气动弹性模型上桥梁根部弯矩与悬挑端加速度之比.按足尺结构计算所得这一比例的目标值为2.72 N·m/g, 由气动弹性模型的实测得到的这一比例为2.68 N·m/g.根据模型几何缩尺λL=1: 40, 计算得到的误差为1.2 %, 可以认为满足精度要求.
结构阻尼比采用自由振动法测定.测得模型结构阻尼比为0.17%, 然后采用在模型上增加黏性贴条的方式将模型结构阻尼比调整到0.5%的标准值.
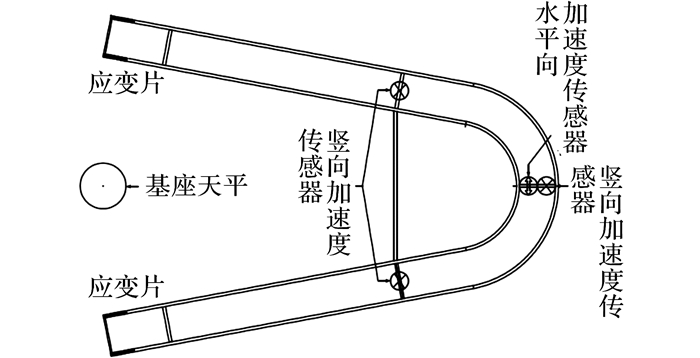
3 气动弹性模型试验与结果 3.1 气动弹性模型的测试仪器气动弹性模型风洞试验中的测试仪器由加速度传感器、动态应变片和六分量动态天平组成.在模型的悬挑端分别安装竖直向与水平向2个加速度传感器, 用以测定廊桥的风致竖向振动与横向振动.在约2/3的悬挑长度的廊桥两侧另外安装2个竖向加速度传感器, 用以测定廊桥的风致扭转振动.加速度传感器的标定则是借助激光位移计将其按已知的频率与振幅作简谐振动完成的.在模型根部的骨架上布置了应变片, 用以测定廊桥箱梁固端的总弯矩.应变片的标定是通过在模型上施加一组已知荷载并测试应变片的信号输出完成的.整个模型被安装在六分量动态天平上, 用以测定作用在整桥上总的风荷载(力和力矩)在各个方向上的分量.气动弹性模型的测试仪器布置图可见图 8.
|
图 8 气动弹性模型的测试仪器布置图 Fig. 8 Instrumentation layout |
从图中可以看出, 所设计的模型风致响应测试仪器能提供一定的测试赘余量, 例如由应变片与动态天平都可得到整桥上总的风荷载;由加速度传感器结合式(1)的关系式也可得到与应变片相应的数据.赘余量的设置对保证模型试验的可靠度是非常重要的.试验数据分析中需要对所有测试工况进行赘余量一致性检验, 以确保在整个试验过程中模型状态没有发生改变, 测试仪器工作正常.
测试中的信号采样频率换算成足尺后为45 Hz, 满足对动态响应的分辨率要求.采样时长换算成足尺后不小于10 min.
3.2 气动弹性模型试验的风场设置根据山体地貌模型的试验结果确定了抗风设计中需要考虑的风场工况(见表 3), 表中, U为平均风速;I为总湍流度;α1为风向角,α2为风攻角.风向角以风的来流方向与顺桥方向之间的夹角定义为风向角, 0°风向角即为顺桥方向.正风攻角定义为从下往上吹的风, 而负攻角则为从上往下的风.
| 表 3 气动弹性模型试验的风场参数 Table 3 Wind properties for aeroelastic model testing |
气动弹性模型安装在风洞试验段的转盘上, 通过转动模型来模拟风向角.根据相似准则可以得到与设计风速对应的风洞风速.实际测试时是对每一工况测试一组不同风速, 其大小涵盖略小于1 a回归期风速到略大于气动稳定性验算风速.1 a回归期风速下的结构振动主要用于评估桥梁的舒适度性能指标.在本研究中, 1 a回归期风速约等于15 m/s.风场模拟中的湍流度是通过在风洞试验段的上风口设置被动式湍流发生装置以及在沿风洞方向布置地板粗糙元实现的.气弹模型的根部支座周围设置了局部的山体模型, 以得到由爬坡风造成的顺桥向风攻角.侧风向的风攻角模拟由局部山体模型和支座转动机构共同完成.局部的山体模型还保证了模型的支座部分屏蔽于风场, 这样由测试仪器得到的数据仅反映作用在廊桥悬挑部分的风效应.如图 9所示为试验中的廊桥气动弹性模型.

|
图 9 试验中的气动弹性模型 Fig. 9 Aeroelastic model during testing |
由支座天平和骨架应变片的测试数据可以求算风荷载的平均分量与脉动分量, 由加速度传感器的测试数据进行频谱分析并结合式(1)的关系式可以得到各模态的惯性力分量, 这样不但可以对各测试通道的可靠性进行相互校核, 而且可以将总的风荷载分离为平均分量、背景分量与惯性力分量3部分.这一分离对于确定下述的等效静力风荷载分布是至关重要的.
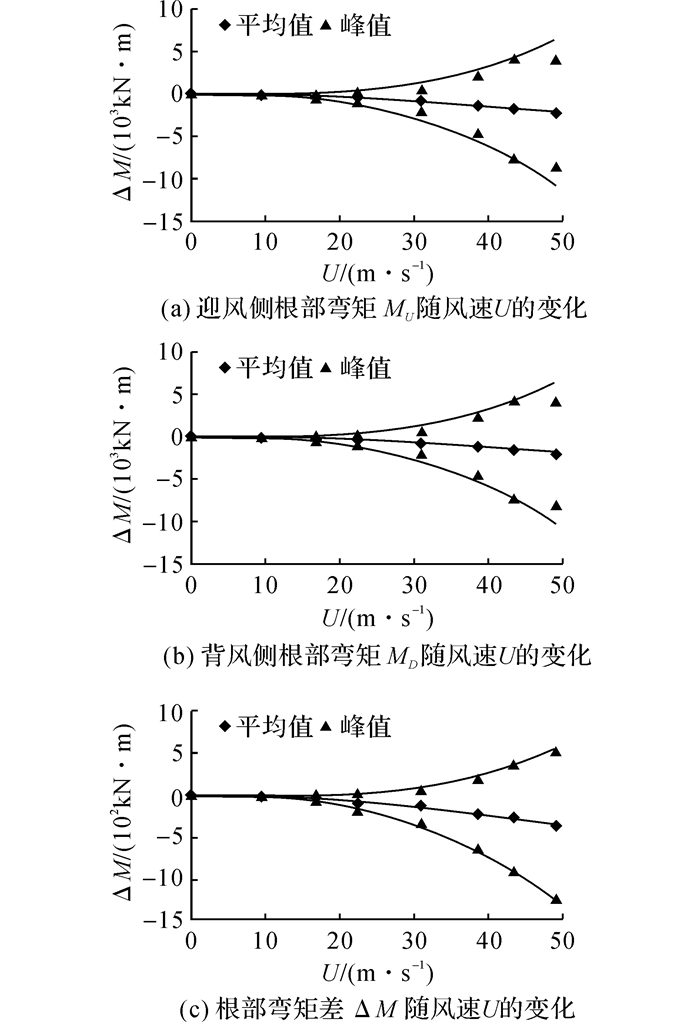
作为风致结构响应的典型示例, 图 10给出在α1=45°得到的廊桥根部箱梁上的竖向弯矩, 图中Mu为迎风侧根部弯矩,Mp为背部侧根部弯矩.
|
图 10 廊桥根部的风致箱梁弯矩α1=45°, α2=+10°) Fig. 10 Wind-induced bending moments at cantilever base (α1=45°, α2=+10°) |
从图中可以看出, 在α2=+10°攻角下, 端部弯矩的平均值是负的, 代表箱梁下部受拉, 上部受压.迎风侧根部和背风侧根部的竖向弯矩差值ΔM代表桥梁承受的绕顺桥向的扭转风荷载, 主要由45°风向角下迎风侧与背风侧的竖向荷载差造成.分析结果表明风荷载中的主要成分是振动引起的动态惯性力.与平均荷载相比, 惯性荷载对风速变化更为敏感.平均荷载与风速的平方成正比, 而惯性荷载则受风力谱中湍流能量分布的影响, 在所关心的约化频率范围内湍流功率谱值随风速而提高, 使得惯性荷载近似与风速的3至3.5次方成正比[16]
图 10还表明在所测试的风速范围内, 没有出现气动不稳定或涡激共振现象.事实上在所有测试工况内, 均没有观测到气动不稳定或涡激共振现象, 表明这一桥梁是空气动力稳定的.抗风设计的关注重点应当是与抖振响应有关的风荷载与风致振动.
由风洞试验只能确定结构风响应(风荷载和风致振动)与风速风向的函数关系.为了考虑实际场地上风速风向出现概率的气候特点, 需要将风洞试验结果结合当地的风气候统计模型进行概率分析才能得出满足设计回归期定义的最大风荷载.本研究中根据桥址周围3个独立气象站近30 a的逐时风速风向记录建立风速风向联合概率分布模型, 然后采用超越概率分析方法将风速风向联合概率分布模型与风洞试验数据相结合.超越概率分析是目前风洞试验技术中相对最为精确可靠的方法, 并已被成功应用于处理气动弹性模型试验数据[7, 17].
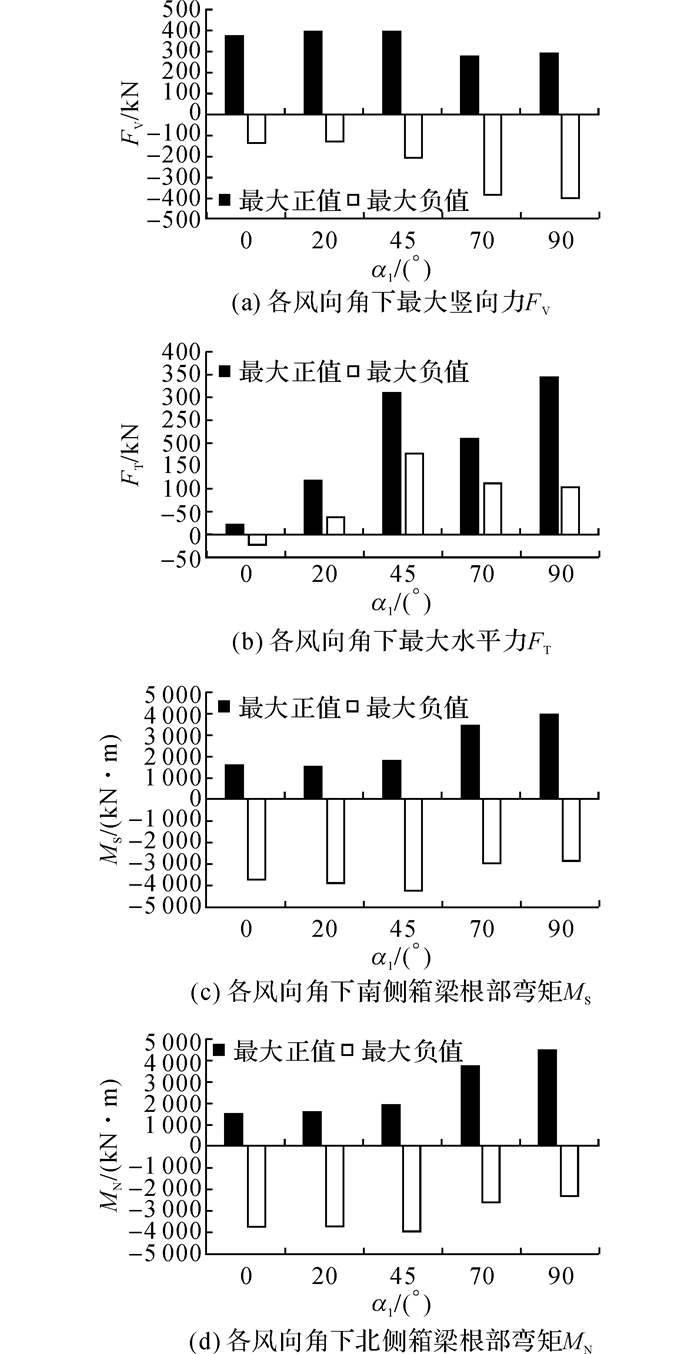
廊桥根部箱梁是结构抗风设计的关键部位.图 11给出按超越概率分析后得到的50 a回归期不同风向角下出现的最大/最小内力, 从图中可以看出不同分量的最大(小)荷载并不出现在同一风向角下.事实上由于总荷载中动态分量占主要成分, 不同分量的最大(小)荷载一般也不同时出现.为了避免不必要的保守设计, 需要分析实际的荷载组合, 并在此基础上以等效静力荷载分布的形式给出结构设计荷载.确定等效静力荷载分布是实现风洞试验研究的工程价值最重要的组成部分.
|
图 11 廊桥根部最大设计风荷载 Fig. 11 Maximum design wind loads of main girders at cantilever base |
等效静力荷载分布定义为由指定静力荷载分布得到的荷载效应不小于相应的实际动态荷载效应的峰值.借助影响函数确定等效静力荷载分布.
首先将结构分成N段, 每一段上的等效静力荷载以向量Plik表示, 其中脚标l代表与第l荷载效应等效;i代表作用在第i分段上;k=x、y、z代表 3个作用力方向.
这样某一荷载效应(如某断面弯矩)可一般地表示为
| $ {e_l}\left( t \right) = \sum\limits_{i = 1}^N {\sum\limits_{k = 1}^3 {\left( {{{\overline F }_{ik}} + {{\widetilde F}_{ik}}\left( t \right) + {m_i}\sum\limits_{j = 1}^M {{\varphi _{jik}}} {a_j}\left( t \right)} \right)} } {I_{lik}}. $ | (3) |
式中:Fik为第i段沿k方向的平均荷载,
考虑到廊桥的动态响应中, 由振动引起的惯性荷载占主导, 而背景荷载则由于相关性的原因数值较小, 可据此将等效静力荷载分布的形式简化为
| $ {\mathit{\boldsymbol{P}}_{lik}} = {\widetilde P_{ik}} + \sum\limits_{j = 1}^M {{g_j}{m_i}{\varphi _{jik}}{D_{li}}{\sigma _{aj}}} . $ | (4) |
式中:
Dlj为第j模态对第l荷载效应的参与系数, 由下式求出.
| $ {D_{Ij}} = \frac{{\sum\limits_{i = 1}^N {\sum\limits_{k = 1}^3 {{m_i}{I_{lik}}{\varphi _{jik}}} } }}{{\sqrt {\sum\limits_{{i_1} = 1}^N {\sum\limits_{{i_2} = 1}^N {\sum\limits_{{k_1} = 1}^3 {\sum\limits_{{k_2} = 1}^3 {{m_{{i_1}}}{m_{{i_2}}}} {I_{l{i_1}{k_1}}}{I_{l{i_2}{k_2}}}{\varphi _{j{i_1}{k_1}}}{\varphi _{j{i_2}{k_2}}}} } } } }}. $ | (5) |
式中的下标i1和i2代表对所有分段求和, k1和k2则代表对所有方向求和.
由式(4)可见, 等效静力荷载分布中需要详细了解平均荷载在各段的分布, 而除非进行单独的风压试验, 气动弹性模型是无法提供相应数据的.考虑到平均荷载远小于动态荷载(见图 10), 对平均荷载分布作一定近似处理不至于造成最终结果的显著差别, 因此可以根据箱梁各截面尺寸及其平均风场, 对平均风荷载分布做了估计, 并对照其根部的测试值进行标定.由此得到可供设计采用的等效静力荷载分布.然后按荷载包络的原则, 对各等效静力荷载分布进行分类归纳, 最后简化成以下6种静力荷载工况.工况1:代表风向为顺桥向, 此时顺桥向荷载最大, 同时向上的荷载也较大; 工况2:代表风向与顺桥方向成20°, 此时向上的荷载为所有工况中最大; 工况3:代表风向与顺桥方向成45°, 此时向上的荷载较大, 同时还有较大的横桥向荷载; 工况4:与工况3类似, 但对称轴两侧向上的正向荷载差达到最大, 即最大正扭转, 所以其中某一固定端的弯矩会较大; 工况5:代表风向为横桥向, 此时向下的荷载为所有工况中最大, 同时横桥向荷载也为所有工况中最大; 工况6:与工况5类似, 但对称轴两侧的负向荷载差达到最大, 即最大负扭转.
在评估桥梁的振动舒适度时, 应当综合考虑各项性能指标.显然当室外风环境已不满足游客舒适度的情况下(例如桥面风速过大以致游客无法正常行走等)评估桥梁的振动舒适度并没有实际意义.参照行人风环境评估标准, 评估桥梁的振动舒适度时可以仅考虑桥面风速不大于15 m/s的情况.
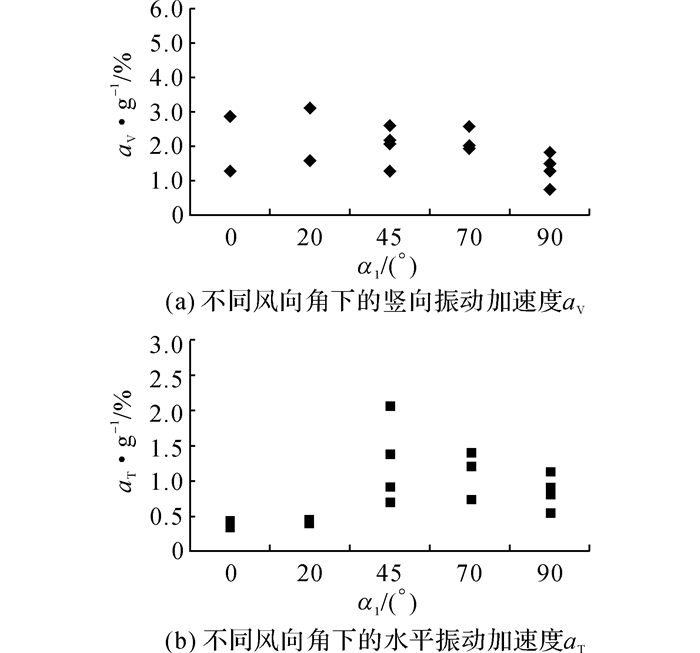
图 12给出在该验算风速下各风向角的振动加速度.按一般振动舒适度评估标准, 这里将振动加速度表示为重力加速度g的百分比.从图中可以看出, 最大加速度发生在偏离顺桥向20°至45°的风向角范围内.最大竖向加速度约为3%g, 最大水平向加速度约为2%g, 这已满足一般的舒适度要求[18].
|
图 12 验算风速下预计最大振动加速度 Fig. 12 Predicted maximum accelerations at design speed |
(1) 本文介绍的全气动弹性模型研究方法克服了经典桥梁风振理论的局限性,可用于解决片条假定不成立的复杂风场下人行桥梁的三维风响应问题.
(2) 研究结果表明,在复杂的山体地貌影响下,悬挑梁桥不但会经受爬坡风造成的正攻角风场作用,而且会经受下洗气流导致的负攻角强风荷载.后者对结构设计更为不利,并且在一般工程实践中往往容易被忽略.本文介绍的全气动弹性模型大攻角风洞模拟方法可以对这种风场情况予以准确把握.
(3) 本文介绍的相似参数取值与工艺设计在一定程度上减低了全气动弹性模型的制作难度,使得全气动弹性模型方法易于在工程实践中应用.所提出的模型验证方法与赘余量测试原则有助于提高试验结果的可靠性,对类似试验研究具有参考价值.
(4) 所提出的静力等效风荷载求算方法大大拓展了全气动弹性模型试验作为设计检验的传统功能,使得全气动弹性模型试验可以成为结构设计与优化的主要依据.相关的研究方法与技术路线对研究其他复杂空间结构的风效应也具有一定的普遍适用性.
| [1] | XIE J, HUNTER M, IRWIN P. Experimental and analytical approaches in wind engineering studies for bridges[C]//Proceedings of IABSE Symposium on "Responding to Tomorrow's Challenges in Structural Engineering". Budapest, Hungary:IABSE. 2006, 92(14):9-16. https://trid.trb.org/view.aspx?id=707629 |
| [2] | 项海帆. 现代桥梁抗风理论与实践[M]. 北京: 人民交通出版社, 2005: 50-97. |
| [3] | SIMIU E, SCANLAN R H. Wind effects on structures-fundamentals and applications to design[M]. 3rd Edition. New York: John Wiley & Sons, New York NY, 1996: 446-486. |
| [4] | STRØMMEN E N. Theory of brid-ge aerodynamics[M]. Berlin Heidelberg: Springer-Verlag, 2006: 91-208. |
| [5] | GE Y, TANAKA H. Aerodynamic flutter analysis of cable-supported bridges by multi-mode and full-mode approaches[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 86(2/3): 123–153. |
| [6] | DING Q, CHEN A, XIANG H. Coupled buffeting response analysis of long-span bridges by the CQC approach[J]. Structural Engineering and Mechanics, 2002, 14(5): 505–520. DOI:10.12989/sem.2002.14.5.505 |
| [7] | XIE J, YANG D. Wind Engineering Studies for Provencher Pedestrian Bridge[C]//Proceedings of 7th International Conference on Short and Medium Span Bridges. Montreal, Quebec, Canad:CURRAN, 2006, 1:203-313. |
| [8] | XIE J, TANAKA H, WARDLAW R L, et al. Buffeting Analysis of long span bridges to turbulent wind with yaw angle[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1991, 37(1): 65–77. DOI:10.1016/0167-6105(91)90005-H |
| [9] | DIANA G, CHELI F, ZASSO A, et al. Suspension bridge response to turbulent wind:comparison of a new numerical simulation results with full scale data[C]//Proceedings of 10th International. Conference on Wind Engineering. Copenhagen Denmark:AA Balkema 1999:871-878. https://core.ac.uk/display/55185836 |
| [10] | XU Y L, SUN D K, KO J M, et al. Fully coupled buffeting analysis of tsing ma suspension bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 85(1): 97–117. DOI:10.1016/S0167-6105(99)00133-6 |
| [11] | ZHU L D, XU Y L. Buffeting response of long cable-supported bridges under skew winds-part Ⅰ:Theory[J]. Journal of Sound and Vibration, 2005, 281(3/5): 647–673. |
| [12] | BENNISON S J. Designing the Grand Canyon's new laminated glass walkway[R]. Glass performance days, 2007. https://ar.scribd.com/document/239938574/Extended-Abstract |
| [13] |
高斐, 冯文焕. 高墩大跨连续刚构桥气弹模型风洞试验研究[J].
现代交通技术, 2012, 9(5): 33–37.
GAO Fei, FENG Wen-huan. Long-span continuous rigid frame bridge with high-rise piers gas model wind tunnel test study[J]. Modern Transport Technology, 2012, 9(5): 33–37. |
| [14] |
李永乐, 郑史雄, 廖海黎. 泰安长江大桥最大单悬臂状态气弹模型风洞试验研究[C]//中国铁道学会中国交通土建工程学术暨建设成果交流会. 成都: 铁道学会, 2003, 432: 26-37.
LI Yong-le, ZHENG Shi-xiong, LIAO Li-hai.Taian Yangtze river bridge's largest single cantilever state gas bomb model wind tunnel test research[C]//China Communications Construction of Academic and Civil Engineering of China Railway Society Communication Meeting. cheng du:Railway society, 2003, 432:26-37. http://d.wanfangdata.com.cn/Conference/5300160 |
| [15] |
周健, 熊龙, 王骑, 等. 大跨扁平钢箱梁悬索桥全桥气弹模型设计[J].
重庆交通大学学报:自然科学版, 2014, 33(6): 1–4.
ZHOU Jian, XIONG Long, WANG QI, et al. Large-span flat steel box girder suspension bridge gas model design[J]. Journal of Chongqing Jiao-tong University:Natural Science Edition, 2014, 33(6): 1–4. |
| [16] | Canadian Commission of Building and Fire Codes.User's Guide-NBC 2010 Structural Commentaries (Part 4 of Division B)[S]. Ottawa, Canada:NRCC, 2010. https://search.library.utoronto.ca/details?8852816 |
| [17] | IRWIN P A, GARBER J, HO E. Integration of wind tunnel data with full scale wind climate[C]//Proceedings of 10th Ameri.cas Conference on Wind Engineering. Baton Rouge, Louisiana, USA:ASCE, 2005. http://koreascience.or.kr/article/ArticleFullRecord.jsp?cn=KJKHCF_2014_v18n4_347 |
| [18] | Committee on Loads and Forces of the Committee on Bridges of the Structural. Division. Recommended design loads for bridges[J]. Journal of Structural Division, Proceeding of ASCE, 1981, 107(7): 1161–1213. |



