轻质的岩棉夹芯复合屋面板广泛应用于大跨度建筑中.此类屋面板由上、下面层压型金属薄板和中间岩棉夹芯层构成[1].工程中, 上层金属板一般为镁锰合金的铝板, 下层板为镀锌钢板, 夹芯岩棉层承担保温、隔声等功能.目前大跨度屋盖结构的设计中, 结构风振[2-3]计算时并不考虑屋面板的影响.一般认为屋面板的刚度足够大, 因此可将屋面风压直接传递到主结构上, 且结构风振效应计算模型中也不包括屋面板.然而, 屋面板的实际抗弯刚度很弱, 远不能满足刚性板的假定.更为重要的是, 岩棉一类的纤维夹芯材料还属于高阻尼材料.直观地理解, 此类夹芯屋面板相当于是屋盖主体结构表面覆盖的一层“缓冲垫”.因此, 当作用于屋面的脉动风压在通过屋面板传递给主体结构时, 风压幅值和频谱特性会发生怎样的改变以及由此会对结构的风致振动效应产生怎样的影响, 是值得研究的问题.
近年来针对该问题已开展了一些基础性研究工作, 但主要以岩棉材料的力学(含阻尼)性能[4]以及复合屋面板的结构阻尼性能[5]为重点.关于屋面板有限刚度和阻尼性能对风压脉动特性以及主体结构风振响应的影响特点, 相关研究还非常少, 也不能给出一些定量的、规律性的结论.本文以结构阻尼理论和已有的岩棉夹芯材料力学性能测试结果为基础, 通过数值分析对以下3方面的问题展开讨论:采用模态应变能法分析典型檩距岩棉夹芯复合屋面板的阻尼特性;将脉动风压施加到屋面板上, 通过对屋面板支座反力的分析, 考察屋面板的刚度和阻尼性能如何改变风压的脉动特征;借助一个30 m跨度的交叉拱壳, 分析屋面板刚度和阻尼对主体结构风振响应的影响规律.
1 基本理论和假定 1.1 岩棉的材料阻尼损耗因子η[6]是材料阻尼最简单的一种表达形式, 定义为一个振动周期内材料耗损的能量和材料弹性应变能的比值, 其数值越大则表明材料的阻尼耗能能力越强.一般情况下, η与频率相关, 且常用的结构阻尼比ξ与损耗因子η近似满足ξ=η/2[7].王宸等[4]采用振动梁法测得了不同频率下复合屋面板常用岩棉材料的损耗因子, 基于试验数据拟合得到该材料损耗因子ηv与频率f的关系式:
| $ {\eta _{\rm{v}}} = 0.513 - 4.71 \times {10^{ - 4}}f. $ | (1) |
根据式(1)易知, 当f在0~200 Hz的范围内, 岩棉材料的损耗因子为0.513~0.419, 表现出高阻尼的特性.
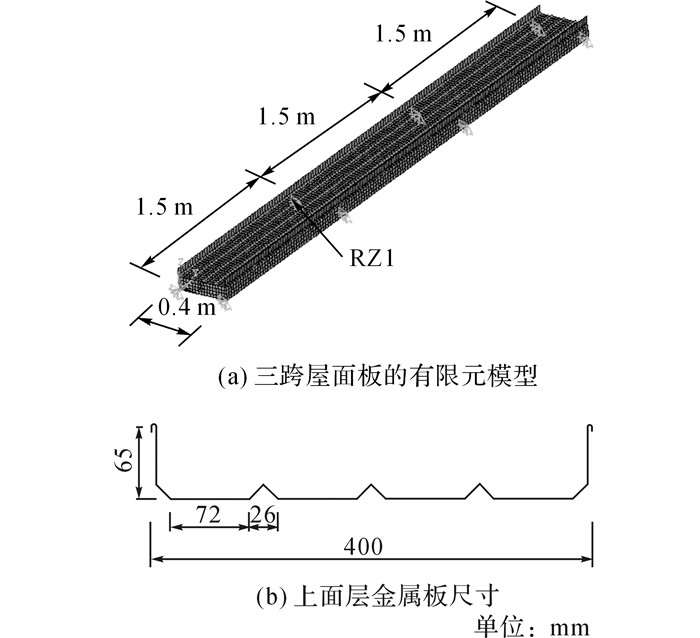
1.2 屋面板的简化有限元模型如图 1所示为一块典型的岩棉夹芯复合屋面板.在工程中, 此类屋面板的檩距约为1.5 m, 上层铝合金压型板厚为0.9~1.0 mm, 下层压型钢板厚为0.4~0.5 mm, 岩棉厚度主要由保温要求决定, 常用厚度约为100 mm.可以看出, 屋面板实际上是一个复杂的结构系统.借助有限元分析软件ANSYS建立一个1.5 m典型檩距的三跨岩棉夹芯屋面板模型(R1), 如图 2(a)所示.模型中上、下层金属板采用壳单元shell63模拟, 上层板的截面尺寸见图 2(b), 下层压型钢板由于波高较小, 简化为平板.岩棉夹芯层定义为实体单元solid45, 沿厚度方向单元分为5等份.该屋面板基本模型的主要参数如表 1所示.复合屋面板的上、下面层金属板与岩棉夹芯层实际上无黏结, 但考虑到风荷载的作用方向垂直屋面板, 平均风分量一般会先将上下面层金属板和岩棉夹芯层压紧(相当于预紧力), 因此在建立以上基本模型时将上、下面层壳单元与相邻夹芯层实体单元对应节点的z向位移耦合来简化模拟, 但不考虑两者x、y向位移的耦合.屋面板边界支承条件为在每个支座(檩条上支点)处x、y、z三向线位移约束, 以此来模拟屋面板T形连接件(如图 1)的固定作用.

|
图 1 岩棉夹芯复合屋面板 Fig. 1 Composite roof panel with rock wool core |
|
图 2 岩棉夹芯复合屋面板有限元基本模型 Fig. 2 Basic FEmodel of composite roof panel with rock wool core |
| 表 1 岩棉夹芯复合屋面板基本模型参数 Table 1 Parameters of the basic model of composite roof panel with rock wool core |
上、下金属面板(铝合金和钢)均定义为各向同性材料, 岩棉假定为正交异性材料.王宸等[4]也给出了试验测得的岩棉材料的质量密度、弹性模量和泊松比等力学指标, 且进一步计算出岩棉材料正交异性本构模型的完整参数.3种材料本构模型的力学参数如表 2所示, 其中Ex、Ey、Ez分别为正交异性材料x、y、z方向的弹性模量, μxy、μyx、μyz、μxz、μzx、μzy为材料的泊松比, ρ为材料的质量密度.
| 表 2 岩棉夹芯复合屋面板基本模型材料力学参数 Table 2 Mechanical parameters of materials in basic model of composite roof panel with rock wool core |
风荷载作用下屋面板的动力方程为
| $ \mathit{\boldsymbol{M\ddot x}} + \mathit{\boldsymbol{C\dot x}} + \mathit{\boldsymbol{Kx}} = \mathit{\boldsymbol{F}}\left( t \right). $ | (2) |
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;
令x = Φy, 其中Φ为振型矩阵, y为广义位移向量.考虑Φ对于M和K的正交性, 并假定阻尼矩阵C也同样满足振型正交条件, 若结构自由度数为n, 则式(2)可以化简为如下n个独立的方程:
| $ {\ddot y_i} + 2{\xi _i}{\omega _i}{\dot y_i}{\rm{ + }}\omega _i^2{y_i} = {f_i}\left( t \right)/{m_i}, i = 1, 2, \cdots, n. $ | (3) |
式中:yi、ωi、ξi分别为i阶模态的广义位移、圆频率和模态阻尼比, 且ωi2=ki/mi, ξi=ci/(2miωi).而mi=φiTMφi、ki=φiTKφi、ci=φiTCφi分别为结构第i阶模态的质量、刚度和阻尼, φi为第i阶振型;fi(t)=φiTF(t)为结构第i阶模态的广义荷载.
如果已知各阶模态阻尼比ξi, 则可以求得该阶模态的阻尼系数ci=2miωiξi, 进而根据式(3)可求得结构阻尼矩阵为
| $ \mathit{\boldsymbol{C}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} c}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}. $ | (4) |
式中:c=diag{…, ci, …}为由ci构成的对角矩阵.
在传统采用Rayleigh阻尼模型的结构分析中, 为简化计算一般假定各阶模态的阻尼比ξi相同, 然后取两阶典型模态(通常取第一、二阶模态)反算出Rayleigh阻尼模型中的系数α、β.但这种方法显然不准确.理论上, 结构各阶模态的阻尼系数是不同的.对于岩棉夹芯复合屋面板而言, 式(1)就已经表明其夹芯材料阻尼与频率的相关性.根据复阻尼理论[7], 可以计算每一阶模态对应的损耗因子ηi, 由此计算对应的阻尼比ξi=ηi/2, 进而代入式(4)来构建结构阻尼矩阵C.
1.5 模态应变能法模态应变能法是一种求解由多种不同阻尼材料构成的复合结构模态损耗因子的方法[8].该方法是基于阻尼损耗因子的定义, 以该振型中各种材料的应变能为权数, 对所有材料的损耗因子进行加权平均, 按下式计算该模态的整体屋面板损耗因子ηi:
| $ {\eta _i} = \frac{{\sum\limits_m {{\eta _{mi}}} {W_{mi}}}}{{\sum\limits_m {{W_{mi}}} }} = \frac{{\sum\limits_m {{\eta _{mi}}} {W_{mi}}}}{{{W_i}}}. $ | (5) |
式中:ηmi为材料m对应于模态i频率的材料损耗因子;Wmi为模态i振型下材料m所储存的应变能, Wi为模态i振型下结构所有材料的应变能之和.
对于岩棉夹芯复合屋面板, 其上、下面层金属板材料阻尼很小, 通常可以忽略.因此本文中, 在采用式(5)计算屋面板的结构阻尼时, 仅考虑夹芯层的阻尼贡献.
采用ANSYS进行屋面板的动力时程计算前, 先需要对屋面板模型进行模态分析, 并采用式(5)计算出各阶模态的损耗因子ηi以及阻尼比ξi.然后, 利用软件中提供了一个“模态综合阻尼比ξid”参数来引入各阶模态的阻尼比ξi[9].
2 屋面板的结构阻尼对如图 2所示的三跨岩棉夹芯复合屋面板模型进行动力模态分析, 并利用式(5)计算各阶模态的损耗因子.前50阶模态对应的自振频率f、岩棉的材料损耗因子ηv、夹芯层模态应变能Wvi与整体屋面板模态应变能Wi的比值以及屋面板的模态损耗因子ηi、屋面板的模态阻尼比ξi一并列于表 3.屋面板的前8阶振型如图 3所示.
| 表 3 岩棉夹芯复合屋面板模态损耗因子 Table 3 Modal loss factors of composite roof panel with rock wool core |

|
图 3 典型檩距屋面板的前8阶振型 Fig. 3 First 8 mode shapes of composite roof panel with typical purlin distance |
如表 3所示, 夹芯层模态应变能与屋面板模态应变能比值在前15阶模态变化幅度较大, 最小为第2阶的0.298, 最大达到第4阶和第5阶的0.999.从第16阶开始夹心层模态应变能比值基本保持在0.6以上.屋面板前50阶振型的模态损耗因子都较大, 除了第2阶的0.152、第3阶的0.199和第14阶的0.196外, 其他各阶模态损耗因子值都大于0.2, 并且在第4阶和第5阶模态达到最大的0.506.相比于一般建筑结构0.02~0.05的阻尼比(相当于损耗因子0.04~0.10), 该类复合屋面板由于受夹芯层高阻尼的贡献, 在频率为4.56~69.3 Hz的宽频段内均表现出高阻尼特性.实际上, 大于50阶的各阶模态依然具有较高的阻尼, 但限于篇幅, 本文未予列出.
对于4、5、11、12、19等阶模态, 其振型主要是以岩棉夹芯层的变形为主, 该振型下屋面板的应变能主要存储在岩棉中, 其夹芯层模态应变能占整体屋面板模态应变能的比例高达0.9以上.以屋面板整体弯曲变形为主的2、3阶振型(如图 3所示), 面层金属板的应变能占总的模态应变能的比例较大, 模态损耗因子虽然低至0.152和0.199, 但阻尼性能依然显著.
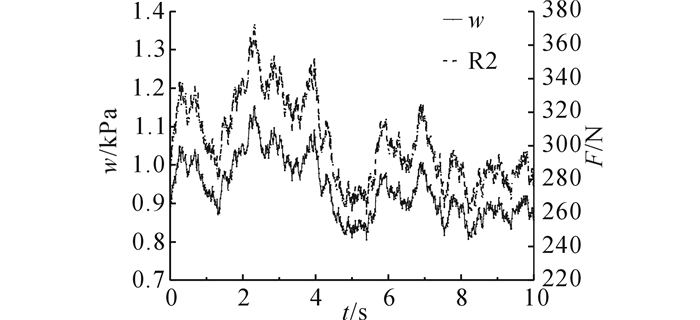
3 屋面板对风压脉动特性的影响 3.1 刚度和阻尼的影响将人工生成的风荷载(如图 4所示)垂直向上(吸力)施加到图 2所示的屋面板上, 通过分析支座反力来考察屋面板在传递风荷载过程中对风压脉动特性产生的影响.图 4中的风压时程w(t)是由满足Davenport谱[3]的风速时程v(t)(单位m/s)根据公式w(t)=v2(t)/1 630计算得到(令屋面风压满足准定常假定)[10], 其中地面粗糙度系数k=0.002 15(相当于地面粗糙度为B类), 平均风速v10=35 m/s.风速时程v(t)又是采用线性滤波法[11]模拟得到.风压时程长度为10 s, 时间步长为0.01 s.
|
图 4 人工模拟风压时程 Fig. 4 Time history of artificial wind pressure |
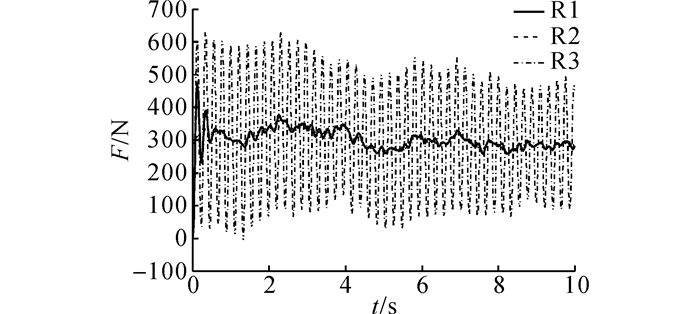
为进一步考察岩棉夹芯复合屋面板的有限刚度和高阻尼特性对其力学性能的影响, 通过对基本模型R1的刚度和阻尼参数进行调整, 增加了刚性板无阻尼(R2)和实际刚度无阻尼(R3)这2个对比模型, 具体如表 4所示.对3个模型施加如图 4所示的脉动风压并进行时程分析.注意, 由于3个模型均不考虑屋面板自重, 脉动风压按向上(吸力)或向下(压力)施加并不影响后续对计算结果的分析.如图 5所示为3个模型所计算得到的屋面板支座RZ1(z向)(见图 2(a))的反力时程F(t).3个模型反力时程的最大值及其相对比值如表 5所示, 其中FRimax分别为模型Ri的支座RZ1反力最大值(i=1, 2, 3).但为避免数值计算中突加荷载的初始放大效应, 表 5中的反力最大值均取0.5 s以后的数据.
| 表 4 岩棉夹芯复合屋面板有限元模型 Table 4 FE models of composite roof panel with rock wool core |
|
图 5 模型R1、R2、R3支座反力RZ1时程 Fig. 5 Time histories of reaction forces RZ1 of Models R1, R2 and R3 |
| 表 5 模型R1、R2和R3支座RZ1反力最大值 Table 5 Reaction forces RZ1 of Models R1, R2 and R3 |
将刚性板模型R2的支座反力时程F(t)列于图 4中, 可以发现与施加在屋面板上的风压时程一致, 两者仅相差一个比例系数.这实际上相当于直接将风荷载按照负荷面积比例分配到各支座上.进一步对比图 5中的模型R2和R3的结果, 在不考虑阻尼的前提下, 屋面板实际有限刚度会显著放大脉动风压幅值, 模型R3支座反力最大值是R2的1.698倍(表 5).但是如果在模型R3的基础上进一步考虑屋面板的阻尼性能, 即模型R1, 则R3振荡放大的反力又被显著地抑制, 最大反力值降低到59.8%, 表现出屋面板夹芯层的高阻尼减振特性.
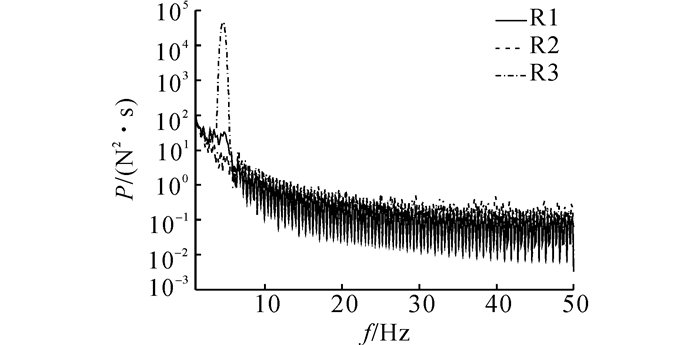
如图 6所示为3个模型反力时程的功率谱P(f).从图 5可以看到, 模型R1和R2在0.5 s以后的反力时程非常接近, 表明屋面板刚度对脉动风压的动力放大效应与屋面板夹芯层的阻尼减振效应相当.但是从如图 6所示的各模型反力时程的功率谱可以看出, 模型R3的功率谱密度在屋面板基频处(4.56 Hz)明显增大, 表明当考虑屋面板的有限刚度后, 风荷载经屋面板传递到支座后其脉动特性发生了变化, 脉动风能量在屋面板基频处有集中效应.模型R1的支座反力功率谱密度在0~50 Hz的频域段内都较R3小, 尤其在屋面板基频处显著降低, 表明屋面板的阻尼在整个频域段内对脉动风能量都有明显的抑制作用.
|
图 6 模型R1、R2、R3支座RZ1反力功率谱 Fig. 6 Power spectra of reaction forces RZ1 of Models R1, R2 and R3 |
在实际工程中, 岩棉夹芯复合屋面板的檩距和面层金属板厚度的变化幅度一般较小, 但夹芯层厚度根据保温要求变化较大.由于会直接影响到屋面板的阻尼性能, 因此在工程意义上有必要考察夹芯层厚度对风压脉动特性的影响.对于图 2所示的屋面板模型, 在其他参数不变的前提下将夹芯层厚度改变为150 mm(模型R4)和200 mm(模型R5), 重新计算屋面板的模态损耗因子并重构阻尼矩阵, 然后同样计算图 4风压作用下的RZ1反力时程并分析其功率谱.
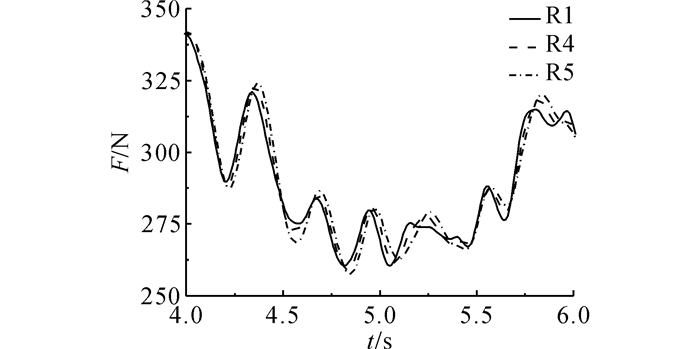
如图 7所示为模型R1、R4和R5的支座RZ1反力时程F(t)的对比, 为清楚表示仅选取4~6 s时段.表 6给出了3个模型支座反力整个时程内统计指标的对比, 表中
|
图 7 模型R1、R4、R5支座反力RZ1时程 Fig. 7 Time histories of reaction forces RZ1 of Models R1, R4 and R5 |
| 表 6 模型R1、R4和R5支座RZ1反力对比 Table 6 Reaction forces RZ1 of Models R1, R4 and R5 |
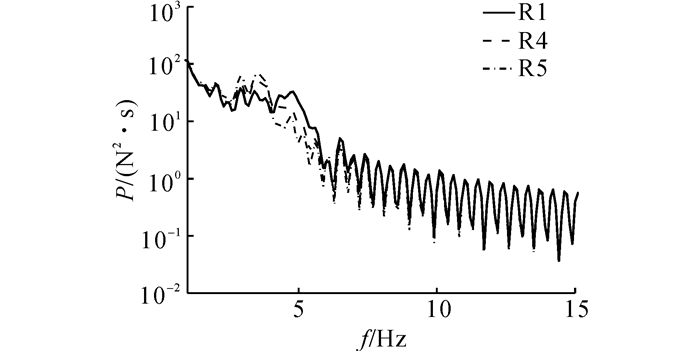
3个模型支座RZ1反力的功率谱如图 8所示.可以看到, 夹芯层材料厚度的不同会引起支座反力从图 8中功率谱在屋面板基频处出现错峰现象, 这是由于屋面板刚度和质量变化造成基频变化而引起的.夹芯层厚度从100增大到150和200 mm, 岩棉夹芯层质量增加对基频影响大于刚度, 造成基频减小, 故支座反力功率谱曲线峰值向左移动, 脉动风能量的集中效应稍往低频段偏移.
|
图 8 模型R1、R4、R5支座RZ1反力功率谱 Fig. 8 Power spectra of reaction forces RZ1 of Models R1, R4 and R5 |
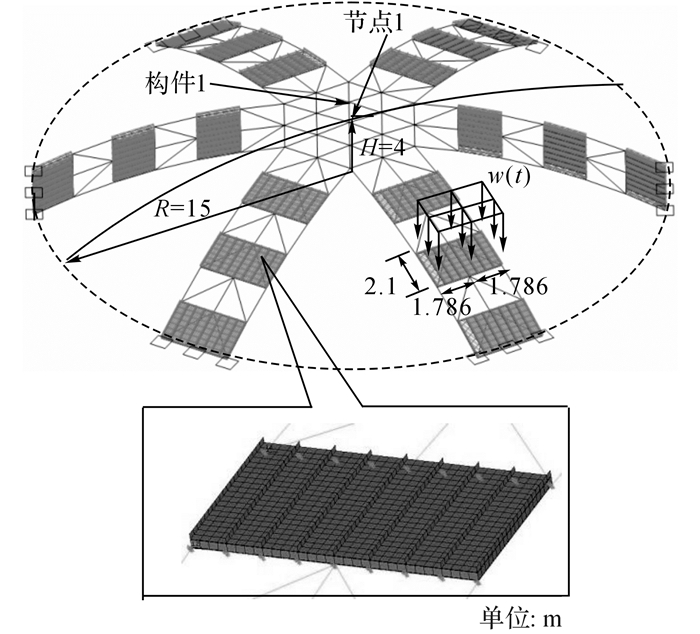
利用如图 9所示一个30 m跨度的交叉拱壳结构假想算例来考察屋面板刚度和阻尼性能对主体结构风致振动效应的影响.该拱壳由轴对称的三向平行拱构成.每向平行拱由3根单拱组成, 水平间距为1.786 m, 拱高为4 m.由拱脚垂直于单拱方向间距2.1 m布置横梁(檩条).主体结构中所有杆件间刚接, 除单拱间斜杆为截面200 mm×4 mm的方钢管外, 其他杆件均为450 mm×200 mm×6 mm的矩形钢管, 在Ansys中用梁单元beam4模拟.钢材密度取7 850 kg/m3.约束拱脚支座节点(如图 9中的“□”所示)的竖向和水平切向位移.通过改变拱脚支座的水平径向约束刚度和钢材的弹性模量来调节主体结构的自振频率(计算时均考虑了屋面板质量), 共考虑主体结构基频为2.23、5.0和7.5 Hz这3种情况.3种基频模型对应的水平径向约束刚度分别为1、7.46 kN/mm和该自由度完全被约束;前2种基频模型对应的钢材弹性模量为206 GPa, 第3种基频模型为244.5 GPa.
|
图 9 整体结构模型 Fig. 9 Model of whole structure |
研究表明, 有限元分析中如果屋面板按满布建模, 结构的蒙皮效应[12]是非常显著的.但实际结构中, 复合屋面板中的金属面板一般较薄, 容易发生局部屈曲, 而且屋面与檩条间为防止温度应力也常采用柔性连接, 故蒙皮效应实际上较有限元模拟的情况要弱很多.为避免蒙皮效应的影响, 将岩棉夹芯复合屋面板在平行拱网格上隔跨布置, 并采用表 1和2相同的参数建立屋面板的精细模型.屋面板在直立锁边处与横梁(檩条)对应节点三向线位移耦合.应该指出的是, 图 9中模型的屋面板跨度为2.1 m.同样参照图 2所示模型建立一个单跨跨度为2.1 m的三跨屋面板模型, 可以求得屋面板的基频为4.56 Hz.
将图 4所示的风压时程垂直屋面板区域进行施加, 不考虑脉动风空间相关性.根据整体结构基频、是否包括屋面板、风荷载加载方式和结构阻尼取值的不同, 建立如表 7所示的12个整体结构有限元模型, 其中fn为结构基频.应该指出, RM0、RM0-5和RM0-7.5为目前结构风振计算的常用模型, 即模型中不含屋面板, 风荷载和屋面板质量等代到主体结构节点上, 结构阻尼按常阻尼比0.02考虑.RM1~RM3、RM1-5~RM3-5和RM1-7.5~RM3-7.5为包含屋面板的模型.RM1、RM1-5和RM1-7.5的风荷载依然作为等代节点荷载施加在主体结构上, 而RM2、RM2-5和RM2-7.5将风荷载直接作用在屋面板上, 但6个模型依然采用常阻尼比0.02.相比之下, RM3、RM3-5和RM3-7.5在考虑屋面板实际刚度的基础上进一步精确考虑屋面板的阻尼, 在进行动力时程计算之前, 采用模态应变能法计算前200阶模态的损耗因子, 以建立整体结构模型的阻尼矩阵.
| 表 7 整体结构有限元模型描述 Table 7 Description on finite element models of wholestructure |
通过对比以上12种模型中同一跨中构件1(见图 9)的弯矩和轴力风振系数以及跨中节点1位移风振系数的大小, 来分析屋面刚度和阻尼对主体结构风振效应的影响.风振系数为
| $ \beta = 1 + \frac{{\mu \sigma }}{x}. $ | (6) |
式中:σ为响应时程的均方差;x为响应时程均值;μ为保证因子, 本文简化统一取3.5[10].
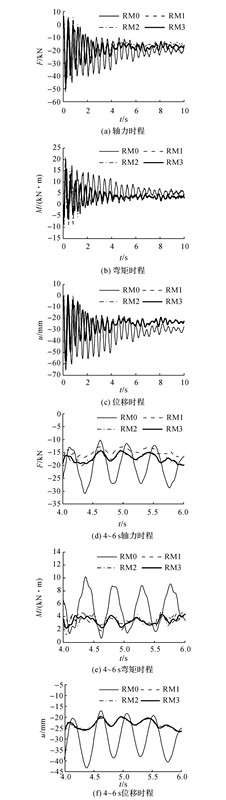
4.2 4种计算模型的风振响应对比首先对主体结构基频为2.23 Hz的情况进行讨论.针对4种计算模型进行结构的风振响应分析, 可求得杆件1的轴力F(t)、跨中弯矩M(t)以及节点1竖向位移u(t)的响应时程, 分别如图 10(a)~(c).尽量忽略前期风荷载突加效应的影响, 图 10(d)~(f)还给出了以上3个参数4~6 s的时程以便于对比.采用4~10 s的时程数据并统计其均值F、M、u和均方差σF、σM、σu", 利用式(6)计算构件1的轴力、弯矩以及节点1竖向位移风振系数.4个模型的计算结果分别如表 8~10所示.表中,F、σF、βF分别为模型RM0~RM3构件1轴力均值、均方差、风振系数;M、σM、βM分别为模型RM0~RM3构件1轴弯矩均值、均方差、风振系数;u、σu、βu分别为模型RM0~RM3节点1竖向位移均值、均方差,风振系数.
|
图 10 模型RM0~RM3构件1轴力、弯矩和节点1竖向位移时程 Fig. 10 Time histories of axial force and bending moment of Member 1 as well asvertical displacement of Node 1 for Models RM0~RM3 |
| 表 8 模型RM0~RM3构件1轴力风振系数 Table 8 Wind-induced vibration coefficients of axial forces of Member 1 for Models RM0~RM3 |
| 表 9 模型RM0~RM3构件1弯矩风振系数 Table 9 Wind-induced vibration coefficients of bending moments of Member 1 for Models RM0~RM3 |
| 表 10 模型RM0~RM3节点1竖向位移风振系数 Table 10 Wind vibration coefficient of vertical displacements of Node 1 for Models RM0~RM3 |
从轴力、弯矩和节点位移风振系数均能够看出, 无屋面模型RM0的风振系数最大.以弯矩风振系数为例, 其值高达2.094, 表明平均风效应和脉动风效应基本相当.对应引入屋面板的模型RM1, 下部交叉拱壳结构对平均风(注意该风荷载为非平稳荷载)和脉动风的内力响应均有较大幅度的下降, 3类风振系数均明显减小, 其中弯矩风振系数减小到1.526.观察该模型的位移响应, 发现屋面板对于主体结构发生了较大的相对变形, 表明作用在主体结构节点上的风荷载主要是激发了屋面板的振动(相当于增加一个调频质量阻尼块(TMD)), 从而大大降低了其自身的动力响应.对于风荷载施加在屋面板上的模型RM2, 风振系数相比于RM1略有增大, 体现出屋面板有限刚度在传递风荷载的过程中对脉动风压的放大效应.进一步考虑屋面板的阻尼后, 模型RM3相对RM2会降低风振系数, 但降幅不大.
总体来看, 相对于目前风振计算的做法(即模型RM0), 考虑屋面板刚度和阻尼后, 结构的内力和位移风振系数均明显降低.模型RM3构件1的轴力风振系数与模型RM0相比从1.642下降到1.313, 弯矩风振系数从2.094下降到1.615, 节点1的竖向位移风振系数从1.578下降到1.284.
4.3 下部结构刚度的影响如上所述, 通过改变支座约束刚度和材料弹性模量调节主体结构的刚度, 使结构基频分别达到5和7.5 Hz.针对以上2种基频情况, 同样分别建立4个模型进行结构风振计算, 如表 7所示.以上2种基频情况的构件1轴力、弯矩响应时程和节点1的位移响应时程分别如图 11、12所示, 图中仅给出4~6 s的时程以忽略前期风荷载突加效应的影响.同样采用4~10 s的时程数据并统计其均值和方差, 利用式(6)计算构件1的轴力、弯矩以及节点1位移风振系数.对应于2种主体结构基频, 8个模型的计算结果分别如表 11~16所示.
|
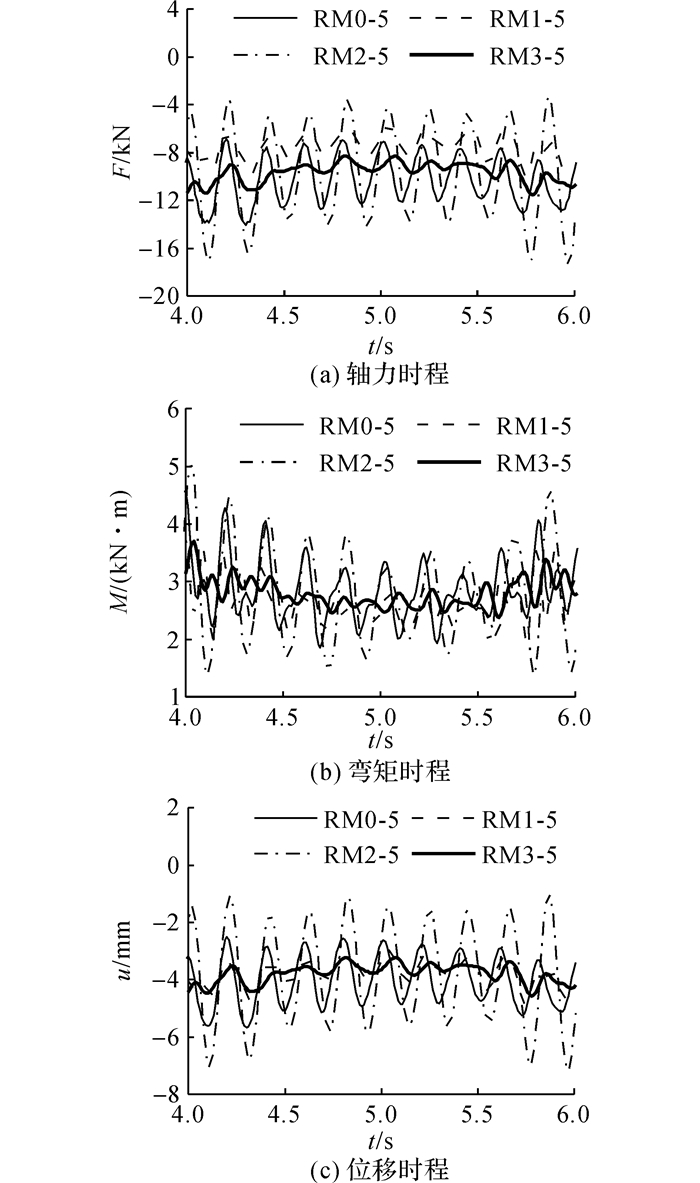
图 11 模型RM0-5~RM3-5构件1轴力、弯矩和节点1竖向位移时程 Fig. 11 Time histories of axial force and bending moment of Member 1 as well as vertical displacement of Node 1 for Models RM0-5~RM3-5 |
|
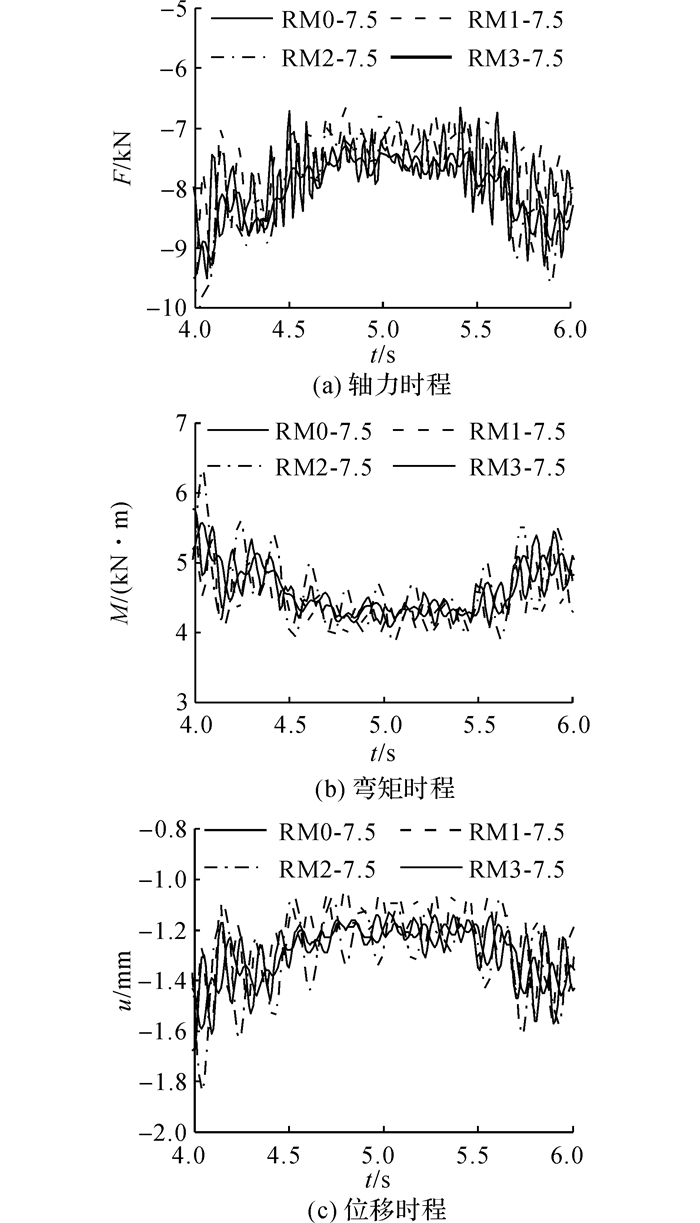
图 12 模型RM0-7.5~RM3-7.5构件1轴力、弯矩和节点1竖向位移时程 Fig. 12 Time histories of axial force and bending moment of Member 1 as well as vertical displacement of Node 1 for Models RM0-7.5~RM3-7.5 |
| 表 11 模型RM0-5~RM3-5构件1轴力风振系数 Table 11 Wind-induced vibration coefficients of axial forces of Member 1 for Models RM0-5~RM3-5 |
| 表 12 模型RM0-5~RM3-5构件1弯矩风振系数 Table 12 Wind-induced vibration coefficients of bending moments of Member 1 for Models RM0-5~RM3-5 |
| 表 13 模型RM0-5~RM3-5节点1竖向位移风振系数 Table 13 Wind vibration coefficient of vertical displacements of Node 1 for ModelsRM0-5~RM3-5 |
| 表 14 模型RM0-7.5~RM3-7.5构件1轴力风振系数 Table 14 Wind-induced vibration coefficients of axial forces of Member 1 for Models RM0-7.5~RM3-7.5 |
| 表 15 模型RM0-7.5~RM3-7.5构件1弯矩风振系数 Table 15 Wind-induced vibration coefficients of bending moments of Member 1 for Models RM0-7.5~RM3-7.5 |
| 表 16 模型RM0-7.5~RM3-7.5节点1竖向位移风振系数 Table 16 Wind vibration coefficient of vertical displacements of Node 1 for Models RM0-7.5~RM3-7.5 |
当主体结构的基频发生变化后, 从表 11~16可以发现轴力、弯矩和位移风振系数的变化与上一小节的结果存在明显不同.
对于5 Hz的4个模型, 模型RM0-5无论是轴力、弯矩还是位移风振系数都不再是最大.对于增加了屋面板的模型RM1-5, 由于主体结构的基频与屋面板的基频(4.56 Hz)相当, 发现该模型位移响应中屋面板相对主体结构的变形明显减小, 基本上与主体结构协调振动, 因此屋面板对主体结构的减振性能下降.以轴力风振系数为例, RM0-5和RM1-5的数值分别为1.570和1.382.对于风荷载施加在屋面板上的模型RM2-5, 屋面板有限刚度在传递风荷载的过程中将脉动风压的能量集中在屋面板基频附近, 而由于屋面板基频与主体结构的基频又十分接近, 一定程度诱发了主体结构的共振效应, 故构件轴力、弯矩和节点位移风振系数分别高达2.260、2.008和2.422.虽然屋面板刚度大大放大了主体结构的风致振动响应, 但是考虑屋面板的实际阻尼后, 模型RM3-5的风振效应又被强烈抑制, 其构件轴力、弯矩和节点位移风振系数急剧下降到1.259、1.277和1.277.可以看出, 对于主体结构基频为5 Hz的情况, 屋面板刚度和阻尼对主体结构风振效应的放大和平抑效应均非常明显.
对于主体结构刚度大、基频高达7.5Hz的4个模型, 风振系数的差异均较小.无屋面板的模型RM0-7.5的构件轴力、弯矩和节点位移风振系数分别为1.247、1.233和1.273左右, 表明结构对脉动风的动力效应敏感性较小.增加屋面板后(模型RM1-7.5), 屋面板与主体结构完全协调振动, 其对结构的减振效果小到可以忽略.对于将风荷载施加到屋面板上的模型RM2-7.5和RM3-7.5, 可以发现屋面板的有限刚度和阻尼特性虽然对主体结构的风振效应也体现出放大和平抑作用, 但效果非常有限.
5 结论在已有岩棉夹芯材料的材性试验和本构模型研究成果的基础上, 本文通过数值分析对岩棉夹芯复合屋面板的阻尼性能以及对主体结构风振效应的影响进行了研究.虽然分析模型还可以更精细化, 但分析结果总体上可反映岩棉夹芯复合屋面板有限刚度和阻尼性能对结构风振效应的影响规律和原因.主要结论有:
(1) 典型檩距的岩棉夹芯复合屋面板从其基频开始的较宽频段内, 各阶振型基本呈现出高阻尼的特性.文中算例的大多数振型的损耗因子高达0.30~ 0.50, 较低阻尼振型的损耗因子也都高于0.15.
(2) 岩棉夹芯复合屋面板对结构风振响应的影响首先体现为在传递风压过程中, 其有限刚度和阻尼性能对风压脉动特性产生的影响.文中算例表明, 考虑岩棉夹芯复合屋面板实际刚度后的支座反力最大幅值与采用刚性板假定的计算结果相比增大近70%.更为重要的是, 脉动风能量被集中到屋面板的基频附近传递给支座.这些都体现了屋面板有限刚度对脉动风效应的动力放大作用以及对其频谱特性的改变.然而当进一步考虑屋面板的结构阻尼后, 支座反力的最大幅值可降低40%, 表明夹芯层的阻尼减振性能也非常显著.
(3) 屋面板对主体结构风振效应的影响取决于主体结构的基频、屋面板的基频以及屋面板的阻尼, 其影响机理是明确的:首先当屋面板与主体结构刚度差异较大而不能协调振动时, 屋面板相对过大的振动可对主体结构起到明显的减振作用;其次在传递风荷载的过程中, 屋面板有限刚度又会放大脉动风压并改变其频谱特性;再者, 岩棉夹芯层的阻尼又会明显平抑脉动风的效应.综合上述3个影响因素来看, 经过岩棉夹芯复合屋面板的传递后, 风荷载对主体结构的风振效应减弱.
(4) 以上3方面因素对主体结构风振效应的综合影响与主体结构的基频最为相关.算例分析表明, 当主体结构基频较低时(跨度较大的屋盖结构一般属于此类), 常用的无屋面板风振计算模型会明显高估结构的风振效应.此时屋面板不能与主体结构协调振动是主要影响因素, 其次才是屋面板刚度和阻尼对脉动风压的放大和平抑作用的影响.当主体结构基频与屋面板基频接近时, 其影响又转变为屋面板对脉动风压频谱特性的改变诱发主体结构的共振, 因此大大增加主体结构的风振效应, 但与此同时, 屋面板高阻尼特性却又能有效地对共振效应进行阻止.与常用无屋面板风振计算模型的计算结果相比, 两者综合作用下计算的内力风振系数要减小约20%.但对于主体结构刚度大、基频高的结构, 屋面板的有限刚度和阻尼特性虽然对主体结构的风振效应也体现出放大和平抑作用, 但影响都非常小并可以忽略.
| [1] |
蔡昭昀. 我国金属屋面工程发展现状[J].
中国建筑防水, 2010, 13(3): 19–22, 30.
CAI Zhao-yun. Current situation about metal roofing in China[J]. CBW-Roofing Engineering, 2010, 13(3): 19–22, 30. |
| [2] |
吴迪, 武岳, 杨庆山, 等. 大跨屋盖结构风振响应参数灵敏度分析[J].
工程力学, 2015, 32(2): 171–177.
WU Di, WU Yue, YANG Qing-shan, et al. Parameter sensitivity analysis of wind-induced response of long-span roofs[J]. Engineering Mechanics, 2015, 32(2): 171–177. |
| [3] | SIMIU E, SCANLAN R H. Wind effects on structures:fundamentals and applications to design[M]. New York: John Wiley, 1996. |
| [4] |
王宸, 邓华, 黄莉. 岩棉夹芯金属屋面板的阻尼性能研究[J].
振动与冲击, 2013, 32(20): 55–60.
WANG Chen, DENG Hua, HUANG Li. Damping properties of metallic sandwich roof panels with rock wool core[J]. Journal of Vibration and Shock, 2013, 32(20): 55–60. DOI:10.3969/j.issn.1000-3835.2013.20.011 |
| [5] |
邓华, 黄莉, 王宸. 聚氨酯夹芯屋面板的风致动力性能分析[J].
浙江大学学报:工学版, 2013, 47(12): 2125–2131, 2175.
DENG Hua, HUANG Li, WANG Chen. Analysis on wind-induced dynamic behaviors of polyurethane sandwich roof panels[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(12): 2125–2131, 2175. |
| [6] | 戴德沛. 阻尼技术的工程应用[M]. 北京: 清华大学出版社, 1991: 36. |
| [7] | 曹树谦, 张文德, 萧龙翔. 振动结构模态分析——理论、实验与应用[M]. 天津: 天津大学出版社, 2001: 8-11. |
| [8] | JOHNSON C D, KIENHOLZ D K. Finite element prediction of damping in structures with constrained viscoelastic layers[J]. AIAA Journal, 1982, 20(9): 1284–1290. DOI:10.2514/3.51190 |
| [9] | 王新敏. ANSYS结构动力分析与应用[M]. 北京: 人民交通出版社, 2014: 7-9. |
| [10] | 黄本才, 汪丛军. 结构抗风分析原理及应用[M]. 2版. 上海: 同济大学出版社, 2008: 23-24. |
| [11] |
李春祥, 都敏, 韩兵康. 基于AR模型模拟超高层建筑的脉动风速时程[J].
地震工程与工程振动, 2008, 28(3): 87–94.
LI Chun-xiang, DU Min, HAN Bing-kang. Simulation of fluctuating wind speed time series of super-tall buildings based on AR model[J]. Journal of Earthquake Engineering and Engineering Vibration, 2008, 28(3): 87–94. |
| [12] |
王卫乐. 聚氨酯夹芯板的受力蒙皮抗剪性能研究[D]. 重庆: 重庆大学, 2006.
WANG Wei-le. Research on the stressed skin diaphragm properties of polyurethane sandwich panels[D]. Chongqing:Chongqing University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10611-2006148760.htm |



