工况是汽车产品研发、匹配、评价的基础, 也是汽车节能和排放测试评价的重要依据, 对车辆在实际道路、环境条件下的燃料经济性、排放、舒适性和可靠性具有决定性影响[1].相关标准均沿用国际循环工况, 影响了我国车辆技术水平的评价及开发.本文以郑州市乘用车为例, 但研究方法可以类推到某个地区或国家的某一类车辆.目前, 郑州市乘用车保有量已突破100万辆, 市区单位面积乘用车污染物排放远远高于非市区部分, 而且郑州市乘用车污染物人均排放比例已超过全国水平1倍以上[2-3];因此, 构建代表郑州市乘用车的行驶工况, 为改善车辆性能奠定基础.由于道路特征、地理特征、交通状况及驾驶习惯等方面的差异, 世界范围内现行的乘用车测试用行驶工况不能真实反映其他国家或地区车辆的实际排放和燃料消耗量水平, 因此国内外学者对构建本土化的循环工况纷纷进行相关研究, 且多采用短行程分析法构建行驶工况[4-9];其中大多学者均采用主成分分析和k-均值聚类分析算法, 但未对特征参数进行优选且k-均值聚类分析算法的初始聚类中心多为随机选取, 聚类中心易陷入局部最优, 从而影响工况拟合的精度.秦大同等[10]提取了与油耗相关的工况特征参数, 但未对初始聚类中心进行优化;王楠楠等[11-12]利用单一的全局优化算法对初始聚类中心进行优化, 易出现“早熟”, 并且寻优效率不高;石琴等[13]利用SOFM神经网络算法和k均值聚类算法相结合的组合聚类, 其中SOFM神经网络能够改进初始聚类中心, 但输入节点通过权值与输出层节点相连, 初始权值的设置会影响学习的结果和k均值聚类的效果.
本文在利用短行程分析法构建行驶工况的同时, 结合因子分析对特征参数进行选取;引入Isight优化平台, 联合多岛遗传算法(multi-island GA,MIGA)和序列二次规划算法(NLPQL)建立组合优化算法, 对初始聚类中心进行优化, 实现了全局动态寻优, 有效克服了全局优化算法后期寻优速度较慢的缺点[14].拟合出更加精确的行驶工况, 有助于车辆的认证和一致性检查, 真实反映了车辆在该地区的油耗和排放.
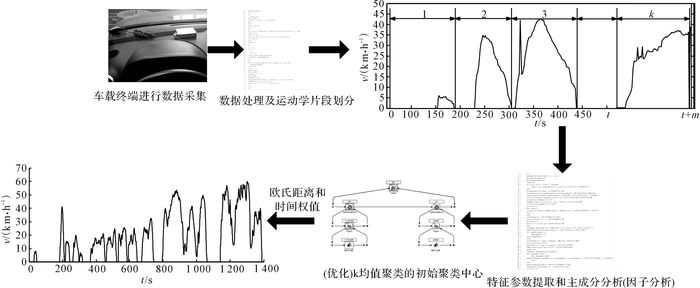
1 行驶工况的试验设计国内外各研究机构和政府部门对汽车行驶工况纷纷进行相关的研究工作, 尽管在数据采集方式、数据分析方法、工况解析及合成手段等方面形式多样, 但总的技术流程可以归纳为如图 1所示的流程.

|
图 1 汽车行驶工况开发技术流程 Fig. 1 Vehicles with cycles to develop technical processes |
乘用车按用途一般可以分为私家车、出租车和公务用车, 项目预选70辆乘用车, 其中选取15辆出租车、15辆公务用车及40辆私家车.车辆根据用途的不同, 呈现出不同的运行特点, 其中出租车和公务车的出行目的随意性强, 无规律, 不需预先规划试验路线和行驶时间, 由驾驶员按正常目的驾驶车辆.私家车多呈现规律性, 通常行驶在居住地点和工作地点之间, 但存在出行目的随意的特点, 因此该类车辆应在不影响驾驶员出行目的的前提下,根据驾驶员常出入的驾驶区域来选取试验车辆,实现以少量试验数据反映全局特征的目的.
试验车辆数据采集一般分为2种方法[15], 针对车辆用途及车型的不同, 选用不同的数据采集方法.本文的私家车、出租车和公务用车均根据出行目的随意的特点, 采用自主行驶法由驾驶员正常驾驶试验车辆以完成试验数据的采集.
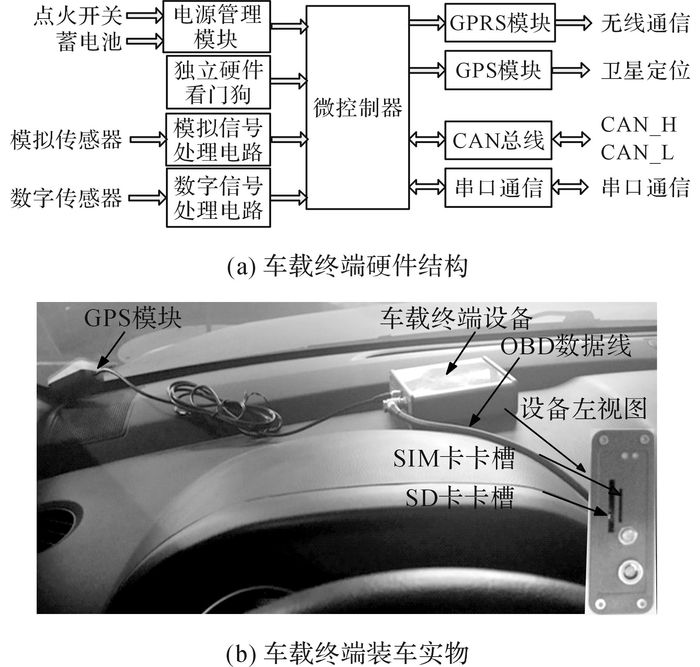
车辆行驶数据由车载终端设备采集, 采样频率为1 Hz, 在正常工作状态下, 车载终端与整车的ECU进行通讯, 采集CAN总线的信息, 获取车辆当前状态下的相关参数;通过外置的GPS天线接收时间、位置等信息, 采用卫星授时方式同步时钟, 同时连接GPRS网络, 将采集到的信息发送到远程服务器数据库, 实现对车辆数据的实时采集, 硬件结构及装车实物如图 2所示.1个月采集有效数据603 077条.
|
图 2 车载终端硬件结构及装车实物 Fig. 2 Vehicle terminal hardware structure and loading object |
根据郑州市日常的交通强度、乘用车的行驶特点, 选用短行程分析法作为工况解析方法, 具体流程如图 3所示.图中, v为车速, t为运行时间.为了拟合更高精度的行驶工况, 在整体解析方法不变的情况下, 改进其中的合成步骤, 具体可以分为3种构建方案, 如表 1所示.表中,“√”表示采用该方法,“-”表示未采用该方法.
|
图 3 构建工况的解析流程 Fig. 3 Construction driving cycle resolution process |
| 表 1 工况构建的3种方案 Table 1 Driving cycle of building three kinds of scheme |
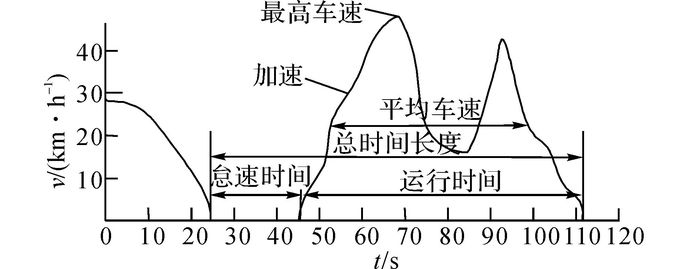
车辆从起步出发到目的地停车, 受道路交通状况的影响, 期间会经过多次起步、停车, 将车辆从一个怠速开始到下一个怠速开始之间的运动定义为运动学片段(简称片段), 如图 4所示.对试验车辆的有效行驶数据可以划分为5 668个具有不同特征的片段.
|
图 4 运动学片段示意图 Fig. 4 Kinematics schematic fragment |
初提取各片段的15个特征参数(见表 2), 构成5 668×15的特征参数矩阵.
| 表 2 提取各片段的15个特征参数 Table 2 15 extracted characteristic parameters of each fragment |
为了避免选用所有特征参数作为分类指标, 导致信息重叠, 对5 668×15的特征参数矩阵进行主成分分析.通过构造原变量的一系列线性组合, 使各线性组合在彼此不相关的前提下, 尽可能多地反映原变量的信息, 为特征参数矩阵实现主成分的提取编写相关程序实现主成分分析, 保留原有信息的80%左右, 具体方法如下.
为了消除特征参数间不同量纲的影响, 对特征参数进行标准差标准化, 使各特征参数转化为均值为0、方差为1的正态分布.数据标准差的标准化公式如下:
| $\left. \begin{align} &\quad \quad \bar{x}=\frac{\sum\limits_{i=1}^{n}{{{x}_{i}}}}{n}, \\ &\text{st}{{\text{d}}_{i}}=\sqrt{\frac{\sum\limits_{i=1}^{n}{{{\left( {{x}_{i}}-\bar{x} \right)}^{2}}}}{n-1}}, \\ &\quad \quad x_{i}^{'}=\frac{{{x}_{i}}-\bar{x}}{\text{st}{{\text{d}}_{i}}}. \\ \end{align} \right\}$ | (1) |
式中:x为特征参数均值, stdi为标准差, xi为运动学片段库中的第i列特征值, n为片段个数.
特征参数之间的协方差为
| $\operatorname{cov}\left( x_{i}^{'},x_{j}^{'} \right)=\frac{\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{n}{\left( x_{i}^{'}-\overline{x_{i}^{'}} \right)\left( x_{j}^{'}-\overline{x_{j}^{'}} \right)}}}{n-1}.$ | (2) |
式中:x′i和x′j为第i个和第j个标准差标准化后的特征参数,
利用Matlab编程求得协方差矩阵的特征向量、特征值及贡献率, 如表 3所示.第q特征值为Zq, 累计贡献率约为80%时应保留的主成分为
| 表 3 各主成分的特征值、贡献率和累计贡献率 Table 3 Characteristic value, contribution rate and cumulative contribution rate of each principal component |
| $m = \min \left( {\frac{{\sum\limits_{k = 1}^{k \le q} {{\lambda _k}} }}{{\sum\limits_{i = 1}^q {{\lambda _i}} }} \approx 80\% } \right).$ | (3) |
式中:m为主成分的个数, λk为第k个主成分的贡献率, q为特征值的个数.
特征参数与第几主成分相关系数的绝对值最大, 表明该特征参数可以隶属于该主成分, 对应的相关系数如表 4所示.表中, P1、P2、P3分别为第一主成分、第二主成分及第三主成分与各特征参数的相关系数.
| 表 4 特征参数与各主成分的相关系数 Table 4 Correlation coefficient characteristic parameters of each main component |
确定了保留的主成分个数的同时, 得到了因子的个数, 对因子矩阵进行Kaiser标准化的正交旋转, 直至收敛;因子载荷aij为某个因子与原变量的相关系数, 主要反映该公共因子对相应变量的贡献力;变量共同度ai反映了所有公共因子对该原变量的方差的解释程度;相关公式如下:
| ${y_i} = {a_{i1}}{f_1} + {a_{i2}}{f_2} + \cdots + {a_{im}}{f_m}.$ | (4) |
式中:yi为第i个特征向量, fm为第m个公共因子,
| ${a_i} = {a_{i1}} + {a_{i2}} + \cdots + {a_{im}}.$ | (5) |
根据公共因子与15个特征参数的相关系数(见表 5), 得到与3个公共因子f1、f2、f3最相关的特征参数, 分别为平均运行速度、怠速时间比(运行时间比)、加速度标准差.
| 表 5 公共因子与原变量的相关系数 Table 5 Correlation coefficient common factor with originalvariables |
运动学片段聚类的准确性会直接影响工况拟合的精度, 但利用k均值聚类算法对各片段进行聚类, 初始聚类中心的随机选取无法避免聚类陷入局部最优这一缺点, 因此对初始聚类中心进行优化选取实现最优聚类.优化算法可以分为数值型和探索型2种, 其中采用数值型优化算法可以快速找到局部最优点, 但不能很好地进行全局寻优;采用探索型优化算法能够寻优到全局最优解附近, 但是存在后期寻优效率低、局部寻优效果不佳的特点.结合2种优化算法, 可以充分利用2种优化算法的各自优点, 提高优化效率, 改善优化质量.选取MIGA和NLPQL构成组合优化算法, 在优化前期, 充分发挥MIGA的全局优化能力;在全局优化后期, 借助NLPQL快速定位全局最优区域, 进行局部快速寻优, 最终得到全局最优解.
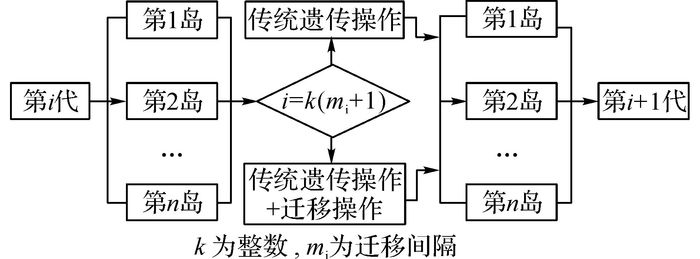
2.3.1 算法基础MIGA是在传统遗传算法的基础上发展起来的.该算法继承了遗传算法的基本思想, 两者的最大区别在于后者将众多种群分成若干个子种群(也被称为岛), 在子种群中执行遗传算法的选择、交叉、变异等操作, 并且周期性地在不同岛之间有针对性地进行移民操作.如此反复操作, 尽可能避免局部最优解, 从而抑制了“早熟”现象的发生, 但大群体增加了个体适应性评价的计算量, 降低了收敛速度.MIGA相邻两代的进化流程如图 5所示.
|
图 5 多岛遗传算法相邻两代之间的进化流程图 Fig. 5 Evolutionary flowchart generations between adjacent multi-island genetic algorithm |
NLPQL是局部优化的数值型优化算法, 用来解决带有约束的非线性数学规划问题.二次连续规划法(SQP)是NLPQL的核心算法, 将目标函数以二阶泰勒级数展开, 并将约束条件线性化, 原非线性问题转化为一个二次规划问题, 通过解二次规划得到下一个设计点.该算法很稳定, 且是局部优化收敛速度最快的一种算法, 主要的优点是很容易和一个非常健壮的算法一起使用.
由于多岛遗传算法和序列二次规划算法的优缺点能够相互弥补, 采用这两种算法构成组合优化算法进行寻优, 能够提高优化效率, 改善优化质量.如图 6所示为优化流程图.
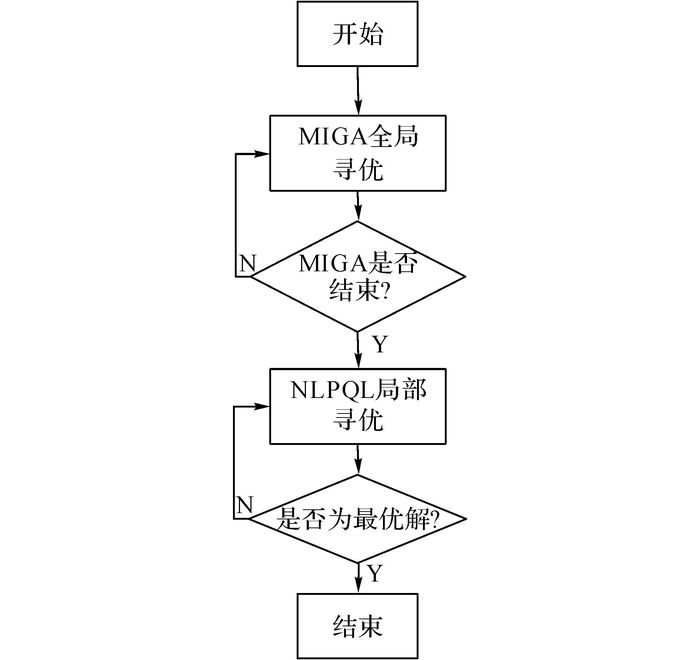
|
图 6 初始聚类中心优化流程图 Fig. 6 Initial clustering center optimization flow chart |
利用k均值聚类算法, 将各片段分为拥堵片段、市区片段、市郊片段及高速片段4类.随机选取初始聚类中心容易受到噪声和孤立点的干扰, 甚至会导致聚类的失败, 最终影响聚类效果.针对该缺点, 综合考虑同类相似性和异类差异性的评价指标, 以综合指标F为优化目标, 利用组合优化算法优化初始聚类中心, 优化数学模型如下.
| $\left. \begin{array}{l} \max F = \frac{{{D_{\rm{M}}}}}{{{d_{\rm{m}}}}},\\ {D_{\rm{M}}} = \sum\limits_{j = 1}^r {{{\left\| {{{\bar x}^{\left( j \right)}} - {{\bar x}^{\left( h \right)}}} \right\|}^2}} ,j \ne h,\\ {d_{\rm{m}}} = \sum\limits_{j = 1}^r {\sum\limits_{i = 1}^{{n_j}} {{{\left\| {x_i^{\left( j \right)} - {{\bar x}^{\left( j \right)}}} \right\|}^2}} } ;\\ {\rm{s}}.\;{\rm{t}}.\;{g_k}\left( x \right) \ge 0,k = 1,2, \cdots ,m;\\ x_u^1 \le {x_u} \le x_u^{\rm{h}},u = 1,2, \cdots ,n. \end{array} \right\}$ | (6) |
式中:F为目标函数, F取最大, 表明该聚类是最合理的聚类;DM为各类中心之间的距离之和;dm为各类样本点到各类中心的距离之和的各平均值相加的和;r为类别数目(本文取r=4);x(j)为第j类的聚类中心, x(h)为第h类的聚类中心, xi(j)为第j类中的第i个运动学片段的特征值;nj为第j类的运动学片段个数;gk(x)≥0为约束条件;m为约束条件个数;xuh和xul分别为第u个变量的上限和下限.优化变量、约束条件等如表 6所示.表中, c(j)表示第j类的初始聚类中心.Isight平台优化界面及流程如图 7所示.
| 表 6 k均值聚类的优化变量及内容 Table 6 k-means clustering of optimized variables and content |
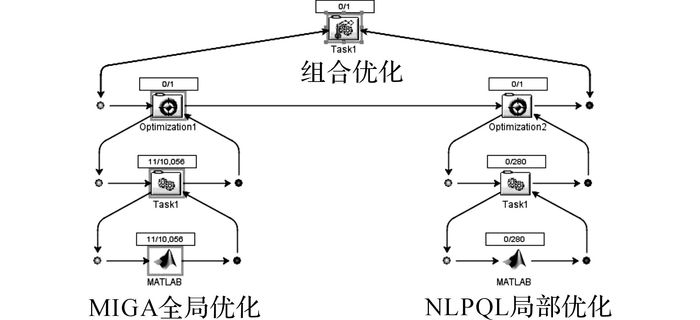
|
图 7 Isight的优化界面及流程 Fig. 7 Isight optimization interface and process |
基于上述3种方案, 对得到的5 668个片段分别进行聚类, 利用每个片段与4个聚类中心间的欧式距离和贴近度准则, 确定所属的类别.片段与各类聚类中心的欧氏距离为
| $\begin{align} &{{d}_{ij}}= \\ &\sqrt{{{\left( x_{i1}^{'}-\bar{x}_{1}^{\left( j \right)} \right)}^{2}}+{{\left( x_{i2}^{'}-\bar{x}_{2}^{\left( j \right)} \right)}^{2}}+\cdots +{{\left( x_{im}^{'}-\bar{x}_{m}^{\left( j \right)} \right)}^{2}}}. \\ \end{align}$ | (7) |
式中:dij为第i个片段到第j类聚类中心的欧氏距离, x′im为第i个片段的第m个特征要素, xm(j)为第j类聚类中心的第m个特征要素.
若出现片段要素到各类中心的最小欧氏距离相等而无法判断的情况, 引入贴近度这一准则进行判断, 公式如下:
| ${{\partial }_{0}}\left( \overline{{{A}_{i}}},\overline{{{B}_{m}}} \right)=\frac{1}{2}\left[ \overline{{{A}_{i}}}\circ \overline{{{B}_{m}}}+\left( 1-\overline{{{A}_{i}}}\otimes \overline{{{B}_{m}}} \right) \right].$ | (8) |
式中:Ai为运动学片段库中的任一个运动学片段的向量要素;Bm为待识别的对象要素, 此处为聚类分析的聚类中心;
根据式(8), 利用Matlab编写程序分别进行聚类, 不同方案下各片段所属的类别如图 8所示.
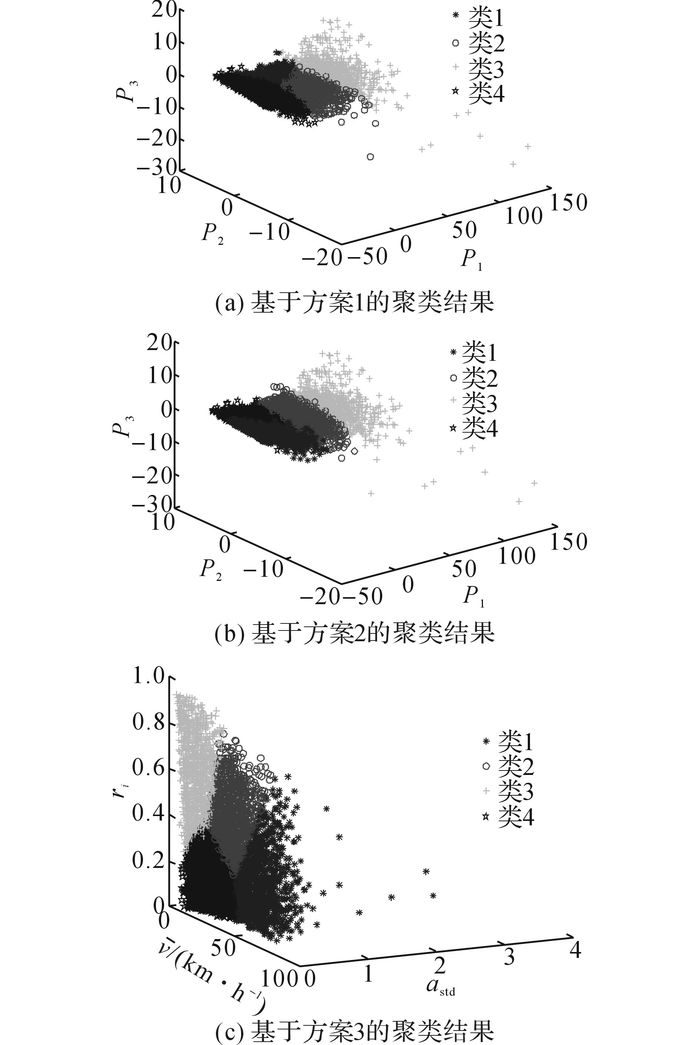
|
图 8 3种不同方案的聚类结果 Fig. 8 Clustering results of three different programs |
根据CVS和国外工况合成的经验可知, 行驶工况的时间长度为1 200~1 500 s.根据同一类中的欧式距离来选择备选片段, 由各类在整个数据中所占的时间比例, 确定各类片段在最终工况合成中所占的时间及个数, 具体公式如下:
| $\left. \begin{align} &{{t}_{i}}=\frac{\sum\limits_{j=1}^{{{n}_{j}}}{{{T}_{ij}}}}{{{T}_{\text{all}}}}{{t}_{\text{cycle}}}, \\ &{{k}_{i}}=\frac{{{t}_{i}}{{n}_{j}}}{\sum\limits_{j=1}^{{{n}_{j}}}{{{T}_{ij}}}}. \\ \end{align} \right\}$ | (9) |
式中:ti为第i类在工况合成中所占的时间, nj为第i类中片段的个数, Tij为第i类中第j个片段所持续的时间, Tall为样本中所有片段持续的总时间, tcycle为工况合成所需的时间, ki为第i类片段在拟合的工况中的片段个数.
依据上述3种不同方案得到的聚类结果分别拟合出时间长度为1 491、1 549及1 373 s的3条郑州市乘用车行驶工况, 如图 9所示.
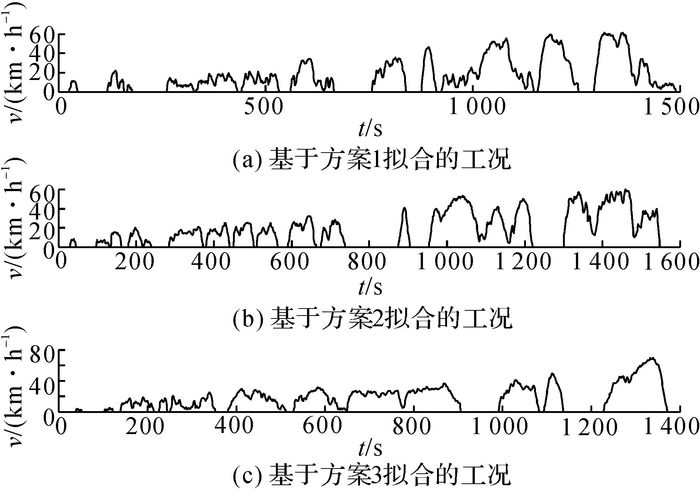
|
图 9 基于3种不同方案构建的郑州市乘用车行驶工况 Fig. 9 Driving cycles of passenger cars in Zhengzhou based on three different schemes |
卡方检验是一种用途较广的计数资料的假设检验方法, 属于非参数检验的范畴, 主要是比较2个及2个以上样本率以及2个分类变量的关联性分析.根本思想是比较理论频数和实际频数的吻合程度或拟合优度问题.基于3种方案拟合的行驶工况与整体有效数据, 开展加速度分布频数检验.其中实验组1、2、3分别为基于方案1、2、3拟合的行驶工况的加速度分布频数, 对照组为整体有效数据的加速度分布频数, 确定这3种方案的检验水准.具体流程如图 10所示, 过程如下.

|
图 10 卡方检验流程图 Fig. 10 Chi-square test flow chart |
1) 首先建立检验假设.H0:3个实验组和对照组加速度分布频数无差异;H1:3个实验组和对照组加速度分布频数有差异, α=0.05.
2) 比较各实验组和同一样本组, 各实验组间不须比较, α′=α/(2(k-1))=0.008 33.
3) 确定χ2和自由度v.如表 7所示为4组数据加速度分布频数.表中, aa为加速频数, ac为匀速和怠速频数, ad为减速频数.
| 表 7 4组数据加速度分布频数 Table 7 Four sets of data acceleration frequency distribution |
4) 查χ2界限表可得如下结论.实验组1和对照组比较可知, χ2=6.80, 0.025<P<0.05;实验组2和对照组比较可知, χ2=4.05, P>0.05;实验组3和对照组比较可知, χ2=0.058, P>0.05.按α′=0.008 33的检验水准, 接受H0, 可以认为3个实验组和对照组加速度分布频数无差异, 表明3次合成的行驶工况均可以代表整体数据的交通特征;同时,χ2越小, P越大, 表明实际频数和理论频数的吻合程度越高, 拟合出的行驶工况更精确.实验组2的χ2比实验组1小, 证明了优化选取初始聚类中心的有效性.实验组3基于方案3拟合的行驶工况较实验组1和实验组2更能够反映整体有效行驶数据的交通特征.选取基于方案3拟合的行驶工况, 供后续研究.
为了便于车辆在底盘测功机上模拟道路试验和实车道路试验时能够更好地复现和跟随工况, 通过移动平均滤波器将拟合的工况进行高频噪声处理, 在不改变数据本身特性的同时, 使工况曲线更加平滑.滤波器的定义公式为
| ${{v}_{\text{smo}}}\left( t \right)=\frac{1}{n}\sum\limits_{i=0}^{n-1}{v\left( n-i \right)}.$ | (10) |
式中:vsmo(t)为第n次采样值经滤波后的输出值, v(n-i)为第n-i次采样值, n为递推平均的项数.
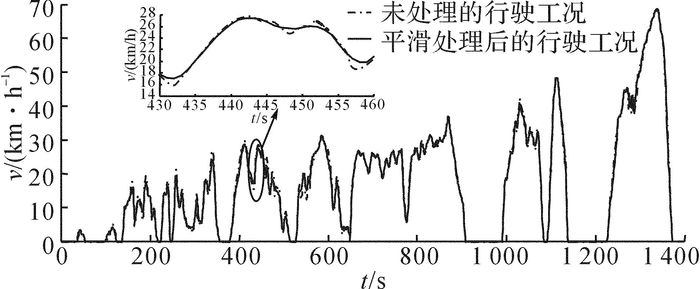
如图 11所示为未经平滑处理的工况与平滑处理后的工况对比.可知, 噪声点能够被移动平均滤波器消除.
|
图 11 平滑处理前、后的工况对比 Fig. 11 Smoothing driving cycle before and after comparison |
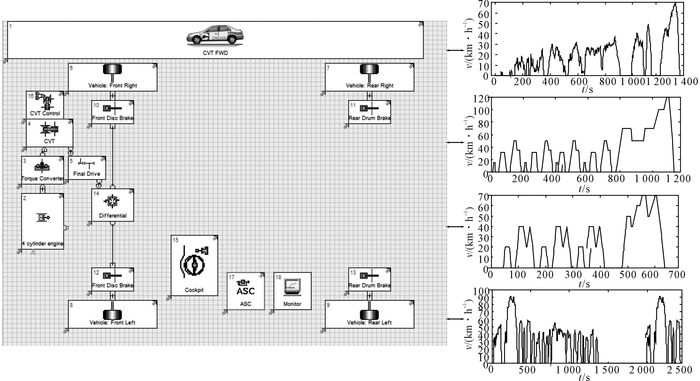
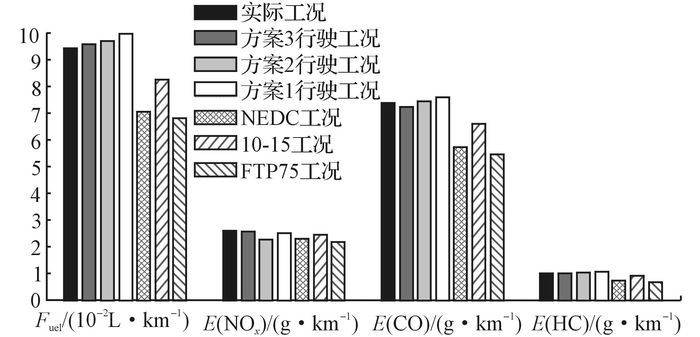
利用AVL-Cruise平台搭建整车动力学模型, 整车的具体参数如表 8所示, 建立的整车仿真模型如图 12所示.分别加载各行驶工况文件得到对应的油耗Fuel和排放量E(NOx)、E(CO)、E(HC), 仿真结果如图 13所示.
| 表 8 整车参数表 Table 8 Vehicle parameters table |
|
图 12 基于Cruise的整车不同工况下性能仿真 Fig. 12 Cruise-based vehicle performance simulation under different driving cycles |
|
图 13 所有试验工况下的整车油耗和排放对比 Fig. 13 All test driving cycles of vehicle fuel consumption and emissions |
比较同一整车模型与各工况的仿真结果可知, 实际行驶工况与国际通用工况的相对误差ε较大(见表 9), 有必要构建本土化的行驶工况.3种方案拟合的工况与实际工况相比, 车辆加载方案3拟合的工况百公里油耗和排放与实际工况的相对误差最小, 分别为1.15%、1.17%、1.8%和1%, 表明3种方案中基于方案3拟合的工况精度更高.
| 表 9 实际工况较其他试验工况的油耗和排放相对误差 Table 9 Relative error of actual driving cycles than other fuel consumption and emissions |
(1) 针对不同用途的车辆选用不同的试验方案, 并利用车载终端设备进行数据采集.结合因子分析对运动学片段的15个特征参数进行分析, 得到平均运行速度、怠速时间比(运行时间比)和加速度标准差3个更具代表性的特征参数.
(2) 利用组合优化算法, 对k均值聚类算法的初始聚类中心进行优化, 得到了最优的聚类效果.运用行驶工况与整体试验数据的加速度分布频数进行卡方检验, 证明了聚类优化和工况合成的有效性.
(3) 采用AVL-Cruise仿真平台的整车模型分别加载各工况进行油耗和排放的对比分析可知, 我国乘用车一直沿用欧洲NEDC循环测量的污染物测试结果不能完全反映本土的实际交通状况特征.有必要构建反映这一地区实际交通的行驶工况, 且依据方案3拟合的行驶工况较前2种方案更接近于实际工况, 工况的拟合精度更高.
| [1] |
郑天雷. 全球车辆循环工况调查与对比[R]. 天津: 中国汽车技术研究中心, 2011.
ZHENG Tian-lei. Research and comparisons of vehicle driving cycle in the world[R]. Tianjin:China Automotive Technology and Research Center, 2011. |
| [2] |
赵新燕. 郑州市机动车污染排放特征与控制措施研究[D]. 长春: 吉林大学, 2014.
ZHAO Xin-yan. Research on vehicle pollution emission characteristics and control measures in Zhengzhou[D]. Changchun:Jilin University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10183-1014295448.htm |
| [3] |
张文凯. 郑州市机动车排放清单建立及减排情景研究[D]. 郑州: 郑州大学, 2015.
ZHANG Wen-kai. Research on establishment of vehicle emission inventory and its abatement scenarios in Zhengzhou[D]. Zhengzhou:Zhengzhou University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10459-1015301430.htm |
| [4] | FOTOUHI A, MONTAZERI-GH M. Tehran driving cycle development using the k-means clustering method[J]. Scientia Iranica, 2013, 20(2): 286–293. |
| [5] | NESAMANI K S, SUBRAMANIAN K P. Development of a driving cycle for intra-city buses in Chennai[J]. Atmospheric Environment, 2011(45): 5469–5476. |
| [6] |
万霞, 黄文伟, 强明明. 深圳市乘用车道路行驶工况构建[J].
深圳大学学报:理工版, 2016, 33(3): 281–287.
WAN Xia, HUANG Wen-wei, QIANG Ming-ming. Construction of driving cycle for passenger vehicles in Shenzhen[J]. Journal of Shenzhen University:Science and Engineering, 2016, 33(3): 281–287. |
| [7] |
石敏. 轻型汽车行驶工况构建的研究[D]. 天津: 天津理工大学, 2013.
SHI Min. Research of construction of the light-duty vehicles driving cycle[D]. Tianjin:Tianjin University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10060-1015516460.htm |
| [8] |
杨小娟, 王建. 北京市重型客车行驶工况的构建与研究[J].
环境工程技术学报, 2015, 5(6): 455–463.
YANG Xiao-juan, WANG Jian. Construction andresearch of heavy-coach's driving cycle in Beijing city[J]. Journal of Environmental Engineering Technology, 2015, 5(6): 455–463. |
| [9] |
胡志远, 秦艳, 谭丕强, 等. 基于大样本的上海市乘用车行驶工况构建[J].
同济大学学报:自然科学版, 2015, 43(10): 1523–1527.
HU Zhi-yuan, QIN Yan, TAN Pi-qiang, et al. Large sample based car driving cycle in Shanghai city[J]. Journal of Tongji University:Natural Science, 2015, 43(10): 1523–1527. |
| [10] |
秦大同, 詹森, 漆正刚, 等. 基于K-均值聚类算法的行驶工况构建方法[J].
吉林大学学报:工学版, 2016, 46(2): 383–389.
QIN Da-tong, ZHAN Sen, QI Zheng-gang, et al. Driving cycle construction using K-means clustering method[J]. Journal of Jilin University:Engineering and Technology Edition, 2016, 46(2): 383–389. |
| [11] |
王楠楠. 城市道路行驶工况构建及油耗研究[D]. 合肥: 合肥工业大学, 2012.
WANG Nan-nan. Construction of the urban road driving cycle and research of the fuel consumption[D]. Hefei:Hefei University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10359-1012520684.htm |
| [12] |
詹森, 秦大同, 曾育平. 基于遗传优化k均值聚类算法工况识别的混合动力汽车能量管理策略[J].
中国公路学报, 2016, 29(4): 130–137.
ZHAN Sen, QIN Da-tong, ZENG Yu-ping. Energy management strategy of HEV based on driving cycle recognition using genetic optimized K-means clustering algorithm[J]. China Journal of Highway and Transport, 2016, 29(4): 130–137. |
| [13] |
石琴, 仇多洋, 周洁瑜. 基于组合聚类法的行驶工况构建与精度分析[J].
汽车工程, 2012, 34(2): 164–169.
SHI Qin, QIU Duo-yang, ZHOU Jie-yu. Driving cycle constrution and accuracy analysis based on combined clustering technique[J]. Automotive Engineering, 2012, 34(2): 164–169. |
| [14] | GAO Jian-ping, LIU Zhen-nan, GUO Zhi-jun, et al. Optimization of hybrid electric bus control strategy with hybrid optimization algorithm[C]//2013 International Conference on Energy Research and Power Engineering. Zhengzhou:Energy Research and Power Engineering, 2013:924-930. |
| [15] | 陈全世, 朱家琏, 田光宇. 先进电动汽车技术[M]. 2版. 北京: 化学工业出版社, 2014: 15-27. |


