2. 重庆大学 汽车工程学院, 重庆 400030
2. College of Automotive Engineering, Chongqing University, Chongqing 400030, China
现有的数值分析方法, 在中频下振动噪声的计算精度和效率通常难以满足要求, 对于汽车工业而言, 主要为400~1 000 Hz, 探寻适合中频振动噪声的预测分析方法成了当下亟待解决的问题.对此, 学者们提出了较多手段, 如对确定性的有限元、边界元算法进行向高频的拓展[1-6], 但该类方法都存在着基于单元方法的局限, 即需要小尺寸单元和更多自由度来提高精度;对统计性的方法, 如统计能量法(statistical energy analysis, SEA)进行向低频的拓展[7-8]以及综合运用统计性方法与确定性方法[9-11]如FEA-SEA混合方法, 利用统计性的方法得到的是空间与频域的统计平均, 无法得到局部的细节响应特性, 且需要满足统计分析方法的理论假设前提, 即频带模态数达到一定的要求.基于Treffz理论的一系列方法[12-14]是一类完全不同于传统基于单元网格建模的确定性方法, 其中的波函数法是很有前途与应用价值的方法[15].
波函数法以高收敛度、少自由度和高精度的特点, 在结构和声腔的振动及声学响应预测中, 显现出了该方法的巨大优势[16-18].然而, 该方法只局限于规则的直边结构或圆边结构的声学域, 限制了该方法在如汽车车内声腔这种复杂几何边界的应用.对波函数法几何应用的拓展十分必要.样条曲线是当下计算机辅助设计(computer aided design, CAD)的造型设计阶段广泛运用的基本手段.利用波函数法实现这类边界的声学预测, 在很大程度上提高了波函数法的几何适应度, 丰富了对样条边界声学域的中频预测手段.本文以包含的B样条边界的二维声学域为例, 分析波函数法与B样条理论.运用数值分析方法实现波函数在该声学域的声学响应预测, 与传统的有限元方法进行对比, 验证了该方法的有效性与高效性.
1 波函数法基本理论对于稳态声学域, 内部声压分布满足Helmholtz方程[19]:
| ${\nabla ^2}p\left( r \right) + {k^2}p\left( r \right) = - {\rm{j}}\rho \omega \delta \left( {r,{r_q}} \right)q.$ | (1) |
式中:拉普拉斯算子
波函数法是一种间接Treffz方法, 不同于有限元方法.波函数法通过运用严格满足控制方法的波函数, 将各点响应计算转化为对各波函数系数求解.将r处的声压p(r)近似表示为一系列波函数的叠加:
| $p\left( r \right) \simeq \sum\limits_{i = 1}^{{n_i}} {{p_{{\rm{w}}i}}{\phi _i}\left( r \right) + {p_{\rm{q}}}\left( r \right)} = \Phi \left( r \right){P_{\rm{w}}} + {p_{\rm{q}}}\left( r \right).$ | (2) |
式中:pwi为未知的权系数, ϕi(r)为满足Helmholtz控制方程的波函数;pq(r)为非齐次微分方程的特解, 物理意义为声学域内的点声源.
对于二维声学域, 波函数选取Desmet推荐的形式[15]:
| ${\phi _i}\left( {x,y} \right) = \left\{ \begin{array}{l} \cos \left( {{k_{xi{\rm{r}}}}x} \right)\exp \left( { - {\rm{j}}{k_{yi{\rm{r}}}}y} \right),\left( {{k_{xi{\rm{r}}}},{k_{yi{\rm{r}}}}} \right) = \left( {\frac{{{n_{\rm{r}}}{\rm{\pi }}}}{{{L_x}}}, \pm \sqrt {{k^2} - k_{xi{\rm{r}}}^2} } \right);\\ \exp \left( { - {\rm{j}}{k_{xi{\rm{s}}}}x} \right)\cos \left( {{k_{yi{\rm{s}}}}y} \right),\left( {{k_{xi{\rm{s}}}},{k_{yi{\rm{s}}}}} \right) = \left( { \pm \sqrt {{k^2} - k_{yi{\rm{s}}}^2} ,\frac{{{n_{\rm{s}}}{\rm{\pi }}}}{{{L_y}}}} \right). \end{array} \right.$ | (3) |
式中:nr、ns=0, 1, 2, …;Lx、Ly分别为声学域外轮廓尺寸.
定义2(nr+ns+1) 为模型的波函数数量, 即模型需要求解的自由度.
在边界运用加权余量法构造余量公式, 求得各波函数系数, 再代回式(2), 可得声学域的声压分布.
| ${R_V} = {{\cal L}_V}\left( {p\left( r \right)} \right) - {{\bar v}_n}\left( r \right) = 0;r \in {\mathit{\Omega }_{\rm{v}}}.$ | (4) |
| ${R_p} = p\left( r \right) - {{\bar p}_n}\left( r \right) = 0;r \in {\mathit{\Omega }_{\rm{p}}}.$ | (5) |
| ${R_Z} = {{\cal L}_V}\left( {p\left( r \right)} \right) - {p_n}\left( r \right)/{{\bar Z}_n}\left( r \right) = 0;r \in {\mathit{\Omega }_Z}.$ | (6) |
式中:
波函数法理论的收敛前提是要求几何域为凸域, 即波函数法对于任何曲边边界的凸域声学域都是可适用的, 但现在该方法都只应用于规则的直边或圆弧.非均匀有理B样条曲线是一种具有代表性且在CAD几何造型中广泛应用的样条曲线.将波函数法应用于B样条边界, 能够在很大程度上扩展波函数法的几何适用性.将p阶的B样条曲线C(u)定义[20]为
| $C\left( u \right) = \left( {x\left( u \right),y\left( u \right)} \right) = \sum\limits_i^n {{N_{i,p}}\left( u \right){P_i}} .$ | (7) |
式中:a、b为样条基函数范围, a≤u≤b;Pi为第i个控制点;Ni, p(u)为第i个基于节点向量的基函数,
| ${N_{i,0}}\left( u \right) = \left\{ \begin{array}{l} 1,{u_i} \le u < {u_{i + 1}};\\ 0,{u_i} > u \ge {u_{i + 1}}. \end{array} \right.$ | (8) |
| $\begin{array}{l} {N_{i,p}}\left( u \right) = \\ \;\;\frac{{u - {u_i}}}{{{u_{i + p}} - {u_i}}}{N_{i,p - 1}}\left( u \right) + \frac{{{u_{i + p + 1}} - u}}{{{u_{i + p + 1}} - {u_{i + 1}}}}{N_{i + 1,p - 1}}\left( u \right). \end{array}$ | (9) |
由B样条曲线定义可知, 只要控制点在凸多边形上, 形成的内部声学域是凸域, 保证了波函数法的收敛.
由波函数法的边界积分公式可知, 计算系统矩阵时, 须得到曲线的外法向量.样条曲线C(u)的k阶导数[20]为
| ${C^{\left( k \right)}}\left( u \right) = \sum\limits_i^n {N_{i,p}^{\left( k \right)}\left( u \right){P_i}} ;a \le u \le b.$ | (10) |
式中:
| $N_{i,p}^{\left( k \right)}\left( u \right) = \frac{{p!}}{{\left( {p - k} \right)!}}\sum\nolimits_{j = 0}^k {{a_{k,j}}{N_{i + j,p - k}}\left( u \right)} .$ | (11) |
| $N_{i,0}^{\left( k \right)}\left( u \right) = \left\{ \begin{array}{l} 1,{u_i} \le u < {u_{i + 1}};\\ 0,{u_{i + 1}} \le u < {u_i}. \end{array} \right.$ | (12) |
| $\left. {\begin{array}{*{20}{c}} {{a_{0,0}} = 1,}\\ {{a_{k,0}} = \frac{{{a_{k - 1,0}}}}{{{u_{i + p - k + 1}} - {u_i}}},}\\ {{a_{k,j}} = \frac{{{a_{k - 1,j}} - {a_{k - 1,j - 1}}}}{{{u_{i + p + j - k + 1}} - {u_{i + j}}}},}\\ {{a_{k,k}} = \frac{{ - {a_{k - 1,k - 1}}}}{{{u_{i + p + 1}} - {u_{i + k}}}}.} \end{array}} \right\}$ | (13) |
当k取1时, C(1)(u)=(x(1)(u), y(1)(u))为曲线的切线, 切线方向的单位向量为
| $\mathit{\boldsymbol{V}}\left( u \right) = \left[ {\frac{{{x^{\left( 1 \right)}}\left( u \right)}}{{{\rm{norm}}\left( {{C^{\left( 1 \right)}}\left( u \right)} \right)}},\frac{{{y^{\left( 1 \right)}}\left( u \right)}}{{{\rm{norm}}\left( {{C^{\left( 1 \right)}}\left( u \right)} \right)}}} \right].$ | (14) |
垂直方向是所求的法向量.
3 样条边界积分根据定义可知, 波函数在声域内是严格满足Helmholtz方程的, 即在声学域内部没有误差的产生.波函数法的误差仅仅来自边界, 因此该方法的实现与计算精度的保证关键在于边界积分.下面针对2种常用的数值积分方法进行阐述, 对2种方法进行比较.
3.1 Gauss积分Gauss积分因高精度、高效率的特点, 被工程上广泛运用.Gauss-Legendre是使用插值多项式, 将积分变成所有积分点函数值的加权和.积分点在-1, 1上分布, 需要对积分边界进行坐标变换, 本文B样条基函数端点值取-1, 1.
由Gauss-Legendre积分的定义可知, 对f(x)在Ω上积分的公式[21]为
| $\int\limits_\mathit{\Omega } {f\left( x \right){\rm{d}}x} = \int\limits_{ - 1}^1 {f\left( \xi \right)\left| \mathit{\boldsymbol{J}} \right|{\rm{d}}\xi } = \sum\limits_{i = 0}^{{N_{\rm{g}}}} {{H_i}f\left( {{q_i}} \right)\left| \mathit{\boldsymbol{J}} \right|} .$ | (15) |
式中:Hi为Gauss权值; qi为Gauss积分点, -1≤qi≤1;|J|为坐标变换的雅可比矩阵的行列式,
| $\left| \mathit{\boldsymbol{J}} \right| = \sqrt {{{\left( {\frac{{{\rm{d}}x}}{{{\rm{d}}u}}} \right)}^2} + {{\left( {\frac{{{\rm{d}}y}}{{{\rm{d}}u}}} \right)}^2}} .$ | (16) |
由式(14) 可知,
| $\left( {\frac{{{\rm{d}}x}}{{{\rm{d}}u}},\frac{{{\rm{d}}y}}{{{\rm{d}}u}}} \right) = \left( {{x^{\left( 1 \right)}}\left( u \right),{y^{\left( 1 \right)}}\left( u \right)} \right).$ |
样条曲线不是直边, 因此各点的|J|不同.在得到曲线一阶导数的基础上, 得到各点的法向量为
| ${\bf{n}}{{\bf{g}}_i} = \left[ {\begin{array}{*{20}{c}} {{\rm{n}}{{\rm{i}}_x}}\\ {{\rm{n}}{{\rm{i}}_y}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \left( {\arctan \left( {{V_i}\left( u \right)} \right) + 0.5{\rm{ \mathsf{ π} }}} \right)}\\ {\sin \left( {\arctan \left( {{V_i}\left( u \right)} \right) + 0.5{\rm{ \mathsf{ π} }}} \right)} \end{array}} \right].$ | (17) |
式中:Vi为斜率.各点坐标以Gauss积分点表示如下:
| $\left( {{x_i},{y_i}} \right) = r\left( {{q_i}} \right).$ | (18) |
以Gauss-Legendre积分方法在样条边界上对任意函数Z、Ψ积分表示为
| $\begin{array}{l} \int\limits_s {Z\mathit{\Psi }{\rm{d}}\mathit{s}} = \\ \;\;\;\;\;\sum\nolimits_{i = 1}^{{N_{{\rm{ng}}}}} {{H_i}g\left( {{x_i},{y_i}} \right)h\left( {{x_i},{y_i}} \right)\left| {\mathit{\boldsymbol{J}}\left( {r\left( {{q_i}} \right)} \right)} \right|} . \end{array}$ | (19) |
式中:g(xi, yi)=Z(r(qi)), h(xi, yi)=Ψ(r(qi)).
3.2 Newton积分Newton积分为最直接的积分方法, 主要思想是将积分转化为离散点间的面积求和.采用Newton积分(梯形)法对该样条边界进行积分, 须先确定B样条函数, 获得曲线上相应点的位置坐标:
| $\left( {{x_i},{y_i}} \right) = C\left( {{u_i}} \right).$ | (20) |
对于积分要求的各点法向量, 转化为求各点的斜率(微分), 各点垂直于斜率方向上的单位向量是所需的单位法向量.各点的斜率表示为
| ${V_i} = \frac{{{y_{i + 1}} - {y_i}}}{{{x_{i + 1}} - {x_i}}}.$ | (21) |
该点的法向量表示为
| $\begin{array}{l} {\mathit{\boldsymbol{n}}_i} = \left[ {\cos \left( {\arctan \left( {{V_i}} \right) + 0.5{\rm{ \mathsf{ π} }}} \right),} \right.\\ \;\;\;\;\;\;\left. {\sin \left( {\arctan \left( {{V_i}} \right) + 0.5{\rm{ \mathsf{ π} }}} \right)} \right]. \end{array}$ | (22) |
式中:(xi+1, yi+1)、(xi, yi)分别为两相邻离散点的坐标.
各波函数的边界积分可以表示为
| $I = \sum\nolimits_{i = 1}^{{N_{n - 1}}} {\psi \left( {f\left( {{x_i},{y_i}} \right),g\left( {{x_i},{y_i}} \right)} \right)} .$ | (23) |
定义
| $\begin{array}{l} \psi \left( {f\left( {{x_i},{y_i}} \right),g\left( {{x_i},{y_i}} \right)} \right) = \\ \frac{{f\left( {{x_{i + 1}},{y_{i + 1}}} \right)g\left( {{x_{i + 1}},{y_{i + 1}}} \right) + f\left( {{x_i},{y_i}} \right)g\left( {{x_i},{y_i}} \right)}}{2} \times \\ {n_i}\sqrt {{{\left( {{y_{i + 1}} - {y_i}} \right)}^2} + {{\left( {{x_{i + 1}} - {x_i}} \right)}^2}} . \end{array}$ | (24) |
Newton积分方法在样条边界对任意函数Z、Ψ的积分表示为
| $\int\limits_s {Z\mathit{\Psi }{\rm{d}}\mathit{s}} = \sum\nolimits_{i = 1}^{{N_{{\rm{nc}} - 1}}} {\mathit{\Psi }\left( {g\left( {{x_i},{y_i}} \right),h\left( {{x_i},{y_i}} \right)} \right)} .$ | (25) |
式中:g(xi, yi)=Z(xi, yi), h(xi, yi)=Ψ(xi, yi).
4 数值验证为了验证前述推导方法的正确性, 选取含B样条边界的二维声学域进行相应的数值验算.以该确定的模型参数, 阐述波函数法在含有样条边界声域的建模方法.
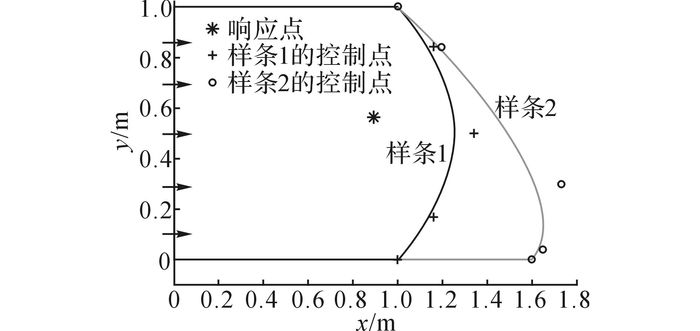
4.1 算例描述对于如图 1所示的声学域, v=1 m/s, 最大边界尺寸分别为Lx1=1.25 m, Lx2=1.65 m, Ly1=Ly2=1 m, 空气声速c=340 m/s, 密度ρ=1.225 kg/m3.右边界为3自由度的B样条.通过改变B样条的控制点来改变边界形状, 两条曲线的节点向量均为U=[-1, -1, -1, -1, 0, 1, 1, 1, 1], 控制点坐标如表 1所示.左边界施加vn=1 m/s的法向速度边界, 其他设定为刚性边界, 设定点(0.894 m, 0.565 m)为响应点.运用波函数法, 分别对由不同样条边界组成的二维声学域进行声学响应预测.
|
图 1 几何声学域 Fig. 1 Geometry of acoustic domain |
| 表 1 B样条控制点坐标 Table 1 Coordinate of control node |
针对该数值模型, 输入为速度边界, 其他边界为刚性边界, 因此该模型的边界余量积分公式取为
| $\int\limits_{{\mathit{\Omega }_{\rm{v}}}} {\tilde p\left( r \right)\left( {{{\cal L}_V}\left( {p\left( r \right)} \right) - {{\bar v}_{\rm{n}}}\left( r \right)} \right){\rm{d}}\mathit{\Omega }} = 0.$ | (26) |
运用类似有限元法采用的伽辽金加权余量法, 定义权函数:
| $\tilde p\left( r \right) = \sum\limits_{i = 1}^{{n_i}} {{\phi _i}\left( r \right)} .$ | (27) |
整理后, 可得包含各波函数系数Pi的系统矩阵方程:
| $\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{P}}_i} = \mathit{\boldsymbol{b}}.$ | (28) |
式中:
| $\mathit{\boldsymbol{A = }}\int\limits_{{\mathit{\Omega }_{\rm{v}}}} {\mathit{\Phi }\left( r \right){{\cal L}_V}\left( {{\mathit{\Phi }^{\rm{T}}}\left( r \right)} \right){\rm{d}}\mathit{\Omega }} ,$ | (29) |
| $\mathit{\boldsymbol{b}} = \int\limits_{{\mathit{\Omega }_{\rm{v}}}} {\mathit{\Phi }\left( r \right)\left[ {{{\bar v}_{\rm{n}}}\left( r \right) - {{\cal L}_V}\left( {{p_q}\left( r \right)} \right)} \right]{\rm{d}}\mathit{\Omega }} .$ | (30) |
求解式(28), 可得各波函数系数.将式(28) 代入式(2), 可得该域的声学响应.
结合推导的样条边界积分公式, A的2种数值积分表达式为
| $\begin{array}{l} {A_{{\rm{GL}},mn}} = \sum\limits_{i = 1}^{{N_{{\rm{ng}}}}} {{H_i}\left[ {{\mathit{\Phi }_m}\left( {r\left( {{q_i}} \right)} \right){{\cal L}_V}\left( {{\mathit{\Phi }_n}\left( {r\left( {{q_i}} \right)} \right)} \right)n{g_i} \times } \right.} \\ \left. {\left| {\mathit{\boldsymbol{J}}\left( {r\left( {{q_i}} \right)} \right)} \right| + {\mathit{\Phi }_m}\left( {r\left( {{q_i}} \right)} \right){{\cal L}_V}\left( {{\mathit{\Phi }_n}\left( {r\left( {{q_i}} \right)} \right)} \right)} \right]. \end{array}$ | (31) |
| $\begin{array}{l} {A_{NC,mn}} = \sum\limits_{i = 1}^{{N_{{\rm{nc}} - {\rm{1}}}}} {\psi \left[ {{\mathit{\Phi }_m}\left( {{x_i},{y_i}} \right),{{\cal L}_V}\left( {{\mathit{\Phi }_n}\left( {{x_i},{y_i}} \right)} \right)} \right]} + \\ \;\;\;\;\sum\limits_{i = 1}^{{N_{{\rm{ng}}}}} {{H_i}{\mathit{\Phi }_m}\left( {r\left( {{q_i}} \right)} \right){{\cal L}_V}\left( {{\mathit{\Phi }_n}\left( {r\left( {{q_i}} \right)} \right)} \right)} . \end{array}$ | (32) |
这两种不同积分方法的波函数建模与计算均在MATLAB2016a中编程实现.为了验证该方法的有效性, 分别将两样条边界构成的声学域运用不同单元尺寸的有限元方法进行计算.以广泛使用的LMS.SYSNOISE开展有限元的建模与计算.
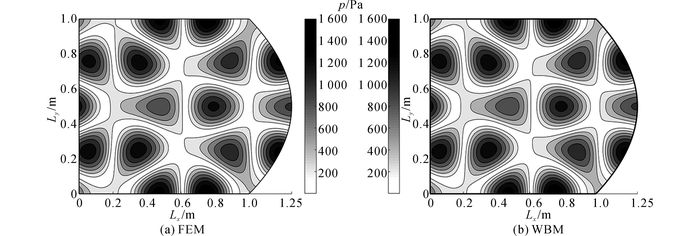
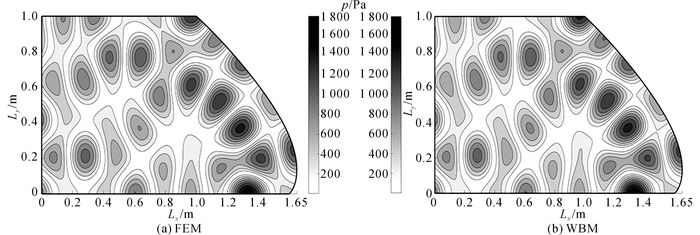
4.3 结果分析 4.3.1 波函数法与有限元法对比如图 2所示为样条1边界模型在800 Hz下的声压云图, 如图 3所示为样条2边界模型在1 000 Hz下的响应云图.图 2、3中, p为声压.经过有限元法的计算结果对比可知, 2种样条边界模型下, 采用波函数法都能够得到很好的结果, 与有限元的计算结果非常吻合.
|
图 2 样条1边界800 Hz时的声压云图对比 Fig. 2 Acoustic contour plot of model with spline 1 at 800 Hz |
|
图 3 样条2边界1 000 Hz时的声压云图对比 Fig. 3 Acoustic contour plot of model with spline 2 at 1 000 Hz |
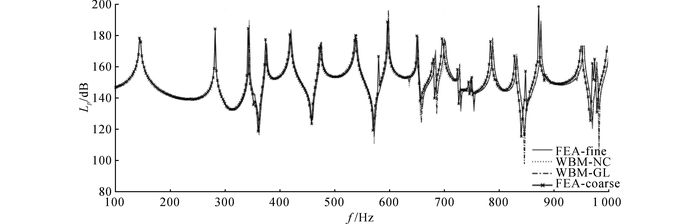
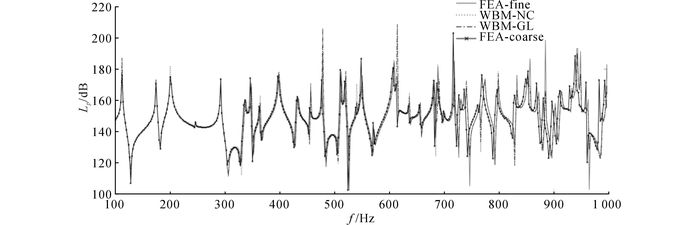
为了反映波函数法在中、低频段的计算精度, 分别运用有限元与波函数法计算响应点在100~1 000 Hz下的声学响应.响应点的频响曲线如图 4、5所示.图中,Lp为声压级, WBM-GL为Gauss积分WBM结果, WBM-NC为Newton积分的WBM计算结果, FEA-coarse为非精细模型, FEA-fine为精细模型.可以看出, 采用波函数法与精细单元计算的结果吻合得很好, 采用2种积分方法得到的结果只在一些峰值有差别.在网格单元不精细的情况下, 有限元计算的结果基本在300 Hz以后出现偏移, 频率越高, 偏移越明显.该特征限制了有限元法对大型或复杂分析域在更高频率下的应用.通过与现有方法的对比, 验证了将B样条引入到波函数法中的方法的正确性.
|
图 4 样条1边界响应点的声压级对比 Fig. 4 Acoustic response of model with spline 1 |
|
图 5 样条2边界响应点的声压级对比 Fig. 5 Acoustic response of model with spline 2 |
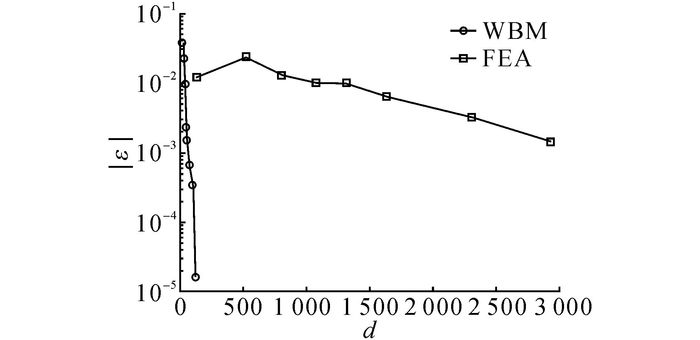
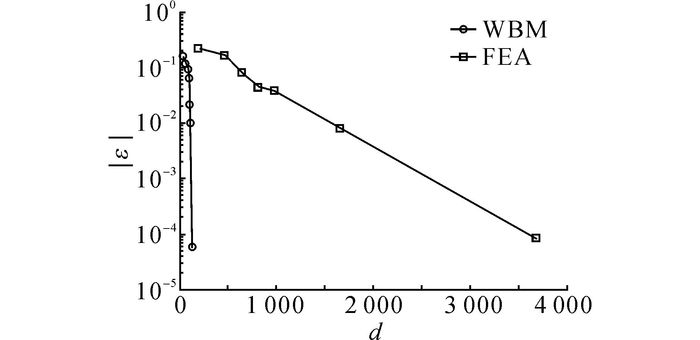
计算精度和计算效率是数值方法的基本评价指标.在时效性的科学预测或产品重复设计时, 计算效率显得更加关键.以两种方法计算得到的响应点在500 Hz时所需自由度结果为参考, 分析2种方法的收敛情况, 定义相对误差|ε|=‖P-Pref‖/‖Pref‖, 其中Pref取精细建模有限元结果.图 6、7中,d为自由度.如图 6、7所示, 波函数法的收敛速度非常快, 通常在波函数(自由度)取100左右时可以达到很高的精度.在同样的计算精度下, FEM所需的计算量较波函数法大出几个量级, 特别是在分析中、高频率问题时, 单元尺寸必须足够小, 才能反映短波特征, 从而导致模型和计算成本陡增, 这是有限元法主要适用于低频声振分析的一大原因.
|
图 6 样条1边界响应点在500 Hz声压收敛曲线 Fig. 6 Convergence of model with spline 1 at 500 Hz |
|
图 7 样条2边界响应点在500 Hz声压收敛曲线 Fig. 7 Convergence of model with spline 2 at 500 Hz |
运用波函数法对B样条边界声域进行响应预测与分析的另一大优势是在变参数的设计与分析时非常便捷.由前述的计算过程可知, 对于结构(样条)的改变, 波函数法中只需改变控制点坐标.运用FEM分析时, 改变B样条参数后, 分析模型只能通过重新划分网格来构建.利用波函数法能够极大地方便对有着不同样条参数的边界进行分析, 特别是在结构设计与优化阶段的优势明显.
4.3.2 2种积分方法的对比由前面2个样条边界的响应曲线可以看出, 2种积分方法下的波函数法计算结果基本一致.牛顿积分在部分频率下的结果有偏差, 主要是由该积分法决定的.利用该方法求得的各点法向量是两点的近似, 积分是两点间的面积近似, 所以对于同一边界, 牛顿需要将样条曲线离散得很细, 即要求很多的积分点才能更加逼近理论解.在高斯积分法中, 各点的法向量是基于样条曲线求导的理论解;利用该方法能够在较少的积分点得到高精度的解, 使得结果更加准确.
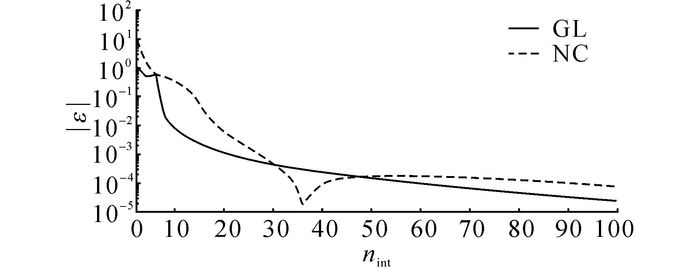
为了进一步对比2种积分方法的计算效率, 分析响应点在500 Hz时2种积分方法在积分点增加时的收敛情况.如图 8所示, nint为积分点数,GL为高斯积分, NC为牛顿积分.从对比结果可以看出, 高斯积分点取到10以后平稳收敛;牛顿积分在取50个点以后, 收敛曲线才较平稳光滑.运用高斯积分能够更高效地得到计算结果, 在无法得到边界函数和法向量时, 例如只有离散边界时, 只能采用牛顿积分方法来近似逼近.
|
图 8 高斯积分与牛顿积分的收敛曲线 Fig. 8 Convergent curves of Gaussian and Newton integral |
本文研究波函数法理论和二维B样条理论, 结合Gauss积分和梯形积分理论, 推导了在含有B样条边界声学域的中频响应方法, 数值验证了该方法的有效性.不同单元尺度的FEM计算结果说明了FEM对复杂结果、中高频声学预测的限制, 与波函数法计算结果进行对比, 展现了该方法在精度和效率的巨大优势.在包含样条曲线这类不规则边界的二维声学域中引入波函数法, 可以在很大程度上拓展波函数法的几何适用度.下一步将研究波函数法在实际复杂边界(如汽车内部声腔)声学域中的应用.
| [1] | WANG D, MONK N A. A least-squares method for the Helmholtz equation[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 175(1/2): 121–136. |
| [2] | BABUŠKA I, IHLENBURG F. A generalized finite element method for solving the Helmholtz equation in two dimensions with minimal pollution[J]. Computer Methods in Applied Mechanics and Engineering, 1995, 128(3/4): 325–359. |
| [3] | LOULA A, FERNANDES D T. A quasi optimal Petrov-Galerkin method for Helmholtz problem[J]. International Journal of Numerical Methods Engineering, 2009, 80(12): 1595–1622. DOI:10.1002/nme.v80:12 |
| [4] | MELEN K, BABUSKA I. Approximation with harmonic and generalized harmonic polynomials in the partition of unity method[J]. Computer Assisted Mechanics and Engineering Sciences, 1997, 4(3): 607–632. |
| [5] | E PERREY D, TREVELYAN J, BETTESS P. Wave boundary elements:a theoretical overview presenting applications in scattering of short waves[J]. Engineering Analysis with Boundary Elements, 2004, 28(2): 131–141. DOI:10.1016/S0955-7997(03)00127-9 |
| [6] | HARARI I, HUGHES T. Galerkin/least-squares finite element methods for the reduced wave equation with non-reflecting boundary conditions in unbounded domains[J]. Computer Methods in Applied Mechanics and Engineering, 1992, 98(3): 411–454. DOI:10.1016/0045-7825(92)90006-6 |
| [7] | MACE B, SHORTER P. Energy flow models from finite element analysis[J]. Journal of Sound and Vibration, 2000, 233(3): 369–389. DOI:10.1006/jsvi.1999.2812 |
| [8] | MAXIT L, GUYADER J. Estimation of SEA coupling loss factors using a dual formulation and FEM modal information, part I:theory[J]. Journal of Sound and Vibration, 2001, 239(5): 907–930. DOI:10.1006/jsvi.2000.3192 |
| [9] | LANGLEY R S, BREMNER P. A hybrid method for the vibration analysis of complex structural acoustic systems[J]. Journal of the Acoustical Society of America, 1999, 105(3): 1657–1671. DOI:10.1121/1.426705 |
| [10] | SAPENA J. Interior noise prediction in high-speed rolling stock driver's cab:focus on structure-borne paths (mechanical and aero sources)[J]. Mathematical Problems in Engineering, 2011, 118: 445–452. |
| [11] | SHORTER P, LANGLEY R. Modeling structure-borne noise with the hybrid FE-SEA method[C]//6th International Conference on Structural Dynamics. Paris:Cambridge University Press, 2005:1205-1210. |
| [12] | SULEAU P. Element-free Galerkin solutions for Helmholtz problems:formulation and numerical assessment of the pollution effect[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 162(1-4): 317–335. DOI:10.1016/S0045-7825(97)00350-2 |
| [13] | FARHAT C, HARARI I, FRANCA C. The discontinuous enrichment method[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(48): 6455–6479. DOI:10.1016/S0045-7825(01)00232-8 |
| [14] | EZE R. The variational theory of complex rays:a predictive tool for medium frequency vibrations[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(28): 3301–3315. |
| [15] | DESMET W. A wave based prediction technique for coupled vibro-acoustic analysis[D]. Leuven, Belgium:University of Leuven, 1998:2053-2063. http://adsabs.harvard.edu/abs/1998phdt.......158d |
| [16] | VERGOTE K, VANMAELE C, VANDEPITTE D. An efficient wave based approach for the time-harmonic vibration analysis of 3D plate assemblies[J]. Journal of Sound and Vibration, 2013, 332(8): 1930–1946. DOI:10.1016/j.jsv.2012.11.018 |
| [17] | DECKERS E, BERGEN B, GENECHTEN B V. An efficient Wave Based Method for 2D acoustic problems containing corner singularities[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 241-244(9): 286–301. |
| [18] | GENECHTEN B V, ATAK O, BERGEN B. An efficient Wave Based Method for solving Helmholtz problems in three-dimensional bounded domains[J]. Engineering Analysis with Boundary Elements, 2012, 36(1): 63–75. DOI:10.1016/j.enganabound.2011.07.011 |
| [19] | 马大猷. 现代声学理论基础[M]. 北京: 科学出版社, 2004: 10-15. |
| [20] | PIEGL L, TILLER W. The NURBS book[M]. 2nd ed. Berlin: Springer, 1997: 50-99. |
| [21] | KIUSALAAS J. Numerical methods engineering with MATLAB[M]. 2nd ed. Cambridge: Cambridge University Press, 2009: 182-249. |



