地铁已成为世界上各大城市用于缓解城市交通压力的一个最重要的手段[1-2].随着城市化扩张的加速, 地铁列车若从80 km/h提速到160 km/h, 气动阻力将为原来4倍, 成为制约地铁进一步提速的重要因素, 必须认真考虑地铁列车的气动阻力问题[3-4].
地铁列车的空气动力学问题研究基本沿用了高速列车[5-7]的相关研究思路, 主要采用理论研究、数值模拟计算与模拟试验、实车试验相结合的方法[8-13].Choi等[14]针对GTX(Great Train eXpress)高速地铁系统的构想, 系统研究200 km/h地铁列车头型长度、地铁隧道横截面积对在隧道中运行的地铁列车气动阻力的影响.列车所受的气动阻力与列车外形有密切的关系[15].梁习锋等[16]研究列车流线型头部长度、宽度、高度及耦合外形对列车交会压力波、空气阻力和升力的影响以及对应的车隧耦合空气动力效应, 得到一系列的理论关系式;张在中等[17-18]对高速列车等的气动外形进行优化研究, 讨论流线型列车头部结构的设计方法;多目标优化及仿生学在列车外形优化中得以应用[19-20].
本文采用数值仿真方法, 研究隧道内地铁列车头型几何参数对列车气动阻力的影响规律及气动阻力对头型几何参数的敏感性, 对地铁列车头型气动阻力进行优化.
1 物理模型 1.1 数学模型列车在隧道中运行, 使得流场呈现较强的非定常性, 必须考虑空气的压缩性;列车周围流场的雷诺数Re一般大于5×105, 即列车周围流场处于湍流状态.采用非定常、黏性、可压缩流的N-S方程和标准k-ε湍流模型来求解整个流场.
计算采用Fluent 6.3在国家超算广州中心的天河2号集群, 速度-压力耦合计算采用SIMPLE(semi-implicit method for pressure linked equation)算法, 扩散项采用二阶精度的中心差分格式离散.
1.2 计算模型头型外形优化计算模型为简化3车编组模型(见图 1), 车宽2.8 m, 为B型地铁列车.参考文献[16]的长细比公式, 将列车头型参数分为头型长度L、车体横断面积S、俯视轮廓线等效长度l1和纵向轮廓线等效长度l2四类.

|
图 1 头型外形优化计算模型 Fig. 1 Calculation model of head shape optimization |
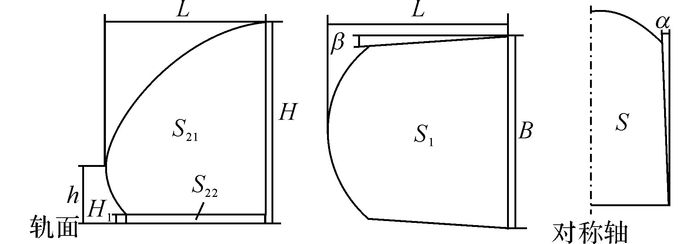
l1为车头流线型部分俯视图轮廓线的等效长度, l1=S1/B, 其中S1为车头流线型部分俯视图轮廓线所围成的面积, B为车头宽度;l2为车头流线部分纵向投影轮廓线等效长度, l2=S2/H, 其中H为车头高度, S2=S21+S12, S21为控制列车头部主视图轮廓线所围成的面积, S22=L×H1, 如图 2所示.
|
图 2 参数模型头型的参数参照 Fig. 2 Parameter reference of model head type |
根据4类参数, 选定研究对象为头型长度、车身侧墙倾角α、车头俯视轮廓线倾角β及鼻锥高度h.针对研究对象设置10个列车模型, 裙板距轨面高度H1为0.2 m, 车头高度H为3.8 m, 其他具体参数见表 1.不同参数研究的对应模型如表 2所示.
| 表 1 不同参数模型头型参数对照表 Table 1 Different model parameters comparison table |
| 表 2 四类头型参数研究内容与模型对应表 Table 2 Four kinds of parameter research content and model corresponding table |
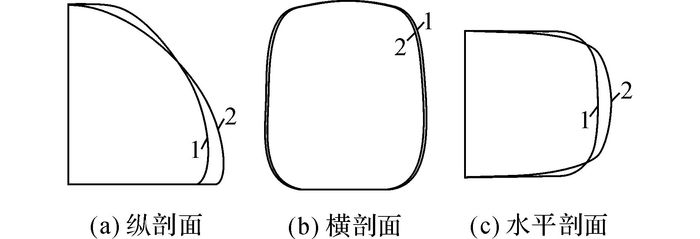
通过参数化研究, 对地铁列车头型进行优化, 优化模型(160 km/h)及原模型(80 km/h)三视图如图 3所示, 头型相关参数如表 3所示.
|
1-原列车模型(80 km/h);2-优化模型(160 km/h) 图 3 原地铁列车头型与优化地铁列车头型三视图 Fig. 3 Original metro train head type and optimized subway train head type three views |
| 表 3 原地铁列车头型与优化地铁列车头型参数 Table 3 Original metro train head type and optimized subway train head type parameters |
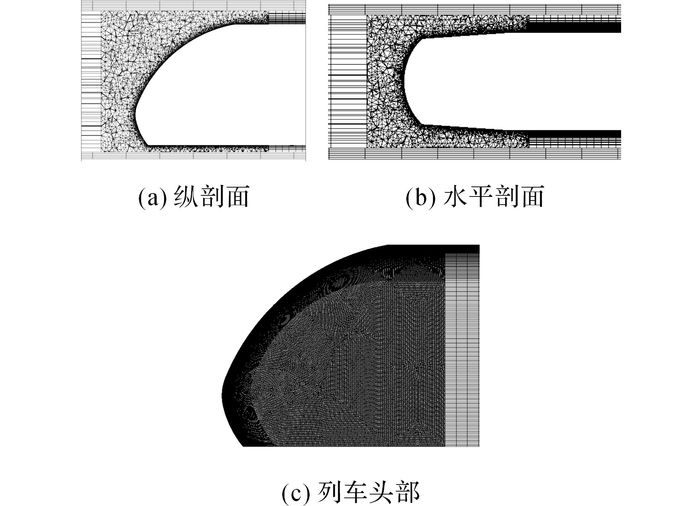
在网格划分中, 为了准确地模拟车体周围流场的变化, 对曲面变化较大的车头处流场区域采用四面体网格且进行加密处理, 车头壁面网格尺寸为0.01 m, 对光滑的车体采用六面体网格.所有工况网格量约为1 300万, 车体表面网格及体网格如图 4所示.
|
图 4 头型参数模型仿真计算网格示意图 Fig. 4 Head parameter model simulation of grid schematicdiagram |
为了模拟列车和隧道之间存在相对运动, 采用滑移网格法进行数值计算(见图 5).当列车向前运动时, 区域1和列车以同样的速度向前运动, 区域2静止, 静止区域和运动区域之间的边界定义为交换面, 静止区域和运动区域之间的信息交换通过交换面进行.

|
图 5 参数研究的滑移网格示意图 Fig. 5 Schematic diagram of sliding mesh for parametric study |
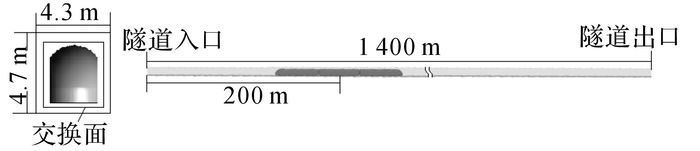
参考文献[21]初选隧道长度, 通过分析计算结果, 调整隧道长度使得列车在隧道中的气动阻力能稳定, 最终选择设置隧道长度为1.4 km, 列车在隧道中的初始位置为列车中心点距隧道入口200 m处;隧道横截面选择简化的地铁长方形隧道截面(4.3 m×4.7 m), 阻塞比约为0.45.隧道壁面、隧道地面、列车与交换面的相对位置及隧道示意图如图 6所示.
|
图 6 头型外形参数研究的计算域 Fig. 6 Computational domain of head parameter research |
如图 6所示, 列车壁面设置为无滑移壁面(wall)边界条件;隧道入口设置为压力入口(pressure-inlet)边界条件;隧道出口为压力出口(pressure-outlet)边界条件, 相对压强pout =0 Pa;隧道壁面及地面设置为无滑移壁面(wall)边界条件;交换面边界条件设置为内部面(interface).区域1滑移速度设置为160 km/h, 区域1两端口设置为压力出口(pressure-outlet), 列车运行方向为x正方向.气体材料设置为可压空气(idea-gas, 在Fluent中的idea-gas具有黏性).
1.4 系数定义为了便于分析, 定义系数如下:
| ${{C}_{\text{d}}}=\frac{D}{0.5\rho {{v}^{2}}S},$ | (1) |
| ${{C}_{\text{p}}}=\frac{\Delta p}{0.5\rho {{v}^{2}}}.$ | (2) |
式中:Cd为气动阻力系数;Cp为列车表面压力系数;ρ为空气密度, 是1. 225 kg/m3;v为列车运行速度;S为车体横截面积(不同工况下的车体横截面积见表 1);D为阻力;Δp为流场该处压力与无穷远处压力之差.
为了分析不同参数变化对列车气动阻力影响的敏感性, 定义敏感系数为
| $s=\frac{\Delta {{C}_{\text{d}}}/{{C}_{\text{d}}}}{\Delta x/x}.$ | (3) |
式中:Δx/x为基准参数x的变化率;ΔCd/Cd为当基准参数x变化Δx时, Cd的相应变化率.
2 算法验证从文献[14]可知, 当阻塞比为0.281, 头型长度为0.5 m, 运行速度为200 km/h时, 压差阻力占总阻力的68%, 列车压差阻力主要与列车外形有关, 摩擦阻力不受头型长度的影响.本文研究头型外形参数对列车气动阻力的影响规律, 主要影响压差阻力.压差阻力是由列车前、后部压力差引起的, 表达式[15]为
| ${{F}_{\text{p}x}}=\oint{{{p}_{\text{b}x}}}\text{d}{{S}_{\text{F}}}.$ | (4) |
式中:Fpx为列车空气压差阻力;pbx为列车表面压力pb在x方向的分量;pb为空气垂直作用在列车表面单位面积上的力, 其方向垂直于列车表面, 以指向作用面方向为正方向, 大小为列车外表面的静压与环境大气压之差.
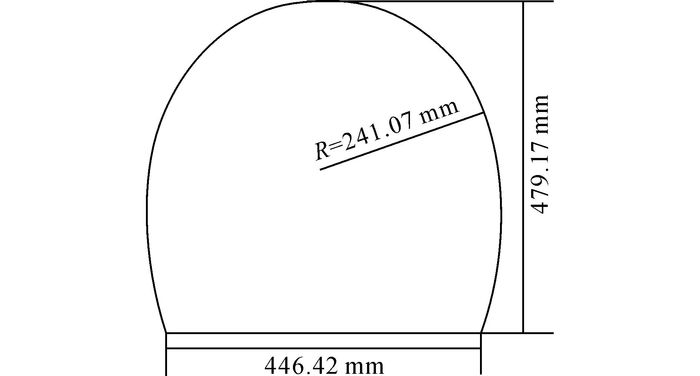
由式(4) 可知, 压差阻力由列车表面压力积分而得, 可以通过与动模型试验监测的压力结果对比, 验证该研究所用数值方法的正确性, 保证计算结果的可靠性与准确度.动模型实验的模型比例为1:16.8(见图 7), 列车模型采用CRH2三车编组(见图 8), 车宽为167 mm;模型隧道长度为59.5 m, 模拟实际长度为1 000 m的隧道, 隧道模型净空截面面积为0.209 m2(见图 9), 模拟实际面积为59 m2的隧道模型.

|
图 7 动模型实验隧道及列车模型 Fig. 7 Dynamic model experimental tunnel and train model |

|
图 8 CRH2缩比模型 Fig. 8 CRH2 scale model |
|
图 9 动模型实验隧道净空横截面积 Fig. 9 Cross-sectional area of experimental tunnel ofdynamic model |
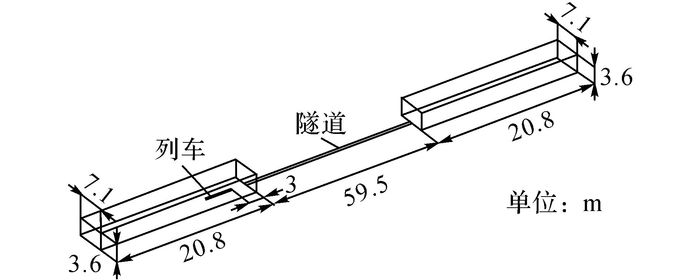
在仿真计算中, 建立与试验相同的缩比模型, 监测隧道壁面离入口3 m(实际50 m)处以及列车鼻尖点处的压力变化.数值仿真采用滑移网格, 速度与试验相同, 为350 km/h, 计算域如图 10所示.
|
图 10 验证数值仿真方法的计算域 Fig. 10 Numerical simulation domain |
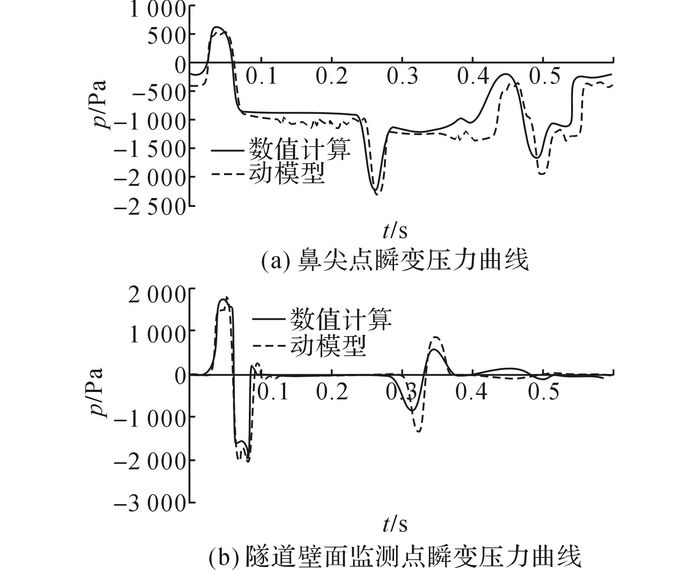
将仿真结果与试验数据进行对比, 通过数值计算所得监测点的压力变化时程曲线规律与动模型一致, 结果吻合良好,如图 11所示.图中,p为瞬变压力.列车鼻尖点与隧道壁面监测点的压力幅值及最大压力梯度列于表 4.可以看出, 仿真计算结果与动模型实验结果相差在5%以内, 因此采用滑移网格的数值仿真方法计算隧道内气动阻力, 具有可靠性.
| 表 4 数值模型与动模型实验表面压力对比 Table 4 Comparison of surface pressure of numerical simulation and dynamic model test |
|
图 11 头车鼻尖点与隧道壁面压力曲线对比 Fig. 11 Comparison of pressure curve of numerical simulation and dynamic model test |
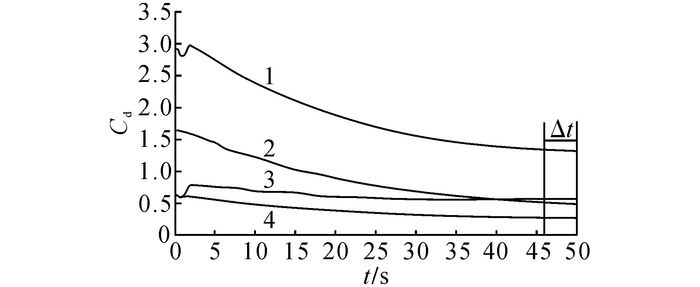
列车模型在隧道中共运行50 s, 选取参数模型4分析隧道内气动阻力.为了便于分析, 将气动阻力通过式(1) 无量纲化, 如图 12所示为模型4在隧道中运行时的气动阻力系数时程曲线图.可以看出, 随着列车在隧道中运行时间的增加, 气动阻力趋于稳定.对于列车气动阻力分析, 选取Δt(4 s)内的气动阻力系数平均值, 作为参考值.在Δt内气动阻力系数波动的相对误差为10-5.整车气动阻力随时间的变化趋势与头车的变化趋势相似.
|
1-整车;2-头车;3-尾车;4-中间车 图 12 气动阻力系数-时间曲线 Fig. 12 Aerodynamic drag coefficient-Time |
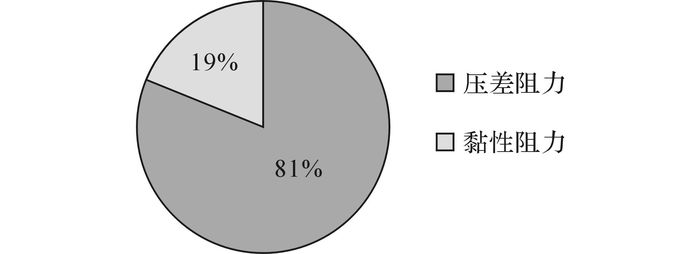
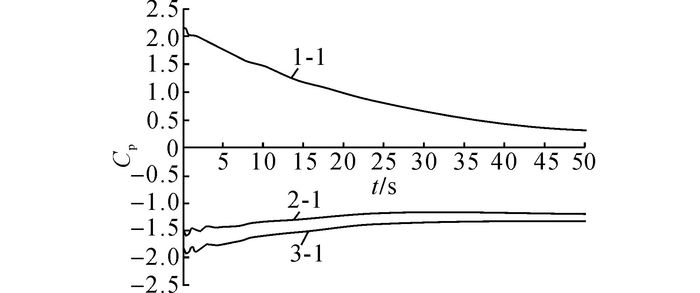
在列车运行稳定后, 压差阻力、黏性阻力占总阻力的比例如图 13所示.可以看出, 当阻塞比约为0.45, 头型长度为3 m, 车速为160 km/h时, 压差阻力占总阻力的81%, 占据主导地位.压差阻力与列车表面压力分布相关.如图 14所示为列车表面压力系数随时间的变化曲线, 监测点如图 15所示.点1-1是头车鼻尖点, 压力曲线的变化趋势与头车气动阻力的变化趋势一致.已知头车鼻尖点压力为最大正压, 通过式(4) 可知, 鼻尖点压力全贡献于压差阻力, 因此气动阻力与鼻尖点压力的变化趋势一致, 具有合理性, 证实压差阻力在气动阻力中占主导地位.点2-1与点3-1分别位于中间车与尾车车身, 压力都为负值, 且尾车负压更大, 与气动阻力的规律一致, 尾车的气动阻力比中间车大.随着时间的变化, 列车表面压力逐渐稳定, 稳定后中间车与尾车车身的压力绝对值大于头车鼻尖点压力, 但车身侧面压力不完全贡献给气动阻力, 因此中间车的气动阻力不比头车大.
|
图 13 压差阻力与黏性阻力占总阻力的比例 Fig. 13 Aerodynamic drag ratio analysis |
|
图 14 监测点的瞬变压力曲线 Fig. 14 Transient pressure curve at monitoring point |

|
图 15 参数模型4的布点图 Fig. 15 Parameter model 4 monitoring points |
为了比较隧道与明线气动阻力, 对模型4进行明线仿真计算, 仿真结果见表 5.表中,Cd1、Cdm、Cd2、Cdw分别为头车、中车、尾车、整车气动阻力系数.通过表 5, 对比明线与隧道两种工况下列车的气动阻力.可以看出, 头车气动阻力的变化最大, 增加最多;当阻塞比约为0.45时, 隧道气动阻力是明线的3倍.
| 表 5 160 km/h明线与隧道气动阻力系数 Table 5 Aerodynamic drag coefficient of 160 km/h open field and tunnel |
对于头型优化, 通过头型的横向(横截面积)、纵向(头型长度、纵向轮廓线等效长度)及水平(俯视轮廓线等效长度)三方位进行参数研究, 为优化模型选取合适的外形参数.在限界与实际中, 纵向参数对外形的影响最大, 其中头型长度最关键.首先通过研究头型长度对列车气动阻力的影响规律, 选取符合工程实际要求的头型长度.在选取的头型长度上, 依次探讨纵向轮廓线等效长度、横截面积、俯视轮廓线等效长度的影响规律, 为优化模型选择较优的外形参数.
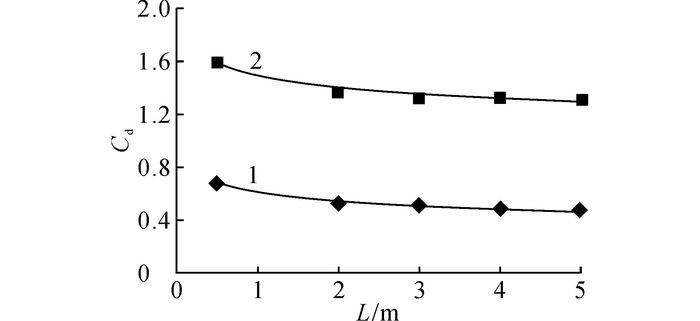
3.2.1 头型长度L头型长度是影响气动阻力的重要因素之一.选择模型4~8, 研究头型长度对列车气动阻力的影响.对于L≤5 m的列车, 整车及头车气动阻力与头型长度符合对数关系(见图 16), 即气动阻力随头型长度增加的下降幅度减小.
|
1-头车;2-整车 图 16 气动阻力系数-头型长度 Fig. 16 Aerodynamic drag coefficient-head type length |
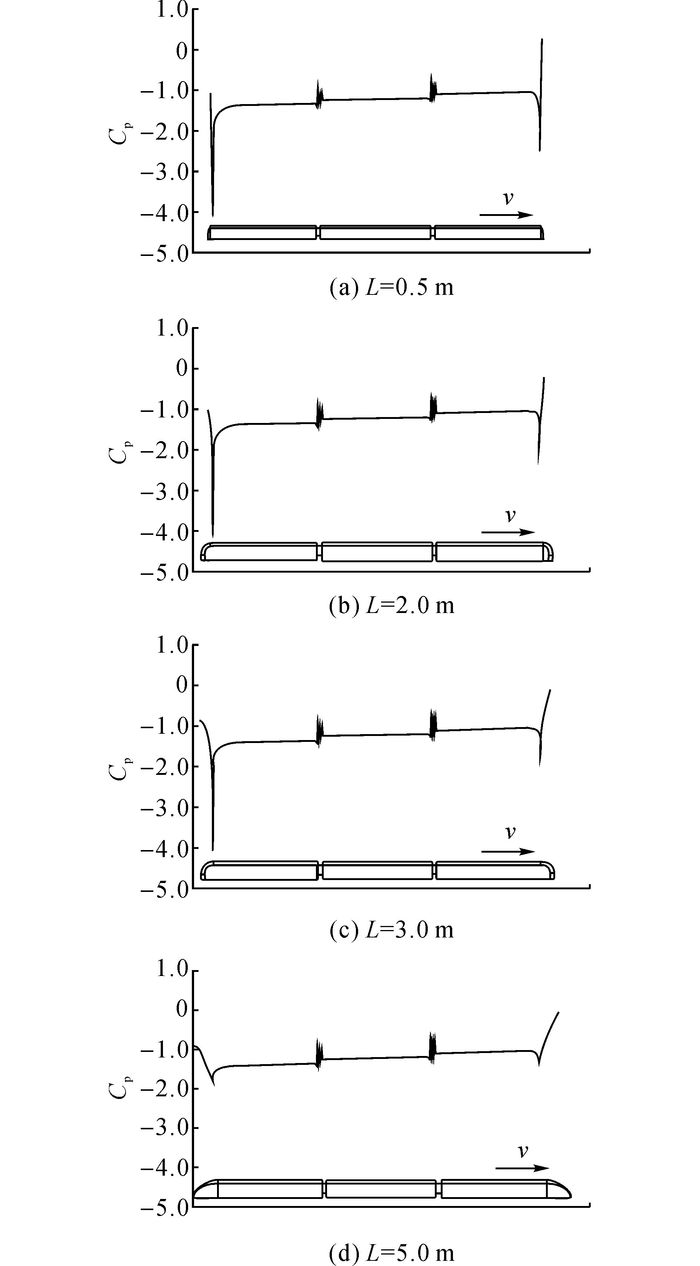
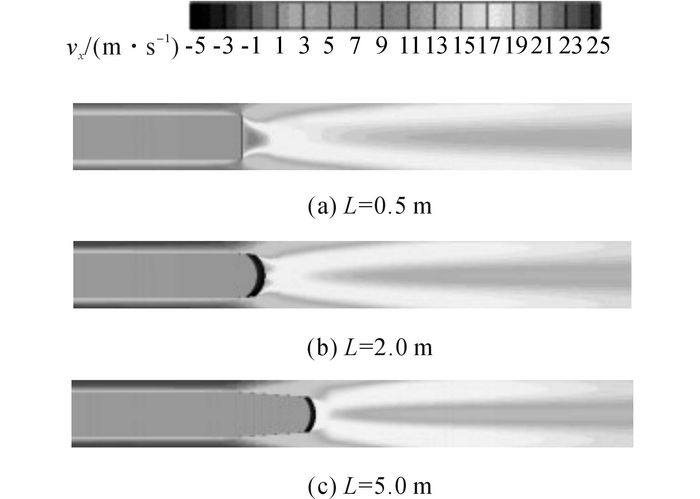
气动阻力与表面压力分布有关, 比较不同头型长度列车的表面压力分布(见图 17).钝头型列车头部过渡段的负压分布变化急剧、迅猛(见图 17(a));流线型列车头部过渡段的负压变化较缓和(见图 17(d)).头型由钝头到流线型, 头型头部过渡段压力减小, 尾车压力恢复变快.如图 18所示为46 s时列车在鼻锥高度的截面上x方向的尾流流速vx.可以看出, 流线型列车靠近头部尾流速度小于钝头车.这是由于流线型头部形状是逐渐变化的, 意味着流线型头部附近的流体流动更顺利.随着头型长度的增加, 鼻端与尾端的压力差降低, 即气动阻力减小.
|
图 17 46 s时列车模型的表面压力 Fig. 17 Surface pressure model trains at 46 s |
|
图 18 46 s时列车x方向尾流流速(z=1.2 m截面) Fig. 18 x-direction flow velocity at 46 s |
以L=5 m的列车模型作为基准, 通过式(3) 分析气动阻力对头型长度的敏感性.从图 19可以看出, 当L为0.5~2.0 m时, 敏感系数的下降速率最大, 这表明随着头型长度的增加, 头型长度对列车气动阻力的影响减小.L为2.0~3.0 m, 头车气动阻力对头型长度的敏感性保持稳定, 整车敏感性下降.比较不同列车头型的气动阻力, 应以整车阻力作为比较标准[20].L为3.0~4.0 m, 整车气动阻力对头型长度的敏感性增加.综合考虑敏感性与气动阻力, 当L≤5.0 m时, 头型长度选择3.0~4.0 m较合适.在工程实际中, 地铁列车头型不宜过长, 本文的优化模型选择L=3 m.

|
1-头车;2-整车 图 19 列车敏感系数-头型长度 Fig. 19 Train sensitivity coefficient-head type length |
当L=3 m时, 选择模型1、9、10对纵向轮廓线等效长度l2进行探讨, 其中l2的变化是由鼻锥高度h变化引起的.气动阻力的计算结果见表 6.可知, h增加, l2减小, 列车气动阻力减小.l2为2.29~2.32 m, 整车气动阻力的减小幅度更大.
| 表 6 纵向轮廓线等效长度不同的列车模型气动阻力系数 Table 6 Aerodynamic drag coefficient of trainmodel with different equivalent length of longitudinal contour |
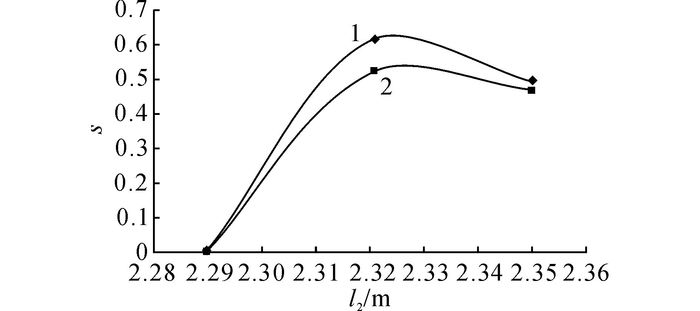
以气动阻力最小的模型10为基准, 探讨气动阻力对l2的敏感性.从图 20可以看出, 整车及头车气动阻力对l2的敏感性曲线趋势一致;当l2=2.32 m时, 敏感系数处于峰值.当l2为2.29~2.32 m时, 敏感系数呈上升趋势, 气动阻力随l2的减小而减小, 综合考虑, l2选择2.32±0.005 m较合适, 利用率最高.优化模型l2选取峰值2.32 m.
|
1-头车;2-整车 图 20 列车敏感系数-纵向轮廓线等效长度 Fig. 20 Train sensitivity coefficient-longitudinal profile line equivalent length |
当L=3 m, l2=2.32 m时, S对列车气动阻力的影响如表 7所示.S减小3.1%, 整车气动阻力下降1.4%, 车体横截面积的变化对列车气动阻力的影响很大.
| 表 7 不同横截面积列车模型的气动阻力系数 Table 7 Different cross-sectional model train aerodynamic drag coefficient |
以模型2为基准, 头车与整车气动阻力对横断面积的敏感系数分别为1.452与0.437, 气动阻力对S的敏感性很高.在实际允许的情况下, 应尽可能减小横断面积, 以降低列车气动阻力.优化模型横断面积为9.56 m2, 减小了0.83%.
3.2.4 俯视轮廓线等效长度l1在L=3 m, l2=2.32 m, S=9.56 m2的情况下, 对具有不同俯视轮廓线等效长度l1的列车模型气动阻力进行探讨研究, 其中l1的变化是由俯视轮廓线倾角β变化引起的.从表 8可以看出, 随着β的增加, l1减小, 列车气动阻力减小.
| 表 8 l1不同的列车模型气动阻力系数 Table 8 Aerodynamic drag coefficient of l1 different train model |
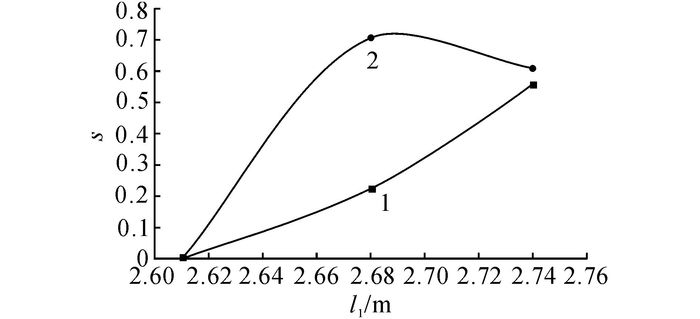
选择模型4为基准, 绘制灵敏度曲线, 分析列车气动阻力对l1的敏感系数.从图 21可以看出, 随着l1的增大, 头车气动阻力对l1的敏感系数增加;整车气动阻力对l1的敏感系数在l1=2.68 m处于峰值.整车气动阻力随l1的减小而减小, 从整车气动阻力与灵敏度角度综合考虑, l1选择(2.68±0.01) m较合适.对于l1, 在实际工程中可以适当牺牲敏感性减小l1, 从而降低气动阻力, 本文优化模型l1选取2.61 m.
|
1-头车;2-整车 图 21 列车敏感系数-俯视轮廓线等效长度 Fig. 21 Train sensitivity coefficient-top contour lineequivalent length |
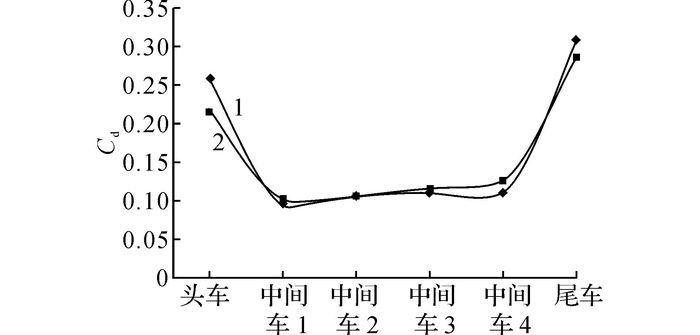
根据研究参数对气动阻力影响规律获取的参数取值, 得到优化的160 km/h地铁列车模型(80 km/h原模型与160 km/h优化模型三视图如图 3所示).为了节约计算资源, 在明线160 km/h工况下对6车编组带转向架的原模型与优化模型气动阻力进行仿真计算, 各节车气动阻力系数见图 22.可知, 优化模型的头车气动阻力减小16.3%, 中间车4气动阻力上升, 但整车气动阻力下降了3.7%, 优化的模型对降低气动阻力有效果.
|
1-原模型(80 km/h);2-优化模型(160 km/h) 图 22 各节车气动阻力系数 Fig. 22 Aerodynamic drag coefficient of each section of train |
(1) 当阻塞比约为0.45时, 隧道气动阻力是明线的3倍, 压差阻力占总阻力的81%.
(2) 当L≤5 m时, 列车气动阻力与头型长度符合对数关系.考虑头型长度对气动阻力的敏感性, 当L≤5.0 m时, 头型长度选择3.0~4.0 m较合适.
(3) 车体横截面积对列车气动阻力的影响较大, 灵敏度很高.在实际允许的情况下, 可以适当减小横截面积, 降低列车气动阻力.
(4) 当L=3 m时, 考虑敏感性, l1选择(2.68±0.01) m, l2选择(2.32±0.005) m较合适.
(5) 对80 km/h地铁列车头型进行气动阻力优化, 得到160 km/h优化模型(L=3 m, l1=2.61 m, l2=2.32 m, S=9.56 m2).优化后的列车模型头车气动阻力下降16.3%, 整车气动阻力下降3.7%.
| [1] | JURAEVA M, LEE J, SONG D J. A computational analysis of the train-wind to identify the best position for the air-curtain installation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(5): 554–559. DOI:10.1016/j.jweia.2011.02.004 |
| [2] |
汪波, 李军, 杨国纪, 等. 快速地铁列车不同司机室头型空气动力学影响分析[J].
电力机车与城轨车辆, 2015, 38(4): 36–39.
WANG Bo, LI Jun, YANG Guo-ji, et al. Analysis on aerodynamics of rapid metro vehicles with different cab shapes[J]. Electric Locomotives and Mass Transit Vehicles, 2015, 38(4): 36–39. |
| [3] |
刘凤华, 余以正. 地铁列车隧道气动力学试验与仿真[J].
大连交通大学学报, 2013, 34(4): 7–11.
LIU Feng-hua, YU Yi-zheng. Comparison of subway train tunnel aerodynamic test and simulation analysis[J]. Journal of Dalian Jiaotong University, 2013, 34(4): 7–11. |
| [4] |
熊骏, 朱冬进, 徐世南, 等. 裙板结构对地铁车辆气动性能的影响[J].
铁道车辆, 2015, 53(3): 16–20.
XIONG Jun, ZHU Dong-jin, XU Shi-nan, et al. Effect of the apron structure on aerodynamic performance of metro vehicles[J]. Rolling Stock, 2015, 53(3): 16–20. |
| [5] | MUOZ-PANIAGUA J, GARCÍA J, CRESPO A. Genetically aerodynamic optimization of the nose shape of a high-speed train entering a tunnel[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 130(7): 48–61. |
| [6] | BAKER C. The flow around high speed trains[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(6): 277–298. |
| [7] |
孔繁冰, 李明, 韩璐, 等. CRH380BL高速动车组气动外形优化设计[J].
铁道机车车辆, 2013, 32(6): 9–12.
KONG Fan-bing, LI Ming, HAN Lu, et al. Optimization design of aerodynamic shape for CRH380BL EMU[J]. Railway Locomotive and Car, 2013, 32(6): 9–12. |
| [8] | KIM J Y, KIM K Y. Experimental and numerical analyses of train-induced unsteady tunnel flow in subway[J]. Tunneling and Underground Space Technology, 2007, 22(2): 166–172. DOI:10.1016/j.tust.2006.06.001 |
| [9] | HUANG Y D, GAO W. A numerical study of the train-induced unsteady airflow in a subway tunnel with natural ventilation ducts using the dynamic layering method[J]. Journal of Hydrodynamics, 2010, 22(2): 164–172. DOI:10.1016/S1001-6058(09)60042-1 |
| [10] | HUANG Y, GONG X, PENG Y, et al. Effects of the ventilation duct arrangement and duct geometry on ventilation performance in a subway tunnel[J]. Tunneling and Underground Space Technology, 2011, 26(6): 725–733. DOI:10.1016/j.tust.2011.05.005 |
| [11] |
祝岚, 张东, 苏振旭, 等. 基于乘客舒适性的快速地铁隧道压力波分析[J].
都市快轨交通, 2015, 28(1): 87–91.
ZHU Lan, ZHANG Dong, SU Zhen-xu, et al. Analysis of pressure waves of high-speed subway tunnel based on passenger comfort[J]. Urban Rapid Rail Transit, 2015, 28(1): 87–91. |
| [12] | KIM T K, KIM K H, KWON H B. Aerodynamic characteristics of a tube train[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(12): 1187–1196. DOI:10.1016/j.jweia.2011.09.001 |
| [13] | GONZÁLEZ M L, VEGA M G, ORO J M F, et al. Numerical modeling of the piston effect in longitudinal ventilation systems for subway tunnel[J]. Tunneling and Underground Space Technology, 2014, 40(2): 22–37. |
| [14] | CHOI J K, KIM K H. Effects of nose shape and tunnel cross-sectional area on aerodynamic drag of train traveling in tunnels[J]. Tunneling and Underground Space Technology, 2014, 41(3): 62–73. |
| [15] | 田红旗. 列车空气动力学[M]. 北京: 中国铁道出版社, 2007: 214-265. |
| [16] |
梁习锋, 田红旗. 列车气动性能评估参数研究[J].
中国铁道科学, 2003, 24(1): 38–42.
LIANG Xi-feng, TIAN Hong-qi. Research on evaluating parameters of train aerodynamic performance[J]. China Railway Science, 2003, 24(1): 38–42. |
| [17] |
张在中, 周丹. 不同头部外形高速列车气动性能风洞试验研究[J].
中南大学学报:自然科学版, 2013, 44(6): 2603–2608.
ZHANG Zai-zhong, ZHOU Dan. Wind tunnel experiment on aerodynamic characteristic of streamline head of high speed train with different head shapes[J]. Journal of Central South University:Science and Technology, 2013, 44(6): 2603–2608. |
| [18] |
张洁, 梁习锋, 刘堂红, 等. 强侧风作用下客车车体气动外形优化[J].
中南大学学报:自然科学版, 2011, 42(11): 356–362.
ZHANG Jie, LIANG Xi-feng, LIU Tang-hong, et al. Optimization research on aerodynamic shape ofpassenger car body with strong crosswind[J]. Journal of Central South University:Science and Technology, 2011, 42(11): 356–362. |
| [19] |
姚拴宝, 郭迪龙, 孙振旭, 等. 基于Kriging代理模型的高速列车头型多目标优化设计[J].
中国科学:技术科学, 2013, 43(2): 186–200.
YAO Shuan-bao, GUO Di-long, SUN Zhen-xu, et al. Multi-objective optimization of the streamlined head of high-speed trains based on the Kriging model[J]. Science China:Technology Science, 2013, 43(2): 186–200. |
| [20] |
杜健, 龚明, 田爱琴, 等. 基于仿生非光滑沟槽的高速列车减阻研究[J].
铁道科学与工程学报, 2014, 11(5): 70–76.
DU Jian, GONG Ming, TIAN Ai-qin, et al. Study on the drag reduction of the high-speed train based on the bionic non-smooth riblets[J]. Journal of Railway Science and Engineering, 2014, 11(5): 70–76. |
| [21] | 建设部. 地铁设计规范: GB50157-2003[S]. 北京: 中国计划出版社, 2003: 12-20. |



