桥梁结构在外界荷载的长期作用下会出现构件损伤或材料性能退化等问题, 累积损伤最终可能会导致桥梁坍塌.及时准确地识别桥梁结构损伤或材料性能退化一直是桥梁工程领域研究的热点问题.国内外已有许多国家和地区的桥梁布设了结构健康监测系统, 用来开展桥梁结构状况评估, 张启伟等[1-5]基于结构健康监测数据作了大量的研究工作.结构损伤识别作为结构健康监测的重要任务, 得到广泛关注[6-7].
中性轴为受弯梁中性层与梁横截面的交线, 是所有梁式结构共有的结构参数.理论上, 在未损伤的状况下受弯梁横截面的中性轴位置不会发生变化.当横截面发生损伤(开裂、分层、材料性能退化等)时, 横截面质心随之改变, 中性轴位置会发生移动.中性轴位置的改变可以反映梁截面刚度的变化, 也可以反映其他影响梁截面质心的结构行为, 如预应力损失、截面材料性能退化、截面应力重分布等.中性轴位置可以用于梁式结构的结构损伤识别、性能预测与状态评估.
目前, Sigurdardottir等[8]研究基于中性轴位置的结构损伤识别.Plude等[9]对多主梁组合钢箱梁桥采用有限元模拟, 开展损伤识别研究, 发现在固有频率、应变分布与中性轴位置3种损伤识别参数中, 中性轴位置具有较高的敏感性.O’Brien等[10]指出桥面板上荷载分布位置会引起中性轴位置改变.Gangone等[11]在一座即将摧毁的桥梁上开展控制试验, 发现中性轴位置对桥梁结构的不均匀沉降具有敏感性.
本文采用九堡大桥结构健康监测系统获得的应变数据, 基于中性轴位置参数进行损伤识别分析.基于小波多分辨率分析对长期监测数据进行处理, 去除应变监测数据中的低频(温度)组分.采用卡尔曼滤波方法对高频(交通荷载)组分进行滤波处理.采用滤波后的应变数据得到梁截面中性轴的变化情况, 对梁的损伤状况进行识别.
1 受弯梁中性轴位置确定 1.1 受弯梁变形分析基于材料力学的基本理论可知, 受弯梁在纯弯矩荷载下发生弯曲变形.假设梁是由无数层纵向纤维组成, 中性层是梁上拉伸区与压缩区的分界面, 中性层与横截面的交线为中性轴, 如图 1所示.o-o、o′-o′为变形前、后的中性轴, c-c、c′-c′为变形前、后的纵向纤维;Δx、Δx′为变形前、后的纤维长度;h为c-c纤维距中性轴的距离;ρ为受弯梁的曲率半径;dθ为夹角.c-c纤维的应变可以通过下式计算:

|
图 1 受弯梁变形 Fig. 1 Beam bending behavior |
| $ \varepsilon = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta x' - \Delta x}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\left( {\rho + h} \right){\rm{d}}\theta - \rho {\rm{d}}\theta }}{{\rho {\rm{d}}\theta }} = \frac{h}{\rho }. $ | (1) |
式中:ε为c-c纤维的应变.
纵向纤维的应变与其距中性轴的距离成正比, 即截面应变沿梁厚度方向呈线性分布.另外, 与中性轴距离为h的应变可由下式求解:
| $ \varepsilon = \frac{{Mh}}{{EI}}. $ | (2) |
式中:M为弯矩, E为材料弹性模量, I为截面惯性矩, h方向取中性轴向下为正.
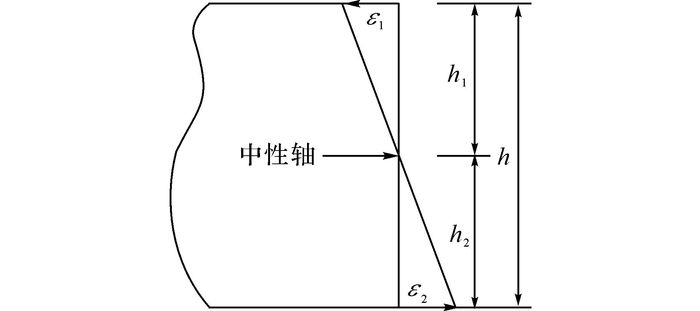
1.2 中性轴位置基于欧拉-伯努利梁理论可知, 受弯梁横截面应变可以根据几何关系确定.受弯梁横截面的应变分布见图 2.图中, ε1、ε2为应变, 均取应变的绝对值;h1、h2为应变距中心轴的距离.根据几何关系, 可知:
| $ \frac{{{\varepsilon _1}}}{{{\varepsilon _2}}} = \frac{{{h_1}}}{{{h_2}}}. $ | (3) |
|
图 2 受弯梁横截面应变分布 Fig. 2 Strain distribution of cross section of bendingbeam |
式中:ε1、ε2可以通过传感器测量.
取r表示受弯梁中性轴位置, 中性轴位置可以通过下式[12]求解:
| $ r = \frac{{{\varepsilon _1}}}{{{\varepsilon _1} + {\varepsilon _2}}} = \frac{{{h_2}}}{h}. $ | (4) |
一般情况下, 根据结构应变监测数据推算结构应力不容易, 因为应变监测数据通常为多组分数据(包含荷载效应、温度效应与噪声等).一方面, 各组分所引起的结构应力不同.比如, 温度效应引起的桥面应变虽然很大, 但伸缩缝位移与温度应变呈线性关系[13], 通过伸缩缝位移不一定会产生结构应力.解决该问题的有效方法是将多组分数据进行单组分分解.小波多分辨率分析可以很好地实现该目标[13].
信号变换域处理为使用一组基函数将信号从信号域转换到转换域.小波变换作为一种变换域信号处理方法, 选择某一特定函数(母小波)表示信号, 通过改变母小波的尺度参数, 即伸缩平移运算, 将信号分解并重构成多种不同尺度的信号.基于小波变换的多分辨率分析过程是对信号进行多尺度分解与重构的过程.
使用函数F(t)表示母小波, 小波变换过程可以表示为
| $ {\left( {{W_F}f} \right)_{\left( {a,b} \right)}} = \frac{1}{{{{\left| a \right|}^{1/2}}}} \times \int_{ - \infty }^\infty {f\left( t \right)\bar F\left( {\frac{{t - b}}{a}} \right){\rm{d}}t} ;a > 0. $ | (5) |
式中:(WFf)(a, b)为小波变换过程, a为尺度参数, b为时间参数, F(t)中上横线表示共轭, f(t)为输入信号函数.f(t)可以通过对(WFf)(a, b)双重积分得到:
| $ f\left( t \right) = \frac{1}{{{C_F}}} \times \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{W_F}f\left( {a,b} \right)\bar F\left( {\frac{{t - b}}{a}} \right)\frac{1}{{{a^2}}}{\rm{d}}a{\rm{d}}b} } . $ | (6) |
式中:CF为容许条件参数.
一般情况下, 由于a与b的离散性, 通常采用离散小波变换进行实际信号的处理.为了提高小波变换过程的有效性, 尺度参数与时间参数均采用二进制表示.选择F(t)作为母小波表示原始信号, 相应的离散小波{Fj, k}可以用尺度参数与时间参数表示为
| $ {F_{j,k}}\left( t \right) = {2^{j/2}} \times F\left( {{2^j}t - k} \right). $ | (7) |
式中:{Fj, k}为属于L2(R)空间的标准正交基.f(t)可以表示为
| $ f\left( t \right) = \sum\limits_j {\sum\limits_k {{\alpha _{j,k}}{F_{j,k}}\left( t \right)} } , $ | (8) |
| $ {\alpha _{j,k}} = \int_{ - \infty }^\infty {f\left( t \right){F_{j,k}}{\rm{d}}t} . $ | (9) |
式中:αj, k为变换参数.如果用Dj、Aj表示j级的细节部分与近似部分, 则
| $ {D_j} = \sum\limits_{k \in Z} {{\alpha _{j,k}}{F_{j,k}}\left( t \right)} , $ | (10) |
| $ {A_J} = \sum\limits_{j > J} {{D_j}} , $ | (11) |
| $ f\left( t \right) = {A_J} + \sum\limits_{j \le J} {{D_j}} . $ | (12) |
式中:J为级数.
式(7)~(12) 给出小波多分辨率分析的树形结构分解和重建过程.通过小波多分辨率分析可知, 原始信号可以分解为多尺度信号.其中, 细节部分具有原始信号的高频信号特征, 近似部分具有原始信号的低频信号特征.
选取的小波种类不同会引起小波变换结果的差异, 小波函数的正交性、支撑集、正则性、消失矩阶数等特性决定了在数据处理应用中如何进行选择[14].Daubechies小波简称db小波, 是90年代初由法国学者Daubechies提出.db族小波具有正交性并且是紧支撑集, 小波分解系数可以精确重构并降低分解信号时的能量散失.正则性和消失矩阶数特性可以保证小波更好地刻画信号特征, 具有较好的滤噪能力[14], 缩短因支撑集太大造成的计算时间冗长.
2.2 卡尔曼滤波1960年, 匈牙利裔鲁道夫·卡尔曼提出采用递归方法进行离散数据线性滤波的方法, 即卡尔曼滤波方法.卡尔曼滤波过程是一个信号处理与更新过程, 实质为根据实时观测的数据(包含噪声及其他误差), 以最小均方误差估计作为最佳估计准则, 获得更趋于真实的观测数据[15-18].卡尔曼滤波方法的优势是可以适用于平稳与非平稳数据的滤波, 具有很好的抗噪声干扰能力[12].
卡尔曼滤波理论认为线性系统可以描述为由状态方程与观测方程构成.
| $ {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{A}}_k} \times {\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{B}}_k} \times {\mathit{\boldsymbol{u}}_k} + {\mathit{\boldsymbol{w}}_k}, $ | (13) |
| $ {\mathit{\boldsymbol{Z}}_k} = {\mathit{\boldsymbol{C}}_k} \times {\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{v}}_k}. $ | (14) |
式中:Xk、Zk为系统k时刻的状态变量与观测变量, Xk-1为系统k-1时刻的状态变量;uk为系统k时刻的控制变量;wk、vk为系统k时刻过程噪声变量与观测噪声变量, 通常假设两者为均值为0、相互独立的白噪声;Ak、Bk、Ck分别为状态转移矩阵、状态控制矩阵和观测矩阵.式(13) 为状态方程, 式(14) 为观测方程.
卡尔曼滤波过程可以通过下列迭代方程实现:
| $ {{\mathit{\boldsymbol{\bar X}}}_k} = {\mathit{\boldsymbol{A}}_k} \times {\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{B}}_k} \times {\mathit{\boldsymbol{u}}_{k - 1}}, $ | (15) |
| $ {\mathit{\boldsymbol{P}}_k} = {\mathit{\boldsymbol{A}}_k} \times {{\mathit{\boldsymbol{\bar P}}}_{k - 1}} \times \mathit{\boldsymbol{A}}_k^{\rm{T}} + \mathit{\boldsymbol{R}}, $ | (16) |
| $ {\mathit{\boldsymbol{X}}_k} = \frac{{{\mathit{\boldsymbol{P}}_k} \times \mathit{\boldsymbol{C}}_k^{\rm{T}}}}{{{\mathit{\boldsymbol{C}}_k} \times {\mathit{\boldsymbol{P}}_k} \times \mathit{\boldsymbol{C}}_k^{\rm{T}} + \mathit{\boldsymbol{Q}}}}, $ | (17) |
| $ {\mathit{\boldsymbol{X}}_k} = {{\mathit{\boldsymbol{\bar X}}}_k} + {\mathit{\boldsymbol{K}}_k} \times \left( {{\mathit{\boldsymbol{Z}}_k} - {\mathit{\boldsymbol{C}}_k} \times {{\mathit{\boldsymbol{\bar X}}}_k}} \right), $ | (18) |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\bar P}}}_k} = \left( {\mathit{\boldsymbol{G}} - {\mathit{\boldsymbol{K}}_k} \times {\mathit{\boldsymbol{C}}_k}} \right) \times {\mathit{\boldsymbol{P}}_k} \times {\left( {\mathit{\boldsymbol{G}} - {\mathit{\boldsymbol{K}}_k} \times {\mathit{\boldsymbol{C}}_k}} \right)^{\rm{T}}} + \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{K}}_k} \times \mathit{\boldsymbol{R}} \times \mathit{\boldsymbol{K}}_k^{\rm{T}}. \end{array} $ | (19) |
式中:G为单位矩阵, R、Q为过程噪声协方差矩阵与观测噪声协方差矩阵, uk-1为系统k-1时刻的控制变量, Xk为k时刻的估计值, Pk为k时刻的误差协方差, Pk-1、Pk为k-1、k时刻的更新估计误差协方差, Kk为卡尔曼增益.式(15) 为状态估计方程, 若没有确定的控制变量, 则右边第2项可以略去;式(16) 为状态估计下的误差协方差方程;式(17) 为卡尔曼增益方程;式(18) 为更新状态估计方程;式(19) 为更新估计误差协方差方程.
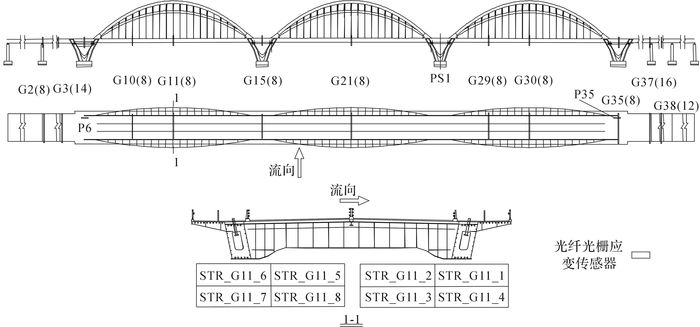
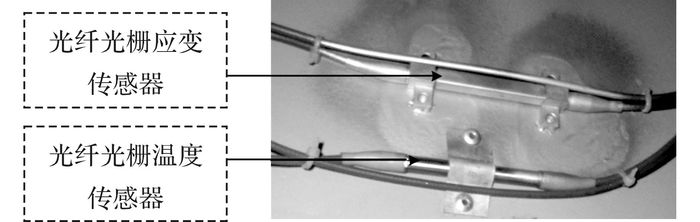
3 基于中性轴位置损伤识别应用 3.1 应变监测系统一般情况下, 大跨径钢箱梁桥在交通荷载作用下发生弯曲时, 可以将钢箱梁视为受弯梁.九堡大桥是一座横跨钱塘江的钢混组合拱桥, 全长1 855 m, 如图 3所示.桥梁建成后布设了长期结构健康监测系统, 通过对多种荷载作用下的桥梁结构响应进行实时采集与分析, 评估大桥在运营期间的健康状况和工作性能.结构应变监测是健康监测系统的组成部分, 九堡大桥在拱肋、钢箱梁内部共布设166个光纤光栅应变传感器, 对应变状况进行在线监测, 钢箱梁光纤光栅应变传感器布设见图 4.图中, STR_G11_1表示传感器的编号, 其中STR表示应变传感器, G11表示梁截面编号, 1表示该截面上传感器的序号.如图 5所示为实际安装在桥面板上的光纤光栅传感器实物图.

|
图 3 九堡大桥 Fig. 3 Jiubao Bridge |
|
图 4 钢箱梁应变传感器布置 Fig. 4 Layout of strain sensors on steel box beam |
|
图 5 应变传感器安装 Fig. 5 Installation of strain sensors |
选择钢箱梁下游截面(G11) 中的STR_G11_1与STR_G11_4两个传感器的监测数据进行截面损伤识别.如图 6所示为钢箱梁顶板与底板一周时间内的应变时程.可以发现, 温度的日循环周期变化导致应变时程存在周期性变化的趋势;温度的周期性变化引起钢箱梁发生顺桥向周期性的收缩或膨胀.

|
图 6 钢箱梁应变时程 Fig. 6 Strain history of steel box beam |
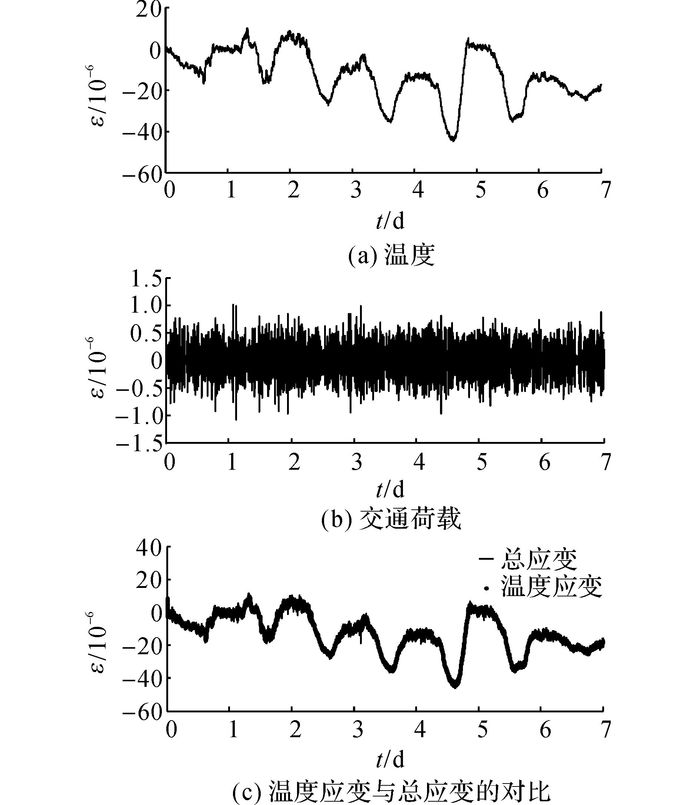
采用小波多分辨率分析方法, 对顶板应变时程进行多尺度分析.采用db4小波对应变时程进行多层分解, 基于变换参数进行细节应变(交通荷载组分)与近似应变(温度组分)的重构.应变时程多分辨率分解如图 7所示.图 7表明, 温度引起的应变比荷载引起的大, 但因伸缩缝位移会将温度引起的应变释放, 对钢箱梁应力的影响较小, 在进行中性轴位置损伤识别时要去除温度的影响.使用小波多分辨率分析方法分离信号中高、低频组分, 具有很好的效果.
|
图 7 多尺度分解应变时程 Fig. 7 Strain time history of multi-scale decomposition |
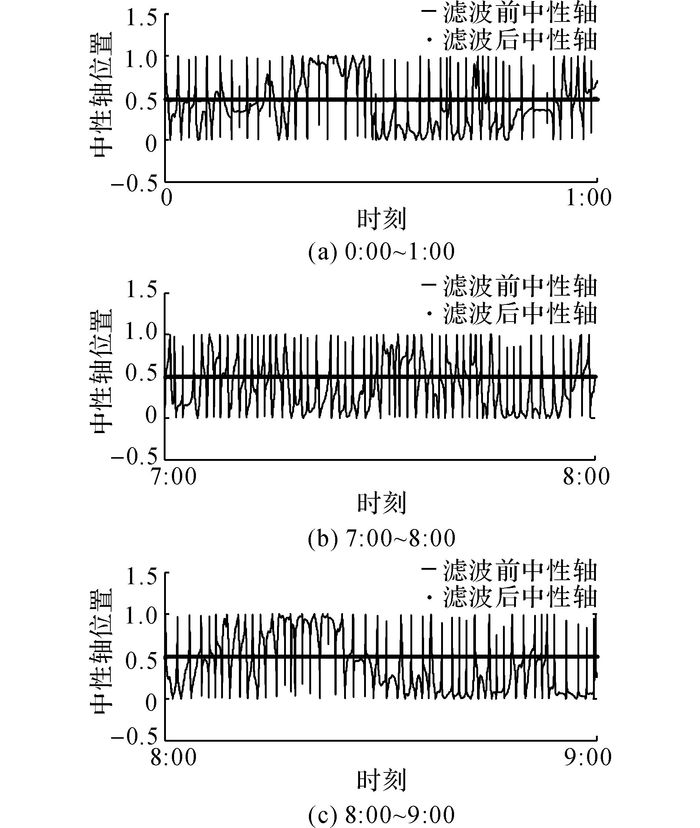
选择一周内某一天3个时间段(0:00~1:00, 7:00~8:00, 8:00~9:00) 的应变数据, 采用卡尔曼滤波方法滤波, 确定中性轴位置的变化情况, 结果如图 8所示.图 8表明, 在交通荷载的作用下, 滤波后的中性轴位置的波动幅度较滤波前的小很多.在不同时间段, 卡尔曼滤波方法均具有很好的稳定性.在不同荷载作用下, 经过卡尔曼滤波后的中性轴位置没有发生较大的移动, 均在0.5附近.
|
图 8 中性轴位置 Fig. 8 Neutral location |
卡尔曼滤波通过对系统状态的初始值和过程噪声与观测噪声协方差矩阵参数赋值, 基于前一时刻对当前时刻的估计值与当前时刻的观测值, 根据迭代公式实现对当前时刻的估计值的更新, 从而完成观测数据的滤波工作, 有效地降低了噪声对应变数据的影响.滤波后的结果表明, 卡尔曼滤波具有很好的稳定性和较强的抗噪声干扰能力.
3.4 损伤识别标准差能够反映一组数据的离散程度, 采用标准差对卡尔曼滤波效果进行评定.滤波前、后的标准差对比见表 1.可以发现, 经过卡尔曼滤波方法处理的信号标准差较小, 卡尔曼滤波方法具有很好的抗噪声能力.在不同时间段内, 滤波后的中性轴位置与均值的变化波动为-2.24%与2.87%, 滤波前的中性轴位置与均值的变化波动为10.6%与-14.7%, 表明在交通荷载作用下, 基于应变监测数据计算的中性轴位置会发生波动, 但均围绕理论均值位置变动, 即发生可回复性变动, 钢箱梁截面未产生损伤.
| 表 1 基于卡尔曼滤波的中性轴位置估计 Table 1 Estimated neutral-axis position by Kalman filter |
若采用未进行滤波的数据对结构进行损伤识别, 因数据存在较大的离散程度, 不同时间段内的均值具有较大的误差, 基于该均值进行损伤识别容易造成误判.
4 结论(1) 基于中性轴位置方法, 对九堡大桥桥面板进行损伤识别, 应变数据来自于九堡大桥结构健康监测系统.采用小波多分辨率分析方法去除监测数据中的温度组分, 采用卡尔曼方法对监测数据进行滤波.通过研究发现, 基于交通荷载作用下的应变数据计算的中性轴位置会发生变动, 若截面未发生损伤, 则中性轴会围绕理论均值变动, 不会发生不可回复的变动.
(2) 采用小波多分辨率分析与卡尔曼滤波方法, 获得了较好的效果, 但小波多分辨率分析具有高频段分辨率低的缺点, 卡尔曼滤波方法需要已知监测数据中噪声的先验知识, 初始值的选择对滤波结果有较大影响.
(3) 在结构未发生损伤的情况下, 基于应变监测数据分析获得桥面板中性轴位置发生的可回复移动特性.对于如何实现基于中性轴位置的结构损伤定量评估以及如何确定中性轴变动阈值, 需要进一步的研究.
| [1] |
张启伟. 大型桥梁健康监测概念与监测系统设计[J].
同济大学学报, 2001, 29(1): 65–69.
ZHANG Qi-wei. Conception of long-span bridge health monitoring and monitoring system design[J]. Journal of Tongji University, 2001, 29(1): 65–69. |
| [2] | NI Y Q, YE X W, KO J M. Monitoring-based fatigue reliability assessment of steel bridges:analytical model and application[J]. Journal of Structural Engineering, 2010, 136(12): 1563–1573. DOI:10.1061/(ASCE)ST.1943-541X.0000250 |
| [3] | YE X W, NI Y Q, WONG K Y, et al. Statistical analysis of stress spectra for fatigue life assessment of steel bridges with structural health monitoring data[J]. Engineering Structures, 2012, 45: 166–176. DOI:10.1016/j.engstruct.2012.06.016 |
| [4] | NI Y Q, YE X W, KO J M. Modeling of stress spectrum using long-term monitoring data and finite mixture distributions[J]. Journal of Engineering Mechanics, 2012, 138(2): 175–183. DOI:10.1061/(ASCE)EM.1943-7889.0000313 |
| [5] | HOUSNER G W, BERGMAN L A, CAUGHEY T K, et al. Structural control past present and future[J]. Journal of Engineering Mechanics, 1997, 123(9): 897–971. DOI:10.1061/(ASCE)0733-9399(1997)123:9(897) |
| [6] |
杨秋伟. 基于振动的结构损伤识别方法研究进展[J].
振动与冲击, 2007, 26(10): 86–100.
YANG Qiu-wei. A review of vibration-based structural damage identification methods[J]. Journal of Vibration and Shock, 2007, 26(10): 86–100. DOI:10.3969/j.issn.1000-3835.2007.10.019 |
| [7] |
宗周红, 钟儒勉, 郑沛娟, 等. 基于健康监测的桥梁结构损伤预后和安全预后研究进展及挑战[J].
中国公路学报, 2014, 27(12): 46–57.
ZONG Zhou-hong, ZHONG Ru-mian, ZHENG Pei-juan, et al. Damage and safety prognosis of bridge structures based on structural health monitoring:progress and challenges[J]. China Journal of Highway and Transport, 2014, 27(12): 46–57. |
| [8] | SIGURDARDOTTIR D H, GLISIC B. The neutral axis location for structural health monitoring:an overview[J]. Journal of Civil Structural Health Monitoring, 2015, 5(5): 703–713. DOI:10.1007/s13349-015-0136-5 |
| [9] | PLUDE S, CHRISTENSON R, DEWOLF J, et al. Quantifying damage measures for a composite steel girder bridge using finite element analysis[C]//Structural Health Monitoring 2011:Condition-Based Maintenance and Intelligent Structures. Palo Alto:StanfordUniversity, 2013:1831-1838. |
| [10] | O'BRIEN E J, KEOGH D L. A discussion on neutral axis location in bridge deck cantilevers[J]. Computers and Structures, 1999, 73(1-5): 295–301. DOI:10.1016/S0045-7949(98)00248-X |
| [11] | GANGONE M V, WHELAN M J, JANOYAN K D, et al. Development of performance assessment tools for a highway bridge resulting from controlled progressive monitoring[J]. Structure and Infrastructure Engineering, 2014, 10(5): 551–567. DOI:10.1080/15732479.2012.757329 |
| [12] | XIA H W. SHM-based condition assessment ofin-service bridge structures using strain measurement[D]. Hong Kong:The Hong Kong Polytechnic University, 2011. http://journals.sagepub.com/doi/abs/10.1260/1369-4332.16.8.1401 |
| [13] | NI Y Q, XIA H W, KO J M. In-service conditionassessment of bridge deck using long-term monitoring data of strain response[J]. Journal of Bridge Engineering, 2012, 17(6): 876–885. DOI:10.1061/(ASCE)BE.1943-5592.0000321 |
| [14] |
杨晓楠, 唐和生, 陈镕, 等. 钢结构损伤识别中Db族小波函数选择[J].
同济大学学报:自然科学版, 2006, 34(12): 1568–1572.
YANG Xiao-nan, TANG He-sheng, CHEN Rong, et al. Selection on Db's family wavelet functions in steel structural damage identification[J]. Journal of Tongji University:Natural Science, 2006, 34(12): 1568–1572. |
| [15] |
孙继平, 李晨鑫. 基于卡尔曼滤波和指纹定位的矿井TOA定位方法[J].
中国矿业大学学报, 2014, 43(6): 1127–1133.
SUN Ji-ping, LI Chen-xin. Mine time of arrival positioning method based on Kalman filtering and fingerpint positioning[J]. Journal of China University of Mining and Technology, 2014, 43(6): 1127–1133. |
| [16] |
杨兆升, 朱中. 基于卡尔曼滤波理论的交通流量实时预测模型[J].
中国公路学报, 1999, 12(3): 63–67.
YANG Zhao-sheng, ZHU Zhong. A real-time traffic volume prediction model based on the Kalman filtering theory[J]. China Journal of Highway and Transport, 1999, 12(3): 63–67. |
| [17] | DING F, LIU X M, MA X Y. Kalman state filtering based least squares iterative parameter estimation for observer canonical state space systems using decomposition[J]. Journal of Computational and Applied Mathematics, 2016, 301: 135–143. DOI:10.1016/j.cam.2016.01.042 |
| [18] |
于滨, 杨忠振, 曾庆成. 基于SVM和Kalman滤波的公交车到站时间预测模型[J].
中国公路学报, 2008, 21(2): 89–92.
YU Bin, YANG Zhong-zhen, ZENG Qing-cheng. Bus arrival time prediction model based on support vector machine and Kalman filter[J]. China Journal of Highway and Transport, 2008, 21(2): 89–92. |


