水利水电工程是一个复杂、动态且带有随机性的系统, 国内外学者对该系统的研究已经开展了很多年, 大部分集中在机械配置优化、物料调度优化等方面, 对施工期间场内道路交通流及道路安全的研究较少.
采用施工仿真方法研究和分析大型土木、水利水电工程施工过程被证明是一种行之有效的方法.国内外有关研究人员开发了一些常用的仿真系统[1-3], 并将它们应用到了实际的工程中.钟登华等[4]分析经验方法在交通运输系统的组织设计中的不足, 提出采用循环网络模拟技术研究复杂地下洞室群施工交通运输系统的方法.陈先明等[5]在分析传统仿真方法的优缺点的基础上, 提出基于元胞自动机(CA)模型的施工运输系统的模糊仿真方法, 更加形象、精确地对运输系统进行仿真.杨兴国等[6]运用生产线平衡原理和层次分析法对地下洞室群施工全过程进行系统仿真, 对施工交通运输可行性进行论证并优化了机械配置方案.在上述仿真方法中, 交通运输过程均作为整个系统的一部分, 模型比较简单, 以服从某一分布产生的随机数作为运输时间来表示运输过程, 且假设在交通运输过程中无交通事故, 这与实际情况存在较大差异.
为了深入研究交通运输过程, 必须建立较准确的交通流模型.多年来, CA模型以简单性和易操作性, 越来越多地被应用到交通流模型的研究中.Nagel等[7]在184号模型[8]的基础上, 提出4条元胞演化规则用以模拟高速公路交通流(NaSch模型).Barlovic等[9]改进了NaSch模型, 将NaSch模型中固定的随机慢化概率定义为车辆速度的函数, 得到依赖于速度的随机慢化模型(VDR模型).Chowdhury等[10]扩展了NaSch模型, 引入车辆换道规则, 提出单向双车道CA模型(STCA模型).此后, 学者们在上述基本模型的基础上进行不同的改进, 如考虑驾驶员特性、动态车间距等, 以适应各自不同的研究需求[11-14].上述CA模型都是基于平直道路的假设, 模型中的车辆多为小汽车和卡车.由于我国的水电工程大都建在高山峻岭之间, 施工场内的道路存在一定的坡度, 同时水电工程施工场内的车辆以运输物料的自卸汽车为主, 其与城市中的小汽车、卡车、公交车等在加速性能、制动性能等方面存在相当大的差异, 因此上述CA模型无法直接应用于水电工程中的交通系统.
在实际的水电工程施工场内, 经常由于交通事故导致道路阻塞, 从而影响物料运输, 最终影响施工工期, 工期延误意味着施工成本的提高和后期发电收入的减少.以某水电站为例, 建成后日发电量为5 200万千瓦时, 每千瓦时售价为0.28元, 工期延误一天相当于损失1 456万元, 这对投资方来说是难以接受的.如何减少施工场内的交通事故, 保证施工进度不受影响是非常重要的.
针对水电工程施工场地的特点, 基于CA模型, 考虑道路坡度对车辆加速和减速的影响以及驾驶员心理素质的差异和车辆性能的差异, 本文提出适用于水电工程施工场内的交通流模型, 对该模型进行验证.在该模型的基础上, 首次引入场地交通事故发生概率模型, 通过仿真分析在不同车头距下发生交通事故的可能性, 给出合理的安全距离建议, 为进一步制定施工交通运输安全标准提供支持.
1 模型描述假设道路由单向的两条车道组成, 每条车道是由L个格点组成的一维离散格点链, 每个格点在t时刻可能的状态为:空格点(即没有车)或者被一辆车占据.根据水电工程施工场内的实际情况可知, 道路上的车辆有空载自卸汽车和满载自卸汽车, 每辆车占n个元胞.两类车以一定混合比例行驶在道路上, 混合比例为1:β.每一种类型的车辆状态由速度v表示, v∈[0, vmax], 其中vmax为车辆允许的最大速度.为了描述车辆状态的演化, 定义Xi(t)表示第i辆车在t时刻车头的位置;gapi(t)=Xi+1(t)-Xi(t)-n表示第i辆车在t时刻与前方紧邻车辆之间的间距;gapi, f(t)=Xi, f(t)-Xi(t)-n表示第i辆车在t时刻与邻道前方紧邻车辆之间的间距, 其中Xi, f(t)表示t时刻邻道前方紧邻车辆车头的位置;gapi, b(t)=Xi, b(t)-Xi(t)-n表示第i辆车在t时刻与邻道后方紧邻车辆之间的间距, 其中Xi, b(t)表示t时刻邻道后方紧邻车辆车头的位置.图 1描述了各变量及它们之间的关系.

|
图 1 车辆状态示意图 Fig. 1 Schematic of vehicles' states |
水利水电工程大部分位于高山峻岭地带, 施工场内的道路存在一定坡度, 因此需要考虑道路的坡度对行车的影响.由于车辆在上坡、下坡时的行驶情形类似, 只对车辆上坡时的情形进行描述.上坡时车辆在加速和减速两种情况下的受力分析如图 2所示.
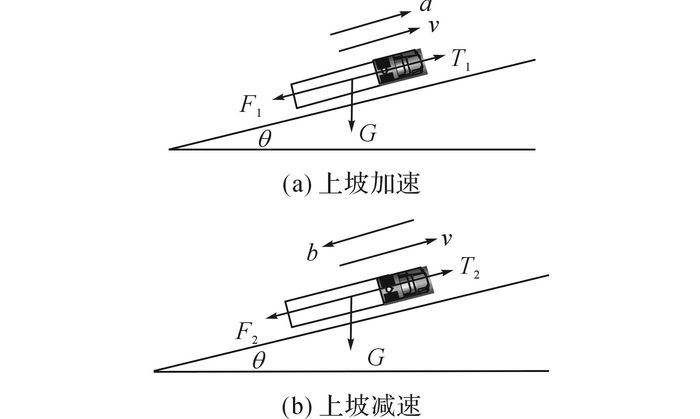
|
图 2 车辆上坡时的受力分析 Fig. 2 Vehicle's stress analysis on uphill road |
加速过程为
| $ {T_1} - {F_1} - G\sin \theta = ma, $ | (1) |
| $ a = \frac{{{T_1} - {F_1}}}{m} - g\sin \theta . $ | (2) |
减速过程为
| $ {F_2} + G\sin \theta - {T_2} = mb, $ | (3) |
| $ b = \frac{{{F_2} - {T_2}}}{m} + g\sin \theta . $ | (4) |
式中:T1、T2为牵引力, F1、F2为阻力, G为重力, g为重力加速度, a为加速度, b为减速度, θ为道路的坡角.
由图 2可知, 重力G在坡道上的分量Gsin θ对车辆行驶产生了减速效应.为了将纵坡的减速效应在CA中体现, 需要将减速效应离散化处理, 即以一定概率一次性减速[15].定义车辆在平直道路上的最大加速度和最大减速度分别为am和bm(即式(2)、(4) 中θ=0°时的值), 则在坡角为θ的道路上车辆每一个时步的加速度为
| $ a = {a_{\rm{m}}} + C. $ | (5) |
式中:
| $ C = \left\{ {\begin{array}{*{20}{c}} { - {a_{\rm{m}}},以概率\;{p_{\rm{a}}};}\\ {0,其他.} \end{array}} \right. $ | (6) |
其中,
| $ {p_{\rm{a}}} = g\sin \theta /{a_{\rm{m}}}. $ | (7) |
同理, 车辆在每一个时步的减速度为
| $ b = {b_{\rm{m}}} + D. $ | (8) |
式中:
| $ D = \left\{ {\begin{array}{*{20}{c}} {{b_{\rm{m}}},以概率\;{p_{\rm{b}}};}\\ {0,其他.} \end{array}} \right. $ | (9) |
其中,
| $ {p_{\rm{b}}} = g\sin \theta /{b_{\rm{m}}}. $ | (10) |
由于θ一般都很小, 可以认为sin θ≈tan θ=η.在实际工程中, 经常用坡比η来描述道路的陡度.由此得到:
| $ {p_{\rm{a}}} = g\eta /{a_{\rm{m}}}, $ | (11) |
| $ {p_{\rm{b}}} = g\eta /{b_{\rm{m}}}. $ | (12) |
CA模型中的随机慢化主要是描述由于实际行驶中各种不确定因素的存在, 导致驾驶员产生随机减速的行为.在实际中, 随机慢化不仅与车辆的速度有关, 还与驾驶员的心理素质有关, 定义随机慢化概率为一个与车辆速度和驾驶员心理素质相关的函数,
| $ {p_{\rm{s}}}\left( {{k_1},v} \right) = {k_1}\exp \left( { - v/{\gamma _1}} \right). $ | (13) |
式中:k1~N(μ1, σ12), 表示驾驶员的心理素质水平.γ1为比例系数, 用于使随机慢化概率处在一个合理的范围.
基于上述描述, 可得如下CA模型中的跟驰规则.
1) 确定随机慢化概率:
| $ p = {p_{\rm{s}}}\left( {{k_1},v} \right). $ | (14) |
2) 加速:
| $ {v_i} = \left( {t + \frac{1}{3}} \right) = \min \left\{ {{v_i}\left( t \right) + a,{v_{\max }}} \right\}. $ | (15) |
3) 减速:
| $ {v_i}\left( {t + \frac{2}{3}} \right) = \min \left\{ {{v_i}\left( {t + \frac{1}{3}} \right),{\rm{ga}}{{\rm{p}}_i}\left( t \right)} \right\}. $ | (16) |
4) 随机慢化:
| $ {v_i}\left( {t + 1} \right) = \left\{ \begin{array}{l} \max \left\{ {{v_i}\left( {t + \frac{2}{3}} \right) - b,0} \right\},以概率\;p;\\ {v_i}\left( {t + \frac{2}{3}} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他. \end{array} \right. $ | (17) |
5) 位置更新:
| $ {X_i}\left( {t + 1} \right) = {X_i}\left( t \right) + {v_i}\left( {t + 1} \right). $ | (18) |
车辆换道是一种常见的行为, 为了将实际道路上的换道行为在CA模型中表现, 需要建立相应的换道规则.考虑驾驶员的心理素质水平、车辆的性能和道路的纵坡坡度对换道行为的影响, 建立如下的换道规则.
1) 换道动机:
| $ {\rm{ga}}{{\rm{p}}_i}\left( t \right) < \min \left\{ {{v_i}\left( t \right) + {a_{\rm{m}}},{v_{\max }}} \right\}, $ | (19) |
| $ {\rm{ga}}{{\rm{p}}_{i,{\rm{f}}}}\left( t \right) > {\rm{ga}}{{\rm{p}}_i}\left( t \right). $ | (20) |
车辆在该车道上无法按照期望速度行驶, 旁道上的行驶条件比该车道好.
2) 安全条件:
| $ {\rm{ga}}{{\rm{p}}_{i,{\rm{b}}}}\left( t \right) > {d_{{\rm{safe}}}}. $ | (21) |
式中:dsafe是为了确保不发生碰撞的换道安全距离.
当同时满足换道动机和安全条件以后, 车辆以概率pc进行换道.定义pc是一个与驾驶员心理素质水平、车辆性能和道路坡度有关的函数:
| $ {p_{\rm{c}}}\left( {{k_1},{k_2},\eta } \right) = {k_1}{k_2}\exp \left( { - \eta /{\gamma _2}} \right). $ | (22) |
式中:k1~N(μ1, σ12), 表示驾驶员的心理素质水平;k2~N(μ2, σ22), 表示车辆性能;γ2为比例系数, 使换道概率位于一个合理的范围.
1.3 交通事故在施工场内, 由于驾驶员的超速、急刹、随意变道等不文明驾驶行为的存在导致交通事故时有发生.为了将实际道路上的交通事故在CA模型中体现, 模型中采用Boccara等[16]提出的交通事故发生的3个条件:
| $ {\rm{ga}}{{\rm{p}}_i}\left( t \right) \le {v_{\max }}, $ | (23) |
| $ {v_{i + 1}}\left( t \right) > 0, $ | (24) |
| $ {v_{i + 1}}\left( {t + 1} \right) = 0. $ | (25) |
式(23) 指车辆与前车间距小于等于以最大速度行驶一个时步的距离, 式(24)、(25) 指前车在该时刻速度大于0, 而在下一时刻速度等于0.当上述3个条件同时满足时, 第i辆车会以一定概率pd与第i+1辆车发生碰撞, 引发交通事故.
2 案例仿真研究根据所建的CA模型进行数值模拟.可以将每一个时步划分为2个子时步:1) 车辆按照换道规则进行换道;2) 车辆按照跟驰规则进行状态更新.
2.1 模型参数定义与设置设每个元胞的大小为0.5 m, 道路长度L=10 000个元胞, 即5 km, 道路上随机分布着空载自卸汽车和满载自卸汽车.其他相关参数值如表 1所示.
| 表 1 元胞自动机模型仿真参数取值 Table 1 Utilized parameter values in cellular automata model |
表 1中参数的取值是根据实际场内的真实数据和部分参考文献, 在实际仿真时, 将am和bm转换成元胞大小进行仿真计算.
定义道路的平均密度为
| $ \rho = \frac{N}{{2L}} = \frac{{{N_{\rm{f}}} + {N_{\rm{e}}}}}{{2L}}. $ | (26) |
式中:N为总车辆数, Nf为满载自卸汽车的数量, Ne为空载自卸汽车的数量.
平均速度定义为
| $ V = \frac{1}{{T - {t_0} + 1}}\sum\limits_{t = {t_0}}^T {\left( {\frac{1}{N}\sum\limits_{i = 1}^N {{v_i}\left( t \right)} } \right)} . $ | (27) |
式中:t0为开始进行数据计算的时间点, T为一次仿真的总时间长度.
平均流量定义为
| $ J = \rho V. $ | (28) |
事故率定义为
| $ {P_{{\rm{ac}}}} = \frac{{{N_{{\rm{ac}}}}}}{N}. $ | (29) |
式中:Nac为发生交通事故的总次数.
模拟时采用周期性边界条件, 每个时步长为1 s, 每次仿真运行1 000个时步(T=1 000).为了消除暂态影响, 取每次仿真最后300个时步的数据进行计算(t0=701);同时为了消除随机性的影响, 取50次仿真数据的平均值作为最后结果.
2.2 交通流模型仿真及验证通过改变道路的纵坡坡度和驾驶员的心理素质水平进行多组仿真, 将仿真得到的密度和平均流量按照实际的单位转换为相应的数值,如图 3所示.然后利用某水电工程施工场内的实际数据, 对交通流模型进行验证.
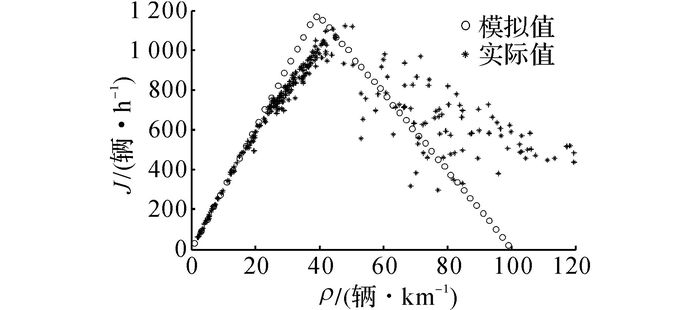
|
图 3 元胞自动机模型仿真结果与实际数据的流量-密度对比图(η=3%, μ1=0.8) Fig. 3 Comparison diagram between simulation of cellular automata model and real data with η=3% and μ1=0.8 |
如图 3所示为其中一组参数下的仿真结果, 图中的流量和密度都转化到了当量小汽车, 在本文中自卸汽车的当量小汽车换算系数是3.0[17].
从图 3可以看出, 该水电工程施工场内道路的交通流大部分处于自由流状态, 因此实际数据大部分集中在低密度和中密度区域, 在高密度区域的实际数据较少, 本文的研究重点主要集中在低密度和中密度区域.
表 2中,Js、Ja分别为仿真平均流量和实际平均流量,ε为相对误差.从表 2可知, 在低密度区域(0~30辆/km), 仿真结果与实际数据非常接近,相对误差都小于5%;在中密度区域(30~50辆/km), 仿真结果比实际结果的值偏大, 当密度为30~40辆/km时, 相对误差为18.79%<20%, 在可接受的范围之内.同时, 实际数据和仿真数据在低密度和中密度区域, 都表现出了流量随密度近似线性增加的趋势, 这种现象符合相关的交通流理论.由于水电工程施工场内道路大部分处于低密度和中密度, 可以认为建立的交通流模型具有可信度.
| 表 2 元胞自动机模型仿真结果误差分析 Table 2 Error analysis of simulation result in cellularautomata |
上述水电工程施工场内的交通流模型具有普适性, 可以根据实际场内的道路情况、车辆性能、驾驶员整体水平等调整模型参数, 使建立的交通流模型适用于相应的施工场地.同时, 该交通流模型对于后期的物料调度优化模型、机械配置优化模型等有重要意义, 因为这些模型的基础是交通流模型.
2.3 事故率与安全距离交通事故在水电工程施工场内时有发生, 并且成为影响施工工期的一个重要因素.实际的交通事故通常是由于驾驶员的粗心或者前车急停造成的.
图 4给出在不同最大速度下事故率Pac与密度ρ的关系.可以看出, 当密度小于临界密度ρc的时候, 几乎不发生交通事故.因为在该密度区域, 车辆之间的间距很大, 即使前车突然停车, 后车也有足够的距离减速, 以避免与前车碰撞.随着密度的增加, 车辆之间的间距减小, 此时若前车突然停车, 则后车很有可能与前车碰撞, 引发交通事故, 这是图 4中事故率上升的原因.在高密度区域, 道路处于堵塞状态, 车辆都以非常低的速度行驶, 在这种情况下, 当后车发现前车突然停车时, 拥有足够的距离进行减速, 因此事故率在该密度区域迅速减小.从图 4可以看出, 随着最大速度的增大, 事故率明显增大.这是因为当最大速度增大时, 车辆会尽可能以更快的速度行驶, 此时当前车突然停车时, 后车没有足够的间距减速.在水电工程施工场内, 进行限速很有必要.
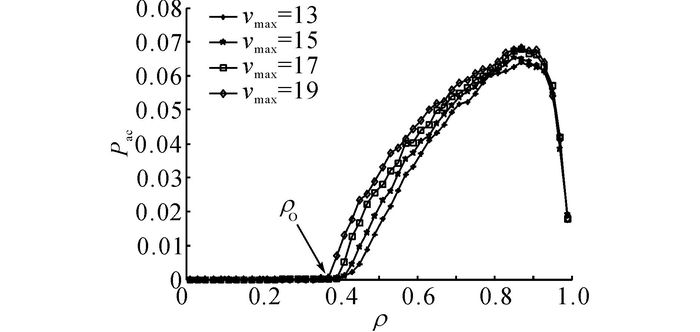
|
图 4 不同最大速度下事故率与密度的关系图(η=3%, μ1=0.8) Fig. 4 Probability of Pac as function of density under various vmax with η=3% and μ1=0.8 |
限速能够从一定程度上降低事故率, 但不能完全杜绝.为了进一步降低事故率, 应该设置安全距离.为了研究车头距与事故率之间的关系, 基于CA模型, 在仿真中统计了在不同车头距下发生交通事故的次数Nac(d), 其中d为车头距;以此为基础, 研究Nac(d)的分布情况.仿真分析分别针对低速(30.6 km/h)和中速(54 km/h)两种情况, 这是因为实际水电工程施工场内车辆的平均速度都较小, 不会出现高速行驶的情况.仿真结果如图 5所示.
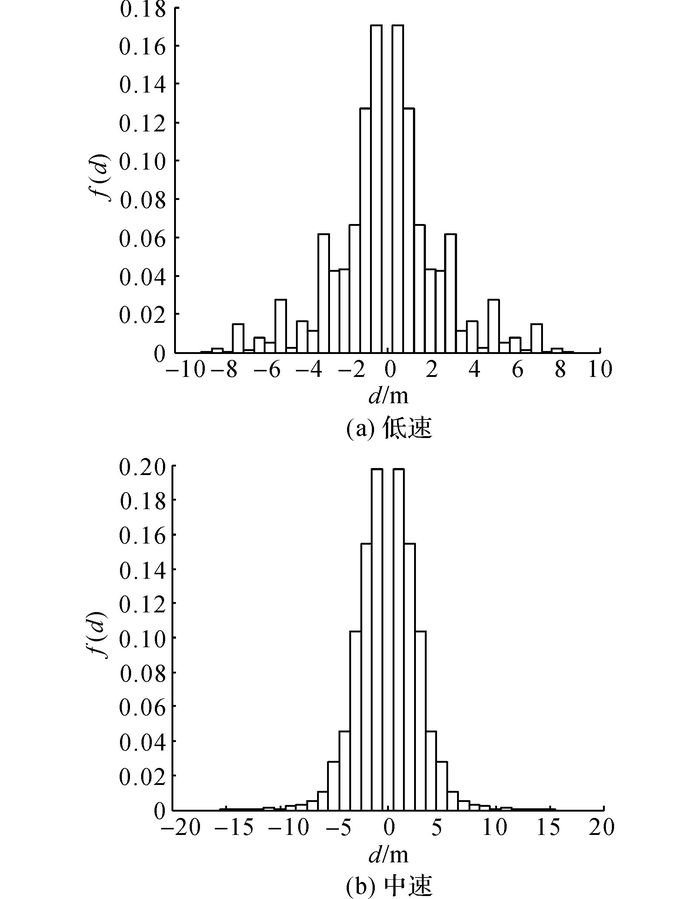
|
图 5 Nac(d)的频率分布直方图 Fig. 5 Probability density histogram of Nac(d) |
图 5中的车头距是有方向的, 定义当前车辆与前车的车头距为正, 当前车辆与后车的车头距为负, 因此每辆车有一正一负两个车头距.根据图 5中低速和中速两种情况的频率分布直方图形状, 利用正态分布的概率密度曲线拟合车头距与事故概率密度之间的关系, 并估计下式的参数:
| $ f\left( x \right) = \frac{1}{{\sqrt {2{\rm{\pi }}} \sigma }}\exp \left[ { - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}} \right]; - \infty < x < + \infty . $ | (30) |
式(30) 为正态分布的概率密度表达式.为了估计其中的参数μ和σ, 建立平方误差损失函数, 利用梯度下降法求解.
| $ {\rm{Loss}} = \frac{1}{{2k}}\sum\limits_{j = 1}^k {{{\left[ {P\left( {{d_j}} \right) - f\left( {{d_j}} \right)} \right]}^2}} . $ | (31) |
式中:k为车头距的个数.
目标函数为
| $ \mathop {\min }\limits_{\mu ,\sigma } {\rm{Loss}}. $ | (32) |
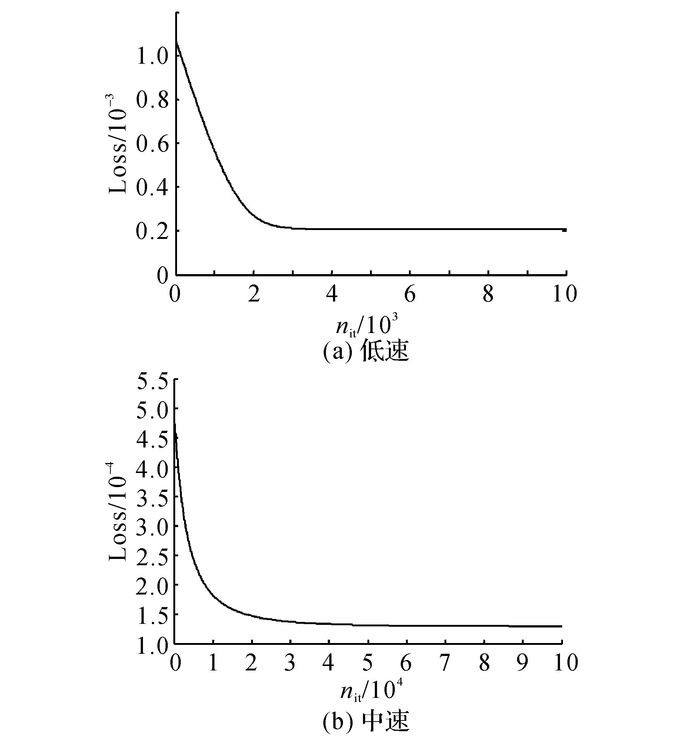
选择合适的初始值、学习率和迭代次数nit, 分别对低速和中速两种情况下的Loss进行迭代计算.迭代过程如图 6所示.
|
图 6 损失函数迭代曲线 Fig. 6 Iteration curve of loss function |
从图 6可得, 在低速情况下迭代3 000次左右已经收敛, 最终计算得到μL=0.01, σL =1.33.在中速情况下, 迭代50 000次左右收敛, 最终计算得到μM=0.02, σM =3.15.为了验证不同车头距下发生交通事故的次数Nac(d)服从正态分布, 利用χ2拟合检验法进行验证.
从表 3可得, χ2=Σfi2/(Nacpi)-Σfi=342.943 4-334=8.943 4.表 3将车头距d分成了5个组, 且有两个未知参数, 因为χ0.012(5-2-1)=9.21>8.943 4, 在置信水平0.01下接受H0, 即可认为在不同车头距下Nac(d)服从正态分布.同理, 对中速情况进行验证, 得到在置信水平0.01下接受H0.
| 表 3 χ2检验计算表(低速) Table 3 Calculation table of chi square test (low speed) |
为了设置合理的安全距离, 尽量避免交通事故的发生, 采用“4σ”法则进行分析.对于低速情况, 车辆的最大速度是8.5 m/s(30.6 km/h), 最大减速度是3 m/s2, 则车辆的最大刹车时间为2.83 s.假设驾驶员的反应时间是1 s, 则整个刹车过程持续的时间为3.83 s, 取整得到为4 s.每一秒都采用“4σ”法则, 则当保持车头距4(μL+4σL)=21.32 m时, 整个刹车过程发生交通事故的可能性为1-(99.993 6%)4=0.026%.当保持安全距离22 m行驶时, 车辆发生交通事故的可能性为0.026%, 这是一个非常小的概率, 可以认为车辆保持这个距离行驶, 几乎不发生事故.在中速情况下进行同样的计算可得, 当车辆保持距离76 m行驶时, 车辆发生交通事故的可能性为0.038%.
在现有的施工场地内, 目前没有具体的车辆安全行驶标准, 无法利用实际数据对计算结果进行验证.现在施工场内的车辆行驶大都遵守《厂矿道路设计规范(GBJ_22-87)》[18], 该规范较粗略地给出车辆在实际行驶时应该保持的距离.规范中给出山岭重丘和平原微丘两种地形、多种行驶速度下的停车视距, 但实际中不同施工场地的道路、车辆等存在差异, 因此该规范具有一定的局限性, 但可以作为研究安全距离时的一种参考.为此, 将上述计算结果与《厂矿道路设计规范(GBJ_22-87)》中的数据进行对比.该规范中规定在山岭重丘地带的厂矿道路, 当行车速度为30 km/h时, 应保持30 m的停车视距;当行车速度为60 km/h时, 应保持75 m的停车视距, 上述数值与本文低速(30.6 km/h)和中速(54 km/h)两种情况下的计算结果在数值上虽有一定偏差, 但在数量级上大致相同, 因此可以认为建立的交通流模型和交通事故模型具有可信度.
在实际的水电工程施工场内, 车辆安全行驶标准必不可少, 否则会大大增加发生交通事故的可能性, 造成重大损失.针对不同施工场地可能存在不同的情况, 需要建立普适性的车辆安全行驶标准.本文的安全距离模型可以根据施工场地的不同情况, 给出具体的安全距离, 对建立普适的车辆安全行驶标准具有重要意义.
3 结语针对水电工程施工场内道路与城市道路存在的差异, 在考虑道路的纵坡坡度以及驾驶员的心理素质差异和车辆性能差异的基础上, 提出适用于水电工程施工场内的交通流模型.利用仿真以及实际水电工程场内的数据对模型进行验证, 结果表明, 所建模型具有可信度.
通过模型与仿真, 研究施工场内影响交通事故的因素, 首次引入场内交通事故发生概率模型.仿真结果表明, 车辆的最大速度越大, 事故率越高, 因此在场内需要有一定限速.通过在低速和中速两种情况下对安全距离的仿真研究与分析, 得到的结果与《厂矿道路设计规范》的数值较接近, 结果可信.
目前建立的水电工程施工场内交通流模型只考虑道路的纵坡坡度, 未来的研究将会考虑道路的曲度、平整度等属性, 建立更加准确的交通流模型.同时, 将研究更多影响交通事故的因素, 提出更完善的场地车辆安全行驶的参考标准.
| [1] | HALPIN D W. CYCLONE-method for modeling job site processes[J]. Journal of the Construction Division, 1977, 103(3): 489–499. |
| [2] | CHANG D Y, CARR R I. RESQUE:a resource oriented simulation system for multiple resource constrained processes[C]//Proceedings of 1987 PMI Seminar/Symposium. Milwaukee:[s. n.], 1987:4-19. |
| [3] | IOANNOU P G. UM-CYCLONE discrete event simulation system user's guide[M]. Ann Arbor, Michigan:[s. n.], 1990. http://www.cem.umich.edu/Ioannou/CYCLONE/userguid.pdf |
| [4] |
钟登华, 李景茹. 复杂地下洞室群施工交通运输系统仿真与优化研究[J].
系统仿真学报, 2002, 14(2): 140–142.
ZHONG Deng-hua, LI Jing-ru. Simulation and optimum for the traffic and transportation system of complex underground structure group[J]. Journal of System Simulation, 2002, 14(2): 140–142. |
| [5] |
陈先明, 肖焕雄. 水利工程施工运输系统元胞自动机模糊仿真模型研究[J].
系统工程理论与实践, 2002, 22(5): 120–124.
CHEN Xian-ming, XIAO Huan-xiong. Study on fuzzy simulation model for hydro-electric engineering transportation with cellular automation[J]. Systems Engineering:Theory and Practice, 2002, 22(5): 120–124. |
| [6] |
杨兴国, 王烈恩, 曹鹏飞, 等. 大型地下洞室群施工交通运输仿真分析[J].
四川大学学报:工程科学版, 2008, 40(2): 49–52.
YANG Xing-guo, WANG Lie-en, CAO Peng-fei, et al. Construction traffic and transport simulation of large-scale underground adits[J]. Journal of Sichuan University:Engineering Science Edition, 2008, 40(2): 49–52. |
| [7] | NAGEL K, SCHRECKENBERG M. A cellular automaton model for freeway traffic[J]. Journal de Physique I, 1992, 2(12): 2221–2229. DOI:10.1051/jp2:1992262 |
| [8] | WOLFRAM D. Statistical mechanics of cellular automata[J]. Reviews of Modern Physics, 1983, 55(3): 601–644. DOI:10.1103/RevModPhys.55.601 |
| [9] | BARLOVIC R, SANTEN L, SCHADSCHNEIDER A, et al. Metastable states in cellular automata for traffic flow[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 1998, 5(3): 793–800. DOI:10.1007/s100510050504 |
| [10] | CHOWDHURY D, WOLF D E, SCHRECKENBERG M. Particle hopping models for two-lane traffic with two kinds of vehicles:effects of lane-changing rules[J]. Physica A:Statistical Mechanics and its Applications, 1997, 235(3/4): 417–439. |
| [11] |
花伟, 林柏梁. 考虑行车状态的一维元胞自动机交通流模型[J].
物理学报, 2005, 54(6): 2595–2599.
HUA Wei, LIN Bo-liang. One-dimensional traffic cellular automaton model with considering the vehicle moving status[J]. Acta Physica Sinica, 2005, 54(6): 2595–2599. DOI:10.7498/aps.54.2595 |
| [12] |
彭莉娟, 康瑞. 考虑驾驶员特性的一维元胞自动机交通流模型[J].
物理学报, 2009, 58(2): 830–835.
PENG Li-juan, KANG Rui. One-dimensional cellular automaton model of traffic flow considering drivers' features[J]. Acta Physica Sinica, 2009, 58(2): 830–835. DOI:10.7498/aps.58.830 |
| [13] |
张柠溪, 祝会兵, 林亨, 等. 考虑动态车间距的一维元胞自动机交通流模型[J].
物理学报, 2015, 64(2): 303–309.
ZHANG Ning-xi, ZHU Hui-bing, LIN Heng, et al. One-dimensional cellular automaton model of traffic flow considering dynamic headway[J]. Acta Physica Sinica, 2015, 64(2): 303–309. |
| [14] | YANG D, QIU X P, YU D, et al. A cellular automata model for car-truck heterogeneous traffic flow considering the car-truck following combination effect[J]. Physica A:Statistical Mechanics and its Applications, 2015, 424: 62–72. DOI:10.1016/j.physa.2014.12.020 |
| [15] |
梁国华, 马荣国, 沈翔, 等. 高速公路爬坡车道设置的有效性[J].
长安大学学报:自然科学版, 2014, 34(1): 23–30.
LIANG Guo-hua, MA Rong-guo, SHEN Xiang, et al. Effectiveness of building climbing lane on expressway[J]. Journal of Chang'an University:Natural Science Edition, 2014, 34(1): 23–30. |
| [16] | BOCCARA N, FUKS H, ZENG Q. Car accidents and number of stopped cars due to road blockage on a one-lane highway[J]. Journal of Physics A:Mathematical and General, 1997, 30(10): 3329–3332. DOI:10.1088/0305-4470/30/10/012 |
| [17] | GB50220-95, 城市道路交通规划设计规范[S]. 北京: 中华人民共和国建设部, 1995. http://www1.planning.org.cn/law/uploads/2013/1384007153.pdf |
| [18] | GBJ 22-87, 厂矿道路设计规范[S]. 北京: 中华人民共和国交通部, 1988. http://www.zys168.net/Upload/DownLoad/DownLoadFile/2010719119674.pdf |



