2. 国网河南省电力公司电力科学研究院 输电线路舞动防治技术重点实验室, 河南 郑州 450052
2. Power Transmission Line Galloping Prevention and Control Technology Laboratory, State Grid Henan Electric Power Research Institute, Zhengzhou 450052, China
我国是输电线路冰灾最严重的国家之一.2008年1月中旬至2月下旬, 我国南方部分省市发生了严重的冰冻雨雪灾害, 对电网造成了极严重的破坏.分析输电线路冰灾的原因, 研究相应的防治措施对电网的安全运行和电力的稳定供应具有重要的意义.
以往对输电线路冰雪灾害的研究主要着重于过载、覆冰闪络、导线的脱冰振动、导线舞动等方面, 忽略了覆冰对导线风偏特性的影响.导线的覆冰形状受线路走向、海拔高度、风速、风向、气温等多种因素的影响, 往往极不规则.肖正直等[1]在结冰风洞中, 研究导线覆冰量及覆冰形状随风速的变化规律发现, 随着风速条件的不同, 导线的覆冰可能呈新月形(准椭圆形)以及扇形(或D形)等典型形状.
非均匀覆冰对导线风偏特性的影响主要体现在以下2个方面:1) 使导线自重增加, 进而改变导线的动力特性;2) 改变导线的截面形状和迎风面积, 使阻力系数发生变化.我国现行输电线路设计规范[2-3]对覆冰导线的阻力系数取单一值, 仅通过引入覆冰风荷载增大系数来考虑线路实际覆冰情况与圆截面标准状况的差异对导线风荷载的影响, 这一规定的合理性值得探讨.
目前, 国内外已有不少关于覆冰导线气动力的试验研究.Keutgen等[4]在风洞内测定典型非对称覆冰导线的气动三分力系数;马文勇等[5]通过刚性模型测压试验, 研究准椭圆形覆冰导线在不同雷诺数下的风压分布规律;张宏雁等[6-8]分别对扇形、新月形和D形等多种覆冰分裂导线的气动力特性及影响因素进行试验研究.上述工作均侧重于研究非均匀覆冰导线的平均气动力特性随风攻角的变化规律, 并将这些规律应用于导线驰振稳定性分析;对于覆冰导线气动力的脉动特性及冰风条件下的风偏响应分析, 现有文献尚无涉及.
本文以D形和新月形两种典型的覆冰导线为对象, 研究冰风工况下的风偏响应.通过刚性模型高频天平测力风洞试验, 测定导线的气动力, 获得两类覆冰导线的气动力系数随风攻角的变化规律, 验证了覆冰导线顺风向脉动风荷载的准定常假定.通过频域计算研究2类覆冰导线的风偏特性, 从覆冰导线的气动力和风偏特性两方面对规范相关规定的合理性进行探究.
1 覆冰导线气动力特性风洞试验该试验按1:1的几何缩尺比采用玻璃钢材料制作导线模型, 导线型号选用LGJ-500/45, 直径d=30 mm.D形覆冰导线模型的几何尺寸和实物如图 1所示, 新月形覆冰导线直径模型的几何尺寸和实物如图 2所示.模型长度L=800 mm.

|
图 1 D形覆冰导线模型的几何尺寸和实物 Fig. 1 Geometric dimensions and real object ofD-shaped iced conductor model |

|
图 2 新月形覆冰导线模型的几何尺寸和实物 Fig. 2 Geometric dimensions and real object of crescent iced conductor model |
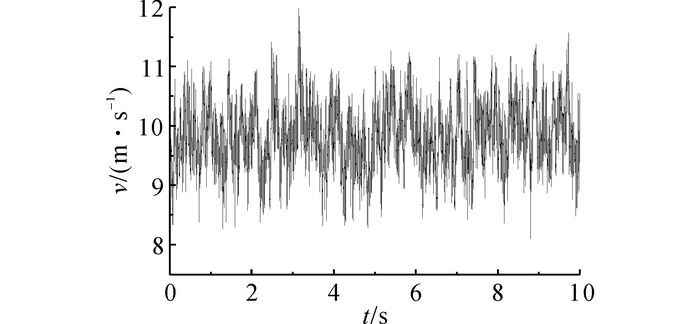
该试验在浙江大学边界层风洞ZD-1中进行, 试验段尺寸为4 m×3 m×18 m.我国输电线路设计规范规定的最不利工况下的覆冰导线设计风速为15 m/s.实际上, 在常见的风速范围内, 导线的雷诺数均处于亚临界范围, 风速变化对导线气动力的影响不大[9], 因此试验平均风速选为10 m/s.采用均匀湍流场, 湍流强度为5%.采用热膜热线风速仪, 测定来流风速时程, 如图 3所示.
|
图 3 均匀湍流场 Fig. 3 Homogeneous turbulent flow |
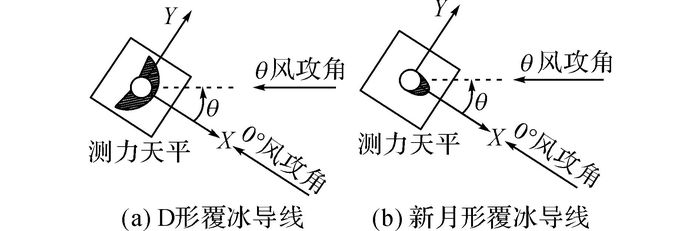
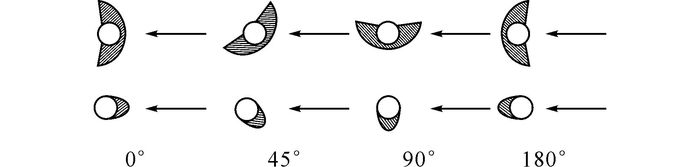
覆冰可能形成于导线截面的不同位置, 从而风攻角不同.导线风攻角的定义如图 4所示.图 5给出几种典型风攻角与覆冰位置的关系.为了全面地研究导线气动力随风攻角的变化情况, 试验风攻角范围选为0°~180°, 间隔为5°.
|
图 4 风攻角的定义 Fig. 4 Definition of wind attack angle |
|
图 5 典型风攻角与覆冰位置的关系 Fig. 5 Relationships between typical wind attack angles and ice accretion positions |
高频测力天平的采样频率为500 Hz, 每一工况的采样时间均为30 s.试验装置如图 6所示.

|
图 6 导线气动力试验装置 Fig. 6 Experimental setup for test of conductor aerodynamic forces |
我国规范计算导线风荷载时, 将覆冰导线截面等效为圆截面, 根据覆冰面积相等的原则来确定覆冰导线的等效直径.为了便于与规范进行对比, 将覆冰导线的气动力系数定义为
| ${C_\alpha } = \frac{{\overline {{F_\alpha }} }}{{\frac{1}{2}\rho {{\bar V}^2}L{d_{{\rm{eq}}}}}};\alpha = {\rm{D,L}}.$ | (1) |
式中:
| 表 1 覆冰导线模型的基本参数 Table 1 Basic parameters of iced conductor models |
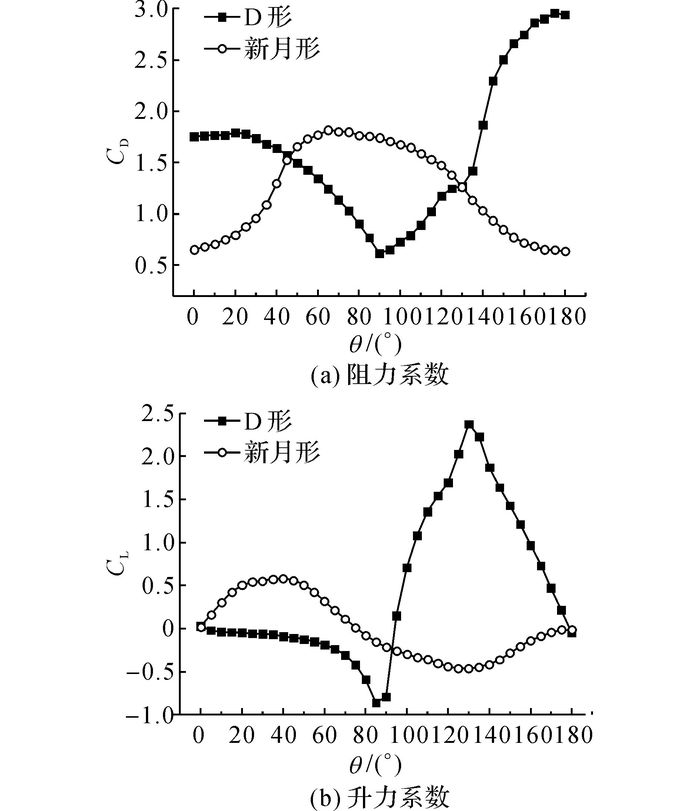
通过该试验测得的2类覆冰导线在各风攻角θ下的阻力系数和升力系数如图 7所示. D形覆冰导线的阻力系数为0.62~2.94, 新月形覆冰导线的阻力系数为0.63~1.82.可见, 覆冰导线阻力系数与覆冰形状、风攻角有关, 变化范围很大.我国规范对覆冰导线阻力系数统一取1.2, 对于D形覆冰导线70°~120°以及新月形导线0°~35°、135°~180°风攻角工况, 规范阻力系数取值偏大;对于2类覆冰导线的其他风攻角工况, 规范取值偏小.由于导线截面形状的非均匀性, 大多数风攻角下, 2类覆冰导线的升力平均值均不为0;我国规范将覆冰导线等效成均匀圆截面, 未考虑升力.
|
图 7 不同风攻角下的覆冰导线气动力系数 Fig. 7 Aerodynamic coefficients of iced conductors at different wind attack angles |
当结构顺风向风荷载的脉动主要受来流湍流的影响时, 由准定常假定[10]可知,
| ${S_{\rm{p}}}\left( f \right) = {f^2}C_{\rm{D}}^2{{\bar V}^2}{S_{\rm{v}}}\left( f \right).$ | (2) |
式中: SP(f)为单位面积上的顺风向脉动风荷载谱, Sv(f)为脉动风速谱.
对于裸导线而言, 准定常假定的适用性已得到认可[11].非均匀覆冰的存在可能会使导线的气动力特性发生变化, 准定常假定的适用性尚需验证.
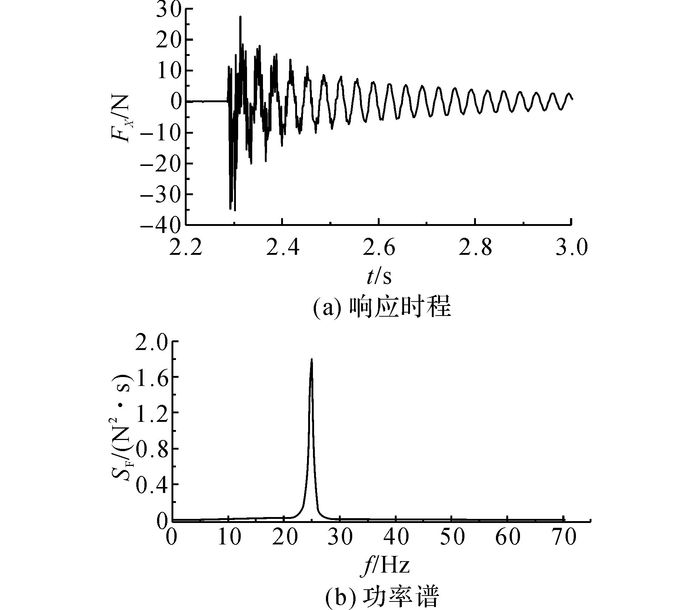
利用高频天平可以测得模型底部的顺风向合力时程, 由于选材的局限性, 试验模型1阶自振频率处于荷载谱的频带内, 共振效应非常明显.利用天平测得的合力时程不仅包含风荷载成分, 而且包含模型振动的惯性力成分.在研究导线气动力的脉动特性前, 需要对测力结果进行频响修正.通过锤击法标定模型-天平系统的自振频率, 图 8给出锤击激励下模型的响应时程及功率谱.可以看出, 模型-天平系统的1阶自振频率为24.97 Hz.
|
图 8 锤击法识别模型-天平系统自振频率 Fig. 8 Identification of natural frequency of model-balance system with hammer excitation method |
采用吴承卉等[12]提出的修正方法, 在频域内对试验数据进行1阶共振效应消除, 计算公式为
| ${S_{{F_{\rm{D}}}}}\left( \omega \right){\rm{ = }}\frac{{S_{{F_{\rm{D}}}}^*\left( \omega \right)}}{{1 + {{\left| {{H_1}\left( \omega \right)} \right|}^2}\left( {{\omega ^4} + 4\zeta _1^2\omega _1^2{\omega ^2}} \right)}}.$ | (3) |
式中:SFD*(ω)为利用高频测力天平测得的底部顺风向合力功率谱; SFD(ω)为修正后的导线顺风向脉动风荷载谱; H1(ω)为模型顺风向1阶振型的频响函数; ω1和ζ1分别为1阶自振角频率和阻尼比.
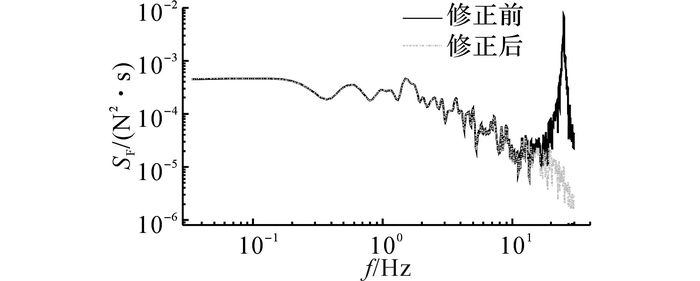
图 9给出修正前、后的新月形覆冰导线模型荷载谱对比.可以看出, 处理前的荷载谱在1阶自振频率处有一明显的共振峰, 可以采用式(3) 进行有效的修正.
|
图 9 修正前、后的新月形覆冰导线模型荷载谱对比 Fig. 9 Comparison between power spectral densities of crescent iced conductor model before and after correction |
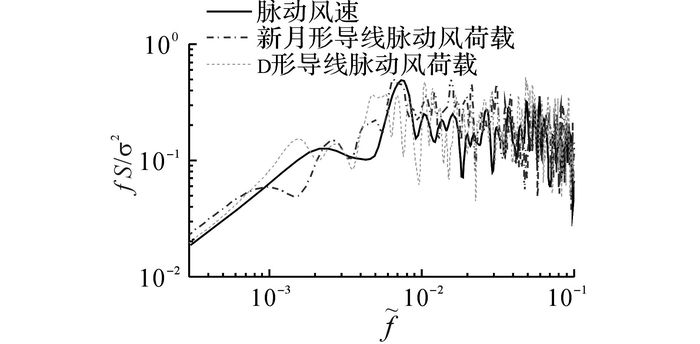
通过风洞试验测得的脉动风速以及2类覆冰导线模型脉动风荷载的归一化功率谱对比如图 10所示.图中,
|
图 10 归一化脉动风速谱和荷载谱对比 Fig. 10 Comparison between power spectral densities of normalized fluctuating wind speed and wind loads |
我国输电线路设计规范对覆冰导线阻力系数取单一值, 仅通过引入覆冰风荷载增大系数来考虑线路实际覆冰情况对导线风荷载的影响, 计算方法过于简化;采用静力方法计算导线风偏响应, 可能会引起较大误差, 有必要采用动力方法精确计算覆冰导线的风偏响应, 以验证规范方法的合理性.
现有文献大多采用时域法[13-14]计算导线风偏, 可以得到具体的风偏响应时程, 计算精确, 表达直观, 但耗时较长.由于导线是1种具有大变形特性的几何非线性结构, 无法直接采用频域法求解导线的动力风偏响应.为此, 可以将导线在自重和平均风荷载作用下的静力平衡形态作为初始计算条件, 受脉动风荷载作用而产生的位移可以视为小变形[15], 从而满足频域法的适用条件.本文分别采用频域法与基于规范荷载的静力方法对2类覆冰导线的风偏响应进行计算.
3.1 频域法通过有限元非线性静力分析, 获得导线的静力平衡构型, 同时得到导线的平均风偏位移响应.对静力平衡形态下的导线进行模态分析, 得到各阶自振频率和振型, 即可以通过振型分解法在频域内计算导线的风偏响应的脉动部分.采用完全二次方结合法(complete quadratic combination, CQC), 计算导线风偏脉动位移响应均方值:
| $\sigma _{ui}^2 = \sum\limits_{k = 1}^N {\sum\limits_{l = 1}^N {{\phi _{ik}}{\phi _{il}}} } {\mathop{\rm Re}\nolimits} \left[ {\int_0^\infty {{S_{{q_k}{q_l}}}\left( f \right){\rm{d}}f} } \right].$ | (4) |
式中:N为参与计算的振型阶数,
| ${S_{{q_k}{q_l}}}\left( f \right) = H_k^*\left( f \right){H_l}\left( f \right){S_{{Q_k}{Q_l}}}\left( f \right).$ | (5) |
其中, Hk(f)为第k阶机械导纳函数, Hk*(f)为相应的复共轭; SQkQl(f)和Sqkql(f)分别为第k、l阶广义荷载和广义响应的互功率谱,
| ${S_{{Q_k}{Q_l}}}\left( f \right) = \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^M {{\phi _{ik}}{\phi _{il}}\sqrt {{S_{{f_i}}}\left( f \right){S_{{f_j}}}\left( f \right)} {\rm{Co}}{{\rm{h}}_{ij}}} } \left( f \right).$ | (6) |
M为导线模型质点总数, Sfi(f)为导线i位置的脉动风荷载谱, 由准定常假定, 有
| ${S_{{f_i}}}\left( f \right) = {\rho ^2}C_{\rm{D}}^2{d^2}L_i^2\bar V_i^2{S_{{v_i}}}\left( f \right).$ | (7) |
式中: Svi(f)为导线i位置的脉动风速谱.
导线上各位置的峰值位移响应为
| ${U_{i,\max }} = {{\bar U}_i} + g{\sigma _{ui}}.$ | (8) |
式中: Ui为通过非线性静力分析得到的导线i位置的平均位移;g为响应的峰值因子, 我国荷载规范[16]取g=2.5.
3.2 基于规范荷载的静力方法我国规范将覆冰导线截面等效为圆截面, 认为覆冰厚度是均匀的, 并引入覆冰风荷载增大系数来考虑覆冰形状不规则导致的风荷载增大.按规范方法计算得到的导线i位置的风荷载为
| ${F_i} = \frac{1}{2}\rho \bar V_i^2{C_{\rm{D}}}{d_{{\rm{eq}}}}{L_i}B.$ | (9) |
式中: Vi为导线i位置所在高度的平均风速, deq为覆冰导线的等效直径, Li为导线i位置的控制长度, B为覆冰风荷载增大系数.
规范给出的风荷载是静力荷载, 将式(9) 的风荷载施加于有限元模型, 通过非线性静力分析得到导线的风偏响应.
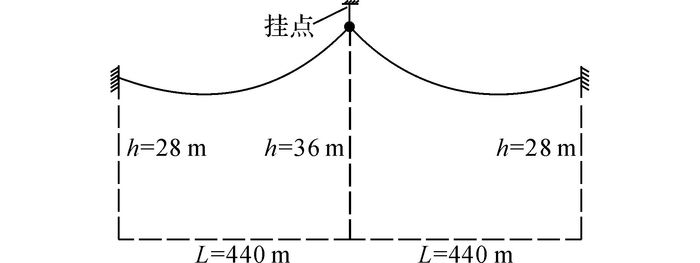
4 风偏响应计算实例 4.1 线路模型及荷载某500 kV输电线路2跨耐张段所在场地的粗糙度类别为B类, 线路两端为耐张塔, 中间为直线塔, 基本的几何参数如图 11所示.线路所采用的导线型号为LGJ-500/45, 裸导线的主要物理参数如下:计算截面为531.68 mm2, 外径为30.00 mm, 弹性模量为65 GPa, 线密度为1 688 kg/km, 年运行张力为32.03 kN.悬垂绝缘子串型号为FXBW-500/180, 主要的物理参数如下:长度为5 m, 质量为34 kg, 弹性模量为30 GPa, 泊松比为0.3.
|
图 11 计算线路的几何参数 Fig. 11 Geometric parameters of calculation line |
利用大型通用有限元分析软件ANSYS, 建立多跨导线与绝缘子串的有限元模型.导线单元类型选用三维仅受拉杆单元LINK10, 绝缘子串选用三维杆单元LINK8.整个耐张段共划分91个单元.建模时, 考虑覆冰引起的导线自重增加, 覆冰密度取900 kg/m3.由于导线覆冰的密实度通常不高, 沈国辉等[17]认为导线覆冰的弹性模量不超过100 MPa, 远远小于导线的弹性模量, 忽略覆冰对导线轴向刚度的影响.
为了对比裸导线和覆冰导线的风偏特性, 分别对两者进行验算.对于裸导线, 我国规范规定风偏验算所采用的10 m高度平均风速v0为27 m/s;对于覆冰导线, 考虑到覆冰和大风同时出现的概率很小, 规范规定最不利工况下v0取15 m/s, 本文取该值进行计算.风向垂直于导线档距方向.脉动风速谱采用修正的Davenport谱[18], 采用Davenport经验公式[19]考虑脉动风荷载的空间相关性.导线不同高度处的平均风速以及脉动风速均方根按我国荷载规范给出的平均风速剖面以及湍流强度剖面确定.
为了比较频域法与规范方法的计算结果, 分别采用2种方法对覆冰导线进行计算.当采用规范方法计算时, 根据表 1可知, 将D形覆冰导线等效为deq=52.12 mm的圆截面导线, 新月形覆冰导线等效为deq=36.73 mm的圆截面导线.
在频域法计算中, 覆冰导线的阻力系数按本文试验结果进行取值.升力对覆冰导线风偏响应有一定的影响, 由图 7可知, 在2类覆冰导线的风偏最不利风攻角(即阻力系数最大的攻角)下, 相应的升力系数绝对值均较小, 对风偏响应的影响不大.本文算例暂不考虑覆冰导线的升力.裸导线阻力系数参考文献[20], 取1.05.在规范方法计算中, 导线阻力系数CD及覆冰风荷载增大系数B均按规范规定进行取值.根据覆冰量, 对于52.12 mm规范覆冰导线, 取B=1.3;对于36.73 mm规范覆冰导线, 取B=1.1.
该算例的计算工况如表 2所示.工况3、4为规范方法静力计算, 工况1、2、5为频域法动力计算.在动力计算中, 导线的气动阻尼效应不可忽略.采用文献[11]的推荐方法, 以等效附加阻尼比ζa的形式进行考虑.导线自身结构阻尼比ζs取0.005.
| 表 2 导线风偏响应计算工况 Table 2 Calculation cases of wind-induced conductor swing response |
覆冰导线的动力特性受覆冰重量、覆冰形状及风攻角等多种因素的影响.一方面, 覆冰会导致导线的质量增加, 使导线的自振频率减小; 另一方面, 导线在荷载作用下会产生几何刚度, 使自振频率增大, 覆冰的形状以及风攻角的改变会引起导线自重荷载以及风荷载的变化.不同计算工况下, 覆冰导线的动力特性是不同的. 表 3给出0°和90°风攻角工况下D形和新月形覆冰导线在自重与平均风荷载作用平衡形态下的前7阶自振频率和振型.表中, n为振型阶数, f0为自振频率.可以看出, 两类覆冰的导线自振频率不同.由于D形覆冰导线的覆冰重量远大于新月形导线, 两个风攻角下D形覆冰导线的自振频率均明显低于新月形导线.对于同一类覆冰导线, 不同风攻角下导线的阻力系数不同, 所受的风荷载不同, 故自振频率略有差异.
| 表 3 D形、新月形覆冰导线自振频率和振型 Table 3 Natural frequencies and mode shapes of D-shaped and crescent iced conductors |
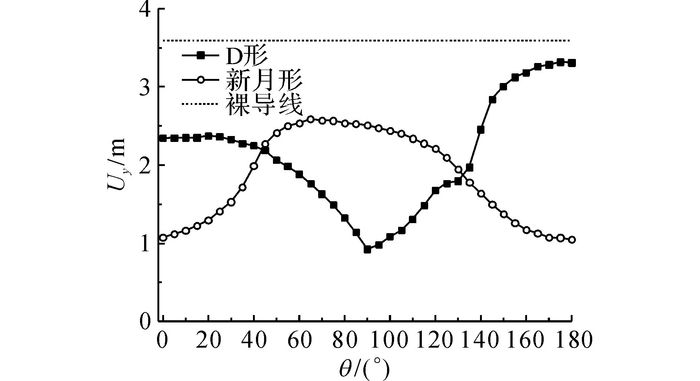
在风偏计算中, 应重点考察悬垂绝缘子串的位移.图 12给出采用频域法计算得到的大风工况下裸导线以及各风攻角工况下的D形和新月形覆冰导线悬垂绝缘子串处的顺风向风偏峰值响应Uy的对比.可以看出, 新月形覆冰导线各风攻角工况下的风偏响应均明显小于裸导线, 这是因为覆冰导线风偏验算基本风速较小, 且新月形导线各风攻角下的阻力系数均不大.虽然D形覆冰导线的质量大于裸导线, 且验算风速比裸导线低得多, 但由于阻力系数较大, 某些风攻角工况下的风偏响应已经接近大风工况下的裸导线.
|
图 12 裸导线与覆冰导线的绝缘子串风偏响应 Fig. 12 Wind-induced responses of suspended insulator strings between bare conductors and iced conductors |
考虑几种典型的风攻角情形, 如表 4所示.可以看出, 当覆冰存在于导线的背风面, 即风攻角约为180°时, D形覆冰导线悬垂绝缘子串处的风偏位移达到最大, 接近大风工况下的裸导线.由此可以推断, 在极端冰风条件下, 风速很可能大于规范规定的验算风速, 此时比裸导线大风工况更不利.考虑到线路存在覆冰时绝缘子串的绝缘性能降低, 覆冰导线将更容易发生风偏闪络事故.建议重视冰风条件下的风偏验算.
| 表 4 典型风攻角下D形覆冰导线与裸导线风偏响应对比 Table 4 Comparison between wind-induced responses ofD-shaped iced conductors at typical wind attack angles and bare conductors |
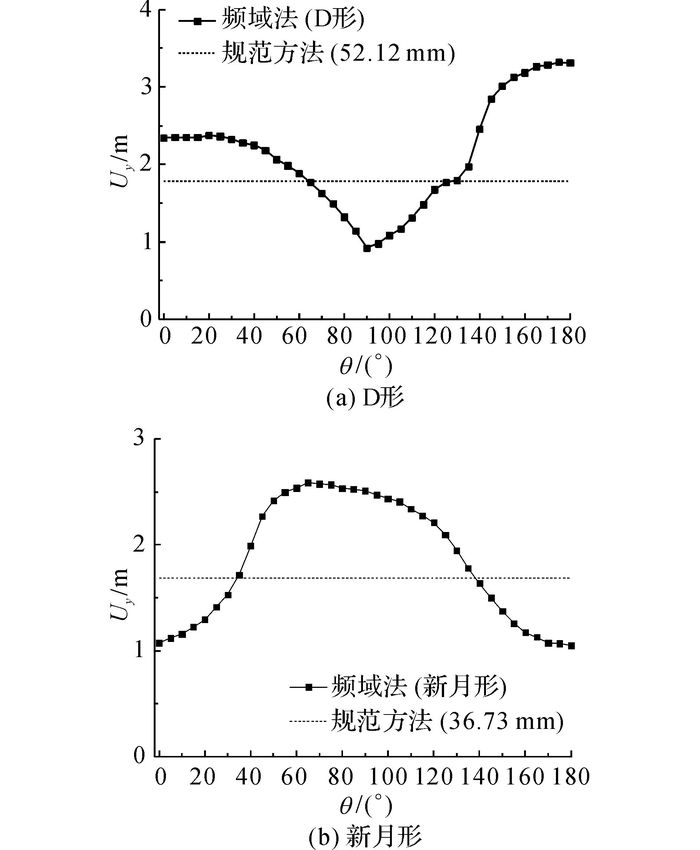
以悬垂绝缘子串处的位移作为考察对象, 利用频域法与规范方法计算得到的2类覆冰导线顺风向风偏峰值响应Uy的对比如图 13所示.对于D形导线, 当风攻角约为90°时, 规范计算结果偏大;当风攻角约为0°~45°或180°时, 规范方法计算结果偏小.对于新月形导线, 当风攻角约为0°或180°时, 规范计算结果偏大;当风攻角约为45°或90°时, 规范计算结果偏小.可见, 不同覆冰形状、不同风攻角工况下导线的风偏响应差异很大, 我国规范对覆冰导线的阻力系数取单一值, 仅通过覆冰风荷载增大系数来考虑覆冰量的影响, 这样的做法是欠妥的.总体来说, 采用规范风荷载来计算覆冰导线风偏不能得到较精确的结果.
|
图 13 覆冰导线风偏峰值响应频域法与规范方法计算结果对比 Fig. 13 Comparisons of wind-induced peak responses of iced conductors calculated with frequency-domain method and code method |
(1) 覆冰导线的气动力与覆冰形状、风攻角有关, 我国规范对覆冰导线阻力系数取单一值.对于D形覆冰导线以及新月形覆冰导线的个别工况, 规范阻力系数取值偏小; 对于新月形覆冰导线的大部分工况, 规范取值偏大.
(2) D形和新月形覆冰导线顺风向风荷载的脉动以来流湍流为主, 准定常假定是适用的.
(3) D形覆冰导线在某些风攻角、15 m/s风速工况下的风偏响应已接近大风工况下裸导线的风偏.在极端冰风条件下, 风速很可能大于规范规定的验算风速, 此时比裸导线大风工况更不利;考虑到覆冰会使绝缘子串的绝缘性能降低, 覆冰导线将更容易发生风偏闪络事故.建议重视冰风条件下的风偏验算.
(4) 覆冰导线的风偏响应受覆冰形状、风攻角等因素的影响, 我国规范计算风荷载时未能全面地考虑这些因素, 采用规范风荷载按静力方法计算得到的覆冰导线风偏响应在大多数工况下偏小.
| [1] |
肖正直, 晏致涛, 李正良, 等. 八分裂输电导线结冰风洞及气动力特性试验[J].
电网技术, 2009, 33(5): 90–94.
XIAO Zheng-zhi, YAN Zhi-tao, LI Zheng-liang, et al. Wind tunnel and aerodynamic characteristics tests for ice-covering of transmission line adopting 8-bundled conductor[J]. Power System Technology, 2009, 33(5): 90–94. |
| [2] | GB 50545-2010. 110kV~750kV架空输电线路设计规范[S]. 北京: 中国计划出版社, 2010: 31-32. |
| [3] | DL/T 5154-2012, 架空输电线路杆塔结构设计技术规定[S]. 北京: 中国计划出版社, 2012: 18-19. |
| [4] | KEUTGEN R, LILIEN J. Benchmark cases for galloping with results obtained from wind tunnel facilities-validation of a finite element model[J]. IEEE Transactions on Power Delivery, 2000, 15(1): 367–374. DOI:10.1109/61.847275 |
| [5] |
马文勇, 顾明, 全涌, 等. 准椭圆形覆冰导线气动力特性试验研究[J].
同济大学学报:自然科学版, 2010, 38(10): 1409–1413.
MA Wen-yong, GU Ming, QUAN Yong, et al. Testing study on aerodynamic force characteristics of quasi-oval shape iced conductor[J]. Journal of Tongji University:Natural Science, 2010, 38(10): 1409–1413. |
| [6] |
张宏雁, 严波, 周松, 等. 覆冰四分裂导线静态气动力特性试验[J].
空气动力学学报, 2011, 29(2): 150–154.
ZHANG Hong-yan, YAN Bo, ZHOU Song, et al. Static test on aerodynamic characteristics of iced quad bundled conductors[J]. Acta Aerodynamica Sinica, 2011, 29(2): 150–154. |
| [7] |
林巍. 覆冰输电导线气动力特性风洞试验及数值模拟研究[D]. 杭州: 浙江大学, 2012.
LIN Wei. Wind tunnel test and numerical simulation study on aerodynamic characteristics of iced transmission lines[D]. Hangzhou:Zhejiang University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10335-1012310568.htm |
| [8] | LOU W, LV J, HUANG M F, et al. Aerodynamic force characteristics and galloping analysis of iced bundled conductors[J]. Wind and Structures, 2014, 18(2): 135–154. DOI:10.12989/was.2014.18.2.135 |
| [9] | CHABART O, LILIEN J L. Galloping of electrical lines in wind tunnel facilities[J]. Journal of Wind Engineering and Industrial Aerodynam ̄ics, 1998, 74(6): 967–976. |
| [10] | DAVENPORT A G. The application of statistical concepts to the wind loading of structures[J]. Proceedings of the Institution of Civil Engineers, 1961, 19(4): 449–472. DOI:10.1680/iicep.1961.11304 |
| [11] | LOREDO-SOUZA A M. The behavior of transmission lines under high winds[D]. London:The University of Western Ontario, 1996. http://ir.lib.uwo.ca/cgi/viewcontent.cgi?article=3649&context=digitizedtheses |
| [12] |
吴承卉, 黄铭枫, 姜雄, 等. 基于半刚性模型风洞试验的锅炉塔架风振分析[J].
空气动力学学报, 2015, 33(3): 353–359.
WU Cheng-hui, HUANG Ming-feng, JIANG Xiong, et al. Wind-induced vibration analysis of lattice-truss tower installed with a boiler based on semi-rigid model test[J]. Acta Aerodynam ̄ica Sinica, 2015, 33(3): 353–359. |
| [13] |
刘小会, 严波, 林雪松, 等. 500kV超高压输电线路风偏数值模拟研究[J].
工程力学, 2009, 26(1): 244–249.
LIU Xiao-hui, YAN Bo, LIN Xue-song, et al. Numerical simulation of windage yaw of 500kV UHV transmission lines[J]. Engineering Me ̄chanics, 2009, 26(1): 244–249. |
| [14] |
李黎, 肖林海, 罗先国, 等. 特高压绝缘子串的风偏计算方法[J].
高电压技术, 2013, 39(12): 2924–2932.
LI Li, XIAO Lin-hai, LUO Xian-guo, et al. Windage yaw calculation method of UHV insu ̄lator strings[J]. High Voltage Engineering, 2013, 39(12): 2924–2932. DOI:10.3969/j.issn.1003-6520.2013.12.013 |
| [15] | ABOSHOSHA H, DAMATTY A E. Dynamic response of transmission line conductors under downburst and synoptic winds[J]. Wind and Structures, 2015, 21(2): 241–272. DOI:10.12989/was.2015.21.2.241 |
| [16] | GB 50009-2012, 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012: 58. |
| [17] |
沈国辉, 徐晓斌, 楼文娟, 等. 导线覆冰脱冰有限元模拟方法的适用性分析[J].
工程力学, 2011, 28(10): 9–15.
SHEN Guo-hui, XU Xiao-bin, LOU Wen-juan, et al. Applicability analysis of finite element methodologies to simulate the ice-accreting and ice-shedding on transmission lines[J]. Engineering Mechanics, 2011, 28(10): 9–15. |
| [18] |
楼文娟, 杨悦, 吕中宾, 等. 考虑气动阻尼效应的输电线路风偏动态分析方法[J].
振动与冲击, 2015, 34(6): 24–29.
LOU Wen-juan, YANG Yue, LV Zhong-bin, et al. Windage yaw dynamic analysis methods for transmission lines considering aerodynamic damping effect[J]. Journal of Vibration and Shock, 2015, 34(6): 24–29. |
| [19] | SIMIU E, SCANLAN R H. Wind effects on structures[M]. 2nd ed. New York: Wiley, 1986. |
| [20] |
楼文娟, 李天昊, 吕中宾, 等. 多分裂子导线气动力系数风洞试验研究[J].
空气动力学学报, 2015, 33(6): 787–792.
LOU Wen-juan, LI Tian-hao, LV Zhong-bin, et al. Wind tunnel test on aerodynamic coefficients of multi-bundled sub-conductors[J]. Acta Aerodynamica Sinica, 2015, 33(6): 787–792. |