管片拼装机是盾构机中关键的一部分, 负责管片的拼装工作.在盾构施工过程中, 随着盾构机的开挖、推进和出碴, 挖好的隧道需要用预先制好的混凝土管片进行永久性支护, 管片拼装机负责将管片准确地安装到刚开挖的隧道表面, 用6~8个管片组成衬砌环来实现支护[1-3].从单环管片拼装角度分析可知, 通常完成该环管片的拼装耗时大于完成该环管片的推进耗时[4].研究管片拼装机回转系统高速工作可以大大提高盾构施工的效率, 具有极大的工程意义.
管片拼装机回转系统具有管片质量大、回转半径大且回转角度大的特点, 导致转动惯量大且负载力矩大, 系统在启动阶段存在很大的冲击力矩, 不易进行控制.目前在用的管片拼装机回转系统的最大回转速度为1.5 r/min, 采用开环控制, 手动调整回转角度, 控制精度低且冲击较大.Shi等[5]研究管片拼装机回转系统的速度闭环控制, 分析不同控制信号对系统冲击的影响发现, 当给定信号为半正弦波信号时, 启动冲击较平滑;Wang等[6]对管片拼装机回转系统进行闭环控制分析, 分别研究速度控制和位置控制2种控制方式, 发现速度和位置复合控制的效果较好, 可以实现较高的控制精度和较小的冲击力矩, 最大转速可达4.73 r/min.杨旭等[7]对直径为2 m的管片拼装机进行设计研究发现, 最大转速达到6.25 r/min, 但没有研究分析其中的系统冲击情况.
已有的研究成果或是研究如何降低当前转速下的冲击力矩, 或是致力于提高转速而忽略了系统冲击, 未能在大幅提高转速的前提下减小冲击力矩.为了解决该问题, 本文设计采用蓄能器回路变速积分控制的方法, 利用变速积分闭环控制的控制策略对系统速度进行控制, 利用蓄能器对系统回路进行改进.通过AMESim软件搭建系统模型, 并与实验结果进行对比, 发现一致性较好;对仿真模型参数进行分析设计, 使系统最大转速可以达到6 r/min, 且冲击力矩小于当前采用的转速为1.5 r/min的系统, 为进一步将该系统运用到盾构管片拼装机中提供一定的理论支撑.
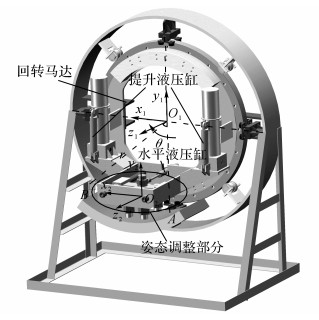
1 管片拼装机回转系统工作原理 1.1 回转机构为了实现管片的拼装功能, 管片必须能够进行6个方向的运动, 如图 1所示, 即:z1方向直线运动(沿隧道轴线)、y1方向直线运动(隧道断面方向)、绕z1轴回转运动(绕隧道轴线)以及实现管片姿态调整的3个方向的运动(分别绕x2、y2、z2方向的回转运动).与管片运动相对应, 管片拼装机能够实现6个方向的运动, 分别由比例方向阀控制液压马达或液压缸实现.
|
图 1 管片拼装机结构及运动示意图 Fig. 1 Schematic diagram of structure and movementabout segment erector |
回转机构由液压马达、减速器、回转支承等零部件组成.液压马达与减速器一体, 回转架通过回转轴承安装在移动架上, 液压马达动力经过减速器, 通过齿轮啮合, 将动力传至回转架, 驱动回转架进行周向回转, 即图 1中绕z1轴进行回转运动.相较其余几个自由度的运动, 回转机构运动行程长、速度低, 是限制管片拼装速度的主要原因.本文主要研究回转运动的控制方法, 该方法可以应用于平移和提升系统.
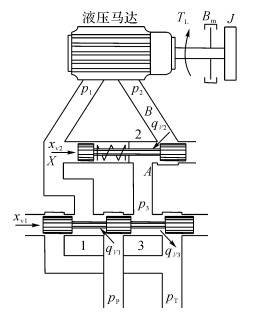
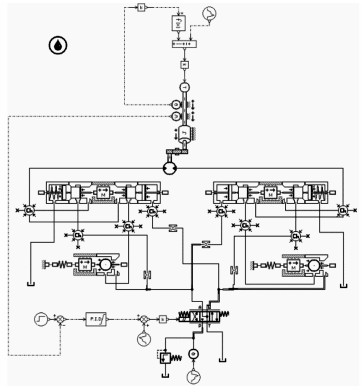
1.2 电液控制系统管片拼装机回转系统的液压原理图如图 2所示, 比例方向阀1控制系统进油量及进油方向, 进而控制液压马达5的转速及转向.平衡阀2用来保证马达转动的平稳性, 确保在超越负载下系统不会失稳.溢流阀4起保护系统的作用, 在负载过大时及时卸油防止系统憋坏.通过压力表 3对系统压力进行实时监控.

|
图 2 管片拼装机回转系统的液压原理图 Fig. 2 Schematic diagram of hydraulic about rotary system in segment erector |
| 表 3 新系统与旧系统动态特性对照表 Table 3 Comparison of dynamic behaviours between new and old systems |
为了开展管片拼装机运动学和动力学分析, 建立如图 1所示的坐标系.回转运动圆心为O1, 设位置A为坐标原点, 管片顺时针旋转, 则位置B的坐标为θ.管片在运动过程中负载随着回转角度变化, 忽略摩擦较小因素的影响, 负载的变化规律为
| $ T = Mgr\sin \theta = {T_{\max }}\sin \theta . $ | (1) |
式中:M为回转系统的质量;g为重力加速度, g=9.8 m/s2;r为回转机构重心至回转运动圆心的距离;θ为管片拼装机回转机构转动角度, -200°≤θ≤+200°;Tmax为回转系统的最大驱动力矩.
管片拼装机回转系统的转动惯量很大, 在运动状态发生改变时会产生很大的冲击载荷.过大的冲击载荷会严重影响管片拼装机的寿命和系统的可靠性, 故管片拼装机回转系统的冲击载荷是一项重要的系统评价指标.
若将系统原点选为0势能参考点, 则管片拼装机回转运动的拉格朗日函数为
| $ L = {E_{\rm{k}}} - {E_{\rm{p}}} = \frac{1}{2}J\dot \theta - Mgr\cos \theta . $ | (2) |
式中:Ek和Ep分别为系统的总动能和总势能, J为回转系统的转动惯量.
管片拼装机回转运动的关节力矩可以表示为
| $ T = \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial \dot \theta }}} \right) - \frac{{\partial L}}{{\partial \theta }} = J\ddot \theta - Mgr\sin \theta . $ | (3) |
冲击力矩为
| $ {\mathit{T}_1} = J\ddot \theta . $ | (4) |
如图 3所示为根据图 2作出的管片拼装机回转电液控制系统的功能简图, 平衡阀中液压油从A端到B端可以自由通过, 但是从B端到A端需要X端的压力油将平衡阀口打开, 平衡阀开口大小受X端压力的影响.由于中位机能不影响方向阀的数学模型, 现以中位机能为O型机能的比例方向阀建立数学模型.图 3中, 比例方向阀为0开口四边滑阀, 系统供油压力为pP, 回油压力为pT, 液压马达进油口压力为p1, 回油口压力为p2, 平衡阀另一工作油口压力为p3.在下文分析中, 设p1为高压油, p2为低压油.
|
图 3 管片拼装机回转系统功能简图 Fig. 3 Function diagram of rotary system about segment erector |
节流口1的体积流量[8]为
| $ {q_{V1}} = {C_{{\rm{d}}1}}{A_1}\sqrt {\frac{{2\left( {{p_{\rm{P}}} - {p_1}} \right)}}{\rho }} . $ | (5) |
式中:Cd1为比例方向阀节流口流量系数, A1为节流口1的开口面积, ρ为液压油密度.
比例方向阀节流口3的体积流量为
| $ {q_{V3}} = {C_{{\rm{d}}1}}{A_1}\sqrt {\frac{{2\left( {{p_{\rm{3}}} - {p_{\rm{T}}}} \right)}}{\rho }} . $ | (6) |
忽略平衡阀阀芯运动对系统流量的影响, 马达高压腔的体积流量连续性方程为
| $ {q_{V1}} = {D_{\rm{m}}}\frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}} + {C_{{\rm{ip}}}}\left( {{p_1} - {p_2}} \right) + {C_{{\rm{ep}}}}{p_1} + \frac{{{V_1}}}{{{\beta _{\rm{e}}}}}\frac{{{\rm{d}}{p_1}}}{{{\rm{d}}t}}. $ | (7) |
式中:Dm为液压马达的排量, φ为液压马达转角, Cip为液压马达内泄漏系数, Cep为液压马达外泄漏系数, V1为液压马达进油腔的容积, βe为等效体积弹性模量.
平衡阀中油液从B到A的体积流量为
| $ {q_{V2}} = {C_{{\rm{d}}2}}{A_2}\sqrt {\frac{{2\left( {{p_{\rm{2}}} - {p_{\rm{3}}}} \right)}}{\rho }} . $ | (8) |
式中:Cd2为平衡阀节流口流量系数, A2为平衡阀节流口2的开口面积.
忽略平衡阀阀芯的动态特性, 则阀芯的力平衡方程为
| $ {A_3}{p_1} = {k_{\rm{c}}}\left( {{x_{\rm{v}}} + {x_{\rm{d}}} + {x_{\rm{k}}}} \right). $ | (9) |
式中:A3为平衡阀阀芯截面积, kc为平衡阀控制阀芯的弹簧刚度, xv为平衡阀阀口开度, xd为平衡阀阀芯的死区长度, xk为平衡阀控制阀芯弹簧的预压缩量.
忽略平衡阀阀芯运动对系统体积流量的影响, 马达低压腔的体积流量连续性方程为
| $ {q_{V2}} = {D_{\rm{m}}}\frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}} + {C_{{\rm{ip}}}}\left( {{p_1} - {p_2}} \right) + {C_{{\rm{ep}}}}{p_2} - \frac{{{V_2}}}{{{\beta _{\rm{e}}}}}\frac{{{\rm{d}}{p_2}}}{{{\rm{d}}t}}. $ | (10) |
式中:V2为液压马达出油腔的容积.
平衡阀2节流口到比例方向阀3节流口的体积流量连续性方程为
| $ {q_{V3}} = {q_{V2}} - \frac{{{V_3}}}{{{\beta _{\rm{e}}}}}\frac{{{\rm{d}}{p_3}}}{{{\rm{d}}t}}. $ | (11) |
式中:V3为平衡阀至比例方向阀B节流口的容积.
液压马达输出力矩与外负载的平衡方程为
| $ {D_{\rm{m}}}\left( {{p_1} - {p_2}} \right) = J\frac{{{{\rm{d}}^2}\varphi }}{{{\rm{d}}{t^2}}} + {B_{\rm{m}}}\frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}} + {T_{\rm{L}}}. $ | (12) |
式中:J为液压马达与负载折算到马达转轴上的总转动惯量, Bm为液压马达及负载的黏性阻尼系数, TL为作用在液压马达上的外负载.
2.3 速度反馈控制模型忽略平衡阀对管片拼装机回转运动动态性能的影响, 管片拼装机回转系统可以看作典型的阀控马达系统, 从比例换向阀控制电流到马达转速的传递函数[9]可以简化为
| $ \frac{{\dot \varphi }}{{{I_{\rm{v}}}}} = \frac{{{K_{{\rm{sv}}}}}}{{\frac{{{s^2}}}{{\omega _{{\rm{sv}}}^2}} + \frac{{2{\zeta _{{\rm{sv}}}}}}{{{\omega _{{\rm{sv}}}}}}s + 1}} \cdot \frac{{{K_{\rm{h}}}}}{{\frac{{{s^2}}}{{\omega _{\rm{h}}^2}} + \frac{{2{\zeta _{\rm{h}}}}}{{{\omega _{\rm{h}}}}}s + 1}}. $ | (13) |
式中:
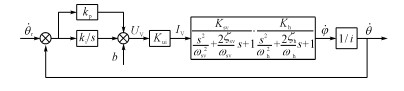
管片拼装机回转系统的速度反馈控制模型如图 4所示.图中, kp和ki分别为控制器比例系数和积分系数, b为系统的零漂、死区等误差补偿.由于采用微分控制会降低系统稳定性, 采用PI控制, 既能够较快地达到响应速度, 又能够提高控制精度.
|
图 4 速度反馈控制系统图 Fig. 4 Block diagram of speed control system |
管片拼装机回转系统的运动速度与系统输入之间的关系为
| $ \begin{array}{l} \dot \theta = \\ \frac{{{K_{{\rm{ui}}}}{K_{{\rm{sv}}}}{K_{\rm{h}}}\left( {{k_{\rm{p}}} + \frac{{{k_{\rm{i}}}}}{s}} \right){{\dot \theta }_{\rm{r}}}}}{{i\left( {\frac{{{s^2}}}{{\omega _{{\rm{sv}}}^2}} + \frac{{2{\zeta _{{\rm{sv}}}}}}{{{\omega _{{\rm{sv}}}}}}s + 1} \right)\left( {\frac{{{s^2}}}{{\omega _{\rm{h}}^2}} + \frac{{2{\zeta _{\rm{h}}}}}{{{\omega _{\rm{h}}}}}s + 1} \right) + {K_{{\rm{ui}}}}{K_{{\rm{sv}}}}{K_{\rm{h}}}\left( {{k_{\rm{p}}} + \frac{{{k_{\rm{i}}}}}{s}} \right)}}. \end{array} $ | (14) |
式中:Kui为比例方向阀放大器增益,
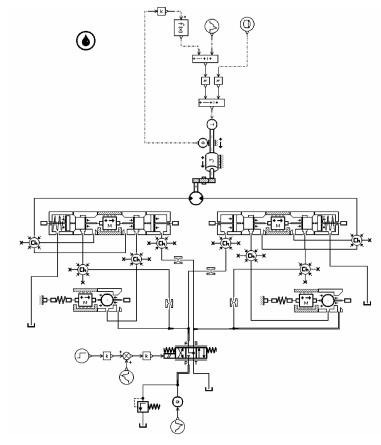
根据图 2建立的开环控制管片拼装机回转系统如图 5所示, 由于液压系统具有典型的非线性, 液压元件的一些性能参数, 如阀口流量系数, 在建模时无法准确确定[10], 利用HCD库对平衡阀和溢流阀进行建模.考虑到平衡阀主阀芯惯性对动态性能的影响, 建模时用质量块模型表示阀芯的惯性[11];管片拼装缩尺实验平台如图 6所示.该实验系统按照实际系统进行了一定比例的缩小, 实验中所用的管片质量为107 kg, 溢流阀设定压力为31.5 MPa, 数据采集卡采集频率为20 Hz.
|
图 5 开环控制管片拼装机回转系统AMESim模型 Fig. 5 AMESim model of rotary system for segmenterector with open-loop control |

|
图 6 管片拼装机实验平台 Fig. 6 Segment erector test model |
液压系统仿真模型的验证包括稳态性能验证和动态性能验证两个方面.稳态性能是指系统稳态时的输出结果;动态性能是指系统运行过程中一些随时间变化的特征量, 如压力和输出速度等, 这些特征量均可以视为随机变量, 进行一致性验证.由于系统为开环系统, 在实验过程中管片从初始位置开始旋转, 系统负载不断增加, 故系统转速缓慢下降, 不是稳定值, 只开展动态性能的一致性验证.
在2 s时, 给系统一阶跃信号, 观测信号响应, 获得马达两侧压力及系统转速的结果.将仿真系统设置相同的参数, 将所获结果与实验结果进行对比, 如图 7所示.

|
图 7 管片拼装机实验台及仿真模型结果 Fig. 7 Results of segment erector test model and AMESim model |
从图 7(a)、(b)可知, 实验台开始存在一定的初始压力, 且与仿真模型相比, 压力冲击较大, 由于各种干扰因素, 压力存在一定的波动, 在系统稳定后, 两者的压力差距不大.从图 7(c)可知, 实验台和仿真模型转速虽然都有一定的波动, 但总体趋势相同, 对AMEsim模型与管片拼装机实验台进行进一步的一致性验证.
动态性能的一致性验证可以通过TIC不等式系数法开展.TIC不等式系数法是一种定性分析两时间序列一致性程度的方法, 原理简单, 计算量小, 该方法的基本原理如下.
设xt为仿真模型输出序列, yt为实际系统输出序列, 取数据长度为N, 则定义TIC系数:
| $ \rho \left( {x,y} \right) = \frac{{\sqrt {\sum\limits_{t = 1}^N {{{\left( {{x_t} - {y_t}} \right)}^2}} } }}{{\sqrt {\sum\limits_{t = 1}^N {x_t^2} } + \sqrt {\sum\limits_{t = 1}^N {y_t^2} } }}. $ | (15) |
通过ρ的大小判断2组数据的一致性好坏, 0≤ρ≤1.当TIC接近于0时, 表明xt和yt基本一致;当TIC≤0.3时, 表明仿真效果很好[12].
基于上述原理, 分别对液压马达进油口压力、回油口压力及系统转速进行TIC系数的计算, 分别记为ρ1、ρ2以及ρ3.当计算ρ1和ρ2时, 由于实验台中开始存在一定的压力, 为了排除该影响, 从2 s之后各点开始计算, 可得ρ1=0.023 6, ρ2=0.028 6, ρ3=0.012 2, 均远小于0.3, 故仿真模型与实验台的动态数据样本一致性很好, 可以认为仿真模型是实验台的再现, 可以用仿真系统代替实验台进行接下来的研究.
4 管片拼装机回转系统模拟分析管片拼装机回转系统可以采用位置控制和速度控制2种控制方式.位置控制信号指令较大, 响应时间较长, 通过速度变化来实现控制.如果能够直接对速度进行控制, 可以很好地控制精度及冲击, 实现理想的控制效果.本文采用速度控制, 设计速度反馈控制系统.
首先对开环控制1.5 r/min进行仿真分析, 得到速度及加速度响应.分析结果可以发现, 启动阶段存在较大的振荡冲击;在开环控制条件下, 将转速提高到6 r/min, 发现冲击力矩远大于1.5 r/min的工况.为了更好地对速度进行控制, 设计闭环控制系统对高速度进行控制, 对不同参数进行对比发现, 闭环变速积分控制能够很好地降低冲击力矩;在闭环变速积分控制的基础上, 利用蓄能器对回路进行改进, 减小了系统的冲击振荡.
4.1 开环控制模拟分析仿真系统模型如图 5所示, 仿真参数如表 1所示.该系统的主要设计参数参照北京地铁五号线施工用盾构机[13], 最高转速为1.5 r/min, 最大驱动力矩为150 kN·m.在实际系统中, 有2个液压马达工作, 仿真时设置最大负载为75 kN·m.
| 表 1 开环控制管片拼装机回转系统仿真参数 Table 1 Simulation parameters of rotary system for segment erector with open-loop control |
图 5中, 假设比例方向阀A口通高压油, B口通低压油, 开始时B口低压油不足以克服左侧平衡阀弹簧力, 高压油经左侧单向阀进入液压马达;A口高压油克服右侧平衡阀弹簧力, 低压油通过右侧阻尼孔回油, 逐渐达到平衡状态.
管片拼装机在运行时主要存在2种工况:1) 管片从初始位置运送到指定位置, 此时系统在启动时重力负载为0, 且负载随回转角度成正弦规律变化;2) 管片未到达指定位置已停下, 并再次启动, 此时可能会存在较大的负载, 为了使结果通用, 将该工况下的启动负载设置为管片拼装机最大负载.之后的仿真对应这2种工况, 分别为0重力负载启动和带负载启动, 系统在运行时不允许出现管片运动超过指定位置.
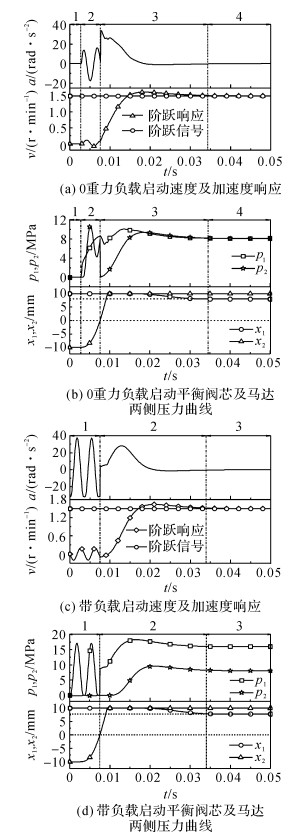
如图 8所示为低速开环控制的仿真结果, 系统转速为1.5 r/min.图中, x1和x2分别为对应图 5中左、右两平衡阀的阀芯位移.
|
图 8 低速开环控制仿真结果 Fig. 8 Simulation results of open-loop control in low speed |
从图 8(a)中的速度及加速度响应曲线可以看出, 系统启动分为4个阶段:系统在1阶段没有响应;在2阶段出现了速度波动, 加速度存在正、负变化;刚进入3阶段时出现了最大加速度, 速度逐步提高;进入4阶段后, 系统达到稳定状态.对照图 8(b)的压力及阀芯位移对启动过程进行分析可知, 在1阶段,液压油尚未进入到马达中, 此时系统无响应;在2阶段,液压油开始进入马达, 左侧压力逐渐升高, 但该压力不足以打开右侧平衡阀, 马达出油口不能回油, 导致出油口压力上升, 在出油口压力大于进油口压力后, 马达反转, 出现了速度波动;在3阶段, 系统压力逐渐升高, 右侧平衡阀阀芯打开, 在阀芯打开一瞬间出现了系统的最大加速度, 此后系统逐步进入稳定状态, 到达状态4.
如图 8(c)、(d)所示为带负载启动工况.从速度及加速度响应曲线可以看出, 系统启动分为3个阶段:在阶段1, 速度有一正负波动, 系统存在较大的振荡冲击加速度;在阶段2, 速度逐步增加并接近给定信号;阶段3系统进入稳定状态.结合图 8(d)分析该过程,可得以下结论.在阶段1, 系统压力尚未建立, 右侧平衡阀未打开, 马达无法回油, 系统在负载的作用下出现了负向速度, 但液压油不能从左侧平衡阀流走;在左侧平衡阀与马达之间形成的封闭空间被压缩, 当压缩到一定值时, 液压油张力使马达开始正转, 该过程往复进行了两次.当系统压力可以将右侧平衡阀阀芯开启后, 系统进入阶段2, 马达两侧压力逐步升高到稳定工作压力, 系统转速不断接近给定信号;在系统稳定后, 进入阶段3.
若在不改变系统及控制方式的基础上, 只是将对应液压元件的选放大型号, 将转速提高到6 r/min后, 与之前1.5 r/min开环控制的速度及加速度响应对比如图 9所示.可以看出, 将转速信号提高之后, 响应过程与之前类似, 但最大冲击加速度急剧增大, 具体数据如表 2所示.表中, am为加速过程中的最大冲击加速度, T1m为除启动点外的最大冲击力矩, k为T1m与系统最大驱动力矩的比值.

|
图 9 高低速开环控制速度及加速度响应对比 Fig. 9 Contrast of speed and acceleration responses with open-loop control between high and low speed |
| 表 2 高低速开环控制冲击数值表 Table 2 Numerical table of impact with open-loop control in high and low speed |
从表 2可以看出, 若不改变系统及控制方式, 将转速变为之前4倍后, 在0重力负载启动时, 最大冲击力矩是原先的2.78倍, 已到达系统最大驱动力矩的2.965倍;在带负载启动时, 最大冲击力矩是原先的1.87倍, 为系统最大驱动力矩的2.112倍.要提高管片拼装机回转系统的转速, 需要解决2个问题:1) 转速提高后系统的冲击变大的问题;2) 能否减小或消除启动阶段的冲击振荡问题.
4.2 闭环控制模拟分析为了更好地对管片拼装机回转系统的速度进行控制, 设计高速闭环控制系统.采用PI控制, 如图 10所示, 系统中各元件的原理与低速开环控制相同, 对应的型号相对较大.设计最大转速由1.5r/min提高到6 r/min, 分析该管片拼装机回转系统的动态特性.
|
图 10 高速闭环控制系统AMESim模型 Fig. 10 AMESim model of closed-loop control in high speed |
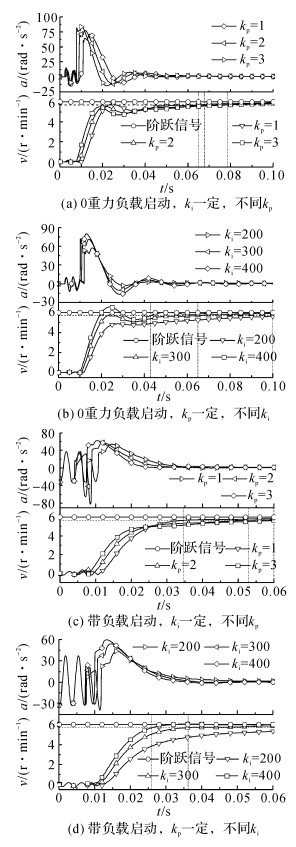
如图 11所示为高速闭环控制的速度及加速度响应.图 11(a)、(c)中, ki=300, kp分别为1、2和3;图 11(b)、(d)中, kp=1, ki分别为200、300和400, 竖线对应的时间为调整时间, 图 11(d)中ki=200的情况, 调整时间已超出坐标轴, 未画出.
|
图 11 高速闭环控制速度及加速度响应 Fig. 11 Speed and acceleration responses with closed-loop control in high speed |
从图 11可以看出, 不论管片拼装机是0重力负载启动还是带负载启动, 都有以下结论.1) 在一定的ki下, 对于不同的kp, 响应过程类似, 虽然较大的kp响应较快, 但调整时间相差不多, 且除启动点外最大冲击加速度较大, 故大的kp对系统的有利影响较少, 可以选用较小的kp.2) 在一定的kp下, 对于不同的ki, ki越大, 系统响应越快, 且调整时间相差较大, 但冲击加速度越大, 这是因为较大的ki可以更快地使控制信号达到最大.
考虑采用较小的kp, 并使ki在一定范围内可变;当误差信号较大时, 采用较小的ki, 减小启动阶段的冲击;当误差信号较小时, 采用较大的ki, 增强系统的稳定性及快速性.
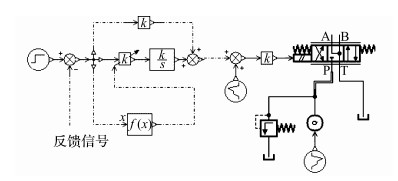
4.3 变速积分控制模拟分析利用上述方法, 设计变速积分的控制策略, 控制模型如图 12所示.图中, f(x)为上述控制策略, ki为100~400.ki由给定信号与反馈信号之差控制, 控制策略为
|
图 12 变速积分控制AMESim模型 Fig. 12 AMESim model of variable speed integral control |
| $ {k_{\rm{i}}} = - 8{e^2} + 400. $ | (16) |
式中:e为给定信号与控制信号之差.
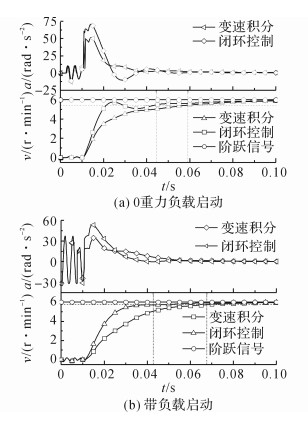
如图 13所示为高速变速积分控制与闭环控制的速度及加速度响应对比.在高速变速积分控制中, ki设置如前所述, kp设置为1;在闭环控制中, ki为300, kp设置为1.系统在变速积分控制下, 与普通闭环控制相比, 在0重力负载启动和带负载启动2种工况下, 响应过程类似, 调整时间稍有延长, 但最大冲击加速度能够减小约20 rad/s2, 最大冲击力矩可以减小约1/3, 与预想结果相同, 可以很好地减小启动冲击, 延长系统寿命.
|
图 13 高速变速积分控制与闭环控制速度及加速度响应 Fig. 13 Speed and acceleration responses with variable speed integral control and closed-loop control in high speed |
为了解决系统在启动阶段的冲击振荡问题, 考虑在系统中加入蓄能器.利用蓄能器吸收启动阶段的压力冲击, 蓄能器回路高速变速积分控制模型如图 14所示, 调节蓄能器参数, 使系统消去在启动阶段的冲击振荡.

|
图 14 蓄能器回路高速变速积分控制AMESim模型 Fig. 14 AMESim model of accumulator circuit with variable speed integral control in high speed |
图 14中, 除了变速积分控制策略外, 各元件参数与之前系统相同, 变速积分控制策略为
| $ {k_{\rm{i}}} = - 10{e^2} + 380. $ | (17) |
该系统选用工程中常用的皮囊式蓄能器, 反应灵敏, 适合用于消除流量脉动.该蓄能器的受力简化模型如图 15所示.图中An为蓄能器进油阀处横截面面积.

|
图 15 蓄能器受力简化模型 Fig. 15 Simplified mechanical model of accumulator |
皮囊式蓄能器预充压力与容积间的关系[14]为
| $ H\left( s \right) = \frac{{{V_{\rm{a}}}}}{{{p_1}}}\frac{{nA_{\rm{a}}^2}}{{{m_{\rm{e}}}{s^2} + \left( {{B_{\rm{e}}} + {C_{\rm{e}}}} \right)s + \left( {\frac{{k{p_{{\rm{a}}0}}A_{\rm{a}}^2}}{{{V_{{\rm{a}}0}}}} + {K_{\rm{e}}}} \right)}}. $ | (18) |
式中:Aa为蓄能器进油腔横截面面积,n为An与Aa之比,me为进油腔油液的等效质量,Be为进油腔油液的等效黏性阻尼系数,Ce为预充气体的等效气体阻尼系数,k为气体多变指数,pa0和Va0分别为蓄能器的预充压力和体积,Ke为预充气体的刚度系数.
整理后, 可得
| $ H\left( s \right) = \frac{{{V_{\rm{a}}}}}{{{p_1}}} = \frac{{nA_{\rm{a}}^2{V_{{\rm{a}}0}}}}{{k{p_{{\rm{a}}0}}A_{\rm{a}}^2 + {k_{\rm{e}}}{V_{{\rm{a}}0}}}}\frac{{\omega _{\rm{n}}^2}}{{{s^2} + 2\zeta {\omega _{\rm{n}}} + \omega _{\rm{n}}^2}}. $ | (19) |
式中:ωn为蓄能器无阻尼固有频率,
| $ {\omega _{\rm{n}}} = \sqrt {\left( {\frac{{k{p_{{\rm{a}}0}}A_{\rm{a}}^2}}{{{V_{{\rm{a}}0}}}} + {K_{\rm{e}}}} \right)/{m_{\rm{e}}}} ; $ |
ζ为蓄能器等效阻尼比,
| $ \zeta = \frac{{{B_{\rm{e}}} + {C_{\rm{e}}}}}{2}{\left[ {\sqrt {\left( {\frac{{k{p_{{\rm{a}}0}}A_{\rm{a}}^2}}{{{V_{{\rm{a}}0}}}} + {K_{\rm{e}}}} \right)/{m_{\rm{e}}}} } \right]^{ - 1}}. $ |
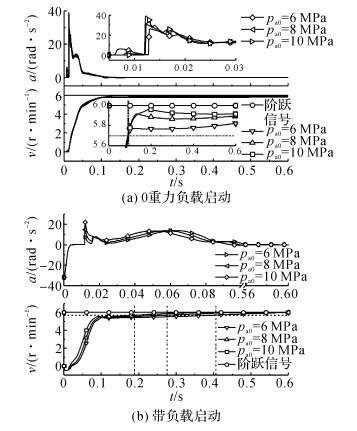
从式(18)、(19) 可以看出, ωn和ζ与蓄能器油腔的预充气体压力、体积以及系统工作压力、气体多变指数、油液的黏性阻尼系数、气体的黏性阻尼系数等参数有关.假设后3项指标不变, 则蓄能器的无阻尼固有频率和等效阻尼比仅与预充气体压力、体积及系统压力相关.当蓄能器预充压力为系统工作压力的80%~90%时, 既能够有效地吸收系统的压力冲击, 又能够保证系统的快速稳定性[15].在该系统中, 蓄能器容量设为1 L, 为了找到合适的预充气压力, 对不同的预充压力进行试验对比, 如图 16所示.
|
图 16 蓄能器回路高速变速积分控制速度及加速度响应 Fig. 16 Speed and acceleration responses of accumulator circuit with variable speed integral control in high speed |
从图 16可以看出, 在2种工况下, 系统在启动阶段的系统振荡冲击均得到了很好的抑制.在0重力负载启动时, 蓄能器预充气压力对系统响应时间的影响不大, 但预充气压力越大, 系统的最大冲击加速度越大;在带负载启动时, 蓄能器预充气压力越大, 加速过程中的最大冲击加速度越大, 但调整时间越长.
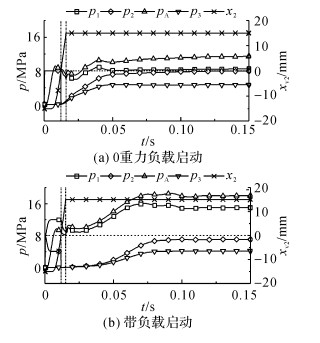
蓄能器回路系统在启动阶段的压力及阀芯位移响应如图 17所示.图中, 蓄能器容积为1 L, 预充气压力为8 MPa, pA为方向阀A油口压力.对于图 17(a)所示的0重力负载启动工况, 当右侧平衡阀阀芯位移为负时, 两平衡阀与马达之间形成了一个封闭空间, 此时马达不会转动;当方向阀A油口压力上升到可以开启右侧平衡阀时, 马达出油口压力迅速下降, 快速启动;当右侧平衡阀阀芯完全打开时, 系统开始逐步稳定.对于图 17(b)所示的带负载启动工况, 在右侧平衡阀阀芯未打开之前, 对于两平衡阀及马达组成的封闭空间, 在负载作用下马达出现了反转, 导致马达左侧压力上升右侧压力下降;在右侧平衡阀阀芯打开之后, 马达右侧压力迅速下降, 马达开始正转;当右侧平衡阀阀芯完全打开之后, 系统逐步稳定.
|
图 17 蓄能器回路高速变速积分控制压力及阀芯位移响应 Fig. 17 Pressure and spool displacement responses of accumulator circuit with variable speed integral control in high speed |
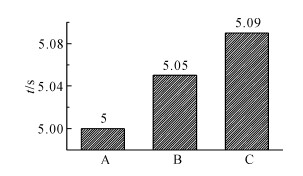
在引入蓄能器之后带来了一个问题, 即系统的响应变慢.以图 16中预充气压力为8 MPa为例, 与无蓄能器回路, 即图 13, 对比可知, 加入蓄能器后, 系统在0重力负载启动时, 调整时间约为之前的2倍;系统在带负载启动时, 调整时间约为之前的5倍.虽然系统速度在0.1 s内可以接近给定速度, 但要达到给定速度还需较长时间, 因为这段时间内系统会对蓄能器进行充液.假设管片需要运送到最大角度180°处, 若以理想的速度6 r/min运动, 所需时间为5 s;若以图 16中响应最慢的曲线A计算, 则管片运动到180°时所需的时间如图 18所示.图中, A为以理想转速运动;B为蓄能器预充气压力为6 MPa, 0重力负载启动;C为蓄能器预充气压力为6 MPa, 带负载启动.从图 18可以看出, 三者相差不大, 实际上不会出现带负载启动转动180°的情况, 引入蓄能器导致系统响应变慢的影响不大.
|
图 18 不同响应运动到180°所需的时间 Fig. 18 Time requirements to 180 degrees for differentresponses |
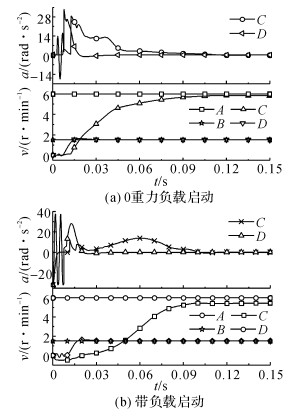
将蓄能器回路中蓄能器预充压力设为7 MPa, 其余参数同上回路, 与低速开环控制管片拼装机回转系统的速度及加速度响应进行对比, 如图 19所示.图中, A表示高速工作的速度阶跃信号, B表示低速工作的速度阶跃信号, C表示蓄能器回路高速变速积分控制, D表示低速开环控制.
|
图 19 蓄能器回路高速变速积分控制与低速开环控制速度及加速度响应对比 Fig. 19 Contrast of speed and acceleration responses between accumulator circuit with variable speed integral control in high speed and open-loop control in low speed |
从图 19可以看出, 蓄能器回路高速变速积分控制与低速开环控制的管片拼装机回转系统相比, 消除了启动阶段的冲击振荡, 减小了最大冲击加速度, 可以大大提升系统的寿命, 但系统调整时间变长, 具体的数值对比如表 3所示.表中, 新系统指蓄能器回路高速变速积分控制系统;旧系统指低速开环控制系统;ts为调整时间, 允许误差为±5%;n为加速度正、负变化的次数, 在发生符号变化后加速度须大于5 rad/s2;T1为除启动点外的最大冲击力矩.
从表 3可以看出:在0负载启动工况下, 新系统没有了冲击振荡, 除了启动点外, 最大冲击力矩减小约15%;在带负载启动工况下, 新系统振荡次数大大减小, 除了启动点外, 最大冲击力矩比旧系统减小约64%.由此可见, 新系统在提高工作效率的同时, 能够大大提高系统的寿命.新系统在减小冲击的同时牺牲了调整时间, 2种工况下的调整时间都有较大的延长.
5 结论(1) 将所建仿真模型与实验台进行对比发现, 两者无论是液压马达两侧压力, 还是系统转速, TIC均小于0.3, 仿真模型与实验台的动态数据样本一致性很好, 可以认为仿真模型是实验台的再现.
(2) 对于本管片拼装机回转系统, 采用普通PI控制时, 增加比例系数对系统响应速度的影响不大, 但最大冲击会增大;增加积分系数可以使系统响应加快, 但最大冲击会增大.采用较小的比例系数及变速积分控制可以将系统最大冲击减小约1/3, 有效地减小最大冲击.
(3) 当系统中加入蓄能器之后, 若选取合适的预充气压力, 则可以消除启动阶段的系统振荡, 但系统响应会变慢.在0重力负载启动时, 系统调整时间约为原回路的2倍;在带负载启动时, 调整时间约为原回路的5倍.
(4) 在采用蓄能器回路并使用变速积分进行控制后, 可以将系统回转速度由1.5 r/min提高到6 r/min, 消除了启动阶段的冲击振荡.在0重力负载启动时, 除启动点外, 最大冲击力矩减小约15%;在带负载启动时, 除启动点外, 最大冲击力矩减小约64%, 可以很好地延长系统寿命, 更加符合高效隧道施工的要求.
| [1] | GUO W T, GUO W Z, GAO F, et al. Innovative group-decoupling design of a segment erector based on GF set theory[J]. Chinese Journal of Mechanical Engineering, 2013, 26(2): 264–274. DOI:10.3901/CJME.2013.02.264 |
| [2] | LI G, CHEN Y D, WANG B, et al. Dynamics simulation of a six-dof tunnel segment erector for tunnel boring machine based on virtual prototype[J]. Applied Mechanics and Materials, 2013, 251: 231–234. |
| [3] | SHI H, GONG G F, YANG H Y, et al. Energy saving analysis of segment positioning in shield tunneling machine considering assembling path optimization[J]. Journal of Central South University, 2014, 21(12): 4526–4536. DOI:10.1007/s11771-014-2457-7 |
| [4] |
戴仕敏. 上海虹桥枢纽迎宾三路隧道新建工程综述[C]//地下交通工程与工程安全. 上海: 同济大学, 2011: 132-140.
DAI Shi-min. Summarize of new tunnel project about shanghai hongqiao yingbin road[C]//Underground Transportation Projects and Work safety. Shanghai:Tongji University, 2011:132-140. |
| [5] | SHI H, GONG G F, YANG H Y, et al. Positioning speed and precision control of segment erector for shield tunneling machine[C]//2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Montreal:IEEE, 2010:1076-1080. http://yadda.icm.edu.pl/yadda/element/bwmeta1.element.ieee-000005695863 |
| [6] | WANG L T, GONG G F, YANG H Y, et al. The development of a high-speed segment erecting system for shield tunneling machine[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(6): 1713–1723. DOI:10.1109/TMECH.2013.2282873 |
| [7] |
杨旭, 龚国芳, 杨华勇, 等. 管片拼装实验台回转电液控制系统设计及试验分析[J].
工程设计学报, 2014, 21(2): 180–197.
YANG Xu, GONG Guo-fang, YANG Hua-yong, et al. Design and test analysis of rotary electro-hydraulic control system for a segment assembly test bed[J]. Chinese Jour-nal of Engineering Design, 2014, 21(2): 180–197. |
| [8] | 王春行. 液压控制系统[M]. 北京: 机械工业出版社, 1999: 14-15. |
| [9] | WANG L T, GONG G F, SHI H, et al. Positioning preci-sion and impact force control of segment erector for shield tunneling machine[C]//20123rd International Conference on Digital Manufacturing and Automation.Guilin:IEEE, 2012:612-617. |
| [10] |
李永堂, 雷布芳, TINGK L. 液压锤液压系统的建模与仿真[J].
中国机械工程, 2004, 15(6): 481–483.
LI Yong-tang, LEI Bu-fang, TING K L. Modeling and simulation of the hydraulic system in hydraulic hammer using"Gray-box" modeling method[J]. China Mechanical Engineering, 2004, 15(6): 481–483. |
| [11] |
袁士豪, 殷晨波, 刘世豪. 基于AMESim的平衡阀动态性能分析[J].
农业机械学报, 2013, 44(8): 273–280.
YUAN Shi-hao, YIN Chen-bo, LIU Shi-hao. Working properties of counterbalance valve based on AMESim code[J]. Transactions of the Chinese Society for Agri-cultural Machinery, 2013, 44(8): 273–280. DOI:10.6041/j.issn.1000-1298.2013.08.047 |
| [12] |
刘兴刚, 张国志, 郝丽娜, 等. 冷连轧轧制力仿真模型的可信度评估[J].
东北大学学报:自然科学版, 2008, 29(4): 537–540.
LIU Xing-gang, ZHANG Guo-zhi, HAO Li-na, et al. Confidence level evaluation for simulation model of con-tinuous cold-rolling force[J]. Journal of Northeastern University:Natural Science, 2008, 29(4): 537–540. |
| [13] |
乐贵平. 浅谈北京地区地铁隧道施工用盾构机选型[J].
现代隧道技术, 2003, 40(3): 14–30.
LE Gui-ping. Selection of shield machines for Beijing metro construction[J]. Modern Tunnelling Technology, 2003, 40(3): 14–30. |
| [14] |
王纪森, 王海涛, 李仕辉. 蓄能器在液压实验台中的参数分析与仿真[J].
机床与液压, 2010, 38(15): 89–91.
WANG Ji-sen, WANG Hai-tao, LI Shi-hui. The parameter analysis and simulation of the accumulator in hydrau-lic test-bed[J]. Machine Tool and Hydraulics, 2010, 38(15): 89–91. DOI:10.3969/j.issn.1001-3881.2010.15.028 |
| [15] |
马登成, 杨士敏, 陈筝, 等. 蓄能器对工程机械液压系统影响的仿真与试验[J].
中国公路学报, 2013, 26(2): 183–190.
MA Deng-cheng, YANG Shi-min, CHEN Zheng, et al. Simulation and experimental study on impact of accumu-lator on engineering machinery hydraulic system[J]. China Journal of Highway and Transport, 2013, 26(2): 183–190. |



