随着激光扫描技术的不断成熟与发展, 基于点云的三维建模技术得到了广泛应用, 三维点云数据[1]配准是曲面建模与识别领域的热点研究问题.在复杂自由曲面物体的三维扫描中, 受测量仪器范围约束或被测实物表面本身遮挡等诸多因素[2]的影响, 一次扫描难以得到曲面的完整三维几何信息.需要在多视角下对被测物体表面局部进行测量, 获得各自基于自身坐标系下的点云数据;将局部坐标系下的点云数据拼接配准, 建立被测物体表面的全局精确描述, 即点云配准.
目前应用较广泛的配准算法是Besl等[3]提出的迭代最近点(iterative closest point, ICP)算法及各种变形[4-6].至今, 该类算法已经得到了很大改进, 但由于误差测度是定义在点-点、点-切面或者点-曲面距离之上的, 对应点对中存在不精确对应的问题, 使得该类算法受偏离点的影响很大.王蕊等[7]通过提取几何特征点, 再匹配特征点(matching feature points, MFP)以实现粗略拼接, 但该方法精度不高, 且特征点提取比较耗时;Basdogan等[8]提出用K邻近方法估算局部邻域点, 同时采用点-点之间的欧氏距离来选取匹配点对, 该方法对噪声较敏感.国内, 高鹏东等[9]提出利用深度图像重叠区域间的空间体积作为误差度量的精确配准算法.该算法对初始运动参数不敏感, 收敛速度较快且具有较强的鲁棒性和较高的配准精度, 抗噪声能力较强, 但在海量数据下, 该算法的效率不够高.
本文结合现实复杂三维物体, 提出基于适应性距离函数(adaptive distance function, ADF)和迭代最近曲面片(iterative closest surface, ICS)的激光点云精细配准方法.首先根据空间点相对位置在刚体变换下的不变特性, 用曲率不变特征和归一化零均值互相关系数(normalized zero-mean cross-correlation coefficient, NZCC)构造有效的初始匹配点对数组, 基于单位四元数对匹配的特征点对进行坐标变换求解, 完成数据粗略配准;在此基础上, 运用适应性距离函数和改进迭代最近曲面片精细匹配技术, 将不同视角点云在三维空间进行最优化匹配, 实现了点云数据精确配准.结合复杂三维曲面物体对算法进行验证, 试验结果表明, 本文提出的精细配准算法, 在配准精度和配准速度上得到了明显提高.本文的2点创新点和亮点如下:1) 引进新的点-曲面距离函数, 构造更加精确的点-曲面距离误差度量指标;2) 提出ICS精细配准算法, 用局部曲面片代替离散点作为配准的目标几何单元, 减少了采样密度对配准精度的影响, 保证了算法的精度.
1 粗略配准 1.1 曲率不变特征在三维空间R3中, 离散曲面的典型代表是Monge曲面, 参数方程可用下式[10]描述:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{r}}\left( {u,v} \right) = {\left[ {\begin{array}{*{20}{c}} {u,}&{v,}&{h\left( {u,v} \right)} \end{array}} \right]^{\rm{T}}};\\ u = 1,2, \cdots ,m,v = 1,2, \cdots ,n. \end{array} \right\} $ | (1) |
式中:u-v平面为三维空间RS3的参考平面, h(u, v)为离散曲面到参考平面点(u, v)的距离.曲面在点r(u, v)的切平面平行于ru与rv张成的矢量平面, 则曲面r(u, v)的单位法线方向矢量为
| $ \mathit{\boldsymbol{n}} = \frac{1}{{\sqrt {h_u^2 + h_v^2 + 1} }}{\left[ { - {h_u}, - {h_v},1} \right]^{\rm{T}}}. $ | (2) |
r(u, v)可以表示成两种基本量, 第一基本量描述曲面的内在性质[11]:
| $ \begin{array}{l} I\left( {{\rm{d}}u,{\rm{d}}v} \right) = {\rm{d}}\mathit{\boldsymbol{r}} \cdot {\rm{d}}\mathit{\boldsymbol{r}} = \left( {{\mathit{\boldsymbol{r}}_u}{\rm{d}}u + {\mathit{\boldsymbol{r}}_v}{\rm{d}}v} \right) \cdot \left( {{\mathit{\boldsymbol{r}}_u}{\rm{d}}u + } \right.\\ \;\;\;\left. {{\mathit{\boldsymbol{r}}_v}{\rm{d}}v} \right) = E{\rm{d}}{u^2} + 2F{\rm{d}}u{\rm{d}}v + G{\rm{d}}{v^2}. \end{array} $ | (3) |
式中:du、dv为u、v方向的微小量;E、F、G为第一基本量参数,
| $ E = 1 + h_u^2,F = {h_u}{h_v},G = 1 + h_v^2. $ | (4) |
第二基本量表示曲面的弯曲程度[10]:
| $ \begin{array}{l} II\left( {{\rm{d}}u,{\rm{d}}v} \right) = - {d_\mathit{\boldsymbol{r}}} \cdot {d_\mathit{\boldsymbol{n}}} = \\ \;\;\;\;\;\;\left( {{\mathit{\boldsymbol{r}}_{uu}}{\rm{d}}{u^2} + 2{\mathit{\boldsymbol{r}}_{uv}}{\rm{d}}u{\rm{d}}v + {\mathit{\boldsymbol{r}}_{vv}}{\rm{d}}{v^2}} \right) \cdot \mathit{\boldsymbol{n}} = \\ \;\;\;\;\;\;L{\rm{d}}{u^2} + 2M{\rm{d}}u{\rm{d}}v + N{\rm{d}}{v^2}. \end{array} $ | (5) |
式中:L、M、N为第二基本量参数,
| $ \begin{array}{l} L = \frac{1}{{\sqrt {h_u^2 + h_v^2 + 1} }}{h_{uu}},M = \frac{1}{{\sqrt {h_u^2 + h_v^2 + 1} }}{h_{uv}},\\ N = \frac{1}{{\sqrt {h_u^2 + h_v^2 + 1} }}{h_{vv}}. \end{array} $ | (6) |
E、F、G、L、M、N这6个参数唯一地确定了曲面的2种基本量, 高斯曲率K、平均曲率H以及主曲率k1、k2可用这些参数表示[12]:
| $ K = \frac{{{h_{uu}}{h_{vv}} - h_{uv}^2}}{{{{\left( {h_u^2 + h_v^2 + 1} \right)}^2}}},H = \frac{{EN + GL - 2FM}}{{2\left( {EG - {F^2}} \right)}}, $ | (7) |
| $ {k_1} = H + \sqrt {{H^2} - K} ,{k_2} = H - \sqrt {{H^2} - K} . $ | (8) |
K和H以及k1、k2包含了曲面的形状信息.H可由曲面函数的微商表示为
| $ H = \frac{1}{2}\frac{{\left( {1 + h_v^2} \right){h_{uu}} + \left( {1 + h_u^2} \right){h_{vv}} - {h_u}{h_v}{h_{uv}}}}{{{{\left( {1 + h_u^2 + h_v^2} \right)}^{\frac{3}{2}}}}}. $ | (9) |
相应的单位主方向矢量分别为
| $ \left. \begin{array}{l} \mathit{\boldsymbol{u}} = \pm \frac{{\left( {{k_1}G - N} \right){\mathit{\boldsymbol{r}}_u} + \left( {M - {k_1}F} \right){\mathit{\boldsymbol{r}}_v}}}{{\left| {\left( {{k_1}G - N} \right){\mathit{\boldsymbol{r}}_u} + \left( {M - {k_1}F} \right){\mathit{\boldsymbol{r}}_v}} \right|}},\\ \mathit{\boldsymbol{v}} = \pm \frac{{\left( {{k_2}G - N} \right){\mathit{\boldsymbol{r}}_u} + \left( {M - {k_2}F} \right){\mathit{\boldsymbol{r}}_v}}}{{\left| {\left( {{k_2}G - N} \right){\mathit{\boldsymbol{r}}_u} + \left( {M - {k_2}F} \right){\mathit{\boldsymbol{r}}_v}} \right|}}. \end{array} \right\} $ | (10) |
设待配准的两片相邻视角扫描点云数据分别为P={pi|pi∈R3, i=1,2,…,NP}, Q={qi|qi∈R3, i=1,2,…,NM}(Q为基准点云). 利用点云数据固有的微分不变特征, 获取初始匹配点对.对于P和Q中的每个点, 首先根据1.1节方法计算法矢量、主曲率以及相应的主方向矢量, 并选取法矢量n的方向, 使得所有法矢量均指向点云曲面的同一侧;同时选取主方向矢量u、v方向, 使得u、v、n构成右手坐标系.然后引用Zhang等[11]提出的方法来确定pi和mj的对应邻域, 从而获取初始匹配点数组.
1.3 粗略配准参数估算利用离散的对应特征点进行粗略配准, 以估计初始位姿.基于对应特征点的配准方法是在2个相邻视图的有效点云模型和QS (基准点云模型)中选取Nt(Nt≥3) 组特征点对(或称为对应特征点), 每一组特征点对都对应实际物体的同一特征点.利用点云模型PS中的Nt个特征点{p1, p2, …, pNt}和点云模型QS中的Nt个特征点{q1, q2, …,qNt}的变换关系qi=R0pi+t0(i=1, 2, …, Nt), 采用文献[13]的四元素和线性最小二乘法来求解刚性变换初值(R0, t0), 将(R0, t0)应用到点云模型PS上, 可得刚性变换后的点云模型P′S=R0PS+t0, 从而将两个点云模型PS和QS粗略配准到了同一坐标系(其中QS为基准点云模型), 实现粗略配准.
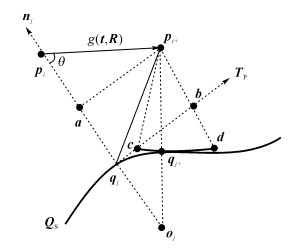
2 基于ADF和ICS的精细配准 2.1 适应性距离函数ADF如图 1所示, 对于移动测量数据pi∈PS, 在目标测量数据点集QS={q1, q2, …, qNt}中搜索最近点qj, 若nj代表qj处的单位外法矢, 定义qj处的切平面TP:TP={x|njT(x-qj)=0}.经过刚体变换参数g=(t, R)作用后, 若pi在三维空间的新坐标点表示为pi+, 则连接更新点pi+和qj处的曲率圆心oj, 可以求得目标数据上的交点qj+.
|
图 1 点pi与目标曲面QS间的适应性距离pi+c Fig. 1 Adaptive distance pi+c from point pi to target surface QS |
在欧式空间中, ‖pi+qj+‖是经过刚体变换后移动点与目标点集最小距离的近似值, ‖pi+qj+‖2被看作点-曲面之间最小的平方距离来构建目标函数, 以优化刚体运动参数g.‖pi+qj+‖和顶点主曲率半径相关, 不能用平方距离来构造目标函数, 原因如下:1) 主曲率是物体曲面的二阶微分信息, 容易受噪声干扰;2) 对于所有的pi, 都需要计算与曲率半径相关的‖pi+qj+‖, 计算过程极其繁琐.
给出点-曲面最近距离的一个替代形式——适应性有向距‖pi+qj+‖, 将点pi+沿qj+处的法线n和切平面T投影到坐标点a、b, 以pi+为圆心, ‖pi+qj+‖为半径构造弧
| $ \begin{array}{l} d_{{\rm{ADF}}}^2\left( {g,{\mathit{\boldsymbol{Q}}_{\rm{S}}}} \right) = {\left\| {{\mathit{\boldsymbol{p}}_i} + \mathit{\boldsymbol{c}}} \right\|^2} = \left( {1 - \mu } \right){\left\| {\mathit{\boldsymbol{n}}_j^{\rm{T}}\left( {{\mathit{\boldsymbol{p}}_{i + }} - {\mathit{\boldsymbol{q}}_j}} \right)} \right\|^2} + \\ \;\;\;\;\;\;\;\;\;\;\mu {\left\| {\mathit{\boldsymbol{t}}_j^{\rm{T}}\left( {{\mathit{\boldsymbol{p}}_{i + }} - {\mathit{\boldsymbol{q}}_j}} \right)} \right\|^2};\mu \in \left[ {0,1} \right]. \end{array} $ | (11) |
1) 当μ=0时, dADF2(g, QS)转变为误差度量dTDF2(g, QS)=‖njT(pi+-qj)‖2.此时, dTDF2(g, QS)对应图 1的点-切面距离函数‖(pi+b)‖2, 是应用于Pottmann等[14]提出的TDM算法的度量指标.
2) 当μ=1时, dADF2(g, QS)转变为dPDF2(g, QS)=‖pi+-qj‖2.此时, dPDF2(g, QS)对应图 1的点-点距离函数‖pi+qj‖2, 是应用于Besl等[3]提出的ICP算法的度量指标.
3) 若点qj位于低曲率区域(例如平面), 则dTDF2(g, QS)是描述点-点距离的简单而合理的度量指标, dPDF2(g, QS)将产生距离偏差εPDF=(‖pi+qj‖-‖pi+qj+‖)2.相反, 当qj位于某高曲率区域(例如半径很小的球)时, dTDF2(g, QS)将产生εTDF=‖bd‖2=(‖pi+qj+‖-‖pi+b‖)2, 偏差与qj处的曲率有关.
dTDF2(g, QS)和dPDF2(g, QS)是dADF2(g, QS)的两种特殊形式, 在描述具有不同曲率特征的点-曲面距离误差时, 绝对的点-切面距离和点-点距离可能会出现较大的距离偏差:εPDF或εTDF.在适应性距离函数中, 通过选择适当的μ引入部分切向距离, 来反映曲率特征对距离误差的影响.对于具有低曲率特征的曲面, 采用较小的改正系数(μ≈0) 来描述点-曲面最近距离;相反, 对于具有高曲率特征的曲面, 采用较大的改正系数(μ≈1) 来描述点-曲面最近距离.相比传统的点-点距离dPDF2(g, Q)误差测度和点-切面距离dTDF2(g, Q)误差测度, dADF2(g, Q)是更加精确的点-曲面距离误差测度指标.
2.2 改正系数μ的确定确定μ时, 应该从以下两方面考虑.
1) 不同的移动点, 在目标数据中对应不同曲率特征的最近点, 必须采用不同的改正系数μ来描述点-曲面最近距离.
2) 因为测量视角的随意性, 移动数据与目标数据间的相对位置关系是不确定的, 必须采用恰当的μ来保证初始阶段的收敛性.在进行配准前, 曲面物体曲率特征与初始位置是未知的.从Levenberg-MarqUard (LM)优化角度确定μ, 无须考虑曲率特征与初始位置对μ的影响.
赋初值k=0,μ0、μ的确定步骤如下.
1) 用μk定义适应性距离函数dADF2(g, Q).
2) 构造目标函数
3) 计算∨xk=pi+-pi并更新pi.
4) 采用k-d树[15]查询pi点的最近点qj.
5) 令w(pi)=[njT(qj-pi)], wk表示k次迭代后的向量:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{w}}_k} = {{\left( {w\left( {{\mathit{\boldsymbol{p}}_1}} \right),w\left( {{\mathit{\boldsymbol{p}}_2}} \right), \cdots ,w\left( {{\mathit{\boldsymbol{p}}_N}} \right)} \right)}^{\rm{T}}},}\\ {{\mathit{\boldsymbol{A}}_k} = \nabla {\mathit{\boldsymbol{w}}_k},{\mathit{\boldsymbol{G}}_k} = {{\left( {{\mathit{\boldsymbol{A}}_k}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{A}}_k}.} \end{array} $ |
6) 计算均值误差:
| $ {\varepsilon _k} = \frac{1}{{{N_{\rm{t}}}}}\sum\limits_{i = 1}^{{N_{\rm{t}}}} {{{\left\| {\left( {{\mathit{\boldsymbol{p}}_i} - {\mathit{\boldsymbol{q}}_j}} \right)} \right\|}^2}} . $ |
7) 若εk≥εk-1, a)计算γk+1=2+(εk-εk-1)/((∨xk)T(Ak)Twk);b)如果γk+1 < 2, 设γk+1=2, 如果γ>10, 设γk+1=10;c)如果μk≤0.001, 设μk+1=γk+1, 否则设μk+1=γk+1μk并转到1).
8) 若εk < εk-1, 则
a)计算
| $ \begin{array}{l} {\beta _k} = - 2{\left( { \vee {\mathit{\boldsymbol{x}}_k}} \right)^{\rm{T}}}{\left( {{\mathit{\boldsymbol{A}}_k}} \right)^{\rm{T}}}{\mathit{\boldsymbol{w}}_k} + {\left( { \vee {\mathit{\boldsymbol{x}}_k}} \right)^{\rm{T}}}{\mathit{\boldsymbol{G}}_k} \vee {\mathit{\boldsymbol{x}}_k},\\ {\gamma _{k + 1}} = \left( {{\varepsilon _k} - {\varepsilon _{k - 1}}} \right)/{\beta _k}. \end{array} $ |
b)如果0.75≤γk+1≤1.2, 设μk+1=μk/4, 否则设μk+1=μk.
9) 输出改正系数μk+1.
设定ADF函数中μ的取值为{0.01, 0.05, 0.10, 0.15, 0.20, 0.40, 0.60, 0.80, 1.0}, 不同改正系数下均值误差em的计算结果如图 2所示.图中,IN为迭代次数.

|
图 2 不同改正系数均值误差(等于15表示算法发散) Fig. 2 Mean error under different correction coefficient (if it equals 15 indicates algorithm divergence) |
图 2的数据表明, 当ADF算法使用不同的改正系数时, 收敛均值误差区别很大.当改正系数取值过小时(如μ=0.01), 绝对切向距离不能拟合点-曲面最近距离, 导致拼合算法最终发散.当改正系数取值过大(如μ=0.8或μ=1.0) 时, 虽然算法稳步收敛, 但收敛的速度非常缓慢.该试验的最佳改正系数μ=0.05.在实际应用中, 采用2.2节介绍的方法适应性地改变改正系数, 连续提高法向距离比例, 加快收敛速度[16].
2.3 ICS精细配准设函数f为映射RS3→RS.用f的零水平集近似表示曲面PS上一点p的邻域NBr(p), 记作:
| $ {f_{{\rm{p}},r}}\left( \mathit{\boldsymbol{x}} \right) = 0. $ | (12) |
式中:NBr(p)为曲面PS在点p处的r闭球域.对于目标数据QS中的任一点qi和NBr(qi), 都可以构造曲面片fqi, r(x)=0, 其中NBr(qi)是定义在点集QS上的闭球域.将曲面PS近似表示成一组曲面片fqi, r(x)=0(i=1, 2, …, Nt).
三角网格用一组平面片表示曲面片PS, 当映射f为线性函数时, 定义为
| $ f\left( \mathit{\boldsymbol{x}} \right) = f\left( \mathit{\boldsymbol{y}} \right) + \nabla f{\left( \mathit{\boldsymbol{y}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right). $ | (13) |
当映射f为非线性函数时, 定义为
| $ f'\left( \mathit{\boldsymbol{x}} \right) = f\left( \mathit{\boldsymbol{y}} \right) + \nabla f{\left( \mathit{\boldsymbol{y}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right). $ | (14) |
式中:▽f(y)T为f在点y处的梯度, y为f的正则点, 则使x和y的距离‖y-x‖最小, 且满足f(x)=0的点x由下式算出:
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{y}} - {\left[ {\nabla f{{\left( \mathit{\boldsymbol{y}} \right)}^{\rm{T}}}} \right]^ + }f\left( \mathit{\boldsymbol{y}} \right). $ | (15) |
式中:[▽f(y)T]+为▽f(y)T的广义逆.
在对应曲面片配准的基础上, 提出ICS迭代对应曲面片配准算法.ICS配准算法用局部二次曲面片代替离散点作为配准的目标几何体, 减少了采样密度对配准精度的影响.与移动数据中的一点p对应的曲面片应为所有曲面片中到点p的距离最近的曲面片, 其中的距离由式(11) 近似.
定义ICS算法中的目标函数为
| $ F = \frac{1}{2}\sum\limits_{i = 1}^N {d_{{\rm{ADF}}}^2\left( {g,\mathit{\boldsymbol{Q}}} \right)} . $ | (16) |
用Y=C(PS, QS)表示移动点集PS在目标点集QS中的对应曲面片的集合, (g, ε)=PS(PS, Y)表示点集PS向对应曲面片集Y的坐标变换计算, 其中ε为对应点和曲面匹配的误差.初始化PS0=PS, 迭代次数k=0.g的初始值根据1.3节来估计.ICS算法的第k次迭代过程如下.
1) 计算最近曲面片集Yk=C(PSk, QS), 其中PSk是第k-1次迭代中得到的坐标变换gk-1作用于移动点集PS0生成的点集.
2) 构造目标函数
3) 建立如下非线性优化模型:
| $ \begin{array}{l} \min \;\;\;\;{F_k} = \frac{1}{2}\sum\limits_{i = 1}^N {d_{{\rm{ADF}}}^2\left( {{g_{k + 1}},{\mathit{\boldsymbol{Q}}_{\rm{S}}}} \right)} ;\\ {\rm{S}}.\;{\rm{t}}.\;\;{g_{k + 1}} = \left( {{\mathit{\boldsymbol{t}}_{k + 1}},{\mathit{\boldsymbol{R}}_{k + 1}}} \right),{\mathit{\boldsymbol{Q}}_{{{\rm{S}}_0}}} = \left\{ {\mathit{\boldsymbol{q}}_1^k,\mathit{\boldsymbol{q}}_2^k, \cdots ,\mathit{\boldsymbol{q}}_{{N_t}}^k} \right\} \subset {\mathit{\boldsymbol{Q}}_{\rm{S}}},\\ \;\;\;\;\mathit{\boldsymbol{q}}_j^k = \left\{ {\mathit{\boldsymbol{q}}\left| {\min \left\| {\mathit{\boldsymbol{p}}_i^k - \mathit{\boldsymbol{q}}} \right\|} \right.} \right\}. \end{array} $ |
4) 计算变换(gk, εk)=PS(PS0, Yk), 其中
| $ \begin{array}{l} {\varepsilon _k} = \varepsilon \left( {{g_k}} \right) = \\ \frac{1}{{{N_{\rm{t}}}}}\sum\limits_{i = 1}^{{N_{\rm{t}}}} {{f_i}{{\left( {{\mathit{\boldsymbol{p}}_i}\left( {{g_k}} \right)} \right)}^2}{{\left[ {\nabla {f_i}{{\left( {{\mathit{\boldsymbol{p}}_i}\left( {{g_k}} \right)} \right)}^{\rm{T}}}\nabla {f_i}\left( {{\mathit{\boldsymbol{p}}_i}\left( {{g_k}} \right)} \right)} \right]}^{ - 1}}} . \end{array} $ |
式中:pi(gk)为点pi∈PS在形位gk时的坐标, fi为Yk中pi(gk-1)所对应的曲面片.这一步的时间复杂度为O(NTLM), 其中TLM为文献[17]中LM算法的平均迭代次数.
5) 对移动点集PS0进行坐标变换gk, 可得PSk+1.
6) 对给定的误差τ>0或Nk>0, 当εk-εk-1 < τ或k>Nk时, 终止迭代并输出最优变换g*=g0×g1…gk;否则, 令k=k+1, 返回1).
3 算法实例结果分析对斯坦福大学提供的Armadillo模型的36视角激光扫描数据进行配准, 限于篇幅, 只显示2视角, 如图 3所示.根据图 2可知, 该试验的最佳改正系数μ=0.05.

|
图 3 2个视角Armadillo点云数据 Fig. 3 Points cloud data of 2 views Armadillo |
第1、2视角下2组点云的配准如图 4所示.如图 4(a)所示为用该算法对图 3(a)、(b)所示第1、2个视角点云的粗略配准结果图, 相应的初次配准误差为4.5×10-7.如图 4(b)所示为图 4(a)经Delaunay三角化后的光照模型;从图 4(a)、(b)可以看出, 该方法的粗略效果良好, 基本上实现了两片点云数据的正确配准.在某些区域, 如Armadillo的脚、胸部、嘴巴处, 配准点云出现轻微的漏洞.经过基于ADF和ICS算法的精细配准后, 大致可以补齐, 如图 4(c)所示, 相应的精细配准误差为2.1×10-7;如图 4(d)所示为图 4(c)经Delaunay三角化后的光照模型.

|
图 4 第1、2视角下2组点云的配准 Fig. 4 Registration of 2 group points cloud from view 1 and view 2 |
采用第1片为基准点云, 其他片点云依次序贯配准到基准坐标下的全局配准方法, 得到36视角配准结果对比, 如图 5所示.如图 5(a)所示为利用该算法得到的36视角Armadillo点云数据的整体配准结果;如图 5(b)所示为图 5(a)经Delaunay三角化后的光照模型;如图 5(c)所示为利用文献[18]算法得到的整体配准点云数据;如图 5(d)所示为图 5(c)经Delaunay三角化后的光照模型.比较图 5(b)、(d)可以看出, 本文的配准结果更加精确.

|
图 5 36视角配准结果对比 Fig. 5 Comparison of registration results of 36 views |
如表 1所示为图 5中配准结果的定量比较.该结果是在Pentium Ⅳ、3.10 GHz CPU、8 GB内存的PC机上计算得到的, 开发平台是VC++6.0和MA TLAB7.0.表 1列出了2种算法的迭代次数及配准误差.可以看出, 本文算法更加高效精确.
| 表 1 图 5中配准结果的定量比较(τ=10-6 mm) Table 1 Quantitative comparison of registration result in Fig. 5 (τ=10-6 mm) |
如图 6所示为图 5中2种配准算法收敛速度的比较, 显示了2种算法迭代150次的误差分布.图中,eR为配准误差.由于满足条件曲面片对的数量远远小于对应点对的数量, 因此本文算法只需较少的时间就可以计算出新的空间位置变换关系, 从而保证了每一次迭代的运行时间和文献[18]算法相比差距不大;考虑迭代次数可知, 本文算法具有更快的收敛速度.

|
图 6 图 5中2种算法的配准误差和迭代次数、收敛速度对比 Fig. 6 Comparison of registration error, iteration number and convergence rate of 2 algorithms in Fig. 5 |
为了说明本文算法的适用性, 对Bunny模型18视角激光扫描数据(取自于斯坦福大学)进行配准.图 7给出视角1、2两视角点云.

|
图 7 2视角Bunny点云数据 Fig. 7 Points cloud data of 2 views Bunny |
如图 8(a)所示为利用本文算法对图 7(a)、(b)所示视角1、2点云粗略配准的结果.如图 8(b)所示为图 8(a)经Delaunay三角化后的光照模型;经过基于ICS算法的精细配准后, 如图 8(c)所示;如图 8(d)所示为图 8(c)经Delaunay三角化后的光照模型.

|
图 8 第1、2视角下2组点云的配准 Fig. 8 Registration of 2 group points cloud from view 1 and view 2 |
如图 9(a)所示为利用本文算法得到的18视角Bunny点云数据的整体配准点云数据;如图 9(b)所示为图 9(a)经Delaunay三角化后的光照模型;如图 9(c)所示为利用文献[18]算法得到的18视角Bunny点云数据的整体配准点云数据;如图 9(d)所示为图 9(c)经Delaunay三角化后的光照模型.比较图 9(b)、(d)可知, 本文的配准结果更加准确.

|
图 9 18视角配准结果对比 Fig. 9 Comparison of registration results of 18 views |
为了说明本文粗配准的健壮性, 增加Armadillo初始位置相差较大的算例, 图 10给出120°和180°点云数据.

|
图 10 2个相差较大视角的Armadillo点云数据 Fig. 10 Armadillo points cloud dada from two large difference views |
如图 11(a)所示为利用本文算法对图 10(a)、(b)所示2视角点云粗略配准的结果, 如图 11(b)所示为图 11(a)经Delaunay三角化后的光照模型.
4 结论(1) 根据已有的点-点距离函数和点-切面距离函数, 引进一种新的点-曲面距离函数, 构造更加精确的点-曲面距离误差度量指标.
(2) 在传统ICP算法配准的基础上, 提出ICS配准算法.用局部二次曲面片代替离散点作为配准的目标几何体, 减少了采样密度对配准精度的影响, 保证了算法的精度和效率.
| [1] |
左超, 鲁敏, 谭志国, 等. 一种新的点云拼接算法[J].
中国激光, 2012, 39(12): 1212004-1–1212004-8.
ZUO Chao, LU Min, TAN Zhi-guo, et al. A novel algorithm for registration of point clouds[J]. Chinese Journal of Lasers, 2012, 39(12): 1212004-1–1212004-8. |
| [2] | SAHILLIOGLU Y, YEMEZ Y. Coarse-to-fine surface reconstruction from silhouettes and range data using mesh deformation[J]. Computer Vision and Image Understanding, 2010, 114(3): 334–348. DOI:10.1016/j.cviu.2009.12.003 |
| [3] | BESL P J, MCKAY N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239–256. DOI:10.1109/34.121791 |
| [4] | CHOW C K, TSUI H T, LEE T. Surface registrationusing a dynamic genetic algorithm[J]. Pattern Recognition, 2004, 37(1): 105–117. DOI:10.1016/S0031-3203(03)00222-X |
| [5] |
林洪彬, 刘彬, 张玉存. 逆向工程中散乱点云变尺度配准算法研究[J].
机械工程学报, 2011, 47(14): 1–6.
LIN Hong-bin, LIU Bin, ZHANG Yu-cun. Research on a variable scale registration algorithm for scattered point clouds in reverse engineering[J]. Journal of Mechanical Engineering, 2011, 47(14): 1–6. |
| [6] |
秦绪佳, 王建奇, 郑红波, 等. 三维不变矩特征估计的点云拼接[J].
机械工程学报, 2013, 49(1): 129–134.
QIN Xu-jia, WANG Jian-qi, ZHENG Hong-bo, et al. Point clouds registration of 3D moment invariant feature estimation[J]. Journal of Mechanical Engineering, 2013, 49(1): 129–134. |
| [7] |
王蕊, 李俊山, 刘玲霞, 等. 基于几何特征的点云配准算法[J].
华东理工大学学报, 2009, 35(5): 768–773.
WANG Rui, LI Jun-shan, LIU Ling-xia, et al. Registration of point clouds based on gemotric properties[J]. East China University of Science and Technology, 2009, 35(5): 768–773. |
| [8] | BASDOGAN C, OZTIRELI A C. A new feature based method for robust and efficient rigid-body registration of overlapping point clouds[J]. The Visual Computer, 2008, 24(7-9): 679–688. DOI:10.1007/s00371-008-0248-6 |
| [9] |
高鹏东, 彭翔, 李阿蒙, 等. ICP框架下基于表面间平均体积测度的深度像配准[J].
计算机辅助设计与图形学学报, 2007, 19(6): 719–724.
GAO Peng-dong, PENG Xiang, LI A-meng, et al. Range image registration with ICP frame using surface mean inter-space measure[J]. Journal of Computer-Aided Design and Computer Graphics, 2007, 19(6): 719–724. |
| [10] | 陈维桓. 微分几何[M]. 北京: 北京大学出版社, 2006: 77-184. |
| [11] | ZHANG Mei, WEN Jing-hua, FAN Yong-long. A new registration method for scattered point clouds from multi-views[J]. Information Technology Journal, 2013, 12(19): 5005–5010. DOI:10.3923/itj.2013.5005.5010 |
| [12] | 孙龙祥, 程义民, 王以孝, 等. 深度图像分析[M]. 北京: 电子工业出版社, 1996. |
| [13] |
张梅, 文静华, 张祖勋, 等. 基于欧氏距离测度的激光点云配准[J].
测绘科学, 2010, 35(3): 5–8.
ZHANG Mei, WEN Jing-hua, ZHANG Zu-xun, et al. Laser points cloud registration using Euclid distance measure[J]. Science of Surveying and Mapping, 2010, 35(3): 5–8. |
| [14] | POTTMANN H, HUANG Q X, YANG Y L, et al. Geometry and convergence analysis of algorithms for registration of 3D shapes[J]. International Journal of Computer Vision, 2006, 67(3): 277–296. DOI:10.1007/s11263-006-5167-2 |
| [15] |
刘宇, 熊有伦. 基于有界k-d树的最近点搜索算法[J].
华中科技大学学报:自然科学版, 2008, 36(7): 73–76.
LIU Yu, XIONG You-lun. Algorithm for searching nearest-neighbor based on the bounded k-d tree[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2008, 36(7): 73–76. |
| [16] |
李文龙. 复杂曲面零件数据拼合与精密加工技术研究[D]. 武汉: 华中科技大学, 2010.
LI Wen-long. Research on the data registration and precision machining technologies towards complex surfaces[D]. Wuhan:Huazhong University of Science and Technology, 2010. http://www.cqvip.com/QK/90288X/201221/44060144.html |
| [17] | PRESS W H, TEUKOLSKY S A, VWTTERLING W T, et al. Numerical recipes in C:the art of scientific computing[M]. 2nd ed. Cambridge:Cambridge University Press, 1992. http://www.doc88.com/p-33778736875.html |
| [18] |
薛耀红, 梁学章, 马婷, 等. 扫描点云的一种自动配准方法[J].
计算机辅助设计与图形学学报, 2011, 23(2): 223–231.
XUE Yao-hong, LIANG Xue-zhang, MA Ting, et al. An automatic registration method of scanned point clouds[J]. Journal of Computer-Aided Design and Computer Graphics, 2011, 23(2): 223–231. |



