2. 浙江大学 电气工程学院, 浙江 杭州 310027
2. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China
随着遥感技术的发展, 在同一地区获得多时相高光谱遥感影像成为可能, 高光谱遥感变化检测研究逐渐引起了关注.高光谱图像的变化检测分为像元级变化检测和亚像元级变化检测[1-2], 本文主要研究像元级变化检测.
分类后比较是最简单的像素级变化检测方法.由于高光谱图像空间分辨率的限制, 混合像元普遍存在, 导致传统分类方法的精度不高[3].虽然光谱解混可以提高分类精度, 但对所有像元分类后比较进行变化检测, 分类误差对变化检测结果的影响较大.变化向量分析(change vector analysis, CVA)[4]是先比较、后分类的多类变化检测方法.Liu等[2]提出二维自适应光谱变化向量表示算法(adaptive spectral change vector representation, 2-D ASCVA)用于高光谱图像的变化检测.该方法需要人机交互实现变化区域的分类.Dawelbait等[5]结合光谱混合分析和CVA, 提出SU_CVA(spectral unmixing and change vector analysis, SU_CVA).SU_CVA方法的不足是没有考虑不同时相图像的端元可能不一致, 只能直接检测两类地物的变化, 如何实现多类变化检测是一个问题.
本文提出结合CVA和光谱解混实现高光谱变化检测方法(change vector and spectral unmixing, CVA_SU), 利用CVA的变化强度, 经阈值分割判断变化与非变化区域, 对变化区域基于光谱解混分类确定变化类型.CVA_SU方法解决了CVA方法无法确定具体变化信息的问题, 结合CVA利用所有波段信息判断变化区域的优势, 与直接用分类后比较的方法相比, 可以减少分类精度对变化检测结果的影响.
1 高光谱图像光谱解混高光谱数据R是一个I×J×L的图像立方体, 其中I、J和L分别对应图像的行数、列数和光谱维(代表高光谱图像的波段个数).基于线性光谱混合模型(linear spectral mixing model, LSMM), 坐标为(i, j)的像元Rij∈RL可以形式化[6]为
| $ {\boldsymbol{R}_{ij}} = \boldsymbol{E}{\boldsymbol{S}_{ij}} + {\boldsymbol{n}_{ij}}. $ | (1) |
满足约束:
| $ {e_{lp}} \ge 0,1 \le l \le L. $ | (2) |
| $ 0 \le {S_{ijp}} \le 1,\sum\limits_{p = 1}^P {{S_{ijp}} = 1.} $ | (3) |
式中:E=[e1, e2, …, ep, …, eP]∈RL×P为P个端元构成的端元矩阵, Sij∈RP中的每一个元素对应于像元Rij中相应端元所占的比例(丰度), nij为噪声.式(2)、(3) 分别称为非负性约束和全加性约束.
光谱解混是指利用端元提取技术[7]得到端元矩阵E, 再通过混合像元分解技术[8]估计丰度Sij或通过非监督的方法同时得到端元矩阵和丰度[9].
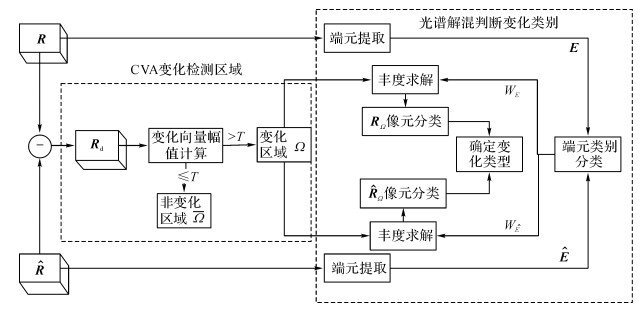
2 CVA结合光谱解混的变化检测算法算法流程如图 1所示.整个算法包含CVA检测变化区域和光谱解混判断变化类别两部分.
|
图 1 变化检测流程 Fig. 1 Flow chart of change detection |
设R和
| $ {\rho _{ij}} = \sqrt {\sum\limits_{l = 1}^L {{{(r_{{\rm{d}}ij}^l)}^2}} } . $ | (4) |
式中:rdijl为Rdij中第l波段的光谱值;ρij包含了两幅图像中坐标为(i, j)像元的变化信息, 当ρij越大时, 变化发生的可能性越大.变化向量的方向代表地物的变化类型.本文只用到ρij.
首先计算所有变化向量的幅值, 然后基于期望值最大化的最小贝叶斯决策算法[10]确定阈值T, 之后比较ρij与T的大小, 判定两幅图像(i, j)位置是否发生了变化, 最后得到变化区域Ω和非变化区域Ω.
2.2 光谱解混判断变化类别光谱解混判断变化区域Ω的类别变化信息, 具体过程分为以下3个步骤.
1) 端元提取.
由于季节变化或其他原因, 同一地区不同时间的地物的类别数以及类别信息不一定完全相同, 需要对R和
2) 端元类别编号确定.
记端元矩阵E中第p个端元ep的类别编号ωp=p, 则E中各端元类别编号集为WE{=ω1, ω2, …, ωP}={1, 2, …, P}.通过相关系数, 判断
| $ \rho (x,y) = \frac{{\sum\limits_{l = 1}^L {({x_l} - \bar x)({y_l} - \bar y)} }}{{\sqrt {\sum\limits_{l = 1}^L {{{({x_l} - \bar x)}^2}} \sum\limits_{l = 1}^L {{{({y_l} - \bar y)}^2}} } }}. $ | (5) |
式中:
| $ \bar x = \frac{1}{L}\sum\limits_{l = 1}^L {{x_l}} ,\bar y = \frac{1}{L}\sum\limits_{l = 1}^L {{y_l}} . $ |
输入:E,
输出:
初始化ρ的阈值为Tρ, n=P;
计算E中各端元间的相关系数, 求最大值(除自相关系数), 记为ρmaxE.
计算
若Tρ≤max(ρmaxE, ρmax
对
计算
如果ρmax>Tρ, 则
其中, γ取值为[0.001, 0.01]比较合适, max (ρmaxE, ρmax
3) 变化类别确定.
设图像R和
| $ \left. \begin{array}{l} {c_{ij}} = \mathop {{\omega _{\arg \max ({S_{ijP}})}},}\limits_p \\ {{\hat c}_{ij}} = \mathop {{{\hat \omega }_{\arg \max ({{\hat S}_{ijP}})}}.}\limits_p \end{array} \right\}. $ | (6) |
逐像元比较, 确定变化类别.
3 实验分析分别采用仿真数据和真实多时相高光谱图像, 验证算法的性能.由于CVA、SU_CVA和2-D ASCVA等方法都无法检测具体的变化信息, 采用光谱解混(spectral unmixing, SU)分类后比较的方法和CVA_SU方法可以检测具体的变化信息, 只对SU和CVA_SU进行实验比较.具体实现中, 采用HFC(Harsanyi-Farrand-Chang, HFC)算法[11]确定高光谱图像中的端元数, 用FNSGA[7]提取端元, 利用全约束最小二乘法[8]求丰度.
3.1 仿真数据实验选取1998年拍摄于加利福尼亚州Salinas峡谷的AVIRIS高光谱图像[12](OL), 该数据有220个波段, 波长为0.4~2.5 μm, 光谱分辨率为10 nm, 空间分辨率为3.7 m.在预处理过程中, 对所有波段进行优化, 去除20个无效波段(波段108~112、154~167、224), 剩余204个波段被用于进一步处理.截取大小为94×217个像素的子图作为参考图像R, 如图 2(a)所示.图 2(a)包含5类地物, 分别为碎秸(stubble), 粗糙的休耕地(fallow_rough_plow), 平滑休耕地(fallow_smooth), 芹菜(celery), 已耕地(soil_vinyard_develop), 表 1列出了所有可能的变化类别.

|
图 2 仿真的多时相图像及变化类型示意图 Fig. 2 Simulated changed images and change referencemap |
| 表 1 所有可能的变化类别 Table 1 All possible change classes |
从R中提取9块子图, 用于替换原图不同位置的像元, 并加入一定信噪比, 仿真得到如图 2 (b)所示的不同时相图像
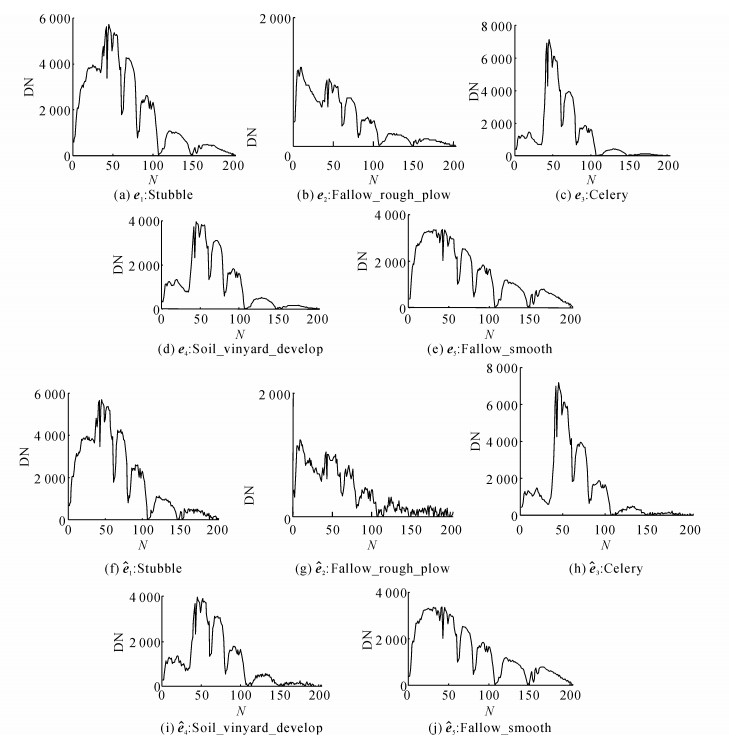
以信噪比SNR=30 dB为例, 分析利用本文算法得到的变化检测结果.用FNSGA方法提取端元, 得到的结果如图 3所示.其中, 图 3(a)~(e)为R的端元, 图 3(f)~(j)为
|
图 3 仿真图像端元光谱曲线 Fig. 3 Spectral curves of endmembers for simulated images (SNR=30 dB) |
| 表 2 R端元光谱相似性 Table 2 Similarity for endmembers in R |
|
表 3 端元光谱相似性
Table 3 Similarity for endmembers in |
|
表 4 R与 |
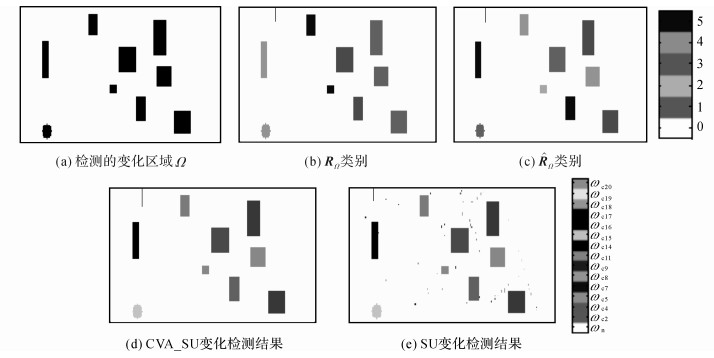
图 4给出通过CVA检测得到的变化区域及变化区域分类和检测结果, 其中变化区域检测阈值T=961.369.与图 2(c)、4(a)相比, CVA检测的变化区域与实际变化区域完全相同.CVA_SU最终检测出8类变化, 分别为{ωc2, ωc4, ωc9, ωc11, ωc15, ωc16, ωc18, ωc20}, 与仿真的变化类型完全一致.与图 4(e)的变化检测结果相比, SU检测出14类, 还检测出了不该出现的类别{ωc5, ωc7, ωc8, ωc14, ωc17, ωc19}.虽然能够检测出仿真的变化类, 但是由于SU对全局进行混合像元分解, 并且受噪声的影响, 产生了一些细小的误差.
|
图 4 变化区域分类和检测结果示意图 Fig. 4 Sketch map of change region classification and detected change results |
为了验证信噪比对算法性能的影响, 分别取SNR=[15, 20, 30, 40] dB, 对误检样本个数、虚警率、总体变化检测精度(overall accuracy, OA)和运行时间进行比较.表 5给出CVA_SU与SU的变化检测结果.可以看出, 对于SU方法, 当SNR=15 dB时, 方法几乎失效;当SNR=20 dB时, 虚警率相对较高, 很多非变化区域都被误检为变化区域, SNR=30 dB时仍有不少误检, 只有SNR=40 dB时效果较好, OA较高且虚警率低.对于CVA_SU方法, 当SNR=15 dB时, 结果不是很好, 可能是由于图像中有几类地物光谱非常相似, 导致光谱解混算法对噪声的鲁棒性降低.在[20, 30] dB下, CVA_SU的虚警率远远低于SU的虚警率, CVA_SU的OA远远高于SU.当SNR=40 dB时, 两者的精度相当.
| 表 5 不同SNR下2种方法的变化检测结果比较 Table 5 Comparison for detected change results for different SNR |
对于两幅N个像元的高光谱图像, 设变化像元数为n个(n≪N), CVA_SU算法的运行时间由4部分组成:N个向量求模的时间、EM求阈值运算时间、端元提取及端元类别确定的时间和2n个像元丰度求解的时间.SU算法的运行时间包含端元提取及端元类别编号确定的时间和2N个像元丰度求解的时间.丰度求解问题是求二次规划最优解的问题, 时间复杂度远大于求模运算, 因此CVA_SU算法只增加了变化区域判断的少量计算量, 大大减少了后续丰度求解的时间.
3.2 真实图像实验该数据来自Hyperion传感器对美国佛罗里达州植被灌溉区域的监测[13](OL), 分别在2004年5月1号和2007年5月8号获得, 如图 5(a)、(b)所示, 部分地物分布呈椭圆形.图像大小为228×211个像素点.Hyperion图像的波长为350~2 580 nm, 光谱分辨率为10 nm, 空间分辨率为30 m.在预处理的过程中, 对波段进行优化, 去除异常波段, 留下153个波段.

|
图 5 不同时相的真实高光谱图像 Fig. 5 Bitemporal hyperion image |
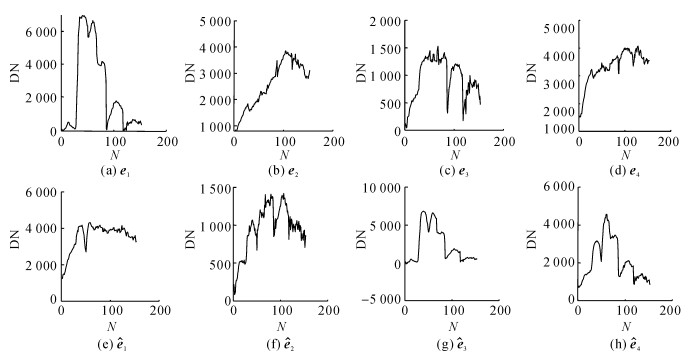
由于该图像得不到真实的地面覆盖信息, 通过视觉定性分析结果的有效性.根据FNSGA算法提取端元, 得到如图 6所示的端元光谱, 其中图 6(a)~(d)为2004年图像端元光谱, 图 6(e)~(h)为2007年图像端元光谱.表 6给出端元间的相关系数, 阈值Tρ=0.918.从图 6可以看出, e1与
|
图 6 真实图像光谱曲线图 Fig. 6 Spectral signatures of endmembers extracted from real images |
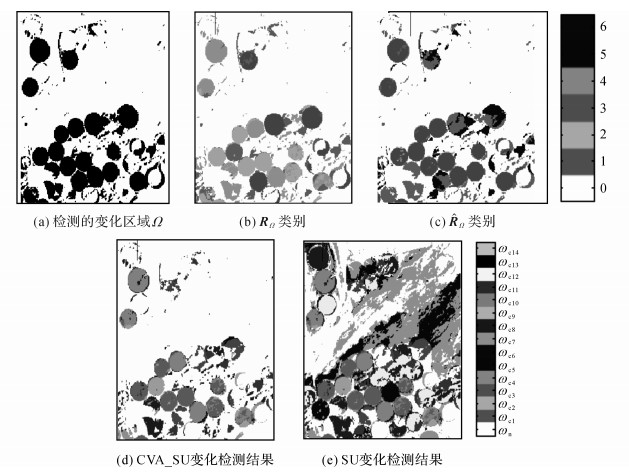
|
图 7 真实高光谱图像变化区域及变化类别检测结果 Fig. 7 Sketch map of change region classification and detected change results for real images |
| 表 6 真实图像端元间的相似性 Table 6 Similarity for endmembers in real images |
| 表 7 真实高光谱图像变化检测结果比较 Table 7 Comparison for results of real images |
本文提出CVA检测变化区域结合光谱解混判断变化类别的高光谱图像多类变化检测新方法.CVA利用高光谱图像的所有波段信息, 提高了变化区域检测的准确性, 降低了后续光谱解混的计算量.光谱解混判断变化类别充分考虑了高光谱图像混合像元普遍存在的特点, 提高了分类精度和变化类别判断的准确性.本文存在一些不足:1) 端元提取和丰度求解都可能引起分类误差, 从而影响整个算法的性能;2) 当两个端元光谱非常相似时, 如果阈值设置不当可能会导致端元类别判断错误而影响变化检测的结果;3) 由于高光谱图像混合像元的普遍存在, 混合像元的类别是一种软分类, 像素级的变化检测是一种较粗的近似变化检测方法.后续研究的工作重点在基于CVA和光谱解混实现高光谱图像各像素更精细的变化检测, 包括像素内不同地物发生变化的比例, 甚至是亚像元级的变化检测.
| [1] | NIELSEN A. The regularized iteratively reweighted MAD method for change detection in multi-and hyperspectral data[J]. IEEE Transactions Image Process, 2006, 16(2): 463–478. |
| [2] | LIU S, BRUZZONE L, BOVOLO F. Sequential spectral change vector analysis for iteratively discovering and detecting multiple changes in hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4363–4378. DOI:10.1109/TGRS.2015.2396686 |
| [3] |
杜培军, 夏俊士, 薛朝辉, 等. 高光谱遥感影像分类研究进展[J].
遥感学报, 2016, 20(2): 236–256.
DU Pei-jun, XIA Jun-shi, XUE Chao-hui, et al. Review of hyperspectral remote sensing image classification[J]. Journal of Remote Sensing, 2016, 20(2): 236–256. |
| [4] | ALP E, ANTONIO P. Informative change detection by unmixing for hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 12(6): 1252–1256. DOI:10.1109/LGRS.2015.2390973 |
| [5] | DAWELBAIT M A A, MORARI F. Landsat, spectral mixture analysis and change vector analysis to monitor land cover degradation in a savanna region in Sudan (1987-1999-2008)[J]. International Journal WaterResources and Arid Environments, 2011, 1(5): 366–377. |
| [6] | 童庆禧, 张兵, 郑兰芬. 高光谱遥感:原理、技术与应用[M]. 北京: 高等教育出版社, 2006. |
| [7] |
王丽姣. 基于单形体体积增长的高光谱图像端元提取及快速实现[D]. 杭州: 浙江大学, 2015.
WANG Li-jiao. Hyperspectral endmember extraction and its fast implementation based on simplex growing theory[D]. Hangzhou:Zhejiang University, 2015. |
| [8] | HEINZ D C, CHANG C I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(3): 529–545. DOI:10.1109/36.911111 |
| [9] |
贾森. 非监督的高光谱图像解混技术研究[D]. 杭州: 浙江大学, 2007.
JIA Sen. Unsupervised hyperspectral unmixing theory and techniques[D]. Hangzhou:Zhejiang University, 2007. http://www.docin.com/p-1397110724.html |
| [10] |
盛辉, 廖明生, 张路. 基于典型相关分析的变化检测中变化阈值的确定[J].
遥感学报, 2004, 8(05): 451–457.
SHEN Hui, LIAO Ming-sheng, ZHANG Lu. Determination of threshold in change detection based on canonical correlation analysis[J]. Journal of Remote Sensing, 2004, 8(05): 451–457. |
| [11] | CHANG C I, DU Q. Estimation of number of spectrally distinct signal sources in hyperspectral imagery[J]. Geoscience and Remote Sensing Letters, 2004, 42(3): 608–619. DOI:10.1109/TGRS.2003.819189 |
| [12] | Hyperspectral remote sensing scenes[EB/OL].[2016-11-01]. http://www.ehu.es/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes. |
| [13] | Earthexplorer[EB/OL].[2016-11-01]. http://earth-explorer.usgs.gov. |



