分类学习作为模式识别领域的一个重要分支, 现在已经在医疗诊断、机器视觉、数据挖掘等领域得到了广泛应用.传统的分类学习方式都是基于经验风险最小化原理(empirical risk minization, ERM)的, 相比这种方法, 以支持向量机(support vector machine, SVM)[1]为代表的基于结构化风险最小原理(structural risk minimization, SRM)的方法更具泛化能力.由于SVM实际上是QP优化问题, 时间复杂度上限是O(dN2), 其中d为数据集维数, N为数据集样本规模, 可见时间花费会随着训练集规模的增加而急剧增加[2].为此, Huang等[2-3]在SVM的基础上进行很多改进性的研究.Huang在单隐层前馈神经网络(single-hidden layer feedforward neural network, SLFN)的基础上, 提出极限学习机(extreme learning machine, ELM)理论[4].该理论能够快速逼近任何连续函数, 具有很好的分类性能和快速的学习效率, 但以ELM为代表的神经网络都缺乏可解释性.
为了提高对实际问题的可解释性, 出现了基于模糊规则的分类器, 特别是Takagi-Sugeno-Kang(TSK)型模糊分类器因其输出的简洁和良好的逼近能力被广泛探讨和运用[5-6].蔡前凤等[7]使用最小二乘支持向量机训练TSK规则, 以提高TSK模糊模型处理高维问题的推广能力;后来提出基于核映射的高阶TS模糊系统, 然而高阶TSK模糊系统会降低系统的可解释性, 且学习效率较低.杨昌健等[8]将0阶TSK模糊系统应用到迁移学习中以解决EEG信号的识别问题;邓赵红等[9]使用模糊子空间聚类模糊聚类算法, 对模糊if-then规则前件进行学习, 提出0阶L2型TSK模糊系统, 然而它们都具有较高的时间花费, 难以解决大规模数据集的分类问题.Leski[10]在FCM的基础上, 提出FCPM模糊聚类算法;将FCPM用来训练模糊规则前件, 使用迭代重加权最小二乘法(iteratively reweighted least squares, IRLS)训练模糊规则后件;提出基于Mamdani的模糊分类器FCPM-IRLS, 但具有时空花费高的不足.除此之外, Starczewski等[11-13]采用如遗传算法、混合模糊神经网络的方法来构建模糊分类器, 然而这些算法都存在时空花费高、鲁棒性较差等问题.
为了提高系统可解释性, 降低时间花费, 同时尽量提高系统的分类性能, 本文在文献[11]的基础上, 利用增量式模糊聚类算法IFCM(c+p) [14]训练模糊if-then规则前件参数、IRLS优化算法训练模糊if-then规则后件, 提出增量式0阶TSK型模糊分类器TSK-IFCIRLS0.为了提高模糊分类器TSK-IFCIRLS0的抗噪性, 本文在伪Huber函数(pseudo Huber, PHub)[15]的基础上, 提出新的代价函数;采用拟牛顿法训练后件参数, 提出另一种具有鲁棒性的增量式0阶TSK型模糊分类器TSK-IFCPHub0.本文所提模糊分类器都是增量式的, 具有很好的数据规模可扩展性.
1 TSK型模糊分类器简介常见的模糊系统包括0阶、一阶及高阶的TSK(Takagi-Sugeno-Kang)型模糊系统、ML(Mamdani-Larsen)型模糊系统以及广义模糊系统(generalized fuzzy system, GFM)[16], 其中0阶TSK型模糊系统得到了广泛应用, 本文在0阶TSK型模糊系统的基础上进行研究.典型的多输入单输出0阶TSK型模糊系统的第i条模糊规则可以表示为
| $ \begin{array}{l} R_i^l:{\rm{if}}\;{\mathit{\boldsymbol{x}}_1}\;{\rm{is}}\;A_{i,1}^l\;\& \;{\mathit{\boldsymbol{x}}_2}\;{\rm{is}}\;A_{i,2}^l\;\& \; \cdots \;\& \;{\mathit{\boldsymbol{x}}_n}\;{\rm{is}}\;A_{i,n}^l,\\ {\rm{Then}}\;\mathit{\boldsymbol{y}}\;{\rm{is}}\;f_i^l\left( \mathit{\boldsymbol{x}} \right),i \in \left[ {1,c} \right]. \end{array} $ | (1) |
其中, c表示模糊规则数, l为输入样本的实际类别, xj=[xj1, xj2, …, xjn], j∈[1, N]表示模糊分类器的输入, y为模糊分类器的输出, n为输入样本的特征数, Ai, dl为在第l类中第i条输入规则的第d个特征对应的模糊子集.该模糊子集对应的隶属函数为μAi, dl(xd),
| $ {\mu _{A_i^l}}\left( \mathit{\boldsymbol{x}} \right) = \exp \left( { - \frac{1}{2}\sum\limits_{d = 1}^n {\frac{{{{\left( {{\mathit{\boldsymbol{x}}_d} - \mathit{\boldsymbol{v}}_{i,d}^l} \right)}^2}}}{{{\rho ^2}s_{i,d}^l}}} } \right). $ | (2) |
式中:vi, dl表示聚类中心;ρ为离散度参数;si, dl为离散度,
| $ s_i^l = \frac{{\sum\limits_{k \in {{\bar \omega }_l}} {u_{ik}^l\left( {{{\left( {{\mathit{\boldsymbol{x}}_k} - \mathit{\boldsymbol{v}}_i^l} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_k} - \mathit{\boldsymbol{v}}_i^l} \right)} \right)} }}{{\sum\limits_{k \in {{\bar \omega }_l}} {u_{ik}^l} }},i \in \left[ {1,c} \right]; $ | (3) |
其中,ωl为属于第l类的样本集合, uikl为经过模糊划分得到的第l类的模糊隶属度.
0阶TSK型模糊系统的输出[11]可以表示为
| $ \begin{array}{l} y_{{\rm{o}}j}^l = f\left( {{\mathit{\boldsymbol{x}}_j}} \right) = \sum\limits_l {\sum\limits_{i = 1}^c {\frac{{{\mu _{A_i^l}}\left( {{\mathit{\boldsymbol{x}}_j}} \right)}}{{\sum\limits_l {\sum\limits_{i = 1}^c {{\mu _{A_i^l}}\left( {{\mathit{\boldsymbol{x}}_j}} \right)} } }}y_i^l} } = \\ \;\;\;\;\sum\limits_l {\sum\limits_{i = 1}^c {\overline {{\mu _{A_i^l}}} \left( {{\mathit{\boldsymbol{x}}_j}} \right)y_i^l} } = g\left( {{\mathit{\boldsymbol{x}}_j}} \right){\mathit{\boldsymbol{y}}^{\rm{T}}};j \in \left[ {1,N} \right]. \end{array} $ | (4) |
式中:
给定输入样本, 具体的类别归属可用下式所示的决策函数表示:
| $ f\left( \mathit{\boldsymbol{x}} \right) = \arg \mathop {\max }\limits_l \left( {\mathit{\boldsymbol{y}}_{\rm{o}}^l} \right). $ | (5) |
针对传统模糊分类器学习效率低下的问题, 提出基于增量式的0阶TSK模糊分类器TSK-IFCIRLS0.为了提高模糊分类器TSK-IFCIRLS0的鲁棒性, 提出基于伪Huber损失函数的增量式0阶TSK模糊分类器TSK-IFCPHub0.
与以往的模糊分类规则相比, 提出的模糊规则具有以下优点.
1) 规则前件:采用增量式模糊聚类算法, 可以大幅提高前件参数的训练时间, 对于某一类已知的数据集将有更好的性能.
2) 规则后件:每条规则的输出都是常数, 保证了TSK模糊分类器的高简洁性, 采用伪Huber形式的损失函数, 提高了模糊分类器的鲁棒性.
3) 提出的2种模糊分类器具有很好的数据规模可扩展性.
2 增量式0阶TSK型模糊分类器建模 2.1 基于IFCM(c+p)的模糊规则前件学习模糊if-then规则的前件学习是将输入样本特征映射到模糊空间中确定模糊划分的过程.Leski[10]提出的模糊分类器采用FCPM模糊聚类算法来训练模糊if-then规则的前件, 但随着数据集规模的增加, 算法的聚类性能显著下降, 甚至会由于样本过大而导致算法失效.李滔等[14]提出适合大规模数据集的增量式模糊聚类算法IFCM(c+p), 通过在整个数据集上进行分块聚类, 将最后一个数据块的聚类结果作为整个数据集的聚类结果.在每一个数据块的聚类过程中, 为了增大数据块间的相互影响程度, 该算法在FCPM的基础上添加了平衡项
模糊规则后件的学习实际上是根据模糊规则前件进行模糊推理, 得到模糊输出的过程.本文首先使用IRLS优化算法对模糊规则后件进行训练, 参照文献[10], 对于二分类问题, 为了尽量区分所有不同类别的训练样本, 应该满足如下代价函数:
| $ \mathop {\min }\limits_\mathit{\boldsymbol{y}} J\left( \mathit{\boldsymbol{y}} \right) = \sum\limits_{j = 1}^N {L\left( {{\theta _j}g\left( {{\mathit{\boldsymbol{x}}_j}} \right){\mathit{\boldsymbol{y}}^{\rm{T}}}} \right)} . $ | (6) |
式中:
| $ {\theta _j} = \left\{ \begin{array}{l} + 1,{\mathit{\boldsymbol{x}}_j} \in {{\bar \omega }_1},\;\;\;j \in \left[ {1,N} \right];\\ - 1,{\mathit{\boldsymbol{x}}_j} \in {{\bar \omega }_2},\;\;\;j \in \left[ {1,N} \right]. \end{array} \right. $ |
选择平方损失函数时, 式(6) 可以表示为
| $ \begin{array}{l} \mathop {\min }\limits_\mathit{\boldsymbol{y}} J\left( \mathit{\boldsymbol{y}} \right) = \sum\limits_{j = 1}^N {{{\left( {{\theta _j}g\left( {{\mathit{\boldsymbol{x}}_j}} \right){\mathit{\boldsymbol{y}}^{\rm{T}}} - 1} \right)}^2}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{y}}^{\rm{T}}} - {\bf{1}}} \right)^{\rm{T}}}\mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{y}}^{\rm{T}}} - {\bf{1}}} \right). \end{array} $ | (7) |
式中:1⊂ RN为所有元素都等于1的向量; G=[θ1g(x1), θ2g(x2), …, θNg(xN)]Τ; H=diag [h1, …, hj, …, hN], 其中hj为第j个样本对应的权值,
| $ {h_j} = \left\{ \begin{array}{l} 0,{e_j} \ge 0,\;\;\;j \in \left[ {1,N} \right];\\ 1,{e_j} < 0,\;\;\;j \in \left[ {1,N} \right]. \end{array} \right. $ | (8) |
ej为第j个样本对应的误差,
| $ \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{y}}^{\rm{T}}} - {\bf{1}}. $ | (9) |
为了找到分类器的最佳输出权重y, 需要通过迭代的方式求解式(7) 所示的优化问题, 对输出权重求导, 可以得到
| $ \mathit{\boldsymbol{y}} = {\left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{HG}}} \right)^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{H}}{\bf{1}}. $ | (10) |
式(10) 是基于IRLS优化算法的模糊分类器的输出权重公式.分类器在求输出权重时, 每次迭代都需要对样本进行重复加权, 以便对误分类样本进行惩罚;于是, 分类器可以在每次的学习中不断调整分离超平面的位置, 以提高分类器的分类性能.
2.3 基于伪Huber损失函数的模糊规则后件学习IRLS算法的核心在于重加权时损失函数的选择, 然而文献[10]采用的非对称平方(asymmetric square, ASQR)型损失函数对噪声数据和离群点较敏感, 缺乏鲁棒性.尽管Leski[10]提及了其他类型的损失函数, 如非对称线性ALIN(asymmetric linear)、非对称哈勃AHUB(asymmetric HUBer), 以增强分类器的鲁棒性, 但前面提到的几种损失函数在实数域上不可导;IRLS算法采用平方误差损失函数, 会对异常值很敏感, 如当样本是重尾分布时(根据估计理论可知, 中值的渐进相关效率会在重尾分布时表现得较差), 采样均值会受少量较大值的影响.伪Huber损失函数[15]可以很好地避免上述问题, 故采用伪Huber函数重新表示代价函数来训练模糊规则后件.伪Huber函数的一般形式如下:
| $ {L_\delta }\left( x \right) = {\delta ^2}\left( {\sqrt {1 + {{\left( {x/\delta } \right)}^2}} - 1} \right). $ | (11) |
式中:δ为可调的阈值参数.从式(11) 可见, 伪Huber函数在整个实数域内都是可导的, 且对异常值不敏感, 具有很好的鲁棒性.式(6) 所示的代价函数用伪Huber损失函数可以表示为
| $ \begin{array}{l} \mathop {\min }\limits_\mathit{\boldsymbol{y}} J\left( \mathit{\boldsymbol{y}} \right) = \\ \;\;\;\sum\limits_{j = 1}^N {{\delta ^2}\left( {\sqrt {1 + {{\left[ {\left( {{\theta _j}g\left( {{\mathit{\boldsymbol{x}}_j}} \right){\mathit{\boldsymbol{y}}^{\rm{T}}} - 1} \right)/\delta } \right]}^2}} - 1} \right).} \end{array} $ | (12) |
式(12) 对y微分可知, 对y微分之后的结果恒大于0, 则J(y)是单调的, 只能通过迭代法求解.拟牛顿法(Quasi-Newton method)[17]是在牛顿法(Newton method)的基础上进行改进的算法.相比牛顿法, 拟牛顿法具有收敛速度快、计算复杂度低的优点, 常用于非线性无约束优化问题的求解.本文采用拟牛顿法求解式(12) 所示的非线性无约束优化问题.
设具有二阶连续偏导的目标函数J(y)的第k次迭代值是yk, 则将J(y)在yk附近进行二阶泰勒展开, 忽略高阶无穷小项, 可得
| $ \nabla J\left( \mathit{\boldsymbol{y}} \right) \approx \nabla J\left( {{\mathit{\boldsymbol{y}}_{k + 1}}} \right) + {\nabla ^2}J\left( {{\mathit{\boldsymbol{y}}_{k + 1}}} \right)\left( {\mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{y}}_{k + 1}}} \right). $ | (13) |
令y=yk, sk=yk+1-yk, βk=▽J(yk+1)-▽J(yk), Hk+1=▽2J(yk+1)(即海塞矩阵), 则式(13) 可以等价表示为
| $ {\mathit{\boldsymbol{\beta }}_k} = {\mathit{\boldsymbol{H}}_{k + 1}}{\mathit{\boldsymbol{s}}_k}. $ | (14) |
式(14) 为拟牛顿条件, 在拟牛顿法中根据拟牛顿条件构造相应的近似海塞矩阵, 从而表示出求解非线性优化问题的迭代公式.本文选取BFGS算法[17]构造近似海塞矩阵.考虑用Bk逼近海塞矩阵Hk, 则BFGS算法中近似矩阵Bk+1的迭代公式可以表示为
| $ {\mathit{\boldsymbol{B}}_{k + 1}} = {\mathit{\boldsymbol{B}}_k} + \frac{{{\mathit{\boldsymbol{\beta }}_k}\mathit{\boldsymbol{\beta }}_k^{\rm{T}}}}{{\mathit{\boldsymbol{\beta }}_k^{\rm{T}}{\mathit{\boldsymbol{s}}_k}}} - \frac{{{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{s}}_k}\mathit{\boldsymbol{s}}_k^{\rm{T}}{\mathit{\boldsymbol{B}}_k}}}{{\mathit{\boldsymbol{s}}_k^{\rm{T}}{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{s}}_k}}}. $ | (15) |
为了高效解决不同规模样本的分类问题, 保证高可解释性和不错的分类性能, 一定要快速建立模糊规则, 即快速完成从输入样本到模糊子空间的模糊划分过程和快速进行模糊推理完成模糊输出的过程.本文采用增量式模糊聚类算法IFCM(c+p)训练模糊规则前件.研究表明, 采用该方法可以很好地提高聚类性能和聚类效率[14].采用该方法可以使得分类器具有很好的数据规模可扩展性.为了在每个类中确定更加合理、更具解释性的规则, 在前件参数的学习中, 需要在相应的类中得到更加稳定的聚类中心.本文借鉴文献[10]的思想, 通过循环迭代的思想获取两个类的聚类中心, 即两个类相互作为已知类别的聚类中心;然后通过IFCM(c+p)算法求另一类的聚类中心, 直至其中一类的聚类中心稳定下来时, 另一类的聚类中心也稳定下来, 此时迭代停止, 可得各类中稳定的聚类中心.将经过迭代产生的聚类结果代入隶属度函数, 可以完成模糊化过程, 即完成了前件参数的学习.在另一方面, 为了能够快速确定模糊规则的后件参数, 采用IRLS优化算法并结合共轭梯度算法以加快输出权重的求取, 可以快速建立TSK-IFCIRLS0模糊分类器模型.算法的具体步骤如下.
1) 对训练集进行分块(尽量随机等分).
2) 确定模糊规则的前件参数.
a)让ω1和ω2类中具有相同聚类个数, 即c=p.
b)使用文献[11]的算法1分别确定ω1和ω2类的初始聚类中心Vuk1、Vuk2.
c)利用Vuk1作为ω1类中未知类的初始聚类中心, 定义一个空集作为已知类的聚类中心, 使用IFCM(c+p)算法获取ω1类的聚类中心V1.
d)使用c)的方法确定ω2类的聚类中心V2.
e)将ω1、ω2类的聚类中心分别作为未知类和已知类的初始聚类中心, 使用IFCM(c+p)算法更新未知类ω1的聚类中心V1.
f)将ω2、ω1类的聚类中心分别作为未知类和已知类的初始聚类中心, 使用IFCM(c+p)算法更新未知类ω2的聚类中心V2.
g)计算V2相对于上一次迭代结果的变化量的Frobenius范数.若该值小于ξ, 则停止迭代;否则回到f)继续计算.
3) 使用IFCM(c+p)算法的样本隶属度计算公式, 确定ω1、ω2类的样本隶属度矩阵U1、U2.
4) 计算ω1、ω2类的离散度矩阵S1、S2.
5) 计算ω1、ω2类中前件的隶属度矩阵μ1、μ2, 然后得到g(x).
6) 确定模糊规则后件参数.
a)初始化样本权值矩阵, 令H=I.
b)计算输出权重y.
c)计算误差向量e=GyT-1.
d)更新样本权值hj(j∈[1, N]).
e)计算输出权重y的变化量的范数.若该值小于ξ, 则迭代停止;否则回到b)继续计算.
通过上述训练过程, 可以建立基于IRLS的模糊分类器模型TSK-IFCIRLS0.其中, I⊂RN×N为单位矩阵, ξ为迭代终止条件.需要对两类的输入样本进行分类识别, 则模糊分类器的决策函数可以表示为
| $ f\left( {{\mathit{\boldsymbol{x}}_j}} \right) = {\mathop{\rm sgn}} \left( {g\left( {{\mathit{\boldsymbol{x}}_j}} \right){\mathit{\boldsymbol{y}}^{\rm{T}}}} \right). $ | (16) |
基于IRLS的增量式0阶TSK模糊分类器TSK-IFCIRLS0采用平方损失函数表示代价函数, 采用ASQR型损失函数计算样本权值将导致模糊分类器TSK-IFCIRLS0对异常值、噪声数据、离群点样本较敏感.为了提高模糊分类器TSK-IFCIRLS0的抗噪性, 在后件参数的学习过程中, 采用伪Huber函数来表示代价函数, 得到另一种鲁棒性更强的增量式0阶TSK模糊分类器TSK-IFCPHub0.该模糊分类器采用增量式模糊聚类算法IFCM(c+p)训练前件参数, 所以具有很好的数据可扩展性.采用拟牛顿法求解式(12) 所示的非线性无约束优化问题, 以获得模糊分类器的输出权重y.算法的具体步骤如下.
1) 使用TSK-IFCIRLS0模糊分类器训练算法的步骤1)~5) 得到前件的隶属度矩阵g(x).
2) 使用BFGS法求解式(12) 的最优解y.
a)定义迭代次数k, 迭代终止条件ξ,初始向量y0, 初始矩阵B0=I, k=0.
b)开始迭代求解, 计算目标函数J(y)在yk处的梯度gk=▽J(yk).若‖gk‖ < ξ, 则迭代停止, 输出近似解y=gk;否则继续步骤c).
c)计算搜索方向, 根据Bkpk=-gk求出pk.
d)从yk开始沿pk方向进行一维搜索, 求满足J(yk+λkpk)=
e)更新yk+1=yk+λkpk.
f)计算gk+1=▽J(yk+1).若‖gk+1‖ < ξ, 则迭代停止, 输出近似解y=yk+1;否则计算Bk+1, 并使k=k+1, 回到c)继续计算.
通过上述算法可以建立基于伪Huber函数的模糊分类器模型TSK-IFCPHub0.其中, 伪Huber函数阈值δ在选择时没有明确的依据, 本文参考文献[18]的相关研究进行取值.通过式(16) 所示的决策函数, 可以确定每个输入样本的实际类别归属.
2.6 时间复杂度分析提出的两种模糊分类器TSK-IFCIRLS0、TSK-IFCPHub0在训练前件时都使用相同的增量式模糊聚类算法IFCM(c+p), 时空花费可以分别表示为O(t′nd(c+p)+t′c)、O((d+c+p+n0)n/s).其中, t′为IFCM(c+p)聚类算法中每个数据块的平均迭代次数, n0为在IFCM(c+p)算法中距每个数据块的聚类中心最近的样本点个数, s为数据块的个数, d为训练集维数.模糊分类器TSK-IFCIRLS0采用IRLS算法训练模糊规则后件, 从式(10) 可以看出, 模糊分类器TSK-IFCIRLS0时空花费主要在求逆运算过程中, 但只会占用O((2c)2)的存储空间, 花费O((2c)3)的时间.此时可以得到模糊分类器TSK-IFCIRLS0的时空复杂度分别为O(t′nd(c+p)+t′c+(2c)3)、O((d+c+p+n0)n/s+(2c)2).后者采用伪Huber函数构造的代价函数来训练模糊规则后件, 时空花费主要为O((2c)2), 则模糊分类器TSK-IFCPHub0的时空复杂度分别为O(t′nd(c+p)+t′c+(2c)2)、O((d+c+p+n0)n/s+(2c)2).其中, c为在模糊聚类过程中的聚类数, 也表示整个模糊系统的模糊规则数.为了提高系统的可解释性及降低系统的时空复杂度, 模糊规则数不能设置得过大.
模糊分类器FCPM-IRLS的时间和空间复杂度分别可以表示为O(tnd(c+p)+tc+(2c)3)、O(n(d+c+p)+(2c)2).与提出的2个模糊分类器相比, FCPM-IRLS具有更高的时间复杂度.
3 实验研究与分析 3.1 实验设置在4个不同规模的二分类数据集上, 对提出的模糊分类器TSK-IFCIRLS0、TSK-IFCPHub0与模糊分类器FCPM-IRLS、ANFIS及RBF在训练时间、分类性能上进行比较.各数据集分别取自LIBSVM、MLDATA及UCI, 其中Skin_nonskin一共有245 057个样本, 随机抽取其中100 000个样本用于本文的验证实验.为了保证仿真实验结果的合理可靠, 所有的分类器都进行5重交叉验证实验, 且对所有的数据集都按特征归一化到[0,1], 训练集、测试集及特征数如表 1所示.
| 表 1 二分类数据集 Table 1 Binary datasets |
所有实验中的最大迭代次数均为100, 迭代终止条件均为ξ=10-3.在IFCM(c+p)算法中, 聚类中心附近的样本点个数n0取5;大规模数据集Cod-rna的数据块大小分别取原始数据集的1%、2.5%, 5%、10%, 其余数据集分别取10%、25%、35%、50%, 每个数据块中的样本均为随机抽取;平衡因子α在取值时保证平衡项
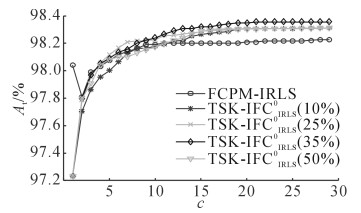
对于一个模糊系统, 为了寻求更好的可解释性和性能, 需要选择合理的模糊规则数.模糊规则数过少将导致系统缺乏可解释性、分类性能降低, 模糊规则数太多会导致模型过于复杂、系统可解释性降低、训练难度增加以至于难于实用.如图 1、2所示分别为模糊分类器FCPM-IRLS、TSK-IFCIRLS0在Twonorm数据集中随着模糊规则数c的变化分类器测试精度At及训练时间ttr的变化情况.从图 2可以看出, 随着模糊规则数的增加, FCPM-IRLS的训练时间快速增加, 模糊分类器TSK-IFCIRLS0的训练时间缓慢增加;从图 1可见, 当模糊规则数增加到一定程度时, 两个模糊分类器的测试精度基本不再变化, 但后者总能保持更好的测试精度.可见, 模糊分类器TSK-IFCIRLS0具有更高的学习效率和更好的分类性能, 且模糊分类器TSK-IFCIRLS0对模糊规则数不是很敏感.
|
图 1 模糊规则数对模糊分类器测试精度的影响 Fig. 1 Influence of fuzzy rules on testing accuracy of fuzzy classifiers |

|
图 2 模糊规则数对模糊分类器训练时间的影响 Fig. 2 Influence of fuzzy rules on training time of fuzzy classifiers |
首先, 提出的模糊分类器TSK-IFCIRLS0、TSK-IFCPHub0以及用于比较的模糊分类器FCPM-IRLS、ANFIS、RBF在不含噪声的数据集中的分类性能及训练时间如表 2所示, 最优结果已用粗体标出.
| 表 2 分类器在不含噪声数据集中的分类性能(Mean±Dev)及训练时间比较 Table 2 Comparison of classification performance (Mean±Dev) and training time of classifiers for different non-noise datasets |
从表 2可得如下结论.1) 与其他几种分类器相比, 本文提出的模糊分类器TSK-IFCIRLS0、TSK-IFCPHub0在各个不含噪声的数据集中的测试精度总能最大程度地接近甚至超过(如在Twonorm数据集中)其他几种分类器, 且总是拥有最短的训练时间, 仅为其他分类器的几分之一到几百分之一, 显然在保持了很好的分类性能的同时, 还具有极高的学习效率.2) 随着数据集规模的增加, 时间花费缓慢增加.模糊分类器TSK-IFCIRLS0、TSK-IFCPHub0在每个数据集中随着数据块大小的增加, 分类性能和时间花费均缓慢增加.3) 其他几种分类器不总是拥有最好的分类性能, 且以花费大量的训练时间为代价来换取分类器不错的分类性能.4) 其他几种分类器随着数据集规模的增加, 时间花费急剧增加, 特别是RBF、ANFIS分类器可能因为数据集规模过大而失效, 如表 2的“/”所示, 显然它们难以在大规模数据集的场景中应用.另一方面, 模糊分类器TSK-IFCIRLS0、TSK-IFCPHub0在不含噪声的数据集中, 前者基本上拥有最高的学习效率和最佳的分类性能.可见, 模糊分类器TSK-IFCIRLS0能够在不含噪声的场景中更好地应用.
3.3.2 噪声数据集中的性能比较在含有20 dB的高斯白噪声的数据集中开展抗噪性实验, 观察各个分类器的分类性能及学习效率.模糊分类器TSK-IFCPHub0针对TSK-IFCIRLS0鲁棒性较差的不足, 采用伪Huber函数重新表示代价函数, 由于伪Huber函数在实数域均可导、对异常值和噪声不敏感, 可以很好地提高分类器的鲁棒性.模糊分类器TSK-IFCIRLS0、TSK-IFCPHub0与FCPM-IRLS、ANFIS、RBF分类器在含5%和20%的高斯噪声的数据集中的分类性能、训练时间比较结果分别如表 3、4所示, 最优结果已用粗体标出.
| 表 3 各分类器在含5%高斯噪声的数据集中的分类性能(Mean±Dev)及训练时间比较 Table 3 Comparison of classification performance (Mean±Dev) and training time of classifiers for different datasets with 5% Gauss noise |
| 表 4 分类器在含20%高斯噪声的数据集中的分类性能(Mean±Dev)及训练时间比较 Table 4 Comparison of classification performance (Mean±Dev) and training time of classifiers for different datasets with 20% Gauss noise |
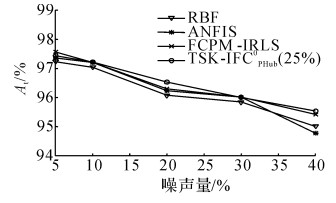
从表 3、4可以得出以下结论.1) 模糊分类器TSK-IFCPHub0、TSK-IFCIRLS0在含有5%噪声的数据集中虽然未能取得最佳的分类性能, 但能够最大程度地接近最佳分类性能且拥有最短的训练时间.2) 在含20%噪声的数据集中, 两者均表现出了不错的分类性能, 都具有最短的训练时间.3) 前者随着数据集中噪声量的增加, 分类性能缓慢降低, 时间花费基本不变, 可见模糊分类器TSK-IFCPHub0学习效率受噪声数据的影响较小, 拥有很好的鲁棒性, 后者受噪声的影响较大, 可见模糊分类器TSK-IFCIRLS0鲁棒性较差.4) 两者随着数据集规模的增加, 时间花费缓慢增加, 在每个数据集中随着数据块大小的增加, 分类性能和训练时间缓慢增加.5) 分类器RBF、ANFIS、FCPM-IRLS随着数据集中噪声量的增加, 分类性能明显下降, 花费了大量的训练时间, 可见这几种分类器的鲁棒性较差.为了进一步验证提出的模糊分类器TSK-IFCPHub0的鲁棒性, 在Twonorm数据集中分别添加了10%、30%、40%的噪声数据, 各个分类器在不同噪声量的Twonorm数据集(数据块大小取25%)中的测试精度如图 3所示.可以看出, 随着数据集中噪声含量的增加, 模糊分类器TSK-IFCPHub0能够保持很好的鲁棒性, 其他分类器的鲁棒性迅速下降.
|
图 3 噪声量对分类器分类性能的影响 Fig. 3 Influence of noise level on classification performance of classifiers |
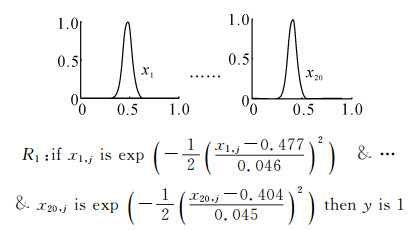
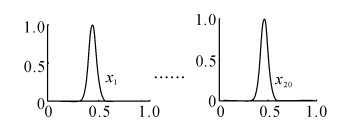
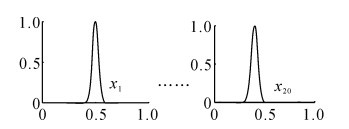
为了通过仿真实验说明提出的2种增量式0阶TSK模糊分类器的高可解释性, 以数据集Twonorm(取数据块大小为25%的情况)为例, 列出2个模糊分类器所得到的一些隶属度函数及模糊规则, 如图 4~6所示.图 4~6中列举的模糊规则都是简洁且容易解释的.可见提出的模糊分类器都是具有高可解释性的.
|
R1:if x1, j is exp |
|
R1:if x1, j is exp |
|
R1:if x1, j is exp |
综上可知, 分类器RBF、ANFIS的性能会随着数据集规模的增大而急剧下降, 模糊分类器FCPM-IRLS通过牺牲大量的训练时间以获取不错的分类性能, 同时这3种分类器对噪声数据较敏感, 可见这3种分类器都难以保证快速的学习效率和较好的鲁棒性.模糊分类器TSK-IFCPHub0、TSK-IFCIRLS0在极个别数据集(如Cod-rna)中没有表现出最佳的分类性能, 但总能最大程度地接近最佳分类性能, 原因主要是模糊规则前件在使用增量式模糊聚类算法进行模糊划分时可能没有达到最佳划分, 但两者在各个数据集(含噪声或者不含噪声)中总能保持最高的学习效率, 因此这种情况是可以接受的.TSK-IFCIRLS0在不含噪声的数据集中具有更好的分类性能, TSK-IFCPHub0在含噪声的数据集中更能表现出最佳的分类性能.模糊分类器TSK-IFCPHub0、TSK-IFCIRLS0都表现出了很好的数据规模可扩展性以及高可解释性.
4 结语本文首先提出增量式0阶TSK模糊分类器TSK-IFCIRLS0, 用以高效解决不同规模数据集的分类问题.为了提高模糊分类器TSK-IFCIRLS0抗噪性, 采用增量式聚类算法IFCM(c+p)训练模糊if-then规则的前件参数, 采用伪Huber函数重新表示代价函数并采用拟牛顿法中的BFGS算法求解非线性无约束优化问题以训练模糊if-then规则的后件参数, 提出另一种具有鲁棒性的增量式0阶TSK模糊分类器TSK-IFCPHub0.与传统的分类器相比, 提出的2种模糊分类器的每一条输入规则都是TSK形式的, 因此都具有很好的可解释性.因为模糊分类器TSK-IFCIRLS0采用平方损失函数而导致抗噪能力下降, 不过能够在不含噪声的数据集中表现出优异的分类性能.另一方面, 因为模糊分类器TSK-IFCPHub0采用伪Huber形式的损失函数, 具有很好的抗噪能力, 能够具有很好的鲁棒性.同时, 两者均可在不同规模数据集的场景中应用, 可见本文算法具有很好的数据规模可扩展性.然而, 2种模糊分类器的可调参数较多, 如何选择更好的参数提高分类器的性能是今后研究的重点.
| [1] | HEARST M A. Support vector machines[J]. IEEE Intelligent Systems, 1998, 13(4): 18–28. |
| [2] | HUANG G B, MAO K Z, SIEW C K, et al. Fast modular network implementation for support vector machines[J]. IEEE Transactions on Neural Networks, 2005, 16(6): 1651–1663. |
| [3] | SUGUMARAN V, RAMACHANDRAN K I. Effect of number of features on classification of roller bearing faults using SVM and PSVM[J]. Expert Systems with Applications, 2011, 38(4): 4088–4096. |
| [4] | HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine:theory and applications[J]. Neurocomputing, 2006, 70(1): 489–501. |
| [5] | JAFARZADEH S, FADALI M S, SONBOL A H. Stability analysis and control of discrete type-1 and type-2 TSK fuzzy systems:Part Ⅱ. control design[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(6): 1001–1013. |
| [6] | FADALI M S, JAFARZADEH S. TSK observers for discrete type-1 and type-2 fuzzy systems[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(2): 451–458. |
| [7] |
蔡前凤, 郝志峰, 杨晓伟. 基于核映射的高阶Takagi-Sugeno模糊模型[J].
控制理论与应用, 2011, 28(5): 681–687.
CAI Qian-feng, HAO Zhi-feng, YANG Xiao-wei. Higher-order Takagi-Sugeno fuzzy model based on kernel mapping[J]. Control Theory and Applications, 2011, 28(5): 681–687. |
| [8] |
杨昌健, 邓赵红, 王士同, 等. 基于0阶TSK型迁移模糊系统的EEG信号自适应识别[J].
计算机应用研究, 2015, 32(8): 2276–2280.
YANG Chang-jian, DENG Zhao-hong, WANG Shi-tong, et al. Adaptive recognition of epileptic EEG signals based on 0-order TSK type transfer fuzzy system[J]. Application Research of Computers, 2015, 32(8): 2276–2280. |
| [9] |
邓赵红, 张江滨, 王士同, 等. 基于模糊子空间聚类的0阶L2型TSK模糊系统[J].
电子与信息学报, 2015, 37(9): 2082–2088.
DENG Zhao-hong, ZHANG Jiang-bin, WANG Shi-tong, et al. Fuzzy subspace clustering based zero-order L2-norm TSK fuzzy system[J]. Journal of Electronics and Information Technology, 2015, 37(9): 2082–2088. |
| [10] | LESKI J M. Fuzzy (c+p)-means clustering and its application to a fuzzy rule-based classifier:towards good generalization and good interpretability[J]. IEEE Transactions on Fuzzy Systems, 2015, 23(4): 802–812. |
| [11] | STARCZEWSKI J T, NOWICKI R K, NOWAK B A. Genetic fuzzy classifier with fuzzy rough sets for imprecise data[C]//IEEE International Conference on Fuzzy Systems. Beijing:IEEE, 2014:1382-1389. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6891857 |
| [12] |
刘淑英. 混合神经模糊分类器的实现[J].
计算机技术与发展, 2013, 12(12): 113–115.
LIU Shu-ying. Hybrid neural fuzzy classifier to achieve[J]. Computer Technology and Development, 2013, 12(12): 113–115. |
| [13] | YANG X, ZHANG G, LU J, et al. A kernel fuzzyc-means clustering-based fuzzy support vector machine algorithm for classification problems with outliers or noises[J]. IEEE Transactions on Fuzzy Systems, 2014, 19(1): 105–115. |
| [14] |
李滔, 王士同. 适合大规模数据集的增量式模糊聚类算法IFCM(c+p)[J].
智能系统学报, 2016, 11(2): 227–233.
LI Tao, WANG Shi-tong. Incremental fuzzy (c+p)-means clustering for large data[J]. CAAI Transactions on Intelligent Systems, 2016, 11(2): 227–233. |
| [15] | HARTLEY R, ZISSERMAN A. Multiple view geometry in computer vision[J]. Cambridge University Press, 2006, 30(9-10): 1865–1872. |
| [16] | 王立新. 模糊系统与模糊控制教程[M]. 北京: 清华大学出版社, 2003: 81-91. |
| [17] | 李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 210-224. |
| [18] |
朱嘉钢, 王士同. Huber-SVR中参数μ与输入噪声间关系的研究[J].
复旦学报:自然科学版, 2004, 43(5): 793–796.
ZHU Jia-gang, WANG Shi-tong. Research on the dependency between μ and the input noise in Huber-support vector regression[J]. Journal of Fudan University:Natural Science, 2004, 43(5): 793–796. |
| [19] | SUN H, WANG S, JIANG Q. FCM-based modelselection algorithms for determining the number of clusters[J]. Pattern recognition, 2004, 37(10): 2027–2037. |
| [20] | YU J, CHENG Q, HUANG H. Analysis of the weighting exponent in the FCM[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetics, 2004, 34(1): 634–639. |
| [21] | JANG J S R. ANFIS:adaptive-network-based fuzzy inference system[J]. IEEE Transactions on Systems Man and Cybernetics, 1993, 23(3): 665–685. |
| [22] | RATSCH G, ONODA T, MULLER K R. Soft margins for AdaBoost[J]. Machine Learning, 2001, 42(3): 287–320. |



