临床路径(clinical pathway)是指针对特定病种制定的有顺序性和时间性的整体服务计划, 目的是使患者获得最佳的服务, 减少康复的延迟和资源的浪费[1].由于临床路径研究起步较晚, 临床路径不够完善, 导致诊疗质量参差不齐, 医疗成本无法控制[2].为了得到高质量标准诊疗流程, 本文采用过程挖掘(process mining)算法, 从实际医疗事件日志中发掘诊疗活动之间的关系, 得到标准诊疗过程模型[3].该模型可以指导和改进现有临床路径, 提高临床路径实施的质量和效率.
过程挖掘在临床路径上的应用研究较少.Peleg等[4]通过挖掘事件日志中的数据, 挖掘诊疗过程中的不合理之处, 给出相应的修改方法.Ghattas等[5]根据过程挖掘思想, 提出自适应诊疗过程模型.该模型可以根据实际诊疗数据来修改原有模型.目前过程挖掘在临床路径上的应用仅限于对原始模型的修正, 利用过程挖掘实现临床路径模型的重构能够更加彻底地改进原有模型.
过程挖掘思想由Cook等[6]提出, 并由Agrawal等[7]最早将过程挖掘应用到工作流管理中.Pinter等[8-9]对Agrawal的算法进行拓展:开始从抽象的角度描述事件日志, 并建立工作流模型.Aalst等[10]提出基于工作流网络(workflow-net, WF-net)行为推理的α算法, 可以在事件日志完备的情况下, 发现合理的工作流网络.为了解决工作流中存在的特殊结构问题, α算法发展成为一系列的算法:α+算法[11]考虑了短循环结构的挖掘;tsinghua-α算法[12]考虑了活动的重合性;α++算法[13]考虑了非自由选择结构的挖掘;α#算法[14]考虑了隐藏活动的挖掘;α*算法[15-16]提出了发现事件日志中的重复活动的规则, 使得α算法的准确度明显提高.α系列算法在工作流模型基本结构和特殊结构的识别上有较高的准确率, 但是无法消除噪音的干扰, 在对含有噪音的事件日志进行挖掘时, 准确率会明显下降.
在临床路径中, 噪音的产生通常是随机的, 因此通过数据预处理的方式来消除噪音比较困难, 直接将α系列算法直接运用到临床路径挖掘不太合适.另一方面, 在临床路径中, 重名的诊疗活动普遍存在, 而重名活动和重复活动在临床路径中存在异议, 因此α*算法中的重复判断规则在临床路径中不适用.本文提出能够识别处理重名活动和减少噪音干扰的统计α算法.该算法不仅可以识别临床路径中的重名活动, 也可以有效规避事件日志中各种噪音的干扰.
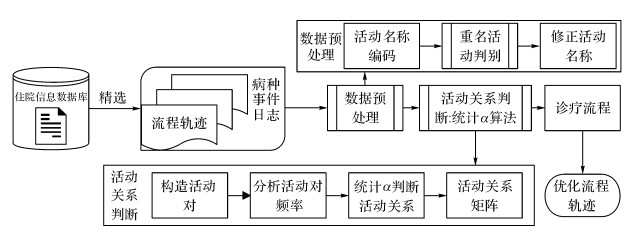
1 临床路径过程挖掘方法体系提出的临床路径过程挖掘方案如图 1所示.在数据库中提取病种的事件日志, 通过活动名称编码、重名活动判别和修正活动名称3个步骤完成数据的预处理工作;通过本文提出的统计α算法进行活动关系判断, 得到标准的诊疗流程.下面给出本文在过程挖掘方案中涉及到的基本概念.
|
图 1 基于重名活动判别与统计α算法的临床路径过程挖掘方案 Fig. 1 Scheme of process mining based on cognominal activities identify and statistical α-algorithm |
在临床路径中, 将一个病种的所有病人的所有记录称作一个事件日志, 记作Wd, 其中下标d表示病种名称.将事件日志中一个病人的记录称为一条流程轨迹, 记作δi, 显然有δi∈Wd.对于一条流程轨迹δi={T1, T2, …, Ti, …}, 其中Ti为诊疗活动代号.在流程轨迹中, 每个活动按照真实的执行时间先后顺序排列, 活动Ti的前一个活动称为活动Ti的前驱活动, 记作TP, TP的前驱活动记作TPP;同样地, 活动Ti的后一个活动称为活动Ti的后继活动, 记作TS, TS的后继活动记作TSS.
如表 1所示, 将活动关系分为4种[10].在临床路径事件日志中, 由于往往只记录了每个活动的开始时间, 没有完成时间, 对事件日志中的活动作如下3点假设:1) 每一个诊疗活动都是一个原子时间, 不考虑事件类型因素的影响.2) 以病人的活动为中心, 不考虑与病人不相关的活动.3) 不考虑资源的等待和约束, 资源问题对整个流程的影响暂时忽略.
| 表 1 活动关系定义 Table 1 Definition of activity relations |
在事件日志的某一条流程轨迹中, 某一活动可能多次出现, 但是每次代表的具体含义可能不同.在活动关系判断之前, 需要对这类活动进行区分, 为了方便描述这一类活动, 给出以下2个定义.
定义1 在任一条流程轨迹中, 若活动A出现一次以上, 则该活动称为重名活动(cognominalactivities).为了区分同一条流程轨迹中的重名活动, 用记号δi(A, ni)来表示在流程轨迹δi中第ni个活动A[15].
定义2 重名活动根据具体活动内容是否相同, 分为两种:活动内容相同的称为重复性重名活动, 简称重复活动(duplicate activities, DA);活动内容不同的称为非重复性重名活动(homonyms activities, HA).提出的重名活动判别规则是为了将重名活动区分为DA和HA, 并对两类重名活动进行不同处理, 以消除HA对过程挖掘的影响.
为了提高重名活动判断效率, 将任意活动A的两个前驱活动TP、TPP和两个后继活动TS、TSS组成的有序集合{TPP, TP, A, TS, TSS}记作一个活动组(activities group), 记作GA, 并以活动组作为重名活动判别的基本单位对于重名活动的判别.
采用内蒙古某三甲医院2010年03月到10月之间7个月的若干病种的事件日志数据, 以活动组为单位, 分析4个病种, 共510条流程轨迹.通过统计发现, 当2个重名活动对应的2个活动组中的元素对应相等, 即活动组中的元素和元素顺序都相同时, 根据Herbst等[17]对于重复活动的定义可知, 这两个重名活动是重复活动的概率高达99.7%, 因此可以得到以下重复活动的定义.
定义3 对于任意流程轨迹δi∈W, 如果δi中存在重名活动δi(A, n), δi(A, m)∈δi, 且两者对应的活动组分别为GA和G′A, GA和G′A中除了活动A之外的其他活动对应相等, 则活动δi(A, n)和活动δi(A, m)可以定义为重复活动(DA).
为了后文叙述方便, 对于任意流程轨迹δi∈W, 如果δi中存在重名活动δi(A, n), δi(A, m)∈δi, 且两者对应的活动组分别为GA和G′A, GA和G′A中包含的除了A之外的元素相同, 但元素排列顺序不同, 则称为两个活动组相等, 记作GA=G′A.
定理 对于任意流程轨迹δi∈W, 如果δi中存在重名活动δi(A, n), δi(A, m)∈δi, TP和TS分别是活动δi(A, n)的前驱任务和后继任务, TPP为TP的前驱活动, TSS为TS的后继活动;T′P和T′S分别是活动δi(A, m)的前驱任务和后继任务, T′PP为T′P的前驱活动, T′SS为T′S的后继活动,活动δi(A, n)和活动δi(A, m)对应的活动组分别为GA和G′A, U为重复活动集合, 则有以下结论.
1) 若GA=G′A, TP=T′P且TS=T′S, 则〈δi(A, n), δi(A, m)∈U.
2) 若GA=G′A, TP=T′P, TS≠T′S, TS=T′SS, 且TSS=T′S, 则〈δi(A, n), δi(A, m)〉∈U.
3) 若GA=G′A, TP≠T′P, TS=T′S, TP=T′PP, 且TPP=T′P, 则〈δi(A, n), δi(A, m)〉∈U.
4) 若GA=G′A, TP≠T′P, TS≠T′S, TP=T′PP, TPP=T′P, TS=T′SS, 且TSS=T′S则〈δi(A, n), δi(A, m)〉∈U.
5) 若GA≠G′A, TP=T′P, TS≠T′S且TS#wT′S, 则〈δi(A, n), δi(A, m)〉∈U.
6) 若GA≠G′A, TP≠T′P, TS=T′S且TP#wT′P, 则〈δi(A, n), δi(A, m)〉∈U.
7) 若GA≠G′A, TP≠T′P, TP#wT′P, TS≠T′S且TS#wT′S, 则〈δi(A, n), δi(A, m)〉∈U.
8) 若GA≠G′A, TP≠T′P, TP#wT′P, TS≠T′S, TS=T′SS且TSS=T′S, 则〈δi(A, n), δi(A, m)〉∈U.
9) 若GA≠G′A, TS≠T′S, TS#wT′S, TP≠T′P, TP=T′PP且TPP=T′P, 则〈δi(A, n), δi(A, m)〉∈U.
对于该定理, 给出基于反证法的证明.
假设〈δi(A, n), δi(A, m)〉∉U, 即活动δi(A, n)和活动δi(A, m)为非重复性重名活动.
对于规则1), 由于〈δi(A, n), δi(A, m)〉∉U, 可以将它们分别记作A和A′.由于TP=T′P且TS=T′S, A和A′只能是选择关系, 根据Aalst等[10]对于选择关系的定义, 有TSS=T′SS;因为GA=G′A, 2个活动组除了A和A′之外, 必须其他元素相同, 因此TPP=T′PP, 此时两个活动组元素顺序相同, 与GA=G′A的定义相矛盾, 〈δi(A, n), δi(A, m)〉∈U成立.
对于规则2), 分为以下2种情况说明.
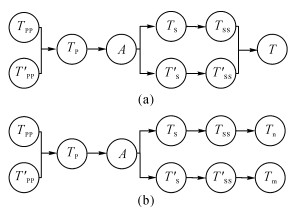
1) 假如TSS和T′SS后继活动相同, 如图 2(a)所示, TSS和T′SS的后继活动都为T, 而TS=T′SS, 且TSS=T′S, 那么按照对于并行关系的定义可知, TS和TSS为并行关系.可以将TS和TSS以及后面的T看作一个活动, 则活动δi(A, n)和活动δi(A, m)的前驱活动和后继活动都相同, 转化成了规则1) 的情况, 得证.
|
图 2 TSS和T′ss后继活动不同情况 Fig. 2 Different situation after TSS and T′SS |
2) 假如TSS和T′SS后继活动不同, 如图 2(b)所示, TSS的后继活动为Tn, T′SS的后继活动为Tm.若Tn和Tm是选择关系或者并行关系, 则可以将Tn和Tm及后面若干活动看作同一活动, 回到情况1);若Tn和Tm是不相关的, 则两条流程轨迹不会归结到同样的结果, 最终得到病人的状态不同, 这与同一病种下痊愈病人的流程轨迹的大前提相矛盾, 因此假设不成立, 〈δi(A, n), δi(A, m)〉∈U.
对于规则3)、4) 的证明, 与规则2) 的证明相同.
对于规则5), 与规则(2) 的证明类似, 分以下2种情况讨论.
1) 假如TSS=T′SS, TS和T′S是选择关系, 可以将TS、T′S和TSS看作一个大活动T, 则重名活动A的前驱活动和后继活动对应相等, 可以转化为规则1) 的情况, 得证.
2) 假如TSS≠T′SS, 则有以下2种情形.
a)在可以预见的若干活动之后, 两条轨迹将合并到同一个活动上.假设这个活动为Tr, 那么可以将活动δi(A, n)和δi(A, m)与活动Tr之间的所有活动合并成一个大活动, 分别记作TC和T′C.由于TC和T′C是由两个互为选择关系的活动TS和T′S开始, 无论TS和T′S后面的活动是因果关系或是选择关系, TC和T′C都可以看作选择关系, 此时将问题转化成第一种情况, 从而得证.
b)在可以预见的若干活动后, 两条轨迹没有合并, 最终得到病人的状态不同, 这与同一病种下痊愈病人的流程轨迹的大前提矛盾, 因此假设不成立, 〈δi(A, n), δi(A, m)〉∈U.
对于规则6)、7) 的证明, 与规则5) 的证明相同.
对于规则8)、9), 证明方法一致, 此处挑选规则9) 进行证明.由于TP=T′PP, TPP=T′P, 且TP和T′P有相同的后继活动A, 可以将TP和T′P看作一个大活动T, 于是, 该问题转化成规则5) 的情况, 因此得证.
以上提出的重复活动判定定理针对同一轨迹中的重名活动, 对于不同轨迹中的重名活动, 利用本文的定理同样可以进行判断.不同轨迹中的重名活动主要分为以下3类.
1) 该重名活动在每条路径中均出现且仅出现一次.该类重名活动是诊疗流程中的日常活动, 利用本文给出的重复活动判定定理可知, 这些活动为重复活动.
2) 重名活动在每条路径中均出现不止一次.该类活动不仅是同一轨迹中的重名活动, 而且是不同轨迹中的重名活动.对于该类活动的判别, 可以采用本文给出的定理, 得到如下结果:位置对应相同的重名活动是重复活动, 位置对应不同的重名活动可以转换为同一路径中的重名活动进行判定.
3) 该重名活动在极少数的情况下在不同轨迹中出现.该类活动利用本文定理判定为非重复性重名活动, 会对该活动执行重命名操作, 不影响后续算法的结果.
本文给出的重名活动判别规则对于不同轨迹中的重名活动同样适用, 但是在本文的过程挖掘方案中对于这种情况没有进一步考虑, 原因如下.
1) 不同轨迹之间必然存在着大量的重名活动, 而且这些重名活动显然是重复活动, 因此不进行多余的判断.
2) 不同轨迹之间的重名活动判别对于本文的核心算法影响较小, 可以不作考虑.
3) 本文的重名活动判别规则虽然针对的是同一流程轨迹中的重名活动, 但是在实际判断过程中是通过多条流程轨迹来共同判断的, 与不同轨迹重名活动判断在一定程度上是重合的, 因此没有进行重复运算.
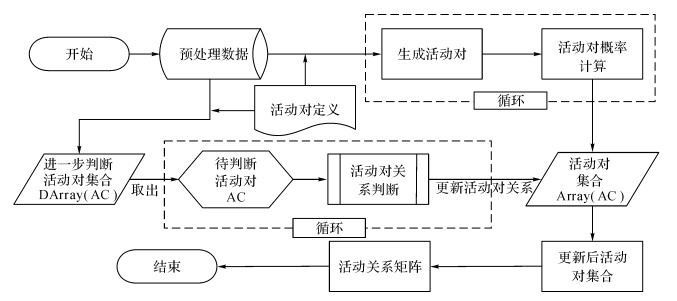
3 基于统计α算法的过程挖掘在临床路径中, 用于过程挖掘的原始事件日志往往包含了大量的数据, 并且同时存在着一定数量噪音数据.经典α算法是在事件日志中无噪音的情况下进行的, 当事件日志存在噪音时, 准确率会明显下降.本文针对性地提出统计α算法(statistic α-algorithm), 利用概率统计的方式去除事件日志中的随机噪音, 有效抑制了噪音的不利影响, 同时保证了算法运行效率, 具体的算法步骤如图 3所示.
|
图 3 统计α算法的步骤 Fig. 3 Procedure of statistical α-algorithm |
1) 活动对检测.本文的统计α算法以活动对为单位, 首先给出活动对的定义.
定义4 对于任意病种的一个事件日志W, 假设有流程轨迹δi={…, Ti, Ti+1, …}⊂W, 流程轨迹中的元素按照执行时间的先后顺序排列.其中任意两个相邻的活动Ti和Ti+1及其出现的次数组成一个结构体, 称为活动对(activities couple, AC).具体定义如下.
Structure活动对{
String FA, 第一个活动名称(Ti);
String SA, 第二个活动名称(Ti+1);
int F, 出现次数=1;
String R, 活动关系=顺序关系(默认);
}
2) 活动对概率统计.遍历事件日志中的所有流程轨迹, 可得一个由不同活动对组成的活动对集合, 记作Array(AC).计算活动对集合Array(AC)中每个活动对的出现概率.考虑到重名活动的存在, 可得活动对AC(Ti, Ti+1)的概率为
| $ P({\rm{AC}}({T_i}, {T_{i + 1}})) = \frac{{{\rm{AC}}({T_i}, {T_{i + 1}}).F}}{{N{n_{\rm{r}}}}}. $ |
式中:AC(Ti, Ti+1).F为活动对AC(Ti, Ti+1)的出现次数, 如果在活动对集合Array(AC)中不存在AC(Ti, Ti+1), 则AC(Ti, Ti+1).F=0;N为流程轨迹数;nr=nr(Ti)+nr(Ti+1)等于活动Ti和活动Ti+1重名活动的数目总和.
3) 检索需要判断活动关系的活动对.对于任意病种的流程轨迹来说, 顺序关系是出现次数最多的活动关系[13].对于可以确定为顺序关系的活动对, 不需要对其进行二次判断.为了简化活动关系的判断流程, 减少判断活动对的数目, 需要对活动对进行筛选.以流程轨迹为单位, 纵向比较每条预处理后的流程轨迹, 排除可以确定为顺序关系的活动对, 得到一个活动关系待定的活动对集合, 记作DArray(AC), 显然DArray(AC)⊆Array(AC).DArray(AC)是所有活动对集合的子集, 它包含了所有活动关系不确定为顺序关系的活动对, 通过对DArray(AC)中的每个元素进行遍历, 分别判断每个活动对的活动关系, 可得所有活动对的活动关系, 进而生成活动关系矩阵.另一方面, 将DArray(AC)作为统计α算法的运算集合, 显著减少了算法的运行次数, 提高了程序运行效率.
4) 判断活动对关系.利用统计α算法进行活动对活动关系判断时, 需要考察与该活动对相关的活动对, 因此给出与之相关的两个活动对:同前活动对和转置活动对的定义.
定义5 同前活动对:对于任意活动对AC(A, B), 若存在一个活动对和它有相同的第一个活动A, 第二个活动不同, 则称为AC(A, B)的同前活动对, 记作#AC(A, B).
定义6 转置活动对:对于任意活动对AC(A, B), 若存在一个活动对的第一个活动等于它的第二个活动, 第二个活动等于它的第一个活动, 则称为AC(A, B)的转置活动对, 记作-AC(A, B).
结合上述定义, 给出统计α算法具体步骤的伪代码如下.
Input Wd//事件日志, α//显著性水平
Output Matrix[Array(AC)]//活动关系矩阵
1. Foreach(σi in Wd)
σi←{T1, T2, …, Tj, Tj+1, …}
j : 1→σi.Length
If (AC(Tj, Tj+1)is exist) then
AC(Tj, Tj+1).F++
Else
AC(Tj, Tj+1).FA←Tj
AC(Tj, Tj+1).SA←Tj+1
P(AC(Tj, Tj+1))=
Array(AC).Add(AC(Tj, Tj+1))
2. Foreach(σ in Wd)
σi←{A1, A2, …, Aj, Aj+1, …}
σk←{B1, B2, …, Bj, Bj+1, …}
j:1→σi.Length
If(Aj≠Bj)
DArray(AC).Add(AC(Aj, Aj+1))
DArray(AC).Add(AC(Aj-1, Aj))
End
Output DArray(AC)
3. Foreach (AC in DArray(AC))
AC←AC(A, B)
#AC(A, B)←AC(A, C)
-AC(A, B)←AC(B, A)
If (P(AC(A, C))> α) then
Dim AC(B, C)
If (P(AC(B, C))> α) then
If (P(AC(C, B))> α) then
B‖wC
Else
B#wC
Else
B#wC
A>wB, A>wC
Else
If (P(AC(B, A))> α) then
A‖wB
Else
A→wB
End.
Output Matrix[Array(AC)]//活动关系矩阵
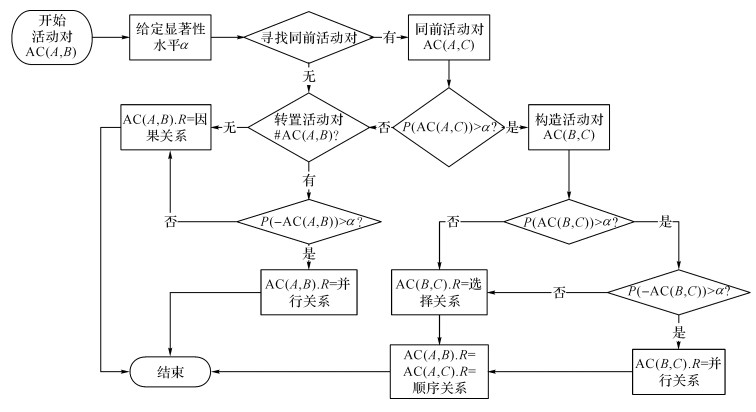
在统计α算法中, 首先需要设定一个显著性系数α, 该系数用于筛选去除出现概率较低的活动对.接着按照图 4的步骤遍历DArray(AC)中所有的活动对, 根据结果不断更新Array(AC)中对应活动对的关系.在遍历完成之后, 根据Array(AC)的最终结果, 可得所有活动之间的活动关系矩阵.
|
图 4 活动对AC(A, B)活动关系判断步骤 Fig. 4 Procedure of activity relations judgment of AC(A, B) |
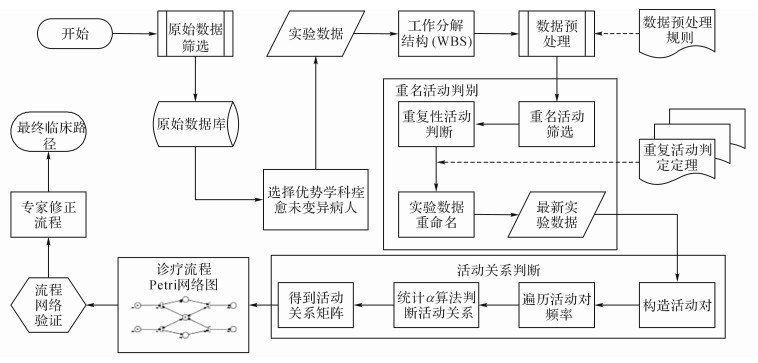
在以上算法的基础上, 给出基于统计α算法的临床路径过程挖掘方法的具体运作流程.如图 5所示, 主要分为以下6个步骤.
|
图 5 基于统计α算法的临床路径过程挖掘综合方案 Fig. 5 Comprehensive scheme of clinical pathway process mining based on statistical α-algorithm |
1) 原始数据的筛选.获取数据库中结构完整、数据量较大的事件日志.
2) 工作分解结构.将一个病种按照其阶段、内容分成若干部分, 减少每一部分包含的活动数目, 降低算法运行时间, 提高准确度.
3) 数据预处理.将原始事件日志中的活动重新命名并统一每条流程轨迹长度.
4) 重名活动判别.以流程轨迹为单位, 开展重名活动判别分析.根据结果重新修正活动命名, 为过程挖掘作准备.
5) 活动关系判断.采用提出的统计α算法, 消除噪音的影响, 得到活动关系矩阵.
6) 得到结果并修正.根据5) 中得到的活动关系矩阵, 将模型问题还原到实际问题中.
4 实验与结果分析本文数据采集于内蒙古某三甲医院2010年03月到10月之间7个月的数据, 具体每个病种对应的病人数量如表 2所示.选取病人数最多的5个病种作为案例, 即:正常分娩、急性阑尾炎、卵巢良性肿瘤、子宫平滑肌瘤和锁骨骨折.
| 表 2 原始数据病种病人数信息 Table 2 Number of patients for each disease |
本文提出的重名活动识别规则基于定义3的假设, 在文献[16]中的重复活动判定定理基于一个假设.为了比较2个假设的重名活动覆盖率及优越性, 取表 2的5个病种作为实验对象, 分别采用本文假设和文献[16]的假设对重名活动进行判断, 得到2种假设对于重复活动的识别结果和运行时间t, 如表 3所示.
| 表 3 基于2种假设的重名活动识别对比 Table 3 Comparison of cognominal activity identify in different assumptions |
从实验结果可以看出, 2种假设对于重复活动的判断结果完全相同, 可以认为2种假设在数据量较大的情况下本质是相同的.分析2种假设相同的具体原因如下.
1)2种假设的具体比较如表 4所示.可以看出, 两者只是在出现较复杂的选择和并行关系时判定的假设不同, 绝大部分情况下假设完全相同.
| 表 4 2种假设的异同点比较 Table 4 Comparison of two assumptions |
2) 当出现复合选择(并行)关系时, 以轨迹δ={(a, b, c, d, x, e, f); (c, d, a, b, x, e, f);…}为例, 活动a、b以及c、d可以看作一个组合活动, 两者之间是选择关系.按照文献[16]的假设可知, 2条轨迹中的x是重复活动.当使用本文给定的活动组假设时, 两条轨迹中活动x对应的活动组显然不相等, 但是对于一个数据量足够的事件日志来说, a、b和c、d作为x的前驱机会是相当的, 按照本文的思想, 将x判定为重复活动, 与文献[16]的结果相同.综上所述, 本文虽然假设与文献[16]不完全相同, 但两者本质是相同的, 在数据量较大的情况下不会出现差异.由于本文假设需要判定的数据量更小, 在算法运行效率上更加有优势.
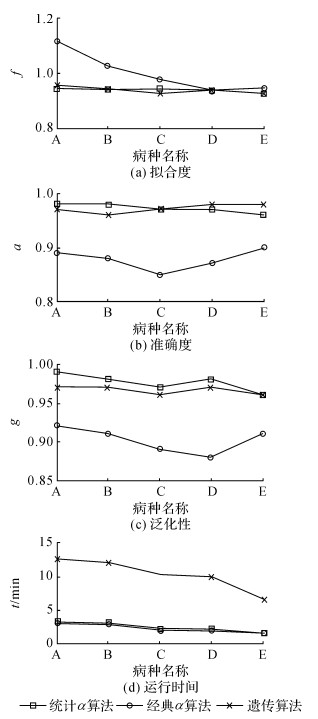
4.2 算法性能实验采用拟合度、准确度和泛化性3个指标, 对统计α算法分析结果进行评判.其中, 拟合度用来反映过程挖掘结果模型对原始数据的拟合程度, 拟合度越接近100%, 结果越好;准确度主要考察结果中活动关系的识别率和准确率;泛化性表示过程挖掘的结果模型在实验数据上应用时的拟合程度.为了使实验结果中的泛化性测试指标更加可靠, 采用10折交叉验证实验:将数据集分成10份, 轮流将其中9份作为训练数据、1份作为测试数据, 开展试验.每次试验都会得出相应的指标结果, 将10次结果的平均值作为最终结果.实验对比算法为经典α算法[10]和基于遗传算法的过程挖掘[18], 实验结果如表 5和图 6所示.表 5中,f为拟合度,a为准确度,g为泛化性.
|
图 6 3个算法的拟合度、准确度、泛化性和运行时间对比 Fig. 6 Comparison of fitness, accuracy, generalization and runtime of three methods |
| 表 5 3种算法性能比较结果 Table 5 Performance comparison of three methods |
实验结果表明:统计α算法在拟合度、准确度及泛化性上略优于遗传算法, 但是前者的运行时间明显少于后者, 算法运行效率更高.统计α算法与经典α算法相比, 前者在拟合度上的表现虽然不如后者, 但是经典α算法出现了过拟合现象, 说明结果受到噪音的影响较明显.另一方面, 统计α算法比经典α算法有更高的准确度和泛化性, 实验结果整体优于经典α算法.
4.3 噪音敏感性分析为了进一步分析噪音对于统计α算法的影响, 选取病种“正常分娩”的真实数据作为样本, 通过人工加噪的方式生成若干组数据进行实验, 采用10折交叉验证实验得到最终结果.人工增加噪音的方法主要分为以下5种[19]:1) 删除流程轨迹的某个活动;2) 调换流程轨迹中的某两个活动;3) 随机替换流程轨迹中的某个活动;4) 随机在流程轨迹中添加一个随机活动;5) 人为地生成重名活动, 并随机替换已有的活动.据此生成5组数据, 噪音规模分别为0、5%、10%、15%和20%.具体的实验结果如表 6所示.
| 表 6 噪音敏感性分析结果 Table 6 Noise sensitivity analysis results |
从实验结果可以看出, 随着噪音规模不断增加, 3种算法的准确度和泛化性都下降.其中经典α算法下降最快, 下降比例和噪音增加比例几乎相同;遗传算法的下降速度略低于噪音增加速度;统计α算法的表现最好.从拟合度指标来看, 由于经典α算法不具有抗噪能力, 拟合度指标一直朝着过拟合的方向发展, 统计α算法的拟合度最稳定.整体而言, 统计α算法在带噪音的临床路径的过程挖掘性能优于其他两种算法.
4.4 敏感性分析实验显著性系数是统计α算法中的重要参数.为了分析该系数对于统计α算法结果的影响, 以病种“正常分娩”和“急性阑尾炎”为实验数据, 将显著性系数分别设定为0.01~0.20, 开展10折交叉验证实验.实验结果如表 7所示.
| 表 7 显著性系数敏感性分析结果 Table 7 Significant level sensitivity analysis results |
从实验结果可以看出:当显著性系数较小和较大时, 结果的准确度和泛化性都会明显下降;拟合度在显著性系数较大时明显下降.具体来看, 当显著性系数较小时, 因果关系和选择关系识别率明显降低, 出现第一类错误;反之, 当显著性系数较大时, 结果受到噪音的影响明显增大, 保留了较多噪音, 出现较多误判的因果关系和选择关系, 出现了第二类错误. 需要保证敏感性系数在一个合理的范围中, 一般可以设定为0.05~0.10.
5 结语本文针对临床路径复杂事件日志的过程挖掘问题, 提出一套集成重名活动判别和统计α算法的过程挖掘算法.主要贡献点如下.1) 在分析了临床路径这一特殊工作流的特点后, 针对性地在分析诊疗活动关系前加入重名活动分析, 识别临床路径中的重名活动, 并且对其进行预处理.2) 基于医院的大量历史数据, 提出统计α算法, 利用统计方法减少事件日志中的噪音干扰, 明显提高了算法的准确率.将统计α算法成功应用到实际的临床路径数据, 并且与经典α算法和遗传算法进行比较, 本文提出的算法在拟合度、准确度、泛化性和运行时间上都具有一定的优势.未来的工作主要是考虑临床路径中出现的非自由选择结构以及不可见任务等问题, 进一步完善过程挖掘算法.
| [1] | LANGAB M, BVRKLE T, LAUMANN S, et al. Process mining for clinical workflows:challenges and current limitations[J]. Studies in Health Technology and Informatics, 2008, 136: 229. |
| [2] |
郑翔, 张寅升, 黄震震, 等. 可扩展的临床决策支持应用集成架构[J].
浙江大学学报:工学版, 2015, 49(9): 1658–1664.
ZHENG Xiang, ZHANG Yin-sheng, HUANG Zhen-zhen, et al. Extensible framework of integration for CDS applications[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(9): 1658–1664. |
| [3] | AALST W M P V D, WEIJTERS A J M M. Process mining:a research agenda[J]. Computers in Industry, 2004, 53(3): 231–244. DOI:10.1016/j.compind.2003.10.001 |
| [4] | PELEG M, SOFFER P, GHATTAS J. Mining process execution and outcomes:position paper[C]//International Conference on Business Process Management. Berlin:Springer, 2007:395-400. http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.95.4315 |
| [5] | GHATTAS J, SOFFER P, PELEG M. Learning business process models:a case study[C]//Business Process Management Workshops. Berlin:Springer, 2008:383-394. http://mis.hevra.haifa.ac.il/~morpeleg/pubs/BPM_Johny.pdf |
| [6] | COOK J E, WOLF A L. Automating process discovery through event-data analysis[C]//International Conference on Software Engineering. Washington:IEEE, 1995:73-82. http://dl.acm.org/citation.cfm?doid=225014.225021 |
| [7] | AGRAWAL R, GUNOPULOS D, LEYMANN F. Mining process models from workflow logs[C]//International Conference on Extending Database Technology. Berlin:Springer, 1998:467-483. http://dl.acm.org/citation.cfm?id=645338.650397 |
| [8] | PINTER S S, GOLANI M. Discovering workflow models from activities' lifespans[J]. Computers in Industry, 2004, 53(3): 283–296. DOI:10.1016/j.compind.2003.10.004 |
| [9] | GRECO G, GUZZO A, PONTIERI L, et al. Discovering expressive process models by clustering log traces[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(8): 1010–1027. DOI:10.1109/TKDE.2006.123 |
| [10] | AALST W M P, WEIJTERS T, MARUSTER L. Workflow mining:discovering process models fromevent logs[J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(9): 1128–1142. DOI:10.1109/TKDE.2004.47 |
| [11] | MEDEIROS A K A, DONGEN B F, AALST W M P, et al. Process mining for ubiquitous mobile systems:an overview and a concrete algorithm[C]//International Workshop on Ubiquitous Mobile Information and Collaboration Systems. Berlin:Springer, 2004:151-165. http://wwwis.win.tue.nl/~wvdaalst/publications/p244.pdf |
| [12] | WEN L, WANG J, AALST W M P, et al. A novel approach for process mining based on event types[J]. Journal of Intelligent Information Systems, 2009, 32(2): 163–190. DOI:10.1007/s10844-007-0052-1 |
| [13] | WEN L, AALST W M P, WANG J, et al. Mining process models with non-free-choice constructs[J]. Data Mining and Knowledge Discovery, 2007, 15(2): 145–180. DOI:10.1007/s10618-007-0065-y |
| [14] | WEN L, WANG J, SUN J. Mining invisible tasks from event logs[C]//Advances in Data and Web Management. Berlin:Springer, 2007:358-365. http://dl.acm.org/citation.cfm?id=1769756 |
| [15] | LI J, LIU D, YANG B. Process mining:extending α-algorithm to mine duplicate tasks in process logs[C]//Advances in Web and Network Technologies, and Information Management. Berlin:Springer, 2007:396-407. |
| [16] |
李嘉菲, 刘大有, 杨博. 过程挖掘中一种能发现重复任务的扩展α算法[J].
计算机学报, 2007, 30(8): 1436–1445.
LI Jia-fei, LIU Da-you, YANG Bo. Process mining:an extended α-algorithm to discovery duplicate tasks[J]. Chinese Journal of Computers, 2007, 30(8): 1436–1445. |
| [17] | HERBST J, KARAGIANNIS D. Workflow mining with InWoLvE[J]. Computers in Industry, 2004, 53(3): 245–264. DOI:10.1016/j.compind.2003.10.002 |
| [18] | MEDEIROS A K A D, WEIJTERS A J M M, AALST W M P V D. Using genetic algorithms to mine process models:representation, operators and results[R]. Eindhoven:Eindhoven University of Technology, 2005. https://www.researchgate.net/publication/221240287_Process_Mining_Extending |
| [19] | AALST W M P, DONGEN B F, HERBST J, et al. Workflow mining:a survey of issues and approaches[J]. Data and Knowledge Engineering, 2003, 47(2): 237–267. DOI:10.1016/S0169-023X(03)00066-1 |


