失速颤振是一种自激振动, 是由于当桨叶经历动态失速时, 气流分离产生的非线性气动力与惯性力、结构相互作用而产生, 其运动形式通常表现为叶片的扭转振动和叶尖的挥舞振动[1-3].该现象不仅存在于直升机的旋翼上, 也存在于大攻角下的固定翼以及风力机的叶片上, 是引起旋翼叶片结构性破坏的因素之一.因此, 为改善控制叶片的工作特性, 并深入了解气动弹性耦合机理, 失速颤振成为旋翼气动弹性响应研究的重点.
对失速颤振的研究主要分为两类.1) 判断颤振稳定性问题.如:最早由Fung[4]提出利用每振动周期的平均力矩系数判定Oates等[5-6]基于正弦振动推导出气的动阻尼表达式, Bowles等[7]利用俯仰力矩以及叶片角度的离散希尔伯特变化推导出具有时间分辨率的气动阻尼表达式, Bhat等[8]使用能量传递函数判别颤振是否持续, 以上研究均为用于判定颤振极限环(limit cycle oscillation, LCO)稳定性的问题.2) 颤振本身的振动特性, 包括扰动引起的非强迫的振动特性以及外部激励引起的振动特性.其中扰动引起的振荡研究包括:O’Neil[9]利用实验和数值分析了结构的3次非线性对进入颤振的临界速度的影响, Amandolese[10]探究了平板随风速变化在俯仰、沉浮运动受到小扰动后的振动特性, Dimitriadis[2]实验探究了NACA 0012翼型随风速变化小扰动引起的颤振极限环特性以及分岔的机理, Shao[11]使用改进的B-L模型、结合Grigoris的实验探究了零度力矩系数为零的严格对称与该值非零的非严格对称翼型的极限环特点以及分岔机理.涉及外部激励引起的颤振振动特性研究如下.Price等[12]利用Gangwani气动力模型探究了NACA 0012翼型在正弦周期力作用下单自由度失速颤振关于周期力振幅以及来流速度的分岔特性和振动特性.Fragiskatos[13]利用Beddose-Leishman气动力模型将Gangwani的探究扩展到不同减缩频率k、平衡位置αm、周期力振幅以及来流速度等4个参数对振动特性的影响.Sarkar等[3]利用ONERA气动力模型探究了k、αm、Q0、U*对强迫振动的影响和αm、U*对自激振动的影响.Tang等[14]实验探究了竖直放置于风洞中的NACA 0012翼型的振动特性, 实验中翼型下端受周期驱动, 而上端无约束.Laxman等[15]为更准确模拟直升机旋翼所经历的振动环境, 利用改进的ONERA模型探究了NACA 0012翼型以周期变距和周期风速为输入的单、双自由度颤振特性.
为更好地设计、控制风力机和直升机旋翼并使之更高效地运作, 近年来国外对于由扰动引起的失速颤振(自激振动)的机理研究方兴未艾.一方面是由于其所描述的是最基础的问题, 涉及因素较少, 能较准确地回答导致不同颤振特性差异的根本原因;另一方面是由于风力机的迅速发展, 叶片多在大攻角状态下工作, 小扰动即可使叶片进入失速状态, 所涉及的问题即属于自激振动而直升机上旋翼所涉及的失速颤振包含但不仅限于上述扰动所引起的振动.当直升机前飞时, 为使旋翼气动合力向某一特定方向偏转, 通过控制自动倾斜器的倾角, 桨叶根部攻角便会随方位角呈周期性变化, 此时桨叶经历的失速颤振则属于强迫振动.这类强迫振动研究的简化建模的思路有2种:一是在动力学方程中加上一项正弦变化的周期力, 二是认为结构之间相对形变产生的弹性作用为强迫振动的力.其中文献[3, 12-13]的研究思路为第一种, 其形式可追溯至Fung[4]所著的气动弹性基础:颤振翼型所受的除非线性气动力以外的其他力, 包括重力、结构弹性力等, 可近似为正弦变化的周期力.气动力模型是最简单的Theodorsen方程, 适用于无分离、小角度的振动;而失速颤振过程伴随动态失速过程, 振动幅度更大, 因此Fung[4]所近似的正弦变化的周期力不再适用, 更为接近真实前飞直升机上叶片失速颤振过程的模型是第二种, 即强迫振动的力随颤振形式而变化, 已知的是周期变化的距(桨叶根部的攻角).文献[14-15]的研究思路即为第二种, 但是文献[14]的实验探究是将1个翼型放置于风洞中, 结构的参数变化对上端颤振形式的影响无法得出;而文献[15]中的计算利用的是半经验模型, 可信度还需要验证.同时文献[14-15]没有回答周期变距下的失速颤振形式都与什么因素有关.
对失速颤振的实验探究多限于由扰动引起的振动, 而鲜有涉及与直升机周期变距相关的问题.基于上述分析发现, 虽然国外已开展了许多关于失速颤振的实验和数值研究, 在扰动引起的振动方面取得了较大的进展, 比如Dimitridias等[2]发现随风速增大颤振极限环由对称变为非对称的机理是“静态发散”.但是, 关于以周期变距为激励的失速颤振研究较少, 因此本文就此问题进行实验探究, 一方面可以更深入地理解失速颤振现象, 另一方面可以作为失速颤振数值模型的验证样本.
本文主要研究在低速风洞中NACA 0012翼型受周期变距激励的单自由度(仅俯仰方向)失速颤振特性以及不同参数下振动特性的差别.
1 实验装置与实验方案实验在上海交通大学复杂流动实验室的风洞中进行, 该回流式风洞可通过更换不同截面实验段, 实现低马赫数到跨声速的要求;本实验采用的试验段采用低速标准, 最大风速可达130 m/s.试验段截面的宽为1.2 m, 高为0.9 m, 长度超过2 m.如图 1所示, 试验装置由翼型模型、支撑系统、驱动系统、传感器和采集系统组成, 其中U为来流速度.翼型模型为3段矩形NACA 0012翼型, 该翼型被广泛用于实验、数值研究.翼型模型翼展为0.9 m, 弦长为0.3 m, 竖直安放在风洞试验段内, 上、下端面与风洞壁面的接触间隙微小, 可以保证绕翼型的流场为准二维流动.上、下两段翼型在前缘后0.115 m处通过轴分别与自由端和扭弹簧相连, 中间翼型与两端翼型以卡扣形式咬合, 并用螺纹紧固, 整个翼型可以绕其1/4弦线处的轴旋转(俯仰运动).驱动方式为电机通过曲柄连杆将圆周运动转化为俯仰方向角度的往复变化, 虽然不是严格的正弦运动, 但符合实际的机械环境.驱动轴与翼型下端通过弹簧机构连结在一起, 在0~10°内弹性机构可以看作是线性扭弹簧, 与线形弹簧之间的误差小于0.5%, 弹性机构由于弹簧有效长度的限制, 最大弹性变形不能超过8.5°.将弹性机构中弹簧换成刚性铁块则认为连接为刚性的.

|
图 1 NACA 0012翼型单自由度失速颤振实验装置与装置示意图 Fig. 1 Experimental facility set-up for investigation in stall flutter of one-degree-of-freedom NACA 0012 airfoil |
翼型的俯仰运动由自由端的传感器测量, 所用传感器为360°磁通量角度传感器, 输出电压与角度呈线性关系, 可用范围大于270°, 对角度感应灵敏, 分辨率为12位, 无最大转速的限制, 刷新频率高达每秒5 000次, 足以测量动态失速中快速变化的动态角度信息.翼型所受的力包括气动力和惯性力, 由中间段翼型内嵌的三分量应变天平传感器测量, 通过角速度信息可以得到动态气动力.传感器测量值由NI公司的采集卡采集, 采集频率fs=4 000 Hz, 远大于振动频率, 符合采样定理;同时采集时间足够长以保证采集到的数据包含足够的振动信息.
本文主要测量了在马赫数Ma=0.1, 雷诺数Re=6.87×105的条件下, 不同减缩频率k,不同扭转刚度弹簧约束和不同变距范围下翼型的攻角变化和受力情况, 其中,
| $k=\frac{\omega c}{2U},$ |
式中:ω为驱动频率, c为翼型弦长, U为来流速度.
如图 2所示为定常情形下, 相同马赫数、雷诺数下翼型的气动力系数与攻角的关系(C1为升力系数,无量纲,Cd为阻力系数,Cm为力矩系数).其气动力失速攻角约为11.76°, 力矩失速攻角约为12.07°.Taylor实验的雷诺数Re=7.50×105, 测得的气动力系数与本文实验系数基本重合, 因此认为本文所用测量天平测得的数据有效.实验方案如表 1所示, 其中Kφ为扭转刚度(1/15Kφ~Kφ), ωn为弹性系统的自然频率, ζ为实验测得系统的阻尼比, θd为驱动角, 振荡范围分别对应刚性连接时的无失速、浅失速和深失速(根据前缘涡大小, McCroskey[16]将动态失速现象归结为浅失速和深失速), 若攻角运动幅度过大导致弹性结构超过前述限度, 则认为所采集的信号无效.实验所用机构的动力学参数通过实验测出, 即通过将采集到的衰减振动信号拟合理论公式得到.由于在强扭转刚度条件下阻尼较大, 衰减曲线较短, 对Kφ与1/5Kφ的弹性机构参数误差为10%~15%, 而其他小扭转刚度的参数反映出的转动惯量均为1.34 kg·m2, 误差小于5%, 可用于验证气动弹性耦合响应的模型.

|
图 2 NACA 0012翼型定常气动力系数验证 Fig. 2 Validation of static aerodynamic coeffients of NACA 0012 airfoil |
| 表 1 NACA 0012翼型单自由度失速颤振实验方案与编号 Table 1 Experimental protocol and numbering for NACA 0012 stall flutter with cyclic pitch input |
如图 5~8所示为实验所得攻角的时域曲线以及相曲线.其中深色曲线为滤波后的攻角值, 浅色曲线为刚性连接时攻角的变化曲线或激励的周期变距曲线.攻角的滤波采用巴斯滤波方法, 所有测得数值的滤波采用同一参数, 最大程度地保证滤波后信号的真实度;角速度为攻角对时间的微分, 数值算法参照文献[17]的方法.通过实际计算对比, 采用拟合样条曲线后中心差分的方法得到角速度.

|
图 5 当扭转刚度为Kφ时,NACA 0012翼型在不同驱动角度下的攻角时序与相平面特性(灰色曲线为“刚性连接”) Fig. 5 Time series and phase plot of NACA 0012 airfoil incidence under different incidence inputswith torsional stiffness of Kφ(grey curves represent "rigid-connection" case) |

|
图 6 当扭转刚度为1/5Kφ时,NACA 0012翼型在不同驱动角度下的攻角时序与相平面特性(灰色曲线为"刚性连接") Fig. 6 Time series and phase plot of NACA 0012 airfoil incidence under different incidence inputswith torsional stiffness of 1/5 Kφ(grey curves represent rigid-connection case) |

|
图 7 扭转刚度1/10Kφ不同驱动角度下翼形攻角时序与相平面图(灰色为“刚性”连接) Fig. 7 With Torsional stiffness 1/10Kφ, the time series and phase plot of the airfoil incidence under different input (grey lines represents "rigid-connection" case) |

|
图 8 扭转刚度1/15Kφ不同驱动角度下翼形攻角时序与相平面图(灰色为“刚性”连接) Fig. 8 With Torsional stiffness 1/15Kφ, the time series and phase plot of the airfoil incidence under different input (grey lines represents "rigid-connection" case) |
实验装置的结构决定其无法达到理想的正弦曲线, 但通过对比曲线差异可规避机械结构引入的因素.由于实验装置中驱动端的周期变距是通过曲柄连杆实现的, 减速器等齿轮结构易造成驱动角度上的损失, 例如5°+5°sin (ωt)的刚性连接最小角度不为0°, 9°+7°sin (ωt)刚性连接时最小角度为4°等.实验通过对比刚性连接与弹性连接条件下攻角运动的差别,即可得到失速颤振中气弹响应的特点, 并进一步理解周期变距激励下的失速颤振.
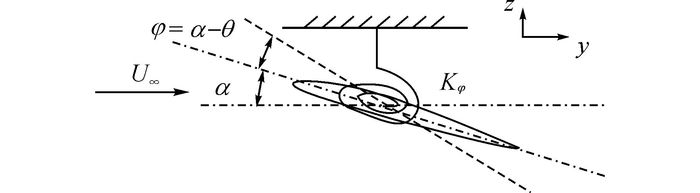
失速颤振最主要的特点之一为“自激振荡”, 表现为自我激励、自我维持在一个限度内[18], 成一个极限环的振动;而在本实验有激励的情况下则表现出比激励变距更大的攻角范围, 并保持在一定限度内, 相平面也形成一个极限环.其中当激励周期变距为“无失速”的5°+5°时, 翼型模型的攻角随着弹性的减弱而出现更大的幅度.因此需要探究当存在激励驱动翼型时, 随着结构刚度的减小以及驱动频率的增加, 增大的振动范围与极限环是否是弹性力本身的作用结果(如:共振),与气动力无关.如图 3所示为本实验装置的简化模型.
|
图 3 单自由度俯仰振荡气动弹性响应实验装置简化模型 Fig. 3 Model for 1-Degree of freedom stall flutter airfoil |
由牛顿第二定律建立模型在俯仰方向上的动力学方程为
| $J\ddot{\alpha }=-C\left( \dot{\alpha }-\dot{\theta } \right)-{{K}_{\varphi }}\left( \alpha -\theta \right)+{{M}_{\text{aero}}}\left( \alpha ,\dot{\alpha },\cdots \right).$ | (1) |
式中:J为翼型关于1/4c的转动惯量;C为阻尼系数;驱动变距θ(t)= θ0+θampsin (ωdt), 其中θ0、θamp、ωd分别为周期变距平衡位置、周期变距振幅以及激励圆频率;Maero为气动力;
| $\ddot{\varphi }+2\zeta {{\omega }_{\text{n}}}\dot{\varphi }+\omega _{\text{n}}^{2}\varphi =\ddot{\theta }.$ | (2) |
式中:
| $\begin{align} &\varphi \left( t \right)=a\text{sin}~\left( {{\omega }_{\text{d}}}t+\delta \right),\text{ }a=\frac{\omega _{\text{d}}^{2}/\omega _{\text{n}}^{2}}{\sqrt{{{\left( \omega _{\text{n}}^{2}-\omega _{\text{d}}^{2} \right)}^{2}}+4{{\zeta }^{2}}\omega _{\text{d}}^{2}\omega _{\text{n}}^{2}}}, \\ &\quad \quad \quad \quad \quad \quad \delta =\text{arctan}\frac{-2\zeta {{\omega }_{\text{n}}}{{\omega }_{\text{d}}}}{\omega _{\text{n}}^{2}-\omega _{\text{d}}^{2}}. \\ \end{align}$ | (3) |
故攻角运动形式为
| $\begin{align} &\alpha \left( t \right)={{\theta }_{0}}+\sqrt{{{a}^{2}}+\theta _{\text{amp}}^{2}+2a\text{cos}~\delta {{\theta }_{\text{amp}}}}\text{sin}\left( {{\omega }_{\text{d}}}t+\gamma \right), \\ &\quad \quad \quad \quad \quad \quad \text{tan }\!\!~\!\!\text{ }\gamma =\frac{a\text{sin }\!\!~\!\!\text{ }\delta }{a\text{cos}~\delta +{{\theta }_{\text{amp}}}}. \\ \end{align}$ | (4) |
根据以上分析可得到如图 4所示的共振曲线.这4种弹簧对应的共振曲线显示,在低频激励时, 攻角的振动幅度将小于周期变距的幅度;在驱动频率仅为5~22 rad/s的区域中, 由于结构阻尼的作用, 翼型攻角振幅集中在αamp/θamp<1的区域中, 且随弹性系数的减小而减小.例如当k=0.075时, αamp/θamp的值为0.93~0.97, 则3种驱动变距应当相差0.4°~0.7°, 而图 5~8中均存在翼型攻角大于刚性驱动的角度的情形.这说明振动幅度增大是气动力的作用.对于驱动的周期变距为无失速时, 振动的幅度仍然有增大.

|
图 4 无气动力时模型俯仰方向振动的共振曲线 Fig. 4 Resonance curves of pitch oscillation of models regardless of aerodynamic forces |
以周期变距为激励的翼型在经历失速颤振时, 攻角不仅表现出增大的现象, 还主要表现出如下3种情况. 1) 在上仰阶段, 攻角向上角速度较刚性偏小, 但最大攻角与刚性相差无几, 在时序图上主要表现出曲线上升变缓、相平面图上表现出最大“V”字形特性;2) 攻角稍微增大或与刚性相同, 时序图上在最大攻角处出现多峰的现象, 而在相平面上出现“额外的圆圈”;3) 最大攻角较刚性明显偏小的情形, 在时序图上表现为峰被“削平”的特性, 在相平面图上显示为横向压扁的特点.与此现象密切相关的是动态失速现象, 从20世纪70年代开始至今的诸多实验结果显示, 是前缘涡生长、脱落引起表面压力振荡, 气动力系数在翼型上仰超过定常的失速角后继续增加, 而后随着前缘涡的脱落和运输, 升力急剧下降且低头力矩陡增[19-20].
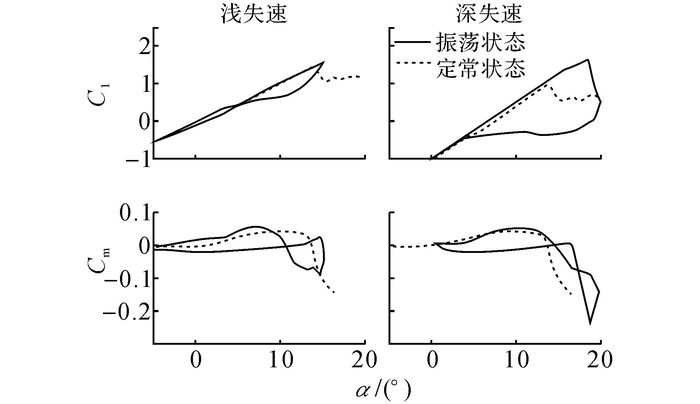
如图 6(b)所示为经历动态失速的俯仰振荡翼型典型的气动力系数[16], 可知在相对于深失速, 浅失速时力矩失速后产生的低头力矩小.同时如图 10所示, 随着减缩频率的增加, 失速角和气动力系数也会不同, 减缩频率越大即翼型的俯仰角速度越大, 失速时低头力矩更大[19].这些动态失速的典型特点也是在弹性过程中攻角曲线展示出不同特性的原因.
|
图 9 典型的浅失速与深失速气动力系数曲线的对比 Fig. 9 Typical aerodynamic coefficients of an oscillating airfoil undergoing light and deep stall |

|
图 10 攻角在不同减缩频率下以15°+10°sin (ωt)振荡时NACA 0012翼型上气动力系数差异(圆圈内气动阻尼Ξ为负, 气动力做正功) Fig. 10 Comparison of aerodynamic coefficients of NACA 0012 airfoil undergoing 15°+10°sin(ωt) pitching oscillation under different reduced frequencies (aerodynamic damping of circle area is negative, aerodynamic moment is positive) |
上述现象可认为是上仰阶段弹性力Fe与气动力Fa相互作用的结果.在情况1) 下, |Fe /Fa|>1, 翼型经过失速角时低头力矩使攻角角速度下降, 但弹性的驱动力稍大, 从而仅出现上升减缓的趋势, 并在相平面图上显示出“V”字型, 即角速度减小的过程, 如图 5(b)中Ⅰ-2-1, 图 5(c)中Ⅰ-3-1、Ⅰ-3-2以及图 6(b)中Ⅱ-2-1所示.当气动力进一步增强, 即|Fe/Fa|≈1时, 翼型的角速度减小为0, 但同时随着前缘涡的脱落与运输, 翼型上方压力振荡、低头力矩减小, 则将出现情况2) 的多峰值的现象.在相平面图上, 翼型攻角由于先减小后增大, 故轨迹为圈型.造成这种现象的本质原因是在动态失速过程中前缘涡的脱落以及二次涡等生成过程中, 低头力矩的振荡, 即只有当前缘涡及时离开翼型上方时, 才可能出现该现象, 如图 7(b)中Ⅲ-2-1以及图 8(b)Ⅳ-2-1所示.若前缘涡驻留时间过长, 且|Fe/Fa|<1时, 上述现象消失, 而出现情况2), 即最大攻角在时间序列上表现出曲线被削平的特点, 如图 6(c)中Ⅱ-3-1/2, 图 7(c)中Ⅲ-3-1/2, 图 8(c)Ⅳ-3-1/2所示, 黑色与灰色曲线最大攻角相差2°~5°; 而前文分析共振曲线时提到, 仅弹性力、结构阻尼作用下的角度最多相差0.7°, 因此该现象说明失速颤振中气动力不总是使最大攻角增加, 亦可以使最大攻角减小.若考虑总的振幅, Ⅲ-3中刚性连接最大与最小攻角差值为18°, 而弹性作用下图 7(c)Ⅲ-3-1/2相同量的值分别为16.97°和15.83°, 而图 8(c)Ⅳ-3-1/2该差值分别为15.71°和16.46°, 即振动幅度减小.若用气动阻尼的概念[1]来解释这种情况, 则该情况在下一个周期展现出正阻尼, 局部可能出现负阻尼.
其他涉及失速过程时振幅增大的结果与上述描述的现象不太相同, 仅当低头力矩在翼型上行出现时, 才有上述3种情况, 而当低头力矩的极大值在翼型上行末端或者下行才出现时, 则上行过程中并无太大阻碍, 并且在下行阶段气动力矩做正功为俯仰振荡输入能量, 从而引起攻角振动幅度的增加.图 10中,当k=0.05以及k=0.15时力矩系数表现出完全不同的特点, 前者负阻尼仅存在于中间段, 而后者负阻尼在几乎占了迟滞回线的一半, 图 6(b)中Ⅱ-2-3/4、图 7(b)中Ⅲ-2-3/4、图 7(c)中Ⅲ-3-3、图 8(b)中Ⅳ-2-3/4、图 8(c)中Ⅳ-3-3振幅增大可能均源于此.图 6(c)中Ⅲ-2-3本应该属于这一类, 相平面图显示上/下行时角速度明显增大, 但可能由于阻尼的作用, 气动力矩的作用被抵消掉, 从而振动幅度并没有表现出增大.另一个相平面图上曲线特征倒“V”型是典型的翼型下行时涡脱落的表现, 伴随出现的是短暂的抬头力矩.
对于攻角变化的频率, 所有时序图皆显示翼型攻角的变化频率变化不大, 在无量纲化时间的时间内, 翼型攻角也表现为5个主要周期, 即主频与驱动频率一致.
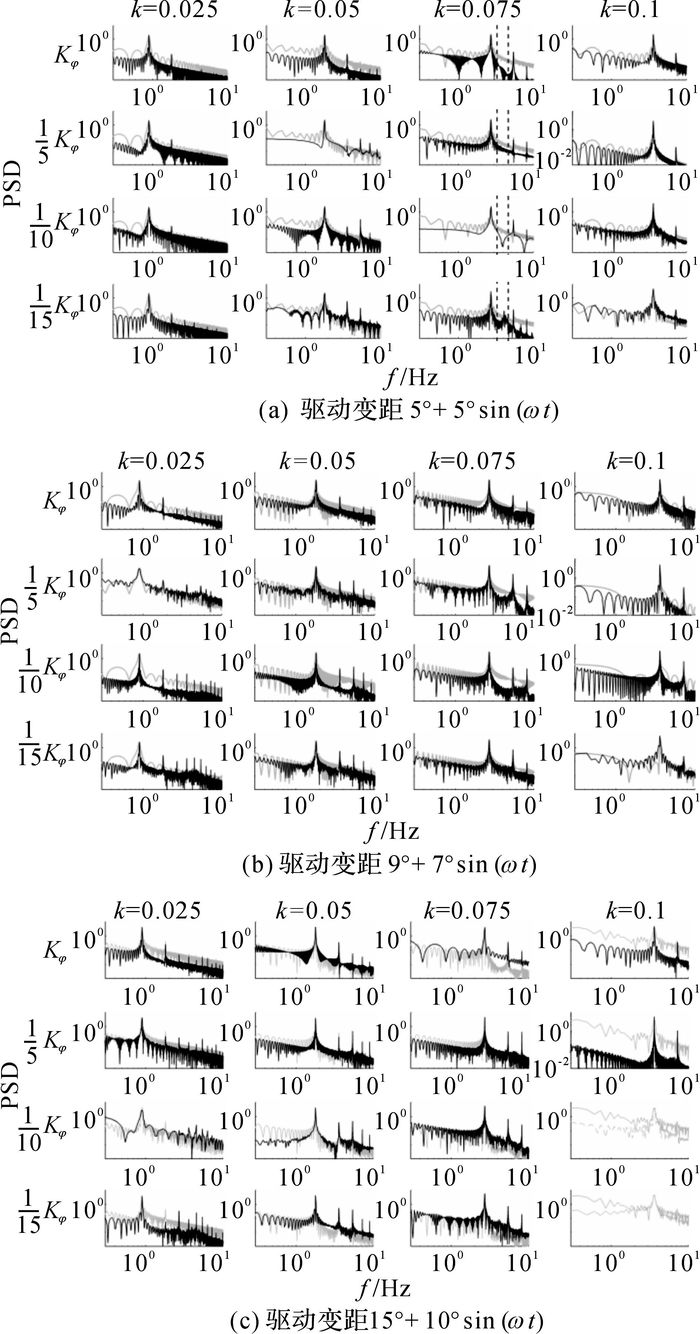
如图 11所示为各激励变距、扭转刚度与驱动频率下攻角的频域特性与刚性运动频域特性的比较.由于选取数据的长度不同, 数据在快速傅里叶变换时存在差异, 各频率处的幅值为归一化后的值.其中主频与驱动频率一致, 这与时序图中判断的一致.随着扭转刚度(自然频率)的下降, 深、浅失速的频谱中整数倍主频相对主频的幅值发生了显著的变化, 其中9°+7°的激励变距在k=0.025和0.050时, 4倍和5倍主频的幅值显著上升, 而2倍主频幅值下降到几乎消失, 当k=0.075和0.100时, 3倍主频幅值显著升高;5°+5°与15°+10°的激励变距与之类似, 高频部分幅值上升.另外, 在5°+5°激励变距作用下, Kφ减小为原来的1/15时, k=0.075时在整数倍主频fmain之间出现了几个特殊的频率为
|
图 11 NACA 0012翼型在不同变距驱动下攻角的频域特性(灰色为刚性连接, 黑色为弹性连接, 全为浅色的两组为无效数据) Fig. 11 Frequency characteristics of NACA 0012 airfoil. (grey lines for rigid and black lines for elastic connection, figure with both light colored curves indicating invalid datas) |
f1=4.04 Hz≈1.5×2.7 Hz=1.5fmain, 即1.5倍主频;
f2=6.77 Hz≈2.5×2.7 Hz=2.5fmain,
即2.5倍主频等.按照庞加莱映射的观点, 若选取一个基频作为参考, 其他频率的整数(N)倍与该基频的整数倍相等, 则这个振动归为N周期振动[17].显然对于该频谱中的1.5fmain、2.5fmain、3.5fmain等, 存在整数N=2满足上述条件, 故归为两周期振动.如图 8(a)中Ⅳ-1-3的时序图所示, 攻角振幅出现一大一小周期呈现的特点, 符合两周期振动的特点.由于气动力作用引起的两周期振动特性是所有实验中出现的显著特点.时序图显示攻角的最大值正好在失速角附近, 因此可能出现间断脱涡的情形.文献[21]利用离散涡的方法计算流场中的涡结构变化周期在某些特定的减缩频率下呈两周期, 在一定程度上佐证了气动力出现两周期正是间断脱涡的结果.若从频率角度理解这个系统, 系统存在固有频率ωn、驱动频率ωd和气动力频率ωa, 这三者决定了翼型运动的运动频率ωm, 而同时该运动频率也决定了气动力频率, 构成耦合系统为
| $f\left( {{\omega }_{\text{n}}},\text{ }{{\omega }_{\text{d}}},\text{ }g\left( {{\omega }_{\text{m}}} \right) \right)={{\omega }_{\text{m}}}.$ | (7) |
这三者的关系即决定了系统的运动特性.一般地, 这些频率之间的某种关系可在一定程度上预测系统的振动特性.在图 8(c)Ⅳ-1-3中, ωn/ωd=26.67/17=1.57≈π/2, 目前还不确定该无理数对系统的影响, 值得进一步探讨.
2.2 弹性约束下的气动力与能量传递上文讨论了攻角的响应特性, 探讨了形成各运动形式可能的原因, 但要更深入了解动态失速对失速颤振所造成影响的根本原因, 需探究各情形下气动力和能量传递的变化过程.由于动态情形下所测力需要修正, 且实验所测数据较多, 现象复杂, 仅以图 5(a)中的Ⅰ-1-1/2/4, 图 5(c)中的Ⅰ-3-1/2/4中气动力系数与能量传递系数为例解释前述观察到的现象, 其余数据将在后续的报告中详细分析.
参考文献[8]的能量系数, 定义
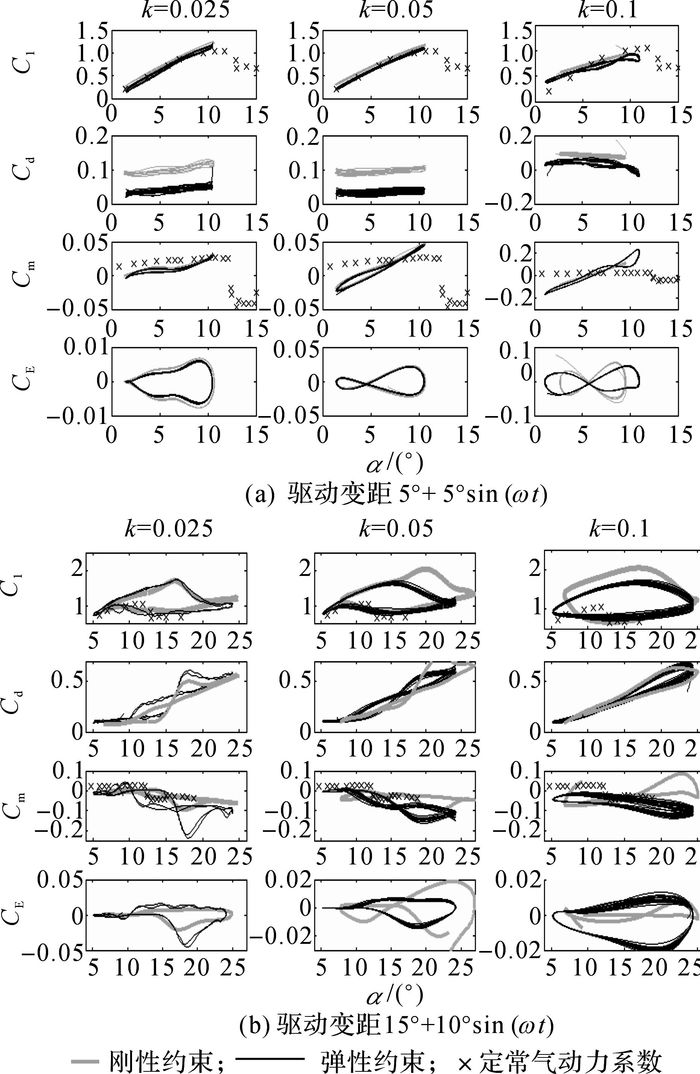
图 12(a)为翼型分别在弹性约束(弹性系数为Kφ)与刚性约束下, 在15°+10°的变距驱动下,气动力系数的对比.在k=0.025以及k=0.050时, 升力沿定常升力系数的曲线上升, 俯仰过程中几乎贴着曲线的两侧, 而阻力系数则小于刚性连接, 力矩系数主要沿着定常力矩曲线, 但随减缩频率增加, 斜率有较大区别.当k=0.100时, 翼型的攻角超过10°, 升力系数展现出类似动态失速过程的曲线, 说明此时有前缘涡脱落, 强度可能较弱.由于攻角正好在升力失速角附近, 按照文献[19]中动态失速实验的结论“翼型超过失速角后升力系数继续上升”, 以及k=0.150时上行阶段不会产生涡脱现象, 判定气动力曲线显示的是由于角速度较小翼型下行时小的前缘涡脱离.因此在右端出现向上的曲线, 同时曲线中间一段下降的曲线正好对应涡脱落后的失速段, 气动力降低.力矩系数同样可以证实这个猜测, 即在下俯阶段前缘涡脱落导致低头力矩(即力矩减小), 这与曲线相符合.根据如图 12(a)所示的能量系数曲线, k=0.025时该系数的曲线呈葫芦状, 而k=0.050时变成8字形, k=0.100时则呈现左下端缺失的类“8”字形图案.其中从葫芦形到类“8”字形的变化是由于力矩系数跨越Cm=0的直线, 在翼型上仰阶段力矩为正.而类“8”字形缺一角则主要源于力矩系数和角速度的不对称或涡的影响.能量系数不对称度变高可能与前缘涡有关, CE-α曲线可判断平均能量系数的符号:若能量系数关于CE=0的轴对称, 则一个周期内气动力输入总能量CE=0;若不对称, 则曲线凸起部分的符号决定一个周期总能量的符号.k=0.100时右下角缺失, 相较于刚性能量系数, 总能量为正向增加, 如表 2所示, 虽然此时气动力做功为负, 但绝对值减小了.在图 5(a)中I-1-4的实验组中攻角幅值超过了10°, 而气动力仍然做负功, 因此翼型获得能量的来源只能是周期变距的激励;而前述已说明若无气动力存在, 攻角无法达到10°, 即气动力的存在改变了原弹性系统的能量传递过程, 使驱动对弹性结构的能量输入增加, 从而使翼型在11°左右达到最大值.刚性连接驱动的翼型在3种驱动频率下能量系数对称度较高, 这是小角度驱动下弹性与刚性连接的重要区别.
| 表 2 不同减缩频率、驱动角度下刚性连接与弹性连接平均能量系数对比 Table 2 Comparison of averaged energy coefficient with rigid and elastic restrains under different driving reduced frequencies and different driving pitches |
|
图 12 弹性约束与刚性约束下, 不同驱动变距驱动时翼形上气动力系数与能量系数的对比 Fig. 12 Comparison of aerodynamic and energy coefficients of NACA 0012 airfoil under elastic connection and rigid connection with different driving pitches |
图 12(b)为翼型分别在弹性约束(弹性系数为Kφ)与刚性约束下在15°+10°的变距驱动下、气动力系数的对比.弹性约束下, k=0.025时气动力系数与刚性连接差不多, 阻力系数在翼型上仰末端及下俯期间略微增大, 而低头力矩系数则在15°附近陡然增加, 并保持到翼型下俯回到10°左右才重新回0.当k=0.050时, 气动力系数出现了很大不同, 升力系数明显小于刚性驱动的测量值, 而阻力系数也在上仰达到20°左右时略小于刚性连接的值, 力矩系数则显示出缓和下降趋势.该弹性连接下翼型攻角最大值小于25°, 同时失速角也较刚性连接时提前.当k=0.1时, 升力系数在上仰阶段偏小, 阻力系数略微偏大, 力矩系数则平缓地下降/回升.能量系数在3个频率下均显示出非对称性, 且呈现上小且平、下凸且大的特点, 通过比较与刚性连接时的曲线可知, k=0.025、k=0.100时气动力做(负)功减小, 而k=0.050时做(负)功增大.前文提到非对称度变高可能是由于前缘涡的关系, 从k=0.025的升力和力矩系数判断可知, 前缘涡脱落后仍可能继续获得能量, 从而有更大的低头力矩.关于此猜想仍需粒子图像测速法(particle image velocimetry, PⅣ)等进一步实验证明.
如表 2所示, 弹性约束的引入, 小角度驱动下气动力做负功减小, 即阻尼向负阻尼方向变化.而大角度驱动(深失速)下则呈现相反的变化, 即气动力所做负功增加, 气动阻尼向正阻尼方向变化.基于刚性的气动力矩系数曲线, McCroskey认为深失速相比浅失速更为稳定[16], 而本实验指出弹性作用下, 深失速的驱动在气动力方面更稳定.这是因为深失速往往伴随着强前缘涡, 而强前缘涡的脱落将造成巨大的低头力矩, 由于弹性结构的存在, 翼型所能达到的最大角度相对减少.但这仅适用于高强度扭弹簧, 实验组Ⅳ-3-4出现的发散现象即是反例.但气动力具有稳定性, 翼型的颤振并不一定也具有稳定性.以往研究均只关注气动力对翼型振动时的能量输入, 但对于直升机这类具有周期变距激励的颤振问题, 气动力即使做负功, 振动幅度也可能增大, 前面已论证能量传递可能会发生变化, 驱动输入能量可能因为气动力作用而大幅增加.
3 结论(1) 随结构扭转刚度的减小, 气动力/弹性力的变化导致攻角的运动规律出现4种主要特点:上升趋缓, 相平面出现“V”字形;出现多峰值情形, 相平面出现多圈曲线;攻角最大值被“削平”, 相平面曲线横向压缩以及振动幅度大幅增加.
(2) 在以周期变距为激励的气动弹性系统中, 驱动力频率、自然频率和气动力频率共同决定了运动的频率, 而运动的频率又决定了气动力频率, 构成耦合系统.随驱动频率增加以及自然频率的减少, 运动主频仍为驱动频率;并出现两周期振动特性, 此时自然频率与驱动频率的比约为π/2.
(3) 弹性约束下气动力系数与刚性运动呈现出较大差别, 在弹性约束下与之对应的气动力对翼型的能量系数也显示出较大差异, 其中小角度驱动下平均能量系数均呈增加趋势, 即趋于气动不稳定;而大角度驱动下平均能量系数大部分呈减小趋势, 即趋于气动稳定.
(4) 不同于由于扰动引起的失速颤振, 周期变距激励下的失速颤振中气动力做功不再是确定振动能量增加/减少的唯一因素, 气动力的作用会引起能量传递的变化, 即翼型从气动力中获得的能量为负, 也可能从激励中获得更高的能量而增大振幅, 即在周期变距为激励的失速颤振中, 气动力可以通过改变弹性机构能量传递来实现振动的加剧.
实验中仍存在许多尚不清楚的问题, 如:在扭转刚度进一步减小时, 为什么当驱动角度为“浅失速”和“深失速”时翼型模型振动会大幅增加?是由于气动力做功还是小角度驱动的能量传递改变?这需要对实验数据继续分析并加以对比总结.另外, 许多相平面上所观测的特点, 仅通过文献对动态失速的总结得出, 还需要进一步结合PⅣ实验进行验证;目前仍不清楚出现两周期振动的原因等.后续工作中将继续改进实验设备并开展流场显示的实验, 一方面为失速颤振紧耦合模型提供验证算例, 另一方面更深入地认识失速颤振.
| [1] | CORKE T C, THOMAS F O. Dynamic stall in pitching airfoils:aerodynamic damping and compressibility effects[J]. Annual Review of Fluid Mechanics, 2015, 47(1): 479–505. DOI:10.1146/annurev-fluid-010814-013632 |
| [2] | DIMITRIADIS G, LI J. Bifurcation behavior of airfoil undergoing stall flutter oscillations in low-speed wind tunnel[J]. AIAA Journal, 2009, 47(11): 2577–2596. DOI:10.2514/1.39571 |
| [3] | SARKAR S, BIJL H. Nonlinear aeroelastic behavior of an oscillating airfoil during stall-induced vibration[J]. Journal of Fluids and Structures, 2008, 24(6): 757–777. DOI:10.1016/j.jfluidstructs.2007.11.004 |
| [4] | FUNG Y C. An introduction to the theory ofaeroelasticity[M]. Chicago: Courier Corporation, 2012: 234-254. |
| [5] | OATES G C. Aircraft propulsion systems technology and design[M]. Ohio: AIAA, 1989. |
| [6] | ARCIDIACONO P J. Prediction of rotor instability of at high forward speeds. Volume I. Steady flight differential equations of motion for a flexible helicopter blade with chordwise mass unbalence[R]. Virginia:U.S. Army Aviation Materiel Laboratiories, 1969. |
| [7] | BOWLES P O, CORKE T C, COLEMAN D G, et al. Improved understanding of aerodynamic damping through the Hilbert transform[J]. AIAA Journal, 2014, 52(11): 2384–2394. DOI:10.2514/1.J052630 |
| [8] | BHAT S S, GOVARDHAN R N. Stall flutter of NACA 0012 airfoil at low Reynolds numbers[J]. Journal of Fluids and Structures, 2013, 41: 166–174. DOI:10.1016/j.jfluidstructs.2013.04.001 |
| [9] | O'NEILL T O, STRGANAC T. Aeroelastic response of a rigid wing supported by nonlinear spring[J]. Journal of Aircraft, 1998, 35(4): 616–622. DOI:10.2514/2.2345 |
| [10] | AMANDOLESE X, MICHELIN S, CHOQUEL M. Low speed flutter and limit cycle oscillations of a two-degree-of-freedom flat plate in a wind tunnel[J]. Journal of Fluids and Structures, 2013, 43: 244–255. DOI:10.1016/j.jfluidstructs.2013.09.002 |
| [11] | SHAO S, ZHU Q, ZHANG C, et al. Airfoil aeroelastic flutter analysis based on modified leishman-beddoes model at low mach number[J]. Chinese Journal of Aeronautics, 2011, 5(24): 550–557. |
| [12] | PRICE S, KELERIS J. Non-linear dynamics of an air foil forced to oscillate in dynamic stall[J]. Journal of sound and Vibration, 1996, 194(2): 265–283. DOI:10.1006/jsvi.1996.0356 |
| [13] | FRAGISKATOS G. Nonlinear response and instabilities of a two-degree-of-freedom airfoil oscillating indynamic stall, in department of mechanical engineering[D]. Montreal Canada:McGill University, 1999. |
| [14] | TANG D M, DOWELL E H. Flutter and stall response of a helicopter blade with structural nonlinearity[J]. Journal of Aircraft, 1992, 29(5): 953–960. DOI:10.2514/3.46268 |
| [15] | LAXMAN V, VENKATESAN C. Chaotic response of an airfoil due to aeroelastic coupling and dynamic stall[J]. AIAA Journal, 2007, 45(1): 271–280. DOI:10.2514/1.24587 |
| [16] | MCCROSKEY W J. Unsteady airfoils[J]. Annual review of fluid Mechanics, 1982, 14(1): 285–311. DOI:10.1146/annurev.fl.14.010182.001441 |
| [17] | PARKER T S, CHUA L. Practical numerical algorithms for chaotic systems[M]. New York: Springer Science and Business Media, 2012: 47-54. |
| [18] | HAM N, YOUNG M. Limit cycle torsional motion of helicopter blades due to stall[J]. Journal of Sound and Vibration, 1966, 4(3): 431–444. DOI:10.1016/0022-460X(66)90138-6 |
| [19] | MCALISTER K W, CARR L W, MCCROSKEY W J. Dynamic stall experiments on the NACA 0012 airfoil. (1978-01-01). https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19780009057.pdf. |
| [20] | LEE T, GERONTAKOS P. Investigation of flow over an oscillating airfoil[J]. Journal of Fluid Mechanics, 2004, 512: 313. |
| [21] | SARKAR S, VENKATRAMAN K. Period-doubling phenomenon observed in the dynamic stall vortex patterns[J]. AIAA Journal, 2007, 45(7): 1786–1791. DOI:10.2514/1.29656 |



