电力电子变压器(power electronic transformer, PET)是一种基于电力电子技术的新型电能变换装置[1].PET被认为在未来电网中有着良好的应用前景, 且在“未来再生电能传输和管理网络”中能够发挥核心作用[2], 对主动型配网的建设也有促进作用[3].相比传统电力变压器, PET能够实现灵活的电流和电压控制, 改善电能质量, 控制潮流和提高稳定性.陈启超等[4]针对可以应用于配电网的PET拓扑结构进行了总结.李子欣等[5]提出了一种将模块化多电平变流器与PET相结合的新型拓扑, 该拓扑面向未来智能配电系统.此外, 功率单向传输的PET拓扑也是该技术在配电领域的研究重点[6-7].
在不同PET拓扑种类中, 被研究最多的是包含高、低压2组直流母线的双交直交拓扑, 因此大部分PET拓扑中的一次侧直流母线都需要安装大容量高压电容器[8].一方面, 高压、高频和大容量的电容器组会提高PET成本;另一方面, 与高压电网相连的直流电容器会影响整个电网的安全性.目前还没有专门针对PET中直流母线电容器的技术标准, 但可以参考具有相似应用场合的电力电容器技术标准.国家标准GB/T 20993-2007规定了高压直流输电系统中的直流侧滤波电容器的相关技术要求:安装于3~35 kV高压直流换电设备中的直流滤波电容器不仅要满足电网过电压、过电流、雷电冲击和热稳定性等试验要求, 而且在其内部还需要安装熔断丝和其他监控来保护附件.由于PET中的高压电容器需要能够承受一定的纹波电压, 通常会选择能够承受高频电流的薄膜电容元件来组成电容组[9].虽然薄膜电容的可靠性优于其他电容, 但是其单位体积的容量较小, 需要多组电容器串并联才能满足电压和容量要求, 降低了PET系统的功率密度;另一方面, 目前还没有研究表明薄膜电容能够满足如标准GB/T 20993-2007所要求的电网安全性测试.PET电路的一次侧通常采用变流器单元级联的结构来满足输入高电压的设计要求, 因而一次侧直流母线电容的存在使得PET的设计需要考虑其级联单元中多个直流母线的均压控制方法[10-11], 同时需要考虑并网启动过程中的母线电容充电问题[12].综上所述, PET中高压电容器不仅会给PET的设计提高难度, 还会带来成本增加和可靠性降低的问题.
针对现有PET拓扑中高压直流母线电容器成本和可靠性等问题, 本文提出一种无需安装高压大容量直流滤波电容的新型PET拓扑.该PET拓扑依靠多脉移相整流技术(multi-pulse rectifier, MPR)[13],避免了高压电容器的安装, 同时具有消除一次侧谐波电流的功能.相比传统PET拓扑, 新型PET取消了高压直流母线电容, 更容易实现柔性并网的功能, 其一次侧多直流母线的均压控制也更加有效.首先提出新型PET的电路拓扑和控制方法, 阐述其在没有一次侧直流母线电容的条件下应用MPR技术消除谐波电流的原理和对不同负载的适应性, 接着分析其柔性并网和多母线均压的问题, 最后通过仿真分析和样机试验结果验证所提PET拓扑的有效性.
1 新型PET拓扑及其控制方法Kang等[14]提出的PET拓扑一次侧采用“交交变流器”电路.虽然该拓扑的高压侧没有大容量滤波电容, 但是不能抑制一次侧电网的谐波电流.本文将MPR技术与PET拓扑的设计进行整合得到新型PET拓扑, 该新型PET拓扑在避免使用高压直流电容的同时具备网侧电流谐波抑制功能.MPR技术是新型PET拓扑的核心, 简称为MPR-PET.
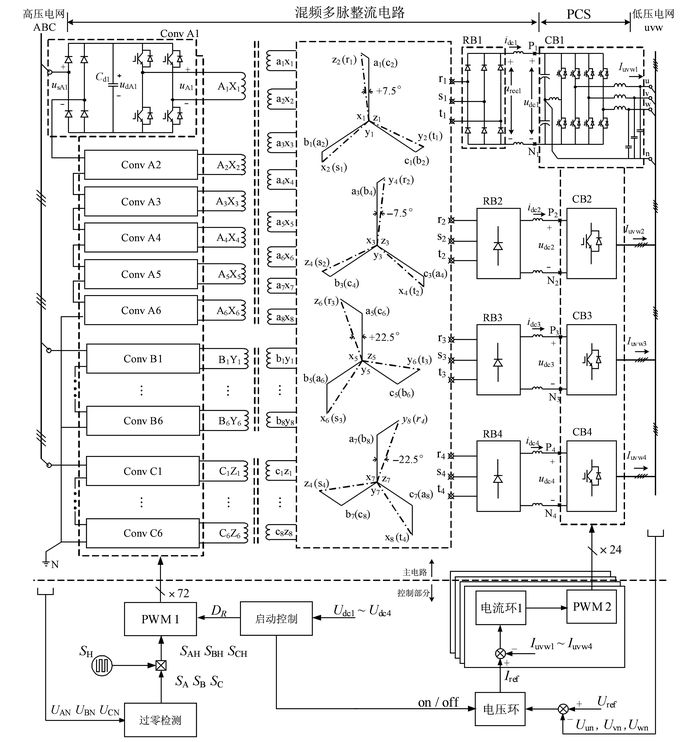
1.1 电路拓扑结构MPR-PET系统的拓扑结构和主要控制部分如图 1所示.与其他PET拓扑一样, MPR-PET电路结构可以分为“一次侧变流器”、“二次侧变流器”和“高频变压器”3个部分.MPR-PET一次侧变流电路由3组相同的单相级联电路组成.每组级联电路的一个输入端分别接一次侧三相电网的一相, 而另一端连接在一起构成中性点N.以A相级联电路为例, 其由6个变流器单元(Conv A1~A6) 依次串联而成, 每个单元的电路结构都一样.如图 1中Conv A1所示, 一次侧每个变流器单元都分别由一个单相全桥不控整流电路和一个单相全桥逆变器组成, 其直流母线上只包含容值小于1 μF的滤波电容, 用于吸收IGBT开关过程中的尖峰电压.高频变压器一次侧的A相包含6个匝数相等的绕组A1X1~A6X6, 依次与Conv A1~A6的输出端相连.Conv A1~A6各个直流母线的电压均衡问题通过绕组A1X1~A6X6能量传递实现, 该方法参考Krishnamoorthy等[15]的研究, 而MPR-PET在解决该电压均衡问题的方面更加有效, 这个问题将在第2.2节中论述.
|
图 1 MPR-PET系统拓扑结构图 Fig. 1 Topology diagram of power electronic transformer with multi-pulse rectifier (MPR-PET) |
MPR-PET中的高频变压器是一个多脉移相变压器, 如图 1所示, 其二次侧A相设计有8个绕组a1x1~a8x8, 三相总共有24个单相绕组, 被接成4组曲折接法的三相绕组r1s1t1~r4s4t4.这4组三相绕组的输出端分别连接三相不控整流电路RB1~RB4.RB1~RB4的输出端经过滤波电路后, 输出4组电压平稳的直流母线P1N1~P4N4.二次侧变流器是将P1N1~P4N4通过4个逆变器(CB1~CB4) 转换成交流电后并联在一起.输出端并联的CB1~CB4构成一个并联逆变器系统(parallel converter system, PCS), 该PCS的输出可以直接连接到380 V低压电网.CB1~CB4是采用“电容中分式”的逆变器拓扑[16], 包含一个“均压”桥臂电路, 用来平衡上下母线电容的电压.4组直流母线的中点都连到三相四线制电网的中性线n, 以便在均压桥臂的配合下提供二次侧负载所需的零序电流.
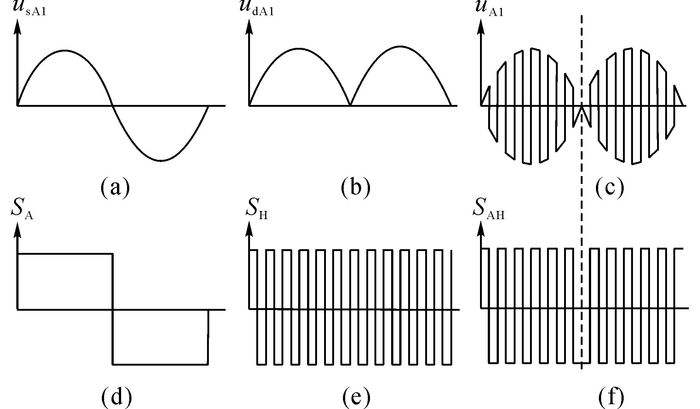
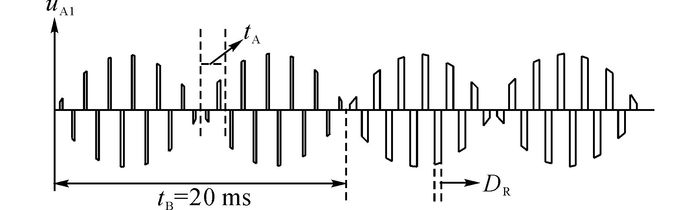
1.2 一次侧变流器控制MPR-PET一次侧A相6个逆变电路的PWM脉冲信号来自同一信号源SAH.图 1中Conv A1的各个电压usA1、udA1和uA1波形如图 2(a)~(c)所示.Conv A1母线电容Cd1是容量仅为1 μF的滤波电容, 因而一次侧直流母线电压udA1波形为如图 2(b)所示的“馒头波”.如图 2(c)所示, 经过逆变部分PWM开关调制后, uA1波形呈现具有正弦包络线的高频波形.参照图 1中的一次侧控制信号框图:以A相为例, 电网相电压反馈信号UAN经过“过零检测”生成开关信号SA(图 2(d)), 将SA和标准方波信号SH(图 2(e))相乘得到一次侧逆变电路的开关信号SAH(图 2(f)).图 2(c)中uA1波形只有正负电平, 在半个开关周期内占空比为100%.实际运行中的uA1波形中有一定时间的零电平, 其控制方法参照刘凤君[17]提出的移相PWM控制技术.占空比调节后的uA1波形如图 3所示:在一个开关周期tA内, 正负电平的时间相等;每个工频周期tB内高频开关的占空比DR保持不变.通过调节占空比DR可以等比例调节二次侧RB1~RB4的输出电压urec1~urec4, 进而调节udc1~udc4和整个MPR-PET输入功率P1.
|
图 2 变流器Conv A1的电压和信号波形 Fig. 2 Voltage and signal waveforms of converter Conv A1 |
|
图 3 占空比可调的一次侧输出电压波形 Fig. 3 First-side output voltage waveforms with duty ratio regulation |
二次侧变流器可以分为整流部分(RB1~RB4) 和逆变部分(CB1~CB4).由于直流母线解耦作用, 这两部分电路可以分别进行分析.
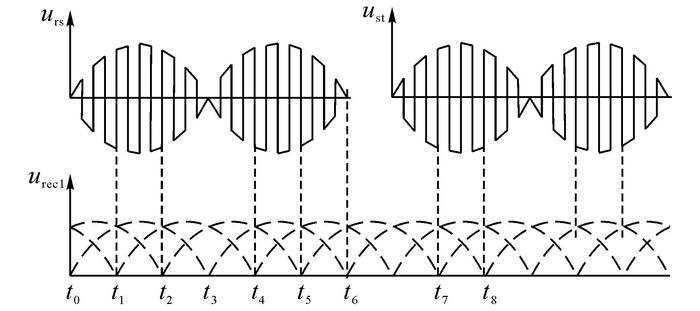
RB1二次侧整流过程的电压波形如图 4所示.图urs为二次侧绕组r1s1t1的r相与s相之间的线电压;ust为s相与t相之间的线电压;urec1为RB1整流器输出电压波形.这2个电压波形和图 2(c)中uA1波形类似, 可以等效为高频分量和工频分量的乘积.ust工频分量的相位比urs工频分量的相位超前了120°, 表明4个绕组r1s1t1~r4s4t4三相电压的工频分量的相位之间会根据接法和绕组匝数不同产生不同偏移.结合工频MPR原理可知:通过绕组之间的相位偏移可以实现网侧谐波电流的消除.在图 4中的一个工频周期(20 ms, t0~t6)内, 根据RB1中二极管导通的情况, urec1可以分为6个工作阶段(对应于三相工频整流的六脉波效应).在t1~t2时间内, RB1仅发生高频整流过程, 即r相与s相对应桥臂的上、下管分别交替导通, 而t相桥臂的二极管保持截止;在t7~t8时间内, RB1中的s相与t相桥臂工作, 而r相桥臂的二极管截止.在t2时刻, RB1会完成从r相到t相桥臂的换流过程, 这类似于三相工频整流电路的换流过程.在整个MPR-PET电路中, 从一次侧电网输入端到母线P1N1~P4N4的这部分可以被看作为一个完整多脉移相整流电路.RB1~RB4的整流过程包含高频过程和工频过程, 因此MPR-PET中的MPR电路可以被称为“混频多脉整流电路”.
|
图 4 RB1二次侧整流过程的电压波形 Fig. 4 Voltage waveforms of RB1 with second-siderectifiers |
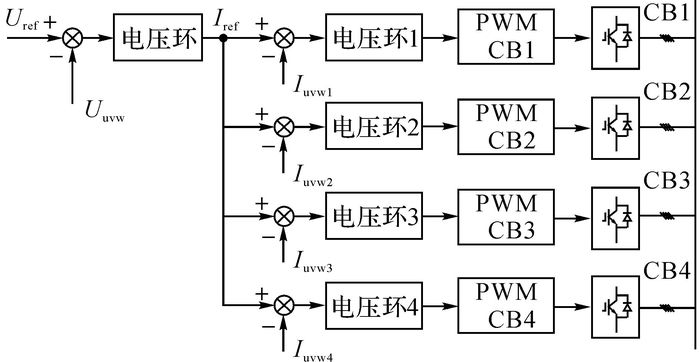
MPR-PET二次侧的逆变部分CB1~CB4组成一个PCS系统.该PCS的均流控制采用了文献[18]提出的主从均流控制方法, 其控制框图如图 5所示.由图可知, PCS系统包含1个电压环调节器, 输出信号Iref同时输入到4个电流环调节器, 作为其三相电流给定值.各个调节器的反馈分别是CB1~CB4的三相电流采样值Iuvw1~Iuvw4(其中Iuvw1为包含iu1、iv1和iw1的三相电流向量,依此类推).电压环和电流环都采用PID控制器, 通过电流环的调节作用实现CB1~CB4输出电流的均衡控制.4个电流环给定信号一致, 因而CB1~CB4对应相的输出电流相等, 实现了PCS的均流控制.
|
图 5 二次侧PCS系统均流控制框图 Fig. 5 Block diagram of current-sharing control forsecond side PCS system |
常规工频MPR电路实现消除谐波的条件包括:1) 各个三相绕组等效匝数相等且相位偏移符合要求;2) 通过均流电抗器或者母线串联的方式保证各个整流桥输出电流相等[20].以课题组试验样机为例, 图 1中变压器绕组的匝数如表 1所示.由于变压器的高频化设计要求, 导致表 1中a2x2、a4x4等绕组匝数比较少.
| 表 1 高频变压器绕组匝数 Table 1 Winding turns of high frequency transformer |
在绕组匝数较少的条件下, 表 1中的绕组接成曲折接法三相绕组r1s1t1~r4s4t4后, 出现了等效匝数不相等的问题, 如表 2所示.等效匝数不同会严重影响MPR电路的正常工作, 无法消除网侧谐波电流.
| 表 2 高频变压器三相绕组等效参数 Table 2 Three-phase windings equivalent parameters of high frequency transformer |
上述问题可以通过PCS系统进行弥补, 因为PCS系统均流控制能够保证CB1~CB4交流侧输出功率相等.忽略CB1~CB4损耗的差异, 各个直流母线P1N1~P4N4的输入功率也相等, 即:
| ${U_{{\rm{dc}}1}}{I_{{\rm{dc}}1}} = {U_{{\rm{dc}}1}}{I_{{\rm{dc}}2}} = {U_{{\rm{dc}}1}}{I_{{\rm{dc}}3}} = {U_{{\rm{dc}}1}}{I_{{\rm{dc}}4}}.$ | (1) |
式中:Udc1为udc1的平均值.
假设输入的三相电压平衡, 以RB1为例, 三相不控整流器输出电压与绕组匝数的关系如下:
| ${U_{{\rm{dc}}1}} = 1.35{U_{{\rm{ea}}}}{\omega _1}.$ | (2) |
式中:Uea为高频变压器A相每匝绕组线圈的感应电压有效值;ω1为绕组r1s1t1的等效匝数.
将式(2) 代入式(1), 得到
| ${\omega _1}{I_{{\rm{dc}}1}} = {\omega _2}{I_{{\rm{dc2}}}} = {\omega _3}{I_{{\rm{dc3}}}} = {\omega _4}{I_{{\rm{dc4}}}}.$ | (3) |
式中:Idc1~Idc4分别为图 1中流入直流母线P1N1~P4N4的电流平均值;ω2~ω4分别为r2s2t2~r4s4t4的等效匝数;ω1~ω4的取值如表 2所示.
参照关于工频MPR电路消除谐波原理的推导[13, 19], 图 1中MPR-PET一次侧A相网侧电流的傅里叶级数展开形式如下:
| $\begin{array}{l} {I_{\rm{A}}} = \frac{1}{{{\omega _{\rm{A}}}}}\sum\limits_{i = 1}^4 {\left[ {\sum\limits_{n = 1,3, \cdots }^{ + \infty } {\frac{{8{k_i}}}{{n{\rm{\pi }}}}} } \right.} \cos \frac{{n{\rm{\pi }}}}{6}\cos \left( {n{\theta _i}} \right) \times \\ \quad \quad \quad \left. {\sin \left( {n\omega t} \right)} \right]{\omega _i}{I_{{\rm{dc}}i}}. \end{array}$ | (4) |
式中:ωA为一次侧所有绕组匝数之和;θ1~θ4为绕组r1s1t1~ r4s4t4的相位偏移.
如表 2所示, θ1~θ4的取值已经基本满足24脉整流电路相位互差15°的设计要求, 有限相位误差不会影响消除谐波的效果[19].式(4) 中匝数ωi和直流母线电流Idci以乘积的形式影响傅里叶级数的结构.因此, 虽然ω1~ω4两两之间的差值较大, 但如果满足式(3), 那么式(2) 中等式右边的3次以上谐波分量的幅值都等于0.PCS系统的均流控制可以使得式(3) 成立, 实现谐波的消除.综上所述, 高频化设计后的绕组匝数破坏了应用MPR电路消除谐波的一般条件, 但可以通过利用PCS的均流控制来克服该问题, 实现网侧电流谐波的消除.
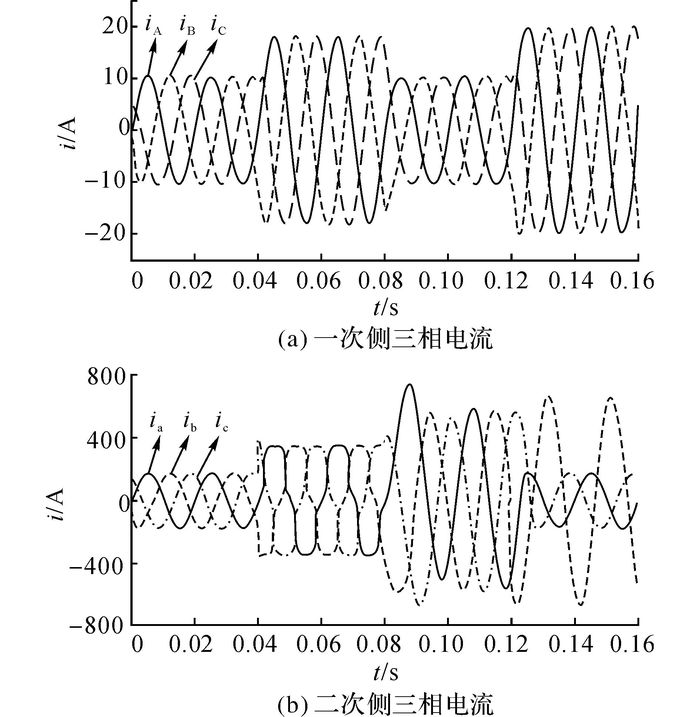
为了验证MPR-PET消除谐波的效果, 同时也为了验证其对无功和三相不平衡负载的适应性, 通过Matlab/Simulink对如图 1所示的MPR-PET电路拓扑进行仿真试验, 仿真参数参考表 1和2, 结果如图 6所示.从图 6(a)可知, 在整个仿真过程中, 一次侧电流波形始终为正弦波且三相电流平衡;在0.08~0.12 s时间段内, 虽然二次侧电流由于感性无功分量增大而出现幅值升高的情况, 但是一次侧的功率因数没有明显变化.从图 6(b)可知, 在仿真开始阶段MPR-PET二次侧负载为纯阻性;在0.04~0.08 s时间段内, 二次侧电流呈现富含谐波的波形;在0.08~0.12 s时间段内, 二次侧加入了一定容量的感性负载;在最后的时间段内, 二次侧出现了严重的三相不平衡问题.仿真结果验证了MPR-PET能够在不同的二次侧负载条件下保证一次侧电网的电能质量.
|
图 6 MPR-PET三相电流仿真波形 Fig. 6 Three-phase simulation current waveforms in MPR-PET |
相比传统PET, MPR-PET避免了在一次侧高压直流母线上安装大容量的电容器, 可以在没有充电电阻及旁路开关的条件下实现柔性并网, 也可以提高一次侧多组直流母线的均压效果.
2.1 柔性并网一次侧高压直流母线包含大容量的储能电容PET拓扑[9-10], 并网过程中一次侧母线电容会和电网的线路电感发生较强的谐振.谐振过电压很可能会损坏功率器件, 严重威胁到电网的安全运行.文献[11]使用与PET一次侧电路类似的级联结构变流器, 通过在启动过程中串入充电电阻来减小并网冲击电流, 在充电结束后采用交流开关将充电电阻旁路掉.PET是一种高压大功率电网设备, 充电电阻和旁路开关的成本和可靠性问题都会制约PET的应用;这种方案也不适合实现快速反复的并网.
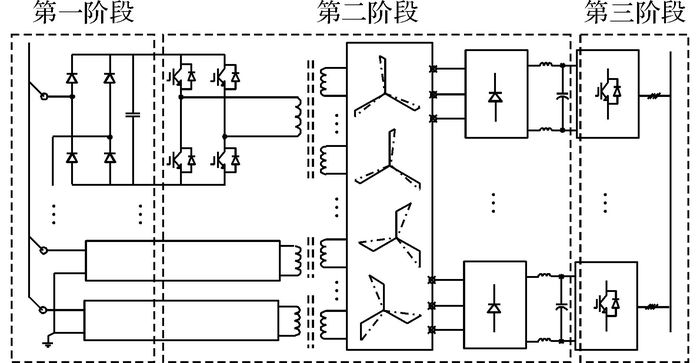
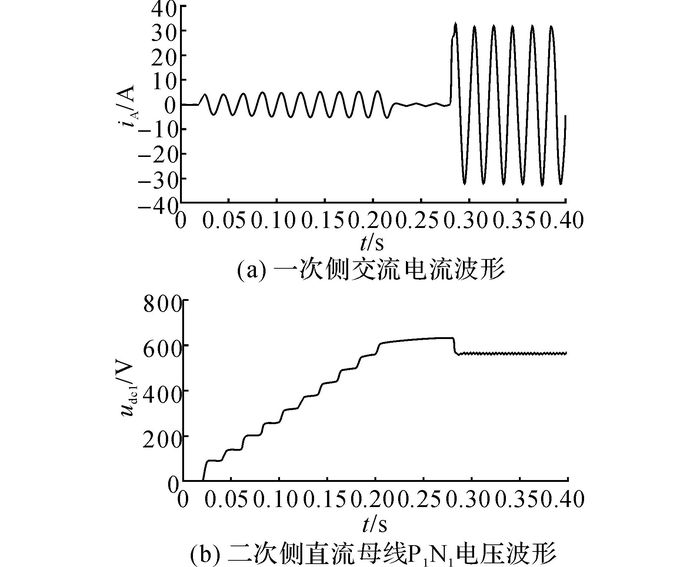
MPR-PET系统的柔性并网过程如图 7所示, 仿真电流电压波形如图 8所示.该过程分为3个阶段, 采用Matlab/Simulink软件进行仿真.第一阶段(0~0.02 s)为对一次侧直流母线进行充电的过程, 一次侧和二次侧变流器中的所有IGBT都保持关断状态, 且由于一次侧母线电容非常小只有约1 μF, 此过程中没有明显的充电电流.第二阶段(0.02~0.28 s)为一次侧的逆变部分开始工作并对直流母线P1N1~P4N4进行充电的过程, 其二次侧逆变部分的IGBT继续保持截止, 且通过调节一次侧的电路输出电压占空比DR使得一次侧变流器的输出电压按照图 3中的规律变化, 从而限制了网侧充电电流, 在0.22 s时二次侧母线电压达到饱和值, 结束充电过程.第三阶段(>0.28 s)为启动二次侧的逆变部分电路, 对负载侧用户进行供电的过程.
|
图 7 MPR-PET柔性并网过程 Fig. 7 Flexible grid-connection process of MPR-PET |
|
图 8 柔性并网仿真过程电流电压波形 Fig. 8 Current and voltage waveforms of flexible grid-connection simulation process |
由图 8可知, 母线电压udc1缓慢上升, 而网侧电流iA维持在较低的幅值, 实现了柔性并网.此外, MPR-PET相比其他PET拓扑更加适应电网重合闸的工况.所谓重合闸是指电网线路故障排除后, 在短时间内闭合断路器恢复供电的一种保护措施.如果PET所在的配网被设计为多次重合闸, 那么PET在单次故障过程中可能会经历连续多次并网过程.在这种工况的考验下, 文献[11]中所采用充电电阻及旁路开关就会出现安全性问题, 而MPR-PET并网过程不依赖任何机械开关, 因此能够很好适应“多次重合闸”这类电网的继电保护过程.
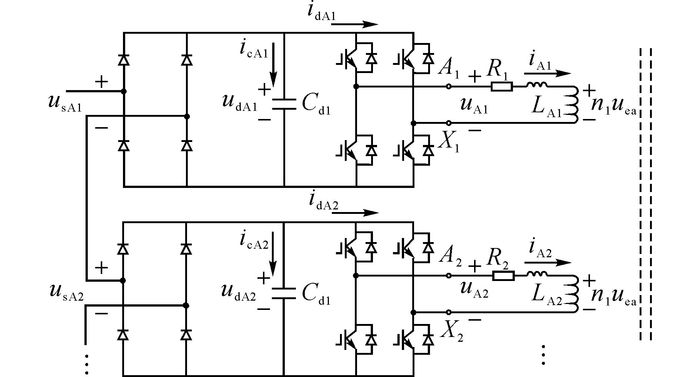
2.2 均压控制MPR-PET拓扑结构是一种输入串联和输出并联的方案, 是解决PET器件限制问题的一般方法[8].MPR-PET一次侧各个级联单元直流母线的电压均衡问题是通过变压器绕组之间能量传递实现的, 其均压控制问题可以简化为针对Conv A1和A2的2组单元的直流母线电压的均衡控制, 如图 9所示.这里“均压控制”的目的是保证udA1和udA2的瞬时值大小时刻相等.
|
图 9 一次侧变流器电路详细拓扑图 Fig. 9 Detailed topology of first side convertors circuit |
由图 9可知, 绕组A1X1与A2X2中每一匝绕组的主磁通的磁通量时刻相等, 且2个绕组的匝数也相等.因此, 2个绕组A1X1与A2X2的感应电压值时刻相等, 都为n1uea, 其中uea为单匝绕组的感应电压.考虑到漏感的问题, 绕组A1X1与A2X2的输入电压与绕组电流之间的关系如下:
| $\left. \begin{array}{l} {u_{{\rm{A}}1}} = {n_{\rm{A}}}{u_{{\rm{ea}}}} + {L_{{\rm{A}}1}}\frac{{\rm{d}}}{{{\rm{d}}t}}{i_{{\rm{A}}1}} + {R_1}{i_{{\rm{A}}1}},\\ {u_{{\rm{A2}}}} = {n_{\rm{A}}}{u_{{\rm{ea}}}} + {L_{{\rm{A2}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}{i_{{\rm{A2}}}} + {R_2}{i_{{\rm{A2}}}}. \end{array} \right\}$ | (5) |
假设变压器一次侧各个绕组的漏感参数和电阻参数分别相等, 即令LA=LA1=LA2, R=R1=R2.将式(5) 的上、下两式相减后得到
| ${u_{{\rm{A}}1}} - {u_{{\rm{A2}}}} = {L_{\rm{A}}}\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{i_{{\rm{A}}1}} - {i_{{\rm{A2}}}}} \right) + R\left( {{i_{{\rm{A}}1}} - {i_{{\rm{A2}}}}} \right).$ | (6) |
根据图 9中的节点电流关系和电容电压变化关系可得:
| ${i_{{\rm{dA}}1}} - {i_{{\rm{dA2}}}} = {i_{{\rm{cA2}}}} - {i_{{\rm{cA1}}}} = - {S_{{\rm{AH}}}}{C_{{\rm{d1}}}}\frac{{{\rm{d}}\left( {{u_{{\rm{A}}1}} - {u_{{\rm{A2}}}}} \right)}}{{{\rm{d}}t}}.$ | (7) |
式中:Cd1=1 μF, 为图 9中高压母线电容的容值.
令变量ΔuA= uA1-uA2, 其幅值也等比例于直流母线电压udA1与udA2之差.结合式(6) 和式(7) 得
| ${{L}_{\text{A}}}{{C}_{\text{d1}}}\Delta u_{\text{A}}^{''}+R{{C}_{\text{d1}}}\Delta u_{\text{A}}^{'}+\Delta {{u}_{\text{A}}}=0.$ | (8) |
由于Cd1取值非常小, 该微分方程满足欠阻尼振荡的条件, 其通解表达式为
| $\Delta {u_{\rm{A}}} = A{{\rm{e}}^{ - \alpha t}}\sin \left( {\beta t + \varphi } \right).$ | (9) |
式中:
从通解的形式上看, 电压差ΔuA表现为角频率为β的欠阻尼振荡.在LA和Cd1足够小的情况下, 频率β/2π远大于一次侧IGBT开关频率, 意味着ΔuA会在一个开关周期内多次波动并衰减到0.因而, 可以近似认为uA1=uA2, 实现有效均压控制.由式(9) 可知, 如果Cd1的取值增大, 将导致ΔuA的波动频率降低, 出现直流母线电压不均衡的问题;如果Cd1进一步增大到破坏欠阻尼振荡的条件, 那么各个母线电压之间将出现明显的不平衡.因此, MPR-PET中的级联电路无大容量直流滤波电容的设计有利于提高通过变压器绕组之间的能量传递来实现均压控制的效果.
3 实验结果 3.1 样机实物图本实验课题组搭建的MPR-PET实验样机实物如图 10所示, 其结构完全按照图 1中的拓扑进行安装.图 10(a)为24脉移相整流变压器;图 10(b)为一次侧变流器柜, 由18个变流器单元构成;图 10(c)为二次侧变流器柜, 由4组并联的变流器单元构成.

|
图 10 MPR-PET样机实物图 Fig. 10 Physical pictures of MPR-PET prototype |
功率器件和拓扑结构是提高PET电压和容量水平的2个主要因素.在功率器件耐压和容量一定的条件下, 采用串联输入和并联输出的结构能够提高PET一次侧的耐压水平和二次侧的通流量, 这也是MPR-PET的优点之一.MPR-PET实验样机的一次侧变流器全部采用英飞凌公司的1 700 V普通IGBT(型号为BSM100GB170DLC);样机运行过程中每个IGBT的承受电压不超过820 V;整个三相级联电路能够承受线电压为6 kV电网电压.二次侧变流器全部采用英飞凌公司的1200 V/150 A普通IGBT(型号为BSM150GB120DLC);4组逆变器电路输出总功率超过200 kVA.一次侧级联电路中各个直流母线的“均压”和二次侧PCS系统中各个逆变器的“均流”是包括MPR-PET在内的“串联输入并联输出”型电力电子拓扑稳定运行的重要条件, 如2.2节和1.3节所述, MPR-PET拓扑在这两方面都具有一定优势.
MPR-PET样机的主要设计参数如表 3所示.表中f1和f2分别为一次侧和二次侧逆变电路开关频率;Cd1和Cd2分别为一次侧和二次侧直流母线电容的容值;Cf和Lf分别为二次侧逆变器的滤波电容值和电感值;LA和La分别为变压器一次侧和二次侧绕组的漏感典型值.
| 表 3 MPR-PET试验样机主要参数 Table 3 Main parameters of MPR-PET prototype |
对于变压器铁芯材料, 课题组最初研究过非晶、纳米晶和铁氧体等材料, 并且认为这些材料中以非晶和纳米晶为代表的新型铁磁材料未来最有可能应用于大容量的PET产品[20].由于国内非晶或者纳米的铁芯切口工艺的限制, 样机高频铁芯材料还是采用铁氧体.变压器绕组材料采用利兹线, 样机中的高频变压器具有高频低损的特性.在20 kHz工作频率的空载运行条件下, 变压器铁芯部分的温升不超过5 ℃;在负载运行条件下, 铁芯温升不超过15 ℃.
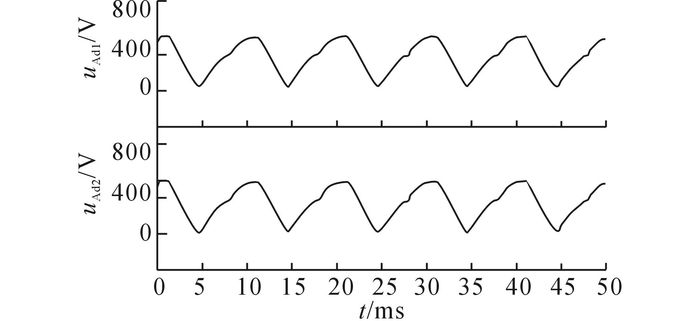
3.2 实验结果实验中的一次侧A相2组直流母线的电压udA1、udA2的波形如图 11所示.由图可知, 2个电压的瞬时值时刻相等, 实现了可靠的均压.该结果验证了利用高频变压器绕组和铁芯的能量传递实现级联变流器单元的直流母线均压的方法.
|
图 11 一次侧2组直流母线电压波形 Fig. 11 Voltage waveforms of two DC buses in first side |
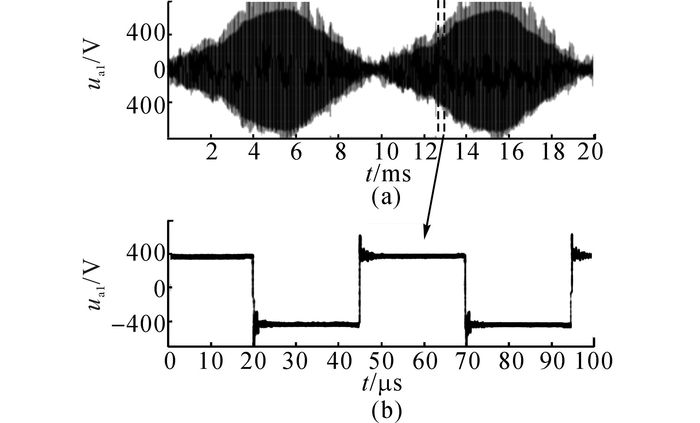
二次侧绕组a1x1电压ua1/V的波形如图 12所示.图中ua1波形呈现出了正弦波包络的高频方波特征(图 12(b)是图 12(a)图部分波形的放大图).其中每个开关周期的正负半周都出现了一次超高频谐振过程, 这是由变压器漏感与二次侧二极管结电容引起的[21].
|
图 12 二次侧绕组a1x1电压波形 Fig. 12 Voltage waveforms of second side winding a1x1 |
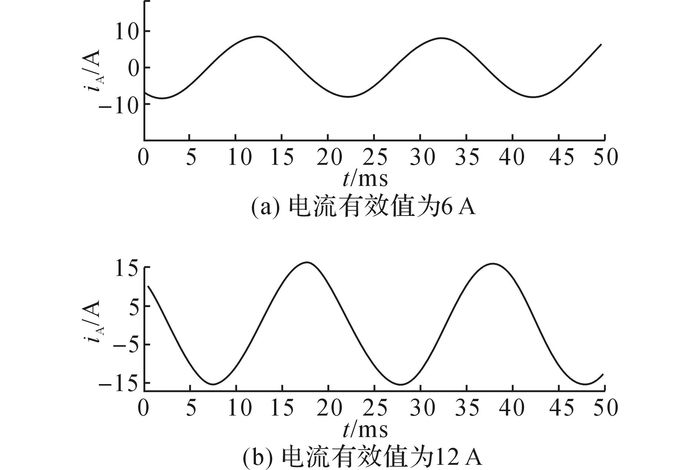
不同负载条件下的一次侧输入电流波形如图 13所示.由图 13(a)可知, 当网侧电流有效值为6 A时, 电流波形呈现24脉阶梯波形状, 说明了试验样机是按照24脉整流电路原理进行工作的.由图 13(b)可知, 当网侧电流有效值增大到12 A时, 电流波形不再具有明显阶梯波的特征, 而是比较接近于正弦波波形, 说明MPR-SST基本消除了一次侧电流谐波分量.
|
图 13 不同负载条件下的一次侧输入电流波形 Fig. 13 Current waveforms of first side input current under different load conditions |
以上实验结果表明:MPR-PET在没有一次侧直流母线电容的条件下使得其内部的混频多脉整流电路按照工频MPR电路的原理工作, 实现网侧谐波电流的消除.
4 结语本文提出了一种基于多脉整流技术的电力电子变压器拓扑(MPR-PET), 分析该新型拓扑的电路结构和控制方法, 提出了通过PCS系统的均流控制技术克服变压器的高频化对MPR电路消除谐波电流不利影响的方案.由于MPR-PET一次侧高压直流母线无电容的特点, 该拓扑能够在无需充电电阻的条件下实现柔性并网的功能, 并且其一次侧多个母线的均压控制更加有效.样机的实验结果进一步验证了MPR-PET的混频整流工作特性与消除网侧谐波电流的功能有效性.相比其他PET拓扑, MPR-PET一次侧直流母线避免了使用高压大容量电容, 同时能够保留对网侧谐波电流的抑制功能, 在可行性、可靠性和成本方面均有独特优势.
| [1] | 毛承雄. 电子电力变压器[M]. 北京: 中国电力出版社, 2010: 1-218. |
| [2] | HUANG A Q, CROW M L, HEYDT G T, et al. The future renewable electric energy delivery and management (FREEDM) system:the energy internet[J]. Proceedings of the IEEE, 2011, 99(1): 133–148. DOI:10.1109/JPROC.2010.2081330 |
| [3] |
李鹏, 窦鹏冲, 李雨薇, 等. 微电网技术在主动配电网中的应用[J].
电力自动化设备, 2015, 35(4): 8–16.
LI Peng, DOU Peng-chong, LI Yu-wei, et al. Application of microgrid technology in active distribution network[J]. Electric Power Automation Equipment, 2015, 35(4): 8–16. |
| [4] |
陈启超, 纪延超, 潘延林, 等. 配电系统电力电子变压器拓扑结构综述[J].
电工电能新技术, 2015, 34(3): 41–48.
CHEN Qi-chao, JI Yan-chao, PAN Yan-lin, et al. Review of power electronic transformer topologies applied to distribution system[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(3): 41–48. |
| [5] |
李子欣, 王平, 楚遵方, 等. 面向中高压智能配电网的电力电子变压器研究[J].
电网技术, 2013, 37(9): 2592–2601.
LI Zi-xin, WANG Ping, CHU Zun-fang, et al. Research on medium-and high-voltage smart distribution grid oriented power electronic transformer[J]. Power System Technology, 2013, 37(9): 2592–2601. |
| [6] | A MAITRA, A SUNDARAM, M GANDHI, et al. Intelligent universal transformer design and applications[C]//Conference and Exhibition on Electricity Distribution-Part 2. Prague:CIRED, 2009:1-7. |
| [7] | W van der MERWE, T MOUTON. Solid-state transformer topology selection[C]//International Conference on Industrial Technology. Churchill:ICIT, 2009:1-6. |
| [8] | XU S, BURGOS R, GANGYAO W, et al. Review of solid state transformer in the distribution system:From components to field application[C]//Energy Conversion Congress and Exposition. Edinburgh:ECCE, 2012:4077-4084. |
| [9] | ORTIZ G. High-power DC-DC converter technologies for smart grid and traction applications[D]. Zurich:Swiss Federal Institute of Technology Zurich, 2014:115-118. |
| [10] | A TRIPATHI, D PATEL, K MAINALI, et al. Solid-state transformer and MV grid tie applications enabled by 15 kV SiC IGBTs and 10 kV SiC MOSFETs based multilevel converters[J]. IEEE Transactions on Industry Applications, 2015, 51(4): 3343–3360. DOI:10.1109/TIA.2015.2412096 |
| [11] | XU S, HUANG A Q, XI J N. Current sensorless power balance strategy for DC/DC converters in a cascaded multilevel converter based solid state transformer[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 17–22. DOI:10.1109/TPEL.2013.2256149 |
| [12] | MAHARJAN L, INOUE S, AKAGI H. A transformerless energy storage system based on a cascade multilevel PWM converter with star configuration[J]. IEEE Transactions on Industry Applications, 2008, 44(5): 1621–1630. DOI:10.1109/TIA.2008.2002180 |
| [13] |
孟凡刚, 杨世彦, 杨威. 多脉波整流技术综述[J].
电力自动化设备, 2012, 32(2): 9–22.
MENG Fan-gang, YANG Shi-yan, YANG Wei. Overview of multi-pulse rectifier technique[J]. Electric Power Automation Equipment, 2012, 32(2): 9–22. |
| [14] | KANG M, ENJETI P N, PITEL I J. Analysis and design of electronic transformers for electric power distribution system[J]. IEEE Transactions on Power Electronics, 1999, 14(6): 1133–1141. DOI:10.1109/63.803407 |
| [15] | KRISHNAMOORTHY H S, ENJETI P S, PITEL I J, et al. New medium-voltage adjustable speed drive (ASD) topologies with medium-frequency transformer isolation[C]//IEEE Power Electronics and Motion Control Conference. Haerbing:IPEMC, 2012:814-819. |
| [16] |
朱婷婷, 邓智泉, 王晓琳, 等. 一种三电平三相四桥臂逆变器中点电位平衡策略[J].
电工技术学报, 2012, 27(6): 77–82.
ZHU Ting-ting, DENG Zhi-quan, WANG Xiao-lin, et al. A novel strategy of neutral point potential balancing for three-level three-phase four-leg inverters[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 77–82. |
| [17] | 刘凤君. 现代高频开关电源技术及应用[M]. 北京: 电子工业出版社, 2004: 125-126. |
| [18] |
朱明磊, 赵荣祥. 基于快速分布式主从控制的PCS系统[J].
浙江大学学报:工学版, 2013, 47(11): 2031–2037.
ZHU Ming-lei, ZHAO Rong-xiang. Parallel convertor system with high speed distributed master-slave control method[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(11): 2031–2037. |
| [19] |
李松, 韩冬杰. 多脉波移相整流变压器匝数查找的遍历法实现[J].
变压器, 2014, 51(10): 26–28.
LI Song, HAN Dong-jie. Realization of turns number searching with traversing method of multipulse phase-shifting rectifier transformer[J]. Transformer, 2014, 51(10): 26–28. |
| [20] |
赵争菡. 电力电子变压器中高频变压器磁芯和绕组特性的研究[D]. 河北: 河北工业大学, 2014.
ZHAO Zheng-han. Research on high-frequency transformer's magnetic core and winding characteristic in power electronic transformer[D]. Hebei:Hebei University of Technology, 2014. http://d.wanfangdata.com.cn/Thesis/D680424 |
| [21] | HONNYONG C, LIHUA C, RONGJUN D, et al. An alternative energy recovery clamp circuit for full-bridge PWM converters with wide ranges of input voltage[J]. IEEE Transactions on Power Electronics, 2008, 23(6): 2828–2837. DOI:10.1109/TPEL.2008.2003131 |



