2. 中航工业庆安集团有限公司, 陕西 西安 710077
2. Aviation Industry Corporation of Qing'an Group Co., Xi'an 710077, China
近年来, 随着人们生活水平的提高和环保意识的增强, 对汽车空间、舒适度以及油耗都提出了较高要求.混合动力汽车, 由于其自身兼具内燃汽车动力足、电动汽车低污染排放的优点, 日益受到人们的青睐.混合动力汽车一般采用内燃机和电池作为动力来源, 传统起动机和发电机结构复杂, 燃油经济指标低, 无法满足未来汽车的需求.近年来, 具备起动/发电一体化功能的一体化起动/发电机成为混合动力汽车技术领域的研究热点[1-2].
一体化起动/发电系统利用电机的可逆原理, 实现一机两用, 不仅可以减轻车载重量, 还能够提高系统运行的稳定性.特别是永磁起动/发电机具有结构简单、无励磁系统损耗、功率密度高和结构可靠性好并且适合高速运行的优点, 从而在中、小功率车载起动/发电机系统中占明显优势[3-5].随着新型永磁材料的问世, 高性能电力电子器件和现代控制技术的发展, 永磁起动/发电机系统集成度、自动化程度和控制策略都实现了提升, 控制参数更容易调节, 对性能的优化意义重大.然而永磁起动/发电(integrated starter/generator, IGS)系统既要满足起动工况的性能指标需求, 又要满足发电工况的电能质量输出要求, 特别是车载燃油发动机的特性也对起动/发电机系统提出了低速大转矩、宽转速范围、高发电运行效率、高功率重量比等要求.因此在系统设计阶段, 为满足起动和发电的需求, 对包含电机和控制器在内的起动/发电系统进行匹配标定设计显得尤为重要.
针对混合动力汽车用永磁起动/发电系统一体化的特点, Bonthu等[6]使用差分进化优化算法对起动/发电机进行优化设计, Legranger等[7-10]采用了优化的磁路结构和有效的控制策略提高了系统效率.夏永洪等[11-12]分别对永磁起动/发电机系统的新型励磁结构和漏磁情况进行了研究, 李艳明等[13-16]则主要进行了弱磁控制策略方面的研究, 都取得了一定的研究成果, 但一体化电机很难兼顾快速动态响应和高质量电能输出的问题仍然存在.对于系统参数匹配的研究主要集中在驱动电机功率、转矩和转速等外特性参数的匹配上[17], 郑维等[18-19]分析了永磁同步电机中永磁体磁链和直轴电感对扩速范围的影响规律, 但获得的结论并不适用于既要电动运行又要发电运行的起动/发电机.
本文从燃油经济指标最优的角度, 在满足整车性能要求的前提下, 对混合动力汽车用永磁起动/发电机本体和功率变换器进行参数匹配标定, 分析参数匹配各环节对系统结构参数的影响规律.搭建永磁起动/发电机的一体化系统仿真模型和基于dSPACE硬件在回路的实验平台, 验证电动和发电工况下控制策略的有效性和可行性.
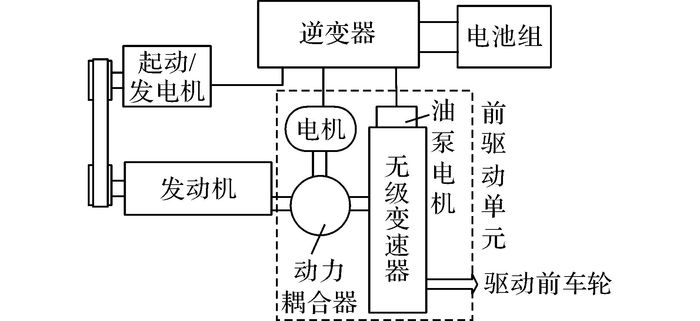
1 永磁起动/发电系统数学模型所设计的永磁起动/发电机系统用于混联式混合动力汽车系统, 结构简图如图 1所示.其中, 永磁起动/发电系统利用电机的可逆原理, 发电机兼作起动机, 一台电机两种用途可减少系统体积和重量, 有效地提高系统可靠性, 是整个设计的核心.功率变换器也要求能够在一套设备中实现逆变和整流.当永磁起动/发电机起动运行时, 三相全桥电路做逆变运行, 将车载蓄电池的直流电逆变为三相正弦电向永磁起动/发电机供电, 控制绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)的开通与关断, 在永磁起动/发电机中产生旋转磁场, 带动内燃机运行;当永磁起动/发电机发电运行时, 三相全桥电路将永磁起动/发电机产生的三相交流电整流为直流电存储在蓄电池中.
|
图 1 混联式混合动力系统结构示意图 Fig. 1 Sketch map of series-parallel hybrid power trainstructure |
引入凸极比和弱磁系数对永磁起动/发电机系统的主要执行机构电机进行模型重构, 其数学模型可表示为
| ${\mathit{\boldsymbol{e}}_{\rm{b}}} = {\omega _{\rm{r}}}\frac{{{L_d}{\mathit{\boldsymbol{i}}_{\lim }}}}{\delta } = {u_{\rm{s}}} + j{\mathit{\boldsymbol{i}}_{\rm{s}}}{X_{\rm{L}}} + {R_{\rm{s}}}{\mathit{\boldsymbol{i}}_{\rm{s}}},$ | (1) |
| ${T_{\rm{e}}} = \frac{3}{2}{n_{\rm{p}}}{i_q}\left[ {\frac{{{L_d}{i_{\lim }}}}{\delta } + {L_d}\left( {1 - \chi } \right){i_d}} \right],$ | (2) |
| ${u_{\rm{s}}} = {\omega _{\rm{r}}}{\mathit{\Psi }_{\rm{s}}},$ | (3) |
| $\left[ {\begin{array}{*{20}{c}} {{\mathit{\Psi }_d}}\\ {{\mathit{\Psi }_q}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{L_d}}&0\\ 0&{\chi {L_d}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{L_d}{i_{\lim }}/\delta }\\ 0 \end{array}} \right],$ | (4) |
| $\delta = \frac{{{L_d}{\mathit{\boldsymbol{i}}_{\lim }}}}{{{\psi _{\rm{f}}}}},\;\;\;\;\chi = \frac{{{L_q}}}{{{L_d}}}.$ | (5) |
式中:eb为三相反电动势向量, Te为电磁功率, ωr为转子的角速度, Ld和Lq分别为定子直轴电感和定子交轴电感, XL和Rs分别为定子绕组的电抗和电阻, Ψs为定子磁链向量, Ψd和Ψq分别为Ψs在直轴和交轴分量, us和is分别为定子三相电压和电流向量, id和iq分别为is的直轴和交轴分量, np为极对数, χ为永磁起动/发电机凸极比, δ为永磁起动/发电机弱磁系数, ilim为电流极限值(当id=0时, 此值为iq), Ψf为永磁体的磁链.
起动/发电机一体化数学模型有效描述了控制策略和电机本体参数对弱磁系数和凸极比的影响, 是系统匹配标定设计的基础.
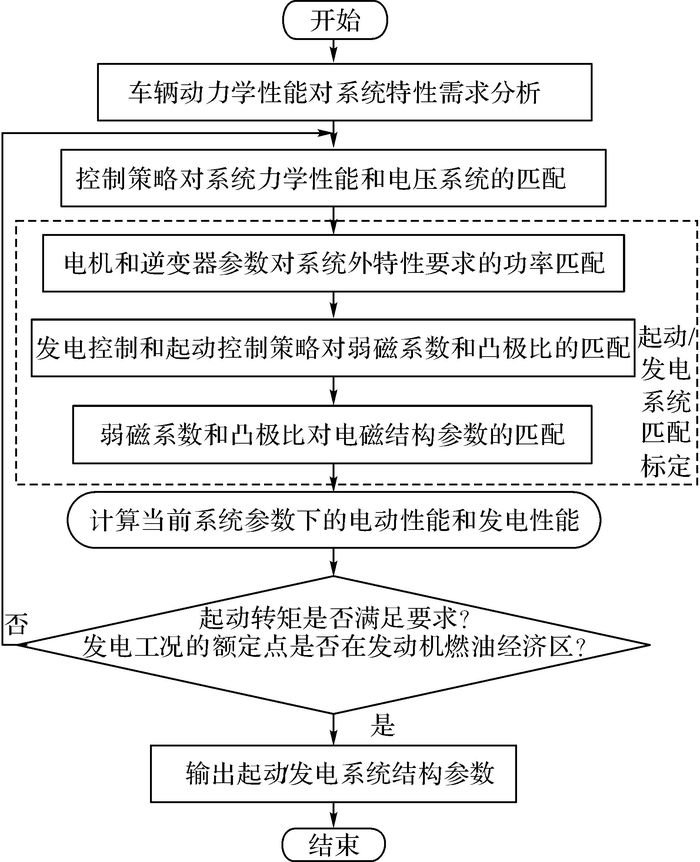
2 永磁起动/发电系统匹配标定设计根据混联式混合动力汽车的能量流动模式, 永磁起动/发电机主要有2种工况:车辆起动时, 起动/发电机迅速拖动发动机越过怠速区, 要求起动/发电机具有良好的加速性能和较大的瞬时转矩输出能力;发动机起动后, 起动/发电机切换到发电状态, 给电池供电, 要求起动/发电机在宽转速范围内具有良好的发电质量.在设计过程中既要考虑起动过程的外特性要求又要兼顾发电过程的性能指标, 因此需要对系统进行匹配标定设计.主要考虑以下3个方面的匹配关系:1) 起动/发电机和逆变器参数与整车对系统外特性要求的功率匹配;2) 电动和发电工况下典型控制策略电压电流约束对弱磁系数和凸极比的匹配;3) 弱磁系数和凸极比对电机本体参数的匹配.系统匹配标定流程如图 2所示.
|
图 2 永磁起动/发电系统匹配标定流程图 Fig. 2 Flow diagram of maching design for permanent magnet integrated starter/generator system |
永磁/起动发电系统为短时运行状态, 主要工作在发电状态, 为了保证系统效率, 要求起动/发电机具有较宽的发电高效区.因此根据整车使用的发动机燃油经济特性曲线对起动/发电机的额定转速点进行设计, 同时保证发电机外特性曲线完全覆盖发动机外特性曲线.最坏工况发生于过载时, 此时的电流决定了续流二极管额定电流的大小, 永磁/起动发电系统的容量
| $P = \frac{{2{\rm{\pi }}{T_{\max }}{n_{\rm{s}}}}}{{2 \times 60 \times 1000}}.$ | (6) |
式中:ns为发动机怠速, Tmax为峰值起动转矩.式(6) 考虑了2倍过载的工况.
电动状态也为短时运行状态, 要求根据发动机参数设计合理的起动转矩, 即起动/发电机的起动转矩必须大于最大阻转矩, 这里设定最大起动转矩为1.5倍的最大阻转矩[20], 即
| ${T_{\max }} \ge 1.5{T_{\rm{p}}},$ | (7) |
| ${P_{\max }} = \frac{{2{\rm{\pi }}{T_{\max }}{n_{\rm{1}}}}}{{60 \times 1000}}.$ | (8) |
式中:Pmax为起动时最大输出功率, Tp为内燃机最大输出阻转矩, n1为恒转矩运行时最高转速.
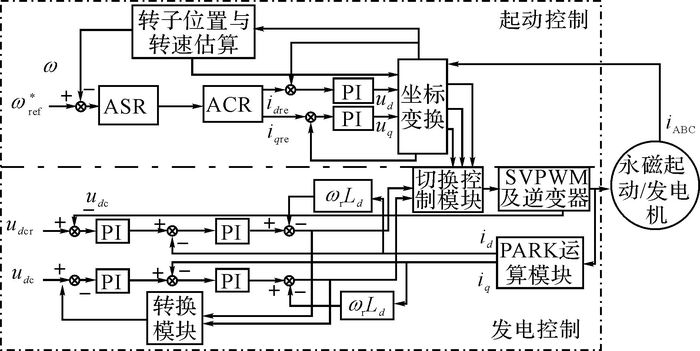
2.2 控制策略匹配标定控制策略是永磁起动/发动一体化系统在工程领域应用的关键技术, 主要包括起动控制和发电控制.本文采用的永磁起动/发电机一体化控制策略结构图如图 3所示, 图中自动转速调节器(automatic speed regulator, ASR)用于调节起动工况下的转速, 自动电流调节器(automatic current regulator, ACR)用于调节起动工况下的电流, 空间矢量脉宽调制(space vector pulse width modulation, SVPWM)用于控制功率变换器运行, 比例积分(proportion integration, PI)控制器用于对被控对象的控制, udc为直流母线电压, udcr为直流母线参考电压, ωref*为目标转速, idre和iqre分别为直轴目标电流和交轴目标电流, ud和uq分别为直轴电压和交轴电压.
|
图 3 永磁起动/发电一体化系统控制结构框图 Fig. 3 Control system diagram of permanent magnet starter/generator system |
在车辆起动时, 永磁起动/发电机为电动运行状态, 辅助发动机起动, 要求快速跟踪给定的目标速度, 在较短的时间内将发动机带动到目标速度, 即永磁起动/发电机提供发动机起动运行的辅助能量, 且要求超调量较小或无超调量.如图 3所示, 电动状态采用id=0控制实现转速快速跟踪, 在起动时刻负载不大的情况下, 能够有效避免功率因数的降低, 提高电流利用率.起动过程中功率P和转矩T与凸极比和弱磁系数的关系表示为
| $\frac{T}{{{T_{\rm{N}}}}} = \delta \cos \alpha + 0.5\left( {1 - \frac{1}{\chi }} \right){\delta ^2}\cos 2\alpha ,$ | (9) |
| $\frac{P}{{{P_{\rm{N}}}}} = \frac{\Omega }{{{\Omega _{\rm{N}}}}}\left[ {\delta \cos \alpha + 0.5\left( {1 - \frac{1}{\chi }} \right){\delta ^2}\cos 2\alpha } \right].$ | (10) |
式中:TN为额定转矩, PN为额定功率, α为电流极限圆和起动控制曲线交点处的电流相角, Ω为机械角速度, ΩN为额定机械角速度.
当发动机被辅助带动至目标转速运行, 为充分利用化石燃料产生的能量, 将永磁起动/发电机切换至发电状态.随着车速的提升, 输出侧电压增大容易导致功率变换器的过调制[21], 使负载能力和母线电压质量降低.因此, 在发电状态使用弱磁控制策略提高发电质量, 提高发电状态带负载能力.发电过程中功率和转矩与凸极比和弱磁系数的关系表示为
| $\frac{T}{{{T_{\rm{N}}}}} = \frac{{\delta \cos \theta }}{{\sqrt {{{\left( {\delta \cos \alpha /\chi } \right)}^2} + {{\left( {1 + \delta \sin \alpha } \right)}^2}} }},$ | (11) |
| $\frac{P}{{{P_{\rm{N}}}}} = \delta \cos \theta .$ | (12) |
式中:θ为功率因数角.此时电机机械角速度表示为
| $\mathit{\Omega = }\frac{{{u_{\lim }}}}{{{n_{\rm{p}}}\sqrt {{{\left( {{L_{\rm{q}}}{i_{\lim }}\cos \alpha } \right)}^2} + {{\left( {{\psi _{\rm{f}}} + {L_{\rm{d}}}{i_{\lim }}\sin \alpha } \right)}^2}} }}.$ | (13) |
式中:ulim为电动机端电压最大值.
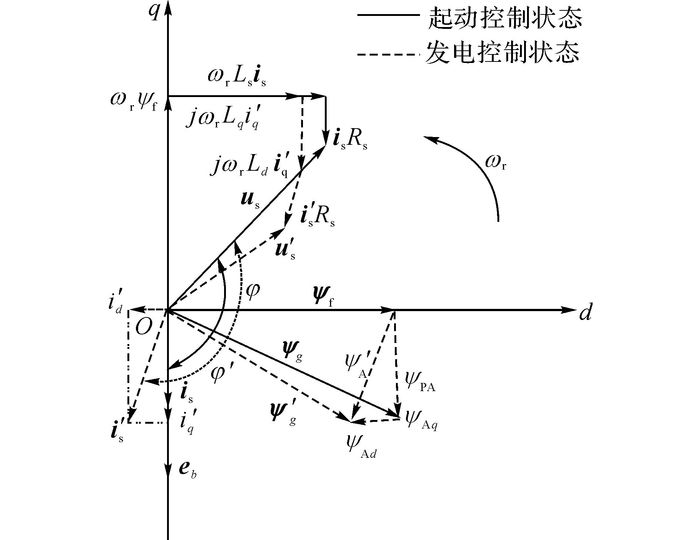
结合起动/发电机数学模型可获得起动控制和发电控制下永磁起动/发电机一体化系统的相量图, 如图 4所示.采用电动机惯例, 统一规定电流表示输入电流, 因此发电状态交轴电流为负.根据图 4, 横坐标为代表转子磁极中心线方向的d轴, 纵坐标为代表磁极间的轴线方向的q轴, ψAd和ψAq为A相定子磁链的d轴和q轴分量, φ为功率因数角, Ψg为气隙磁链, 发电过程中随着弱磁直轴电流增大功率因数增大, 说明弱磁控制有利于提高电机的负载能力.
|
图 4 起动控制和发电控制下永磁起动/发电机一体化系统的相量图 Fig. 4 Vector diagrams for starting and generating control in permanent magnet integrated starter/generator system |
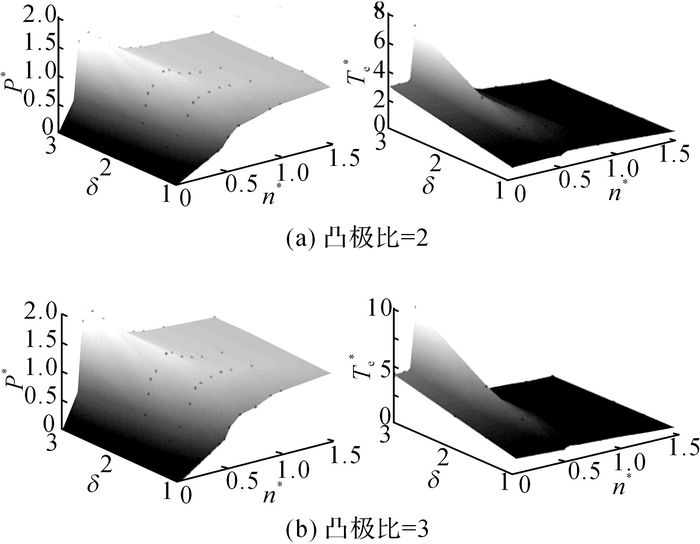
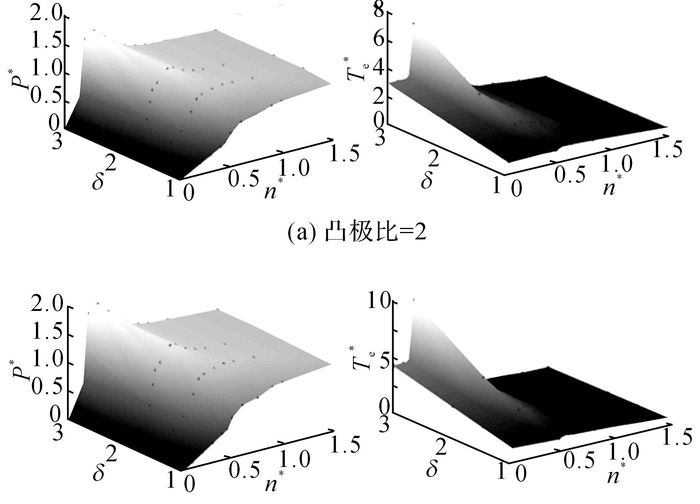
由上述分析, 可获得永磁起动/发电机系统在起动和发电工况下, 凸极比和弱磁系数对输出功率和转矩的影响关系, 如图 5和6所示, P*为表示功率标幺值, Te*为电磁转矩标幺值, n*为转速标幺值, 随着弱磁系数的增大, 最大输出功率增加, 最大输出功率对应的转速降低, 最大转矩增加;随着凸极比的增加, 电机最大转矩增大, 对应的电机恒转矩区转速范围减小.
|
图 5 起动工况凸极比和弱磁系数对永磁起动/发电机一体化系统功率和转矩的影响 Fig. 5 Influence of saliency ratio and flux weakening ratio saliency on power and torque for motoring in permanent magnet integrated starter/generator system |
|
图 6 发电工况凸极比和弱磁系数对永磁起动/发电机一体化系统功率和转矩的影响 Fig. 6 Influence of saliency ratio and flux weakeningratio saliency on performance for generating in permanent magnet integrated starter/generatorsystem |
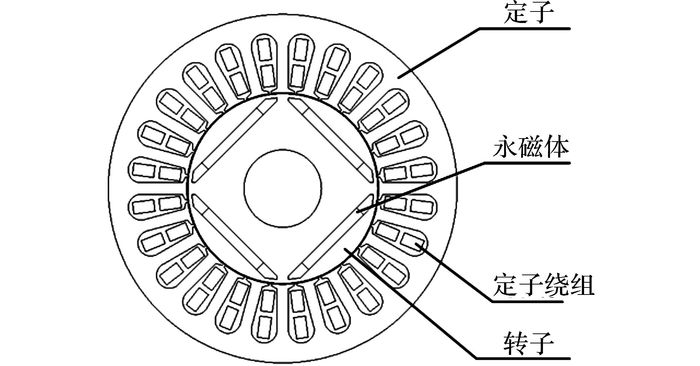
本文所设计的永磁起动/发电机的整体结构如图 7所示.进行永磁起动/发电机设计时, 为了提高电机效率, 需要充分考虑各参数之间的制约关系, 主要根据凸极比和弱磁系数对电机的交直轴电感和永磁体磁链进行设计.
|
图 7 永磁起动/发电机结构示意图 Fig. 7 Schematic diagram of permanent magnet starter/generator |
为保证槽面积的有效利用, 同时避免磁密过高、波形畸变大、铁耗增大, 选用底部比顶部宽的梨形半闭口槽.在保证电机功率的前提下使电动势和磁动势谐波分量尽可能小, 减少材料的使用, 降低一体化电机的重量, 同时保证散热效果, 重点对永磁起动/发电机的电磁参数、永磁体参数和电机尺寸进行设计, 使其满足电机高性能、小体积的要求.
根据前述的外特性匹配标定和控制策略匹配标定获得凸极比和弱磁系数分别为2.5和1.13.根据起动和发电过程对系统最大转矩的要求, 最大转矩和凸极比、弱磁系数的关系表示为
| ${T_{\max }} = \left[ {\delta \cos \alpha + 0.5\left( {1 - \frac{1}{\chi }} \right){\delta ^2}\cos 2\alpha } \right]\frac{{p\psi _{\rm{f}}^2}}{{{L_d}}},$ | (14) |
| $\alpha = \arccos \frac{{\sqrt {{{\left( {1/\delta } \right)}^2} + 8{{\left( {1 - 1/\chi } \right)}^2}} }}{{4\left( {1 - 1/\chi } \right)}}.$ | (15) |
结合式(5)、(14) 和(15) 分别对永磁体磁链ψf、直轴电感Ld和交轴电感Lq进行标定.
为保证系统的动态响应速度, 假设电机的时间常数不高于0.02 s[19], 则定子的绕组电阻为
| ${R_{\rm{s}}} \ge 50{L_q}.$ | (16) |
在满足系统效率经济比要求的条件下, 兼顾永磁起动/发电机的性能和电机的生产成本, 根据前述获得的交直轴电感、永磁体磁链、最大转矩和功率, 对永磁起动/发电机的主要尺寸进行匹配设计.定子内径Di和电机轴向长度le的计算方法为
| ${D_{\rm{i}}} = {\left( {\frac{{4{T_{\max }}}}{{\sqrt 2 \beta {\rm{\pi }}{B_{{\rm{\delta 1}}}}A}}} \right)^{3/2}},$ | (17) |
| ${l_{\rm{e}}} = \beta {D_{{\rm{i1}}}}.$ | (18) |
式中:Α为定子的电负荷, Βδ1为气隙磁场磁密的基波幅值, β为长径比.
永磁体的极弧系数αp和径向充磁长度hm的估算方法如下:
| ${\alpha _{\rm{p}}} = \frac{{51{\sigma _0}{\rm{\pi }}{n_{\rm{p}}}{\omega _{\rm{s}}}{T_{\max }}{L_d}{K_{{\rm{Fd}}}}}}{{4{\mu _0}{\mu _{\rm{r}}}m\tau {f^2}{K_{\rm{u}}}{K_\mathit{\Phi }}C{W_{{\rm{BH}}}}{{\left( {N{K_{{\rm{dp}}}}} \right)}^2}{{\left( {\beta {D_{\rm{i}}}} \right)}^{2/3}}}},$ | (19) |
| $\begin{array}{l} {h_{\rm{m}}} = \\ \frac{{4f{\mu _0}{\mu _{\rm{r}}}m\tau {l_{\rm{e}}}{{\left( {N{K_{{\rm{dp}}}}} \right)}^2}\left[ {{\alpha _{\rm{p}}}{\rm{\pi }} - \sin \left( {{\alpha _{\rm{p}}}{\rm{\pi }}} \right) + 2/3\cos \left( {{\alpha _{\rm{p}}}{\rm{\pi /2}}} \right)} \right]}}{{4{\rm{\pi }}{n_{\rm{p}}}\omega \sin \left( {{\alpha _{\rm{p}}}{\rm{\pi }}/2} \right) \cdot {K_{\rm{\delta }}}{L_d}}}. \end{array}$ | (20) |
式中:m为相数, Kdp为绕组因数, KFd为电极短路时每对极的永磁体磁动势为直轴电枢磁动势的倍数, Ku为电压系数, KΦ为电机气隙磁通的波形系数, K为气隙系数, C为永磁体磁能利用系数, WBH为选用的永磁材料的最大磁能积, σ0为空载漏磁系数, μr为永磁体相对磁导率, μ0为空气磁导率, ωs为同步速.
经过以上电磁参数的匹配设计, 可得到永磁起动/发电机的主要参数如表 1所示, do和di分别为定子外径和定子内径, ls为轴向长度, lg为气隙长度, Bδ为气隙磁密, BPM为永磁磁密, q为每极每相槽数, a为绕组并联支数, αi为极弧系数, y为节距, lPM和bPM分别为永磁体的长度和宽度, PN、UN和IN分别为额定功率、额定电压和额定电流, nt为电动转发电转速, Rs为定子相电阻.
| 表 1 永磁起动/发电机主要参数 Table 1 Main parameters of permanent magnet starter/generator |
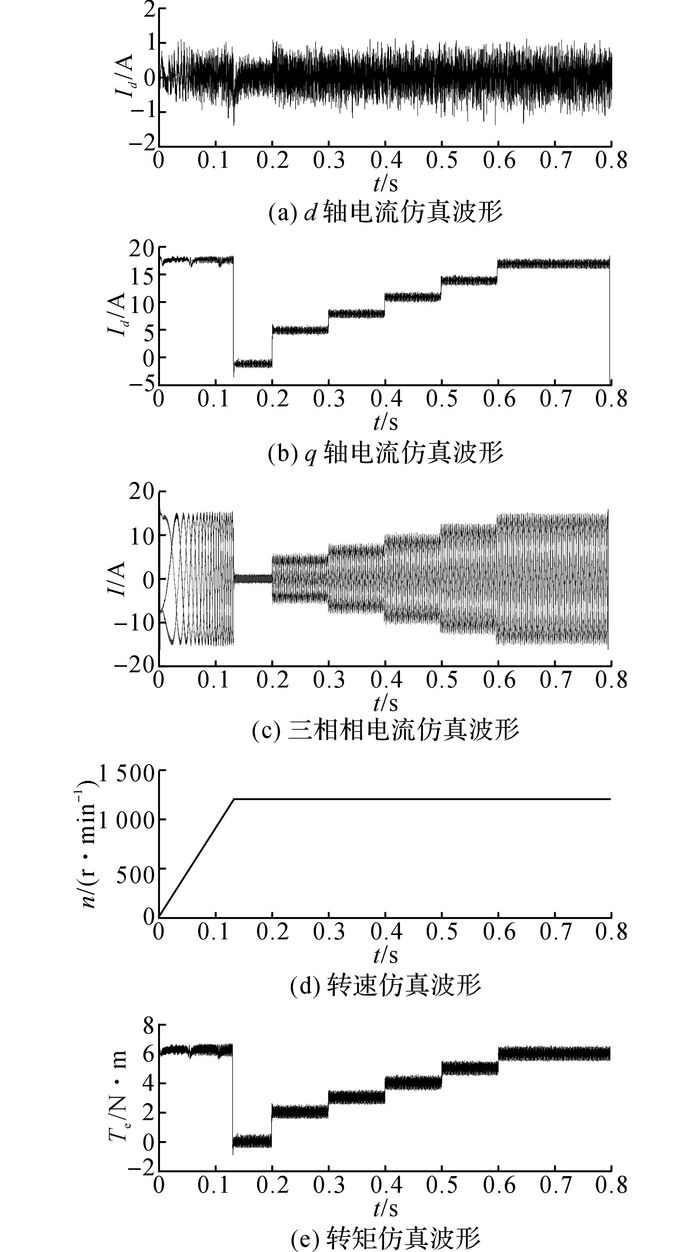
仿真模拟发动机系统的阻力, 将转速提升至1 200 r/min, 并保持稳定, 针对电机不同负载情况进行仿真分析, 仿真结果如图 8所示, t为时间, Id为直轴电流, Iq为交轴电流, I为三相电流, n为转速, Te为电磁转矩.
|
图 8 永磁起动/发电一体化系统起动状态不同负载下电流、转速和转矩参数仿真波形 Fig. 8 Current, speed and torque for starting with different loads in permanent magnet integrated starter/generator system |
仿真过程为:0~0.2 s, 电机空载运行;0.2~0.3 s, 负载转矩为2 N·m;0.3~0.4 s, 负载转矩为3 N·m;0.4~0.5 s, 负载转矩为4 N·m;0.5~0.6 s, 负载转矩为5 N·m;0.6 s之后, 负载转矩为6 N·m.由图 8所示, 电机空载起动, 0.13 s起动完成, q轴电流与转矩成比例.在负载运行的情况下, 电机输出的电磁转矩能够跟随负载转矩的变化, 而且十分稳定.在负载转矩突变的情况下, 转速几乎没有波动, 始终保持平稳,表明永磁起动/发电机具有良好的起动性能.
3.2 发电状态仿真分析如图 9所示为永磁起动/发电机发电仿真波形, UA为A相线电压, U为直流母线电压, Pm为电机功率, 给定整流器输出电压为120 V, 负载电阻为25 Ω, 直流侧电容为1 mF.发电运行时, 给定转速初始1 500 r/min, 电压响应较快, 超调较小.稳定后, 输出恒定120 V直流电压.0.5 s时, 转速给定为2 000 r/min, 电压有所上升, 很快又回到恒定120 V.电机的输出功率取决于发动机投入的机械功率, 当功率保持恒定时, 转速升高, 转矩下降.根据图 9, 直流母线电压稳定, 且线电压正弦度较好, 线电压频率稳定, 表明在弱磁控制下, 永磁起动/发电机具有较高的发电质量.
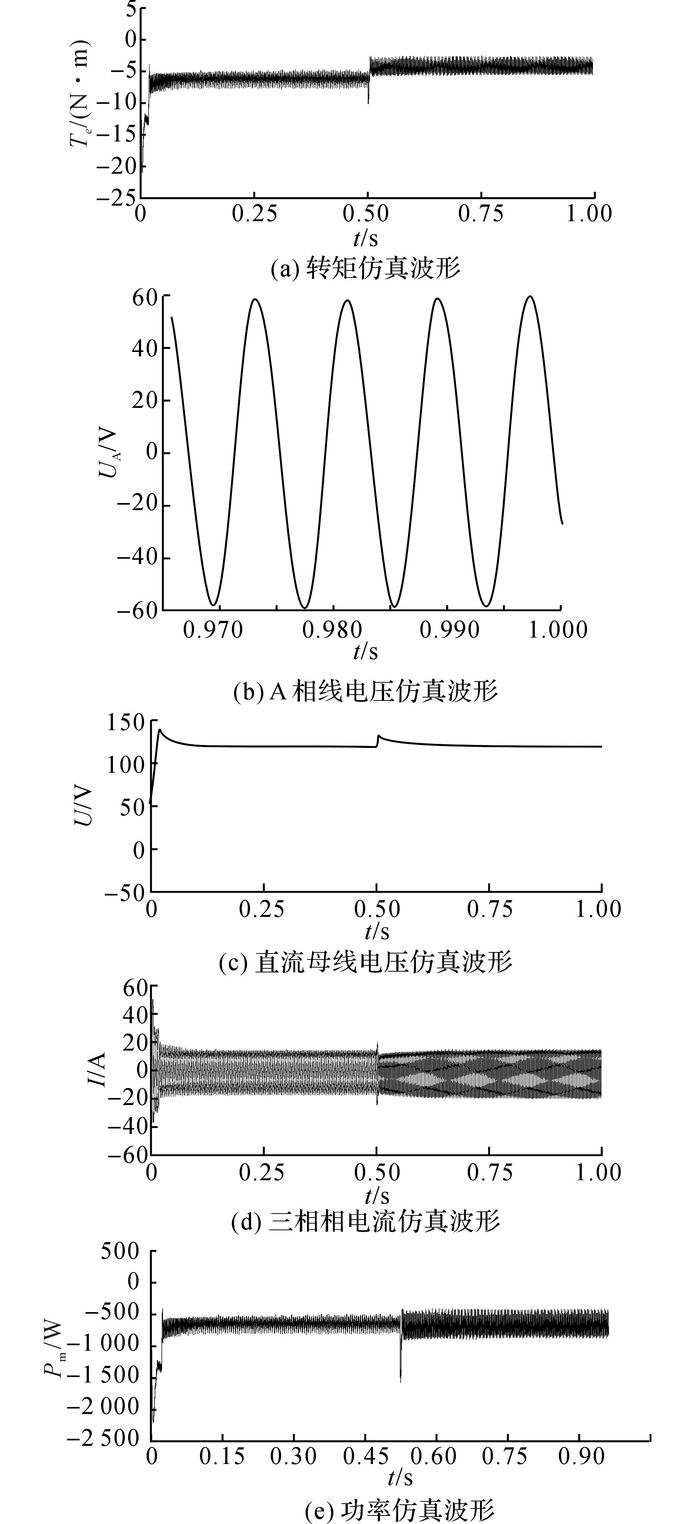
|
图 9 永磁起动/发电一体化系统发电状态不同转速下转矩、电压、电流和功率仿真波形 Fig. 9 Torque, voltage, current and power for generating at different speeds in permanent magnet integrated starter/generator system |
永磁起动/发电系统硬件在回路实验验证平台和3 kW永磁起动/发电机样机实物图分别如图 10和11所示.平台主要设备包括:永磁起动/发电机(样机参数如表 1所示)、异步电机模拟车辆负载、逆变器、硬件在回路仿真控制器和发电回馈单元.

|
1-能量回馈单元;2-永磁起动/发电机驱动单元;3-硬件在回路处理器与接口;4-工控机;5-永磁起动/发电机样机;6-转速转矩测量仪 图 10 永磁起动/发电一体化系统硬件在回路实验验证平台 Fig. 10 Hardware-in-the-loop experiment platform of permanent magnet integrated stater and generator system |

|
图 11 3 kW永磁起动/发电机实验样机实物图 Fig. 11 Physical map of 3 kW permanent magnet integrated starter and generator experiment prototype |
永磁起动/发电机空载起动实验分为给定转速运行和逐步升高转速的实验.当对永磁起动/发电机空载起动指定转速运行时, 分别给定电机转速为600、1 000、1 500 r/min, 其转速如图 12所示, 电机输出的转速能够跟随给定转速的变化, 转速波形较平稳, 且超调量很小, 起动/发电机系统具有良好的空载起动性能.
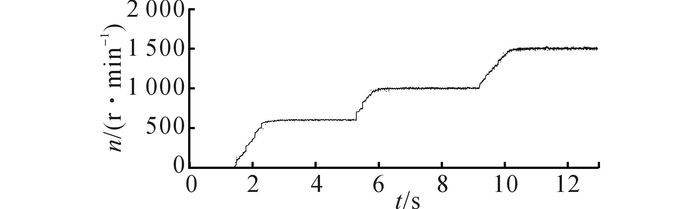
|
图 12 永磁起动/发电一体化系统转速跟随特性空载实验波形 Fig. 12 Speed tracking experiment waveform at no-load for permanent magnet integrated starter/generator system |
实验负载由一台三相异步电机提供, 该电机由矢量控制变频器控制.给定永磁起动/发电机转速600 r/min, 接通逆变器电源, 给负载电机通电, 给定频率10 Hz, 两电机保持同步速.如图 13所示为永磁起动/发电机负载实验波形.实验所采集到的电流、转速波形有很大毛刺, 只有一个数值的尖峰为测量噪声, 其余波动是由于轴系安装不对中所引起.总体趋势正确, 说明该电机带负载情况良好.
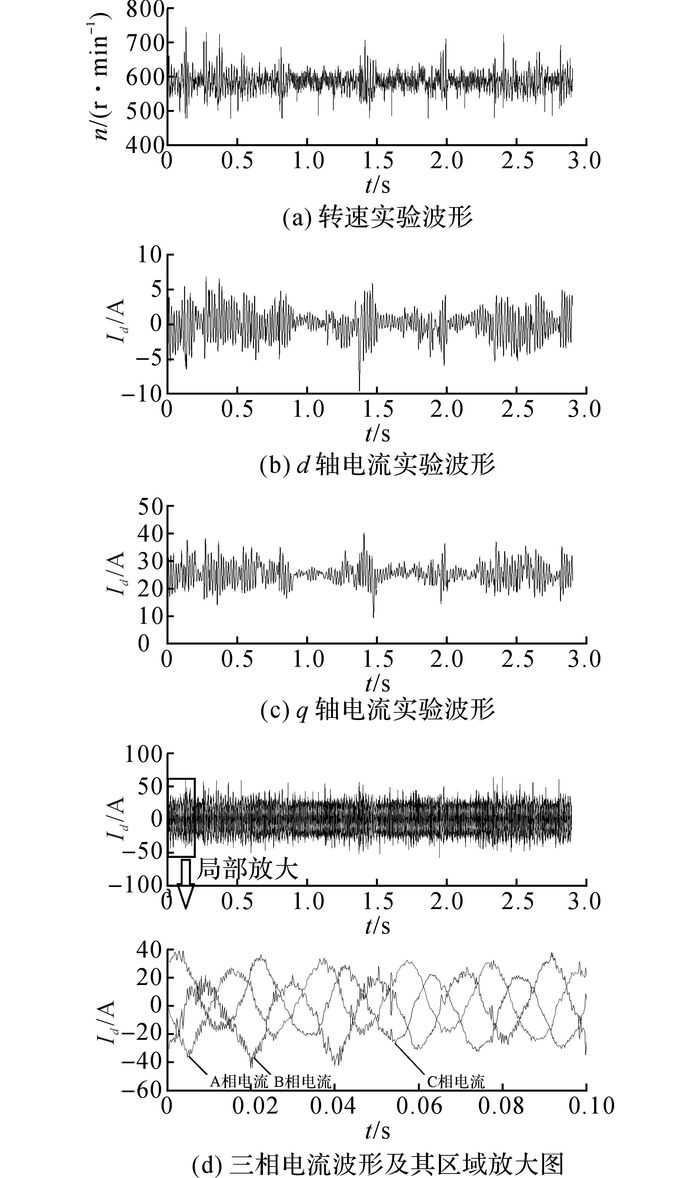
|
图 13 永磁起动/发电一体化系统起动状态负载实验波形 Fig. 13 Experiment waveform at loaded for starting motoring of permanent magnet integrated starter/generator system |
发电实验时, 用异步电动机拖动永磁起动/发电机, 使转子以同步速旋转, 则主磁通在气隙内形成旋转磁场.负载接能量回馈单元.逐步升高永磁起动/发电机的转速, 永磁起动/发电机转速波形如图 14所示, 电机运行到12 s时, 达到电动和发电的切换转速2 000 r/min.整个过程转速上升比较平稳, 且能够较快的跟踪给定转速.
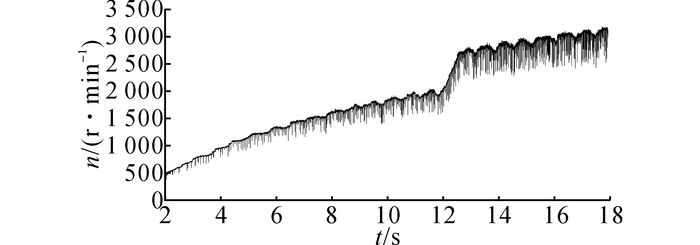
|
图 14 永磁起动/发电一体化系统起动工况和发电工况切换实验转速波形 Fig. 14 Speed waveform of starting and generating condition switching experiment for permanent magnet integrated starter/generator system |
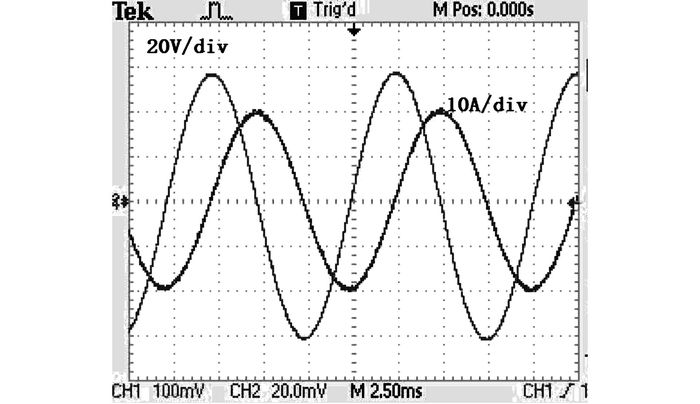
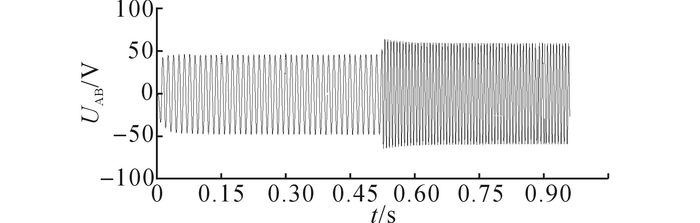
如图 15所示为电机发电相电流和线电压波形, 发电状态下的线电压正弦度较好, 功率因数高.如图 16所示发电状态AB线电压实验波形, UAB为发电机A相和B相间的线电压, 电压幅值和频率稳定, 电能质量好.
|
图 15 永磁起动/发电一体化系统发电状态AB线电压与A相相电流实验波形 Fig. 15 Waves of AB line voltage and phase A current at generating for permanent magnet integrated starter generating system |
|
图 16 永磁起动/发电一体化系统发电状态AB线电压实验波形 Fig. 16 Waves of AB line voltage at generating for permanent magnet integrated starter/generator system |
(1) 外特性参数匹配标定使起动/发电机在满足整车动力学性能需求的情况下实现了电机和逆变器的功率匹配.
(2) 控制策略的匹配标定表明凸极比和弱磁系数是影响控制过程中最大输出功率和最大转矩的主要参数.
(3) 推导了以凸极比和弱磁系数为参变量的电机数学模型, 给出了凸极比和弱磁系数对输出功率和转矩的影响关系, 并以此为依据进行电磁结构参数匹配的设计流程.
(4) 样机实验的结果表明, 采用该匹配设计方法的样机既能够满足起动过程中转矩转速要求, 又能够满足发电工况下对发电质量的要求, 验证了匹配标定理论分析的有效性和可行性, 可以为混合动力汽车用起动/发电系统的匹配设计提供理论基础和工程应用参考.
考虑饱和情况下交直轴电感的交叉耦合对匹配设计的影响是下一步的研究内容.
| [1] | KAMIEV K, MONTONEN J, RAGAVENDRA M P. Design principles of permanent magnet synchronous machines for parallel hybrid or traction applications[J]. IEEE Transactions on Industrial Electronics, 2013, 60(11): 4881–4890. DOI:10.1109/TIE.2012.2221117 |
| [2] | SEO J H, KIM S M, JUNG H K. Rotor-design strategy of IPMSM for 42 V integrated starter/generator[J]. IEEE Transactions on Magnetics, 2010, 46(6): 2458–2461. DOI:10.1109/TMAG.2010.2043417 |
| [3] |
张岳, 曹文平, MARROWJ. 电动车用内置式永磁电机(PMSM)设计[J].
电工技术学报, 2015, 30(14): 108–115.
ZHANG Yue, CAO Wen-ping, MARROW J. Design of an interior permanent magnet synchronous motor (PMSM) for EV traction[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 108–115. DOI:10.3969/j.issn.1000-6753.2015.14.015 |
| [4] |
王晓远, 高鹏, 赵玉双. 电动汽车用高功率密度电机关键技术[J].
电工技术学报, 2015, 30(6): 53–59.
WANG Xiao-yuan, GAO Peng, ZHAO Yu-shuang. Key technology of high power density motors in electric vehicles[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 53–59. |
| [5] |
段建东, 赵克, 孙力, 等. 永磁同步发电机效率最优联合控制[J].
电工技术学报, 2012, 27(3): 49–55.
DUAN Jian-dong, ZHAO Ke, SUN Li, et al. Optimal efficiency joint control for permanent magnet synchronous generators[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 49–55. |
| [6] | BONTHU S S R, BAEK J, ISLAM M Z, et al. Optimal design of five phase permanent magnet assisted synchronous reluctance motor for integrated starter/generator application[C]//2015 IEEE International Electric Machines and Drives Conference (IEMDC). Coeur d'Alene:IEEE, 2015:433-439. |
| [7] | LEGRABGER J, FRIEDRICH G, VIVIER S, et al. Combination of finite-element and analytical models in the optimal multi-domain design of machines:application to an interior permanent-magnet starter/generator[J]. IEEE Transactions on Industry Applications, 2010, 46(1): 232–239. DOI:10.1109/TIA.2009.2036549 |
| [8] | GRIFFO A, WROBEL R, MELLOR P H, et al. Design and characterization of a three-phase brushless exciter for aircraft starter/generator[J]. IEEE Transactions on Industry Applications, 2013, 49(5): 2106–2115. DOI:10.1109/TIA.2013.2269036 |
| [9] | YEOH S S.Control design for PMM-based starter/generator system for more electric aircraft[C]//201416th European Conference on Power Electronics and Applications. Lappeenranta:IEEE, 2014:1-10. |
| [10] | GAO F, BOZHKO S, YEOH S S. Control design for PMM starter-generator operated in flux-weakening mode[C]//Power Engineering Conference (UPEC). Dublin:IEEE, 2013:1-6. |
| [11] |
夏永洪, 王善铭, 黄劭刚, 等. 齿谐波励磁的混合励磁永磁同步发电机[J].
清华大学学报:自然科学版, 2011, 51(11): 1557–1561.
XIA Yong-hong, WANG Shan-ming, HUANG Shao-gang, et al. Hybrid excitation permanent magnet synchronous generator utilizing tooth harmonics for the excitation[J]. Journal of Tsinghua University:Science and Technology, 2011, 51(11): 1557–1561. |
| [12] |
彭兵, 夏加宽, 王成元, 等. 近极槽数表贴式永磁同步电机齿顶漏磁分析与计算[J].
电工技术学报, 2012, 27(1): 114–118.
PENG Bin, XIA Jia-kuan, WANG Cheng-yuan, et al. Axial flux leakage of coordinate structure hybrid excitation synchronous machine and its influence[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 114–118. |
| [13] |
李艳明, 郭宏, 谢清明, 等. 微燃机用高速永磁同步起动发电机驱动控制策略研究[J].
电气传动, 2013, 43(4): 17–21.
LI Yan-ming, GUO Hong, XIE Qing-ming, et al. Research on the drive and control strategy of the high speed permanent magnet synchronous starter/generator used in the microturbine generation system[J]. Electric Drive, 2013, 43(4): 17–21. |
| [14] |
唐朝晖, 丁强, 喻寿益, 等. 内埋式永磁同步电机的弱磁控制策略[J].
电机与控制学报, 2010, 14(5): 68–72.
TANG Zhao-hui, DING Qiang, YU Shou-yi, et al. Research of flux weakening strategy of interior permanent magnet synchronous motor[J]. Electric Machines and Control, 2010, 14(5): 68–72. |
| [15] |
卢东斌, 欧阳明高, 谷靖, 等. 电动汽车永磁同步电机最优制动能量回馈控制[J].
中国电机工程学报, 2013, 33(3): 83–91.
LU Dong-bin, OU Yang-ming-gao, GU Jing, et al. Optimal regenerative braking control for permanent magnet synchronous motors in electric vehicles[J]. Proceedings of the Chinese Society for Electrical Engineering, 2013, 33(3): 83–91. |
| [16] |
李政, 胡广大, 崔家瑞, 等. 永磁同步电机调速系统的积分型滑模变结构控制[J].
中国电机工程学报, 2014, 34(3): 431–437.
LI Zheng, HU Guang-da, CUI Jia-rui, et al. Sliding-mode variable structure control with integral action for permanent magnet synchronous motor[J]. Proceedings of the Chinese Society for Electrical Engineering, 2014, 34(3): 431–437. |
| [17] | KAMIEV K, MONTONEN J, RAGAVENDRA M P, et al. Design principles of permanent magnet synchronous machines for parallel hybrid or traction applications[J]. IEEE Transactions on Industrial Electronics, 2013, 60(11): 4880–4890. |
| [18] |
郑维. 混合动力汽车动力总成参数匹配方法与控制策略的研究[D]. 哈尔滨: 哈尔滨工业大学, 2010: 43-62.
ZHENG Wei. Research on power train parameter matching method and control strategy for hybrid electric vehicle[D]. Harbin:Harbin Institute of Technology, 2010:43-62. http://d.wanfangdata.com.cn/Thesis/D269436 |
| [19] |
曹永霞. 混合动力汽车用永磁同步电机参数匹配与控制算法研究[D]. 吉林: 吉林大学, 2015: 21-42.
CAO Yong-xia. Research on permanent magnet synchronous motor parameter matching and control algorithm for hybrid electric vehicle[D]. Jilin:Jilin University, 2015:21-42. http://cdmd.cnki.com.cn/Article/CDMD-10183-1015597796.htm |
| [20] |
任海英. 双凸极起动/发电机系统一体化设计与实现[D]. 南京: 南京航空航天大学, 2006: 13-17.
REN Hai-ying. Integral design and implementation of doubly salient starter/generator[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2006:13-17. http://d.wanfangdata.com.cn/Periodical/zgdjgcxb200624028 |
| [21] |
罗德荣, 张洪彬, 蔡亚辉, 等. 起发一体机发电模式的弱磁电压控制策略[J].
电网技术, 2015, 39(8): 2291–2296.
LUO De-rong, ZHANG Hong-bin, CAI Ya-hui, et al. Flux-weakening voltage control strategy of the integrated starter/generator motor in generator mode[J]. Power System Technology, 2015, 39(8): 2291–2296. |


