2. 浙江银轮机械股份有限公司, 浙江 台州 317200
2. Zhejiang Yinlun Machinery Co. Ltd, Taizhou 317200, China
导风罩是发动机冷却模块的重要组成部分, 直接影响冷却系统的整体性能, 导风罩结构的差异对散热器性能的影响达到3%~4%[1], 而导风罩结构参数中对模块性能影响最大的参数是导风罩深度[2].多数研究认为加大导风罩深度有利于模块性能的提升[2-6], 但也有研究发现, 导风罩深度并非越深越好, 当导风罩深度从81 mm变化到231 mm时, 空气流量在不同风扇转速下均出现先上升后下降的趋势[7].因此, 在有限空间范围内设计出最优导风罩结构深度, 对实车冷却模块布置具有重要的现实意义.
以往研究大多针对机械风扇冷却模块展开, 随着电子风扇应用的日渐广泛, 人们对电子风扇冷却模块导风罩结构也进行了一些研究[8-10].这些研究涉及的电子风扇与机械风扇在结构上仍十分相似, 仅驱动方式有所不同:风扇自身仍无护风圈和安装结构, 扇叶与电机轴安装成一体结构后再安装到导风罩上.与这种结构的风扇相比, 商用车采用的大风量、高静压的紧凑型电子风扇结构有明显差异:该类型风扇带有独立护风圈、定子和安装结构, 工程应用中通常安装在矩形导风罩上, 再通过导风罩与冷却模块组成多风扇冷却模块.因此, 对于这种多风扇冷却模块, 导风罩截面尺寸一般与散热器截面尺寸相同, 实际应用中需要解决的是在有限安装空间内优化导风罩深度结构, 进而在模块散热量和模块制造成本之间寻求最佳的平衡点.目前相关研究尚不多见, Stephens等[11]利用计算流体动力学(CFD)计算了导风罩深度对模块性能的影响, 但该研究在计算中采用风扇面模型, 不能模拟风扇实际运行中复杂的旋转气流特征;且仅针对单一结构模块进行研究, 未考虑导风罩其他结构参数及应用条件的影响.
为深入研究多风扇冷却模块中导风罩深度结构对模块性能的影响, 建立多风扇冷却模块数值仿真模型, 并进行试验验证;研究导风罩深度对多风扇冷却模块气动和换热性能的影响, 并提出最优导风罩深度的概念;进一步研究不同风扇数量、面积比、长宽比、散热器阻力特性和风扇转速等安装、运行参数对最优导风罩深度的影响.
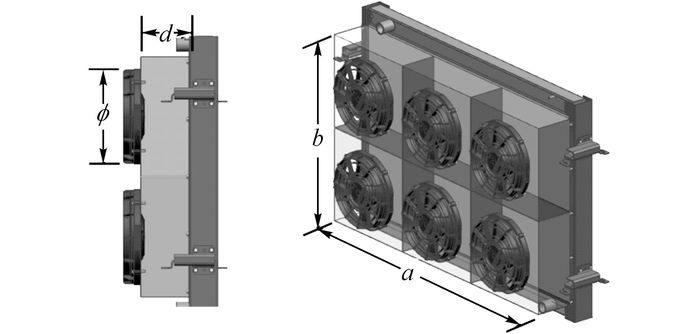
1 数值仿真模型 1.1 物理模型多风扇冷却模块由不同数量的电子风扇和不同尺寸的散热器组成.如图 1所示为六风扇冷却模块实物模型, 图中d为导风罩深度, 是电子风扇轮毂端面到散热器芯子端面的距离.图 1中的导风罩结构为多风扇冷却模块应用中的典型结构, 在导风罩内部采用隔板将各个风扇分隔开, 以减少风扇间的相互影响.为便于后文表述, 结合图 1对相关参数作如下定义:
|
图 1 多风扇冷却模块(MFCP)几何模型 Fig. 1 Geometry model of multi-fans cooling package (MFCP) |
| $\kappa = \frac{{ab}}{{n\left( {{\rm{ \mathsf{ π} }}{\phi ^2}/4} \right)}}.$ | (1) |
式中:κ为面积比, a为散热器芯宽, b为散热器芯高, n为风扇数量, ϕ为风扇直径.设λ为长宽比, λ=a/b.
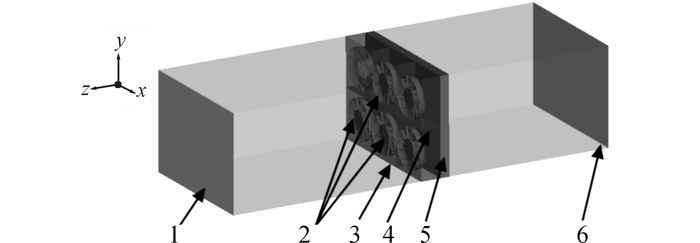
在如图 1所示的实物模型基础上建立数值仿真所需的物理模型:1) 去除安装支架等零部件;2) 忽略散热器室体结构, 仅保留芯体尺寸结构, 并采用多孔介质模型进行简化;3) 保留电子风扇主要结构和导风罩结构;4) 依照所研究的多风扇冷却模块迎风面尺寸, 按一定的比例沿冷却风流向的同轴方向扩展、建立虚拟风洞[12], 如图 2所示.
|
1 -虚拟风洞出口; 2 -电子风扇; 3 -导风罩; 4 -风扇间的分隔板; 5 -简化的散热器; 6 -虚拟风洞进口 图 2 多风扇冷却模块仿真模型 Fig. 2 Simulation model of MFCP |
湍流模型采用标准k-ε模型.连续性方程、动量方程和能量方程等控制方程采用式(2) 的通用形式表示.利用商用软件ANSYS Fluent 14.5提供的有限体积法对方程进行离散, 并选择一阶迎风差分格式和SIMPLE求解算法.
| $\frac{{\partial \left( {\rho \psi } \right)}}{{\partial t}} + {\rm{div}}\left( {\rho \mathit{\boldsymbol{u}}\psi } \right){\rm{div}}\left( {\mathit{\Gamma }{\rm{grad}}\psi } \right) + s.$ | (2) |
式中:ρ为流体密度, ψ为广义变量, u为速度矢量, Γ为扩散系数, s为源项.
风扇模型采用多重参考坐标系(multiple reference frame, MRF)模型.该模型包含风扇几何特征, 不依赖于实验值, 合理选择旋转区域后, 计算精度可达到6%左右[13-15].该方法将风扇非旋转部件定义在绝对坐标系下, 扇叶等旋转部件及其附近区域定义在旋转坐标系下, 对应速度通过下式进行转换:
| ${\mathit{\boldsymbol{v}}_{\rm{r}}} = \mathit{\boldsymbol{v}} - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{r}}.$ | (3) |
式中:vr为旋转坐标系速度, v为绝对坐标系速度, ω为旋转坐标系旋转角速度, r为旋转坐标系内的位置矢量.
由于现有计算能力有限, 将散热器简化为多孔介质模型, 并采用热交换器模型模拟散热器的传热特性.多孔介质模型是在标准动量方程中附加一个能源项:
| ${S_i} = - \left[ {\sum\limits_{j = 1}^3 {\left( {{\mathit{\boldsymbol{D}}_{ij}}\mu {u_j}} \right)} + \sum\limits_{j = 1}^3 {\left( {{\mathit{\boldsymbol{C}}_{ij}}\frac{1}{2}\rho \left| \mathit{\boldsymbol{u}} \right|{u_j}} \right)} } \right].$ | (4) |
对于简单均匀多孔介质, 式(4) 可以简化为
| ${S_i} = - \left( {\frac{\mu }{\alpha }{u_i} + {C_2}\frac{1}{2}\rho \left| \mathit{\boldsymbol{u}} \right|{u_j}} \right).$ | (5) |
式中:D、C为系数矩阵, μ为运动黏度, α-1为黏性阻力系数, C2为惯性阻力系数.
热交换器模型是利用效能-传热单元数法的一维计算模型, 采用下式计算换热单元的效能后计算各单元的换热量, 并求和得到散热器的散热量:
| $\varepsilon = 1 - \exp \left\{ {\frac{{{\rm{NT}}{{\rm{U}}^{0.22}}}}{{{C^*}}}\left[ {\exp \left( { - {C^*}{\rm{NT}}{{\rm{U}}^{0.78}}} \right) - 1} \right]} \right\}.$ | (6) |
式中:ε为传热有效度, ε=q/qmax, 表征热交换器实际传热量和最大可能传热量的比值;C*为热容量速率比值, C*=Cmin/Cmax;NTU为传热单元数NTU=kA/Cmin, 是热交换器传热尺度的无因次度量.
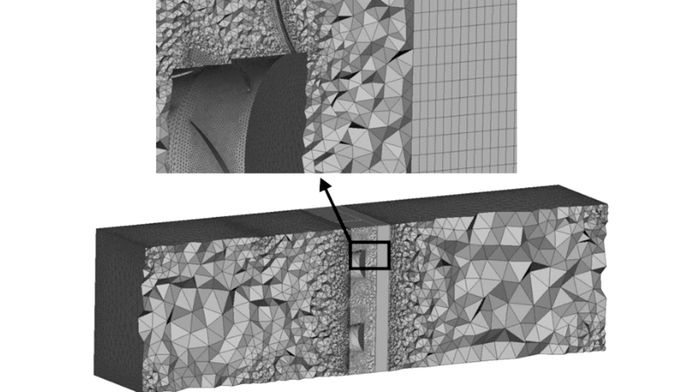
1.3 网格划分和边界条件对如图 2所示的仿真模型进行网格划分, 并沿中截面进行剖视, 如图 3所示.在网格划分时, 为了减少网格数量, 节约计算时间, 依据流场变化情况, 对不同区域的网格进行区别处理:散热器区域采用六面体结构网格, 其他区域采用四面体网格, 其中风扇区域进行局部细化.为了保证计算精度, 进行网格的无关性检验, 最终单个风扇区域网格数约为4.03×106;如图 3所示的整个模型网格总数约为3.20×107.
|
图 3 多风扇冷却模块计算网格 Fig. 3 Computational mesh of MFCP |
冷却空气采用随温度变化的变物性参数;冷却液采用常物性参数;虚拟风洞进、出口分别采用压力进口和压力出口边界条件;扇叶所在流体区域设置在旋转坐标系内, 转速即为风扇转速;扇叶壁面设置为滑移壁面, 与旋转坐标系相对转速为0;其余壁面为无滑移壁面.
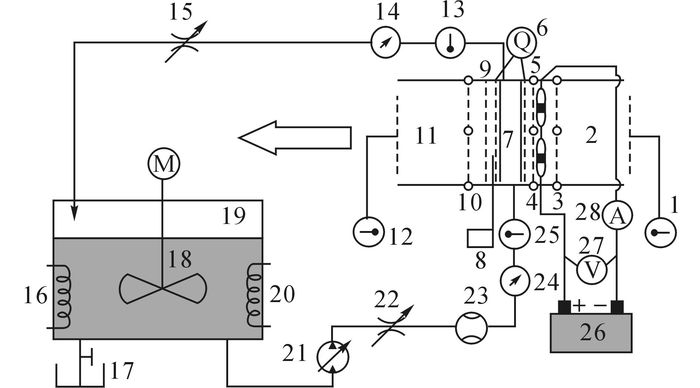
2 试验验证为验证模型精度, 建立如图 4所示的多风扇冷却模块性能测试装置.该试验装置主要由冷却液循环及控制系统、冷却风道和数据采集分析系统等部分组成, 主要采用PT100铂电阻温度传感器测量温度, 采用科氏力质量流量计测量冷却液流量, 采用“斜压管不均匀冷却气流测量”方法[16]测量冷却空气流量, 压差变送器测量压差.
|
1, 12-“钉耙式”温度取样器;2-进风口导风段;3, 5, 10-静压测量孔;4-电子风扇;6-斜压管流量测量仪;7-散热器;8-热线风速仪;9-出风口测温网;11-出风口导风段;13, 25-温度传感器;14, 24-压力传感器;15, 22-流量调节阀;16, 20-电加热器;17-排水管;18-搅拌装置;19-蓄水箱;21-电动水泵;23-流量计;26-直流电源;27-电压表;28-电流表 图 4 多风扇冷却模块性能试验装置示意图 Fig. 4 Schematic diagram of MFCP test equipment |
试验中需确保达到热平衡稳定工况才能采集数据, 具体地:冷却液流量调到设定值、并保持稳定;冷热侧进、出口温度稳定、并持续稳定10 min.尽管如此, 热平衡误差仍不可避免的存在[17], 为统一比较基础, 试验中统一将冷却液侧测得的散热量作为冷却模块的散热量值Q.
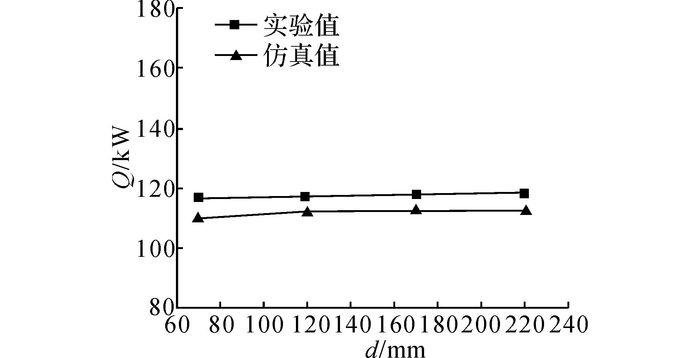
如图 1~3所示的六风扇冷却模块, 散热器芯子尺寸为:1 086 mm(芯宽)×769 mm(芯高)×70 mm(芯厚);导风罩深度d为70、120、170、220 mm.试验条件为:冷却液流量为4.684 kg/s, 气液温差为35 ℃;冷却空气进口温度为25±1 ℃, 风扇转速为4 100 r/min.将上述试验条件作为数值仿真的边界条件进行数值计算, 并同样取冷却液侧的换热量数值作为模块散热量值Q, 对比结果见图 5:仿真值略小于实验值, 最小偏差为-4.27%, 最大偏差为-5.68%.因此, 可以认为, 本文提出的数值仿真模型计算精度符合要求, 可用于后续研究.
|
图 5 多风扇冷却模块传热性能仿真值与实验值对比 Fig. 5 Comparison of calculated and measured thermal performance of MFCP |
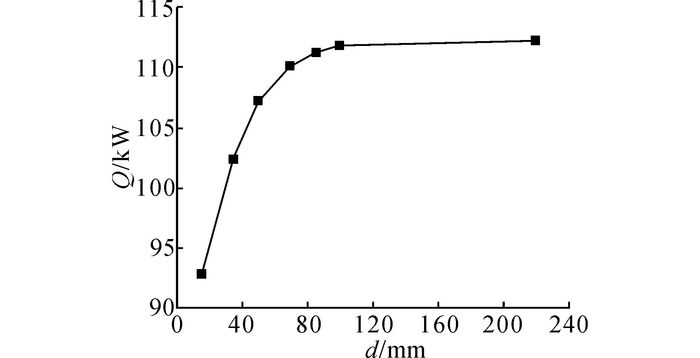
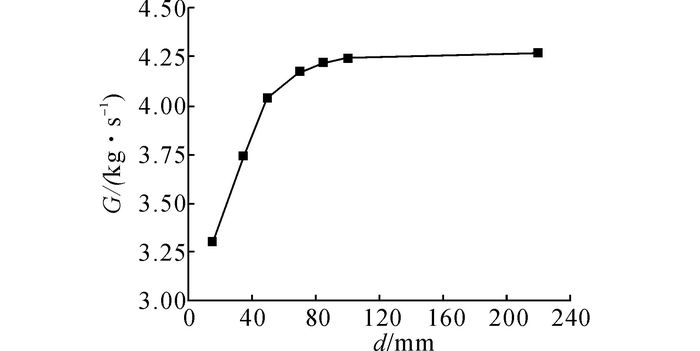
如图 5所示, 导风罩深度对多风扇冷却模块的散热性能影响并不明显, d=220 mm时的模块散热量较d=70 mm时模块散热量仅提高了1.94 %.原因如下, 对于该模块d在70~220 mm变化刚好处于导风罩深度对模块性能作用的平缓区.为此, 扩大d的取值范围, 并保持其他边界条件不变, 继续进行数值仿真计算.如图 6所示, 当d取15、35、50、70、85、100和220 mm时, 冷却模块散热量随导风罩深度的变化关系.由图可见, 扩大取值范围后可以清晰地看到导风罩深度对冷却模块散热性能的影响:随着导风罩深度的增大, 模块散热量不断增大, 但变化速率逐渐变小, 这与Stephens等[11]的研究结论相似.为进一步解释这一现象, 给出了模块冷却风量G随导风罩深度的变化关系, 如图 7所示.由图可见, 冷却风量与散热量的变化规律相同, 原因如下, 由于风扇直接作用的散热器面积有限, 使得进入散热器的冷却空气流场不均匀, 通过增大导风罩深度可以改善流场均匀性, 减少摩擦损失, 进而提高冷却风量和换热量;但随着流场均匀性的改善, 进一步增大导风罩深度带来的改善逐渐变小.
|
图 6 导风罩深度对多风扇冷却模块换热量的影响 Fig. 6 Effect of shroud depth on heat transfer rate of MFCP |
|
图 7 导风罩深度对多风扇冷却模块冷却风量的影响 Fig. 7 Effect of shroud depth on air flux of MFCP |
由于上述导风罩深度对多风扇冷却模块性能的上述影响规律, 在进行模块设计、匹配时, 应在散热性能与安装空间、制造成本之间寻找平衡点.为此, 遵照一般工程应用经验, 可得,当导风罩深度对模块性能影响小于5%时, 进一步增大导风罩深度得不偿失.以最大安装空间下的模块性能为基准, 定义模块性能可以提升的空间, 并将Δ<5%时的导风罩深度定义为最优导风罩深度:
| ${\Delta _G} = \left[ {\left( {{G_{{d_{\max }}}} - {G_{{d_{\rm{i}}}}}} \right)/{G_{{d_{\max }}}}} \right] \times 100\% ,$ | (7) |
| ${\Delta _Q} = \left[ {\left( {{Q_{{d_{\max }}}} - {Q_{{d_{\rm{i}}}}}} \right)/{Q_{{d_{\max }}}}} \right] \times 100\% .$ | (8) |
式中:ΔG为冷却风量可提升率;ΔQ为散热量可提升率;dmax为安装空间允许的最大导风罩深度,本文取dmax=220 mm;Gdmax、Gdi分别为导风罩深度为dmax和di时模块的冷却风量;Qdmax、Qdi分别为导风罩深度为dmax和di时模块的散热量.
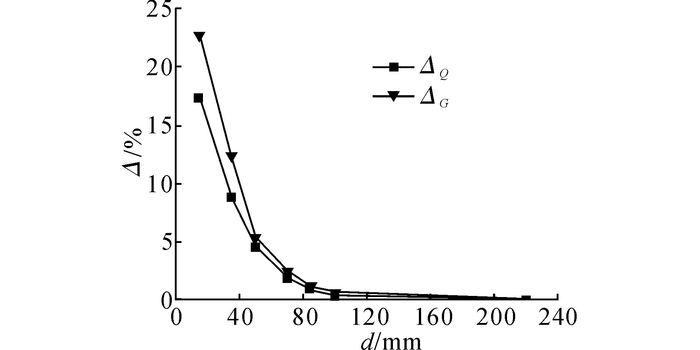
如图 8所示为六风扇冷却模块冷却风量和换热量可提升率随导风罩深度变化的曲线.当d=50时, ΔQ=4.51%<5.00%, 依据本文定义认为50 mm为该模块的最优导风罩深度.此外, 如图 8所示, 利用ΔG和ΔQ判定最优导风罩深度结果一致, 两者相关性好, 因此, 为节约计算时间, 后续研究仅作冷态流场计算.
|
图 8 导风罩深度对多风扇冷却模块性能可提升率的影响 Fig. 8 Effect of shroud depth on performance improvement rate of MFCP |
分别改变模块中风扇数量、面积比、长宽比、散热器阻力和风扇转速等参数, 进一步研究不同结构和运行参数下, 最优导风罩深度的变化规律.
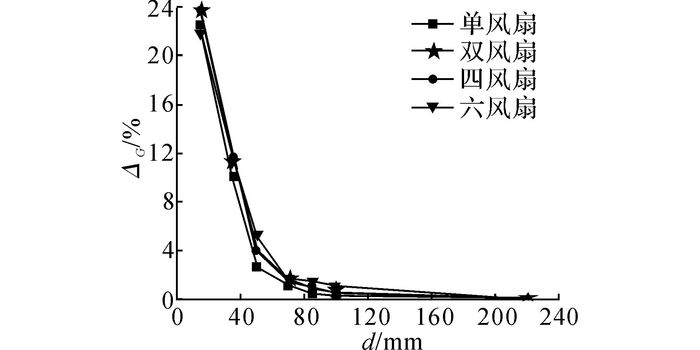
4.1 风扇数量的影响当κ=1.79, λ=1.05, 风扇转速为4 100 r/min时, 不同风扇数量的冷却模块冷却风量可提升率随导风罩深度的变化如图 9所示.由图可见, 随着风扇数量的增加, 对应导风罩深度下的模块性能可提升率略有提高, 但并不显著, 按照性能可提升率小于5%的判断准则, 不同冷却模块的最优导风罩深度均为50 mm.
|
图 9 不同风扇数量时导风罩深度对冷却模块性能的影响 Fig. 9 Effect of shroud depth on cooling package of MFCP with different numbers of fans |
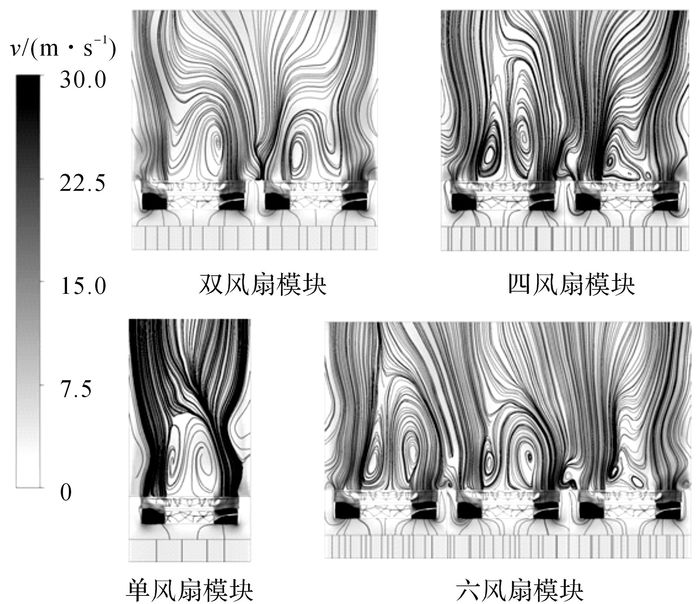
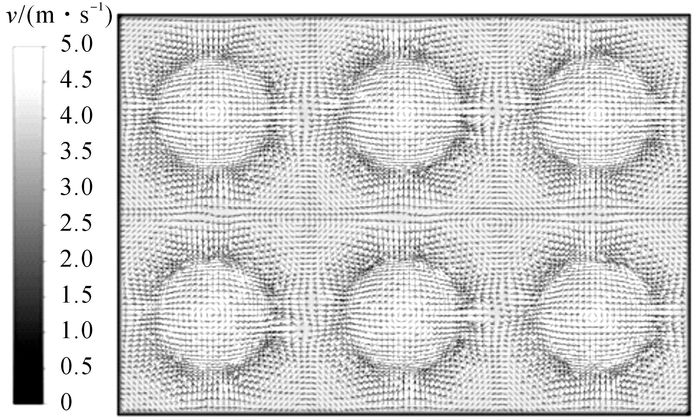
为分析其中原因, 分别给出各模块中截面和六风扇模块出口处速度云图与流线图, 如图 10、11所示, 图中v为冷却风的风速.由图可见, 由于散热器的多孔介质整流作用和模块采用吸风式的布置结构, 通过散热器的冷却空气流向几乎垂直于散热器迎风面, 无旋流作用;此外, 在风扇的定子结构和风扇间的隔板双重作用下, 仅在风扇叶尖投影区域有较强的气流旋转效应, 风扇间的相互作用得以削弱, Stephens等[11]也有相似发现.因此, 各风扇单元结构相同的不同风扇数量的多风扇冷却模块最优导风罩深度基本一致, 对于多风扇冷却模块导风罩结构的研究可简化为单风扇冷却模块.将该结论应用于产品开发实践中, 可以节约大量的计算资源、试制费用和试验资源.
|
图 10 各多风扇冷却模块中截面处速度云图与流线对比 Fig. 10 Velocity contours and pathlines of middle face of MFCP |
|
图 11 多风扇冷却模块中散热器出口处速度云图和矢量图 Fig. 11 Velocity contours and vectors of outlet of radiator of MFCP |
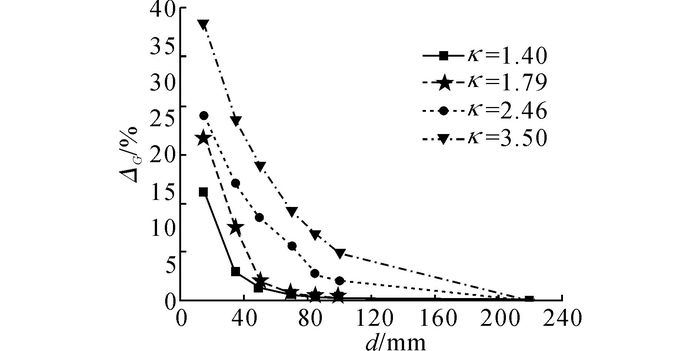
对于单风扇冷却模块, 当λ=1.05, 风扇转速为4 100 r/min时, 不同面积比下的冷却模块冷却风量可提升率随导风罩深度的变化如图 12所示.由图可见, 面积比越大, 同一导风罩深度对应的模块冷却风量可提升率越大.分析其原因可知, 随着面积比的增大, 进入散热器的冷却空气流场不均匀性变大, 使得需要更大的导风罩深度才能提高流场均匀性.在具体应用中, 当前后距离有限时, 应尽量选择截面更大的风扇, 以减小面积比.
|
图 12 不同面积比时导风罩深度对MFCP性能的影响 Fig. 12 Effect of shroud depth on performance of MFCP with different area ratios |
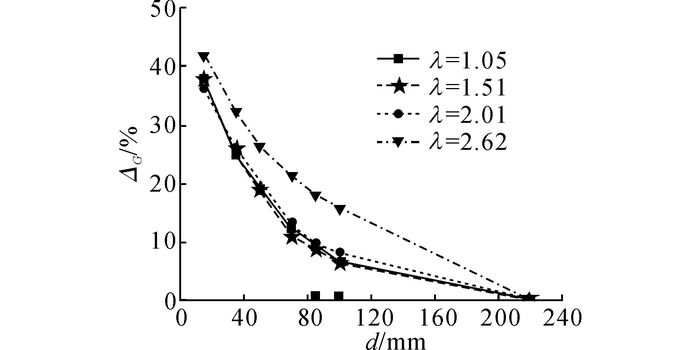
对于单风扇冷却模块, 当κ=3.05, 风扇转速为4 100 r/min时, 不同长宽比下的冷却模块冷却风量可提升率随导风罩深度的变化如图 13所示.由图可见, 当长宽比数值较小, λ≤2.01时, 改变长宽比, 几乎对不同深度下的模块冷却风量可提升率没有影响;只有当长宽比数值较大, 如λ=2.62时, 对应深度下的冷却风扇可提升率才有大幅上升, 也就是最优导风罩深度显著增大.原因如下, 对同一个冷却风扇而言, 尽管面积比一定, 但当长宽比增大到一定程度时, 风扇不能直接作用到的面积增大, 需要更多空间以协调不均匀的来流.因此, 在具体应用中, 应尽量避免“狭长”型结构布置以免导致长宽比过大,需要更大安装空间.
|
图 13 不同长宽比时导风罩深度对MFCP性能的影响 Fig. 13 Effect of shroud depth on performance of MFCP with different length width ratios |
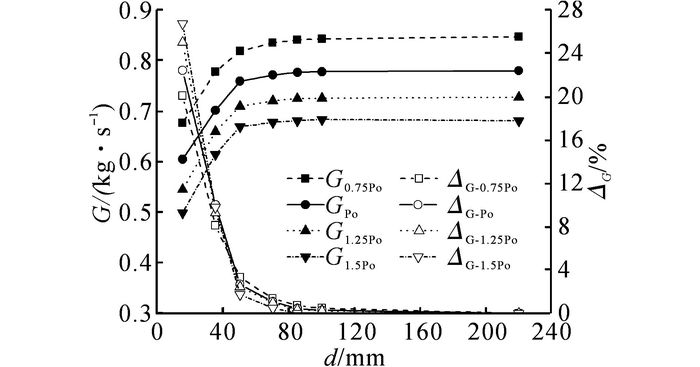
当风扇转速设定为4 100 r/min, 模块结构参数相同时, 将散热器的多孔介质参数在前文原始阻力特性(标记为Po)的基础上分别乘以0.75、1.25和1.5的系数, 构建新阻力特性的散热器, 研究在不同散热器阻力特性下, 导风罩深度对冷却模块性能的影响, 如图 14所示.由图可见, 散热器阻力越大, 通过冷却模块的冷却风量越小;但阻力特性对冷却模块的冷却风量可提升率几乎没有影响, 即模块最优导风罩深度不随阻力特性的改变而改变.
|
图 14 不同阻力特性下导风罩深度对模块性能的影响 Fig. 14 Effect of shroud depth on air flux of MFCP with different resistances |
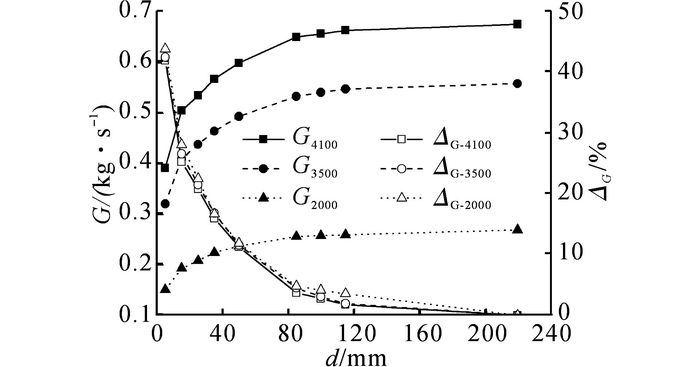
冷却模块结构及安装参数一定, 改变风扇转速, 研究不同运行参数下, 导风罩深度对冷却模块性能的影响.如图 15所示为当风扇转速为2 000、3 500、4 100 r/min时, 不同导风罩深度下的冷却模块性能曲线.如图所示, 风扇转速越小, 通过冷却模块的冷却风量越小;但不同风扇转速下模块冷却风量随导风罩深度变化的幅度相近, 即改变风扇转速不改变最优导风罩深度的选取, 这与4.4节中散热器阻力特性的影响规律相似.
|
图 15 不同风扇转速下导风罩深度对模块性能的影响 Fig. 15 Effect of shroud depth on air flux of MFCP with different speeds of fans |
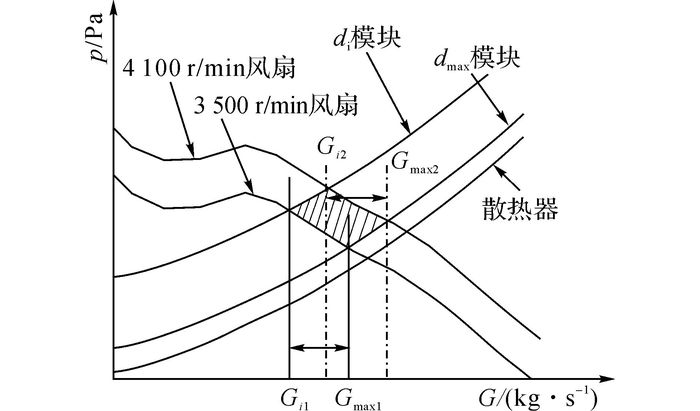
上述研究表明, 由于风扇转速或模块阻力特性的改变, 不同导风罩深度对模块性能影响程度差异不大, 也就是不同模块阻力特征下风扇工作点的改变对最优导风罩深度没有影响.为解释这一规律, 图 16给出了系统阻力匹配图.图中, p为静压,在散热器阻力特性的基础上, 示意了导风罩深度分别为dmax和di的2个模块的阻力特性, 阻力特性曲线与2个风扇转速下风扇性能曲线的交点, 即为对应冷却模块的工作点.由图可见, 4个工作点形成的区域可近似为平行四边形, Gmax1-Gi1与Gmax2-Gi2在数值上相当, 又根据式(7) 分母Gmax2与Gmax1在数值上的细小差异对性能可能提升率影响有限, 因此, 如图 15所示, 风扇转速越小, 导风罩深度对模块性能的影响程度越大, 但变化不大, 这导致各风扇转速下的最优导风罩深度相同.对模块而言, 改变风扇转速与改变模块阻力特性的作用机理相似.
|
图 16 多风扇冷却模块系统阻力匹配示意图 Fig. 16 Resistance match-up scheme of MFCP system aerodynamic performance |
(1) 采用多重参考坐标系模型对风扇建模、多孔介质模型结合热交换器模型对散热器建模, 建立了多风扇冷却模块虚拟风洞仿真模型, 仿真结果与试验值的偏差在5%左右, 可信度高.
(2) 多风扇冷却模块的气动和散热性能受导风罩深度影响较大, 导风罩深度越大, 模块性能越好, 但性能可提升率逐渐变小;考虑安装空间和制造成本等诸多因素, 并遵照一般工程应用经验, 将模块性能可提升率小于5%的导风罩深度定义为最优导风罩深度.
(3) 风扇数量几乎不影响导风罩深度对模块性能的作用, 对多风扇冷却模块最优导风罩深度的研究可简化为对单风扇冷却模块最优导风罩深度的研究, 可大量节约产品开发过程中的试验资源、计算资源以及试制费用.
(4) 面积比越大, 模块所需最优导风罩深度越大;当具体应用中前后距离有限时, 应尽量选择截面更大的风扇, 以减小面积比.
(5) 长宽比只有增大到一定程度, 才对最优导风罩深度有显著影响, 如本文取λ≥2.62;在具体应用中, 应尽量避免“狭长”型结构布置.
(6) 散热器阻力特性和风扇转速对最优导风罩深度几乎没有影响.
| [1] | CELIK E. Truck airflow management influence on cooling module performance-experimental and numerical study[C]//2000 SAE World Congress. Detroit:SAE 2000:1-6. |
| [2] | TAYLOR D O, CHU A C. Wind tunnel investigation of the effects of installation parameters on truck cooling system performance[C]//1976 SAE World Congress. Deroit:SAE, 1976:2070-2682. |
| [3] | HALLQVIST T. The cooling airflow of heavy trucks a parametric study[C]//2008 SAE World Congress.Detroit:SAE, 2008:119-133. |
| [4] |
沈凯, 徐锦华, 朱黎明, 等. 发动机冷却模块安装参数对气动性能的影响[J].
内燃机工程, 2013, 34(1): 27–32.
SHEN Kai, XU Jin-hua, ZHU Li-ming, et al. Influence of installation of cooling components on aerodynamic characteristics[J]. Chinese Internal Combustion Engine Engineering, 2013, 34(1): 27–32. |
| [5] | SRINIVASA V K, RENJITH S, SHOME B. Design of experiments enabled CFD approach for optimizing cooling fan performance[C]//2014 SAE World Congress. Detroit:SAE, 2014:2014-01-0658. |
| [6] |
田海勇, 马文肖, 孙会来, 等. 工程车辆发动机冷却风扇的设计与优化[J].
矿山机械, 2014, 42(6): 40–45.
TIAN Hai-yong, MA Wen-xiao, SUN Hui-lai, et al. Design and optimization of cooling fan for the engine of construction vehicle[J]. Mining and Processing Equipment, 2014, 42(6): 40–45. |
| [7] |
刘佳鑫. 工程机械散热模块传热性能研究[D]. 长春: 吉林大学, 2013: 28.
LIU Jia-xin. Research on heat transfer performance of heat-dissipation module for construction machinery[D]. Changchun:Jilin University, 2013:28. http://cdmd.cnki.com.cn/Article/CDMD-10183-1013192581.htm |
| [8] | AP N S, GUERRERO P, JOUANNY P. Influence of front end vehicle, fan and shroud on the heat performance of A/C condenser and cooling radiator[C]//2002 SAE World Congress. Detroit:SAE, 2002:2002-01-1206. |
| [9] |
贾青, 杨志刚. 汽车前端部件结构对冷却性能的影响[J].
同济大学学报:自然科学版, 2014, 42(8): 1221–1226.
JIA Qing, YANG Zhi-gang. Influence of front end structure on vehicle cooling performance[J]. Journal of Tongji University:Natural Science, 2014, 42(8): 1221–1226. |
| [10] | MANNA S, KUSHWAH Y S.Optimization of a vehicle under hood airflow using 3D CFD analysis[C]//2015 SAE World Congress.Detroit:SAE, 2015:2015-01-0349. |
| [11] | STEPHENS T, CROSS T.Fan and heat exchanger flow interactions[C]//2005 SAE World Congress.Toronto:SAE, 2005:2005-01-2004. |
| [12] |
李永乐, 陈宁, 蔡宪棠, 等. 桥塔遮风效应对风-车-桥耦合震动的影响[J].
西南交通大学学报, 2010, 45(6): 875–881.
LI Yong-le, CHEN Ning, CAI Xian-tang, et al. Wake impact of bridge tower on coupling vibration of wind-vehicle-bridge system[J]. Journal of Southwest University, 2010, 45(6): 875–881. |
| [13] | GULLBERG P, LOFDAHL L, ADELMAN S, et al.An investigation and correction method of stationary fan CFD MRF simulations[C]//2009 SAE World Congress.Detroit:SAE, 2009:2009-01-3067. |
| [14] | GULLBERG P, LOFDAHL L, NILSSON P, et al.Continued study of the error and consistency of fan CFD MRF models[C]//2010 SAE World Congress.Detroit:SAE, 2010:2010-01-0553. |
| [15] | GULLBERG P, LOFDAHL L, NILSSON P.Cooling airflow system modeling in CFD using assumption of stationary flow[C]//2011 SAE World Congress.Detroit:SAE, 2011:2011-01-2182. |
| [16] |
吕峰. 商用车冷却模块匹配设计方法研究[D]. 杭州: 浙江大学, 2011: 84-86.
LV Feng.The investigation on match and design of commercial vehicle cooling module[D].Hangzhou:Zhejiang University, 2011:84-86. http://d.wanfangdata.com.cn/Thesis/Y2215076 |
| [17] | 全国内燃机标准化技术委员会. 内燃机水散热器技术条件: JB/T 8577-2015[S]. 北京, 机械工业出版社, 2016. |



