近年来, 在非线性非稳态的电能质量扰动信号处理方法中, 传统方法包括短时傅里叶变换[1~3]、小波变换[4~6]和S变换[7~9]等.这些方法在分解过程中不仅需要预先选择加窗函数和小波基函数, 而且分析函数一旦确定以后其分解尺度就保持不变, 因此其分解过程本质上都是非自适应处理.经验模态分解(empirical mode decomposition, EMD)是希尔伯特-黄变换的核心部分[10], 可以根据信号极值点分布特性, 将信号自适应分解成一系列的固有模态函数(intrinsic mode functions, IMF),其分解过程完全基于信号局部时间尺度特征, 无需人为选择基函数的自适应性, 因此在信号处理领域得到了深入的研究.
虽然EMD方法应用范围广泛[11], 但当受到间断信号干扰时, 会造成极值点分布不均匀,导致模态混叠效应[12].模态混叠效应的产生使得分解的个别IMF物理意义不明确、降低EMD分解性能.针对上述问题, WU等[13]提出了一种噪声辅助分解方法:集总经验模态分解(ensemble empirical mode decomposition, EEMD), 通过对原始待分解信号加入不同幅值白噪声进行EMD分解, 将分解结果进行集总平均得到最终的IMF分量.Yeh等[14]提出了互补集总经验模态分解(complementary ensemble empirical mode decomposition, CEEMD)的分解方法, 通过加入正负成对的白噪声克服EEMD存在的残余噪声大、分解不完备的缺点.为了解决加噪幅值不同产生不同的IMF个数以及虚假分量的问题, Torres等[15]提出了自适应完全经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN), 在每一阶的分解过程中加入经过EMD自适应分解的白噪声达到改进效果.
虽然上述方法通过加入辅助噪声分解达到改进目的.但是加噪的幅值A和集总分解次数N都是通过经验方法确定的, 大大削弱了EMD的自适应性分解性能.在分解过程中A和N只停留在理论性描述上,并没有进行严格的数学证明分析, 这类经验参数并不适合所有的分解信号.通过大量的集总次数消除残余分量, 依旧存在计算量较大的缺点.
事实上, EMD分解是采用插值方法对信号局部极值点拟合成上下包络线求得均值曲线得到IMF分量, 因此极值点分布特性是分解结果的决定性因素[16].但间断信号会影响极值点的均匀分布, 在包络拟合时会出现局部均值扭曲的过冲和欠冲现象以及端点效应, 从而导致不同时间尺度无法准确分解的模态混叠效应.加噪辅助的分解方法, 通过加入受控噪声改善原始信号极值点的分布, 使极值点分布趋于均匀从而抑制模态混叠效应的发生.从理论上来说, 加入较小幅值噪声分解误差更小,可以取得更好的分解效果, 而噪声幅值较小却不能改变原始信号极值点的分布, 但加噪幅值较大又会产生过大的残余噪声和剩余分量, 虽然通过增加集总次数可以消除残余噪声, 但集总次数的增加又会增加算法的运算量.
对于电能质量信号和噪声信号而言, 极值点的密度间接表示信号的频率, 即频率越高, 极值点分布越密集, 反之亦然.因此可以对原始信号加入小幅值的辅助噪声, 通过改变辅助噪声的频率去影响原始信号极值点的分布,从而使极值点分布趋于均匀得到更好的分解效果.基于上述分析, 针对加噪参数依据经验性确定的不足,以及如何在消除模态混叠的基础上进一步减小计算量, 本文提出一种自适应快速互补集总经验模态分解(adaptively fast complementary ensemble empirical mode decomposition, AFCEEMD)方法.首先, 通过对EEMD加噪准则进行研究, 提出加入噪声采用小幅值高频形式, 而通过建立极值点间距标准差与加噪频率之间对应的函数关系, 自适应寻求最优高频噪声fi.其次, 进一步确定辅助加噪参数采用固定形式.通过仿真信号对比分析, 结果表明AFCEEMD方法不仅解决了模态混叠问题, 而且进一步减少了计算量, 消除了残余噪声的干扰, 具有一定的优越性.最后将所提方法运用在电能质量扰动检测中, 验证了AFCEEMD的可行性与实用性.
1 基本原理 1.1 EEMD原理对于给定的信号s(t), EEMD分解过程如下.
1) 对原始信号s(t)加入零均值的白噪声:
| ${x^i}\left( t \right) = s\left( t \right) + {\xi _0}{n^i}\left( t \right).$ | (1) |
式中:ni(t)为第i次添加的白噪声, i=1, 2, …, N, N为集总分解次数;ξ0为添加白噪声的幅值.
2) 对含噪信号xi(t)进行上述EMD分解得到:
| $s\left( t \right) + {\xi _0}{n^i}\left( t \right)\xrightarrow{{{\text{EMD}}}}\sum\limits_{j = 1}^M {c_j^i\left( t \right) + {r^i}\left( t \right).} $ | (2) |
式中:cji(t)为第i次集总分解得到的第j阶IMF分量, j=1, 2, …, M, ri(t)为分解的剩余分量.
3) 重复步骤1) 和2) 进行N次分解, 每次分解添加不同的幅值白噪声, 对分解得到的IMF进行集总平均, 作为EEMD最终分解的第j个IMF分量:
| $\overline {{c_j}\left( t \right)} = \frac{1}{N}\sum\limits_{j = 1}^M {c_j^i\left( t \right).} $ | (3) |
对于EEMD方法而言, 2个加噪参数(加噪幅值和集总分解次数)需要预先人为确定.Wu等[13]给出了2个参数之间的关系公式:
| $\varepsilon = \frac{A}{{\sqrt N }}.$ | (4) |
式中:A为加噪幅值;N为集总分解次数;ε为分解的标准误差.
分析式(4) 可知, 加噪幅值A与分解误差ε成正比, A越小, 可以获得越小的分解误差, 分解结果更为精确.然而, 一方面,如果A太小, 噪声振动微弱难以改变信号极值点的分布, EEMD方法弱化成EMD方法,无法达到消除模态混叠作用;另一方面, 如果A过大, 分解误差随之增大, 且噪声振动过于剧烈, 使得信号极值均匀分布受到破坏, 信号极值点均由噪声诱发, 产生残余噪声和过多的剩余分量.虽然可以通过增加集总分解次数N消除残余噪声和剩余分量的影响, 但N的增加往往会增加算法的计算量.Wu等[13]通过大量的实验建议:A一般取0.1~0.2 SD(SD表示原始信号标准差), N一般为数百次.但这种经验参数并不适合所有非线性非稳态信号的处理.因此, 如何折中选择上述加噪参数, 使分解性能达到最优, 在消除模态混叠效应的基础上进一步减少计算量体现了算法的优越性.
2.1.1 加噪频率确定通过上述分析可以看出, EEMD方法消除模态混叠效应的原理是通过选择合适的噪声改变原始信号的极值点分布,使其趋于均匀, 利用噪声频率分布均匀特性, 使得原始信号相应成分自动映射到由噪声构建的均匀分布的尺度中, 从而消除模态混叠[16].噪声的频率f分布和极值点特性直接决定了分解效果.针对非线性非稳态信号和噪声而言, 信号的频率间接表示为极值点密度,即频率越高, 极值点密度就越高;反之亦然.因此可以推断高频噪声比低频噪声对极值点分布的改善效果更为明显.
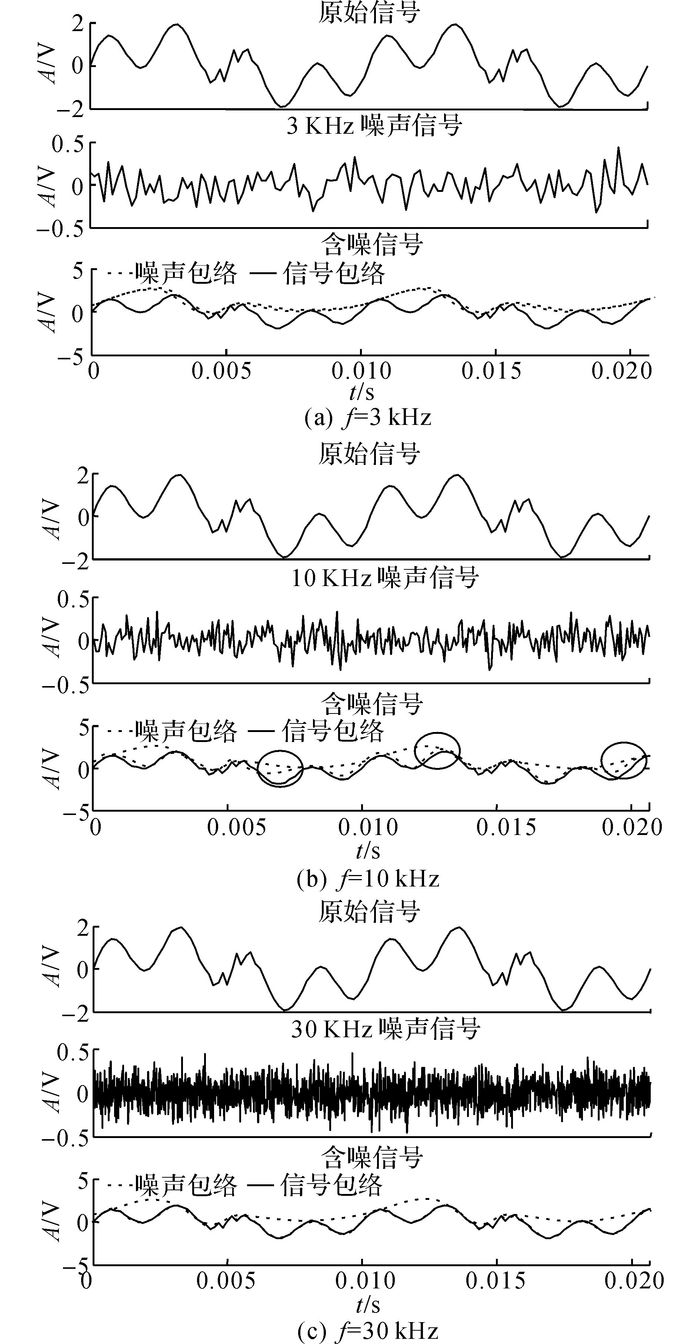
如图 1所示为不同频率的噪声对原始信号极值点分布的影响.分析图 1可以看出, 图 1(a)中原始含噪信号构建的包络与噪声信号包络近乎重合, 表明噪声信号的加入未能改变原始信号极值点的分布, 对消除模态混叠效应作用不是很大;图 1(b)中随着噪声频率增加, 含噪信号极值点分布有了明显改变, 噪声包络逐渐趋于拟合含噪信号, 但拟合程度不高,存在拟合过冲和欠冲现象;图 1(c)中随着加噪频率进一步增加, 含噪信号极值点分布改进更为显著, 所有的含噪信号被噪声包络所包裹拟合, 使含噪信号全部映射到噪声构建的均匀分布尺度中, 表明高密度的噪声信号对原始信号极值点分布改善效果更为明显,更有利于消除模态混叠现象.可以得出,不同的加噪频率对极值点均匀分布特性的影响存在差异, 加噪频率越高, 极值点分布越趋于均匀, 越能取得良好的分解效果.
|
图 1 不同频率噪声下的极值点分布特性(0.1 SD) Fig. 1 Distribution characteristics of extreme points under different frequency noises (0.1 SD) |
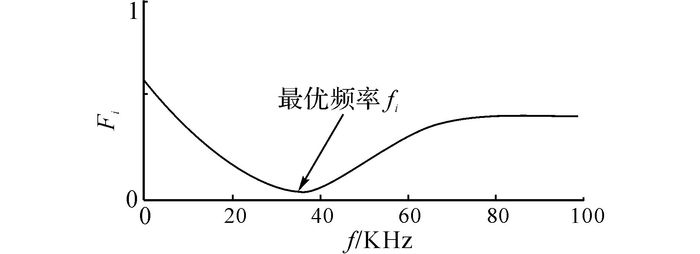
虽然高频噪声相对于低频噪声的性能优势明显, 但加噪频率并不是越高越有效.为了进一步分析极值点分布特征与加噪频率之间的关系, 引入极值点间距标准差作为评价参数[17].当极值点间距变化较小时, 表明波动程度小, 极值分布较均匀;反之亦然.间距差的波动程度可以采用标准差来衡量, 即极值点之间的标准差可以反映极值点均匀分布的情况.因此, 通过改变加入不同频率的白噪声, 采用式(5) 计算极大值和极小值点间的标准差Dmax和Dmin, 通过目标优化参数Fi可自适应确定噪声的优化频率, 自适应加噪频率优化过程如图 2所示.
|
图 2 自适应频率优化过程 Fig. 2 Optimization process of adaptive frequency |
| $\left. \begin{array}{l} {D_{\max }} = {S_{\max }}\left( {l + 1} \right) - {S_{\max }}\left( l \right);\\ {D_{\min }} = {S_{\min }}\left( {k + 1} \right) - {S_{\min }}\left( k \right);\\ {F_i} = \sqrt {D_{\max }^2 + D_{\min }^2} . \end{array} \right\}$ | (5) |
式中:S为标准差计算公式, l=1, 2, …, p, k=1, 2, …, q, l为极大值个数, k为极小值个数.
由图 2可知, 当加噪频率逐渐增大时, 参数Fi随之减小, 说明极值点分布越发趋于均匀;当加噪频率增加到一定程度时, 此时噪声频率破坏了极值点分布的均匀程度, 导致原始信号极值点均被噪声淹没, 极值点间距差变大, Fi呈现增加趋势, 直到趋于稳定.因此, 自适应优化过程的极小值点为所求的最优噪声频率fi.
2.1.2 集总平均次数的确定EEMD方法中分解通过集总次数N的平均来消除, 具体原理分析如下.由于EMD方法的分解完备性特征[18], 式(2) 亦可表达为
| $s\left( t \right) + {\xi _0}{n^i}\left( t \right) = \sum\limits_{j = 1}^M {c_j^i\left( t \right) + {r^i}\left( t \right).} $ | (6) |
将式(3) 最终的分解结果代入式(6) 可得:
| $s\left( t \right) = \sum\limits_{j = 1}^M {\overline {{c_j}\left( t \right)} + \overline {r\left( t \right)} } - \frac{1}{N}\sum\limits_{i = 1}^N {{\xi _0}{n^i}\left( t \right)} .$ | (7) |
式中:
由重构信号定义[19]可知, 将
| $s\left( t \right) = \sum\limits_{j = 1}^M {\overline {{c_j}\left( t \right)} + \overline {r\left( t \right)} } .$ | (8) |
对比式(8) 和(7) 可以发现, EEMD方法分解的重构误差为
| ${R_{{\rm{EEMD}}}}\left( t \right) = - \frac{1}{N}\sum\limits_{i = 1}^N {{\xi _0}{n^i}\left( t \right)} .$ | (9) |
REEMD(t)即为加噪信号存留在分解中的残余噪声, 并不是原始信号的固有成分.虽然根据白噪声的统计特性, 理论上通过增加N可以使得残余噪声减少, 但不断的集总平均使得计算量大幅增加.
在CEEMD方法中, 加噪方式采用正负成对的形式, 因此由同样的分析方法得到CEEMD的残余噪声为
| ${R_{{\rm{CEEMD}}}}\left( t \right) = - \frac{1}{N}\sum\limits_{i = 1}^{N/2} {\left[ {{\xi _0}{n^i}\left( t \right) + \left( { - {\xi _0}} \right){n^i}\left( t \right)} \right]} = 0.$ | (10) |
由式(10) 分析可以看出, 由于CEEMD加噪方式采用正负成对的白噪声, 正负相抵后残余噪声为零, 理论上不需要通过集总次数来消除残余噪声对分解结果的影响, 可以得出残余噪声大小与集总平均次数无关的结论.
为了进一步验证集总次数对分解性能的影响, 利用第3章中的仿真信号y(t), 通过对y(t)加入不同频率的噪声进行CEEMD分解, 计算不同集总次数下的Fi, 自适应寻求最优频率fi, 其中噪声幅值统一为0.1 SD, N对极值点分布影响如图 3所示.

|
图 3 集总分解次数对极值点分布影响 Fig. 3 Influence of ensemble decomposition trials on distribution of extreme points |
表 1列出了不同集总次数下的性能评价指标值, 表中RMSE为原始信号与重构信号间的均方根误差, 用来计算信号中的残余噪声大小.
| 表 1 不同集总次数性能评价指标值 Table 1 Evaluating indicator values in different trails |
分析图 3和表 1可知, 4次集总次数不同的实验, 都在fi=49.6 kHz时达到最优的极小值, 得到的极值点均匀分布参数Fi较为接近, 相互间的误差较小, 增加集总次数N对改善极值点分布的影响可以忽略不计.不同N值对应的残余噪声RMSE数量级都在10-15, 计算误差近似为0, 主要由计算机的计算运差造成.但不同N值下, 计算量存在明显差异, N=2时的计算耗时仅为N=150的计算耗时的1/65, 即通过减少集总次数N, 可以大幅降低计算量, 提高算法运算效率.
综上所述, 在满足获得残余噪声小、Fi近似相同的条件下, 为了进一步减少计算量, 理论上当集总分解次数为2时可以加快计算效率, 因此采用CEEMD正负成对的加噪方式, 固定N=2的分解方法.
2.1.3 加噪幅值确定为了保证良好的分解性能, 使得分解误差较小, 文献[13]规定式(4) 中, ε≤1%.EEMD方法通过加噪幅值A的大小来消除模态混叠, 且A不宜过大和过小.根据前文分析, 提出通过高频噪声来消除模态混叠效应, 采用正负加噪集总平均2次提高运算效率, 在消除模态混叠的同时进一步提高运算效率, 得出加噪幅值A与最终的残余噪声无关的结论.因此, 将ε=0.01、N=2代入式(4) 得到加噪幅值A=0.014, 即采用较小的加噪幅值, 为了进一步简化运算和获得较小的分解误差, 本文采用固定加噪幅值A=0.010的方式.
2.2 AFCEEMD方法基于上述分析, 本文提出AFCEEMD方法, 对于非平稳非线性信号s(t), AFCEEMD方法步骤如下:
1) 采用2.1.1节的方法确定最优加噪频率fi, 其中, 初始加噪频率fb=2fs(fs为信号的采样频率), 截止加噪频率一般取10~20fs, 即加入不同频率的噪声计算Fi, 寻求极小值对应的fi.为了提高计算效率, 对fb~fp进行频带划分:fb~6fs、6fs~8fs和8fs~fp, 对于6fs~8fs频带的加噪频率间隔为0.2fs Hz, 其余2个频带加噪间隔为0.5fs Hz.
2) 对原始信号s(t)加入一对正负白噪声[n(t), -n(t)]得到一组含噪信号[P(t), -N(t)]:
| $P\left( t \right) = s\left( t \right) + n\left( t \right),N\left( t \right) = s\left( t \right) - n\left( t \right).$ | (11) |
式中:噪声±n(t)幅值固定为0.01 SD.
3) 对含噪信号[P(t), -N(t)]分别进行EMD分解, 得到一系列IMF分量与剩余分量:
| $\left. \begin{array}{l} P\left( t \right) = \sum\limits_{j = 1}^M {c_j^ + \left( t \right) + r_m^ + \left( t \right)} ,\\ N\left( t \right) = \sum\limits_{j = 1}^M {c_j^ - \left( t \right) + r_m^ - \left( t \right)} . \end{array} \right\}$ | (12) |
式中:cj+(t)与cj-(t)分别为加入噪声+n(t)与-n(t)对应的第j阶IMF分量, rm+(t)与rm-(t)分别为相对应的剩余分量, M为分解产生得到的IMF个数.
4) 对所有的IMF分量进行2次集总平均得到:
| ${c_j}\left( t \right) = \frac{1}{2}\left[ {c_j^ + \left( t \right) + c_j^ - \left( t \right)} \right].$ | (13) |
式中:cj(t)(j=1, 2, …, M)为AFCEEMD分解得到的最终的第j阶IMF分量, 完成整个分解工作.
3 仿真实验分析为了验证AFCEEMD方法的有效性, 采用复合扰动仿真信号进行仿真验证:
| $\left. \begin{array}{l} y\left( t \right) = {y_1}\left( t \right) + {y_2}\left( t \right) + {y_3}\left( t \right);\\ {y_1}\left( t \right) = 0.5\sin \left( {2{\rm{\pi }}{f_2}t} \right)\left[ {\exp \left( { - \frac{1}{\tau }{{\left( {t - 0.005} \right)}^2}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\exp \left( { - \frac{1}{\tau }{{\left( {t - 0.015} \right)}^2}} \right)} \right];\\ {y_2}\left( t \right) = \sin \left( {2{\rm{\pi }}{f_1}t} \right);\\ {y_3}\left( t \right) = \sin \left( {2{\rm{\pi }}{f_0}t} \right). \end{array} \right\}$ | (14) |
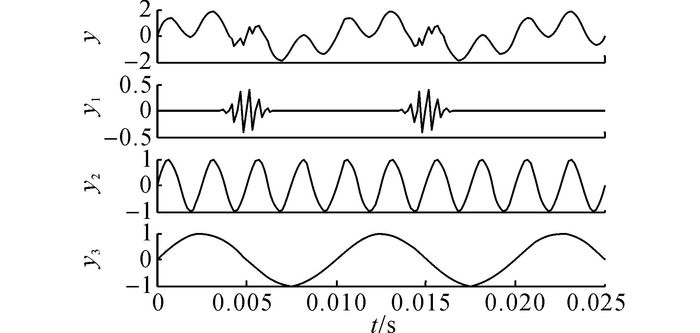
式中:y2(t)和y3(t)为正常的正弦信号, y1(t)为间断扰动信号, f0=100 Hz、f1=400 Hz、f2=2 000 Hz、τ=6×10-7s, 采样频率为8 kHz, 采用时长为0.025 s.仿真信号时域波形如图 4所示.
|
图 4 仿真信号时域波形图 Fig. 4 Time domain waveforms of simulation signals |
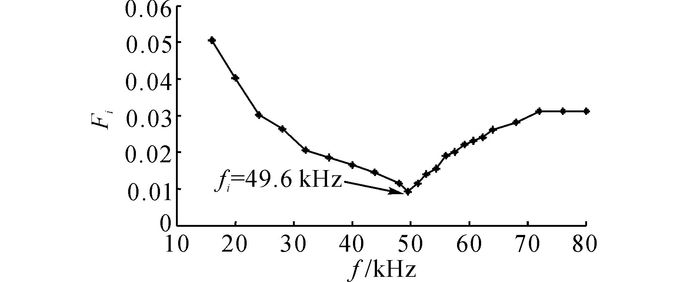
通过对y(t)加入不同频率噪声计算Fi参数求得fi, 其中fb=2fs=16 kHz, fp=80 kHz, 噪声幅值A=0.01 SD.自适应优化频率过程如图 5所示.图 5中Fi先减少再逐渐增大最后趋于稳定, 当Fi达到最小值0.008 92时, 求得最优频率fi=49.6 kHz.
|
图 5 仿真信号最优频率求解过程 Fig. 5 Optimal frequency solution process of simulationsignal |
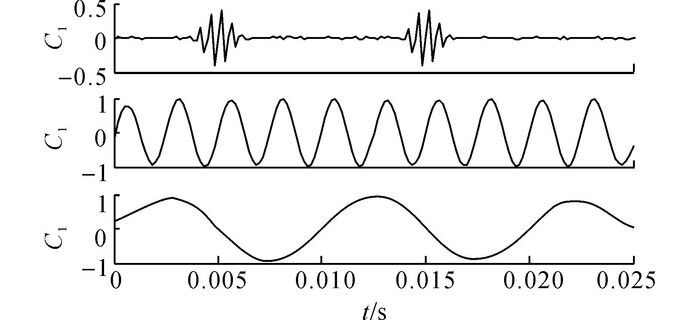
采用AFCEEMD方法对仿真信号进行分解, 其中加噪参数设置如下:fi=49.6 kHz、A=0.01 SD、N=2, 分解结果如图 6所示.
|
图 6 自适应快速互补集总经验模态分解(AFCEEMD)方法的信号分解结果 Fig. 6 Signal decomposition result derived by adaptively fast complementary ensemble empirical modedecomposition (AFCEEMD) method |
为了证实选择高频加噪方式在最优加噪频率时的分解效果, 采用式(15) 和(16) 相关系数和正交系数[20]去衡量不同频率下AFCEEMD方法分解性能:
| $C = \frac{{\sum\nolimits_{i = 1}^N {\left[ {\left( {{p_i} - \bar p} \right)\left( {q - \bar q} \right)} \right]} }}{{\sqrt {\sum\nolimits_{i = 1}^N {{{\left( {{p_i} - \bar p} \right)}^2}} } \sqrt {\sum\nolimits_{i = 1}^N {{{\left( {{q_i} - \bar q} \right)}^2}} } }}.$ | (15) |
式中:p、q分别为信号pi和qi的均值, i=1, 2, …, N.
| $O = \sum\limits_{t = 0}^T {\left( {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^n {\frac{{{I_j}\left( t \right){I_k}\left( t \right)}}{{{y^2}\left( t \right)}}} } } \right)} .$ | (16) |
式中:y(t)表示原始信号, Ik(t)为IMF分量成分, Ij(t)为剩余分量.
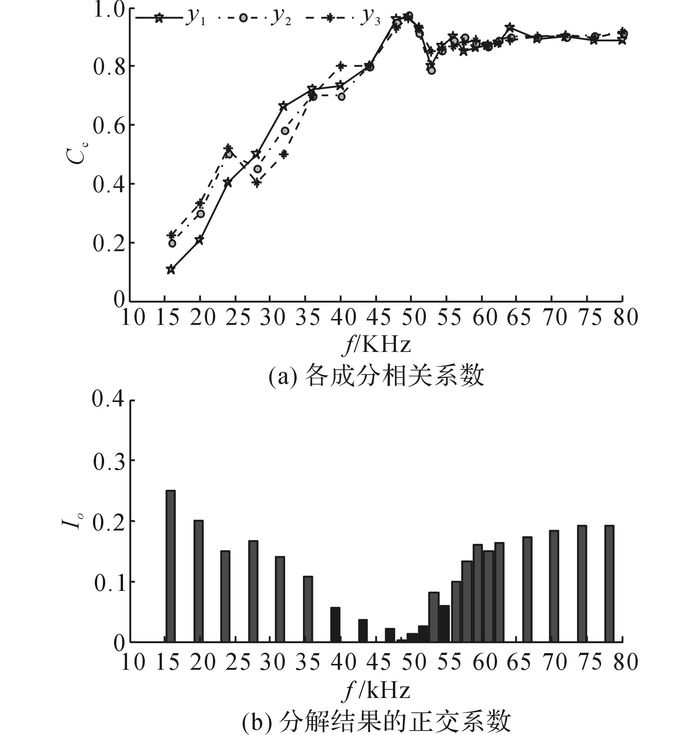
C测试真实信号与分解线号的相关性, C越高表明分解成分越精确, O用来检验分解方法各分量的正交性, O越低表明分解结果频率混叠越小.图 7表示不同频率下C与O的具体值.
|
图 7 不同频率下AFCEEMD分解性能对比 Fig. 7 Comparison of decomposition performance by AFCEEMD method under different frequencies |
结合图 6和图 7分析可以得出:图 6直观反应出AFCEEMD分解性能较好, 各分量成分能准确的分解得到对应的IMF分量, 不存在模态混叠效应和虚假分量成分.图 7通过比较不同频率下的分解结果的C与O值, 当频率都为49.6 kHz时, 分解结果得到最大的相关系数和最小的正交系数, 验证了通过Fi搜寻最优高频加噪方法的有效性.
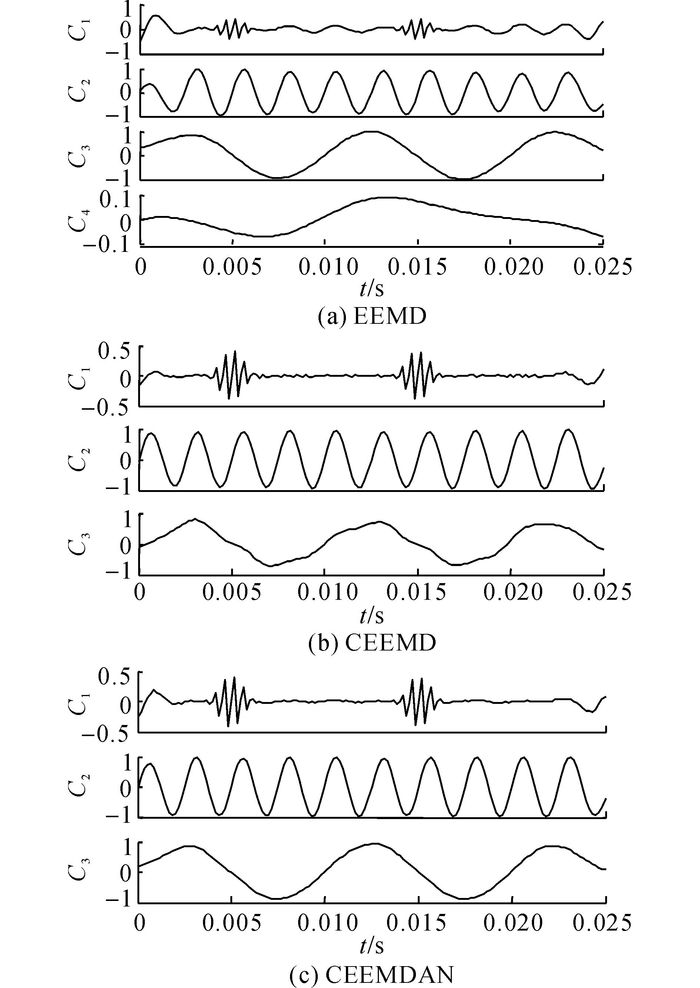
将AFCEEMD与前文所提的EEMD、CEEMD与CEEMDAN加噪辅助方法进行综合比较, 各方法加噪幅值统一设定为0.2 SD, 集总分解次数统一为150.各方法对y(t)的分解结果如图 8所示.
|
图 8 不同经验模态分解(EMD)改进方法信号分解结果 Fig. 8 Decomposition results of signal in differentimproved empirical mode decomposition (EMD)methods |
结合图 6和图 8中各方法的分解结果可以看出, 总体而言, 各方法都能实现对高频间断信号和低频分量的频带分离, 但基于经验性参数选择的3种方法分解效果稍逊, 尤其是对高频间断分量C1分解时出现了模态混叠效应和端点现象, 其中EEMD方法分解得到了虚假分量C4, 而本文方法分解的结果更加清晰和准确.
为了进一步量化分解效果, 4种方法的分解性能指标参数表 2所示.其中, 耗时指标为上述4种方法在配置为4 G内存、2.4 GHz双核CPU笔记本及Matlab2014a运行环境中重复进行50次实验所消耗时间的平均值.
| 表 2 不同经验模态分解(EMD)方法性能评价指标值 Table 2 Evaluating indicator values of different empirical mode decomposition (EMD) methods |
如图 9所示为4种方法分解的残余噪声结果, ε为残余噪声误差,又叫重构误差.通过对表 1和图 9对比分析可知, 本文所提方法可以获得较高的相关系数和较低的正交系数, 充分验证分解性能的精确性;加噪方法采用正负成对的形式, 在分解过程中相互抵消残余噪声的影响, 表明本文方法在分解过程中的完备性.本文方法的计算时间较之其他方法大为减少, 计算性能有了显著的提高.

|
图 9 各经验模态分解改进方法分解结果残余噪声对比 Fig. 9 Contrast of decomposition results residual noise derived by different improved EMD methods |
为了验证本文所提方法的实际检测性能, 在仿真测试的基础上, 搭建电能质量扰动实验平台, 采集真实电能质量扰动数据进行验证, 电能质量扰动实验平台如图 10所示.平台主要实验装置包括:负载电阻(100 Ω、1 000 W)、投切电容(47 μF)、单相整流桥(输入电压220 V、直流输出电流10 A)、交流调压器(1 000 W)、交流电机(220 V、400 W)、DSP控制器(TMS320F28335)、继电器组、示波器和Fluke435电能质量测试仪等.

|
图 10 电能质量扰动实验平台 Fig. 10 Experiment platform of power quality disturbance |
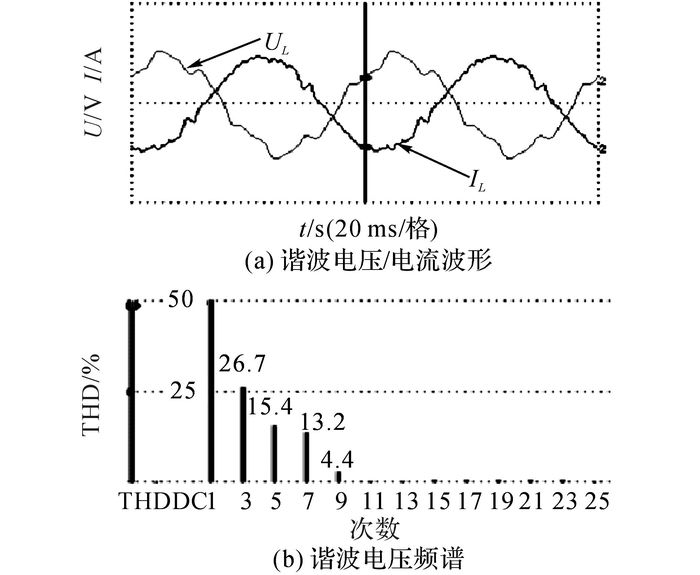
设计整流桥与电容投切的稳态扰动实验, 通过DSP控制器控制继电器组, 在t0时刻投入整流桥与电容, 使得整流桥与电容和负载电阻形成串联电路.在t1时刻切除, 实验中交流调压器原副边变比为4:1, 利用Fluke435对负载侧进行检测, 采样频率为15 kHz, 测得t0~t1时刻实际总电压电流波形、电压频谱含量如图 11(a)、(b)所示.图中,IL为负载电流,UL为负载电压.
|
图 11 稳态扰动实验谐波检测结果 Fig. 11 Harmonics test results of steady state disturbance |
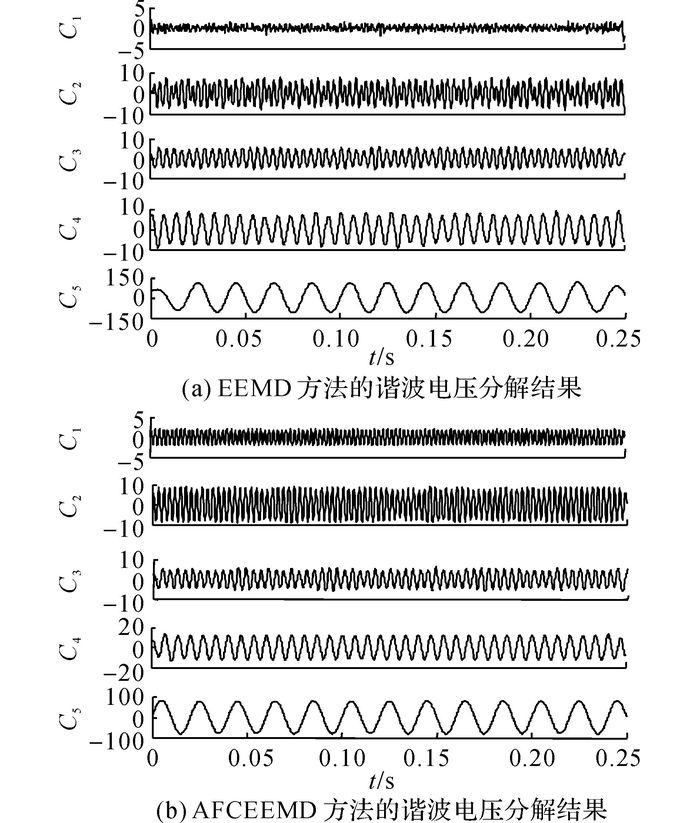
分析图 11可知, Fluke检测到1~9次奇次谐波含量, 3次、5次和7次谐波含量较高, 总谐波畸变率(THD)达到26.7%、15.4%和13.2%, 9次含量相对较少.将实测数据导入Matlab通过EEMD和AFCEEMD方法检测分析, 这2种方法的谐波分解结果如图 12(a)、(b)所示.
|
图 12 EEMD方法与AFCEEMD方法的谐波分解结果 Fig. 12 Harmonic decomposition results derived byEEMD method and AFCEEMD method |
由图 12分解结果直观上可以得出, AFCEEMD方法的谐波分解效果优于EEMD方法, 各次谐波含量能准确分解得到对应的IMF分量, 而EEMD方法得到C1与C2模态分量扰动较大存在模态混叠效应.为了进一步分析频率和幅值特征参数检测结果, 将EEMD方法与AFCEEMD方法分解得到的IMF分量进行Hilbert变换[21]得到具体检测值, 并与Fluke实测结果进行对比分析, 如表 3所示为频率与幅值的具体检测结果.
| 表 3 稳态扰动特征参数检测结果 Table 3 Detection results of characteristic parameters of steady state perturbation |
由表 3检测结果可知, AFCEEMD方法对2个特征参数的检测效果与Fluke仪器检测效果相仿, 而EEMD方法由于分解存在明显的模态混叠效应, C1与C2还检测到432.78 Hz、321.47 Hz的间谐波分量, 特征提取参数精确度逊于其他2种方式.
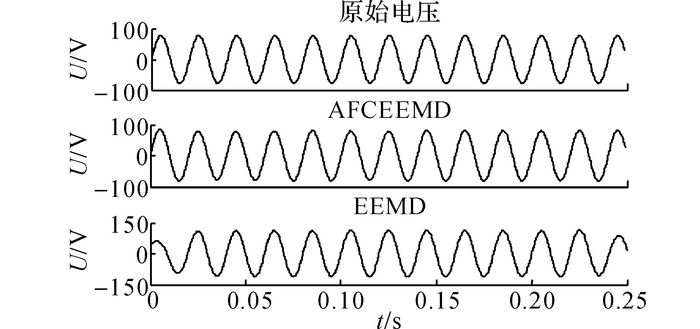
为了具体比较检测结果与实际电压偏差程度, 单独对基波分量分析研究, 图 13为当交流调压器变比为4:1时,不进行投切时的原始电压波形图以及由EEMD方法与AFCEEMD方法分解得到的基波电压波形图.图 13表明, 实测原始电压波形较为标准, 电压范围为-76.82~77.78 V, AFCEEMD方法基波分解波形电压波动范围为-78.66~79.35 V, 基波分解波形更稳定、精确, 偏离范围较小, 而EEMD方法基波电压偏差较大, 电压波形范围为-56.78~68.76 V.
|
图 13 EEMD方法的与AFCEEMD方法的基波分量电压波形 Fig. 13 Fundamental component voltage waveforms byEEMD method and AFCEEMD method |
如表 4所示为各方法检测的频率和幅值与国标工频电压的偏差结果, 为了便于和标准电压有效值220 V进行对比,将Fluke、EEMD以及AFCEEMD所得结果乘以交流调压器变化(4:1),统一转换成原边电压有效值.分析表 4可以得出, 采用Fluke与AFCEEMD方法检测的频率与电压有效值满足国家工频电压偏离标准(频率偏差为±1%, 电压偏差为-10%~7%).EEMD方法检测结果偏差较大, 频率与电压偏差分别为2.62%、-16.10%.
| 表 4 EEMD方法与AFCEEMD方法基波分量分析指标 Table 4 Analysis index of fundamental component by EEMD method and AFCEEMD method |
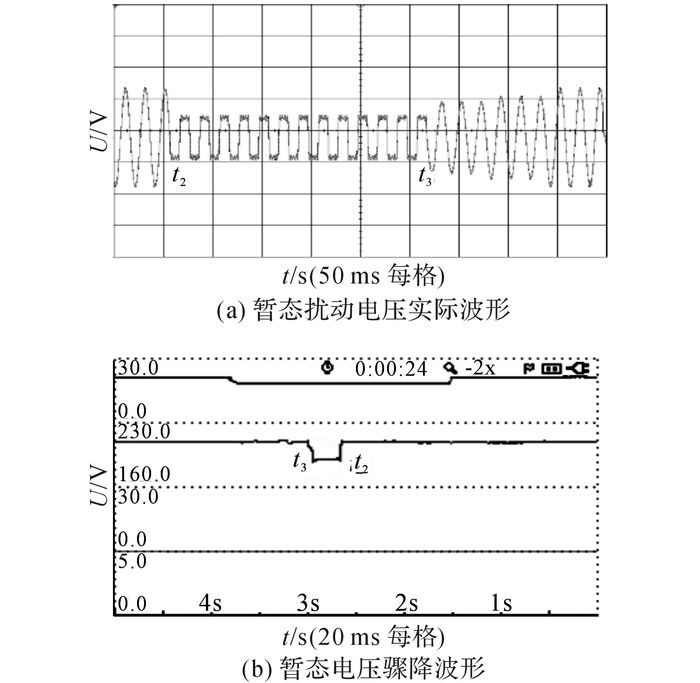
设计交流电机和整流桥投切的暂态扰动实验, 同样通过DSP控制器控制继电器组和电机驱动模块, 在t2时刻投入整流桥与交流电机, 使得电机与整流桥和负载电阻形成并联电路.在t3时刻切除, 实验中交流调压器原副边变比为1:1, 利用示波仪和Fluke435对负载侧进行检测, 采样频率都设置为15 kHz, 测得实际暂态总电压波形、电压幅值骤降波形如图 14(a)、(b)所示.
|
图 14 暂态扰动实验电压骤降检测结果 Fig. 14 Voltage sag test results of steady transient disturbance |
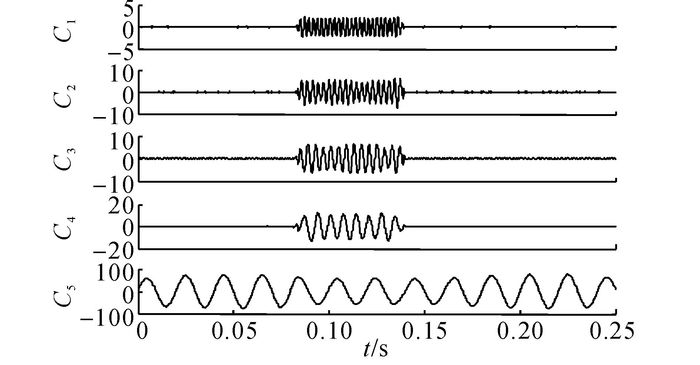
可知, AFCEEMD方法对含有谐波的暂态扰动采取同样的分析方法, 将实测数据运用AFCEEMD方法进行分解, 分解结果如图 15所示.问题, 可以准确分解出各个有效成分, C1~C4为奇次谐波含量, C5为基波成分, 分解效果较为准确.同样, 为了验证算法对暂态扰动的检测效果, 仅将基波分量C5进行Hilbert变换得到扰动瞬时幅值.为了进行检测效果对比, 图 16给出了EEMD采取同样方法的瞬时幅值检测曲线以及将Fluke检测数据导入后绘制的瞬时幅值扰动曲线, 其中时间点采取统一起始点归零化处理.
|
图 15 暂态扰动AFCEEMD分解结果 Fig. 15 Decomposition results of transient disturbance derived by AFCEEMD method |

|
图 16 暂态扰动电压幅值检测结果对比 Fig. 16 Contrast of voltage amplitude detection results of transient disturbance |
通过图 16可知, AFCEEMD方法对暂态扰动跟踪响应性能与Fluke仪器检测性能相当, 扰动时间点定位误差相对较小(3.53%、0.06%), Fluke检测的骤降幅度为0.071 pu, AFCEEMD方法的骤降幅度为0.070 pu, EEMD方法相对Fluke扰动点定位误差为4.5%、3.6%, 跟踪响应性能满足暂态扰动检测要求, 但对瞬时幅值检测误差依旧较大, 骤降幅度达到0.074 pu.
5 结语本文提出的自适应快速互补集总经验模态分解(AFCEEMD)方法解决了EEMD方法分解自适应性不足以及计算效率低的缺点.仿真信号表明,AFCEEMD方法能比现有的噪声辅助分解方法更好地抑制模态混叠效应,使分解残余噪声大幅降低且计算效率有了明显提高.将AFCEEMD方法应用于电能质量扰动检测中, 可以有效地实现对稳态扰动频率、幅值的准确识别以及对暂态扰动时刻、扰动幅值的精确提取,验证了所提方法的有效性和实用性.
尽管如此, AFCEEMD方法也只是一种改进的噪声辅助分解方法, 并未对EMD方法本身进行改进研究, EMD方法采取2次样条插值方式计算耗时依旧过大,分解迭代次数较多, 这将在下一步研究中进行分析与改进.
| [1] |
徐永海, 赵燕. 基于短时傅里叶变换的电能质量扰动识别与采用奇异值分解的扰动时间定位[J].
电网技术, 2011, 35(8): 174–180.
XU Yong-hai, ZHAO Yan. Identification of power quality disturbance based on short-term fourier transform and disturbance time orientation by singular valuedecomposition[J]. Power System Technology, 2011, 35(8): 174–180. |
| [2] |
赵凤展, 杨仁刚. 基于短时傅里叶变换的电压暂降扰动检测[J].
中国电机工程学报, 2007, 7(10): 28–34.
ZHAO Feng-zhan, YANG Ren-gang. Voltage sag disturbance detection based on short time fourier transform[J]. Proceedings of the CSEE, 2007, 7(10): 28–34. DOI:10.3321/j.issn:0258-8013.2007.10.005 |
| [3] | MAHELA O P, SHAIK A G, GUPTA N. A critical review of detection and classification of power qualityevents[J]. Renewable and Sustainable Energy Reviews, 2015, 41(C): 4954–505. |
| [4] | THIRUMALA K, UMARIKAR A C, JAIN T. Estimation of single-phase and three-phase power-quality indices using empirical wavelet transform[J]. IEEE Transactions on Power Delivery, 2015, 30(1): 445–454. DOI:10.1109/TPWRD.2014.2355296 |
| [5] | DE YONG D, BHOWMIK S, MAGNAGO F. An effective power quality classifier using wavelet transform and support vector machines[J]. Expert Systems with Applications, 2015, 42(15): 6075–6081. |
| [6] |
李涛, 夏浪, 张宇, 等. 基于提升复小波的暂态电能质量扰动的检测与定位[J].
中国电机工程学报, 2011, 31(25): 66–72.
LI Tao, XIA Lang, ZHANG Yu, et al. Detection and localization of power quality transient disturbances based on lifting complex wavelet[J]. Proceedings of the CSEE, 2011, 31(25): 66–72. |
| [7] |
张志禹, 满蔚仕, 郗垒, 等. 快速S变换在电能质量分析中的应用[J].
电网技术, 2013, 37(5): 1285–1290.
ZHANG Zhi-yu, MAN Wei-shi, XI Lei, et al. Application of fast S-transform in power quality analysis[J]. Power System Technology, 2013, 37(5): 1285–1290. |
| [8] |
徐方维, 杨洪耕, 叶茂清, 等. 基于改进S变换的电能质量扰动分类[J].
中国电机工程学报, 2012, 32(4): 77–84.
XU Fang-wei, YANG Hong-geng, YE Mao-qing, et al. Classification for power quality short duration disturbances based on generalized S-transform[J]. Proceedings of the CSEE, 2012, 32(4): 77–84. |
| [9] | XIAO X, XU F, YANG H. Short duration disturbance classifying based on s-transform maximum similarity[J]. International Journal of Electrical Power and Energy Systems, 2009, 31(7/8): 374–378. |
| [10] | MANDIC D P, REHMAN N U, WU Z, et al. Empirical mode decomposition-based time-frequency analysis of multivariate signals:the power of adaptive data analysis[J]. IEEE Signal Processing Magazine, 2013, 30(6): 74–86. DOI:10.1109/MSP.2013.2267931 |
| [11] | NORDEN E H, THOMAS Y H. Adaptive data analysis:theory and applications[J]. Philosophical Transactions of the Royal Society A-Mathematical Physical and Engineering Sciences, 2016, 20(12): 141–151. |
| [12] |
汤宝平, 董绍江, 马靖华. 基于独立分量分析的EMD模态混叠消除方法研究[J].
仪器仪表学报, 2012, 33(7): 1477–1482.
TANG Bao-ping, DONG Shao-jiang, MA Jing-hua. Study on the method for eliminating mode mixing of empirical mode decomposition based on independent component analysis[J]. Chinese Journal of Scientific Instrument, 2012, 33(7): 1477–1482. |
| [13] | WU Z, HUANG N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2011, 1(1): 1–41. |
| [14] | YEH J R, SHIEH J S, HUANG N E. Complementary ensemble empirical mode decomposition:a novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135–156. DOI:10.1142/S1793536910000422 |
| [15] | TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[J]. Brain Research Bulletin, 2011, 125(3): 4144–4147. |
| [16] | LEI Y, LI N, LIN J, et al. Fault diagnosis of rotating machinery based on an adaptive ensemble empirical mode decomposition[J]. Sensors, 2013, 13(12): 16950–16964. DOI:10.3390/s131216950 |
| [17] |
孔德同, 刘庆超, 雷亚国, 等. 一种改进的EEMD方法及其应用研究[J].
振动工程学报, 2015, 28(6): 1015–1021.
KONG De-tong, LIU Qing-chao, LEI Ya-guo, et al. The improved EEMD method and its application[J]. Journal of Vibration Engineering, 2015, 28(6): 1015–1021. |
| [18] | HUANG W, CAI N, XIE W, et al. ECG baseline wander correction based on ensemble empirical mode decomposition with complementary adaptive noise[J]. Journal of Medical Imaging and Health Informatics, 2015, 5(8): 1796–1799. DOI:10.1166/jmihi.2015.1647 |
| [19] |
王学伟, 王琳, 苗桂君, 等. 暂态和短时电能质量扰动信号压缩采样与重构方法[J].
电网技术, 2012, 36(3): 191–196.
WANG Xue-wei, WANG Lin, MIAO Gui-jun, et al. An approach for compressible sampling and reconstruction of transient and short-time power quality disturbance signals[J]. Power System Technology, 2012, 36(3): 191–196. |
| [20] | ZHENG J, CHENG J, YANG Y. Partly ensemble empirical mode decomposition:an improved noise-assisted method for eliminating mode mixing[J]. Signal Processing, 2014, 9(6): 362–374. |
| [21] |
李天云, 程思勇, 杨梅. 基于希尔伯特-黄变换的电力系统谐波分析[J].
中国电机工程学报, 2008, 28(4): 109–113.
LI Tian-yun, CHENG Si-yong, YANG Mei. Power system harmonic analysis based on hilbert-huang transform[J]. Proceedings of the CSEE, 2008, 28(4): 109–113. |


