大型立式圆筒形储罐通常由不同厚度或相同厚度的多层壁板焊接而成, 各层壁板厚度与储罐内径的比值很小, 属于典型的薄壁结构[1-2].作为国家战略石油储备库的关键设备, 储罐通常建造于沿海软土地基, 在不均匀的土壤沉积和非均匀分布外载荷作用下, 罐壁底部极易产生沉降[3-4].根据顶部的结构形式, 储罐主要分为固定顶和浮顶2种类型, 浮顶储罐的浮盘随着罐内储液量的变化上下浮动.储罐在底部沉降作用下会发生变形, 当变形逐渐增大时, 可能引起浮盘和罐壁之间密封装置的失效, 造成浮盘出现卡盘现象, 无法继续正常工作[5-6].以往有限元模拟方法较多地被应用在对储罐变形的研究上[7-10], 但这样既耗费计算成本, 而且针对每一个储罐, 都需要进行单独分析, 缺乏统一的评判标准.Kamyab等[5]采用理论方法, 利用不可延展性理论推导储罐的径向位移, 但该理论的前提假设是抗风圈不会对储罐的径向位移产生影响.然而在储罐的实际变形过程中, 顶部抗风圈会对储罐的变形产生很大的影响, 限制储罐顶部的径向位移.在薄膜理论中, Kamyab等[5]考虑了抗风圈的影响, 基于无限长圆柱壳中间设置若干环梁的情况, 计算切向剪应力下环梁处的径向位移, 但并不是针对储罐在沉降下变形的研究.
实测得到的沉降数据, 记录的是储罐底部沿圆周方向有限个离散点的沉降情况, 需要采用傅里叶级数展开方法, 推导出沿储罐底部连续分布的沉降表达式.该沉降表达式由3部分组成:阶数为0的整体均匀沉降、阶数为1的整体倾斜沉降、阶数大于1的不均匀沉降[11].整体均匀沉降分量和整体刚性倾斜分量默认储罐只发生刚体下沉和旋转, 内部储液有可能对发生刚性倾斜的储罐产生一定的应力和变形影响, 但这种影响十分微小, 可以忽略不计[5].尽管沿储罐底部圆周方向的不均匀沉降幅值相对较小, 仍会引起储罐产生明显的变形, 危害储罐的安全稳定性[3, 12].
本文基于实测沉降数据, 研究储罐在不均匀沉降作用下的变形响应.采用薄膜理论, 针对未设置抗风圈的储罐, 推导其在沉降作用下的径向位移表达式.以该理论表达式为基础, 采用双指数衰减函数拟合法, 研究具有不同结构形式、不同尺寸抗风圈的储罐, 在不均匀沉降作用下的变形情况, 推导用于计算具有抗风圈的储罐在不均匀沉降作用下的径向位移理论公式, 并采用数值模拟方法与理论公式进行比较和验证.
1 不均匀沉降下储罐径向位移公式储罐属于典型的薄壁圆柱壳结构, 在受底部沉降作用而产生变形的过程中, 可以忽略弯曲应力的影响.储罐在沉降作用下的平衡方程为
| $\left. \begin{array}{l} {N_\varphi } - {p_r}r = 0,\\ \frac{{\partial {N_{x\varphi }}}}{{\partial x}} + \frac{1}{r}\frac{{\partial {N_\varphi }}}{{\partial \varphi }} + {p_\varphi } = 0,\\ \frac{{\partial {N_x}}}{{\partial x}} + \frac{1}{r}\frac{{\partial {N_{x\varphi }}}}{{\partial \varphi }}{p_x} = 0 \end{array} \right\}$ | (1) |
式中:x为轴向坐标, φ为环向坐标, r为半径, Nx为轴向应力, Nφ为环向应力;Nxφ为剪应力;pr、pφ和px分别为各个方向的外力集中载荷.
通常, 储罐在沉降的初始阶段会产生弹性变形, 随着沉降的不断增大, 储罐的变形也会随之增大, 直至发生屈曲现象, 进而失去稳定性.作用于储罐底部的不均匀沉降是由不同阶数的谐波叠加而成, 因此在储罐的弹性变形阶段, 其径向位移可以通过不同阶数的谐波单独作用产生的径向位移值叠加得到.假设罐底部某一阶谐波表达式为
| $u = {u_n}\cos \left( {n\varphi } \right).$ |
式中:u为罐底部的沉降值, n为阶数, un为对应n阶的沉降幅值.
储罐底部相应的应力表示为
| ${N_x} = {N_n}\cos \left( {n\varphi } \right).$ |
式中:Nn为对应于n阶的应力幅值[5].
储罐在该谐波作用下的径向位移可以采用如下方法求得.对于储罐结构, 外力集中载荷主要指其自身和介质的重量, 与变形时产生的应力相比很小, 可以忽略不计, 即pr=pφ=px=0[12], 则式(1) 转化为
| $\left. \begin{array}{l} {N_\varphi } = 0,\\ {N_{x\varphi }} = {f_1}\left( \varphi \right),\\ {N_x} = - \frac{x}{r}\frac{{\partial {f_1}}}{{\partial \varphi }} + {f_2}\left( \varphi \right). \end{array} \right\}$ | (2) |
式中:f1(φ)和f2(φ)为关于参数φ的待定函数.
浮顶储罐顶部和底部的轴向应力边界条件为
| ${N_x} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{N_n}\cos \left( {n\varphi } \right),}\\ {0,} \end{array}}&\begin{array}{l} x = 0;\\ x = l. \end{array} \end{array}} \right.$ | (3) |
将式(3) 代入式(2) 求解得到各应力的表达式为
| $\left. \begin{array}{l} {N_\varphi } = 0,\\ {N_{x\varphi }} = \frac{{r{N_n}}}{{nl}}\sin \left( {n\varphi } \right),\\ {N_x} = {N_n}\left( {1 - \frac{x}{l}} \right)\cos \left( {n\varphi } \right). \end{array} \right\}$ | (4) |
圆柱壳的弹性本构方程为
| $\left. \begin{array}{l} \frac{{\partial u}}{{\partial x}} = \frac{1}{{E{t_c}}}\left( {{N_x} - v{N_\varphi }} \right),\\ \frac{{\partial v}}{{\partial x}} + \frac{1}{r}\frac{{\partial u}}{{\partial \varphi }} = \frac{{2\left( {1 + v} \right)}}{{E{t_c}}}{N_{x\varphi }},\\ \frac{w}{r} + \frac{1}{r}\frac{{\partial v}}{{\partial \varphi }} = \frac{1}{{E{t_c}}}\left( {{N_\varphi } - v{N_x}} \right). \end{array} \right\}$ | (5) |
式中:u为轴向位移, v为环向位移, w为径向位移, E为弹性模量, tc为圆柱壳的厚度.
储罐底部的位移边界条件如下:当x=0时, w=0, u=un·cos (nφ).结合边界条件, 将式(4) 代入式(5), 求解得到储罐在底部谐波作用下的位移表达式为
| $\left. \begin{array}{l} u = \frac{{{N_n}}}{{E{t_{\rm{c}}}}}\left( {x - \frac{{{x^2}}}{{2l}}} \right)\cos \left( {n\varphi } \right) + {u_n}\cos \left( {n\varphi } \right),\\ v = \frac{n}{r}\left[ {\frac{{{N_n}}}{{E{t_{\rm{c}}}}}\left( {\frac{{{x^2}}}{2} - \frac{{{x^3}}}{{6l}}} \right) + {u_n}x} \right]\sin \left( {n\varphi } \right) + \\ \;\;\;\;\;\;\;\frac{{2\left( {1 + v} \right)r{N_n}x}}{{nE{t_{\rm{c}}}l}}\sin \left( {n\varphi } \right) - \frac{{rv{N_n}}}{{nE{t_{\rm{c}}}}}\sin \left( {n\varphi } \right)\\ w = - \frac{{{n^2}}}{r}\left[ {\frac{{{N_n}}}{{E{t_{\rm{c}}}}}\left( {\frac{{{x^2}}}{2} - \frac{{{x^3}}}{{6l}}} \right) + {u_n}x} \right]\cos \left( {n\varphi } \right) - \\ \;\;\;\;\;\;\;\frac{{\left( {2 + v} \right)r{N_n}x}}{{E{t_{\rm{c}}}l}}\cos \left( {n\varphi } \right) \end{array} \right\}$ | (6) |
根据文献[13]的分析结果可知, 在底部谐波作用下, 储罐弹性变形阶段的轴向应力幅值Nn满足关系式Nn<<Et.化简式(6) 中的相关项, 得到储罐在谐波下的径向位移理论公式为
| $w = - \frac{{{n^2}}}{r}{u_n}x\cos \left( {n\varphi } \right).$ | (7) |
同理, 当储罐底部沉降表达式为u=u′nsin (nφ)时, 采用同样的推导方法求得对应的径向位移理论公式:
| $w=-\frac{{{n}^{2}}}{r}u_{n}^{'}x\sin \left( n\varphi \right)$ | (8) |
因此, 在底部不均匀沉降的作用下, 储罐的径向位移可以通过不均匀沉降表达式中的每一阶谐波产生的径向位移值叠加得到, 叠加后的表达式为
| $w=-\sum\limits_{n=2}^{{{n}_{\max }}}{\left\{ \frac{{{n}^{2}}}{r}x\left[ {{u}_{n}}\cos \left( n\varphi \right)+u_{n}^{'}\sin \left( n\varphi \right) \right] \right\}.}$ | (9) |
式中:nmax为不均匀沉降表达式中的最高阶数.该式即为用于计算储罐在不均匀沉降作用下的径向位移理论公式.
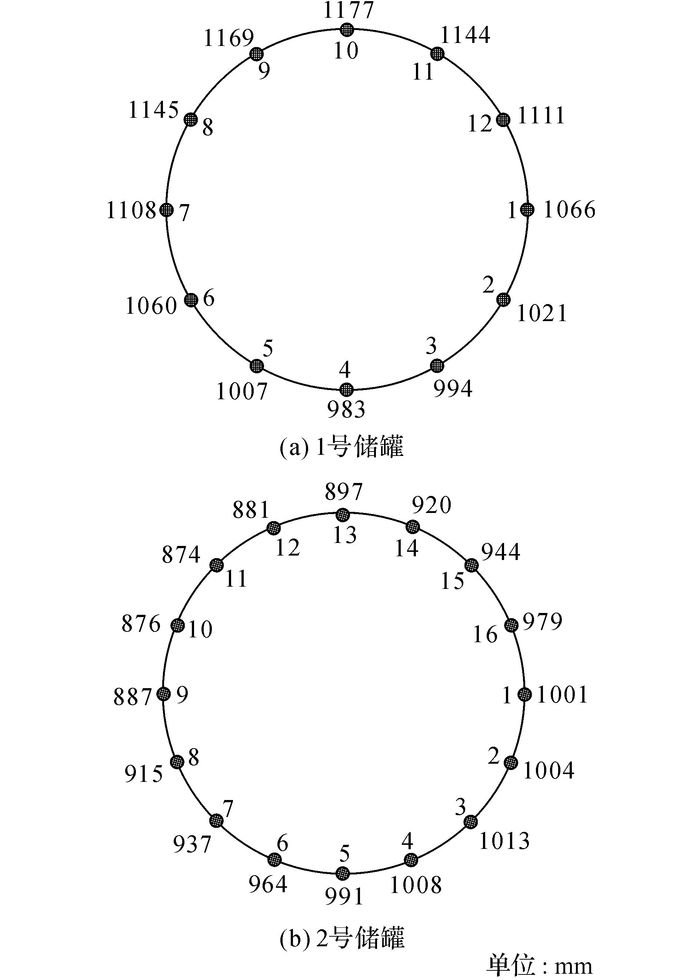
2 有限元分析与比较为了验证不均匀沉降下储罐径向位移理论公式的合理性和准确性, 采用有限元模拟方法对储罐在不均匀沉降作用下的变形进行分析和研究.分别选取3×104 m3和10×104 m3这2种不同容积的浮顶储罐, 分别定义为1号储罐和2号储罐, 基于实测得到的沉降数据, 研究储罐在不均匀沉降作用下的变形响应.储罐材料的弹性模量为206 GPa, 泊松比为0.3.其中,1号储罐内径为46 m, 罐壁总高度为19.35 m;2号储罐内径为80 m, 罐壁总高度为21.7 m.这2种储罐的罐壁结构参数如表 1所示, h为壁板高度, tw为壁板厚度, 底部的实测沉降数据如图 1所示.1号储罐的沉降数据源自宁波某检测机构对某地V2213号储罐实际检验监测结果, 2号储罐的沉降数据引自文献[12].
| 表 1 储罐结构参数 Table 1 Structure parameters of tank |
|
图 1 储罐底部的实测沉降数据 Fig. 1 Measured settlement data of tank bottom |
根据沉降的理论研究[14], 采用傅里叶级数展开的方法, 利用储罐底部各观测点的离散沉降值, 推导得到沿储罐底部连续分布的不均匀沉降表达式, 从而反映储罐的真实沉降情况.通过该方法推导得到的不均匀沉降表达式如式(10) 和(11) 所示, 分别对应于1号和2号储罐:
| $\begin{array}{l} u = 4.25{\rm{cos}}(2\varphi ) + 1.01{\rm{sin}}(2\varphi ) - 0.667{\rm{cos}}(3\varphi ) + \\ 3.167{\rm{sin}}(3\varphi ) + 1.417{\rm{cos}}(4\varphi ) - 2.454{\rm{sin}}(4\varphi ) + \\ 0.37{\rm{cos}}(5\varphi ) - 1.883{\rm{sin}}(5\varphi ) - 0.75{\rm{cos}}(6\varphi ). \end{array}$ | (10) |
| $\begin{array}{l} u = 0.088{\rm{cos}}(2\varphi ) - 0.045{\rm{sin}}(2\varphi ) + 0.944{\rm{cos}}(3\varphi ) - \\ 0.872{\rm{sin}}(3\varphi ) + {\rm{cos}}(4\varphi ) - 2.375{\rm{sin}}(4\varphi ) + \\ 1.746{\rm{cos}}(5\varphi ) - 0.706{\rm{sin}}(5\varphi ) - 0.088{\rm{cos}}(6\varphi ) - \\ 1.545{\rm{sin}}(6\varphi ) + 1.011{\rm{cos}}(7\varphi ) - 0.601{\rm{sin}}(7\varphi ) - \\ 0188{\rm{cos}}(8\varphi ). \end{array}$ | (11) |
将式(10) 代入式(9), 得到1号储罐在不均匀沉降作用下的径向位移理论解为
| $\begin{array}{l} w = [ - 0.739{\rm{cos}}(2\varphi ) - 0.176{\rm{sin}}(2\varphi ) + \\ 0.261{\rm{cos}}(3\varphi ) - 1.239{\rm{sin}}(3\varphi ) - 0.986{\rm{cos}}(4\varphi ) + \\ 1.707{\rm{sin}}(4\varphi ) - 0.402{\rm{cos}}(5\varphi ) + 2.047{\rm{sin}}(5\varphi ) + \\ 1.174{\rm{cos}}(6\varphi )]x{\rm{ }}. \end{array}$ | (12) |
将式(11) 代入式(9), 得到2号储罐在不均匀沉降作用下的径向位移理论解为
| $\begin{array}{l} w = [ - 0.0088{\rm{cos}}(2\varphi ) + 0.0045{\rm{sin}}(2\varphi ) - \\ 0.212{\rm{cos}}(3\varphi ) + 0.196{\rm{sin}}(3\varphi ) - 0.4{\rm{cos}}(4\varphi ) + \\ 0.95{\rm{sin}}(4\varphi ) - 1.091{\rm{cos}}(5\varphi ) + 0.441{\rm{sin}}(5\varphi ) + \\ 0.0792{\rm{cos}}(6\varphi ) + 1.391{\rm{sin}}(6\varphi ) - 1.238{\rm{cos}}(7\varphi ) + \\ 0.736{\rm{sin}}(7\varphi ) + 0.301{\rm{cos}}(8\varphi )]x. \end{array}$ | (13) |
储罐属于典型的薄壁圆柱壳结构, 因此采用薄壳理论推导储罐径向位移理论公式.为了验证理论公式在实际应用中的准确性, 运用有限元模拟方法, 分别采用壳单元和实体单元模拟储罐在不均匀沉降作用下的变形响应, 并将这2种结果与理论公式的计算结果进行比较.
采用通用有限元软件ABAQUS对储罐进行模拟分析.本文主要研究沿储罐罐壁底部一周方向的不均匀沉降对储罐罐壁的影响, 不包含底板本身的沉降性能和失效机理, 为了节约计算成本, 储罐有限元模型不包含底板, 而通过对罐壁底部设置相应的边界条件, 约束储罐底部的径向位移和转角, 从而模拟底板对储罐罐壁的影响.应用几何大变形的静态分析方法, 储罐底部沿轴向施加不均匀沉降表达式, 顶部为自由边界.应用壳单元模拟时, 选用4节点四边形有限薄膜应变线性减缩积分壳单元S4R, 该单元性能稳定, 应用范围广泛, 可以有效地模拟薄壳结构的变形响应.应用实体单元模拟时, 选用8节点六面体线性减缩积分单元C3D8R, 该单元对求解位移问题精确度较高, 在网格存在变形时, 分析精度不会受到大的影响, 适用于模拟具有较大变形和位移的问题[15].
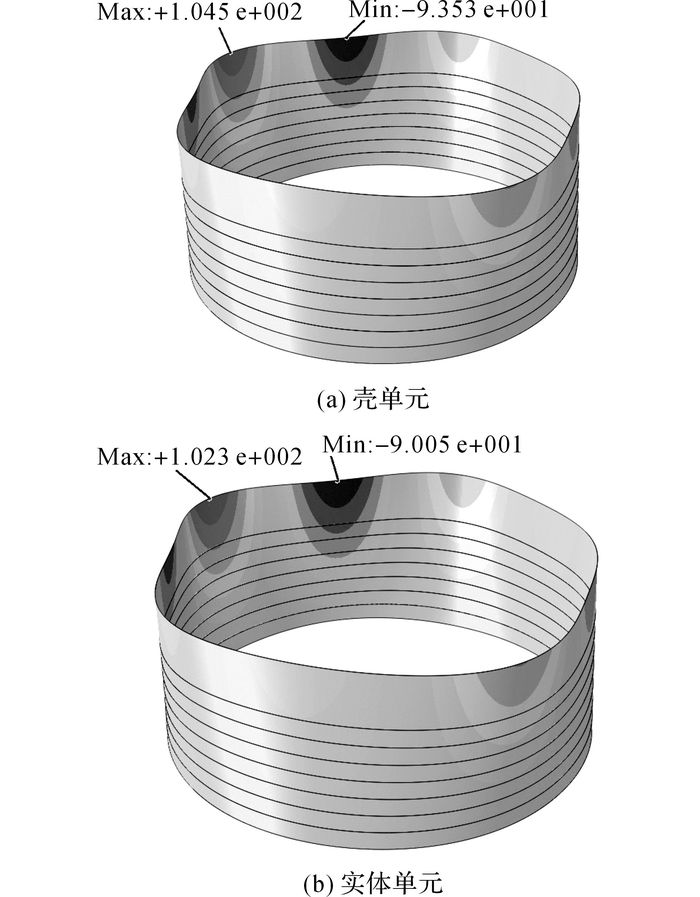
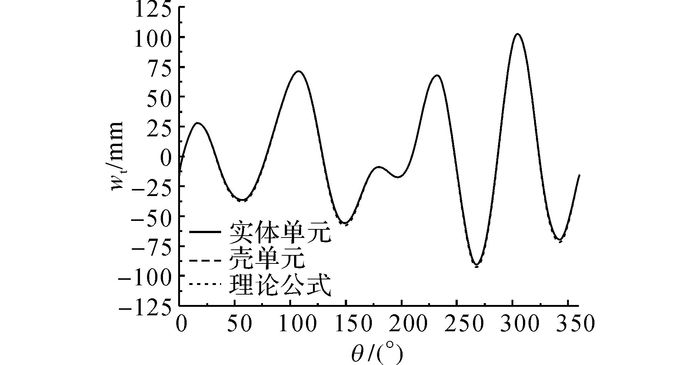
如图 2所示为1号储罐分别采用壳单元和实体单元模拟得到的径向位移云图, 缩放比例系数为20.可以看出, 采用壳单元和实体单元模拟得到的储罐径向位移云图几乎相同, 储罐的最大径向位移发生在罐顶部.以储罐顶部边界的径向位移为研究对象, 分析比较式(12) 所示的理论值与有限元模拟结果之间的关系.采用壳单元的模拟值、实体单元的模拟值和式(12) 计算得到的理论值计算得到的储罐顶部径向位移沿圆周方向的分布情况如图 3所示, 横坐标θ=φ×180/π, 为周向角度, 纵坐标wt为储罐顶部径向位移.
|
图 2 采用壳单元和实体单元模拟得到的1号储罐径向位移云图 Fig. 2 Radial displacement nephograms of tank 1 using shell element and solid element |
|
图 3 由3种不同方法计算得到的1号储罐顶部径向位移沿圆周方向的分布 Fig. 3 Radial displacement distributions of tank 1 top in circumferential direction obtained from three different methods |
如图 3所示, 采用3种不同方法计算得到的罐顶径向位移几乎完全相同.一般认为, 采用实体单元模拟得到的结果能够真实地反映储罐的变形情况.采用壳单元和理论公式计算得到的径向位移与采用实体单元得到的结果几乎相同, 这表明采用壳单元得到的模拟结果和采用理论公式计算得到的理论结果都能够真实地反映储罐的变形情况, 证明式(9) 可以有效地应用于预测储罐在不均匀沉降作用下的径向位移.如表 2所示为运用3种不同方法计算得到的储罐顶部向内和向外的最大径向位移值, 以及采用壳单元和理论公式得到的结果相对于采用实体单元得到结果的误差.wi为向内最大径向位移, wo为向外最大径向位移, δ为相对误差.
| 表 2 由3种不同方法计算得到的1号储罐顶部的最大径向位移 Table 2 Maximum radial displacements of top of tank 1obtained from three different methods |
如表 2所示, 采用壳单元和理论公式计算得到的最大径向位移值与采用实体单元得到的结果非常接近, 其中采用实体单元得到的最大径向位移值略小于采用壳单元和理论公式得到的结果.证明弯曲应力对储罐在不均匀沉降作用下的变形影响非常小, 也证明了采用薄壳理论推导得到的储罐在不均匀沉降作用下的径向位移理论公式是合理和准确的.
虽然在有限元分析过程中考虑了几何非线性, 但由于浮顶储罐直径较大, 在底部沉降作用下, 当罐顶变形已接近或达到了GB50341[16]的容许值100 mm时, 储罐仍处于弹性变形阶段, 几何非线性效应对这一状态下的储罐几乎没有影响, 因此采用本文的理论公式推导得到的变形和有限元分析结果非常吻合.本文推导公式的证明, 可以较好地应用于计算浮顶储罐的罐壁变形, 保障浮顶和密封结构的正常工作.对于固顶罐等在沉降下的非线性变形, 则还需要在未来进行进一步的研究.
采用与上述1号储罐相同的方法, 对2号储罐在不均匀沉降表达式(11) 作用下的变形进行分析和研究, 得到了如表 3所示的最大径向位移比较.2号储罐的分析结果证明了理论公式(式(9))可以准确地应用于计算不同容积储罐的径向位移.
| 表 3 由3种不同方法计算得到的2号储罐顶部的最大径向位移 Table 3 Maximum radial displacements of top of tank 2 obtained from three different methods |
壳单元模拟、实体单元模拟和理论公式这3种不同方法的分析结果表明, 为了节约计算成本和资源, 在不均匀沉降作用下的储罐有限元模拟分析中, 可以采用壳单元替代实体单元, 得到的结果非常接近真实情况.理论公式(式(9))可以有效地预测不同储罐在不均匀沉降作用下的径向位移, 预测结果也与实际变形非常吻合.
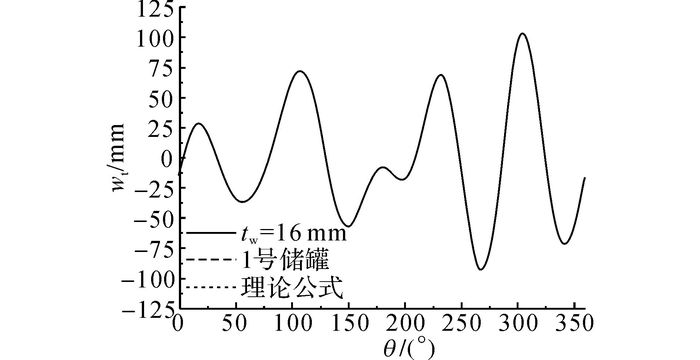
2.2 壁厚的影响在径向位移理论公式的推导过程中, 包含储罐厚度tw的各项均被忽略, 因此理论公式(式(9))中不包含参数tw.这表明作为薄壁结构, 储罐在沉降作用下的变形与其自身厚度无关.为了验证这一结论, 研究具有相同内径、相同高度、不同厚度的储罐在同一沉降作用下的变形情况.以1号储罐的内径和高度为例, 选取tw=12、14、16、18和20 mm这5种壁厚储罐作为研究对象, 采用有限元方法模拟这些储罐在式(10) 所示不均匀沉降作用下的变形响应, 将得到的径向位移与1号储罐以及采用式(9) 计算得到的理论解进行分析和比较, 研究壁厚对储罐变形的影响.如图 4所示分别为tw=16 mm的等壁厚储罐、1号储罐和理论公式(式(9))计算得到的储罐顶部径向位移沿圆周方向的分布情况.如表 4所示为不同厚度储罐顶部向内和向外最大径向位移的比较以及相对于理论公式计算结果的误差.
|
图 4 不同壁厚储罐顶部径向位移沿圆周方向的分布 Fig. 4 Radial displacement distributions of tank with different thicknesses in circumferential direction |
| 表 4 不同壁厚储罐顶部的最大径向位移 Table 4 Maximum radial displacements in top of tanks with different thicknesses |
如图 4所示, 3条径向位移曲线几乎重合, 表 4中各个不同壁厚储罐之间的最大径向位移误差非常微小.这表明在相同内径和高度的情况下, 无论是变壁厚的储罐, 还是不同厚度的等壁厚储罐, 在同一不均匀沉降作用下, 其变形几乎不随厚度的变化而变化.证明作为一种典型的薄壁结构, 储罐在沉降作用下的变形与其自身的厚度无关, 进一步验证了理论公式(式(9))的准确性.
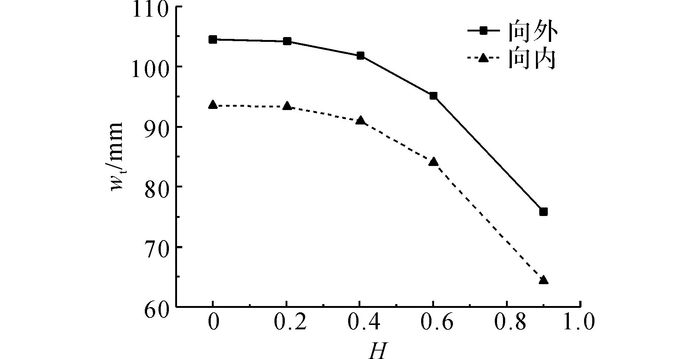
2.3 储液的影响储罐的沉降数据是从其经历冲水预压一直到正常运营的全过程中监测所得, 对于在役石油储罐, 由于运行时间较长, 其地基沉降逐渐由弹性变形转变为塑性变形, 即产生了永久沉降变形.此时地基沉降会随着储罐运行时间的增加而增大, 直到逐渐趋于稳定, 受罐内储液量变化的影响较小.但沉降造成罐壁变形时, 罐内不同的储液量将会对罐壁变形的大小产生一定影响.以1号储罐为例, 选取5种不同储液高度, h=0、3.91、7.77、11.63、17.42 m, 研究不同储液量对储罐变形的影响, 假设罐内介质为水.在这5种不同情况下, 分别对罐壁内侧相应区域施加液柱静压力, 如当h=11.63 m时, 在罐壁内侧h=0到h=11.63 m区域, 施加p=9 800(11.63-x) Pa的内压.如图 5所示为储罐在式(10) 所示不均匀沉降作用下的最大径向位移与储液高度之间的关系, 图中H=h/h0, 其中h0为储液高度.
|
图 5 1号储罐在式(10) 作用下的最大径向位移与储液高度的关系 Fig. 5 Relation of maximum radial displacement and liquid height of tank 1 under Formula Ten |
由图 5可知, 储罐的径向位移随着储液高度的增大而逐渐减小, 表明储罐内的液体可以提高储罐抵抗沉降变形的能力.当罐内具有储液时, 储罐在沉降作用下的变形小于空罐时储罐在相同沉降作用下的变形.因此, 忽略储液影响计算得到的储罐变形, 是对应于储罐在沉降下的最危险工况, 更有利于对储罐的变形失效作出提前预判, 保证储罐的安全运行.
3 含抗风圈储罐的变形研究大型储罐通常建造在沿海地区, 容易遭受较大的风载荷作用, 为了使储罐在风载荷作用下保持圆度, 避免出现局部被风吹瘪的现象, 常在储罐顶部设置抗风圈[17].抗风圈的结构形式采用钢板、型钢或两者组合焊接而成[16], 由于抗风圈结构形式的多样性, 在分析其对储罐变形的影响时, 通常采用截面惯性矩IG来表示不同结构形式、不同尺寸的抗风圈[5].为了便于研究, 本文选取截面形状为矩形的钢板结构抗风圈, 通过改变其宽度和厚度, 获得不同的截面惯性矩IG.对于具有相同内径、相同高度、不同IG值的储罐, 运用有限元模拟方法计算不同IG值对应的储罐变形, 通过分析储罐径向位移与IG之间的关系, 得到不均匀沉降作用下, 包含参数IG的储罐径向位移理论公式.
3.1 理论公式的求解具有顶部抗风圈的储罐, 径向位移值同样可以通过不同阶数的谐波单独作用产生的径向位移值叠加得到.在同一阶谐波作用下, 与没有抗风圈的储罐相比, 具有顶部抗风圈的储罐径向位移将会减小.该径向位移可以通过对没有抗风圈时储罐的径向位移理论公式(即式(7) 或(8))乘以衰减系数An得到, An是关于参数IG的表达式.通过各阶谐波沉降结果的叠加, 得到不均匀沉降作用下的径向位移理论公式为
| $w=-\sum\limits_{n=2}^{{{n}_{\max }}}{\left\{ {{A}_{n}}\frac{{{n}^{2}}}{r}x\left[ {{u}_{n}}\cos \left( n\varphi \right)+u_{n}^{'}\sin \left( n\varphi \right) \right] \right\}}.$ | (14) |
采用非线性拟合法, 求解表达式An.以1号储罐为例, 对于每一阶谐波沉降u=uncos (nφ), 采用有限元模拟方法, 共计算得到40个不同IG下的储罐最大径向位移, 并将不同IG对应的储罐最大径向位移与没有抗风圈的储罐在该谐波沉降作用下的最大径向位移的比值记为K.如表 5所示为部分抗风圈的截面尺寸和对应储罐在谐波沉降un=1 mm, n=3时的最大径向位移, a为抗风圈的宽度, b为抗风圈的厚度.如图 6所示为抗风圈宽度700 mm, 厚度15 mm时, 储罐在该谐波沉降作用下的径向位移云图.
| 表 5 部分抗风圈的尺寸和对应储罐的最大径向位移 Table 5 Dimensions of some eave wind girders and corresponding maximum radial displacements of tanks |

|
图 6 当抗风圈宽度为700 mm、厚度为15 mm时, 储罐在谐波沉降下的径向位移云图 Fig. 6 Radial displacement nephogram of tank under harmonic settlement with eave wind girder's width of 700 mm and its thickness of 15 mm |
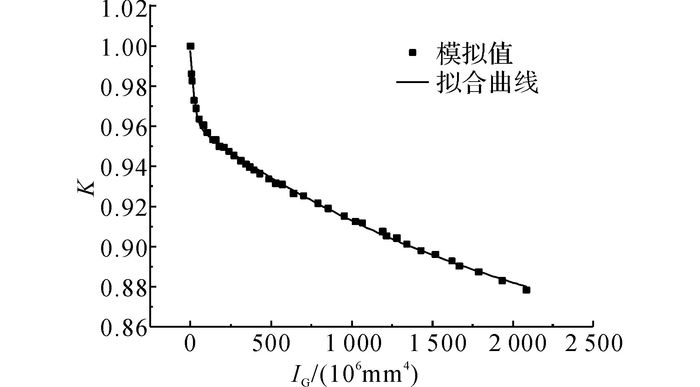
以IG为横坐标, K为纵坐标, 将对应不同抗风圈的计算结果绘制于图 7中.根据图中数据的分布规律, 采用双指数衰减函数对图中数据进行曲线拟合, 拟合结果如图 7所示.拟合曲线的相关系数平方R2=0.998 21, 表明曲线的拟合度非常高, 能够准确地反映储罐径向位移随抗风圈截面惯性矩的变化情况.该拟合曲线即为1号储罐在3阶谐波沉降作用下的衰减系数A3.采用同样的方法, 可以求解1号储罐在各阶谐波沉降作用下的衰减系数An.
|
图 7 1号储罐在3阶谐波沉降下的径向位移模拟值和拟合曲线 Fig. 7 Radial displacement simulation result and fitting curve of tank 1 under harmonic settlement with 3rd order |
对于不同容积的储罐, 均可以采用本文提出的非线性拟合方法, 求解对应于各阶谐波的衰减系数, 代入式(14) 中得到具有不同顶部抗风圈的储罐径向位移理论公式, 预测储罐在不均匀沉降作用下的变形情况.
衰减系数与储罐的尺寸相关, 对于特定的储罐, 求得对应的衰减系数后, 就可以通过检测得到的不同时期的沉降数据, 计算这一时刻的储罐变形.这一方法可以应用于大型石油储备基地的储罐群中, 对储罐群建立相应的数据库, 包括对应于各储罐的衰减系数.应用该数据库, 可以在后续计算中, 通过储罐底部检测得到的沉降数据, 方便地获得储罐变形情况.
3.2 验证与比较为了对理论公式(14) 进行验证, 采用有限元模拟方法, 模拟具有不同抗风圈的1号储罐在式(10) 所示不均匀沉降作用下的变形响应.
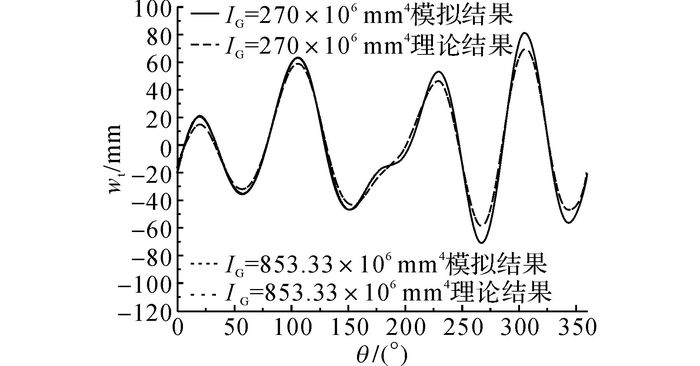
选取2种抗风圈尺寸:宽度为600 mm, 厚度为15 mm, IG=270.00×106 mm4;宽度为800 mm, 厚度为20 mm, IG=853.33×106 mm4.模拟具有这2种抗风圈的1号储罐在式(10) 作用下的变形响应, 得到的径向位移云图如图 8所示.罐顶径向位移沿圆周方向的分布如图 9所示, 包括有限元模拟结果和理论公式(式(14))的计算结果.

|
图 8 1号储罐在式(10) 作用下的径向位移云图(抗风圈截面模量为853.33×106 mm4) Fig. 8 Radial displacement nephogram of tank 1 under Formula Ten (Section modulu of eave wind girder is 853.33×106 mm4) |
|
图 9 式(10) 作用下1号储罐罐顶径向位移沿圆周方向的分布 Fig. 9 Radial displacement distribution of tank 1 top under Formula Ten in circumferential direction |
当抗风圈的截面惯性矩相同时, 采用有限元模拟和理论公式(式(14))计算得到的罐顶径向位移沿圆周方向的分布曲线几乎重合.当抗风圈的截面惯性矩较大时, 储罐在不均匀沉降作用下产生了较小的径向位移, 表明抗风圈有助于减小储罐在不均匀沉降作用下的变形.采用这2种不同方法计算得到的储罐向内和向外最大径向位移以及理论结果相对于有限元模拟结果的误差如表 6所示, 理论公式计算结果相对于有限元模拟结果的误差均小于5%, 表明理论结果非常接近于有限元模拟结果.以上分析均表明式(14) 可以有效地应用于计算储罐具有不同抗风圈时的径向位移, 预测储罐在沉降作用下的变形.
| 表 6 具有不同抗风圈的1号储罐最大径向位移及相对误差 Table 6 Maximum radial displacements and relative errors corresponding to tank 1 with different eave windgirders |
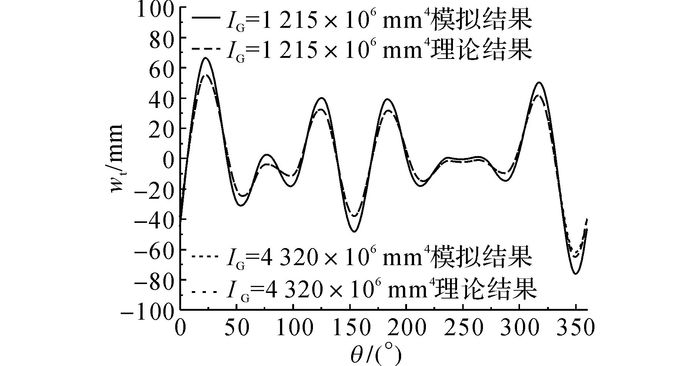
采用同样的方法, 研究具有不同抗风圈的2号储罐在不均匀沉降表达式(11) 作用下的变形情况, 验证理论公式(14) 在不同容积储罐上的应用.对应于2号储罐的各阶衰减系数的求解方法与1号储罐相同.具有抗风圈的2号储罐在式(11) 作用下的径向位移云图如图 10所示, 罐顶径向位移的有限元模拟结果与理论公式计算结果如图 11所示, 两者之间的误差如表 7所示.
|
图 10 2号储罐在式(11) 作用下的径向位移云图(抗风圈截面模量为1 215×106 mm4) Fig. 10 Radial displacement nephogram of tank 2 under Formula Eleven (Section modulus of eave wind girder is 1 215×106 mm4) |
|
图 11 式(11) 作用下2号储罐罐顶径向位移沿圆周方向的分布 Fig. 11 Radial displacement distribution of top of tank 2 under Formula Eleven in circumferentia direction |
| 表 7 具有不同抗风圈的2号储罐最大径向位移及相对误差 Table 7 Maximum radial displacements and relative errors corresponding to tank 2 with different eave wind girders |
与1号储罐的分析结果类似, 如图 11和表 7所示, 采用理论公式(14) 计算得到的储罐径向位移非常接近有限元模拟结果.研究结果表明理论公式(14) 可以有效地应用于预测不同容积储罐在不均匀沉降作用下的变形情况.
3.3 抗风圈结构形式的影响考虑到抗风圈结构形式的复杂多样性, 本文在储罐径向位移理论公式推导过程中, 应用抗风圈的截面惯性矩IG来表示不同结构、不同尺寸的抗风圈.为了便于研究, 采用截面形状为矩形的钢板式抗风圈, 求解储罐的各阶衰减系数.为了验证本文的方法以及理论公式(14) 在不同结构形式抗风圈上的应用, 以工程上最常使用的角钢式抗风圈为例, 研究具有角钢式顶部抗风圈的储罐在不均匀沉降作用下的变形响应.
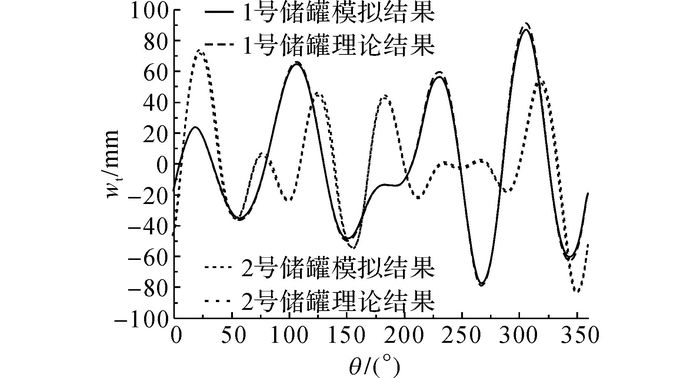
本研究1号储罐选用的角钢抗风圈尺寸如下:长度为L=300 mm, 厚度为d=15 mm, 截面惯性矩为IG=78.348×106 mm4;2号储罐选用的角钢抗风圈尺寸如下:长度为L=500 mm, 厚度为d=15 mm, 截面惯性矩为IG=373.55×106 mm4.作用于1号储罐的不均匀沉降如式(10) 所示, 作用于2号储罐的不均匀沉降如式(11) 所示.分别采用有限元模拟方法和理论公式(式(14))计算得到的储罐顶部径向位移沿圆周方向的分布曲线如图 12所示.采用理论公式(式(14))计算得到的储罐最大径向位移相对于有限元模拟结果的误差如表 8所示.可知, 采用理论公式计算得到的储罐径向位移非常接近有限元模拟结果, 两者之间的误差均小于5%.证明本文提出的分析方法和推导得到的理论公式可以有效地应用于不同结构形式抗风圈储罐的径向位移计算中.
|
图 12 角钢抗风圈储罐顶部径向位移沿圆周方向的分布 Fig. 12 Radial displacement of tank with angle steel eave wind girder in circumferential direction |
| 表 8 角钢抗风圈储罐最大径向位移及相对误差 Table 8 Maximum radial displacement and relative error of tank with angle steel eave wind girder |
(1) 储罐在不均匀沉降作用下的径向位移可以应用理论公式(式(9))计算得到, 理论公式结果与有限元模拟结果几乎相同.
(2) 作为一种典型的薄壁结构, 大型储罐在沉降作用下的变形与其罐壁厚度无关.
(3) 罐内储液可以提高储罐抵抗沉降变形的能力, 随着储液的增多, 储罐在沉降作用下的变形逐渐减小.
(4) 应用理论公式(式(14)), 可以准确地计算具有不同尺寸、不同结构形式抗风圈的储罐在不均匀沉降作用下的径向位移.
| [1] | FAN H G, CHEN Z P, FENG W Z, et al. Buckling of axial compressed cylindrical shells with stepwise variable thickness[J]. Structural Engineering and Mechanics, 2015, 54(1): 87–103. DOI:10.12989/sem.2015.54.1.087 |
| [2] | CHEN Z P, DUAN Y Y, SHEN J M, et al. A simplified method for calculating the stress of a large storage tank wall[J]. Proceedings of the Institution of Mechanical Engineers, Part E:Journal of Process Mechanical Engineering, 2007, 221(3): 119–127. DOI:10.1243/09544089JPME125 |
| [3] | FAN H G, CHEN Z P, SHEN J M, et al. Buckling of steel tanks under measured settlement based on Poisson curve prediction model[J]. Thin-Walled Structures, 2016, 106: 284–293. DOI:10.1016/j.tws.2016.05.009 |
| [4] |
康杰, 徐晓红, 郭寥廓. 软土地基储罐群产生不均匀沉降原因及纠偏[J].
炼油技术与工程, 2010(10): 57–60.
KANG Jie, XU Xiao-hong, GUO Liao-kuo. Analysis and correction of uneven settlement of tank group in soft soil area[J]. Petroleum Refinery Engineering, 2010(10): 57–60. DOI:10.3969/j.issn.1002-106X.2010.10.014 |
| [5] | KAMYAB H, PALMER S C. Analysis of displacements and stresses in oil storage tanks caused by differential settlement[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 1989, 203(1): 61–70. |
| [6] |
傅伟庆, 武铜柱, 许莉. 大型浮顶油罐技术发展[J].
化工设备与管道, 2013, 50(4): 1–5.
FU Wei-qing, WU Tong-zhu, XU Li. Technical development of large floating roof oil tank[J]. ProcessEquipment and Piping, 2013, 50(4): 1–5. |
| [7] | ZHAO Y, CAO Q S, XIE X Y. Floating-roof steel tanks under harmonic settlement:FE parametric study and design criterion[J]. Journal of Zhejiang University SCIENCE A, 2006, 7(3): 398–406. DOI:10.1631/jzus.2006.A0398 |
| [8] | CHEBARO M R, YOOSEF-GHODSI N, YUE H K. Steel storage tank shell settlement assessment based on finite element and API standard 653 analysis[C]//20087th International Pipeline Conference. Calgary:ASME, 2008:395-399. |
| [9] |
石磊, 帅健, 许葵. 基于FEA模型和API653的大型油罐基础沉降评价[J].
中国安全科学学报, 2014, 24(3): 114–119.
SHI Lei, SHUAI Jian, XU Kui. Assessment of large-scale oil tanks foundation settlement based on FEA model and API 653[J]. China Safety Science Journal, 2014, 24(3): 114–119. |
| [10] |
石磊, 帅健, 许葵. 大型油罐基础沉降国内外评价标准对比[J].
油气储运, 2014, 33(8): 862–868.
SHI Lei, SHUAI Jian, XU Kui. Comparison of evaluation standards for large oil tank foundation settlement in China and abroad[J]. Oil and Gas Storage and Transportation, 2014, 33(8): 862–868. |
| [11] | AYARI H, TRUONG D, SEHN J, et al. A nonlinear finite element study on settlement and releveling procedure of a large deformed steel tank[J]. Journal of Pressure Vessel Technology, 2014, 136(3): 034–502. |
| [12] | ZHAO Y, LEI X, WANG Z, et al. Buckling behavior of floating-roof steel tanks under measured differential settlement[J]. Thin-Walled Structures, 2013, 70: 70–80. DOI:10.1016/j.tws.2013.04.015 |
| [13] | CALLADINE C R. Theory of shell structures[M]. Cambridge: Cambridge University Press, 1989: 407. |
| [14] | CHEN D Y, FAN H G, SHEN J M, et al. Research of curve fitting method on the measured settlement of tanks[J]. Procedia Engineering, 2015, 130: 400–407. DOI:10.1016/j.proeng.2015.12.232 |
| [15] | 石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社, 2006: 60-62. |
| [16] | 中华人民共和国住房和城乡建设部. 立式圆筒形钢制焊接油罐设计规范: GB 50341-2014[S]. 北京: 中国计划出版社, 2014: 47. |
| [17] | GONG J, TAO J, ZHAO J, et al. Effect of top stiffening rings of open top tanks on critical harmonic settlement[J]. Thin-Walled Structures, 2013, 65: 62–71. DOI:10.1016/j.tws.2013.01.011 |



