传统的工程机械常采用比例多路阀控制执行器的运行速度, 存在进出口同时节流、节流损失大等不足.针对此问题的解决方案是采用进出口独立控制, 分别控制执行器两腔的压力和流量.Andersson等[1-2]分别采用4个插装阀和4个先导比例节流阀组成进出口独立方式控制系统, 并研究了系统的特性.Yao等[3-5]分别采用5和6个比例节流阀组成进出口独立控制系统, 应用自适应鲁棒性策略进行控制, 并对系统的速度和压力的特性进行研究, 新的研究中进一步增加了流量再生回路.Shenouda[6]采用4个比例插装节流阀组成进出口独立系统以控制挖掘机、伸缩式装载机动臂, 研究了不同工作模式下系统的能量效率和动臂势能再生的控制策略.Eriksson[7-8]采用4个可双向工作的Valvistor型比例流量阀组成进出口独立系统以控制装载机, 并对其能效特性进行研究, 研究表明采用双向比例流量阀可增加能量调控的自由度.Sitte等[9-11]对比分析了两位、三位比例阀、开关阀及其组合等多种进出口独立控制方案, 选择2个两位比例节流阀和4个开关阀组成进出口独立控制系统, 并对采用该系统控制挖掘机铲斗水平移动的能量和压力特性进行研究.
权龙等[12-14]提出了可用于多执行器的泵阀复合进出口独立控制方案, 将其控制原理应用于挖掘机整机控制, 分别对采用LUDV系统和进出口独立系统控制的动臂、斗杆和回转马达3个执行机构的动静态性能和能耗特性进行研究.徐兵等[15]基于进出口独立系统的泵阀联合控制, 设计两层结构的控制器实现系统的运动控制及节能控制, 对采用该系统的挖掘机动臂和斗杆的控制特性和能耗特性进行研究.刘英杰等[16]基于进出口独立控制系统, 采用计算流量反馈和压力闭环的控制策略以控制液压缸的速度和压力.丁孺琦等[17]提出了一种对进出口独立控制系统进行仿真的建模方法, 简化了模型结构, 提高了仿真效率.
现有针对进出口独立控制系统的研究工作主要集中在回路原理、能量效率、控制策略、速度和压力控制特性等方面.随着对工程机械作业智能化和作业质量要求的不断提高[18-19], 在工程机械作业中, 各执行器不仅要满足运行速度和输出力的特性, 而且需要较高的定位精度.为此, 本文在泵阀复合和进出口独立控制系统的基础上, 提出一种基于模式切换的控制策略, 以实现挖掘机动臂运行速度和位置的复合控制.根据目标位置和运行速度的要求, 设计期望的速度和位移曲线;结合挖掘机动臂上升、下降和定位工况给出对应的控制策略, 建立机电液联合仿真模型对提出的控制策略进行仿真分析;以实验室现有的6 t挖掘机为研究对象, 构建采用进出口独立控制方法复合控制动臂速度和位置的试验测试系统, 对动臂的运行特性进行试验研究.
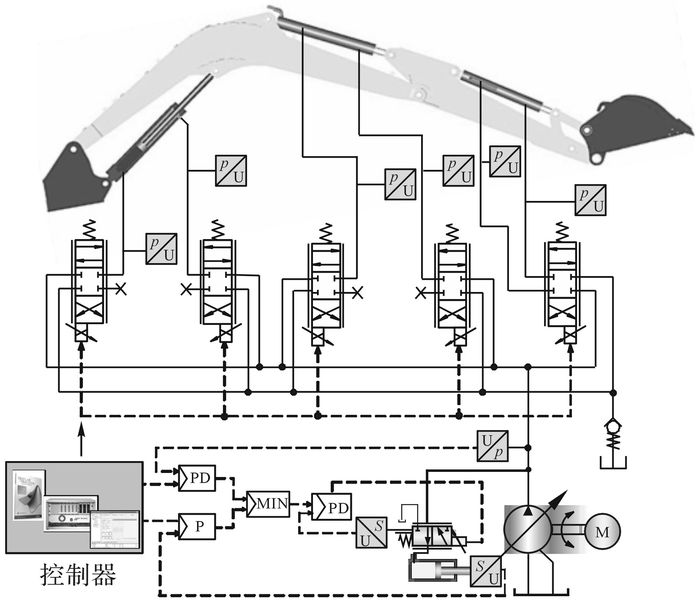
1 工作装置如图 1所示为所采用的进出口独立控制液压挖掘机工作装置的控制回路原理及试验测试系统.动力源采用压力和流量连续可调的电子比例变量柱塞泵, 动臂液压缸和斗杆液压缸均连接2个三位三通比例方向阀, 对液压缸的进出油口进行独立控制.液压缸两腔及变量泵的出口都装有压力传感器, 活塞杆上装有位移传感器, 采用德国dSPACE公司的硬件在环控制系统DS1103进行控制.
|
图 1 进出口独立控制液压挖掘机工作装置的工作原理及试验测试系统 Fig. 1 Working principle and experimental test system of hydraulic excavator's actuators with separate meter-in and meter-out system |
在动臂工作过程中, 从t0到t1时间段泵消耗的能量可以用泵输出的功率表示:
| $ E = \int_{{t_0}}^{{t_1}} {{P_{\rm{s}}}{\rm{d}}t} = \int_{{t_0}}^{{t_1}} {{P_{\rm{s}}}{q_{\rm{s}}}{\rm{d}}t} . $ | (1) |
式中:t0为工作过程的起始时间, t1为工作过程的结束时间, Ps为某一时刻泵的功率, ps为泵出口压力, qs为泵输出流量.由式(1) 可以看出, 在满足工作条件的前提下, 减少能耗的方法有2种途径:一是降低泵出口压力;二是减少泵输出流量.
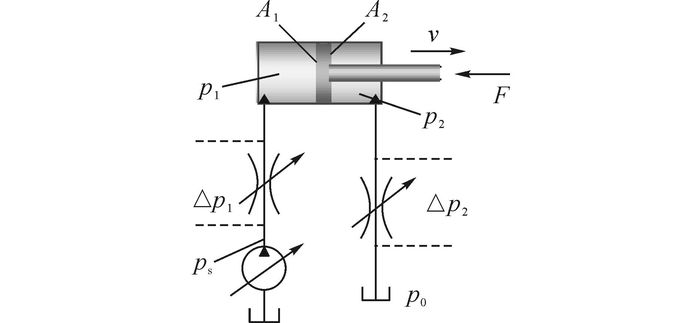
2.1 动臂上升能耗分析动臂上升过程中液压控制原理如图 2所示.其中, p1、p2分别为无杆腔和有杆腔压力, Δp1、Δp2分别为进油路和回油路的节流口所产生的压差, p0为油箱或背压阀压力, A1、A2分别为无杆腔侧和有杆腔侧的活塞面积, 活塞杆在负载力F下以速度v运行, 设A1/A2=R.
|
图 2 动臂上升过程的控制原理 Fig. 2 Control principle of boom rising process |
液压缸受力方程为
| $ {p_1}{A_1} - {p_2}{A_2} = F. $ | (2) |
压力关系为
| $ {p_{\rm{s}}} = {p_1} + \Delta {p_1},{p_2} = {p_0} + \Delta {p_2}. $ | (3) |
故有
| $ {p_{\rm{s}}} = \frac{F}{{{A_1}}} + \frac{{{p_0}}}{R} + \frac{{\Delta {p_2}}}{R} + \Delta {p_1}. $ | (4) |
又因液压缸伸出速度对于两腔是相等的, 故
| $ \frac{{{q_1}}}{{{A_1}}} = \frac{{{q_2}}}{{{A_2}}} \Rightarrow {q_1} = R{q_2}. $ | (5) |
泵输出的流量为
| $ {q_{\rm{s}}} = v{A_1}. $ | (6) |
故
| $ {P_{\rm{s}}} = {p_{\rm{s}}}{q_{\rm{s}}} = Fv + v{A_2}{p_0} + v{A_2}\Delta {p_2} + v{A_1}\Delta {p_1}. $ | (7) |
对应的能量消耗为
| $ \mathit{E} = {\mathit{E}_{\rm{L}}} + {E_0} + {E_2} + {E_1}. $ | (8) |
式中:EL为对负载做功消耗的能量, E0为背压阀消耗的能量, 如果没有背压阀, 则该项为0, E2为有杆腔阀消耗的能量, E1为无杆腔阀消耗的能量.对于不同的控制方式, 会产生不同的能耗.
1) 当采用传统四边联动滑阀时,
| $ {x_1} = {x_2}. $ | (9) |
式中:x1、x2分别为进回油路节流口的开口面积, 则Δp1=R2Δp2;对于负载敏感回路, 阀口两端压差恒定, 记Δp1=Δp, 则
| $ {P_{\rm{s}}} = {p_{\rm{s}}}{q_{\rm{s}}} = Fv + v{A_2}{p_0} + v{A_2}\Delta p/{R^2} + v{A_1}\Delta p. $ | (10) |
2) 当采用进口节流回路时,
| $ \Delta {p_1} = \Delta p,\;\;\;\Delta {p_2} = \Delta {p_{2\min }}. $ | (11) |
式中:Δp2min表示在流量不变情况下, 有杆腔阀口全开时阀口的最小压降, 此时,
| $ {P_{\rm{s}}} = {p_{\rm{s}}}{q_{\rm{s}}} = Fv + v{A_2}{p_0} + v{A_2}\Delta {p_{2\min }} + v{A_1}\Delta p. $ | (12) |
3) 当采用出口节流回路时,
| $ \Delta {p_2} = \Delta p,\;\;\;\Delta {p_1} = \Delta {p_{1\min }}. $ | (13) |
式中:Δp1min表示在流量不变情况下, 无杆腔阀口全开时阀口的最小压降, 此时,
| $ {P_{\rm{s}}} = {p_{\rm{s}}}{q_{\rm{s}}} = Fv + v{A_2}{p_0} + v{A_2}\Delta p + v{A_1}\Delta {p_{1\min }}. $ | (14) |
4) 当采用进出口阀全开, 通过控制泵摆角来控制流量的方式时,
| $ \Delta {p_1} = \Delta {p_{1\min }},\;\;\;\Delta {p_2} = \Delta {p_{2\min }}. $ |
则有
| $ {P_{\rm{s}}} = {p_{\rm{s}}}{q_{\rm{s}}} = Fv + v{A_2}{p_0} + v{A_2}\Delta {p_{1\min }} + v{A_1}\Delta {p_{2\min }}. $ | (15) |
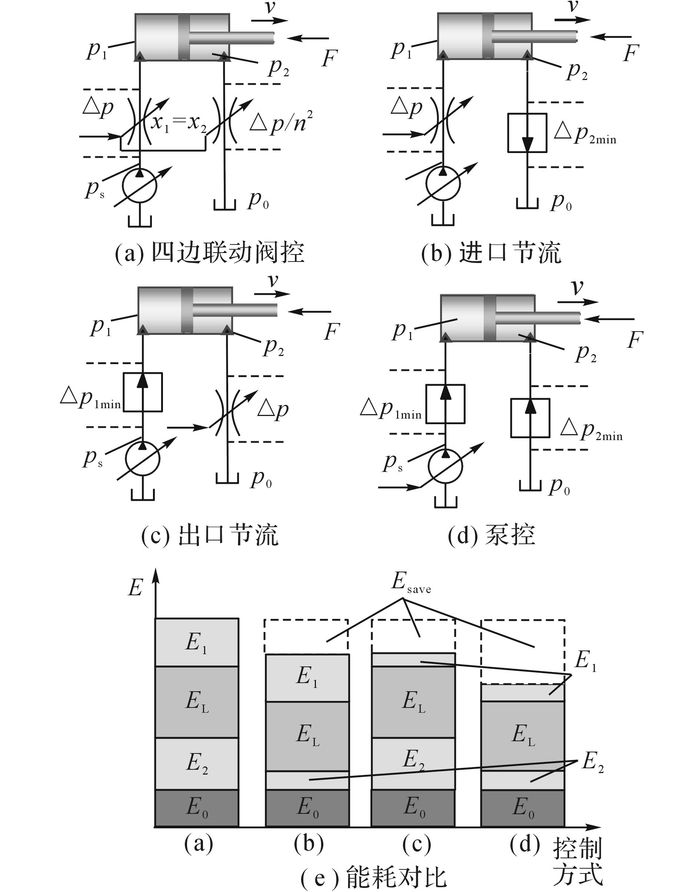
如图 3所示为当动臂上升时不同控制方式及其能耗对比, 图中, Esave为相对于四边联动阀控方式节约的能量.
|
图 3 动臂上升的不同控制方式及其能耗对比 Fig. 3 Comparison of different control methods and corresponding energy consumption for boom rising |
当动臂下降时, 处于超越负载工况, 此时无杆腔的压力必须能够克服动臂自重, 有杆腔需要保持不吸空的压力.此时,
| $ {p_{\rm{s}}} = {p_2} + \Delta {p_2},{p_1} = {p_0} + \Delta {p_1}. $ | (16) |
泵需要提供的流量为
| $ {q_{\rm{s}}} = v{A_2}. $ | (17) |
动臂下行时可采用3种不同的控制方式:传统四边联动阀控、回油节流控制、流量再生.
1) 当采用传统四边联动阀控时, 进油路和回油路的节流面积相同, 则
| $ \Delta {p_2} = \frac{1}{{{R^2}}}\Delta {p_1} = \frac{1}{{{R^2}}}\left( {\frac{F}{{{A_1}}} + \frac{{{p_2}}}{R} - {p_0}} \right). $ | (18) |
则泵出口压力为
| $ {p_{\rm{s}}} = \left( {1 + \frac{1}{{{R^3}}}} \right){p_2} + \frac{1}{{{R^2}}} \cdot \frac{F}{{{A_1}}} - \frac{1}{{{R^2}}}{p_0}. $ | (19) |
因此泵输出功率为
| $ {P_{\rm{s}}} = {p_{\rm{s}}}{q_{\rm{s}}} = \left( {1 + \frac{1}{{{R^3}}}} \right){p_2}v{A_2} + \frac{{Fv}}{{{R^3}}} - \frac{{{A_2}}}{{{R_2}}}v{p_0}. $ | (20) |
2) 当采用出口节流控制时,
| $ {p_{\rm{s}}} = {p_2} + \Delta {p_2} = {p_2} + \Delta {p_{2\min }}. $ | (21) |
此时,
| $ {P_{\rm{s}}} = {p_{\rm{s}}}{q_{\rm{s}}} = {p_2}v{A_2} + \Delta {p_{2\min }}v{A_2}. $ | (22) |
3) 当采用流量再生控制时, 无杆腔和有杆腔接通, 同时经过一个背压阀与油箱连通.由于背压阀的存在, 一部分流量从无杆腔流入有杆腔实现流量再生, 另一部分流量通过背压阀流回油箱.因此, 这个过程中泵不需要输出能量, 即Ps=0.
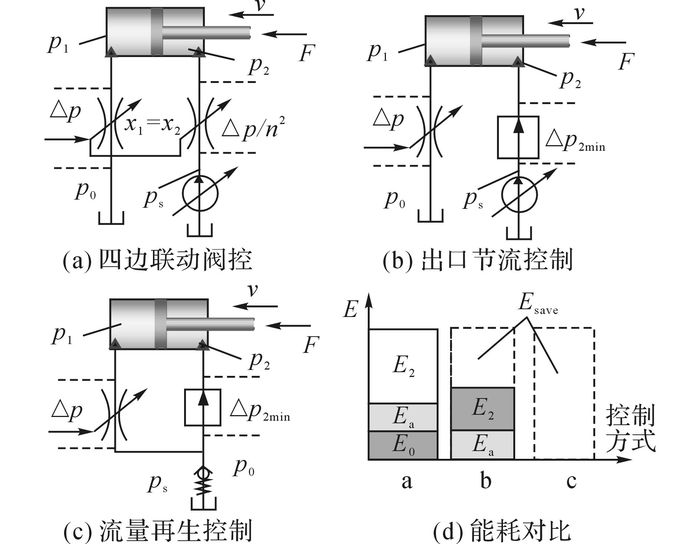
如图 4所示为动臂下降时不同控制方式及能耗对比.其中, Ea为防止有杆腔吸空而消耗的能量.
|
图 4 动臂下降的不同控制方式及其能耗对比 Fig. 4 Comparison of different control methods and corresponding energy consumption for boom lowering |
在动臂升降运行过程中, 应主要考虑其运行特性和能耗特性.根据以上对动臂上升和下降时不同控制方式及其能耗的对比分析可知, 动臂上升时采用泵控、下降时采用流量再生的方式能耗最低, 因此将其作为动臂速度位置复合控制的运行过程中的控制回路.
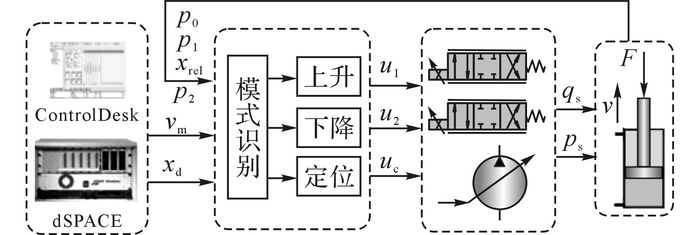
3 控制策略 3.1 总体控制策略如图 5所示为动臂速度位置复合控制总体策略.控制器根据输入的目标指令信号和液压缸反馈信号, 进行工作模式识别.其中, xd为目标位置, xrel为液压缸的位移反馈值, vm为运行速度要求.动臂运行过程中分为3种工作模式:举升、下降和定位, 对于不同的工作模式给出不同的控制方式.控制器输出控制信号u1、u2、uc, 分别控制无杆腔比例阀、有杆腔比例阀和变量泵的摆角, 从而输出系统压力和系统流量, 控制执行器按照预期的速度运行至目标位置, 并保证运行平稳性和定位精度.
|
图 5 速度位置复合控制总体策略 Fig. 5 Overall strategy of velocity and position compound control |
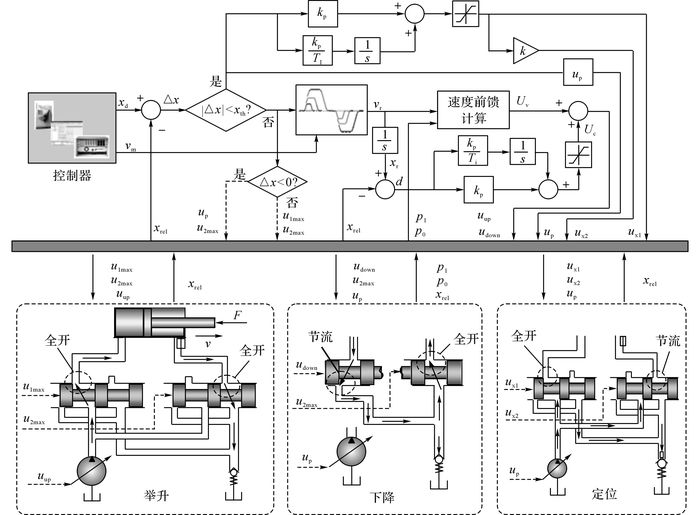
如图 6所示为基于模式切换的速度位置复合控制的流程.其中, vr为期望速度、xr为期望位移, Uv为速度前馈信号, Uc为位置反馈信号, xth为设定的模式切换阈值.图中, xrel为位移反馈值, d为期望位移xr与位移反馈值xrel的差值, u1max、udown、ux1分别为不同模式下无杆腔阀的控制信号, u2max、ux1为有杆腔阀的控制信号, uup、up为泵的控制信号, Kp、kp为比例系数, TI、Ti为积分系数.控制器根据目标位置xd与位移反馈值xrel的差值Δx, 识别挖掘机动臂处于的工作模式.3种工作模式的判别准则如下:
1) 当|Δx|≥xth且Δx>0时, 举升;
2) 当|Δx|≥xth且Δx < 0时, 下降;
3) 当|Δx| < xth时, 定位.
|
图 6 基于模式切换的速度位置复合控制流程 Fig. 6 Velocity and position compound control process based on mode switching |
采用带速度前馈的位置闭环(velocity feedforward position feedback, VFPB)的控制方式.根据位移差值Δx和运行速度vm的要求, 设定期望的速度曲线和位移曲线, 对相应的控制元件进行速度前馈计算, 通过位置反馈对前馈计算进行补偿与修正, 使运行过程中能够尽可能地达到预期的速度.
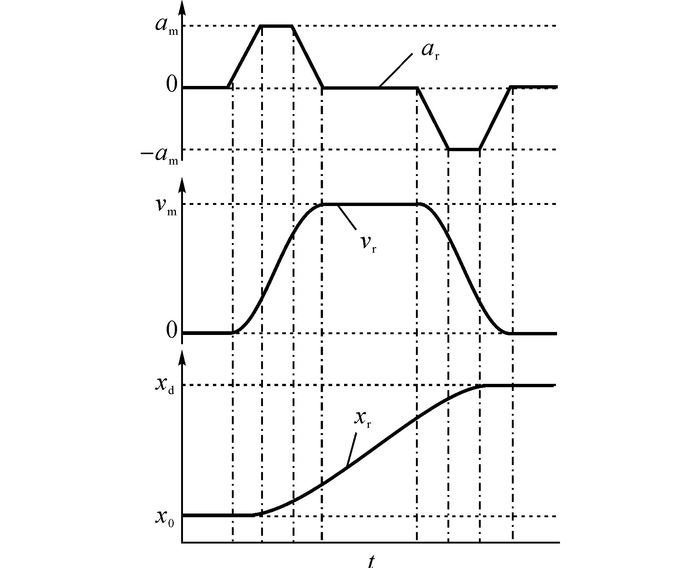
如图 7所示为设定的加速度-速度-位移期望曲线(t为时间).可根据目标位移值xd、运行速度vm和最大加速度am设计出期望的加速度ar、期望速度vr、期望位移xr, 运行过程分为7个阶段.当动臂按此曲线举升时, 其位移和速度都不存在突变, 可避免运行时的刚性冲击和柔性冲击.如图 7所示为动臂举升时生成的速度曲线, 动臂下降时可生成类似的速度曲线.
|
图 7 加速度-速度-位移的期望曲线 Fig. 7 Expected curves of acceleration-velocity-displacement |
如果直接以期望位置xd与实际位置xrel的差值Δx作为位置反馈, 则在运行过程中位置误差较大, 从而使位置反馈输出值较大, 与前馈控制同时起作用, 无法实现运行速度的控制.因此, 以期望位移曲线xr与实际位移xrel的差值d作为位置反馈, 则整个动态运行过程中d始终较小, 保证速度前馈控制起主要作用, 位置反馈起调节作用, 保证运行过程按照期望速度和位移曲线运行.
在动臂举升过程中, 无杆腔阀全开以减少节流损失, 有杆腔阀全开以减小背压, 通过控制泵的摆角来控制活塞杆伸出的速度.对应的无杆腔阀、有杆腔阀和泵摆角的输入量为
| $ \left\{ {{u_1},{u_2},{u_{\rm{c}}}} \right\} = \left\{ {{u_{1\max }},{u_{2\max }},{u_{{\rm{up}}}}} \right\}. $ | (23) |
式中:u1max表示无杆腔阀全开, u2max表示有杆腔阀全开, uup表示动臂上升时泵摆角的控制量, 可由速度前馈计算和位置反馈得到:
| $ {u_{{\rm{up}}}} = {U_{\rm{v}}} + {U_{\rm{c}}}. $ | (24) |
期望速度与前馈信号Uv之间的计算公式为
| $ {U_{\rm{v}}} = \frac{{{v_{\rm{r}}}{A_1}}}{{n{V_{{\rm{pmax}}}}}}. $ | (25) |
式中:n为电机转速, Vpmax为变量泵最大排量.位置反馈信号Uc的计算公式为
| $ {U_{\rm{c}}} = {k_{\rm{p}}} \cdot \left( {d + \frac{1}{{{T_{\rm{i}}}}}\int {d{\rm{d}}t} } \right). $ | (26) |
式中:kp为位置反馈比例系数, Ti为位置反馈积分系数.
由于泵的泄漏及响应速度较慢等原因, 加入位置闭环控制对速度前馈计算进行补偿, 同时控制变量泵的摆角值, 使动臂在举升过程中达到预期的速度.
在动臂下降过程中, 采用流量再生的控制方式, 无杆腔阀和有杆腔阀同时接油箱, 有杆腔阀全开, 通过控制无杆腔阀的开口量来调节速度.由于背压阀的存在, 使得无杆腔的油液一部分回到有杆腔, 实现流量再生, 另一部分油液回到油箱.对应的无杆腔阀、有杆腔阀和泵摆角的输入量为
| $ \left\{ {{u_1},{u_2},{u_{\rm{c}}}} \right\} = \left\{ {{u_{{\rm{down}}}},{u_{2\max }},{u_{\rm{p}}}} \right\}. $ | (27) |
式中:up为变量泵此时处于压力控制, 只需维持较小的压力即可, udown为无杆腔阀的开口量, 可由速度前馈计算和位置反馈得到:
| $ {u_{{\rm{down}}}} = {U_{\rm{v}}} + {U_{\rm{c}}}. $ | (28) |
在期望的速度下, 无杆腔阀流过的流量为
| $ {q_1} = {v_{\rm{r}}}{A_1}. $ | (29) |
对于电液比例阀, 当其阀口全开时, 单边压差为ΔpN所对应的额定流量为qN, 则压差为Δp时所对应的流量q为
| $ q = {q_{\rm{N}}}\sqrt {\frac{{\Delta p}}{{\Delta {p_{\rm{N}}}}}} . $ | (30) |
则无杆腔阀在控制信号为Uv, 压差为Δp时的流量为
| $ {q_1} = {U_{\rm{v}}}{q_{\rm{N}}}\sqrt {\frac{{\Delta p}}{{\Delta {p_{\rm{N}}}}}} . $ | (31) |
当动臂下降时, 无杆腔阀两端压差为
| $ \Delta p = {p_1} - {p_0}. $ | (32) |
整理可得, 无杆腔阀速度前馈计算公式为
| $ {U_{\rm{v}}} = \frac{{6{v_{\rm{r}}}{A_1}}}{{{{10}^5}{q_{\rm{N}}}}}\sqrt {\frac{{\Delta {p_{\rm{N}}}}}{{{p_1} - {p_0}}}} . $ | (33) |
式中:p1与负载有关, vr与期望运行速度有关, 故当期望速度相同、负载不同时, 控制器输出不同的前馈控制量以满足负载变化;当负载相同、期望速度不同时, 控制器输出不同的前馈控制量以满足不同的速度要求.在前馈控制的基础上加入位置反馈, 以调节速度前馈计算值, 使动臂能够按照预期速度运行.
3.3 定位控制策略由于系统泄漏、负载变化等原因, 动臂运行过程中的VFPB控制难以到达较准确的目标位置, 存在一定的偏差, 定位精度不够.为了提高位置精度, 当实际位置值与目标位置值差值的绝对值小于设定的阈值时, 切换为定位(positioning control, PC)控制模式.此时对应的无杆腔阀、有杆腔阀和泵摆角的输入量为
| $ \left\{ {{u_1},{u_2},{u_{\rm{c}}}} \right\} = \left\{ {{u_{1{\rm{x}}}},{u_{2{\rm{x}}}},{u_{\rm{p}}}} \right\}. $ | (34) |
式中:u1x和u2x分别为无杆腔阀和有杆腔阀的控制量, 此时,泵出口压力要能克服动臂重力负载.
|
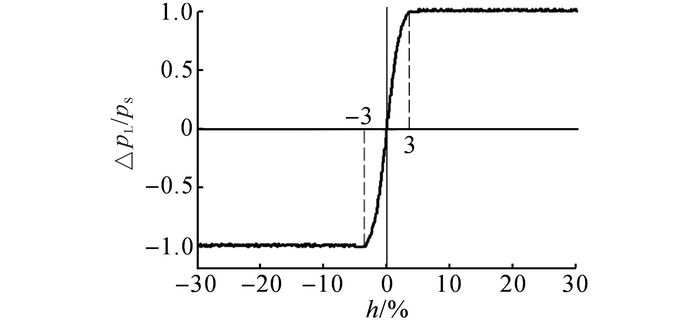
图 8 试验测试阀的压力特性曲线 Fig. 8 Curve of pressure characteristics of test valve |
对于无杆腔阀和有杆腔阀, 在定位模式时应使其具有较高的压力增益以保证定位精度.如图 8所示为试验测试阀的压力特性曲线, h为阀的开口量, ΔpL/ps表示负载压力与泵口压力的比值.四边联动比例滑阀的压力增益较高, 具有定位速度快、位置精度高的特点.为了使进出口独立系统在定位过程中具有与比例阀相近的压力增益, 在液压缸处于定位工作模式时, 通过设定无杆腔阀和有杆腔阀的控制信号, 使两阀联动控制, 其作用类似于一个四通比例滑阀.
由于液压缸两腔面积不同, 若两阀的控制信号相同, 则其作用相当于对称阀控制非对称缸, 系统会存在压力突变、压力超限和气蚀现象[20].为使进出油口的流量与两腔面积相匹配, 对于无杆腔阀和有杆腔阀, 采用不同的开口控制量:
| $ {u_{2{\rm{x}}}} = k{u_{1{\rm{x}}}}. $ | (35) |
式中:k为两阀开口比例, 可根据两腔的面积比值决定.无杆腔阀的控制量计算公式为
| $ {u_{1{\rm{x}}}} = {K_{\rm{p}}}\left[ {\left( {{x_{\rm{d}}} - {x_{{\rm{rel}}}}} \right) + \frac{1}{{{T_1}}}\int {\left( {{x_{\rm{d}}} - {x_{{\rm{rel}}}}} \right){\rm{d}}t} } \right]. $ | (36) |
式中:Kp为定位比例系数, TI为定位积分系数.进出口两阀阀芯位移始终成比例, 相当于一个非对称阀, 故其作用类似于非对称阀控制非对称缸方式, 可以在一定程度上避免非对称缸两腔面积不同所带来的流量和压力不匹配问题.对于两节流口处面积增益不同的非对称阀, 其面积增益是固定的, 只适用于特定面积比的非对称缸.此处通过控制两阀芯的位移实现非对称阀的作用, 两阀芯位移比例可任意设定, 适用于任意面积比的非对称缸的控制.
4 机电液联合仿真分析 4.1 联合仿真模型为了验证控制策略的可行性, 根据液压挖掘机机械结构和液压元件的物理结构, 采用多学科仿真软件Simulation X, 构建能反映液压挖掘机真实工况的机电液联合仿真模型进行仿真研究.
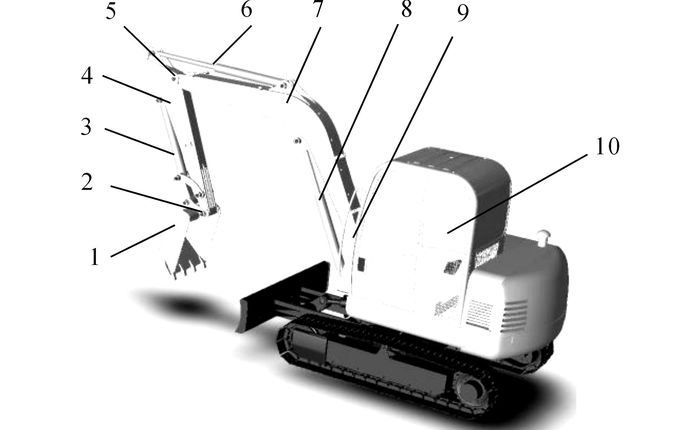
以实验室YC60-8型挖掘机为研究对象, 通过测绘获得挖掘机各重要部件的实际尺寸, 包括动臂、动臂液压缸、斗杆、斗杆液压缸、铲斗、驾驶室等.根据测绘所得各部件的尺寸, 在Solidworks软件中建立挖掘机三维模型, 并且根据各个部件之间的相对位置关系和运动关系进行装配.如图 9所示为所建立的挖掘机三维模型.
|
1-铲斗;2-斗杆铲斗铰接副;3-铲斗液压杆;4-斗杆;5-动臂动臂斗杆铰接副;6-斗杆液压杆;7-动臂;8-动臂液压缸;9-动臂机身铰接副;10-机身 图 9 YC60-8型挖掘机Solidworks三维模型 Fig. 9 3D model of YC60-8 excavator in Solidworks |
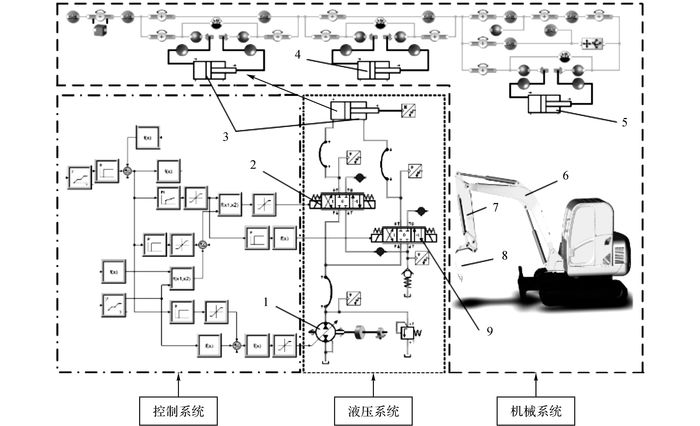
Simulation X仿真软件提供了与其他软件的接口.将建立的三维模型转换为stl格式, 导入Simulation X中, 对其质量、惯性矩及质心坐标进行设置.通过软件中的液压缸、比例阀、泵、管路和油箱等液压模块, 建立挖掘机的进出口独立液压控制系统.通过液压缸模型将工作装置的动力学模型与液压模型连接, 得到其联合仿真模型.如图 10所示为动臂速度位置复合控制策略联合仿真模型.
|
1-变量泵;2-无杆腔阀;3-动臂液压缸;4-斗杆液压缸;5-铲斗液压缸;6-动臂;7-斗杆;8-铲斗;9-有杆腔阀 图 10 动臂速度位置复合控制策略的联合仿真模型 Fig. 10 Joint simulation model of boom's position and velocity compound control strategy |
单纯按液压系统仿真时, 机械系统的转动惯量和等效质量采用常数, 与实际情况不符, 仿真准确性较差.采用机电液联合仿真模型, 能够实时仿真挖掘机各工作姿态时执行机构以及液压系统的动态特性, 实时计算作用在动臂上的等效质量、转动惯量及负载变化, 实现液压系统模型与机械结构模型的无缝连接和实时驱动.
4.2 仿真研究结果如图 11所示为动臂不同控制方式的仿真结果, 为了便于比较, 给出只有速度前馈(velocity feedforward, VF)的开环控制和无定位控制的VFPB的控制结果作为对比.
图 11(a)为只有VF的控制方式, 由于泵的响应时间慢、系统的泄漏等原因, 实际运行速度与期望运行速度相差7 mm/s左右, 实际位置与目标位置偏差约为20 mm.图 11(b)为不加定位控制的VFPB控制方式, 运行过程中加入位置反馈之后, 其速度和位置精度都有所改善, 速度偏差为2 mm/s左右.但是位置反馈的增益值和限幅值都难以直接确定, 需要通过不断调试才能定出一个较为合理的值.在实际工况中, 负载变化、系统泄漏等都会对其参数有较大的影响.图 11(c)为VFPB+PC控制, 在运行过程中, 采用VFPB控制方式, 通过位置闭环对速度前馈的补偿作用, 使其运行速度能够接近预期要求, 实际速度与期望速度偏差小于2 mm/s;在目标位置附近, 转换为PC控制, 提高定位精度, 定位精度小于1 mm, 且定位过程不受运行过程中参数设置的影响.

|
图 11 动臂不同控制方式的仿真结果 Fig. 11 Simulation results of different control modes on boom |
以实验室现有的6 t的挖掘机为试验对象, 构建进出口独立控制系统试验平台, 采用所提出的策略进行控制.试验测试系统工作原理如图 11所示, 试验现场照片如图 12所示.

|
1-变量泵;2-电动机;3-油箱;4-驾驶室;5-动臂进出口阀组;6-动臂;7-动臂液压缸;8-斗杆液压缸;9-斗杆;10-铲斗液压缸;11-铲斗;12-功率仪;13-操作手柄14-Control desk;15-Dspace1103 图 12 挖掘机动臂试验及系统的硬件组成 Fig. 12 Excavator's boom test and system hardwarecomponents |
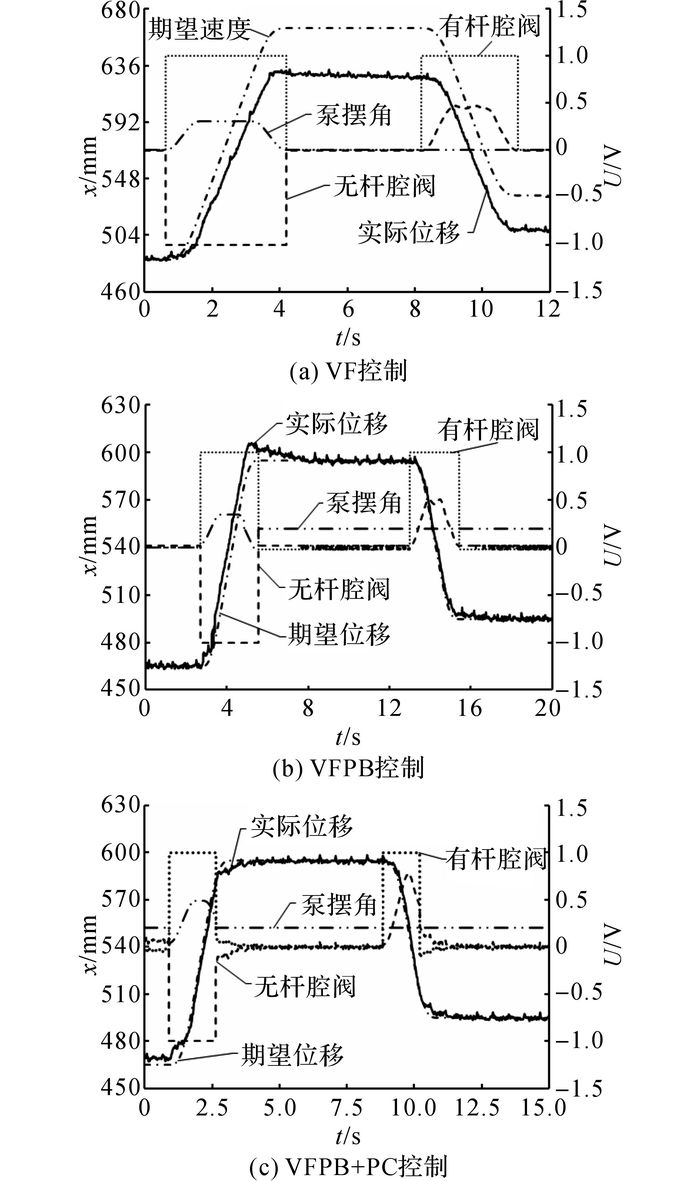
如图 13所示为动臂不同控制方式的试验结果.图 13(a)为仅VF的开环控制, 在动臂上升和下降过程中, 实际运行速度与实际到达位置与预期值都有较大差别.图 13(b)为不加定位控制的VFPB控制, 其速度和位置精度都有所改善.但是在实际控制过程中, 位置闭环的增益值和限幅值都难以直接确定, 需要通过多次试验测试才能定出一个较为合理的值, 且对于不同的工况, 受负载、压力、速度等因素的影响, 其参数可能不同.图 13(b)中位移存在一定的超调值, 原因在于位置闭环限幅值偏大, 导致速度略大于预期速度, 位移产生超调, 之后由于位置闭环的作用再缓慢调节至目标位置, 但是定位至目标位置的时间较长.图 13(c)为VFPB+PC的控制方式, 在运行过程中, 通过位置闭环对速度前馈的补偿作用, 位移与期望位移曲线接近, 运行速度接近期望速度.在2.5 s和10.0 s附近, 其位移值与预期位移值的差值小于模式切换阈值, 切换为PC定位控制方式, 定位误差小于1 mm, 且其定位至目标位置所需时间小于图 11(b)中所需时间.由于系统从运行过程中的VFPB控制切换为定位控制, 其定位精度和定位时间不受运行过程中参数设置的影响.
|
图 13 动臂不同控制方式的试验结果 Fig. 13 Test results of different control modes on boom |
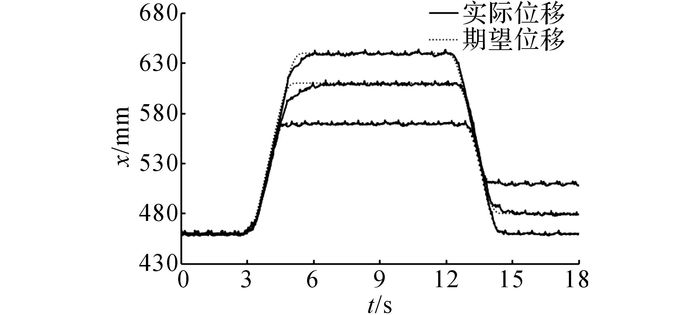
如图 14所示为动臂以相同的最大速度上升和下降至不同的目标位置时的位移曲线.由图可知, 以相同的最大运行速度运行时, 动臂运行过程中的位移变化斜率是相同的, 对于不同的目标位置, 动臂都能按预期的位移曲线到达目标位置.
|
图 14 以相同速度运行至不同目标位置的特性曲线 Fig. 14 Characteristic curves of different target positions with same velocity |
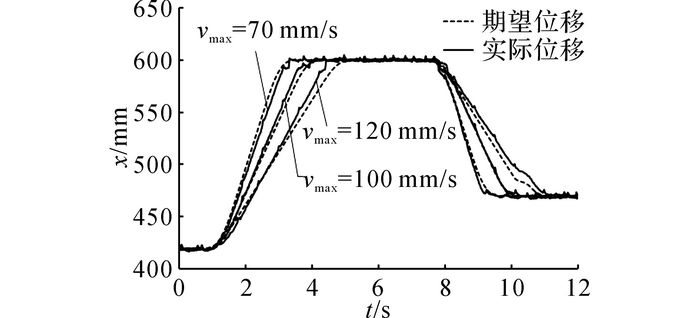
当目标位置相同时, 不同的最大运行速度要求对应不同的预期曲线和运行时间.如图 15所示为动臂以不同的速度上升和下降至相同位置的位移曲线, 最大速度分别为70、100、120 mm/s.由图可知, 对于不同的运行速度, 动臂都能按期望的位移曲线到达目标位置.
|
图 15 以不同速度运行至相同目标位置的特性曲线 Fig. 15 Characteristic curves of same target positions with different velocities |
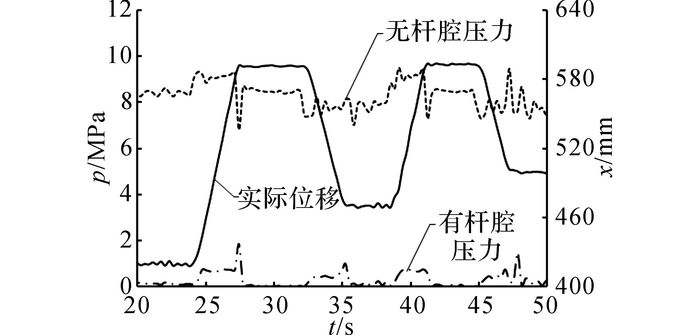
如图 16所示为动臂两次举升和下降过程中动臂液压缸位移和两腔压力的变化曲线.在动臂运行过程中, 无杆腔需要约8 MPa的压力平衡动臂质量, 且在动臂升降过程中该压力变化较小.当动臂上升时, 无杆腔压力只产生一次波动, 幅值约为1 MPa, 压力波动较小, 表明起动平稳性较好.制动时有约为2.3 MPa的压力波动, 原因是切换为定位控制方式时阀芯位移有较大变化, 导致压力产生波动.动臂的2次升降过程都能满足预期设定的速度和位置要求, 表明试验的重复性较好.
|
图 16 动臂运行过程中两腔压力变化曲线 Fig. 16 Pressure curves of two chambers during boom operation |
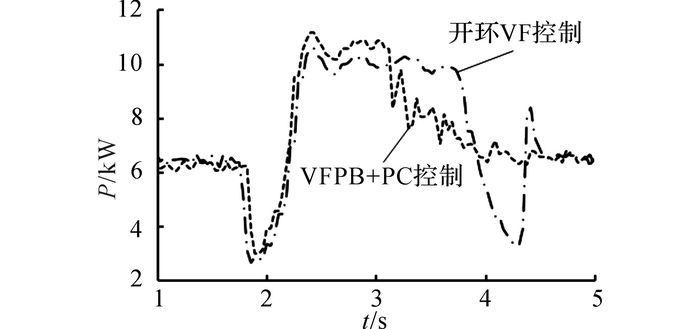
如图 17所示为动臂以相同的速度上升至相同的位置时, 在不同控制方式下电机消耗的功率曲线.对功率进行积分可得, 采用开环VF控制时动臂举升一次消耗20.3 kJ的能量, 采用VFPB+PC控制时, 动臂举升一次消耗20.9 kJ能量, 两者基本相同.由此可知, 采用本文所提控制策略, 可在不增加能耗的前提下提高动臂运行的速度和位置特性.
|
图 17 不同控制方式下的电机消耗功率 Fig. 17 Motor power consumption under different control methods |
(1) 所提出的速度位置复合控制策略能够根据实际工作中不同的目标位置和运行速度要求, 设定相应的预期速度和位移曲线, 使执行器按照预期速度运行到目标位置.仿真表明速度偏差小于2 mm/s, 定位精度小于1 mm.试验结果表明, 运行速度接近期望速度, 压力无明显波动, 定位误差小于1 mm, 平稳性好且定位精度较高.
(2) VF、VFPB和VFPB+PC这3种控制方式的对比结果表明, 采用VFPB+PC控制方式的速度和位置特性较好, 运行过程接近期望速度, 能够较快定位, 且其能耗特性与开环控制基本相同.
(3) 基于进出口独立控制系统, 在动臂升降时, 采用流量匹配和流量再生的控制方式充分利用了进出口独立系统的节能特性, 减少了节流损失, 提高了能量效率.
| [1] | ANDERSSON B. Hydraulic valve means:4662601[P]. 1987-05-05. http://www.freepatentsonline.com/4662601.html |
| [2] | BACKÉ W. Design systematics and perforence of cartridge valve controls[C]//Proceedings of International Conference on Fluid Power. Tampere:ICFP, 1987:1-48. |
| [3] | YAO B, CHRIS D. Energy-saving adaptive robust motion control of single-rod hydraulic cylinders with programmable valves[C]//Proceedings of the American Control Conference.Anchorage:IEEE, 2002:4819-4824. http://ieeexplore.ieee.org/document/1025421/ |
| [4] | YAO B, LIU S. Energy-saving control of hydraulic sys-tems with novel programmable valves[C]//Proceedings of the 4th World Congress on Intelligent Control and Automation. Shanghai:IEEE, 2002:81-91. http://ieeexplore.ieee.org/document/1020129/ |
| [5] | TROXEL N A, YAO B. Hydraulic cylinder velocity control with energy recovery:a comparative simulation study[C]//ASME 2011 Dynamic Systems and Control Conference and Bath/ASME Symposium on Fluid Power and Motion Control. Arlington:ASME, 2011:169-176. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1638344 |
| [6] | SHENOUDA A. Quasi-static hydraulic control systems and energy savings potential using independent metering four-valve assembly configuration[D]. Atlanta:Georgia Institute of Technology, 2006. https://smartech.gatech.edu/bitstream/handle/1853/11553/shenouda_amir_200608_phd.pdf |
| [7] | ERIKSSON B. Control strategy for energy efficient fluid power actuators utilizing individual metering[D]. Linköping:Linköping University, 2007. http://www.diva-portal.org/smash/record.jsf?pid=diva2%3A443&dswid=5396 |
| [8] | ERIKSSON B. Mobile fluid power systems design:with a focus on energy efficiency[D]. Link ping:Link ping University, 2010. http://liu.diva-portal.org/smash/record.jsf?pid=diva2%3A370276&dswid=-2473 |
| [9] | SITTE A, WEBER J. Structural design of independent metering control systems[C]//The 13th Scandinavian International Conference on Fluid Power. Link ping:SICFP, 2013:261-270. http://www.ep.liu.se/ecp/article.asp?issue=092&article=026 |
| [10] | SITTE A, BECK B, WEBER J. Design of independent metering control system[C]//9th International Fluid Power Conference. Aachen:IFK, 2014:428-441. |
| [11] | LUBBERT J, SITTE A, WEBER J. Pressure compensator control:a novel independent metering architecture[C]//10th International Fluid Power Conference. Dresden:IFK, 2016:231-245. http://www.qucosa.de/recherche/frontdoor/?tx_slubopus4frontend%5bid%5d=urn:nbn:de:bsz:14-qucosa-199532 |
| [12] | 权龙, 冯克温, 陈青. 泵阀复合流量匹配进出油口独立控制电液系统: 200710062517. 3[P]. 2008-01-23. http://industry.wanfangdata.com.cn/dl/Detail/Patent?id=Patent_CN200710062517.3&type=Free |
| [13] |
董致新, 黄伟男, 葛磊, 等. 泵阀复合进出口独立控制液压挖掘机特性研究[J].
机械工程学报, 2016, 52(12): 173–180.
DONG Zhi-xin, HUANG Wei-nan, GE Lei, et al. Research on the performance of hydraulic excavator with pump and valve combined separate meter in and meter out circuits[J]. Chinese Journal of Mechanical Engineering, 2016, 52(12): 173–180. |
| [14] |
黄伟男, 权龙, 黄家海, 等. 进出口独立控制液压挖掘机回转系统运行特性[J].
机械工程学报, 2016, 52(20): 159–167.
HUANG Wei-nan, QUAN Long, HUANG Jia-hai, et al. Excavator swing system controlled with separate meter-in and meter-out method[J]. Chinese Journal of Mechanical Engineering, 2016, 52(20): 159–167. |
| [15] |
徐兵, 丁孺琦, 张军辉. 基于泵阀联合控制的负载口独立系统试验研究[J].
浙江大学学报:工学版, 2015, 49(1): 93–101.
XU Bing, DING Ru-qi, ZHANG Jun-hui. Experiment research on individual metering systems of mobile machinery based on coordinate control of pump and valves[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(1): 93–101. |
| [16] |
刘英杰, 徐兵, 杨华勇, 等. 电液比例负载口独立控制系统压力流量控制策略[J].
农业机械学报, 2010, 41(5): 182–187.
LIU Ying-jie, XU Bing, YANG Hua-yong, et al. Strategy for flow and pressure control of electro hydraulic proportional separate meter in and separate meter out control system[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(5): 182–187. |
| [17] |
丁孺琦, 徐兵, 张军辉, 等. 负载口独立控制挖掘机机液耦合模型建立与试验[J].
农业机械学报, 2016, 47(4): 309–31.
DING Ru-qi, XU Bing, ZHANG Jun-hui, et al. Mechanical-hydraulic coupling model of independent metering control excavator and its test verification[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(4): 309–31. DOI:10.6041/j.issn.1000-1298.2016.04.041 |
| [18] |
刘禹廷. 负载口独立挖掘机的智能控制系统研究[D]. 杭州: 浙江大学, 2016.
LIU Yu-ting. Research on intelligent control system for excavator with independent metering[D]. Hangzhou:Zhejiang University, 2016. |
| [19] |
赵鑫. 智能挖掘机轨迹控制研究[D]. 长沙: 中南大学, 2012.
ZHAO Xin. Trajectory control of new intelligent excavator[D]. Changsha:Central South University, 2012. |
| [20] |
李洪人, 王栋梁, 李春萍. 非对称缸电液伺服系统的静态特性分析[J].
机械工程学报, 2003, 39(2): 18–22.
LI Hong-ren, WANG Dong-liang, LI Chun-ping. Static property analysis of electrohydraulic single rod cylinder servo systems[J]. Chinese Journal of Mechanical Engineering, 2003, 39(2): 18–22. |



