旋压成形具有成形力小、可以改善材料性能等优势, 在机械制造领域中占有重要地位.在传统旋压中, 成形件轮廓受到特定形状芯模支撑, 可以获得具有目标形状的产品[1].但是, 特定形状芯模的使用降低了旋压成形的柔性.
无芯模旋压技术采用通用芯模替代特定芯模,解除特定芯模对旋压成形的限制, 增加旋压成形的柔性[2], 该技术适合小批量产品生产及原型试制, 扩大了旋压成形的应用范围, 是一种颇具潜力的新型旋压成形方式.许多学者从成形工艺参数、成形方法和旋轮轨迹等方面对无芯模旋压技术展开了研究[3-7], 以扩大无芯模旋压的应用范围, 改善以形状精度为主的成形质量.
变速成形技术能够改善材料受力状态和变形行为, 降低材料的成形回弹, 提高材料的成形性能[8].变速成形技术较早被引入冲压成形领域, Manabe等[9]于1996年首次研究了变速冲压方法用于成形应变敏感材料的效果.付秀娟[8]研究了成形速度对板料回弹的影响规律, 通过变速成形方法提高了冲压过程中材料成形性能, 改善了冲压成形质量.相比之下, 旋压所用材料应变速率敏感性普遍不高, 成形过程中应变速率跨度较窄.
作为旋压成形中最重要的成形工艺参数[10], 进给比的大小影响应力应变分布和材料流动状态[11], 进给比与旋轮轨迹的匹配程度影响形状精度[12].根据以往研究结果, 在普通旋压中增大进给比有利于降低成形件减薄率, 但同时会降低壁厚均匀性[13-14].旋压件的外径分布、直线度以及椭圆度等尺寸精度随进给比的增加而减小[15].鉴于进给比大小对旋压成形质量和生产效率的重要性, 变速(变进给比)方法不失为无芯模旋压的有效改进方式.在无芯模旋压中进给比对成形质量的影响仍需要进一步探究.
现今数控旋压设备的应用使变速旋压成形技术具备了硬件基础, 变速成形技术在旋压成形领域的应用已成为可能, 然而针对该项技术的研究非常少.作为目前为数不多涉及变进给比旋压的研究, 詹梅等[14]采用首道次与后续道次设置不同进给比的方式研究了改变不同道次中进给比对壁厚分布的影响, 结果表明:首道次成形过程中壁厚极小值随进给比先增大后减小, 后续道次中壁厚分布均匀性随进给比的增大而增加.Ozer等[16]采用单道次普旋过程中进给比线性递增和递减的设计方式调整了道次内进给比, 结果表明:采用递减式进给比设计可以解决产品边缘起皱问题.以上2项研究均属于尝试性定性研究, 未提出进给比定量设计方法.
进给比参数对旋压成形质量具有重要的作用, 如何优化分配和设计进给比及成形时间, 从而改善无芯模旋压成型质量, 提高加工效率, 目前还缺少有效的方法和依据.本文首先进行成形量量化表征, 在此基础上提出道次间及道次内定量设计方法, 使坯料变形速度适应各阶段成形特点, 实现成形时间的道次间及道次内优化分配从而提高成形精度, 改善成形质量.
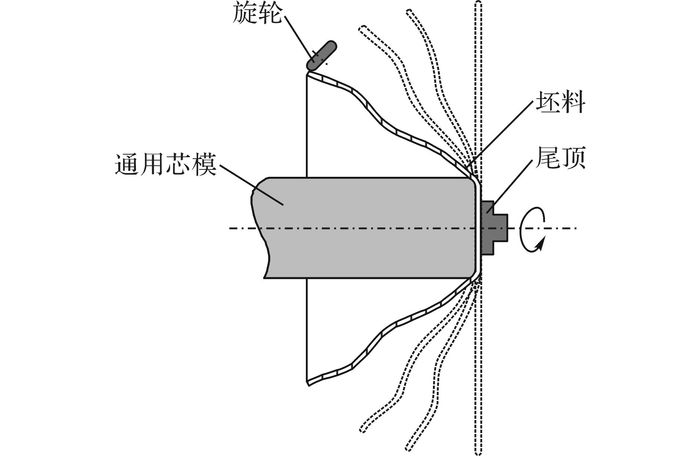
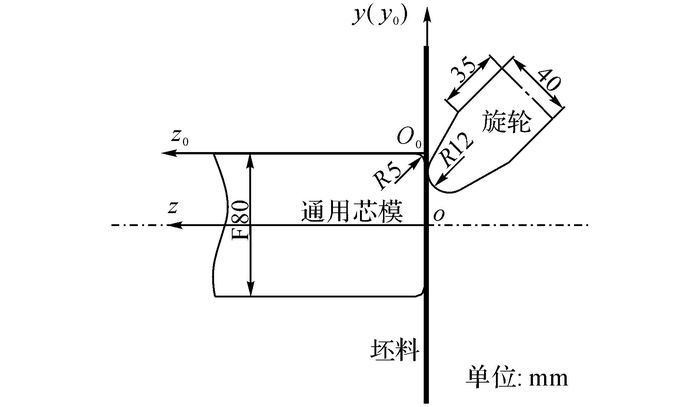
1 无芯模旋压恒进给比实验 1.1 实验设置无芯模旋压坯料成形过程如图 1所示.旋压成形各部分初始位置及其尺寸如图 2所示, 在通用芯模与旋轮共同的对称剖面上建立如图 2所示的主坐标系o-y-z及旋轮轨迹坐标系o0-y0-z0.
|
图 1 无芯模旋压示意图 Fig. 1 Diagram of die-less spinning |
|
图 2 无芯模旋压实验原理图 Fig. 2 Schematic of die-less spinning experiment |
旋压成形实验用圆形坯料切割自SPHC商用钢板, 厚度为1.9 mm, 直径为240 mm.芯模转速为400 r/min.旋轮结构及工艺参数参照文献[17].
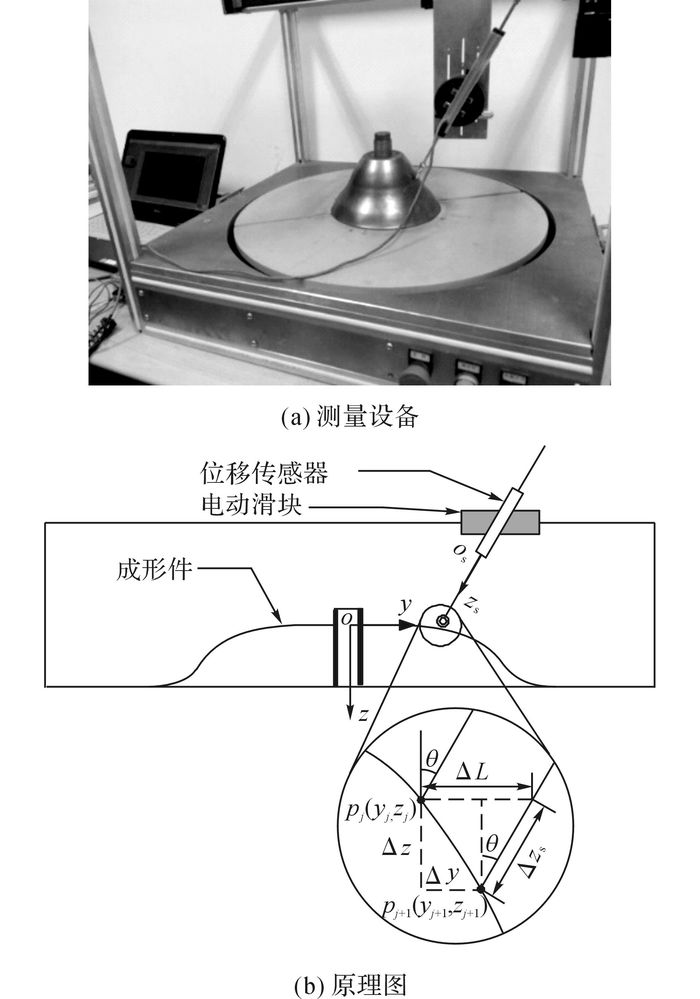
无芯模旋压成形的主要质量参数包括成形件形状误差及壁厚减薄率.其中, 形状误差为成形件轮廓形状与目标形状之差.为获取成形件轮廓形状, 采用如图 3所示的测量方法.根据如图 3(b)所示的几何关系, 成形件轮廓数据可以通过下式的迭代方法获取, 即通过前一采样点Pj的坐标获取采样点Pj+1的坐标:
|
图 3 旋压成形件的轮廓形状测量方法 Fig. 3 Measuring method for contour shape of spinning forming parts |
| $ \left. \begin{array}{l} {z_{j + 1}} = {z_j} + \Delta z = {z_j} + \Delta {z_{\rm{s}}}\cos \theta ,\\ {y_{j + 1}} = {y_j} + \Delta y = {y_j} + \Delta L - \Delta {z_{\rm{s}}}\sin \theta . \end{array} \right\} $ | (1) |
式中:zj及yj分别为采样点pj在如图 3(b)所示的局部坐标系下的坐标值;Δz及Δy为点pj+1和点pj的坐标值差;Δzs为位移传感器采集的位移量;ΔL为单个采样周期位移传感器的y向位移量; θ为位移传感器中轴线与z轴夹角.
采用如图 4所示的PX-7超声波壁厚测量仪获取壁厚数据.由于测量仪探头存在一定面积, 采样点数量受限, 而壁厚极小值点的强度决定成形件强度, 需要对成形件壁厚极值点进行探测.首先在成形件表面绘出等间距的3条母线, 将壁厚仪的探头在成形件表面上沿一条母线探测局部壁厚极值点.

|
图 4 旋压成形件壁厚测量设备 Fig. 4 Measuring device for wall thickness of spinning forming parts |
当所有的壁厚局部极值点都测量完毕后, 在母线上主成形区内再选取几个采样点进行测量, 同时保持采样点沿母线间距基本大于10 mm, 共取7个采样点.
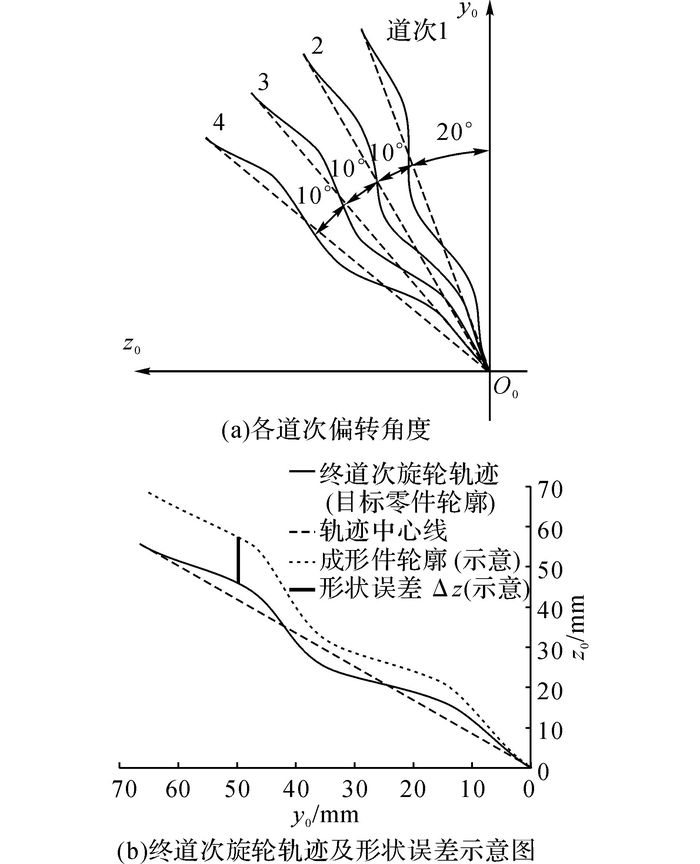
1.2 旋轮轨迹对象旋压过程共4个道次, 为减小对芯模的依赖, 采用偏转式成形方法, 即各道次轨迹形状与成形目标形状相同长度相等, 如图 5所示.目标零件外轮廓与图 5中的终道次轨迹形状相同, 零件设计图如图 6所示.
|
图 5 无芯模旋压成形实验旋轮轨迹示意图 Fig. 5 Sketch of roller trace of die-less spinning forming experiment |

|
图 6 无芯模旋压成形目标零件外轮廓设计图 Fig. 6 Design drawing of outer contour of die-less spinning forming part |
旋压成形中坯料径向受到拉伸,因而坯料径向尺寸逐道次增大, 旋轮轨迹长度逐道次增加.为控制成形件长度同时避免边缘起皱, 采用等长轨迹, 即保持各道次轨迹长度相等, 由此造成坯料边缘堆积多余材料, 如图 7(a)所示.多余部分在后续工艺中通过切割去除.采用延伸轨迹成形的零件如图 7(b)所示.

|
图 7 采用等长和延伸轨迹的成形件轮廓外形对比 Fig. 7 Comparison of formed parts' contour profile with equal length and extended paths |
由于坯料的弹塑性变形特性, 坯料成形到目标形状后, 弹性变形发生恢复性变形(回弹)造成形状误差, 即如图 5(b)加粗线条所示.如图 5(b)所示的成形件目标零件轮廓形状, 同时也是终道次旋轮与坯料的接触点轨迹.
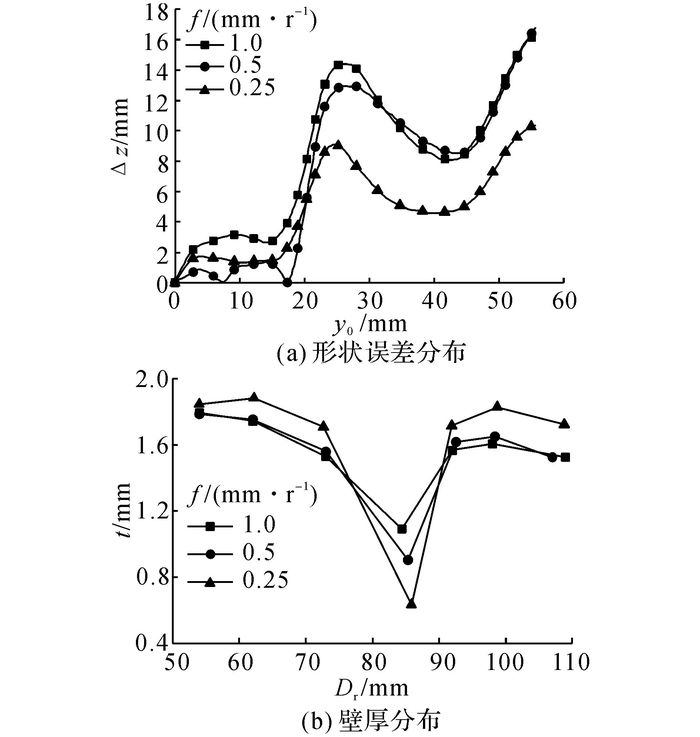
1.3 进给比对成形质量的影响如图 8所示为采用不同恒进给比的成形件质量对比, 其中t为成形件壁厚, Dr为采样点沿母线到点o的距离.如图 8所示, 当进给比f从1.00 mm/r减小至0.25 mm/r, 成形件的形状误差减小, 最大壁厚减薄率增大.
|
图 8 改变恒进给比对成形质量的影响 Fig. 8 Influence of changing feed ratio on forming quality |
形状精度的控制是无芯模旋压研究中的难点与重点, 当f=1 mm/r时, 形状误差较大, 因此当采用不同的变进给比方法时, 形状误差也相对较大, 便于对方法进行对比.选取形状误差较大的f=1 mm/r为研究的基准进给比, 即保持各种设计方法的总成形时间与f=1 mm/r时的总成形时间相同.
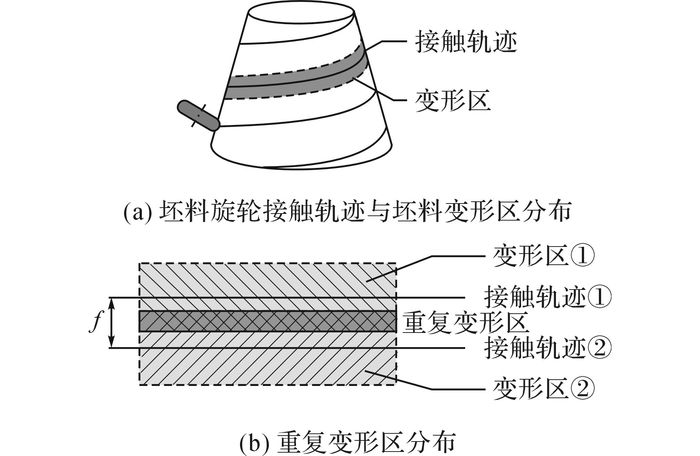
2 基于匀速环向应变的变进给比旋压成形机理 2.1 进给比对成形质量的影响机理旋轮与坯料的空间接触轨迹如图 9(a)所示, 接触轨迹间距与进给比f大小相等.接触轨迹周围为材料变形区.
|
图 9 旋压坯料变形区分布原理图 Fig. 9 Distribution diagram of spinning billet'sdeformation zone |
如图 9(b)所示, 当进给比较小时, 接触轨迹① 与接触轨迹② 的间距较小, 导致变形区发生重叠, 坯料发生重复变形, 产生重复变形区.重复变形区的材料受到旋轮的反复作用, 塑性应变占比增大, 回弹变形受到抑制.
2.2 基于环向应变的成形量量化表征方法道次成形量与旋轮轨迹相关, 为提高道次进给比与其成形量的匹配度, 需要根据各道次旋轮轨迹几何特性进行成形时间分配, 因此成形量的量化算法是变进给比方法的基础.
普通旋压采用道次轨迹偏转角和道次贴模长度对道次成形量进行量化[18-19].无芯模旋压无法采用贴模长度进行计算.对于旋轮轨迹形状较复杂的无芯模旋压, 道次轨迹偏转角无法精确量化其成形量[20].
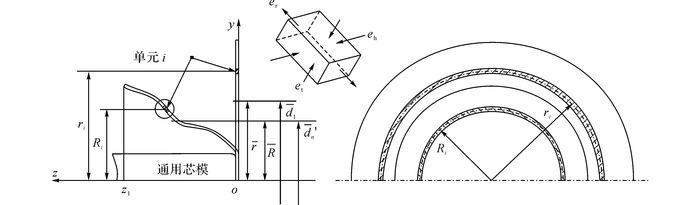
多道次普通旋压的主要目的和特征是改变坯料的直径尺寸[2], 多道次无芯模旋压与其类似.根据该特征, 在坯料变形机理研究的基础上提出根据坯料材料的平均直径尺寸变化量, 即环向应变量对成形量进行参数化表征.本文以如图 10所示的环形材料单元作为研究对象.
|
图 10 无芯模旋压坯料尺寸变化及环向应变示意图 Fig. 10 Schematic of billet size change and hoop strain distribution of die-less spinning |
第i道次的平均环向应变为
| $ {{\bar \varepsilon }_{{\rm{h}}i}} = \ln \frac{{{{\bar d'}_i}}}{{{{\bar d}_i}}}, $ | (2) |
式中:di及d′i分别为第i道次成形前、后坯料的平均直径, 通过曲线积分方法获取:
| $ \bar r = \frac{{\int_0^{{z_1}} {f\left( z \right){\rm{d}}z} }}{{{z_1}}}. $ | (3) |
其中, f(z)为旋轮轨迹曲线方程.
由于di=d′i-1, 整体旋压过程和第i道次的环向应变关系如下:
| $ \begin{array}{l} {{\bar \varepsilon }_{\rm{h}}} = \ln \frac{{{{\bar d'}_n}}}{{{{\bar d}_1}}} = \ln \left( {\frac{{{{\bar d}_2}}}{{{{\bar d}_1}}}\frac{{{{\bar d}_3}}}{{{{\bar d}_2}}} \cdots \frac{{{{\bar d'}_n}}}{{{{\bar d}_n}}}} \right) = \\ \;\;\;\;\;\;\;\ln \left( {\frac{{{{\bar d'}_1}}}{{{{\bar d}_1}}}\frac{{{{\bar d'}_2}}}{{{{\bar d}_2}}} \cdots \frac{{{{\bar d'}_n}}}{{{{\bar d}_n}}}} \right) = \sum\limits_{i = 1}^n {{{\bar \varepsilon }_{{\rm{h}}i}}} . \end{array} $ | (4) |
式(4) 建立了与旋轮轨迹曲线方程相匹配的旋压成形量量化表征方法, 为获取与成形量相适应的进给比设计方案奠定基础.
2.3 基于旋压成形量的变进给比旋压机理假设第一道次平均环向应变小于第二道次, 即εh1 < εh2.当采用恒进给比成形方法时, 由于两道次轨迹长度相同, 两者成形时间相等, 有
对于道次间成形时间分配, 需要使各道次的环向应变速率保持一致:
| $ {\overline {\dot \varepsilon } _{{\rm{h1}}}} = {\overline {\dot \varepsilon } _{{\rm{h2}}}} = \cdots = {\overline {\dot \varepsilon } _{{\rm{h}}n}} = {\overline {\dot \varepsilon } _{\rm{h}}}. $ | (5) |
式中:
在提出成形量算法及变进给比设计思路的基础上, 根据道次间环向应变速率相等的原则进行成形时间分配.总成形时间T为各道次成形时间之和:
| $ T = \sum\limits_{i = 1}^n {\frac{{{{\bar \varepsilon }_{{\rm{h}}i}}}}{{{{\overline {\dot \varepsilon } }_{{\rm{h}}i}}}}} . $ | (6) |
将式(5) 代入式(6) 可得
| $ T = \sum\limits_{i = 1}^n {\frac{{{{\bar \varepsilon }_{{\rm{h}}i}}}}{{{{\overline {\dot \varepsilon } }_{\rm{h}}}}}} = \frac{1}{{{{\overline {\dot \varepsilon } }_{\rm{h}}}}}\sum\limits_{i = 1}^n {{{\bar \varepsilon }_{{\rm{h}}i}}} , $ | (7) |
则基于匀速环向应变的道次成形时间为
| $ {T_i} = T{{\bar \varepsilon }_{{\rm{h}}i}}/\sum\limits_{j = 1}^n {{{\bar \varepsilon }_{{\rm{h}}j}}} , $ | (8) |
各道次的环向应变速率为
| $ {\overline {\dot \varepsilon } _{{\rm{h}}i}} = \frac{1}{T}\sum\limits_{j = 1}^n {{{\bar \varepsilon }_{{\rm{h}}j}}} . $ | (9) |
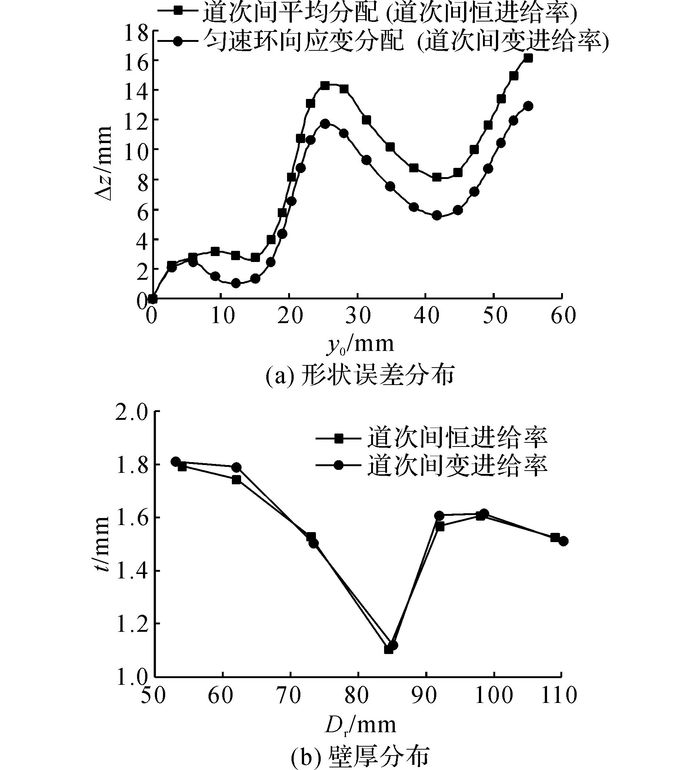
根据式(9), 各道次的环向应变速率仅与成形过程总环向应变和总成形时间有关, 因此道次间的环向应变速率相等, 由此形成基于匀速环向应变的道次间成形时间应变方法.将基于匀速环向应变的成形量分配方法应用于如图 5(a)所示的旋压成形过程,并与传统的恒进给比方法进行对比,如表 1所示, 其中第i道次成形时间在总成形时间中的占比(ηi=Ti/T)根据如图 5(a)所示的道次旋轮轨迹通过式(8) 进行计算, fi为第i道次进给比, 根据道次成形时间进行计算.这2种方法的成形件质量参数对比如图 11所示.
| 表 1 采用不同成形时间分配方法的各道次成形时间占比和进给比对比 Table 1 Comparison of passes' forming time and feed ratios with different processing time allocation methods |
|
图 11 不同道次成形时间分配方法对成形质量的影响 Fig. 11 Influence of different processing time allocation methods between passes on forming quality |
如图 11所示, 与传统道次间恒进给比相比, 根据道次平均环向应变进行成形时间分配的道次间变进给比方法成形件形状误差较小, 壁厚减薄差距不大.
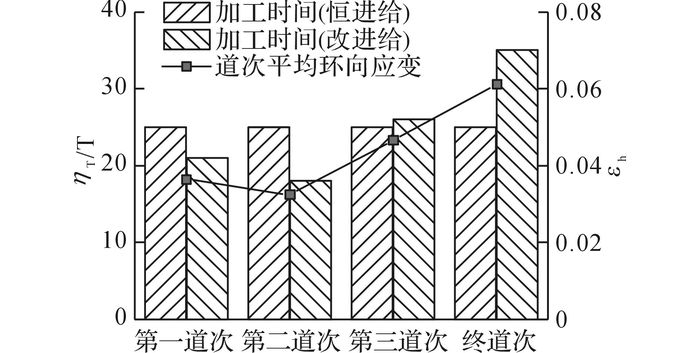
各道次的平均环向应变及采用道次间恒/变进给比的各道次成形时间对比如图 12所示, 其中道次平均环向应变根据图 5(a)所示的道次旋轮轨迹通过式(2) 进行计算, ηT为道次成形时间在总成形时间中的占比, εh为环向应变.
|
图 12 采用不同道次间成形时间分配方法时道次平均环向应变的匹配程度对比 Fig. 12 Matching degree comparison of passes' average hoop strains under different processing timeallocation methods betwee passes |
综上, 保持道次间环向变形速度不变, 能在成形时间不变的前提下提高形状精度, 即实现道次进给比设计的“匀速变形原则”.
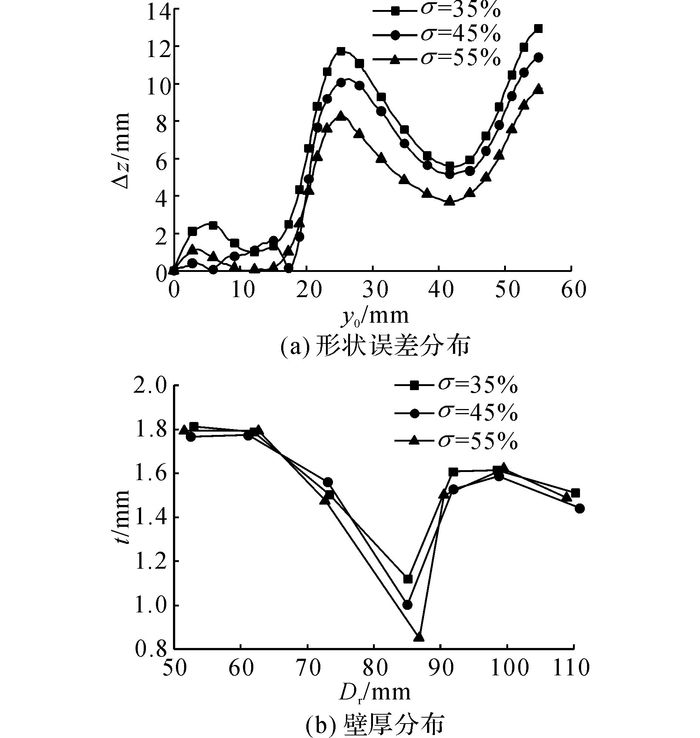
4 基于终道次成形时间占比优化的道次间变进给比终道次(i=4) 是直接决定成型件形状的关键道次, 逐步增大终道次成形时间T4在总成形时间T中的占比σ=T4/T, 相应的各道次进给比设计如表 2所示, 其中终道次成形时间占比按照10%递增, 并保持其他道次占比之间的比值基本不变.相应的成形质量参数如图 13所示.
| 表 2 采用不同终道次成形时间占比时的各道次成形时间分配和进给比 Table 2 Processing time allocation and feed ratios of passes under different final pass processing time percents |
|
图 13 终道次成形时间对成形质量的影响 Fig. 13 Influence of final-pass forming time on formingquality |
根据图 13, 形状误差随着σ增大而减小, 壁厚最小值随着σ增大而减小.在道次成形时间分配时, 优先保证终道次坯料变形充分成形有利于改善形状精度, 即实现道次进给比设计的“终道次充分成形原则”.
增加终道次的成形时间违背了第3章提出的“匀速变形原则”, 在提高成形件形状精度的同时加剧壁厚减薄, 需要在两者之间进行权衡.产品的设计强度要求最小壁厚大于规定值, 在此基础上, 尽量增大终道次成形时间占比.目标产品最小壁厚要求大于1 mm, 由图 13(b)可见, 当σ=45%时成形件最小壁厚值略大于1 mm, 由此得σ优化值约为45%.
5 道次内变进给比鉴于终道次成形对成形件形状的重要影响, 为进一步提高成形精度, 针对终道次进行道次内成形时间优化分配.
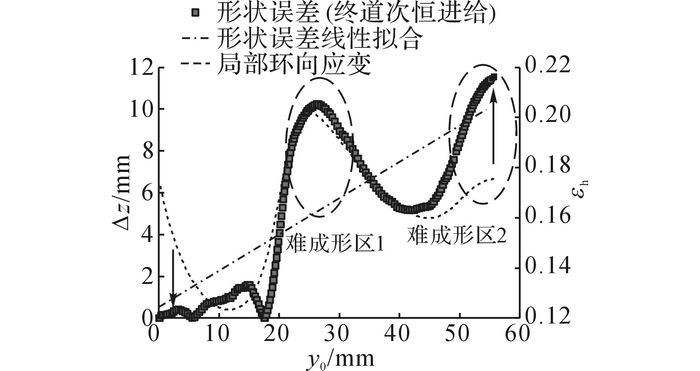
观察如图 14所示的当σ=45%时终道次恒进给成形件形状误差与局部环向应变分布特性, 可以发现两者在主成形区中间的大部分区域有较高的相似度, 相应的环向应变分布曲线由图 5中的终道次旋轮轨迹根据式(2) 计算获得.在y0为20~30 mm及50~60 mm的环向应变极值区, 即图中的难成形区1和2, 形状误差出现局部极值.可见, 随着局部环向应变增大, 成形量增大, 导致局部成形困难, 因此形状误差较大.在y0较小和较大的成形区两端两者差异较大, 其中靠近芯模的部分形状误差相较小, 而在远端相对较大(如图中箭头所示).
|
图 14 形状误差与局部环向应变分布的相似性 Fig. 14 Similarity of shape error and local hoop strain distribution |
从图 14中的形状误差拟合线可以发现, 随着y0增加, 形状误差总体呈增大趋势.这种趋势体现了离芯模越远, 形状误差越大的分布特征, 也是形状误差与局部环向应变两端分布差异的原因.这种形状误差的增大趋势产生原因是坯料绕着通用芯模圆角处发生弯折,如图 1所示,而当旋轮撤出,坯料在弹性变形恢复作用下发生整体回弹.
由于形状误差与轨迹的局部环向应变基本呈正相关, 针对终道次内的进给比设计, 提出基于道次内变进给比成形方法, 即在局部环向应变较大的部分, 减小旋轮进给速度.
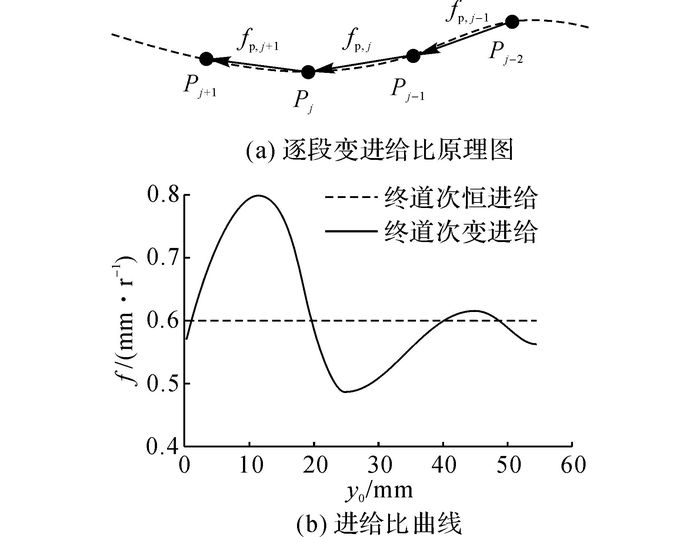
实际成形中采用如图 15(a)所示的直线插补方法控制旋轮运动逼近理论旋轮轨迹, 即通过m+1个点将旋轮轨迹分为m个等距直线段.
|
图 15 单道次内变进给比方法原理图 Fig. 15 Schematic diagram of varying feed ratio method within single pass |
根据道次内各段环向应变速率不变的原则, 各插补段环向应变速率与终道次平均环向应变速率相等:
| $ {{\dot \varepsilon }_{{\rm{h}},1}} = {{\dot \varepsilon }_{{\rm{h}},2}} = \cdots = {{\dot \varepsilon }_{{\rm{h}},j}} = {\overline {\dot \varepsilon } _{{\rm{h}}n}}, $ | (10) |
式中:
第j段的环向应变速率为环向应变与成形时间的比值:
| $ {{\dot \varepsilon }_{{\rm{h}},j}} = \frac{{{\varepsilon _{{\rm{h}},j}}}}{{{t_j}}}. $ | (11) |
式中:εh, j为点pj位置坯料单元的环向应变, 根据如图 5所示旋轮轨迹中该点前一道次及终道次径向位置进行计算;tj为第j个插补段的成形时间.
将式(11) 代入式(10) 可得
| $ \frac{{{\varepsilon _{{\rm{h}},1}}}}{{{t_1}}} = \frac{{{\varepsilon _{{\rm{h}},2}}}}{{{t_2}}} = \cdots = \frac{{{\varepsilon _{{\rm{h}},j}}}}{{{t_j}}} = \cdots = \frac{1}{{{T_n}}}\sum\limits_{k = 1}^m {{\varepsilon _{{\rm{h}},k}}} , $ | (12) |
| $ {t_j} = {\varepsilon _{{\rm{h}},j}}{T_n}/\sum\limits_{k = 1}^m {{\varepsilon _{{\rm{h}},k}}} . $ | (13) |
式中:Tn为终道次总成形时间.
假设各插补线段的长度为lc, 芯模转速为nr, 则第j段的局部进给比fp, j可表示为
| $ {f_{{\rm{p}}.j}} = \frac{{{l_c}}}{{{t_j}{n_{\rm{r}}}}}. $ | (14) |
终道次进给比fn与总成形长度mlc和成形时间Tn、转速nr之间的关系可表示为
| $ {f_n} = \frac{{m{l_{\rm{c}}}}}{{{T_n}{n_{\rm{r}}}}}. $ | (15) |
将式(13) 代入式(14) 可得
| $ {f_{{\rm{p}},j}} = \frac{1}{{m{\varepsilon _{{\rm{h}},j}}}}\frac{{m{l_{\rm{c}}}}}{{t{n_{\rm{r}}}}}\sum\limits_{k = 1}^m {{\varepsilon _{{\rm{h}},k}}} . $ | (16) |
将式(15) 代入式(16) 可得到匀速环向应变条件下第j段的局部进给比:
| $ {f_{{\rm{p}},j}} = \frac{{{f_n}}}{{m{\varepsilon _{{\rm{h}},j}}}}\sum\limits_{k = 1}^m {{\varepsilon _{{\rm{h}},k}}} . $ | (17) |
根据图 15(b)的进给比曲线进行旋压成形试验,获取的成形件质量如图 16所示.

|
图 16 单道次内成形时间分配方法对成形质量的影响 Fig. 16 Effect of processing time allocation method within single pass on forming quality |
采用基于匀速环向应变的终道次变进给比方法的成形件与恒进给相比, 难成形区1的形状误差得到了有效降低, 而难成形区2的形状精度改善效果并不明显.坯料边缘的形状误差的主要成因是坯料的整体回弹, 而通过降低该区域的局部进给比很难有效抑制坯料整体回弹造成的误差.可见增加大环向应变部分的成形时间占比, 使该部分坯料得到充分成形, 能有效降低形状误差, 即道次内进给比设计的“大环向应变充分成形原则”.
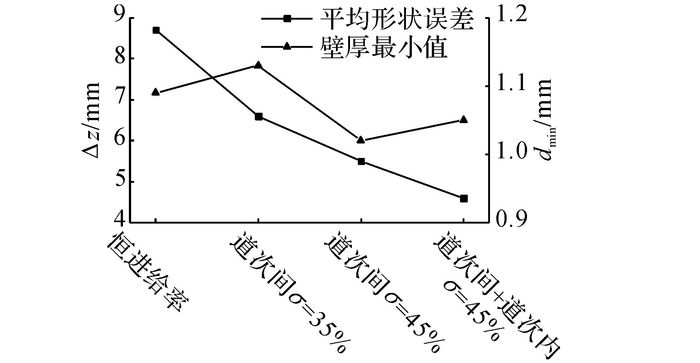
6 进给比方案成形质量比较进给比方案优化思路及相应质量参数实验结果如图 17所示, 其中Δzm为平均形状误差, tmin为壁厚最小值.实验结果显示:采用衡进给比成形方式, 平均形状误差约为8.7 mm;根据“环向应变匀速分解原则”进行道次间变进给比设计, 平均形状误差降低了约24%;在此基础上结合“终道次充分成形原则”进行变进给比设计,平均形状误差降低了约37%, 与普通道次间变进给比方案相比平均形状误差降低约17%;通过道次间及道次内变进给比相结合的方法使形状误差降低了约47%, 与道次内恒进给比方案相比平均形状误差降低了16%.相应的成形件外形轮廓对比如图 18所示.
|
图 17 采用变进给比成形方法对成形质量的影响 Fig. 17 Influence of varying feed ratio forming method on forming quality |

|
图 18 采用不同进给比方案的成形件轮廓 Fig. 18 Contour of formed parts using different feedratio schemes |
(1) 在恒进给比条件下, 降低进给比抑制形状误差会加剧壁厚减薄, 甚至产生开裂.
(2) 保持道次间平均环向应变速度相等, 可以有效降低形状误差, 同时防止壁厚过度减薄, 由此提出道次进给比设计的“匀速变形原则”.根据该原则提出基于道次间匀速环向应变的道次间变进给比方案, 与恒进给方案相比, 平均形状误差降低了24%.
(3) 终道次成形过程直接影响最终成形件轮廓, 增加终道次成形时间占比可以有效提高形状精度, 即道次间进给比设计的“终道次充分成形原则”.根据该原则提出基于终道次成形时间占比优化的道次间变进给比方案, 与普通道次间变进给比方案相比, 平均形状误差降低了17%.
(4) 减小难成型区进给比从而增大其成形时间占比, 可增加成形充分性, 从而有效降低整体形状误差, 即道次内进给比设计的“大环向应变充分成形原则”.根据该原则提出基于道次内匀速环向应变的道次内变进率方案, 与道次内恒进给比方案相比, 平均形状误差降低了16%;与传统恒进给比方案相比, 平均形状误差降低了47%.
目前无芯模旋压仍有一些问题需要解决, 例如:成形件形状偏差整体偏高及壁厚减薄率偏大等, 后续研究可以尝试采用轨迹修正及正反程偏移式成形方法予以克服.此外, 成形件椭圆度等形状指标以及多道次旋压导致材料的硬化等内容需要进一步研究.
| [1] | WONG C C, DEAN T A, LIN J. A review of spinning, shear forming and flow forming processes[J]. International Journal of Machine Tools and Manufacture, 2003, 43(14): 1419–1435. DOI:10.1016/S0890-6955(03)00172-X |
| [2] | MUSIC O, ALLWOOD J M, KAWAI K. A review of the mechanics of metal spinning[J]. Journal of Materials Processing Technology, 2010, 210(1): 3–23. DOI:10.1016/j.jmatprotec.2009.08.021 |
| [3] | LI Y, WANG J, LU G D, et al. Three-dimensional finite element analysis of effects of roller intervals on tool forces and wall thickness in stagger spinning of thin-walled tube[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2013, 227(7): 1429–1440. DOI:10.1177/0954406212466518 |
| [4] | JIA Z, HAN Z R, XU Q, et al. Effects of processing parameters on the surface quality of square sectiondie-less spinning[J]. International Journal of Advanced Manufacturing Technology, 2015, 80(9-12): 1689–1700. DOI:10.1007/s00170-015-7055-9 |
| [5] | LIU C H. The simulation of the multi-pass and die-less spinning process[J]. Journal of Materials Processing Technology, 2007, 192(5): 518–524. |
| [6] | LI Y, WANG J, LU G D, et al. A numerical study of the effects of roller paths on dimensional precision in die-less spinning of sheet metal[J]. Journal of ZhejiangUniversity Science A, 2014, 15(6): 432–446. |
| [7] |
李勇. 无芯模旋压回弹变形特性及多道次轨迹规划方法仿真研究[D]. 杭州: 浙江大学, 2014.
LI Yong. A numerical study of springback deformation properties of die-less spinning and its multi roller path planning method[D]. Hangzhou:Zhejiang University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014173121.htm |
| [8] |
付秀娟. 变速/变载条件下板料冲压成形性能及其变形机理研究[D]. 武汉: 华中科技大学, 2012.
FU Xiu-juan. Study on formability and forming mechanism of sheet metals in variable forming speed/forming loading stamping process[D]. Wuhan:Huazhong University of Science and Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10487-1013010903.htm |
| [9] | MANABE K, KOYAMA H, KATOH K, et al. Intelligent design architecture for process control of deep-drawing[C]//Proceedings of the Second International Conference on Intelligent Processing and Manufacturing of Materials, 1999. IPMM'99. Forrest:IEEE, 1999:571-576. http://ieeexplore.ieee.org/document/792541/ |
| [10] |
MASU J H, 王强. 普旋过程中旋轮道次的制定对产品的影响[J]. 锻压技术, 1989(5): 45-51.
HAYAMA M.Effect of roller pass programming on products in conventional spinning[J]. Forging and Stamping Technology, 1989(5):45-51. http://www.cnki.com.cn/Article/CJFDTOTAL-DYJE198905008.htm |
| [11] | ZHAN M, YANG H, ZHANG J H, et al. 3D FEManalysis of influence of roller feed rate on forming force and quality of cone spinning[J]. Journal of Materials Processing Technology, 2007, 187(12): 486–491. |
| [12] |
曾超, 张赛军, 夏琴香, 等. 旋轮轨迹和工艺参数对多道次拉深旋压成形质量的影响研究[J].
锻压技术, 2014, 39(1): 58–63.
ZENG C, ZHANG S J, XIA Q X, et al. Research on effect of roller-races and process parameters on multi-pass drawing spinning quality[J]. Forging and Stamping Technology, 2014, 39(1): 58–63. |
| [13] |
黄成龙. 普通旋压成形质量分析及控制研究[D]. 广州: 华南理工大学, 2015.
HUANG C L.Research on the forming quality analysis and control of conventional spinning.[D].Guangzhou:South China University of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10561-1015989169.htm |
| [14] |
詹梅, 李虎, 杨合, 等. 大型复杂薄壁壳体多道次旋压过程中的壁厚变化[J].
塑性工程学报, 2008, 15(2): 115–121.
ZHAN M, LI H, YANG H, et al. Wall thickness variation during multi-pass spinning of large complicated shell[J]. Journal of Plasticity Engneering, 2008, 15(2): 115–121. |
| [15] |
袁玉军. 薄壁件精密旋压成形方法及缺陷控制研究[D]. 广州: 华南理工大学, 2013.
YUAN Y J.Research on the thin-walled workpiece's forming method and defect controlling of the accurate spinning[D].Guangzhou:South China University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10561-1014065456.htm |
| [16] | OZER A, SEKIGUCHI A, ARAI H. Experimental implementation and analysis of robotic metal spinning with enhanced trajectory tracking algorithms[J]. Robotics and Computer Integrated Manufacturing, 2012, 28(4): 539–550. DOI:10.1016/j.rcim.2011.12.003 |
| [17] | WANG L, LONG H. Roller path design by tool compensation in multi-pass conventional spinning[J]. Materials and Design, 2013, 46(4): 645–653. |
| [18] | HAYAMA M, KUDO H, SHINOKURA T. Study of the pass schedule in conventional spinning[J]. Journal of the Japan Society of Mechanical Engineers, 1970, 13(65): 1358–1365. |
| [19] | LIN X J, GE T, WANG J, et al. Numerical investigation of effects of deformation allocation on multi-pass conventional spinning process of curvilinear generatrix parts[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2015, 229(18): 3299–3307. DOI:10.1177/0954406215570384 |
| [20] | GUO H, WANG J, LU G, et al. A study of multi-pass scheduling methods for die-less spinning[J]. Journal of Zhejiang University:SCIENCE A, 2017, 18(6): 413–429. DOI:10.1631/jzus.A1600403 |



