2. 中国航天空气动力技术研究院, 北京 100074
2. China Academy of Aerospace Aerodynamics(CAAA), Beijing 100074, China
作为自主水下航行器的一个分支, 水下滑翔机依靠净浮力的改变实现垂直方向的运动, 同时利用机翼上产生的前向升力分量实现前向运动.由于使用净浮力作为动力, 水下滑翔机具有长航时、长航程的特点.自从Stommel[1]于1989年首次提出水下滑翔机的概念, 3个典型的滑翔机类型被开发和利用于海洋探测:Slocum[2]、Spray[3]和Seaglider[4].此后水下滑翔机继续在世界范围内不断发展, 如Fòlaga[5]、Sterne[6]、Gliding Robotic Fish[7-8]和USM hybrid-driven UG[9]等.
水下滑翔机有2种典型的稳态运动模式:垂直面内的锯齿形运动和定常回转螺旋形运动.锯齿形运动是纯二维的运动, 很容易理解.对于螺旋形运动, 早期的滑翔机是按照正螺旋方式运行, 即转弯方向与机翼升力侧向分量的方向一致[10-12].但是, 有的滑翔机遭遇了反螺旋运动模式, 即转弯方向与机翼升力水平分量方向相反,如:滑翔机Sterne[13]在海洋实验当中遭遇了反螺旋运动.由于海洋中存在各种干扰(如:洋流), 反螺旋运动是滑翔机的短暂现象还是固有运动形式不得而知.Phoemsapthawee等[13]使用一个基于势流的模拟器模拟了拥有3个不同面积的尾翼的滑翔机的螺旋运动, 认为不合适的尾翼面积会导致反螺旋运动, 但该结论是纯理论的, 没有任何实验验证;又认为反螺旋运动是所谓的“反常行为”, 应该要设法避免.Liu等[14]从理论和湖水实验两方面详细研究了反螺旋运动, 得出了反螺旋运动可以稳定存在的结论.
本文进一步研究机翼沿着机身中轴线的位置对滑翔机螺旋运动中的转弯方向和转弯速率的影响.通过建立并求解一个描述正/反螺旋运动特性的平衡模型, 获得重心位置以及机翼位置与正/反螺旋运动特性之间的对应关系.这些关系对于滑翔机的设计优化有很好的参考价值.
1 平衡模型滑翔机的平衡方程基于以下2个重要假设[14]:
1) 运动假设:正/反螺旋运动在稳态时可以简单看作是由一个水平面内匀速圆周运动和一个竖直方向的匀速直线运动的叠加运动.假设滑翔机为刚体, 滑翔机浮心的速度可以代表滑翔机的速度, 匀速圆周运动的角速度可以代表滑翔机的角速度.若考虑惯性离心力, 螺旋运动在非惯性系下(见2.1节)可以看作是平衡的, 即说合力和合力矩都为零向量.
2) 流动假设:当攻角、侧滑角、角速度都比较小时(见2.2节), 流体是定常的, 且没有发生分离.
1.1 参考系本文一共用到3个参考系, 都是非惯性参考系, 在稳态时随着滑翔机一起作螺旋运动.
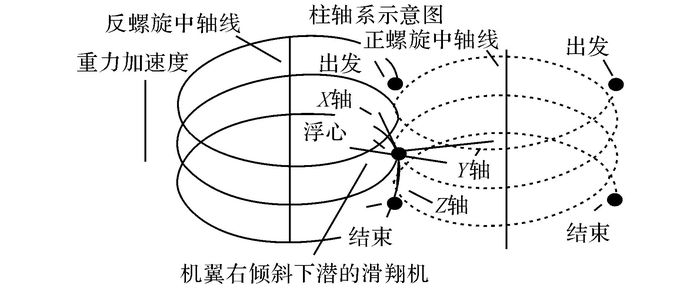
1) 柱轴系.如图 1所示, 原点是浮心(CB), X轴与浮心的水平速度方向一致, Y轴垂直于XZ平面向右(参照飞行员视角), Z轴与重力加速度的方向一致.
|
图 1 柱轴系与螺旋运动轨迹的关系示意图 Fig. 1 Relationship between cylinder coordinate system and spiral trajectory |
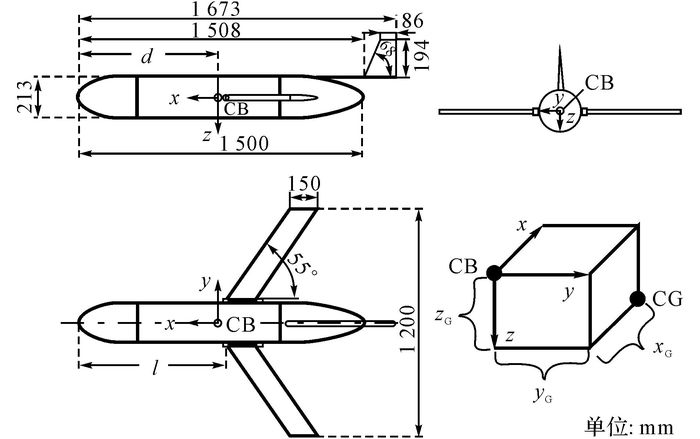
2) 体轴系.该坐标轴的原点在浮心, 坐标轴x、y和z的方向如图 2所示.l为机翼离机头的距离, d为浮心(CB)到机头的距离.本文分析了5个机翼位置不同的滑翔机, 这5个滑翔机的名称及机翼位置如表 1所示.
|
图 2 体轴系及滑翔机外形示意图 Fig. 2 Diagram of body coordinate system and gliderprofile |
| 表 1 滑翔机A、B、C、D、E的机翼位置 Table 1 Wing locations of glider A, B, C, D and E |
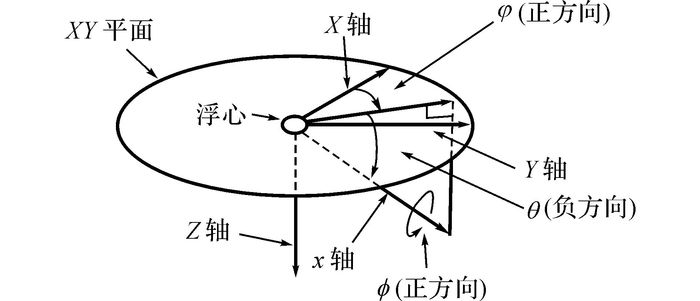
滑翔机螺旋运动稳态时的姿态角由3个欧拉角(ϕ、θ、ψ)来描述, 其含义如图 3所示.ϕ和θ就是水下无人机领域熟知的滚转角和俯仰角, ψ的含义与熟知的含义不同[16-17], 一般ψ代表的是航向角, 是相对于惯性系定义的, 但是本文的ψ是相对于非惯性系定义的, ψ在稳态时不变.
|
图 3 滑翔机螺旋运动姿态角示意图 Fig. 3 Illustration of underwater glider's attitude angles during helical motion |
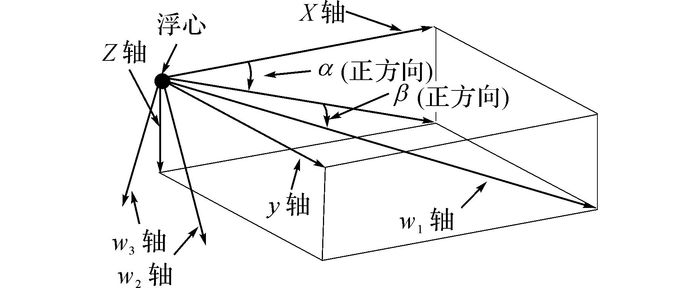
3) 风轴系.如图 4所示, α为攻角, β为侧滑角.4个坐标转换矩阵[9]定义如下:
|
图 4 风轴系与体轴系关系图 Fig. 4 Relationship between wind frame and body frame |
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{R}}_{{\rm{CB}}}} = {{\rm{e}}^{{{\mathit{\boldsymbol{\hat e}}}_3}\psi }} \cdot {{\rm{e}}^{{{\mathit{\boldsymbol{\hat e}}}_2}\theta }} \cdot {{\rm{e}}^{{{\mathit{\boldsymbol{\hat e}}}_1}\theta }},\\ {\mathit{\boldsymbol{R}}_{{\rm{BC}}}} = \mathit{\boldsymbol{R}}_{{\rm{CB}}}^{\rm{T}},\\ {\mathit{\boldsymbol{R}}_{{\rm{BW}}}} = {{\rm{e}}^{ - {{\mathit{\boldsymbol{\hat e}}}_2}\alpha }} \cdot {{\rm{e}}^{{{\mathit{\boldsymbol{\hat e}}}_3}\beta }},\\ {\mathit{\boldsymbol{R}}_{{\rm{WB}}}} = \mathit{\boldsymbol{R}}_{{\rm{BW}}}^{\rm{T}}. \end{array} \right\} $ | (1) |
式中:RCB为从体轴系向柱轴系的转换矩阵, RBW为从风轴系向体轴系的转换矩阵, RBC为RCB的反向转换矩阵, RWB为RBW的反向转换矩阵;e1代表三维空间内沿第一维方向的基向量, e2代表三维空间内沿第二维方向的基向量, e3代表三维空间内沿着第三维方向的基向量;运算符“^”代表反对称矩阵运算, 对于任意的n阶方阵Q, 矩阵指数的运算方法定义如下:
| $ {e^\mathit{\boldsymbol{Q}}} = \sum\limits_{i = 0}^n {\left( {\frac{1}{{n!}}{\mathit{\boldsymbol{Q}}^n}} \right)} . $ | (2) |
滑翔机所受的外力包括水动力、浮力和重力.水动力又包括惯性水动力和黏性水动力, 由于本文研究的是稳态运动, 惯性水动力可以忽略.对于黏性水动力, Leonard等[18]使用了一个由翼型理论和势流理论推导而来的标准模型, 该模型经过了实验验证.Wang等[12]使用了一个潜艇水动力模型来估计其水下滑翔机的黏性水动力.随着CFD技术的发展, 越来越多的研究人员开始接受并使用这个以潜艇为基础的水动力模型.本文使用一个经典的潜艇水动力模型[19]来估计黏性水动力和水动力矩, 孙秀军等[20]对该模型进行了简化.当攻角、侧滑角、角速度在某个特定的范围(见式(6))内时, 该水动力模型可以表示为
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_{\rm{h}}} = \left[ {\begin{array}{*{20}{c}} {C_{\rm{X}}^\alpha }\\ {C_{\rm{Y}}^\beta + C_{\rm{Y}}^P + C_{\rm{Y}}^R}\\ {C_{\rm{Z}}^\alpha + C_{\rm{Z}}^Q} \end{array}} \right] \times 0.5\rho {v^2}S = \\ \;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {X_\alpha ^0 + X_\alpha ^2{\alpha ^2}}\\ {Y_\beta ^1\beta + Y_P^1P + Y_R^1R}\\ {Z_\alpha ^1\alpha + Z_\alpha ^0 + Z_Q^1Q} \end{array}} \right] \times 0.5\rho {v^2}S, \end{array} $ | (3) |
| $ \begin{array}{l} {\mathit{\boldsymbol{M}}_{\rm{h}}} = \left[ {\begin{array}{*{20}{c}} {C_{\rm{K}}^P}\\ {C_{\rm{M}}^\alpha + C_{\rm{M}}^Q}\\ {C_{\rm{N}}^\beta + C_{\rm{N}}^P + C_{\rm{N}}^R} \end{array}} \right] \times 0.5\rho {v^2}SL = \\ \;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {K_P^1P}\\ {M_\alpha ^1\alpha + M_Q^1Q}\\ {N_\beta ^1\beta + N_P^1P + N_R^1R} \end{array}} \right] \times 0.5\rho {v^2}SL. \end{array} $ | (4) |
式中:Fh为作用于浮心的水动力, Mh为作用于浮心的水动力矩(这里所有的向量都是在体轴系下的), ρ为水密度, v为滑翔机速度, S为机翼面积, L为滑翔机长度.ρ=998.2 kg/m3, S=0.15 m2, 滑翔机总质量约为49.193 0 kg, L=1.673 0 m.P、Q、R的定义如下:
| $ P = pL/v,Q = qL/v,R = rL/v. $ | (5) |
其中, p为滑翔机角速度沿着体轴系x轴的分量, q为滑翔机角速度沿着体轴系y轴的分量, r为滑翔机角速度沿着体轴系z轴的分量.式(3) 和(4) 中其余项都是无量纲水动力系数, 相关含义见文献[14], 其数值可以通过CFD技术估计.本文的水动力模型适用于一个特定的范围[17]:
| $ \left| \alpha \right|,\left| \beta \right| \le {10^ \circ },\left| P \right|,\left| Q \right|,\left| R \right| \le 0.06,v \le 1{\rm{m/s}}. $ | (6) |
上文所提到的所有水动力系数都可以通过CFD方法获得.采用ANSYS15.0软件获得的水动力系数如表 2所示(文献[17]详细介绍了获取这些水动力系数的步骤).
| 表 2 对应不同机翼位置的水动力系数 Table 2 Hydrodynamic coefficients corresponding to different wing locations |
柱轴系下的静浮力(浮力与重力的合力)可以表示为
| $ {\mathit{\boldsymbol{F}}_{\rm{n}}} = {\left[ {\begin{array}{*{20}{c}} 0&0&B \end{array}} \right]^{\rm{T}}}. $ | (7) |
式中:B为Fn在Z轴方向的分量, 当滑翔机下潜时, B为正.
浮力对浮心的力矩为零向量, 重力对浮心的力矩可以表示为
| $ {\mathit{\boldsymbol{M}}_{\rm{G}}} = {{\mathit{\boldsymbol{\hat R}}}_{\rm{G}}}\left( {{\mathit{\boldsymbol{R}}_{{\rm{BC}}}}\mathit{\boldsymbol{G}}} \right). $ | (8) |
式中:G=mg, m为滑翔机总质量.g是重力加速度, 在柱轴系下g=[0 0 9.81]T.RG代表重心位置向量, 在体轴系下可以表示为RG =[xG yG zG]T.
利用下式将速度从体轴系转化到柱轴系:
| $ {\mathit{\boldsymbol{V}}_{\rm{C}}} = {\mathit{\boldsymbol{R}}_{{\rm{CB}}}}{\mathit{\boldsymbol{R}}_{{\rm{BW}}}}\mathit{\boldsymbol{v}}. $ | (9) |
式中:v为滑翔机速度向量, 在风轴系下可以表示为v=[v 0 0]T.根据风轴系的定义, v为正;vC为柱轴系下的滑翔机速度, vC=[vX vY vZ]T.
利用下式将角速度从柱轴系映射到体轴系:
| $ {\mathit{\boldsymbol{\omega }}_{\rm{B}}} = {\mathit{\boldsymbol{R}}_{{\rm{BC}}}}\mathit{\boldsymbol{\omega }}. $ | (10) |
式中:ω为柱轴系下滑翔机的角速度, ω=[0 0 ω]T.ωB为体轴系下滑翔机的角速度, ωB= [p q r]T.
1.3 平衡方程组由于使用的是非惯性系, 需要加入惯性力, 稳态的螺旋运动才能看作是平衡的.根据文献[17]中的结论, 柱轴系下作用于浮心的惯性力和惯性力矩可以表示为
| $ {\mathit{\boldsymbol{F}}_{\rm{i}}} = - m{\omega ^2}{\left[ {\begin{array}{*{20}{c}} 0&R&0 \end{array}} \right]^{\rm{T}}}, $ | (11) |
| $ {\mathit{\boldsymbol{M}}_{\rm{i}}} = {{\mathit{\boldsymbol{\hat R}}}_{\rm{G}}}\left( {{\mathit{\boldsymbol{R}}_{{\rm{BC}}}}{\mathit{\boldsymbol{F}}_{\rm{i}}}} \right). $ | (12) |
式中:R为螺旋运动半径, R=vX/ω.
当滑翔机稳态螺旋运动时, 作用于浮心的所有力和力矩为0, 且速度在Y轴的分量为0, 因而有如下平衡方程组:
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{R}}_{{\rm{CB}}}}{\mathit{\boldsymbol{F}}_{\rm{h}}} + {\mathit{\boldsymbol{F}}_{\rm{n}}} + {\mathit{\boldsymbol{F}}_{\rm{i}}} = 0,\\ {\mathit{\boldsymbol{M}}_{\rm{h}}} + {\mathit{\boldsymbol{M}}_{\rm{G}}} + {\mathit{\boldsymbol{M}}_{\rm{i}}} = 0,\\ {v_Y} = 0. \end{array} \right\} $ | (13) |
式(13) 构成了水下滑翔机稳态螺旋运动控制方程, 由7个分量方程组成, 独立的变量有11个, 包括xG、yG、zG、B、v、ω、α、β、ψ、θ和ϕ.将这11个变量归为3类:控制变量、设计参数和运动特性.xG、yG和B可以被滑翔机内可移动质量块和抽水机控制, 称为控制变量.zG在设计时确定, 在实际使用过程中不再发生变化, 称为设计参数.剩下的7个变量可以表征螺旋运动稳态时的运动特性, 称为运动特性变量.
令x={v ω α β ψ θ}T且y ={xG yG zG B}T, 式(13) 可以简化为
| $ \mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = {\bf{0}}. $ | (15) |
式中:G(x, y)为由7个非线性方程所组成的方程组.
当y给定时, 式(15) 可以进一步简化为
| $ \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) = 0. $ | (16) |
式中:F(x)为拥有7个独立变量的7维非线性方程组, 可以通过数值方法[17]求得该方程组的解x.因为x是在y给定情况下求得的, 所以x可以看作是y的函数.需要特别指出的是, 所有运动特性变量的符号和大小都是在y给定以后才确定的, 因而无法提前预知滑翔机到底是按照正螺旋方式运行还是反螺旋方式运行.x与y的关系见第2章.
2 数值结果 2.1 机翼位于过渡区域前面控制变量与运动特性关系的数值求解过程如下.
1) 设B=4.9 N, zG=0.005 m, 则
| $ \begin{array}{l} {\mathit{\boldsymbol{y}}_{ij}} = \left( {{x_{Gij}},{y_{Gij}},0.005,4.9} \right),\\ {x_{Gij}} = {z_{\rm{G}}} \times \tan \left[ {{{15}^ \circ } + \left( {i - 1} \right) \times {5^ \circ }} \right],\\ {y_{Gij}} = {z_{\rm{G}}} \times \tan \left( {j * {{4.5}^ \circ }} \right). \end{array} $ |
式中:1≤i≤11, 1≤j≤10, i∈N, j∈N, yij代表四维空间的一个点.
2) 对于每一个yij, 使用信赖区域反射算法(trust-region reflective algorithm)[17]求得对应的xij ={vij ωij αij βij ψij θij ij}的值.
3) 将所得的结果(xGij yGij vij), (xGij yGij ωij), (xGij yGij αij), (xGij yGij βij), (xGij yGij ψij), (xGij yGij θij), (xGij yGij ϕij)呈现在7个不同的坐标系中.
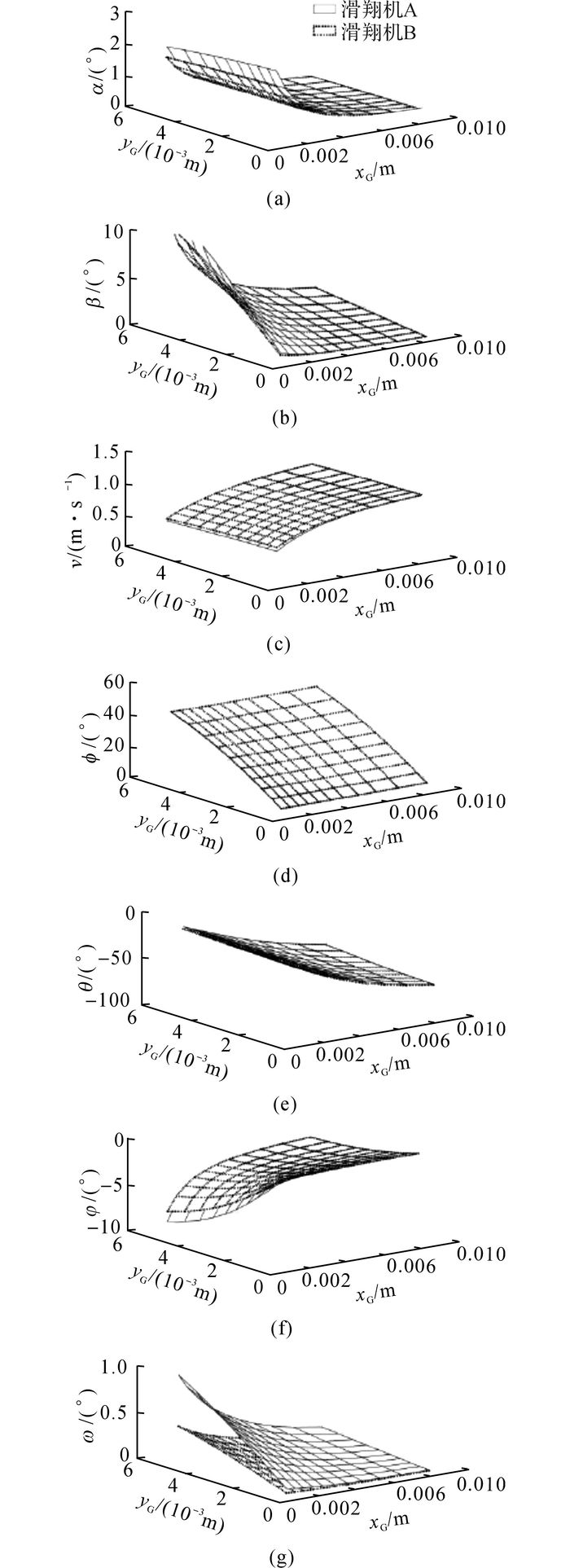
对于滑翔机A和滑翔机B, 所得结果如图 5所示.攻角始终小于2° (在1.2节所提到的范围内)且yG对于攻角几乎没有影响.但是当xG减小时, 攻角会迅速增大.机翼位置对于攻角几乎没有影响.侧滑角始终小于10°(在1.2节所提到的范围内), 且其绝对值大概是攻角的5倍.与攻角不同, xG和yG对于侧滑角都有显著影响, 侧滑角会随着xG的减小而增大, 随着yG的增大而增大.与攻角类似, 机翼位置对侧滑角几乎没有影响.速度始终小于1 m/s(在1.2节所提到的范围内)并且机翼位置对速度影响很小, 随着xG的减小而迅速减小, 也随着yG的增大而迅速减小.对于滚转角, 机翼位置和xG都对其影响很小, 但是滚转角会随着yG的增大而明显增大.对于俯仰角, 机翼位置对其影响很小, 但是俯仰角会随着xG的增大而减小(绝对值增大), 同时会随着yG减小而减小(绝对值增大).角速度在Z轴的分量ω会随着xG减小显著增大, 同时会随着yG的增大而增大.ω的符号始终为正, 这说明滑翔机A和滑翔机B始终按照正螺旋方式运行, 与重心位置无关.在重心位置相同的条件下, 滑翔机A的角速度大约是滑翔机B的角速度的2倍(见图 5), 且滑翔机A的机翼离过渡区域的距离比滑翔机B的更远(见表 1), 这表明增加机翼到过渡区域的距离可以提高旋转速率.
|
图 5 滑翔机A和滑翔机B的运动特性与重心位置关系图 Fig. 5 Relationship between CG location and motion features of glider A and glider B |
这里用到4个典型的重心位置, 分别为CG11、CG12、CG21和CG22,对应的坐标分别为(0.001 3 m, 0.003 6 m), (0.001 3 m, 0.005 0 m), (0.002 3 m, 0.003 6 m), (0.002 3 m, 0.005 0 m).其中,横坐标代表xG的位置, 纵坐标代表yG的位置.对应于典型的4个重心位置, 螺旋运动特性的具体数值如表 3所示.
| 表 3 滑翔机A和滑翔机B与典型重心位置对应的运动特性 Table 3 Motion features corresponding to typical CG locations for glider A and glider B |
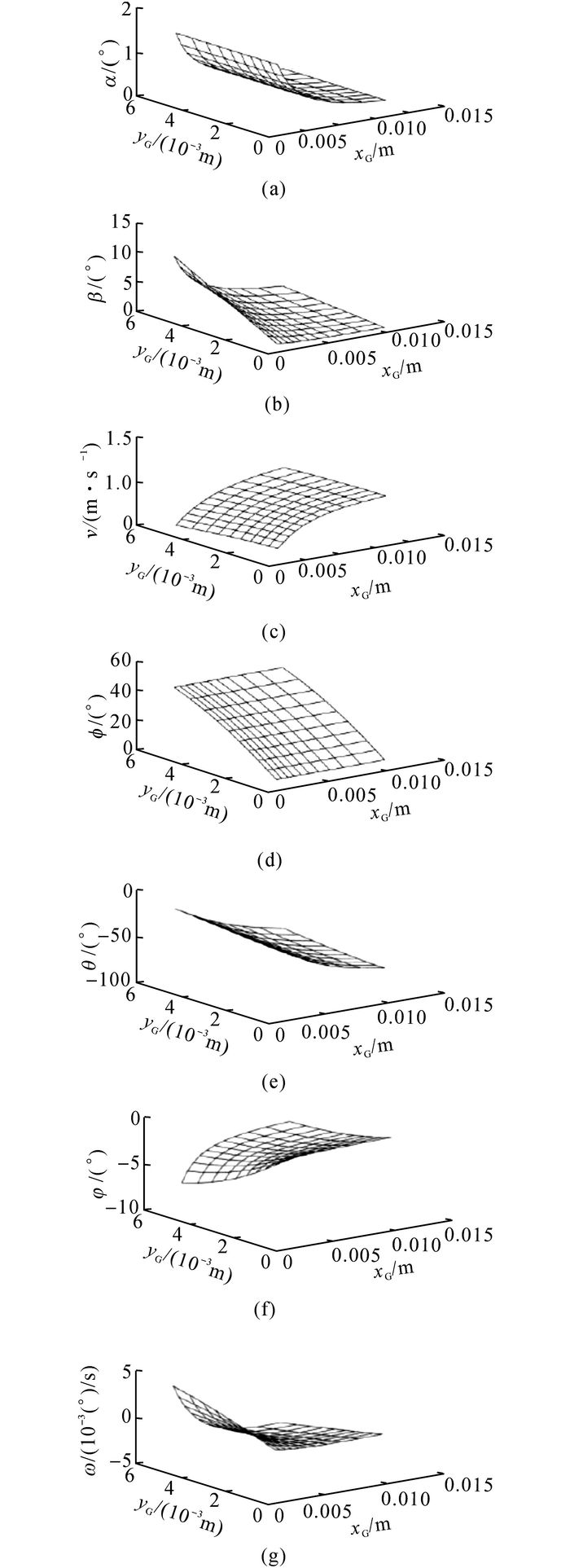
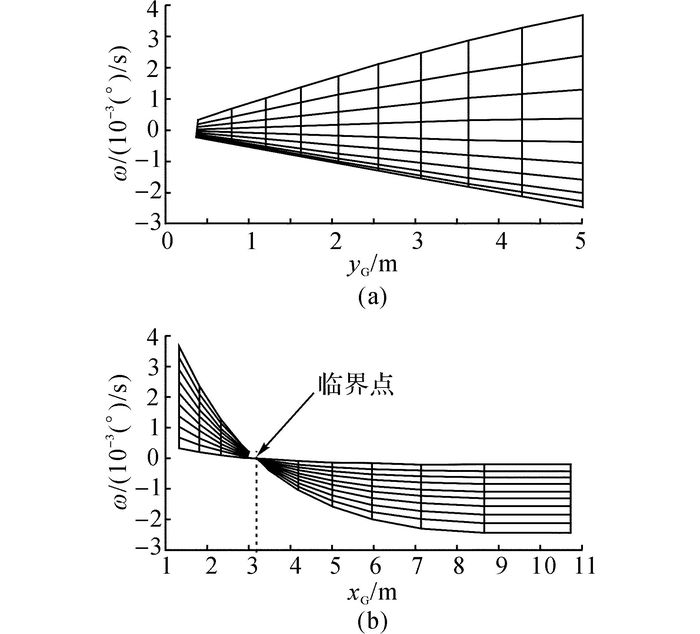
滑翔机C的机翼位于过渡区域内部,其运动特性与其他滑翔机大不相同.如图 6所示为滑翔机C的运动特性随重心位置的变化情况.对比图 5和6可知, 图 6(a)~(f)与图 5(a)~(f)的情况基本相同, 图 6(g)和图 5(g)则大不相同.当xG和yG变化时, ω的符号会发生变化, 这说明滑翔机C可以做正螺旋运动, 也可以做反螺旋运动, 运动形式取决于重心的具体位置.分别从xG轴正向和yG轴正向观察图 6(g), 分析结果如图 7所示.
|
图 6 滑翔机C的运动特性与重心位置关系图 Fig. 6 Relationship between CG location and motion features of glider C |
|
图 7 滑翔机C转向相速度与重心位置的关系 Fig. 7 Relationship between turning velocity of Glider C and CG location |
如图 7(b)所示, 当xG小于某个临界值(critical number)时, ω始终为正(滑翔机C按正螺旋方式转向);但是当xG大于某个临界值时, ω则始终为负(滑翔机C按反螺旋方式转向).如图 7(a)所示, yG对ω的数值大小有影响, 但是不会改变ω的符号.滑翔机C的另一个重要特点是转弯速率很小(如图 7(a)~(b)所示), 这么小的转弯速率在工程实践中是要规避的.
这里所提出的过渡区域概念指的是一个特定区域, 当滑翔机机翼位于这个区域内就会表现出上述特点.需要注意的是, 如果尾翼或者机身等发生变化, 这个过渡区域的具体位置也会发生变化.每个滑翔机都应该有自己固有的过渡区域.如何找到这个特殊区域是设计师在滑翔机设计阶段需要认真分析的(求解方法参见第1章).
过渡区域这一概念的提出对于滑翔机设计师有重要意义.如果设计人员想要自己的滑翔机按照正螺旋方式运行, 就要将机翼尽量设计在过渡区域前面.如果设计人员想要自己的滑翔机按照反螺旋方式运行, 就要将机翼尽量设计在过渡区域后面.无论如何也不能将机翼位置设计在过渡区域内部, 那样的话转弯速率会非常的小.
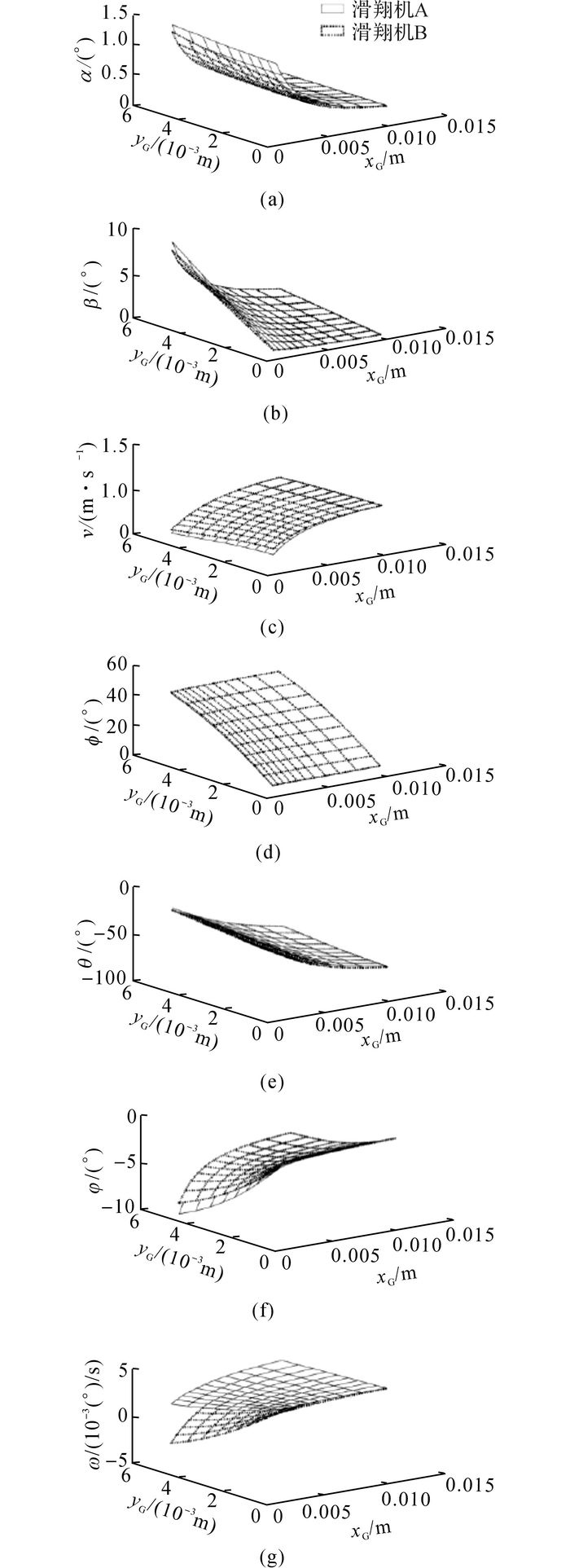
2.3 机翼位于过渡区域后使用2.1节所用的方法求得滑翔机D和滑翔机E的运动特性与重心位置的关系, 如图 8所示.运动特性α、β、V都在1.2节所提到的范围内.与滑翔机A和滑翔机B截然相反的是, 滑翔机D和滑翔机E的旋转速率ω一直是负的.这表明滑翔机D和滑翔机E是按照反螺旋的方式转弯的, 且转弯速率的数值会随着xG的减小和yG的增加而显著增大.在重心位置相同的条件下, 拥有离过渡区域更远机翼的滑翔机E的转弯速率几乎是滑翔机D的2倍.除了ω以外, 机翼位置对于其他运动变量的影响很小, 可以忽略不计, 运动变量的数值如表 4所示.
|
图 8 滑翔机D和滑翔机E的运动特性与重心位置关系图 Fig. 8 Relationship between CG location and motion features of glider D and glider E |
| 表 4 滑翔机D和滑翔机E与典型重心位置对应的运动特性 Table 4 Motion features for glider D and glider E corresponding to typical center of gravity (CG) locations |
与正螺旋运动相比, 反螺旋运动所对应的机翼位置比正螺旋运动要靠后很多, 且该位置越靠后, 转弯速率越大.机翼位置越靠后, 俯仰方向的恢复力矩就越大, 俯仰方向稳定性就越好[15].这是反螺旋运动模式的1个优点.
3 湖试结果为了验证上文的理论分析结果, 课题组在河北省易水湖开展湖试研究.滑翔机装备了1个压力传感器, 1个电子罗盘(TCM5), 1台抽水机以及调重心的丝杠系统.机翼可以通过螺丝钉固定在不同的位置.压力传感器用来记录滑翔机的深度.电子罗盘用来记录滑翔机的姿态角, 包括滚转角、俯仰角以及航向角.虽然航向角ψ的物理含义不同, 但是稳态时的航向角速率与ω的物理含义相同.当滑翔机下潜过程中保持正的滚转角、负的俯仰角以及正的航向角速率时, 可以判定滑翔机在做正螺旋运动;如果滑翔机在下潜过程中保持正的滚转角、负的俯仰角以及负的航向角速率, 则可以判定滑翔机在做反螺旋运动.航向角速率可以通过对航向角差分运算求得.通过丝杆系统调整2个可移动质量块的重心位置, 其中沿体轴系x轴的可移动质量块可以调节xG的大小, 沿体轴系y轴的可移动质量块可以调节yG的大小, 重心位置提前在岸上先调整好, 湖试过程中不再发生变化.抽水机可以通过抽放水来改变净浮力.当水抽满时, 静浮力约为4.9 N, 此时滑翔机总重约为49.19 kg.实验过程中, 抽水机的流速通过单片机控制, 并用流速计记录流速的时间历程.由于滑翔机C的转弯速率太小, 试验中不容易测定, 实验人员只对滑翔机A、B、D、E进行实验.试验中重心位于CG11(xG=0.001 3 m, yG=0.003 6 m)处.该重心位置是在抽水机抽满水的情况下调整并测定的.zG值在设计之初就通过压仓重物调整为约0.005 m.如图 9所示为滑翔机的试验环境.

|
图 9 在湖试中的滑翔机 Fig. 9 Glider during in-lake experiment |
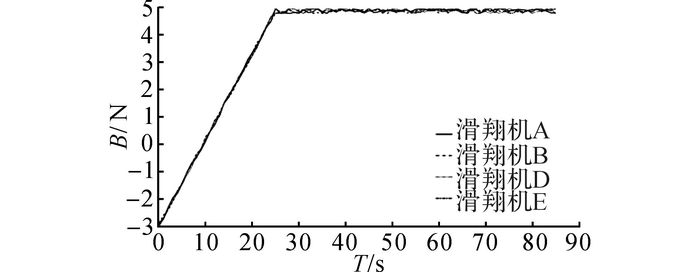
如图 10所示为湖试中滑翔机A、B、D、E的净浮力(B)随时间(T)变化的时间历程, 净浮力可以通过对抽水机流速的时间历程积分获得, 而流速的时间历程可以通过流速计获得.
|
图 10 试验中滑翔机净浮力的时间变化历程 Fig. 10 Time variation history of glider net buoyancy during experiment |
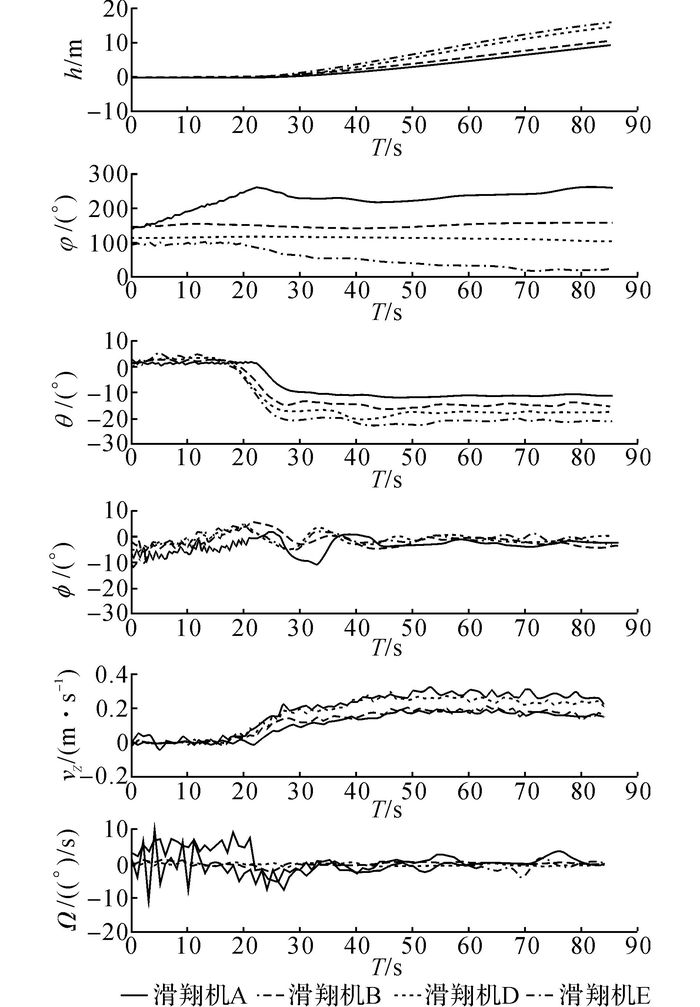
滑翔机深度h, 航向角ψ, 俯仰角θ, 滚转角Φ, 竖直下潜速率vZ以及航向角速率Ω的时间T历程如图 11所示.其中, 下潜速率是通过对滑翔机深度进行差分运算获得.可以看出, 所有的滑翔机在约40 s后达到稳态.在稳态时, 滑翔机A和滑翔机B的滚转角为正, 俯仰角为负且航向角速率为正(见表 5), 这表明滑翔机A和滑翔机B在按照正螺旋方式转弯.但是, 在稳态时, 滑翔机D和滑翔机E的滚转角为正, 俯仰角为负, 航向角速率为负(见表 5),这表明滑翔机D和滑翔机E按照反螺旋方式转弯.
|
图 11 试验中竖直下潜深度、航向角、俯仰角、滚转角、竖直下潜速度以及航向角速度的时间历程 Fig. 11 Time history of depth, yaw angle, pitch angle, roll angle, depth rate and yaw angle rate during experiment |
由于受未知因素的干扰, 航向角速率的符号是变化的(并不是一直为正或者一直为负).为了让实验结果与理论值进行精确的比较, 实验中将40 s后的滚转角、俯仰角、下潜速率以及航向角速率的值求平均, 结果如表 5所示.表中, σ为数值理论结果相对于实验值的百分误差.可以看出, 滑翔机A的转弯速率比滑翔机B明显要大.滑翔机E的转弯速率同样比滑翔机D要大很多.这很好地验证了上文关于机翼离过渡区域越远, 转弯速率就越高的理论结果.
| 表 5 滑翔机A、B、D、E的实验数据与理论数据比较 Table 5 Comparison between experimental and numericalresults during steady state for glider A, B, D and E |
(1) 存在1个决定水下滑翔机转弯方向的过渡区域, 当机翼位于这个区域的前面时, 滑翔机按正螺旋方式转弯;当机翼位于这个区域的后面时, 滑翔机按照反螺旋方式转弯;当机翼位于这个区域内时, 滑翔机的转弯速率很小, 且转弯方向由重心位置决定.
(2) 过渡区域的概念代表了一种特殊的水动力外形布局, 设计师必须避免将滑翔机的机翼设计在这个特殊区域内.每个滑翔机都有其自身固有的过渡区域, 在滑翔机设计阶段, 可按照本文所提供的方法分析并确定这个区域.
(3) 无论滑翔机是按何种方式运行, 机翼距离过渡区域越远, 转弯速率越高.在一定的范围内, 减小xG的绝对值并增大yG的绝对值可以显著提升转弯速率的绝对值.
(4) 相比于正螺旋模式, 采用反螺旋转弯模式的滑翔机的机翼更加靠后, 其俯仰方向的稳定性能更优, 因而反螺旋模式在水下滑翔机领域是一个新的设计方向.
(5) 湖试结果表明:机翼位置可以影响螺旋运动的转弯方向, 且稳态试验数据与数值结果比较吻合, 误差≤15%.
本文的研究成果为水下滑翔机设计开拓了思路, 为该领域注入了新的活力.未来研究将进一步分析正/反螺旋运动的动力学特性, 比如稳定性、可控性以及可观测性, 并开展航向闭环控制器的设计.
| [1] | STOMMEL H. The slocum mission[J]. Oceanog-raphy, 1989, 2(1): 22–25. DOI:10.5670/oceanog |
| [2] | WEBB D C, SIMONETTI P J, JONES C P. Slocum:an underwater glider propelled by environmental energy[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 447–452. DOI:10.1109/48.972077 |
| [3] | SHERMAN J, DAVIS R E, OWENS W B, et al. The autonomous underwater glider "Spray"[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 437–446. DOI:10.1109/48.972076 |
| [4] | ERIKSEN C C, OSSE T J, LIGHT R D, et al. Seag-lider:a long range autonomous underwater vehicle foroceanographic research[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 424–436. DOI:10.1109/48.972073 |
| [5] | ALVAREZ A, CAFFAZ A, CAITI A, et al. Fòlaga:a low-cost autonomous underwater vehicle combining glider and AUV capabilities[J]. Journal of Ocean Engineering, 2009, 36(1): 24–38. DOI:10.1016/j.oceaneng.2008.08.014 |
| [6] | PHOEMSAPTHAWEE S, LEBOULLUEC M, LAURENS J M, et al. Numerical study on hydrodyn-amic behavior of an underwater glider[C]//ASME 201130th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers. Rotterdam:ASME, 2011:521-526. |
| [7] | ZHANG F, TAN X. Tail-enabled spiraling maneuver for gliding robotic fish[J]. Journal of Dynamic Systems Measurement and Control, 2014, 136(4): 041028. DOI:10.1115/1.4026965 |
| [8] | ZHANG F, TAN X. Passivity-based stabilization of underwater gliders with a control surface[J]. Journal of Dynamic Systems Measurement and Control, 2015, 137(6): 061006. DOI:10.1115/1.4029078 |
| [9] | ISA K, ARSHAD M R, ISHAK S. A hybrid-driven underwater glider model, hydrodynamics estimation, and an analysis of the motion control[J]. Ocean Engineering, 2014, 81(2): 111–129. |
| [10] | YU J C, ZHANG A Q, JIN W M, et al. Development and experiments of the sea-wing underwater glider[J]. China Ocean Engineering, 2011, 25(4): 721–736. DOI:10.1007/s13344-011-0058-x |
| [11] | WANG Y H, WANG S X. Dynamic modeling and three-dimensional motion analysis of underwater gliders[J]. China Ocean Engineering, 2009, 23(3): 489–504. |
| [12] | WANG S, SUN X, WANG Y, et al. Dynamic modeling and motion simulation for a winged hybrid-driven underwater glider[J]. China Ocean Engineering, 2011, 25(1): 97–112. DOI:10.1007/s13344-011-0008-7 |
| [13] | PHOEMSAPTHAWEE S, BOULLUEC M L, LAURENS J M, et al. A potential flow based flight simulator for an underwater glider[J]. Journal of Marine Science and Application, 2013, 12(1): 112–121. DOI:10.1007/s11804-013-1165-x |
| [14] | LIU Y, SHEN Q, MA D, et al. Theoretical and experimental study of anti-helical motion for underwater glider[J]. Applied Ocean Research, 2016, 60: 121–140. DOI:10.1016/j.apor.2016.09.001 |
| [15] | FAN S S, YANG C J, PENG S L, et al. Underwater glider design based on dynamic model analysis and prototype development[J]. Frontiers of Information Technology and Electronic Engineering, 2013, 14(8): 583–599. |
| [16] | DANTAS J L D, BARROS E A D. Numerical analysis of control surface effects on AUV manoeuvrability[J]. Journal of Applied Ocean Research, 2013, 42(42): 168–181. |
| [17] | BHATTA P. Nonlinear stability and control of gliding vehicles[D]. Princeton:Princeton University, 2006. http://www.princeton.edu/~naomi/theses/thesis_pradeep_bhatta.pdf |
| [18] | LEONARD N E, GRAVER J G. Model based feedback control of autonomous underwater gliders[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 633–645. DOI:10.1109/48.972106 |
| [19] | 施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995: 19-42. |
| [20] |
孙秀军. 混合驱动水下滑翔器动力学建模及运动控制研究[D]. 天津: 天津大学, 2011.
SUN Xiu-jun. Dynamic modeling and motion control for a hybrid-driven underwater glider[D]. Tianjin:Tianjin University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10056-1012007354.htm |



