2. 吉林大学 吉林省道路交通重点实验室, 吉林 长春 130022;
3. 山东省交通规划设计院, 山东 济南 250000
2. Jilin Provence Key Laboratory of Road Traffic, Jilin University, Changchun 130022, China;
3. Shandong Provincial Key Communications Planning and Design Institute, Jinan 250000, China
从庞大的高速公路交通流数据集中获取有效信息对于准确预测交通状态和改善交通具有重要作用.有关研究表明, 目前高速公路交通流数据中主要存在缺失、错误等故障情况, 降低了数据质量, 影响了交通流预测的精度[1].因此, 如何有效地对故障数据进行修复成了研究的热点.
关于高速公路交通流故障数据修复方法的研究, 已有一定的成果, 其中研究较广的数据修复方法包括时间序列分析法和空间插值法[2-6].时间序列分析法主要依据交通流参数观测值与时间的相关性对故障数据进行估计.空间插值法主要以空间维为研究视角, 认为可以使用相邻地点检测数据来估计缺失数据.传统的空间插值方法对时空数据的分析通常以限定时间范围为前提, 在交通领域对交通流数据进行特性分析时破坏了时空连续域的统一性.因此, 单纯对时间和空间数据进行时间序列分析或空间相关分析, 均会造成时空数据大量有价值信息的丢失.从时空角度进行综合分析能够较好地解决数据信息丢失的问题, 目前时空分析方法已成为多个学科的研究重点[7-9].
在交通领域中针对交通流数据时空特性的研究大多基于数据驱动对其进行时空建模.陆化普等[10]提出了一种基于时空相关性的交通流故障数据修复方法, 将时空模型抽象为双层规划模型, 并用数据驱动法完成时空模型的标定, 对修复方法进行了有效性验证.陆百川等[11]提出了一种基于改进的多尺度主元分析的交通流数据修复模型, 并结合时空相关特性计算故障数据的相关系数从而估算其真实值.邹晓芳[12]从交通流数据的时空特性出发提出了一种自适应权重的两阶段故障数据修复模型, 并结合北京市微波检测器数据进行了验证, 结果表明该方法具有较高的修复精度.此外, 一些研究分别从交通流数据的时空特性出发提出了基于灰色残差GM模型、粗集理论、小波理论等的交通流故障数据修复方法[13-15].
以上方法虽然都对故障数据进行了较为有效的修复, 但随着大数据时代的来临, 高效、准确的处理需求使得传统的模型驱动策略难以展开.例如:现有的研究方法直接将空间位置时序数据代入分析, 并没有对该时间序列进行相关度估计便进行处理, 而基于3D形函数的时空插值方法不仅能将时间维度与空间维度综合考虑, 还能计算数据的相关度, 可以有效地分析不规则数据集[16-18], 这很好地解决了传统方法的弊端, 使得数据的修复结果更加精确.基于此, 本研究提出一种综合考虑交通流数据时空相关性的3D形函数时空插值修复方法, 并对高速公路交通流故障数据进行有效修复.
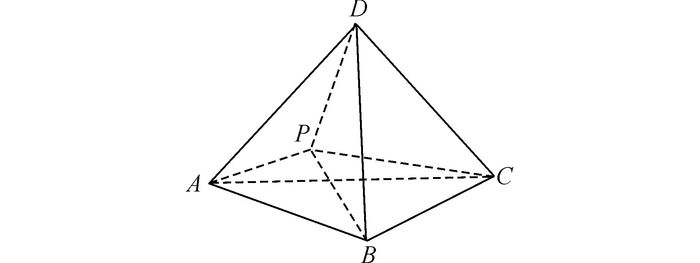
1 3D形函数插值理论形函数在有限元法中指的是一单元内部的连续函数, 又称为试函数[19].形函数作为一种时空插值方法应用较为广泛.3D形函数主要以传统一维时间和二维空间的时空域为例, 将时间维度作为时空域的第三维进行扩展.3D形函数模型可以简化为一个四面体单元, 其函数可以用体积坐标法定义, 如图 1所示为简化后的3D形函数模型示意图.
|
图 1 简化后的3D形函数模型 Fig. 1 Simplified 3D shape function model |
在四面体单元ABCD中任意选取一点P, 点P与四面体的3个顶点构成4个内部四面体PBCD、PCAD、PABD以及PBAC, 其体积与原四面体体积之比用Wi表示, 则点P体积坐标为P(WA, WB, WC, WD), 其中:
| $ {W_A} = \frac{{{V_{PBCD}}}}{{{V_{ABCD}}}},{W_B} = \frac{{{V_{PCAD}}}}{{{V_{ABCD}}}},{W_C} = \frac{{{V_{PABD}}}}{{{V_{ABCD}}}},{W_D} = \frac{{{V_{PBAC}}}}{{{V_{ABCD}}}}, $ |
| $ {V_{ABCD}} = \frac{1}{6}\left[ {\begin{array}{*{20}{c}} 1&{{x_1}}&{{y_1}}&{{z_1}}\\ 1&{{x_2}}&{{y_2}}&{{z_2}}\\ 1&{{x_3}}&{{y_3}}&{{z_3}}\\ 1&{{x_4}}&{{y_4}}&{{z_4}} \end{array}} \right],{V_{PBCD}} = \frac{1}{6}\left[ {\begin{array}{*{20}{c}} 1&x&y&z\\ 1&{{x_2}}&{{y_2}}&{{z_2}}\\ 1&{{x_3}}&{{y_3}}&{{z_3}}\\ 1&{{x_4}}&{{y_4}}&{{z_4}} \end{array}} \right], $ |
| $ {V_{PCAD}} = \frac{1}{6}\left[ {\begin{array}{*{20}{c}} 1&x&y&z\\ 1&{{x_3}}&{{y_3}}&{{z_3}}\\ 1&{{x_1}}&{{y_1}}&{{z_1}}\\ 1&{{x_4}}&{{y_4}}&{{z_4}} \end{array}} \right],{V_{ABPD}} = \frac{1}{6}\left[ {\begin{array}{*{20}{c}} 1&x&y&z\\ 1&{{x_1}}&{{y_1}}&{{z_1}}\\ 1&{{x_2}}&{{y_2}}&{{z_2}}\\ 1&{{x_4}}&{{y_4}}&{{z_4}} \end{array}} \right]. $ |
式中:VABCD、VPBCD、VPCAD、VABPD分别为相应的四面体体积.x、y、z分别为空间四面体的3个维度, 即3个坐标轴.
四面体中任意一点的参数值可由插值形函数[20]表示:
| $ \begin{array}{l} W\left( X \right) = {W_A}W\left( A \right) + {W_B}W\left( B \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{W_C}W\left( C \right) + {W_D}W\left( D \right). \end{array} $ | (1) |
式中:Wi为该插值函数的系数, 表示四面体中任意一点的4个位置坐标, 即相应的四面体体积与原四面体体积之比.由于式(1) 在三维空间有3个维度, 若要对三维空间四面体内部任意一点的函数值进行估计, 则至少需要4个离散点作为参考数据进行计算.
2 交通流时空相关数据分析 2.1 时间相关数据分析由于交通流时序数据的组织方式不同, 可从环比时间序列(指某一检测断面几天内的交通流数据时间序列)和同比时间序列(指某一检测断面特定时间的交通流数据时间序列)两方面进行时间相关性分析.对于二维随机变量(X, Y), 可用相关系数R表示X与Y之间的相关程度[21]:
| $ R = \frac{{{\mathop{\rm cov}} \left( {X,Y} \right)}}{{\sqrt {{\sigma _x}} \sqrt {{\sigma _y}} }} = \frac{{\sum\nolimits_{i = 1}^n {\left[ {{x_i} - {{\bar x}_i}} \right)\left( {{y_i} - {{\bar y}_i}} \right]} }}{{\sqrt {\sum\nolimits_{i = 1}^n {{{\left[ {{x_i} - {{\bar x}_i}} \right)}^2}{{\left( {{y_i} - {{\bar y}_i}} \right]}^2}} } }}. $ | (2) |
式中:cov (X, Y)为X、Y的协方差, σx、σy、xi、yi分别为x、y的方差和平均值.
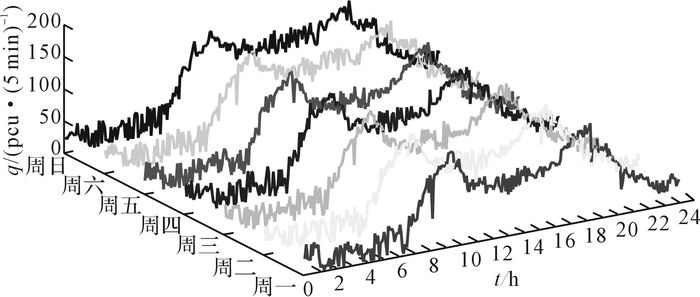
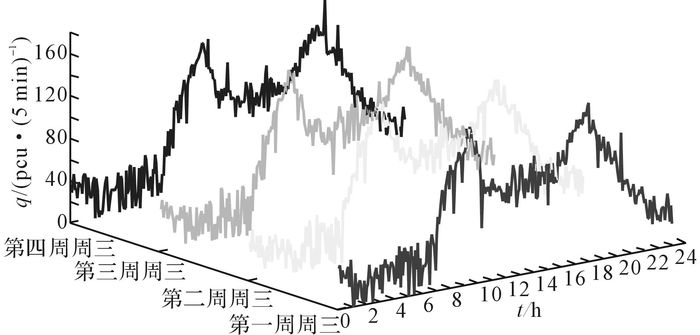
本研究选取山东高速公路威海段的交通流检测数据进行时间相似性和周期性分析, 数据选择的时间范围为2014年10月20日至10月26日及接下来连续4周每周三(特定时间)的检测数据, 位置选取的是K15+985断面的检测数据, 则关于流量q和时间t的序列图如图 2、3所示.
|
图 2 山东高速公路一周内交通流数据时间相似性统计 Fig. 2 Time similarity statistics of traffic flow in one week of Shandong freeways |
|
图 3 山东高速公路特定时间交通流数据周期性统计 Fig. 3 Periodic statistics of traffic flow in specific time of Shandong freeways |
依据式(2) 分别计算交通流量环比和同比时间序列的相关性大小, 结果如表 1、2所示.由表 1可知, 周一到周五的交通流量相关程度均为90%左右, 属于高度相关, 足以作为数据修复模型的参考数据.周六、周日的交通流量相关程度在80%以上, 认为具有较强的相关性, 也可作为数据修复模型的参考数据.但周一到周五与周六、周日相比, 由于交通流高峰时段的起止时间不同, 导致交通流数据序列间的相关程度
| 表 1 高速公路基本路段交通流量环比时间序列相似性分析结果 Table 1 Similarity analysis results of traffic flow sequential time series of basic road in freeways |
| 表 2 高速公路基本路段交通流量同比时间序列相似性分析结果 Table 2 Similarity analysis results of compared traffic flow time series of basic road in freeways |
仅有60%左右, 表明该情况下交通流量间虽具有一定的相关性, 但其相关程度不足以作为修复模型的参考数据.由表 2可知, 该检测断面连续4周每周特定日期的交通流量相关程度均接近90%或在90%以上, 属于高度相关, 足以作为数据修复模型的参考数据.
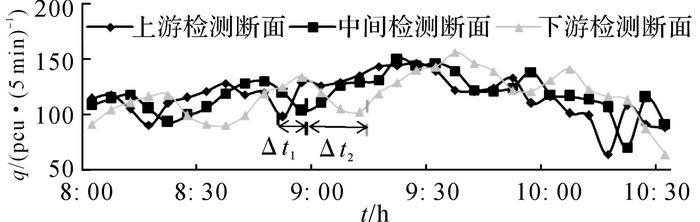
2.2 空间相关数据分析由高速公路交通流的运行特性可知, 路段上、下游间的纵向相关性显然高于相邻车道的横向相关性, 因此选取山东高速公路威海段的3个相邻检测断面的交通流时序数据进行统计分析:断面K12+875、K15+985、K20+793, 分别表示上游、中间和下游检测断面, 则3个断面不同时刻的交通流量检测数据统计结果如图 4所示.
|
图 4 高速公路上、下游路段流量数据统计 Fig. 4 Traffic flow statistics of upstream and downstream roads in freeways |
由图 4可知, 高速公路基本路段上、下游相邻断面间的交通流数据序列存在极强的相似性, 但上、下游间相似性存在一定的延时(上游断面与中游断面的延时为Δt1, 中游断面与下游断面的延时为Δt2), 称为交通流状态空间传播的时滞性.将传播延时Δt定义为时滞参数.断面a、b的交通流数据为Xa={xa, i}iN和Xb={xb, i}iN, 基于时滞参数的互相关系数为
| $ R' = \frac{{{{{\mathop{\rm cov}} }_\tau }\left( {{X_a},{X_b}} \right)}}{{{\sigma _{{X_a}}}{\sigma _{{X_b}}}}}. $ | (3) |
式中:τ为时滞参数, 表示检测器断面i与j处交通状态空间传播的延迟时间, σXa和σXb为交通流时间序列数据的标准差, covτ(Xa, Xb)为基于时滞参数的协方差, 计算公式如下:
| $ \begin{array}{l} {{\mathop{\rm cov}} _\tau }\left( {{X_a},{X_b}} \right) = \\ \;\;\;\;\;\;\;\;\frac{1}{{N - \tau }}\sum\limits_{t = 1}^{n - \tau } {\left[ {\left( {{x_{a,t}} - {\mu _{{x_a}}}} \right)\left( {{x_{b,t + \tau }} - {\mu _{{x_b}}}} \right)} \right].} \end{array} $ | (4) |
式中:xa, t为断面a在t时刻的交通流时序数据, xb, t+τ为断面b在t+τ时刻的交通时序数据, μxa和μxb分别表示Xa和Xb交通流数据序列的均值.
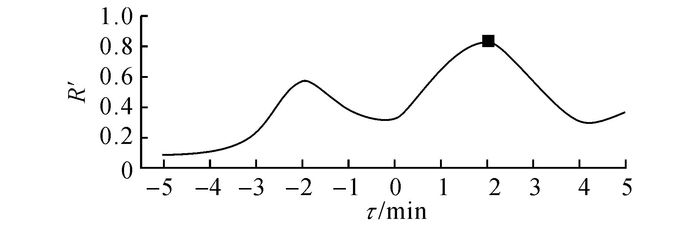
选取上游与中游2个检测断面的交通流时序数据进行统计分析, 时间范围设定为(-5 min, 5 min), 计算该范围内的互相关系数, 并统计其随时滞参数的变化情况, 如图 5所示.从图 5可知, 随着时滞参数的变化, 互相关系数呈现波动特性, 相邻断面交通流互相关系数在τ=2时最大, τ=0时互相关系数没有达到最大, 这是因为上、下游2个断面在同一时刻的数据不能体现上、下游间交通流状态的传播性.
|
图 5 交通流互相关系数随时滞参数的变化 Fig. 5 Change of traffic flow relations coefficient with hysteresis parameters |
基于3D形函数的时空修复模型主要针对交通流故障数据时空插值修复的需求并结合检测器原始数据类型定义.检测器对检测对象产生的数据集可表示为
| $ \begin{array}{l} \;\;\;\;\;\;{\rm{Data}} = \left\{ {{\rm{Date}},t,{\rm{Distance}}\;{\rm{post,Detector}}\;{\rm{No}}{\rm{.}}} \right.\\ \left. {{\rm{Lane}}\;{\rm{No}}{\rm{.}}\;q,v,{o_{\rm{t}}}} \right\}. \end{array} $ |
例如:{2014/10/15, 08: 05, 14400, 0602, 1, 600, 75, 9}表示2014年10月15日08:05时刻K14+400里程桩处“0602”检测器所采集的车道1的交通流量为600 pcu/h, 速度为75 km/h, 时间占有率为9%的数据集.
3.2 输入参量设计研究采用时间间隔(检测断面处故障数据与其他参考数据的间隔时间)、距离参数(两相邻检测器断面的距离)和时滞参数描述交通流数据序列的相关度, 由此确定模型的输入参量, 3D形函数需要4个参考数据序列一同构成时空相关数据组, 因此输入参量的设计步骤如下.
1) 确定时空相关数据组, 与故障数据相关的时空相关数据组表示为Ri=(Ri1, Ri2, Ri3, Ri4, ), Rij计算公式如下:
| $ {R_{i,j}} = \left\{ {{q_i},{v_i},{o_{ti}},\Delta {t_{i,j}}.{d_{i,j}},{\tau _{i,j}}} \right\},j = 1,2,3,4. $ | (5) |
式中:qi、vi、oti为第i组数据中交通参数值, 分别表示流量、速度和时间占有率, Δtij为第i组与第j组数据的时间间隔, dij为第i组与第j组数据所处断面间的距离, τi, j为第i组与第j组数据间的时滞参数.
2) 确定模型输入参量:
| $ {\rm{Paramete}}{{\rm{r}}_i} = \left\{ {{\rm{Parameter}},\Delta t',d',\tau '} \right\}. $ | (6) |
式中:Parameter为流量q、速度v、时间占有率ot, Δt′, d′, τ′为时间间隔、距离、时滞参数的标准值.例如, 当需修复的故障数据为交通流量q时, 模型输入参量为
| $ {q_i} = \left\{ {q,\Delta {{t'}_{i,j}}.{{d'}_{i,j}},{{\tau '}_{i,j}}} \right\},j = 1,2,3,4. $ | (7) |
交通流故障数据时空修复方法的时空插值函数模型可以表示为
| $ \begin{array}{l} W'\left( {\Delta t',d',\tau '} \right) = {{W'}_{\rm{A}}}\left( {\Delta t',d',\tau '} \right) \cdot W'\left( A \right) + \\ {{W'}_{\rm{B}}}\left( {\Delta t',d',\tau '} \right) \cdot W'\left( B \right) + {{W'}_C}\left( {\Delta t',d',\tau '} \right) \cdot W'\left( C \right) + \\ {{W'}_{\rm{D}}}\left( {\Delta t',d',\tau '} \right) \cdot W'\left( D \right). \end{array} $ | (8) |
式中:点A~D表示与故障数据时空相关的参考点, W′(i)表示点A~D四参考点的交通参数属性值q/v/ot, Wi′(Δt′, d′, τ′)表示点A~D四参考点位于四面体坐标中的坐标值, 计算公式如下:
| $ \left. \begin{array}{l} {{W'}_{\rm{A}}}\left( {\Delta t',d',\tau '} \right) = {{V'}_{{\rm{PBCD}}}}/{{V'}_{{\rm{ABCD}}}},\\ {{W'}_{\rm{B}}}\left( {\Delta t',d',\tau '} \right) = {{V'}_{{\rm{PCAD}}}}/{{V'}_{{\rm{ABCD}}}},\\ {{W'}_{\rm{C}}}\left( {\Delta t',d',\tau '} \right) = {{V'}_{{\rm{PABD}}}}/{{V'}_{{\rm{ABCD}}}},\\ {{W'}_{\rm{D}}}\left( {\Delta t',d',\tau '} \right) = {{V'}_{{\rm{PBAD}}}}/{{V'}_{{\rm{ABCD}}}}. \end{array} \right\} $ | (9) |
| $ {{V'}_{{\rm{ABCD}}}} = \frac{1}{6}\left[ {\begin{array}{*{20}{c}} 1&{\Delta {{t'}_1}}&{{{d'}_1}}&{{{\tau '}_1}}\\ 1&{\Delta {{t'}_2}}&{{{d'}_2}}&{{{\tau '}_2}}\\ 1&{\Delta {{t'}_3}}&{{{d'}_3}}&{{{\tau '}_3}}\\ 1&{\Delta {{t'}_4}}&{{{d'}_4}}&{{{\tau '}_4}} \end{array}} \right],{{V'}_{{\rm{PBCD}}}} = \frac{1}{6}\left[ {\begin{array}{*{20}{c}} 1&{\Delta t'}&{d'}&{\tau '}\\ 1&{\Delta {{t'}_2}}&{{{d'}_2}}&{{{\tau '}_2}}\\ 1&{\Delta {{t'}_3}}&{{{d'}_3}}&{{{\tau '}_3}}\\ 1&{\Delta {{t'}_4}}&{{{d'}_4}}&{{{\tau '}_4}} \end{array}} \right], $ |
| $ {{V'}_{{\rm{PCAD}}}} = \frac{1}{6}\left[ {\begin{array}{*{20}{c}} 1&{\Delta t'}&{d'}&{\tau '}\\ 1&{\Delta {{t'}_3}}&{{{d'}_3}}&{{{\tau '}_3}}\\ 1&{\Delta {{t'}_1}}&{{{d'}_1}}&{{{\tau '}_1}}\\ 1&{\Delta {{t'}_4}}&{{{d'}_4}}&{{{\tau '}_4}} \end{array}} \right],{{V'}_{{\rm{ABPD}}}} = \frac{1}{6}\left[ {\begin{array}{*{20}{c}} 1&{\Delta t'}&{d'}&{\tau '}\\ 1&{\Delta {{t'}_1}}&{{{d'}_1}}&{{{\tau '}_1}}\\ 1&{\Delta {{t'}_2}}&{{{d'}_2}}&{{{\tau '}_2}}\\ 1&{\Delta {{t'}_4}}&{{{d'}_4}}&{{{\tau '}_4}} \end{array}} \right]. $ |
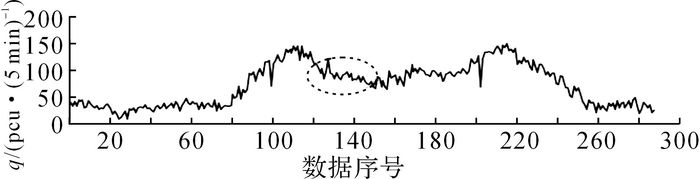
以山东高速公路威海段K10~K25路段为研究对象, 以其路段及相关交通流数据序列为基础数据(检测器每5 min检测到的流量数据), 验证不同时段模型的有效性, 选取日期Di中间车道的交通流量数据序列中连续10个时间点的数据(如图中虚线圆圈内所示,对应的数据序号为136~145) 作为交通流故障数据序列, 则去除故障数据后的交通流原始数据序列如图 6所示.
|
图 6 交通流故障数据序列确定 Fig. 6 Determination of traffic flow failure data sequence |
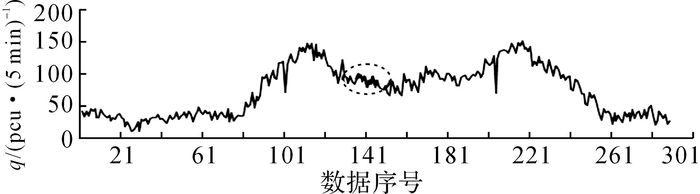
依据对高速公路基本路段交通流时间序列的相似性和周期性的分析, 对故障数据序列某天前一周及当天前两日(Di-7、Di-2和Di-1)相同时段的时序数据(数据序号为136-145) 进行提取, 结果如表 3所示.将所选故障数据序列所在断面记为X, 则上、下游相邻两检测断面分别表示为X-1和X+1.针对5 min统计间隔的交通流数据所得对应的故障数据空间相关数据序列如表 4所示.通过基于3D形函数的时空插值方法对待插值的交通流故障数据时间序列进行修复, 并还原模型输出结果, 修复后的交通流数据结果如表 5所示.
|
图 7 修复后的交通流数据序列 Fig. 7 Repaired traffic flow data sequence |
| 表 3 不同时间交通流故障数据时间序列 Table 3 Time series of traffic flow fault data at different time |
| 表 4 故障数据空间相关数据序列 Table 4 Spatial related data sequence of failure data |
| 表 5 修复后的交通流数据结果 Table 5 Results of repaired traffic flow data |
选取基于空间相关的插值修复法和基于时间相关的序列分析方法与研究所提方法进行对比.基于空间相关的修复法常用的是利用相邻车道数据进行修复, 主要利用相邻车道间历史数据的比例关系, 通过相同时刻相邻车道的实时数据对故障数据进行修复, 以流量为例, 计算公式[22]如下:
| $ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} }_i}\left( k \right) = \frac{1}{{n - 1}}\sum\nolimits_{j - 1}^n {\left[ {\frac{{{q_i}\left( j \right)}}{{{q_i}\left( k \right)}}{q_i}\left( j \right)} \right],j \ne k.} $ | (10) |
式中:
基于时间相关的序列分析方法常采用基于统计与故障数据序列相关性较高的数据对进行修复, 计算公式[23]为
| $ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} }_i}\left( d \right) = \sum\limits_{j = 1}^n {\left[ {\frac{{R\left( {d - j} \right)}}{{\sum R }}{q_i}\left( {d - j} \right).} \right]} $ | (11) |
式中:
最终计算得出时间序列法和空间插值法的修复结果.为了进一步验证研究中所提方法的有效性, 分别选取基于灰色残差GM模型和文献[12]中提到的基于统计相关分析方法进行对比, 通过计算得出这2种方法的交通流故障数据修复结果.最终得出所有对比方法的修复结果,如表 6所示.分别计算各方法修复结果的均绝对误差(MAE)、均方根误差(RMSE)和平均绝对值误差率(MAPE), 对比结果如表 7所示.
| 表 6 各方法交通流故障数据修复结果 Table 6 Repair results of traffic flow fault data of all methods |
| 表 7 各方法修复结果的误差对比 Table 7 Error comparison of the repair results of all methods |
分析表 6可知, 在几种修复结果中, 单一的时间序列法和空间插值法修复后的交通流比较分散, 而考虑时空特性的3种方法(灰色残差GM模型、基于统计相关分析的方法以及时空插值法)修复后的交通流分布更加均匀, 每个时间序号对应的流量值变化不大, 这更接近实际中的交通流数据.由此可见, 考虑时空特性的交通流数据修复方法比单一的考虑时间特性和空间特性的方法更有效.分析表 7可知, 考虑时空特性的3种方法的修复误差远远低于时间序列法和空间插值法.这3种方法中修复误差最低的是基于3D形函数的时空插值法;与灰色残差GM模型和基于统计相关分析的方法相比, 时空插值法的均绝对误差分别降低了21.33%和43.54%, 均方根误差分别降低了12.87%和35.08%, 平均绝对值误差率与灰色残差GM模型一致, 但比基于统计相关分析的方法降低了40%.由此可见, 所提出的交通流故障数据修复算法是可行的, 对高速公路交通流故障数据具有较高的修复能力.
5 结语本研究综合考虑交通流数据的时空特性, 提出了一种基于3D形函数的时空插值修复方法, 较好地实现了对交通流故障数据的修复.实例验证结果表明:本研究所提出的修复方法优于其他方法, 不仅降低了修复误差, 还使得修复结果更接近实际.这说明基于3D形函数的时空插值修复模型是一种有效的数据修复方法, 可用于高速公路交通流故障数据的修复.需要说明的是, 本研究忽略了实际交通流数据序列的缺失程度, 且暂未考虑高速公路交通流状态的复杂动态变化特性对空间传播的影响, 有待后续研究.
| [1] |
王英会. 高速公路交通流异常数据识别及修复方法研究[D]. 北京: 北京交通大学, 2015.
WANG Ying-hui. Research on identification and recovery method for abnormal highway traffic flow data[D]. Beijing:Beijing Jiaotong University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015611715.htm |
| [2] |
陆化普, 屈闻聪, 孙智源. 基于S-G滤波的交通流故障数据识别与修复算法[J].
土木工程学报, 2015(5): 23–128.
LU Hua-pu, QU Wen-cong, SUN Zhi-yuan. Detection and repair algorithm of traffic erroneous data based onS-G filtering[J]. China Civil Engineering Journal, 2015(5): 23–128. |
| [3] | SMITH B, SCHERER W, CONKLIN J. Exploring imputation techniques for missing data in transportation management systems[J]. Transportation Research Record, 2003, 1836(1): 132–142. |
| [4] | 姜桂艳. 道路交通状态判别技术与应用[M]. 北京: 人民交通出版社, 2004: 9-14. |
| [5] | MIN W, WYNTER L. Real-time road traffic prediction with spatio-temporal correlations[J]. Transportation Research Part C:Emerging Technologies, 2011, 19(4): 606–616. DOI:10.1016/j.trc.2010.10.002 |
| [6] |
邹海翔, 乐阳, 李清泉, 叶嘉安, 等. 基于Kriging插值的无检测器路段交通数据插补方法[J].
交通运输工程学报, 2011, 11(3): 118–126.
ZOU Hai-xiang, LE Yang, LI Qing-quan, YE Jia-an, et al. Traffic data interpolation method of non-detection road link based on Kriging interpolation[J]. Journal of Traffic and Transportation Engineering, 2011, 11(3): 118–126. |
| [7] | 王佳璆. 时空序列数据分析和建模[M]. 北京: 科学出版社, 2012. |
| [8] |
甘健胜, 洪伟. 基于时空数据的线性组合插值模型及其应用[J].
福建林学院学报, 2006, 26(4): 318–323.
GAN Jian-sheng, HONG Wei. Linear combination interpolation model based on panel data and its application[J]. Journal of Fujian College of Forestry, 2006, 26(4): 318–323. |
| [9] |
李莎, 舒红, 董林. 基于时空变异函数的Kriging插值及实现[J].
计算机工程与应用, 2011, 47(23): 25–26.
LI Sha, SHU Hong, DONG Lin. Research and realization of Kriging interpolation based on spatial-temporal variogram[J]. Computer Engineering and Applications, 2011, 47(23): 25–26. DOI:10.3778/j.issn.1002-8331.2011.23.007 |
| [10] |
陆化普, 孙智源, 屈闻聪. 基于时空模型的交通流故障数据修正方法[J].
交通运输工程学报, 2015, 16(6): 92–100.
LU Hua-pu, SUN Zhi-yuan, QU Wen-cong. Repair method of traffic flow malfunction data based on temporal-spatial model[J]. Journal of Traffic and Transportation Engineering, 2015, 16(5): 92–100. |
| [11] |
陆百川, 郭桂林, 肖汶谦, 等. 基于多尺度主元分析法的动态交通数据故障诊断与修复[J].
重庆交通大学学报:自然科学版, 2016(1): 134–137.
LU Bai-chuan, GUO Gui-lin, XIAO Wen-qian, et al. Fault diagnosing and modifying of dynamic traffic data based on MSPCA[J]. Journal of Chongqing Jiaotong University:Natural Science, 2016(01): 134–137. |
| [12] |
邹晓芳. 城市快速路交通流故障数据修复方法研究[D]. 北京: 北京京交通大学, 2014.
ZOU Xiao-fang. Research on repair methods of urban expressway traffic flow fault data[D]. Beijing:Beijing Jiaotong University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10004-1014177891.htm |
| [13] |
王晓原, 吴芳, 朴基男. 基于粗集理论的交通流丢失数据补齐方法[J].
交通运输工程学报, 2008(5): 91–108.
WANG Xiao-yuan, WU Fang, PIAO Ji-nan. Filling method of missing data for traffic flow based on rough set theory[J]. Journal of Traffic and Transportation Engineering, 2008(5): 91–108. |
| [14] |
郭敏, 蓝金辉, 李娟娟, 等. 基于灰色残差GM(1, N)模型的交通流数据恢复算法[J].
交通运输系统工程与信息, 2012, 12(1): 42–47.
GUO Min, LAN Jin-hui, LI Juan-juan, et al. Traffic flow data recovery algorithm based on gray residual GM (1, N) model[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(1): 42–47. |
| [15] |
陈淑燕, 王炜, 李文勇. 实时交通数据的噪声识别和消噪方法[J].
东南大学学报, 2006, 36(2): 322–325.
CHEN Shu-yan, WANG Wei, LI Wen-yong. Noise recognition and noise reduction of real-time traffic data[J]. Journal of Southeast University, 2006, 36(2): 322–325. DOI:10.3969/j.issn.1001-0505.2006.02.030 |
| [16] | LI L. Spatiotemporal interpolation methods in GIS[M]. Lincoln: The University of Nebraska-Lincoln, 2003. |
| [17] | LI L, ZHANG X, HOLT J. B, TIAN J, et al. Spatiotemporal interpolation methods for air pollution exposure[C]//Proceedings of the Ninth Symposium on Abstraction, Reformulation and Approximation.:, 2011:75-81. |
| [18] | REVESZ P Z, LI Y. MLPQ:a linear constraint database system with aggregate operators[C]//Database Engineering and Applications Symposium 1997. IDEAS '97. Proceedings.:IEEE, 1997:132-137. |
| [19] | 尹飞鸿. 有限元法基本原理及应用[M]. 北京: 高等教育出版社, 2010. |
| [20] |
尉桂兴. 顾及时序平稳性的时空插值方法研究[D]. 南京: 南京师范大学, 2014.
WEI Gui-xing. A spatio-temporal interpolation method based on the stationarity of time series[D]. Nanjing:Nanjing Normal University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10319-1014340720.htm |
| [21] |
王凯, 冯晅, 刘财. Pearson相关系数法快慢横波波场分离[J].
世界地质, 2012, 31(2): 371–376.
WANG Kai, FENG Xuan, LIU Cai. Wave filed separation of fast-slow shear waves by Pearson correlation coefficient method[J]. Global Geology, 2012, 31(2): 371–376. |
| [22] | SMITH B, CONKLIN J. Use of local lane distribution patterns to estimate missing data values from traffic monitoring systems[J]. Transportation Research Record, 2002, 1811(1): 50–56. |
| [23] | DAVIS G A, NIHAN N L. Using time-series designs to estimate changes in freeway level of service, despite missing data[J]. Transportation Research Part A:General, 1984, 18(5-6): 431–438. DOI:10.1016/0191-2607(84)90018-9 |



