海上风能资源丰富、区域广阔, 是风机安装的理想场所.支撑结构是风机的主要承载部件, 长期遭受随机波浪和风载荷的联合作用, 易于产生疲劳破坏.单一载荷作用下支撑结构的疲劳评估方法已发展成熟.如果只考虑单一载荷的作用, 会明显高估支撑结构的抗疲劳能力[1-2], 且由于疲劳损伤和应力存在非线性关系, 风浪联合作用下塔架结构的疲劳损伤并不等于2个损伤之和[3].因此,考虑风浪载荷的耦合效应对风机支撑结构的疲劳分析有重要意义[4].
考虑风浪载荷耦合效应最直接的方法是建立完整的风机模型进行全时域分析, 如英国的Blyth风电场[5].马永亮等[6-7]对时域疲劳评估方法进行了研究.时域疲劳评估方法具有计算精度高的优点, 但需要进行长周期的瞬态动力学分析, 计算量较大, 在设计的初期阶段难以实现.此外, 风机支撑结构的疲劳分析广泛采用损伤组合方法[8-10], 即分别计算风载荷和波浪载荷引起的损伤, 然后按照一定的方法进行组合.其中风载荷引起的疲劳损伤仍需要进行瞬态动力学分析, 计算量依然较大.因此, 发展一种简单、便捷的风机支撑结构疲劳评估方法是很有必要的.
频域疲劳分析方法具有理论明确、计算效率高的特点, 在船舶与海洋工程领域得到了广泛应用[11-12].但针对风浪联合作用下海上风机支撑结构频域疲劳评估方法的研究较少.本文在现有研究的基础上, 给出一种风载荷作用下疲劳热点应力功率谱密度函数计算方法, 并以导管架式支撑结构为例, 研究风浪联合作用下支撑结构的频域疲劳评估方法.
1 频域分析方法流程海上风浪环境可以通过三维风-波浪散布图来描述, 即采用有效波高、平均跨零周期以及轮毂处的平均风速将风浪环境离散成一系列的工况, 并给出每种工况出现的概率[8].分别计算每种工况产生的疲劳损伤, 然后通过叠加各个工况的损伤, 就可以得到风机支撑结构在整个服役期内的损伤.总损伤的表达式为
| $ D = \sum\limits_{i = 1}^N {\left( {{P_i}{D_i}} \right)} . $ | (1) |
式中:N为总工况数, Di为第i个工况的损伤, Pi为第i个工况出现的概率.
对于每一个工况, 可以认为风和波浪是相互独立的[5-6, 8], 即可分别计算风载荷和波浪载荷在结构上的疲劳应力.对于同一疲劳热点部位, t时刻的总应力σ(t)可以表示为
| $ \sigma \left( t \right) = {\sigma _{\rm{a}}}\left( t \right) + {\sigma _{\rm{w}}}\left( t \right). $ | (2) |
式中:σa(t)为t时刻风载荷引起的应力, σw(t)为t时刻波浪载荷引起的应力.式(2) 是在最大主应力方向相同的情况下得到的.对于最大主应力方向不相同的情况, 式(2) 是保守的, 具体说明见2.2节.
由于风和波浪均可视为平稳高斯随机过程, σ(t)的功率谱密度函数[3, 5, 13]可以表示为
| $ S\left( \omega \right) = {S_{\rm{a}}}\left( \omega \right) + {S_{\rm{w}}}\left( \omega \right). $ | (3) |
式中:ω为圆频率, Sa(ω)为σa(t)的功率谱密度函数, Sw(ω)为σw(t)的功率谱密度函数.
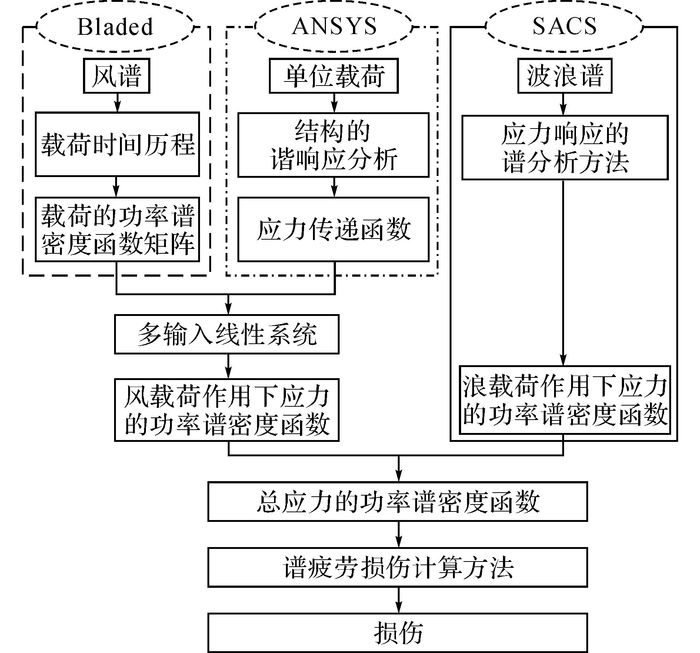
对于线性动力系统来说, Sa(ω)和Sw(ω)可以通过谱分析方法计算得到.有关波浪载荷作用下的谱分析方法已发展成熟, 可以通过专业软件计算得到.本文采用SACS软件进行计算.对于风载荷作用下的谱分析, 目前还没有一致认可的方法.本文采用Bladed软件计算风载荷,采用ANSYS软件计算载荷到应力的传递函数, 并在此基础上根据多输入线性系统理论建立风载荷作用下的谱分析方法.在获得S(ω)后通过谱疲劳损伤计算方法得到疲劳损伤, 总的分析流程如图 1所示.
|
图 1 频域疲劳分析方法流程 Fig. 1 Flow chart of frequency-domain fatigue analysismethod |
支撑结构的非线性行为主要包括2个方面:气动阻尼和桩土相互作用.在使用谱分析方法时, 需要对非线性项进行等效线性化处理.在实际工程中, 气动阻尼取4%的临界阻尼[4-5]; 基础的桩土相互作用采用6倍桩径法来处理[14].对结构动力学性能影响较小的土壤阻尼(Soil damping)以及水动力学阻尼(Hydrodynamic damping), 忽略不计[8].
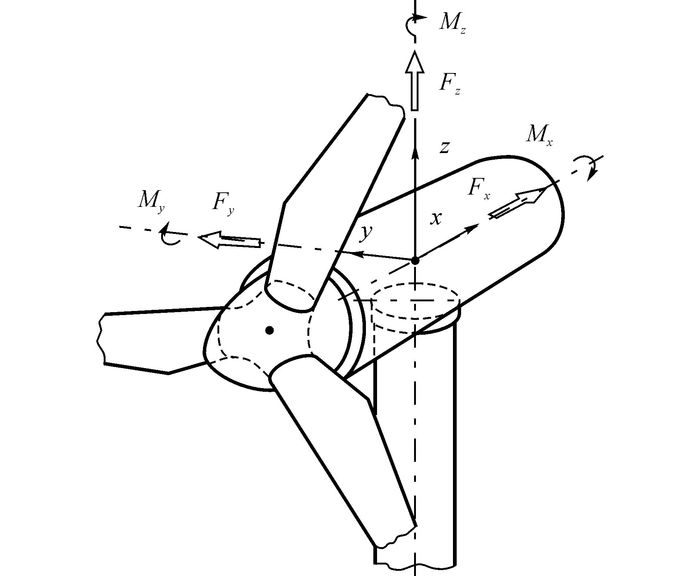
2.2 风载荷作用下应力的功率谱密度函数计算海上风力发电系统主要由叶轮-机舱组件(Rotor-Nacelle Assembly, RNA)和支撑结构[15]两部分组成.在设计支撑结构时, 将叶轮-机舱组件简化为塔顶处的质量点, 并将风载荷直接加载到质量点上.塔顶处的风载荷和坐标如图 2所示.图中坐标系原点位于风轮轴和塔架轴的交点上, 风轮轴方向为x轴, 塔架轴方向为z轴, y轴指向侧向;沿3个坐标轴方向的力和绕3个坐标轴的矩分别为Fx、Fy、Fz和Mx、My、Mz.该方法忽略了气动阻尼.目前, 在支撑结构的设计过程中通常将气动阻尼作为附加结构阻尼来考虑[4-5, 8].
|
图 2 塔顶处的风载荷和总体坐标 Fig. 2 Wind loads and global coordinates at top of tower |
在支撑结构的疲劳评估中, 使用最大主应力作为热点应力计算疲劳损伤.对于焊接结构来说, 疲劳裂纹一般萌生于结构表面, 因而结构的疲劳热点部位处于平面应力状态.由图 2可知, 风载荷作用下的支撑结构属于多输入线性系统.对于多输入线性系统, 载荷和最大主应力之间一般不存在线性关系, 需要进行线性化处理.
2.2.1 多载荷联合作用下的最大主应力线性化(1) 单一载荷作用下的最大主应力.
对于单一载荷Fi作用下的线性结构系统, Fi与疲劳热点部位3个应力分量σx, i、σy, i、τxy, i之间存在线性关系:
| $ {\sigma _{x,i}} = {C_{x,i}}{F_i},{\sigma _{y,i}} = {C_{y,i}}{F_i},{\tau _{xy,i}} = {C_{xy,i}}{F_i}. $ | (4) |
式中:Cx, i、Cy, i、Cxy, i分别为单位载荷作用下疲劳热点部位的3个应力分量.根据弹性理论, 此点的最大主应力可以表示为
| $ {\sigma _{1,i}} = {F_i}\left[ {\frac{{{C_{x,i}} + {C_{y,i}}}}{2} + \sqrt {{{\left( {\frac{{{C_{x,i}} + {C_{y,i}}}}{2}} \right)}^2} + C_{xy,i}^2} } \right] = {F_i}{C_i}. $ | (5) |
对于同一载荷形式和结构, 式(5) 中的Cx, i、Cy, i、Cxy, i是确定的, 因此单位载荷作用下疲劳热点部位的最大主应力Ci也是确定的, 可知Fi和σ1, i之间存在线性关系.
(2) 多载荷联合作用下的最大主应力.
对于n个载荷Fi(i=1, 2, …, n)同时作用下的线性结构系统, 疲劳热点部位的3个应力分量为
| $ {\sigma _x} = \sum\limits_{i = 1}^n {{\sigma _{x,i}},{\sigma _y}} = \sum\limits_{i = 1}^n {{\sigma _{y,i}},{\tau _{xy}}} = \sum\limits_{i = 1}^n {{\tau _{xy,i}}} . $ | (6) |
根据弹性理论, 此点的最大主应力可以表示为
| $ {\sigma _1} = \frac{1}{2}\sum\limits_{i = 1}^n {\left( {{\sigma _{x,i}} + {\sigma _{y,i}}} \right) + \sum .} $ | (7) |
式中:
| $ \sum = \sqrt {{{\left[ {\sum\limits_{i = 1}^n {\left( {\frac{{{\sigma _{x,i}} - {\sigma _{y,i}}}}{2}} \right)} } \right]}^2} + {{\left( {\sum\limits_{i = 1}^n {{\tau _{xy,i}}} } \right)}^2}} . $ |
通过分析可得, Σ与载荷Fi之间的关系是非线性的, 因而σ1与载荷Fi之间的关系也是非线性的.
(3) 多载荷联合作用下最大主应力的线性化.
对各个载荷Fi的最大主应力求和, 得到
| $ \begin{array}{l} {{\sigma '}_1} = \sum\limits_{i = 1}^n {{\sigma _{1,i}}} = \sum\limits_{i = 1}^n {\left( {{F_i}{C_i}} \right)} = \\ \;\;\;\;\frac{1}{2}\sum\limits_{i = 1}^n {\left( {{\sigma _{x,i}} - {\sigma _{y,i}}} \right)} + \sum\limits_{i = 1}^n {\sqrt {{{\left( {\frac{{{\sigma _{x,i}} - {\sigma _{y,i}}}}{2}} \right)}^2} + \tau _{xy,i}^2} } . \end{array} $ | (8) |
从上式可以看出, σ1′与Fi成线性关系.
当最大主应力的方向都相同时, σ1=σ1′.当主应力方向不相同时, 通过数学方法可以严格证明存在如下不等式:
| $ \begin{array}{l} \sum\limits_{i = 1}^n {\sqrt {{{\left( {\frac{{{\sigma _{x,i}} - {\sigma _{y,i}}}}{2}} \right)}^2} + \tau _{xy,i}^2} } \ge \\ \;\;\;\;\;\sqrt {{{\left[ {\sum\limits_{i = 1}^n {\left( {\frac{{{\sigma _{x,i}} - {\sigma _{y,i}}}}{2}} \right)} } \right]}^2} + {{\left( {\sum\limits_{i = 1}^n {{\tau _{xy,i}}} } \right)}^2}} . \end{array} $ | (9) |
结合式(7) 和(8) 可以得出, σ1′≥σ1, 因此采用σ1′代替σ1是一种保守的处理方法.
2.2.2 最大主应力的功率谱密度函数计算根据式(8) 以及多输入线性系统理论[16], 多载荷联合作用下最大主应力的功率谱密度函数为
| $ {S_y}\left( \omega \right) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {H_1^ * \left( {i\omega } \right){H_j}\left( {i\omega } \right){S_{{x_i}{x_j}}}} \right).} } $ | (10) |
式中:Hj(iω)为第j个载荷单独作用时的传递函数, Hi*(iω)为Hi(iω)的共轭复数, Sxixj为输入载荷xi和xj的互功率谱密度函数.
对于互不相关的输入载荷, 式(10) 可以简化为
| $ {S_y}\left( \omega \right) = \sum\limits_{i = 1}^n {\left( {{{\left| {{H_i}\left( {i\omega } \right)} \right|}^2}{S_{{x_i}{x_i}}}} \right).} $ | (11) |
上式可以进一步简化为
| $ {S_y}\left( \omega \right) = \sum\limits_{i = 1}^n {{S_{{y_i}}}\left( \omega \right).} $ | (12) |
同理可得, 单一载荷作用下最大主应力的功率谱密度函数为
| $ {S_{{y_i}}}\left( \omega \right) = {\left| {{H_i}\left( {i\omega } \right)} \right|^2}{S_{{x_i}{x_i}}} $ |
根据以上理论, 风载荷作用下应力的功率谱密度函数计算可分为以下3步.
1) 计算输入载荷的功率谱密度函数矩阵.
根据输入风谱模型, 采用Bladed软件模拟湍流风环境, 并计算风机叶片上的气动载荷, 得到塔顶处的风载荷时间历程.对风载荷时间历程进行傅里叶变换得到风载荷的功率谱密度函数矩阵.
2) 计算单个载荷作用下应力的传递函数.
针对每一载荷, 利用ANSYS软件的谐响应分析, 计算单位载荷作用下结构的应力响应, 得到载荷到应力的传递函数.
3) 根据式(10) 或式(11) 计算最大主应力的功率谱密度函数.
3 谱疲劳损伤的计算在应力范围的概率密度函数已知的情况下, 结合S-N曲线和Miner线性损伤理论, 计算出服役时间TS内的结构的疲劳损伤为
| $ D = \frac{{{T_{\rm{S}}}{n_t}}}{C}\int\limits_0^{ + \infty } {{S^m}{P_{\rm{S}}}\left( S \right){\rm{d}}S} . $ | (13) |
式中:S为应力范围, PS(S)为应力范围的概率密度函数, C和m分别为S-N曲线的疲劳强度系数和疲劳强度指数, nt为单位时间内的平均循环次数.
对于理想窄带高斯随机过程, 应力范围服从Rayleigh分布[12].根据式(13), 可得服役时间TS内的损伤为
| $ {D_{{\rm{NB}}}} = \frac{{{T_{\rm{S}}}{v_0}}}{C}{\left( {2\sqrt {2{\lambda _0}} } \right)^m}\Gamma \left( {\frac{m}{2} + 1} \right). $ | (14) |
式中:ν0为应力的平均跨零率;λ0为应力功率谱密度函数的零阶矩;Γ(·)为伽马函数.
浪载荷作用下应力的功率谱密度函数可近似为窄带, 而风载荷作用下应力的功率谱密度函数则一般为宽带.对于宽带谱, 由于应力范围概率密度函数的理论解不存在, 不能根据式(13) 计算得到损伤结果.目前, 宽带谱的疲劳损伤一般通过近似方法计算.在船舶与海洋工程领域主要采用以下3种方法.
1) 窄带近似方法, 即采用式(14) 计算损伤, 是一种比较保守的方法[11-12].
2) 带宽修正方法, 即对窄带近似方法进行带宽修正, 得到宽带谱的疲劳损伤为
| $ {D_{{\rm{WB}}}} = {\rho _{{\rm{WB}}}}{D_{{\rm{NB}}}}. $ | (15) |
式中:ρWB为带宽修正系数.计算带宽修正系数ρWB的方法主要有Wirsching-Light方法[11-12]、Ortiz-Chen方法[11]以及Lutes-Larson方法[11-12].
3) 采用近似概率密度函数公式计算疲劳损伤, 目前广泛认可的是Dirlik提出的近似公式[17].
此外, 也可以先将应力的功率谱密度函数转化为应力时间历程, 然后采用时域雨流计数方法计算损伤.该方法具有计算精度高的优点, 但会产生大量的时域样本, 因而通常只作为评估谱疲劳方法准确性的工具.为了定量评价各种谱疲劳计算方法的精度, 误差计算方法如下:
| $ \sigma = \frac{{{D_{\rm{c}}} - {D_{{\rm{RF}}}}}}{{{D_{{\rm{RF}}}}}} \times 100\% . $ | (16) |
式中: DRF为采用时域雨流计数方法计算得到的损伤, Dc为采用各种谱疲劳方法计算得到的损伤.
4 实例计算以广东省某海域3 MW导管架式海上风机支撑结构为研究对象, 分析风浪联合作用下频域疲劳.工况条件如下:风场所在海域水深为20 m;纬度为25°N;海面粗糙度为0.02;平均风速服从Weibull分布, 形状参数为1.718 3, 尺度参数为6.947 3, 有效波高为1.75 m, 谱峰周期为6 s, 轮毂处平均风速为12 m/s;纵向紊流强度为10%.
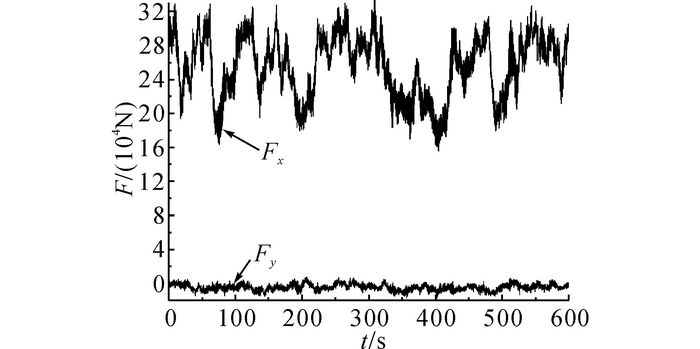
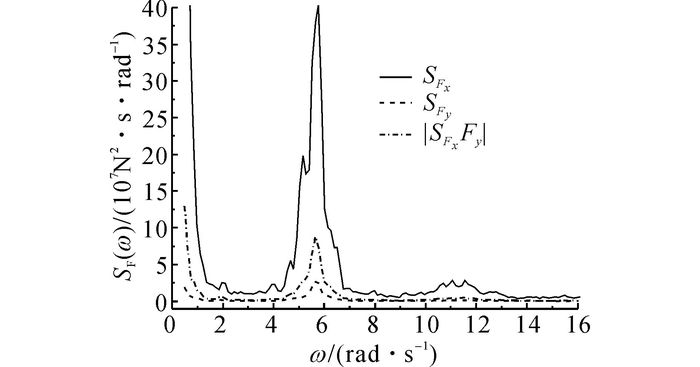
4.1 风载荷作用下的计算结果 4.1.1 塔顶风载荷及其功率谱密度函数采用Bladed软件计算塔顶处的风载荷, 其中风谱采用改进的Von Karman谱.根据DNV-OS-J101规范[10]的要求, 风载荷模拟时长取为10 min.由于塔顶6个载荷分量由同一风谱产生, 载荷分量之间存在一定的相关性.为了和波浪一致, 将风载荷功率谱密度函数的频率转化为圆频率ω, 转化方法参考文献[16].风载荷分量Fx和Fy的时间历程如图 3所示, 对应的自功率谱密度函数SFx、SFy以及互功率谱密度函数SFxFy如图 4所示.由图 3可知, 载荷Fy远小于Fx, 这是风机的偏航角度较小导致的.由图 4可知, 载荷Fx和Fy的互功率谱密度函数介于2个自功率谱密度函数之间, 表明载荷之间存在相关性, 同时可以看出风载荷的谱峰频率为5.8 rad/s.
|
图 3 风载荷分量Fx和Fy的时间历程 Fig. 3 Time history of wind load component Fx and Fy |
|
图 4 风载荷分量Fx和Fy的自功率谱密度函数以及互功率谱密度函数 Fig. 4 Auto and cross power spectrum density functions of wind load component Fx and Fy |
在ANSYS软件的谐响应分析中, 结构阻尼采用瑞利阻尼模型, 模型中参数α、β定义如下:
| $ \alpha = \frac{{2\xi {\omega _1}{\omega _2}}}{{{\omega _1} + {\omega _2}}},\beta = \frac{{2\xi }}{{{\omega _1} + {\omega _2}}}. $ | (17) |
式中:ω1和ω2分别为结构的一阶、二阶固有频率, ξ为结构的实际阻尼与其临界阻尼之比.
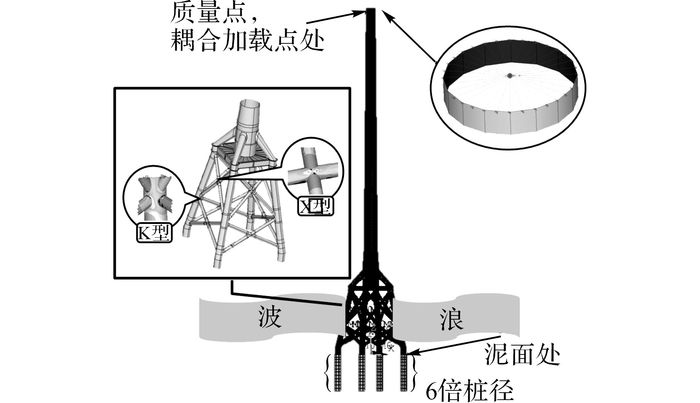
为了确定参数α、β的值, 首先进行模态分析.导管架式支撑结构的有限元模型如图 5所示, 模型中各构件的长度l、外径φ以及壁厚δ如表 1所示.
|
图 5 导管架式支撑结构模型 Fig. 5 Model of jacket-type support structure |
| 表 1 风机支撑结构模型参数 Table 1 Dimension parameters of wind turbine supportstructure |
通过计算可得:ω1=0.328 15 Hz, ω2=2.024 60 Hz.对于支撑结构来说, 实际阻尼包括结构阻尼和气动阻尼.根据DNV-OS-J101的规定[10], 结构阻尼取其临界阻尼的1%;根据文献[4-5], 气动阻尼取其临界阻尼的4%, 因此取ξ=5%.根据式(17) 可得, α=0.028 24, β=0.042 50.
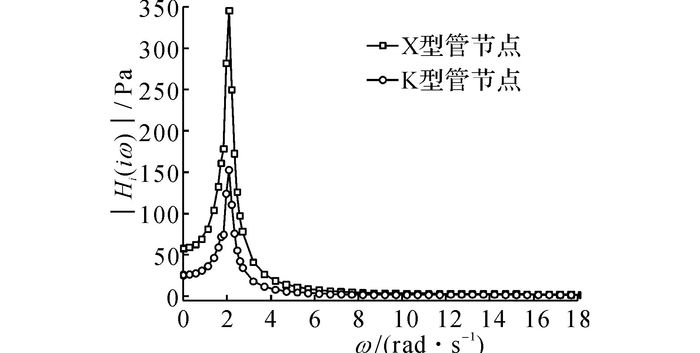
结构疲劳校核的主要部位为图 5中的X型和K型管节点, 管节点的疲劳热点应力插值方法按照DNV-OS-J101[10]进行.针对每一载荷, 使用ANSYS软件分别分析单位载荷作用下的谐响应, 加载方式如图 5所示.根据谐响应分析结果可以得到疲劳热点应力的传递函数Hi(iω).载荷Fx作用下的X型和K型管节点热点应力传递函数的幅值|Hi(iω)|如图 6所示.结构的一阶固有频率转换为圆频率ω=2.062 rad/s.由图 6可知, 应力传递函数的幅值|Hi(iω)|在一阶固有频率处最大;X型管节点的响应大于K型管节点.
|
图 6 X型和K型管节点热点应力传递函数的幅值 Fig. 6 Amplitude of hot-spot stress transfer function for X-type and K-type tubular joints |
风载荷作用下热点应力的功率谱密度函数计算包含结构的线性化和最大主应力线性化.为验证这2个线性化的合理性, 分别进行单一载荷作用下和多载荷联合作用下的热点应力功率谱密度函数分析.
(1) 单一载荷作用下的热点应力功率谱密度函数分析.
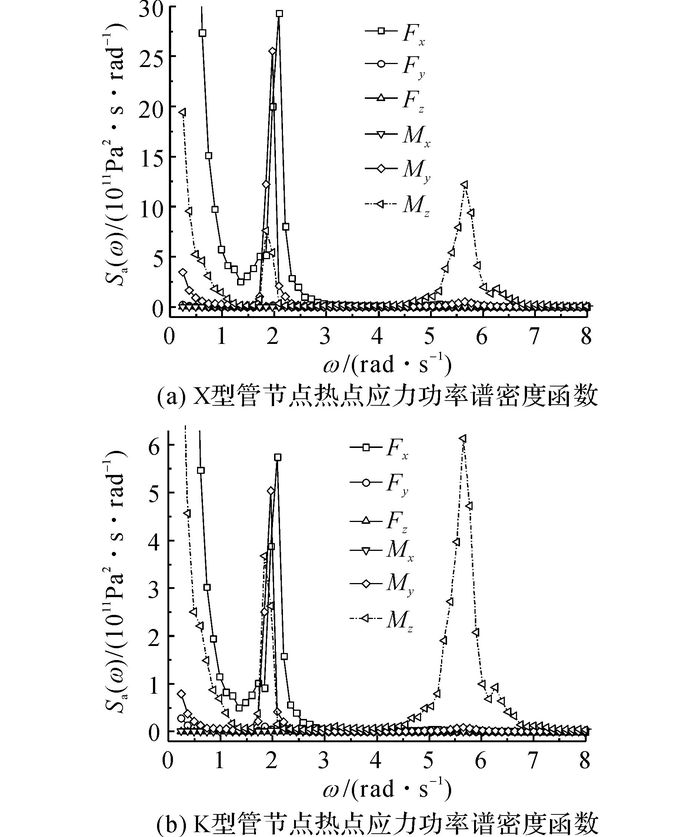
在单一载荷作用下, 载荷和最大主应力之间是线性关系.通过单一载荷作用下的热点应力功率谱密度函数分析验证结构模型等效线性化的合理性;根据载荷的功率谱密度函数以及应力传递函数计算出热点应力的功率谱密度函数.塔顶6个载荷单独作用下热点应力的功率谱密度函数的计算结果如图 7所示.由图 7可知, 对于总热点应力贡献较大的载荷为Fx、My以及Mz, 应力的功率谱密度函数存在2个峰值.根据4.1.1节和4.1.2节的分析可知, 这2个峰值对应的频率分别为结构的一阶固有频率和风载荷的谱峰频率.
|
图 7 单一风载荷分量作用下X型和K型管节点热点应力的功率谱密度函数 Fig. 7 Power spectrum density function of hot-spot stress for X-type and K-Type tubular jointsunder one component of wind load |
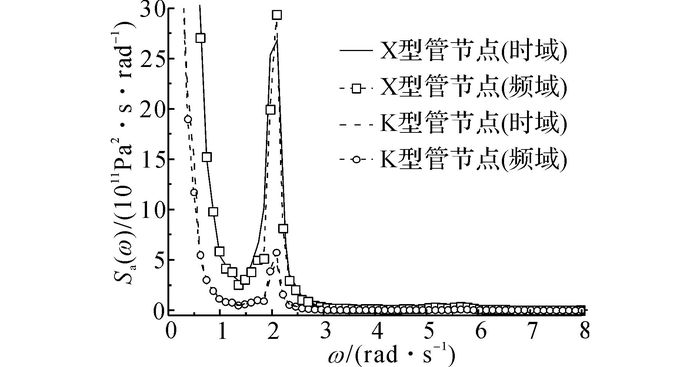
通过ANSYS软件对结构进行瞬态动力学分析;结构模型中的桩土相互作用通过非线性弹簧单元来模拟;桩侧土抗力与侧向位移关系曲线P-y、桩侧摩擦力与轴向位移曲线T-z以及桩端承载力与轴向位移Q-z曲线)来自实际工程勘测.输入单一载荷的时间历程, 得到热点应力的时间历程, 接着对其进行傅里叶变换得到功率谱密度函数.载荷Fx作用下采用2种不同方法(频域和时域)计算得到的功率谱密度函数如图 8所示.由图 8可知, 谱分析方法得到的热点应力功率谱密度函数与时域瞬态动力学的计算结果十分接近.
|
图 8 载荷Fx作用下X型和K型管节点热点应力功率谱密度函数的比较 Fig. 8 Comparison of power spectrum density function of hot-spot stress under load Fx |
为了进一步验证谱分析方法, 分别采用图 8中时域和频域热点应力结果计算X型管节点的疲劳损伤.为了便于比较, 使用带宽修正系数ρWB作为比较参量.当S-N曲线的参数m=3时, 时域方法计算的ρWB为0.626 8, 对应频域方法计算的ρWB为0.615 2.因此, 对于支撑结构的疲劳分析来说, 本文采用的结构系统线性化方法是合理的.
(2) 多载荷联合作用下的热点应力功率谱密度函数分析.
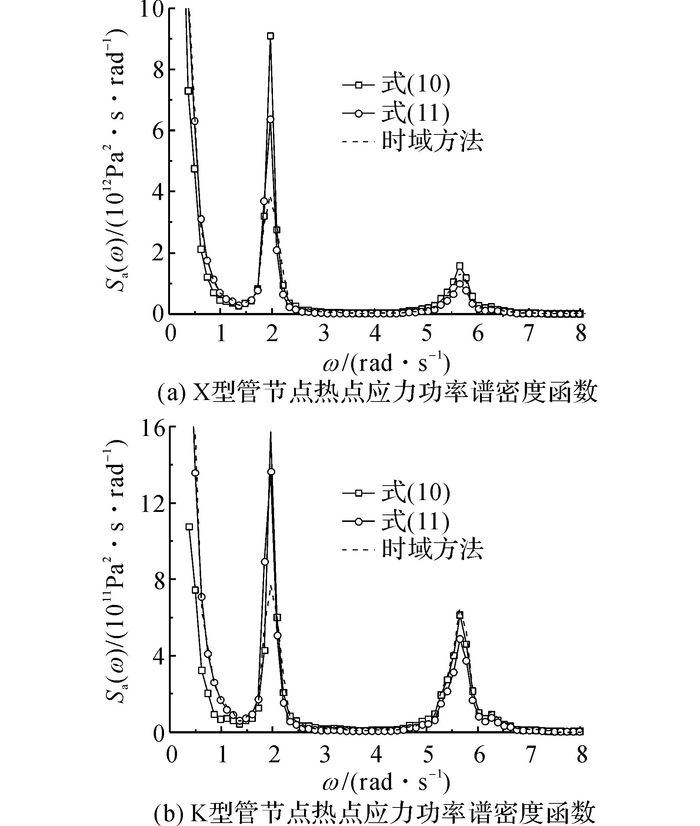
应用式(10) 和式(11) 计算风载荷作用下(6个载荷分量)X型和K型管节点的热点应力功率谱密度函数, 并进行结构的时域瞬态动力学分析.风载荷作用下热点应力功率谱密度函数的比较(频域和时域方法)如图 9所示.由图 9可知, 在低频部分(ω≤1.5 rad/s), 式(11) 的结果和时域模拟一致, 式(10) 的结果反而较小;在结构的一阶固有频率处(ω=2.062 rad/s), 式(10) 的结果最大, 时域模拟最小, 式(11) 的结果介于两者之间;在风载荷的谱峰频率处(ω=5.8 rad/s), 式(10) 的结果和时域结果接近, 并且大于式(11) 的结果.总的来说, 2种频域方法(即式(10) 和式(11))的结果都接近于时域模拟, 但式(11) 不需要计算风载荷分量之间的互功率谱密度函数, 计算相对简便, 因此采用此方法计算Sa(ω).
|
图 9 风载荷作用下热点应力功率谱密度函数的比较 Fig. 9 Comparison of power spectrum density function of hot-spot stress under wind load |
采用SACS软件计算波浪载荷作用下支撑结构的应力谱Sw(ω).使用SACS中的Airy波理论, 并对Morison公式进行等效线性化处理.
根据DNV-OS-J101[10]规范, 选用Pierson-Moskowitz(PM)谱来计算波浪载荷作用下支撑结构的响应, 其中波浪传播方向为x轴正方向.
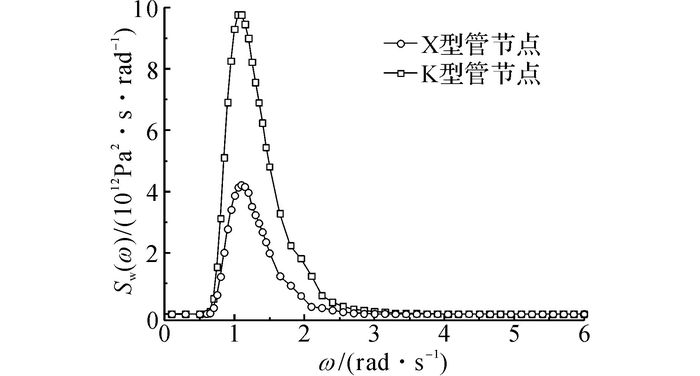
通过SACS软件计算波浪载荷作用下X型和K型管节点热点应力的功率谱密度函数, 结果如图 10所示.可知, K型管节点的响应大于X型管节点;根据波浪的谱峰周期可以得到其谱峰频率为1.05 rad/s;应力的功率谱密度函数只存在1个峰值, 对应频率为谱峰频率.
|
图 10 波浪载荷作用下热点应力的功率谱密度函数 Fig. 10 Power spectrum density function of hot-spot stress under wave loads |
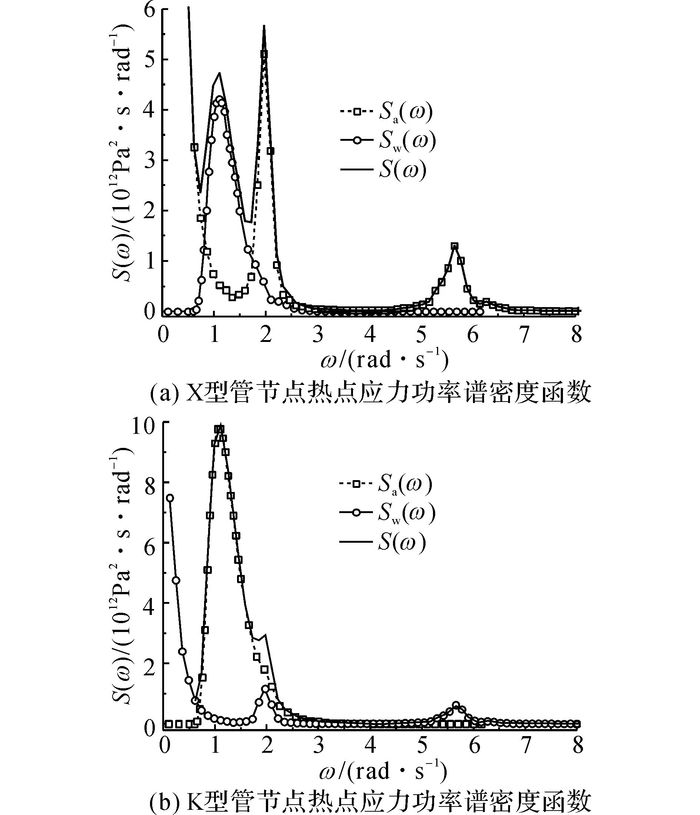
根据式(3) 可得到风浪联合作用下热点应力的功率谱密度函数, 结果如图 11所示.由图 11可知,对于X型管节点, 风荷载和波浪载荷对应力的贡献相当;对于K型管节点, 波浪载荷对应力的贡献大于风载荷;无论是X型管节点还是K型管节点, 总应力的功率谱密度函数都包含3个峰值, 是典型的宽带谱.
|
图 11 风浪联合作用下热点应力的功率谱密度函数 Fig. 11 Power spectrum density function of hot-spot stress under wave and wind loads |
根据DNV-OS-J101规范[10]确定S-N曲线;设计疲劳系数(design fatigue factor, DFF) DFF=2.0, 设计寿命取20 a; 采用第3章中所述的谱疲劳方法计算图 11中X型和K型管节点的损伤, 并将其与时域雨流计数方法进行比较.各种谱疲劳方法的损伤计算结果及误差如表 2所示.
| 表 2 各种谱疲劳方法的损伤计算结果及误差 Table 2 Damage calculation results and error by various spectral fatigue methods |
由表 2可知, 窄带近似方法给出的结果过于保守;Wirsching-Light方法和Ortiz-Chen方法稍显保守;Lutes-Larson和Dirlik方法偏于危险.因此, 在风机的疲劳评估中使用Wirsching-Light方法或Ortiz-Chen方法都是合理的.结合文献[12], 基于计算简便的考虑, 应优先考虑使用Wirsching-Light方法.
5 结论(1) 本文提出了2种风载荷作用下(即式(10) 和式(11))疲劳应力的功率谱密度函数计算方法, 并将其与时域模拟结果进行了比较, 结果表明这2种方法都与时域模拟结果接近, 其中不考虑相关性的计算方法的计算量较小.
(2) 对于不同的疲劳校核部位, 塔顶的6个风载荷分量对应力的贡献各不相同, 其中载荷Fx、My以及Mz对应力的贡献显著.
(3) 对于不同的疲劳校核部位, 风载荷与波浪载荷对应力的贡献不一样.
(4) 在支撑结构的谱疲劳计算方法中, Wirsching-Light方法和Ortiz-Chen方法的计算结果较合理.由于Wirsching-Light方法计算较简便, 建议在评估过程中选用Wirsching-Light方法.
| [1] |
康海贵, 田茂金, 龙丽吉, 等. 基于谱分析的海上风机支撑结构疲劳分析[J].
可再生能源, 2013, 31(7): 41–44.
KANG Hai-gui, TIAN Mao-jin, LONG Li-ji, et al. Spectral-based fatigue analysis of a support structure for offshore wind turbines[J]. Renewable Energy Resources, 2013, 31(7): 41–44. |
| [2] |
莫继华, 何炎平, 李勇刚, 等. 近海风电机组单桩式支撑结构疲劳分析[J].
上海交通大学学报, 2011, 45(4): 565–569.
MO Ji-hua, HE Yan-ping, LI Yong-gang, et al. Fatigue analysis of offshore wind turbine mono-pile structure[J]. Journal of Shanghai Jiaotong University, 2011, 45(4): 565–569. |
| [3] | HUANG W B, MOAN T. A practical formulation for evaluating combined fatigue damage from high and low frequency loads[J]. Journal of Offshore Mechanics and Arctic Engineering, 2007, 129(1): 1–8. DOI:10.1115/1.2426999 |
| [4] |
李红涛, 李林斌. 海上风机支撑结构设计分析[J].
海洋工程, 2011, 29(4): 74–80.
LI Hong-tao, LI Lin-bin. Design analysis for support structure of offshore wind turbine[J]. Ocean Engineering, 2011, 29(4): 74–80. |
| [5] | TEMPLE J V D. Design of support structures for offshore wind turbines[D]. Delft:Delft University of Technology, 2006. |
| [6] |
马永亮, 曲先强, 沙胜义, 等. 风浪联合作用下近海风机塔架结构疲劳评估方法[J].
大连海事大学学报, 2012, 38(3): 36–40.
MA Yong-liang, QU Xian-qiang, SHA Sheng-yi, et al. Fatigue assessment method of the offshore wind turbine tower under the function of combined wind and wave[J]. Journal of Dalian Maritime University, 2012, 38(3): 36–40. |
| [7] |
盛振国, 任慧龙, 甄春博, 等. 基于时域载荷的海上风机基础结构疲劳分析[J].
华中科技大学学报:自然科学版, 2014, 42(4): 96–100.
SHENG Zhen-guo, REN Hui-long, ZHEN Chun-bo, et al. Fatigue analysis for offshore wind turbine foundational structures based on loads in time domain[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2014, 42(4): 96–100. |
| [8] | KUHN M. Dynamics and design optimization of offshore wind energy conversion systems[D]. Delft:Delft University of Technology, 2001. |
| [9] |
韩超帅. 导管架式海上风机支撑结构疲劳性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
HAN Chao-shuai. Research for fatigue performance of jacket offshore wind turbine support structure[D]. Harbin:Harbin Engineering University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014133476.htm |
| [10] | Det Norske Veritas. Design of offshore wind turbine structures:DNV-OS-J101[S]. Oslo:Det Norske Veritas, 2004. |
| [11] | Det Norske Veritas. Recommended practice riser fatigue:DNV-RP-F204[S]. Oslo:Det Norske Veritas, 2010. |
| [12] | American Bureau of Shipping. Commentary on the guide for the fatigue assessment of offshore structures[S]. Houston:American Bureau of Shipping, 2003. |
| [13] | JIAO G, MOAN T. Probabilistic analysis of fatigue due to Gaussian load processes[J]. Probabilistic Engineering Mechanics, 1990, 5(2): 76–83. DOI:10.1016/0266-8920(90)90010-H |
| [14] | 中国船级社. 海上固定平台入级与建造规范[S]. 北京: 中国船级社, 1992. |
| [15] | International Electrotechnical Commission. Design requirements for offshore wind turbines:IEC 61400-3[S]. London:International Electrotechnical Commission, 2009. |
| [16] | NEWLAND D E. An Introduction to Random Vibrations Spectral and Wavelet Analysis[M]. New York: Dover Publications Inc, 2005: 71-73. |
| [17] | DIRLIK T. Application of computers to fatigue analysis[D]. Coventry:University of Warwick, 1985. http://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.372215 |



