近年来, 铝合金因具有轻质高强、耐腐蚀和延展性好等特点被越来越多地应用于建筑结构领域[1], 如上海辰山植物园展览温室、南京牛首山佛宫等, 均采用了铝合金作为主体结构材料[2].焊接会显著降低铝合金材料的力学性能, 现代铝合金结构多采用机械连接, 其中不锈钢螺栓连接应用最为广泛[3].
目前诸多学者对于常温下铝合金板螺栓连接进行了一系列的研究.笔者进行了5组铝合金板件不锈钢螺栓抗剪连接试验, 提出了铝合金受剪螺栓连接的孔壁承压变形失效准则建议, 并通过数值分析给出了孔壁承压强度的建议公式[4].张贵祥等[5]采用ANSYS软件对铝合金构件普通螺栓抗剪连接进行了数值拟合, 提出了孔壁承载力计算公式以及长连接的折减系数公式.王元清等[6]完成了铝合金板件螺栓连接节点的试验研究, 得到了承载力与螺栓孔变形之间的关系, 并给出了铝合金板件孔壁承压强度的建议计算公式.总之, 常温下铝合金板件螺栓连接的研究成果较为丰富, 各国相关规范中亦有详细的明文规定, 如欧洲铝合金规范[7]和中国铝合金结构规范[8]等.
与常温下的研究成果相比, 高温下承载性能的研究成果相对比较匮乏[9].笔者对铝合金板螺栓连接高温下承载性能进行了数值分析, 研究了温度对破坏模式的影响, 结果表明欧规计算方法偏于保守[10].Cai等[11-12]对冷弯薄壁不锈钢单剪及双剪螺栓连接在高温下的性能进行了试验研究, 得到了其极限承载力和破坏模式.对于高温下铝合金板螺栓连接承载力计算, 仅欧洲铝合金结构设计规范EC9[13]采用了强度折减法来进行计算, 而我国《铝合金结构设计规范》[8]尚没有相关规定.可见, 目前对于高温下的铝合金板螺栓连接承载性能亟待进一步研究.
针对上述研究的不足, 本文进行10个常温及高温下的铝合金板螺栓抗剪连接试验, 并建立数值分析模型, 分析各参数对连接承载力的影响, 拟合得到高温下连接承载力的计算公式.
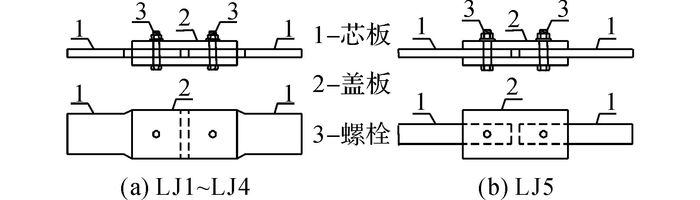
1 试验简介本文共设计10个铝合金板螺栓连接试件, 所有试件均采用国产6061-T6铝合金和A2-70不锈钢螺栓.各试件总长均为290 mm, 螺孔直径比螺栓名义直径大0.5 mm.试件编号和各连接件规格如表 1和图 1所示, 每组试件加工数量为2件.表中, θ为温度, d为螺栓直径, Lx、Bx、tx分别为芯板的长度、宽度和厚度, Lg、Bg、tg分别为盖板的长度、宽度和厚度, ex、eg分别为螺栓与芯板和盖板的端距.所有试件均由双盖板和芯板通过螺栓连接而成, 部分试件照片如图 2所示.
| 表 1 抗剪连接试件信息汇总表 Table 1 Summary of shear connections' information |
|
图 1 连接试件加工图 Fig. 1 Operation drawing of specimen |

|
图 2 连接试件照片 Fig. 2 Photo of connection specimen |
为了对比分析温度对铝合金板螺栓连接性能的影响, 设计了LJ1~LJ3组加载试验, 各试件的板件及螺栓规格均相同, 分别进行20、200和300 ℃恒温加载试验.为了研究除温度外的其他参数对铝合金板螺栓连接性能的影响, 以便在有限的试验数量下获得更多种高温破坏模式和试验数据, 并为验证有限元模型提供更多参考, 增设在200 ℃下进行的LJ4组与LJ5组高温恒温加载试验, 其中LJ4组试件螺栓改用M10, 芯板厚度改为4.5 mm, 芯板端距减小为20.0 mm, 以对比分析;LJ5组试件螺栓为M10, 芯板宽度为25.0 mm.
所有试验均在同济大学工程力学试验中心的岛津高温电子万能试验机上完成, 加热系统为垂直电子高温炉.在试验前拼装节点过程中, 所有螺栓拧至保证连接节点不松动而未过度拧紧, 以便升温过程中板件自由膨胀.试验采用恒温单向拉伸加载的方式, 在确定试件温度达到设定温度后, 保持恒温30 min, 然后进行位移加载, 加载速率约为2 mm/min.加载方式如图 3所示.加载时荷载作用线与试件中心线重合.

|
图 3 加载装置和高温炉 Fig. 3 Loading device and high temperature furnace |
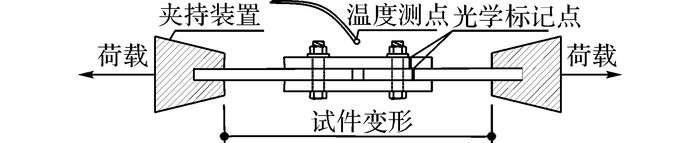
本试验测量内容主要包括加热炉内温度、试验荷载、试件变形以及试件下端螺孔处芯板和盖板的相对位移.炉内温度通过试验机保温炉内部自带的温度热电偶检测, 温度测点靠近试件中心.试验荷载通过油压传感器直接测得.试件变形通过电子万能试验机采集系统自动采集, 变形代表试件上、下夹持端的相对位移.芯板和盖板相对位移的测量采用光学测量的原理, 利用固定位置的位移摄像仪捕捉试件上的标记点, 通过标记点的位移变化计算得到试件标记区段的相对变形, 各测点布置如图 4所示.
|
图 4 测点布置图 Fig. 4 Layout of measuring points |
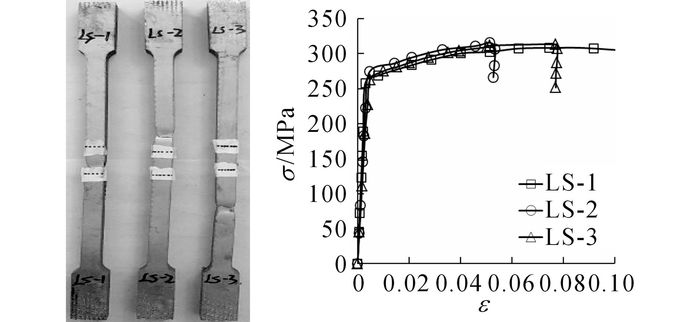
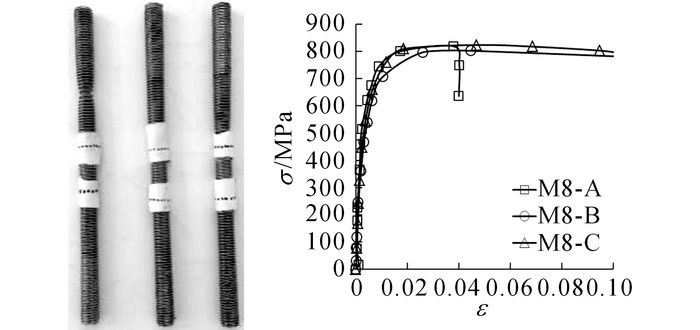
根据《金属材料室温拉伸试验方法》[14]的规定, 试验前利用同一批次的6061-T6铝合金板和A2-70螺栓制作了3个哑铃型铝合金拉伸试件和3个圆棒螺栓拉伸试件, 在电子万能试验机上测定铝合金和螺栓的常温力学性能.铝合金和螺栓破坏后的拉伸试样与名义应力-应变曲线分别如图 5和6所示, 图中σ为名义应力, ε为名义应变.铝合金和螺栓破坏后拉伸试验结果分别如表 2和3所示, 表中E为弹性模量, f0.2为名义屈服强度, fu为极限抗拉强度, δ5为断后伸长率, ψ为断面收缩率.
|
图 5 铝合金的应力-应变曲线 Fig. 5 Stress-strain curve of aluminum alloy |
|
图 6 不锈钢的应力-应变曲线 Fig. 6 Stress-strain curve of stainless steel |
| 表 2 铝合金拉伸试验结果 Table 2 Tensile test results of aluminum alloy |
| 表 3 不锈钢螺栓拉伸试验结果 Table 3 Tensile test results of stainless steel bolt |
试件的典型破坏模式如图 7所示, 各试件的极限承载力、破坏模式和试件的破坏现象如表 4所示, 表中Fu为极限承载力, σu为试件在其对应的破坏模式下破坏部位的极限应力, 即LJ1组、LJ2组的螺栓剪应力, LJ3组的芯板孔壁承压应力, LJ5组的芯板拉应力, 上述应力均根据实测面积计算得到.LJ4组试件由于发生芯板端部冲剪破坏, 孔壁承压性能未完全发挥, 本文未列出其孔壁承压应力.

|
图 7 抗剪连接试件典型破坏模式 Fig. 7 Typical failure mode of shearing connection specimens |
| 表 4 抗剪连接试件破坏情况概述 Table 4 Description of failure mode of shearing connection specimens |
从表 4可以看出, LJ1和LJ2组试件均发生螺杆剪断破坏, 破坏面位于螺杆靠近芯板与盖板的交界处, 常温下螺杆剪断时螺栓截面上的平均剪应力在650 MPa以上, 200 ℃时破坏剪应力下降为550 MPa;LJ3组试件发生孔壁承压破坏, 高温下铝合金材料进入塑性流动状态, 螺栓挤压孔壁铝合金材料从而发生向外的挤压变形, LJ3组试件的破坏模式不同于LJ1和LJ2组的原因在于高温下铝合金的强度和弹性模量的下降快于不锈钢材料, 因此节点破坏模式由螺栓剪断转变为铝合金芯板孔壁承压破坏;LJ4组试件发生芯板端部冲剪破坏, 由图 7可见, 破坏面由螺栓孔向芯板端面发展, 芯板净截面最大应力仅为拉断应力的40%, 这表明当连接板端距不足时, 孔壁端材料受到冲剪作用从而导致连接承载力大幅降低;LJ5组试件芯板净截面拉断, 裂纹由螺栓孔向芯板边缘发展.芯板平均应力接近材料在200 ℃时的抗拉强度.
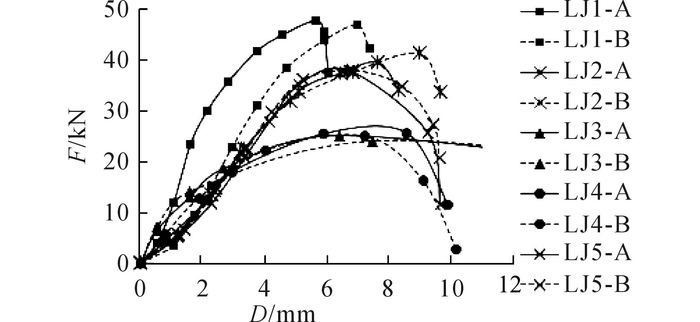
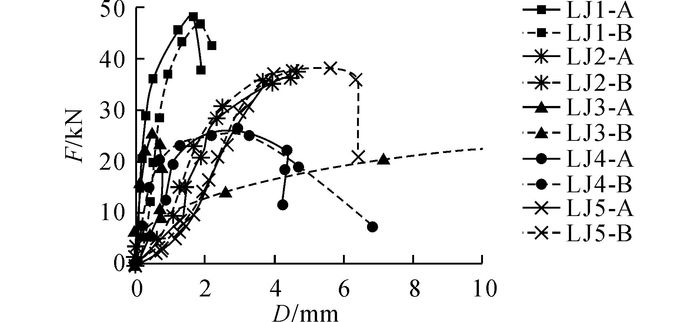
2.3 荷载-位移曲线试验过程中试验机自动记录了试件夹持端的相对位移, 所有试件的荷载-端部位移曲线如图 8所示.通过试件装置中的光学位移捕捉器, 可以得到在螺栓孔附近处芯板及盖板的相对变形, 各试件的荷载-孔壁变形曲线如图 9所示.其中, F为荷载, D为端部位移或相对变形大小.
|
图 8 荷载-夹持端相对位移曲线 Fig. 8 Load-relative displacement curves of clamped end |
|
图 9 荷载-孔壁相对变形曲线 Fig. 9 Load-relative deformation curves of hole wall |
从图 8和9可以看出, 各组试件的承载过程均可分为5个阶段:初期螺栓滑移和嵌固阶段、弹性阶段、屈服阶段、峰值阶段及破坏阶段.加载初期, 由于存在滑移, 荷载位移曲线刚度较小;随着荷载增加, 连接进入孔壁承压阶段, 螺杆受压区或芯板孔壁逐渐出现塑性区域, 承载刚度发生变化;当塑性区域扩展至一定范围时, 荷载-位移曲线趋于平缓, 最终荷载达到螺栓抗剪极限或孔壁承压极限而发生破坏.另外, 随着温度的升高, 试件的极限承载力逐步降低, 而极限变形逐渐变大.
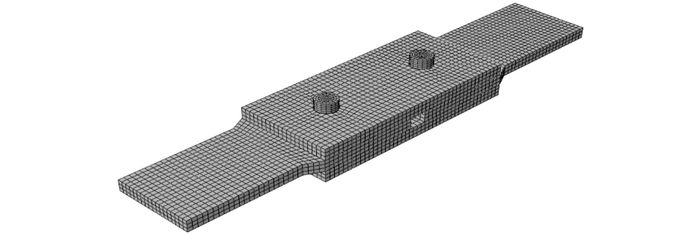
3 有限元模拟 3.1 数值模型采用有限元软件ABAQUS对本次试验中5组试件进行模拟, 典型有限元模型如图 10所示.模型尺寸采用试件名义尺寸, 螺孔直径为螺杆直径大0.5 mm.常温下螺栓和铝合金的材性采用表 2和3的结果, 高温下材性根据欧规EC3[15-16]和EC9[13]的规定对常温的物理力学性能进行折减, 模型中本构关系均为经拉伸试验结果处理得到的真实应力-真实应变关系.铝合金和不锈钢的本构关系均采用Ramberg-Osgood模型.采用C3D8R单元模拟螺栓与铝合金板, 采用扫略技术划分网格, 综合考虑计算精度及效率, 选定铝合金板件网格尺寸近似3 mm, 不锈钢螺栓的网格尺寸近似1.5 mm, 圆孔处网格局部加密;采用罚摩擦模型模拟各接触面之间的接触, 摩擦系数取0.2.试件在装配时所有试件初始状态为恰好相互接触, 连接板与螺杆之间未互相挤压.
|
图 10 抗剪连接有限元模型 Fig. 10 FE model of shear connections |
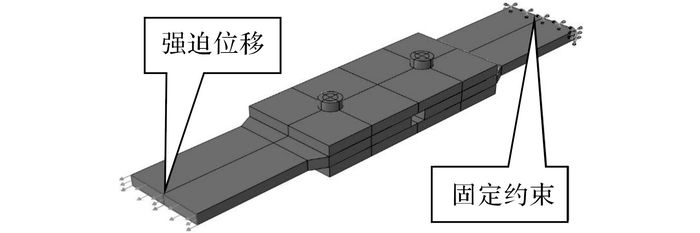
数值模型的荷载及约束如图 11所示.为了研究理想情况下的节点承载性能, 不考虑试件夹持端滑移的影响, 参数分析中的数值模型均将一侧铝芯板的边缘完全固定.为了获得完整的荷载-位移曲线, 数值模型采用位移加载的方式, 对铝合金芯板端部施加位移荷载.
|
图 11 抗剪连接的边界条件 Fig. 11 Boundary conditions of shear connections |
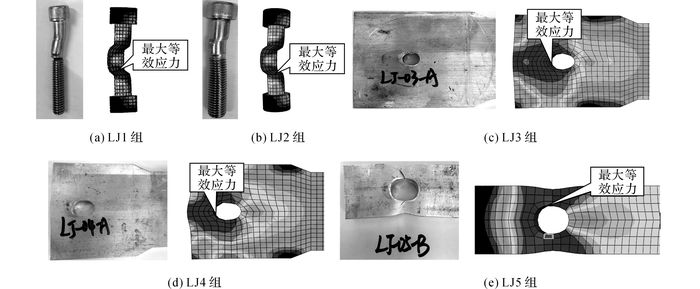
各组试件试验和数值模拟所得的破坏模式及变形情况如图 12所示.可以看出, 数值模型较好地模拟出了各组试验的破坏模式, 数值模型和试验结果吻合度较高.
|
图 12 试验结果与数值模拟的破坏模式对比 Fig. 12 Comparison of failure modes between test and numerical simulation |
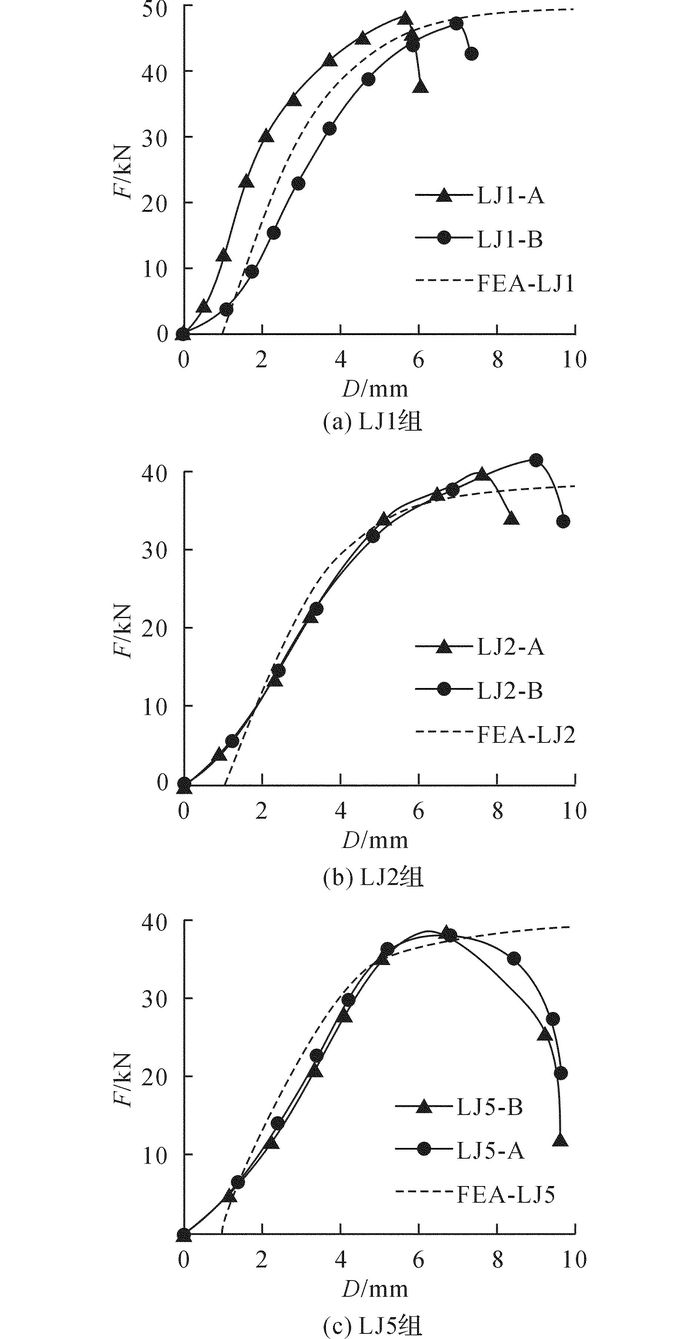
部分试件试验与数值模拟得到的荷载-位移曲线对比如图 13所示.由图可见, 有限元结果和试验结果在加载初期的线弹性阶段较为吻合;进入塑性后, 有限元结果的荷载-位移曲线略比试验值低;试验后期由于板件破坏而自动卸载, 而有限元分析中材料达到极限强度后应力保持不变, 荷载-位移曲线平缓上升.总体而言, 数值模拟中的荷载位移曲线和试验结果吻合良好.
|
图 13 部分抗剪连接试件的荷载-位移曲线 Fig. 13 Load-displacement curve of some shear connection specimens |
各组试件极限承载力的实测值和有限元结果对比如表 6所示, 表中Ft为试验中承载力实测值, FFEA为有限元计算结果, 判断极限状态的孔壁承压失效准则分别为美国钢结构规范[17]规定的0.3d0准则(FFEA-1)以及文献[4]采用的90°嵌入角准则(FFEA-2), δFEA-1和δFEA-2分别为2种失效准则下的数值计算结果与相应试验结果的相对误差.从表 6中可以看出, 准则FEA-2结果比准则FEA-1更保守, LJ4组试件由于提前发生端部冲剪破坏而导致有限元结果偏低, LJ1、LJ2、LJ3和LJ5组试件承载力误差均小于10%, 数值模型所得承载力与试验实测承载力吻合良好.
| 表 6 试验及有限元极限承载力对比 Table 6 Comparison of ultimate capacity between test and numerical simulation |
采用经过试验验证的有限元模型对铝合金板螺栓连接进行参数分析, 主要参数包括温度θ、铝合金芯板宽度B、芯板厚度t、螺栓直径d和螺栓端距e.
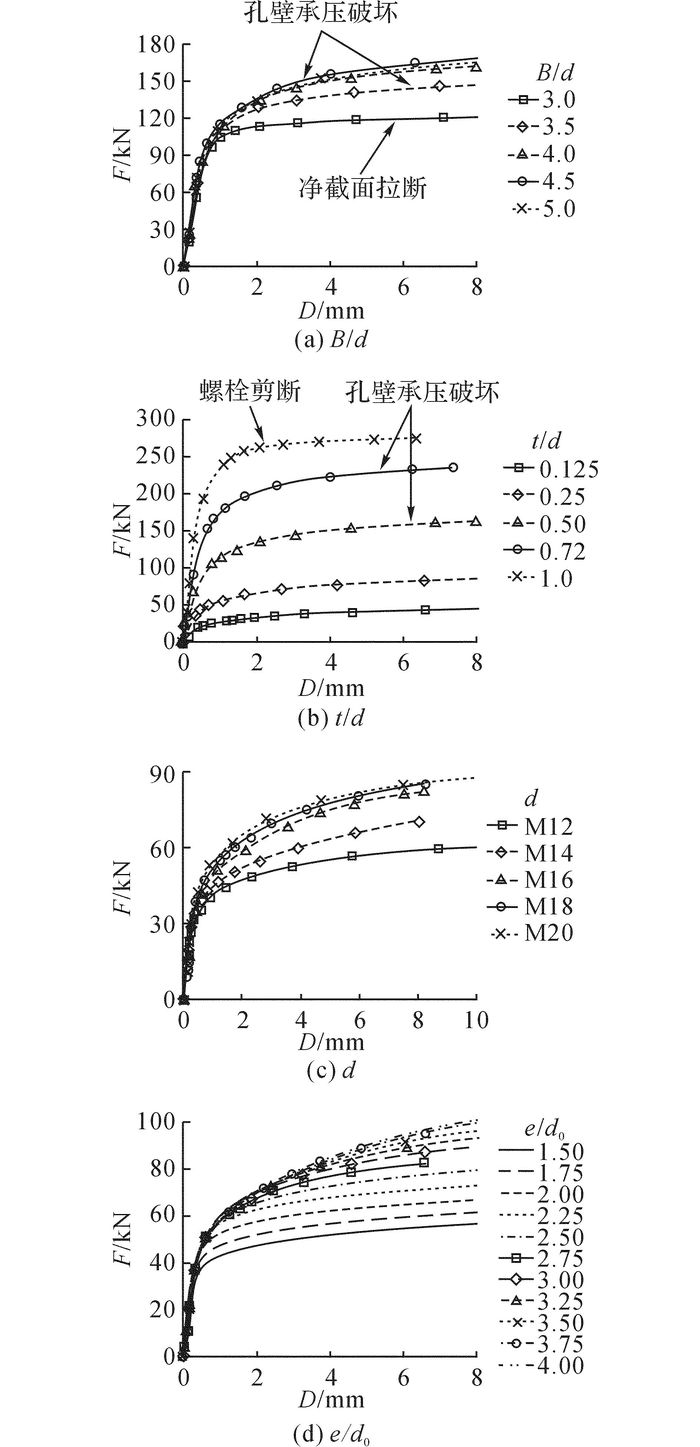
常温下芯板宽度和螺栓直径之比B/d对荷载-孔壁挤压变形曲线的影响如图 14(a)所示.随着芯板宽度的增加, 承载力有所提高, 但初始刚度近似一致.当芯板宽度较小时, 芯板发生拉断破坏;当芯板宽度较大时, 破坏模式变为孔壁承压破坏;此后继续增大芯板宽度对承载力提高不明显.
|
图 14 不同参数对荷载-孔壁变形曲线的影响 Fig. 14 Influence of different parameters on load-hole wall deformation curve |
常温下芯板厚度和螺栓直径之比t/d对荷载-孔壁挤压变形曲线的影响如图 14(b)所示.随着芯板厚度的增加, 节点的承载能力和初始刚度都大幅度提升, 当t/d从0.125增加至1.000时, 承载力提高约6.2倍.当芯板厚度较小时, 发生孔壁承压破坏;当t/d=1.000时, 发生螺栓剪断破坏.
常温下螺栓直径d对荷载-孔壁挤压变形曲线的影响如图 14(c)所示, 本系列模型中的t=5 mm, B/d>4.随着螺栓直径的增加, 孔壁承压破坏程度越发明显, 芯板塑性区变大, 螺栓应力下降, 但各曲线初始刚度有一定区别.当螺栓直径较小时, 发生孔壁承压破坏;当直径达到20 mm时, 发生芯板净截面拉断破坏.
常温下螺栓端距和螺孔直径之比e/d0对荷载-孔壁挤压变形曲线的影响如图 14(d)所示.随着螺栓端距的增加, 孔壁承压能力逐渐增强, 各曲线初始刚度相近.当螺栓端距较小时, 易发生端部冲剪破坏, 孔壁承压能力无法完全发挥;当e>3d0后, 端距的增大对承载性能的贡献变小.
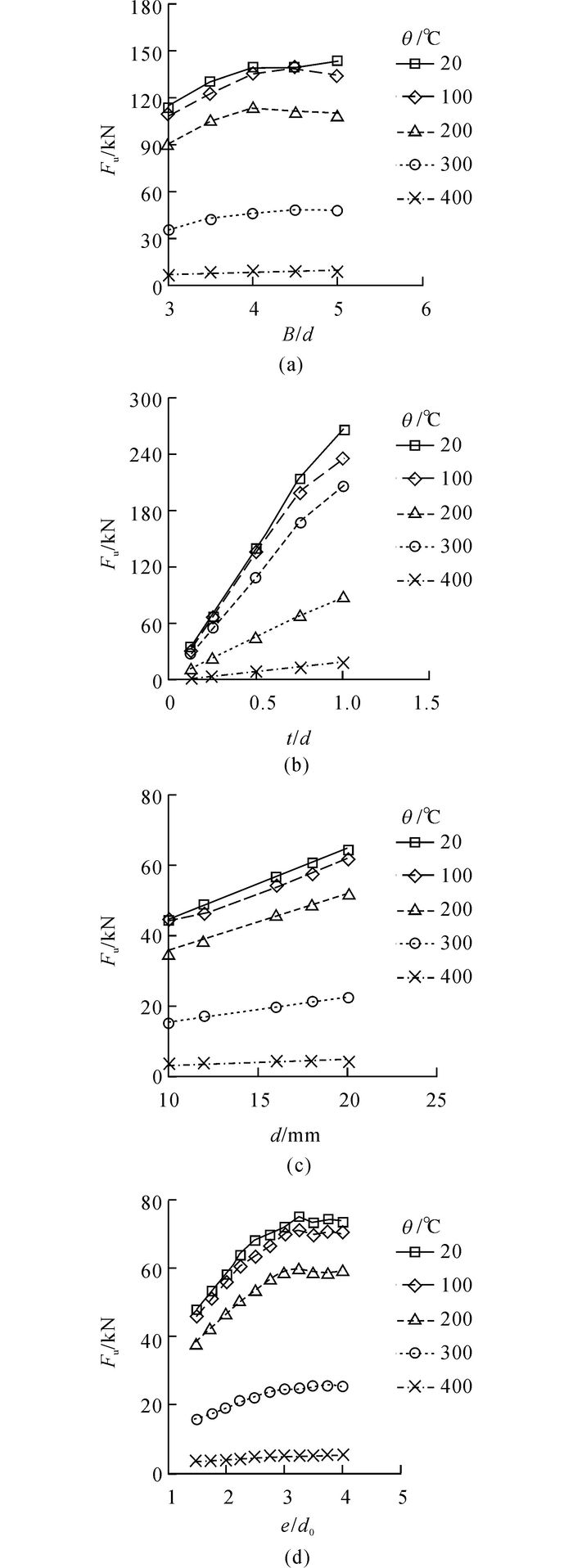
在20、100、200、300和400 ℃这5个温度条件下, 分别以上述4个参数为变量分析连接承载力的变化规律, 计算4个系列共225个数值模型, 得到约3 000个有效数据点.采用较为保守的90°嵌入角准则[4]来确定孔壁承压强度.在各温度下不同参数对节点极限承载力Fu的影响曲线如图 15所示.由图可见, 温度的升高会降低节点的极限承载力.当温度达到400 ℃时, 节点承载力均不足10 kN, 改变任何参数均对节点承载力的提高无明显影响.
|
图 15 不同温度下各参数对抗剪连接极限承载力的影响 Fig. 15 Influence of different parameters on capacity of shear connections under different temperatures |
根据有限元参数分析结果可知, 铝合金板件不锈钢螺栓连接孔壁承压承载力与螺栓直径和连接件厚度成比例关系, 芯板宽度和端距影响着节点破坏模式, 温度对承载力与破坏模式均有影响.当连接在高温下发生孔壁承压破坏时, 其孔壁承压承载力为
| $N_{\rm{c}}^{\rm{b}}\left( T \right) = dt \times f_{\rm{c}}^{\rm{b}}\left( T \right).$ | (1) |
式中:fbc(T)为高温下孔壁承压强度标准值.
在不同螺栓直径和不同温度的条件下,由数值分析得到的螺栓端距对孔壁承压强度的影响曲线如图 16所示.图中,fcb(T)/fu(T)为高温下孔壁承压强度和芯板抗拉强度之比.根据图中承载力随螺栓端距变化的双折线规律,偏保守地采用所有曲线的下包络线来计算孔壁承压强度.据此拟合出的孔壁承压强度标准值的计算公式为

|
图 16 拟合公式与数值模拟结果对比 Fig. 16 Results comparision between fitting formula and numerical simulation |
| $f_{\rm{c}}^{\rm{b}}\left( T \right) = \left\{ {\begin{array}{*{20}{l}} {[0.6e/{d_0} + 0.7]{f_{\rm{u}}}\left( T \right),1.5 \le e/{d_0} < 3;}\\ {2.5{f_{\rm{u}}}\left( T \right),30 < e/{d_0} \le 4.} \end{array}} \right.$ | (2) |
式中:fu(T)为温度T时铝合金抗拉强度标准值, 可按下式计算:
| ${f_{\rm{u}}}\left( T \right) = k\left( T \right) \times {f_{\rm{u}}}.$ | (3) |
其中, fu为常温下的铝合金抗拉强度, k(T)为高温折减系数, 由于我国规范没有相关规定, 建议按照欧洲规范EC9的规定取值.
表 7对比了拟合公式计算结果(Fcb)与发生了孔壁承压破坏的LJ3和LJ4组试验结果, 表中δt和δFEA分别为拟合公式计算结果与试验和数值模拟结果的相对误差, 有限元结果(FFEA)为90°嵌入角准则[4]所对应的承压承载力.可见公式计算结果与试验结果的相对误差小于10%, 且公式结果偏于保守;与有限元结果的相对误差小于6%.因此, 拟合公式具有较高的可靠性.
| 表 7 拟合公式承载力与试验结果对比 Table 7 Comparison of capacity between fitting formula and test |
为了工程应用方便, 表 8列出了根据式(2) 计算得到的国产6061-T6铝合金在高温下的孔壁承压承载力标准值fcb和设计值fcd.其中, 对于国产6061-T6铝合金, fu=265 MPa;连接的抗力分项系数为1.3.
| 表 8 国产6061-T6铝合金在高温下的孔壁承压强度取值 Table 8 Bearing strength at bolt hole of domestic 6061-T6 at elevated temperature |
通过铝合金板件不锈钢螺栓连接的高温抗剪试验和有限元模拟发现, 随着温度升高, 抗剪连接的破坏模式会发生变化;连接板宽度对孔壁承压承载力影响较小;孔壁承压承载力随螺栓直径和连接板厚度近似呈线性变化;孔壁承压承载力在一定范围内随螺栓端距增大而升高.
高温下铝合金板件不锈钢螺栓抗剪连接的孔壁承压强度可按照式(2) 计算;对于国产6061-T6铝合金, 其高温下的孔壁承压强度标准值和设计值可采用表 8中的数值;式(2) 和试验结果吻合良好, 相对误差小于10%.
| [1] |
杨联萍, 韦申, 张其林. 铝合金空间网格结构研究现状及关键问题[J].
建筑结构学报, 2013, 34(2): 1–19.
YANG Lian-ping, WEI Shen, ZHANG Qi-lin. Aluminum reticulated spatial structures:state of the art and key issues[J]. Journal of Building Structures, 2013, 34(2): 1–19. |
| [2] |
杨联萍, 邱枕戈. 铝合金结构在上海地区的应用[J].
建筑钢结构进展, 2008, 10(1): 53–57.
YANG Lian-ping, QIU Zhen-ge. Application of aluminum alloy structures in Shanghai[J]. Progress in Steel Building Structures, 2008, 10(1): 53–57. |
| [3] |
沈祖炎, 郭小农, 李元齐. 铝合金结构研究现状简述[J].
建筑结构学报, 2007, 28(6): 100–109.
SHEN Zu-yan, GUO Xiao-nong, LI Yuan-qi. State of the arts of research on aluminum alloy structures[J]. Journal of Building Structures, 2007, 28(6): 100–109. |
| [4] |
郭小农, 邱丽秋, 徐晗, 等. 铝合金受剪螺栓连接孔壁承压强度[J].
同济大学学报:自然科学版, 2014, 42(1): 36–43.
GUO Xiao-nong, QIU Li-qiu, XU Han, et al. Bearing strength at bolt holes of aluminum alloy[J]. Journal of Tongji University:Natural Science, 2014, 42(1): 36–43. |
| [5] |
张贵祥, 石永久, 王元清, 等. 铝合金构件螺栓连接承压性能分析与设计方法[J].
桂林工学院学报, 2006, 26(4): 501–505.
ZHANG Gui-xiang, SHI Yong-jiu, WANG Yuan-qing, et al. Analysis and design of bearing strength of bolted connection in aluminum alloy[J]. Journal of Guilin University of Technology, 2006, 26(4): 501–505. |
| [6] |
王元清, 袁焕鑫, 石永久, 等. 铝合金板件螺栓连接承压强度试验与计算方法[J].
四川大学学报:工程科学版, 2011, 43(5): 203–208.
WANG Yuan-qing, YUAN Huan-xin, SHI Yong-jiu, et al. Experiments and computational method on bearing capacity of bolted joint for aluminum alloy sheets[J]. Journal of Sichuan University:Engineering Science Edition, 2011, 43(5): 203–208. |
| [7] | CEN. EN 1999-1-1:2007 Eurocode 9:Design of aluminium structures. Part 1-1:general structuralrules[S]. Brussels:European Committee for Standardization, 2007. |
| [8] | 中华人民共和国建设部. 铝合金结构设计规范: GB50429-2007[S]. 北京: 中国计划出版社, 2008. |
| [9] |
郭小农, 梁水平, 蒋首超. 铝合金构件不锈钢螺栓连接高温性能研究综述[J].
建筑钢结构进展, 2015, 17(5): 18–23.
GUO Xiao-nong, LIANG Shui-ping, JIANG Shou-chao. Research review on the mechanical behavior of stainless steel bolted joint for aluminum alloy members at elevated temperatures[J]. Progress in Steel Building Structures, 2015, 17(5): 18–23. |
| [10] |
郭小农, 梁水平, 蒋首超. 铝合金板件不锈钢螺栓连接的高温承载性能数值研究[J].
工业建筑, 2015, 45: 1617–1624.
GUO Xiao-nong, LIANG Shui-ping, JIANG Shou-chao. Numerical study on bearing performance of stainless steel bolted shear connection for aluminum alloy members at elevated temperature[J]. Industrial Construction, 2015, 45(Suppl.): 1617–1624. |
| [11] | CAI Y, YOUNG B. Behavior of cold-formed stainless steel single shear bolted connections at elevated temperatures[J]. Thin-Walled Structures, 2014, 75(2): 63–75. |
| [12] | CAI Y, YOUNG B. High temperature tests of cold-formed stainless steel double shear bolted connections[J]. Journal of Constructional Steel Research, 2015, 104(104): 49–63. |
| [13] | CEN. EN 1999-1-2:2007 Eurocode 9:Design of aluminum structures. Part 1-2:General rules:structural fire design[S]. Brussels:European Committee for Standardization, 2007. |
| [14] | 中华人民共和国国家质量监督检验检疫总局. 金属材料室温拉伸试验方法: GB/T228-2002[S]. 北京: 中国建筑工业出版社, 2002. |
| [15] | CEN. EN 1993-1-2:2005 Eurocode 3:Design of Steel Structures. Part 1-2:Structural fire design[S]. Brussels:European Committee for Standardization, 2005. |
| [16] | CEN. EN 1993-1-4:2006 Eurocode 3:Design of Steel structures. Part 1-4:General Rules-Supplementary Rules for Stainless Steels[S]. Brussels:European Committee for Standardization, 2006. |
| [17] | AISC. Load and resistance factor design specification for structural steel buildings[S]. Chicago:American Institute of Steel Construction, 1993. |



