2. 中国能源建设集团江苏省电力设计院有限公司, 江苏 南京 210036
2. Energy China JSPDI, Nanjing 210036, China
自20世纪初, Richart等[1]进行了混凝土圆柱体在均匀围压和螺旋箍筋约束下的受压试验研究, 提出约束效应公式后, 研究学者们对混凝土在约束力作用下的本构关系进行了三轴受压试验和理论研究分析, 发现在侧向围压状态下, 混凝土的抗压强度和延性都会有所提高[2-4].
基于混凝土多轴受力下的试验和理论研究成果,纤维增强复合材料(fiber reinforced polymer,FRP)约束混凝土开始被广泛应用于结构加固工程中.混凝土受到的侧向约束力随混凝土侧向变形的变化而变化的约束机制称为被动约束.混凝土侧向约束力与变形无关, 为恒定值的约束机制称为主动约束.由于FRP是线弹性材料, FRP约束混凝土施加给混凝土的侧向围压与混凝土的侧向应变成正比关系, 为被动约束;由于钢材为弹塑性材料, 在与混凝土共同受力下, 钢管或钢筋很快达到屈服强度, 混凝土环向约束力保持恒值, 常被简化为主动约束.混凝土是一种静水压力敏感性材料, 具有应力路径相关性[5-6].主动约束与被动约束这2种不同的约束机制, 是2种不同的应力路径, 这2种应力路径下混凝土表现出截然不同的应力-应变关系[6-7].
对于主动约束, 分别采用常规静水三轴试验机和真三轴试验机模拟侧向等围压和侧向不等围压, 直接获得混凝土在多向应力路径下的力学特性.常规静水三轴试验机一般由已有的压力试验机配备一个带活塞的液压油缸以及附属的油泵、油路系统构成.在油泵往油缸内压油时, 试件承受侧向油压, 纵向由试验机通过活塞施加压力, 试件外包有橡胶薄膜,防止高压油进入混凝土裂缝内导致试件强度降低.常规静水三轴试验机可以进行三轴受压试验, 但不能完成二轴受拉试验, 也无法进行三轴拉压试验.
真三轴试验机主要由压力试验机、水平承载框和底部工作平台组成.真三轴试验机在3个相互垂直的方向分别设立独立的液压缸和附属设备以便分别施加三向主应力, 3个方向的加载比例由相应的控制器控制, 可以进行任意应力比例的二轴和三轴应力状态试验.
常规静水三轴试验机和真三轴试验机均无法实现施加双向被动围压, 即围压与位移耦合的加载状态.为了获得混凝土被动约束下本构模型所需的试验数据, 目前广泛采用FRP包裹混凝土圆柱的受压试验, 但此类试验无法通过FRP包裹非圆形截面混凝土柱及偏心受压FRP约束混凝土获取混凝土在两向被动约束力不等情况下的本构关系.
本文结合主动约束装置系统,采用玻璃纤维增强复合(glass fiber reinforced polymer, GFRP) GFRP筋和钢板设计一套具有被动加载机制的新型真三轴试验装置系统[8].该装置结合万能试验机组成新型的真三轴试验装置, 可以实现在某一主应力方向等速率加载的同时, 在另外2个主应力方向随试件的变形自发产生围压荷载, 以此建立均匀被动约束混凝土在三轴应力状态下的本构模型, 进一步研究非均匀被动约束下混凝土的力学性能, 模拟混凝土矩形柱及偏心受压柱在FRP包裹下的力学行为.
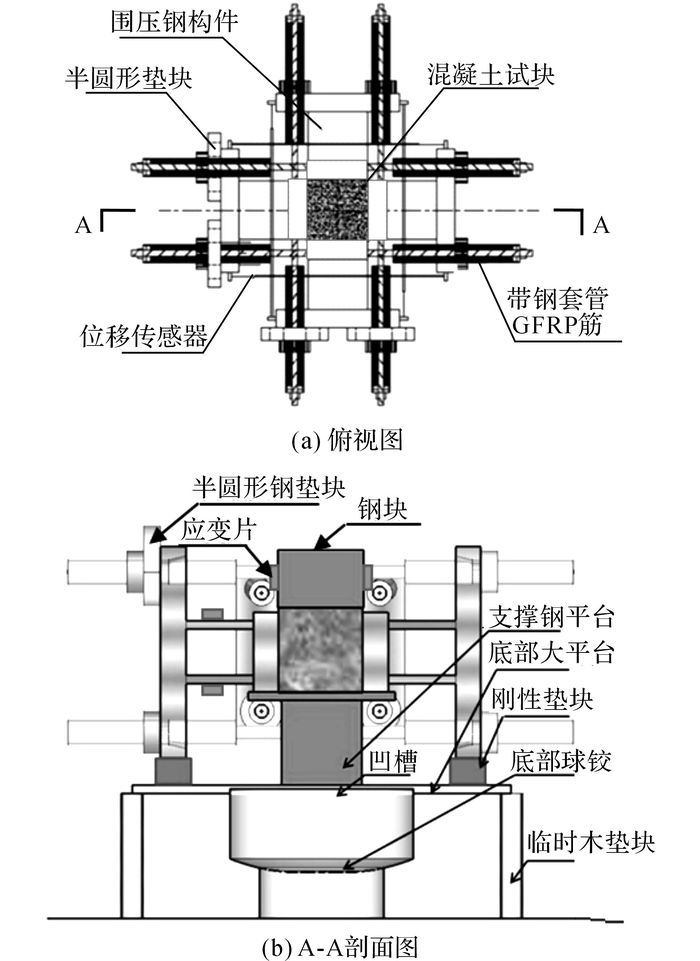
1 试验装置设计本文设计的具有被动加载机制的新型真三轴试验装置系统主要由万能试验机、被动式约束加载装置及位移传感器组成.通过万能试验机向试件施加轴向力, 通过被动式约束加载装置实现与侧向变形成线性耦合关系的侧向力, 通过万能试验机采集荷载信息, 通过外设的位移传感器采集变形数据.该装置系统的核心是变形转化机构, 其转化控制方程决定了该机构的被动围压加载模式, 其中侧向刚度K为侧向约束力与侧向变形的比例系数, 通过调整K值来控制侧向装置提供给混凝土的约束力.当2个侧向的K值不同时, 装置就能实现双向不等的被动约束.为保证混凝土侧向围压与侧向变形之间恒定的线性比例关系, K值在试验过程中需要保持恒定.该新型真三轴试验装置系统主要针对100 mm×100 mm×100 mm的立方体试块进行设计.
GFRP筋有较高的抗拉强度和极限应变[9], 一般情况下极限应变可以达到2%, 且在一定的应力范围内, 应力-应变呈线弹性关系, 因此, 本试验装置系统采用GFRP筋作为侧向围压施加材料, 即采用GFRP筋作为实现侧向变形与侧向约束力转换的构件.通过将GFRP筋锚固于围压钢构件, 基于作用力与反作用力原理, 实现力传输机构的作用.加载体系简图如图 1所示.
|
图 1 新型真三轴试验装置系统简图 Fig. 1 Diagram of new true-triaxial test apparatus system |
本试验装置系统中的K值主要受GFRP筋及其锚固系统组成的侧向围压装置的影响.由GFRP筋及其锚固系统组成的侧向围压装置的变形主要由GFRP筋的弹性变形和GFRP筋在锚固体内的滑移变形2部分组成.视围压钢构件为刚体, 则混凝土的侧向变形等于GFRP筋弹性变形和GFRP筋在锚固体内的滑移变形之和:
| ${\varepsilon _{\rm{c}}}{L_{\rm{c}}} = {\varepsilon _{\rm{r}}}{L_{\rm{r}}} + 2s.$ | (1) |
式中:εc为混凝土某一侧向的应变, Lc为混凝土边长, εr为GFRP筋的应变, Lr为GFRP筋的长度, s为GFRP筋一端的滑移量.
对于两端锚固在钢套管的GFRP筋来说, 力-滑移变形和力-FRP筋弹性应变在微小变形内可视为线性关系[8-9].通过端部黏结力与GFRP筋拉力相互平衡建立GFRP筋滑移量与GFRP筋弹性应变的关系式:
| ${k_{{\rm{slip}}}} = \frac{{{E_{\rm{r}}}{\varepsilon _{\rm{r}}}{A_{\rm{r}}}}}{s}.$ | (2) |
式中:kslip为GFRP筋的滑移模量, Er为GFRP筋的弹性模量, Ar为单根GFRP筋的面积.
将求出的滑移量s代入式(1), 建立GFRP筋应变与混凝土应变的转化关系:
| ${\varepsilon _{\rm{r}}} = {L_{\rm{c}}}{\varepsilon _{\rm{c}}}{\left( {{L_{\rm{r}}} + 2\frac{{{E_{\rm{r}}}{A_{\rm{r}}}}}{{{k_{{\rm{slip}}}}}}} \right)^{ - 1}}.$ | (3) |
该被动加载装置系统最终作用于混凝土试块某一主应力方向上的合力为
| $F = {n_{\rm{r}}}{E_{\rm{r}}}{\varepsilon _{\rm{r}}}{A_{\rm{r}}} = {n_{\rm{r}}}{L_{\rm{c}}}{\varepsilon _{\rm{c}}}{\left( {\frac{{{L_{\rm{r}}}}}{{{E_{\rm{r}}}{A_{\rm{r}}}}} + \frac{2}{{{k_{{\rm{slip}}}}}}} \right)^{ - 1}}.$ | (4) |
式中:nr为某一主应力方向的GFRP筋的根数.
由下式计算得到侧向刚度:
| $K = \frac{{\Delta F}}{{\Delta {\varepsilon _{\rm{c}}}{L_{\rm{c}}}}} = {n_{\rm{r}}}{\left( {\frac{{{L_{\rm{r}}}}}{{{E_{\rm{r}}}{A_{\rm{r}}}}} + \frac{2}{{{k_{{\rm{slip}}}}}}} \right)^{ - 1}}.$ | (5) |
由式(1)~(5) 可知, 当GFRP筋确定后, 该设计可确保K为恒定常数.在实施三轴试验前, 可通过单侧围压装置拉拔试验直接得出侧向力和GFRP筋应变之间的关系, 获得K值.试验装置的约束能力可用约束刚度比表示:
| $\rho = \frac{K}{{{L_{\rm{c}}}{f_{{\rm{c}}0}}}}.$ | (6) |
式中:fc0为混疑土抗压强度.
2 单根GFRP筋力学性能试验试验采用的GFRP筋由上海绩满玻璃钢制品有限公司生产, 样品出厂参数见表 1.表中, D为GFRP筋的规格, 即外围直径设计值, D1为实际外径, D2为实际底径, r为螺距, Ft为抗拉力.
| 表 1 GFRP筋的出厂参数 Table 1 Manufacture parameters of GFRP bar |
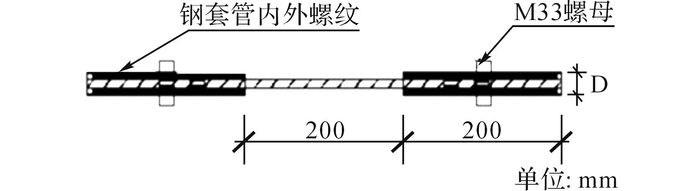
在GFRP筋两端黏结钢套管提供足够的端部刚度, 避免GFRP筋在夹头端部提前发生脆断破坏, GFRP筋与钢套管之间填充环氧树脂作为灌浆材料[10-11].单根GFRP筋两端黏结钢套管长度方向尺寸如图 2所示, 200 mm锚固长度依据ASTM D3916-08[12], 满足最小长度要求.钢套管内螺纹的作用为增大GFRP筋与环氧树脂之间的黏结锚固, 外螺纹用于正式试验时安置螺母.
|
图 2 GFRP筋示意图 Fig. 2 Diagram of GFRP reinforcement |
GFRP筋力学性能试验在同济大学土木工程学院建筑结构试验室进行, 采用2 000 kN SHT4206伺服液压试验机.采集仪型号为DCS-300, 采样频率为1 Hz.试验采用定制的夹具固定位移计, 2个位移计的夹持端设在钢套管边缘, 用于测量GFRP筋全长的变形, 标距为200 mm, 位移计有效行程为30 mm;同时在FRP筋中间位置夹持1个引伸计, 标距为100 mm, 以测量GFRP筋的应变, 如图 3所示.

|
图 3 GFRP拉伸试验加载装置图 Fig. 3 Loading setup of GFRP tensile test |
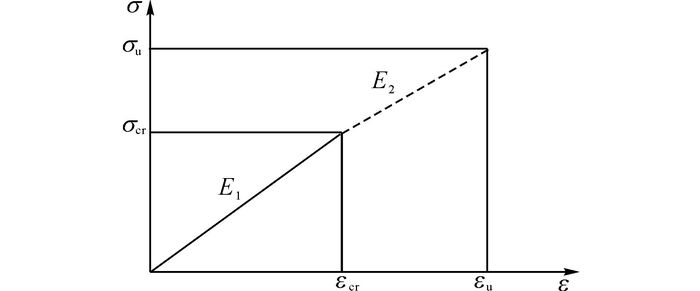
试验采用位移加载, 参照《拉挤玻璃纤维增强塑料杆力学性能试验方法》(GBT 13096-2008) [13], 加载速度为2 mm/min.在同一直径类型的组别中设计3个试件, 其中1个试件加载至破坏, 获得应力-应变曲线, 另外2个试件分别循环加载3次, 即0→σcr(反复3次)→破坏应力σu, 观察其性能随加载次数的变化情况.σcr为应力-应变曲线折点应力(见图 4), 图中,εcr为σcr对应的拉伸应变,εu为破坏应变.根据各规格GFRP筋的单调加载结果, 应力-应变曲线呈现明显的双折线现象, 源于该筋材部分树脂发生破坏, 这与周继凯等[14-15]发现的现象相同, 双折线前后的斜率分别用E1、E2表示.
|
图 4 GFRP筋加载至破坏的应力-应变曲线 Fig. 4 Stress-strain curve of GFRP specimens loaded to failure |
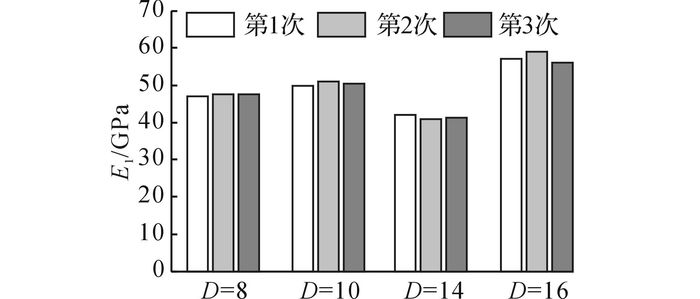
由于试验装置系统中GFRP筋要循环利用, 为分析循环加载对GFRP筋刚度的影响, 对各规格的第2、3个试件循环加载3次, 每次加载到折点荷载.折点应力范围内初始弹性模量E1随循环加载次数的变化如图 5所示.在试验初期, 对试件在折点应力范围内循环加载10次, 发现在折点荷载范围内E1变化不明显, 范围为54.49~55.24 GPa, 方差为0.053, 说明GFRP筋具有较好的抗疲劳特性[16].
|
图 5 折点应力范围内初始弹性模量随循环加载次数的变化 Fig. 5 Variation of initial elastic modulus before critical stress with number of load cycles |
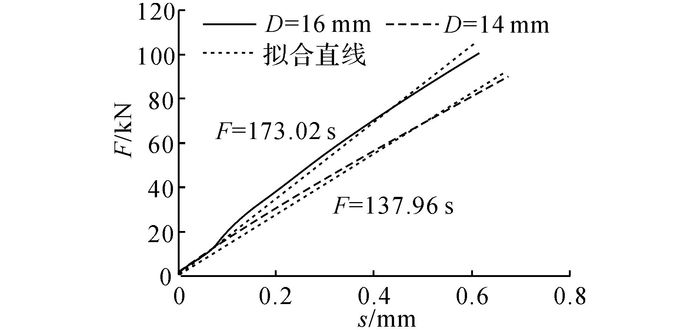
试验所得GFRP筋基本力学参数见表 2.表中,Fu和Fcr分别为对应极限应力和折点应力的拉伸力, Δcr为GFRP筋达到折点应力时引伸计测得的带钢套筒的GFRP筋总变形.可以看出, 不同规格的带钢套管的GFRP筋的折点应变εcr变化相近, 最小为0.80%, 最大为0.93%;折点总变形Δcr变化较大, 最小为2.16 mm, 最大为3.08 mm.试验中以折点应力范围内产生的总变形的最小值为试验装置的最大位移控制量, 为确保试验加载过程中GFRP筋处于线弹性阶段, 达到GFRP筋在装置中重复使用的目的.依据位移计和引伸计的差值, 获取GFRP筋在钢套管内的黏结滑移性能, 如图 6所示.由试验数据可得, 在筋材处于线弹性的应力范围内时, 其与套管的黏结滑移关系为线性.
| 表 2 试验所得的GFRP筋的基本力学参数 Table 2 Mechanical properties of GFRP bar from test |
|
图 6 GFRP筋在钢套管内的荷载-滑移曲线 Fig. 6 Load-slip curve of GFRP bars in steel sleeves |
本试验装置中与混凝土试件4个侧面直接接触的是4块钢板, 其表面加工粗糙度<1 μm.GFRP筋通过围压钢板施加围压给混凝土试件, 围压钢板和GFRP筋实际上构成了一个侧向围压装置.依据所获得的单根GFRP筋力学性能, 采用Abaqus建模设计围压钢板的构造、截面尺寸, 并分析围压钢板的强度、刚度和变形, 保证与混凝土表面直接接触的内部小钢板的弹性变形的均匀分布.围压钢板的构造及截面尺寸见文献[8].由于该三轴试验装置系统的位移采集空间局限性, 将位移计设于端部大钢板间, 端部大钢板和内部小钢板间采用中空形式.通过拉拔试验获取单侧围压装置的性能.
侧向围压装置力学性能试验在同济大学土木工程学院建筑结构实验室进行, 试验装置如图 7所示.采用与筋材拉伸试验相同的试验机和采集系统.采用有效行程为30 mm的位移计和标距为100 mm的夹持式引伸计.采用位移加载方式, 加载速度为2 mm/min.试验中设5个变形数据采集通道.其中4个使用位移计, 2对位移机夹持端分别为两侧端部的大钢板和两侧内部小钢板, 分别用于测量大钢板间的变形Δs和小钢板间的变形Δc;为引伸计用于测量GFRP筋的变形.

|
图 7 GFRP筋结合围压钢板试验图 Fig. 7 Test set-up of confining apparatus with GFRP bars and steel plates |
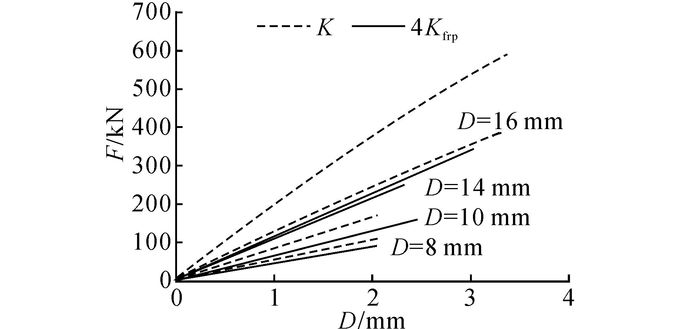
该试验主要是为了测得侧向内部的小钢板间的变形Δc和侧向的围压力F, 从而获得侧向围压装置的侧向刚度K.同时, 端部大钢板受力会产生微小的挠曲变形, 使得端部的大钢板上位移计直接测得的变形Δs小于Δc, 两者存在一个系数k, 使得Δc=kΔs.通过拉拔试验获得Δs和Δc变形转换系数k, 用于三轴试验侧向位移的矫正.在三轴试验中,小钢板间的变形即为混凝土试块的侧向膨胀变形.该试验所得的力变形关系表现出明显的线性, 如图 8所示.由此所得不同规格筋材的单侧围压装置的力学性能见表 3.其中, Kfrp为单根GFRP筋初始刚度;K为围压装置侧向刚度;k为位移转换系数.可以看出, K值比4根带钢套管Kfrp值之和小.结果表明:钢板仍然处于弹性变形阶段, 挠曲变形是引起两者数值不同的主要原因.将试验所得的K值代入式(6), 即可得到控制围压水平的指标ρ值.
|
图 8 围压装置力-变形曲线 Fig. 8 Force-deformation curve of confinement apparatus |
| 表 3 侧向围压装置的力学性能参数 Table 3 Mechanical property parameters of lateral confinement apparatus |
本试验装置系统可分别完成单侧约束、双向等或不等约束试验, 其中双向等约束和双向不等约束的区别在于2个侧向的GFRP筋的规格是否相同.本试验装置系统底部采用球铰来有效降低混凝土偏心受压的可能[17], 在试验结束后, 当万能试验机荷载卸载到0时, 混凝土试件仍存在残余变形.在受拉状态下, GFRP筋的抗扭性能较差, 不能采用扳手直接卸载, 因此在GFRP筋的端部增设半圆形垫块, 竖向荷载完全卸载后通过敲动2个半圆形垫块完成GFRP筋的应力卸载, 实现GFRP筋的重复利用.
以双向约束为例, 本试验装置系统设置13个数据采集通道, 包括6个位移传感器通道、6个应变片通道和1个油压通道.在主动加载方向(竖向)设置2个位移计用于采集混凝土竖向的变形量, 2个应变片用于监测和调整竖向加载的偏心;2个侧向各设置2个位移计采集侧向的变形, 2个应变片贴于围压钢板上, 测量施加的围压, 同时可以对测得的侧向刚度K进行验证;竖向荷载通过万能试验机荷载传感器输出获得.
5 双向均匀被动约束混凝土三轴试验为验证该试验装置的可行性, 制作12个尺寸为100 mm×100 mm×100 mm的混凝土立方体试件进行双向等约束试验, 如图 9所示.混凝土强度等级为C20, 每立方米混凝土用料情况如下:水泥300 kg, 水210 kg, 砂794 kg, 碎石1 096 kg.试验分组及结果见表 4.其中, fcu为混凝土试块峰值强度, εcu为混凝土达到峰值强度时对应的轴向应变.表中, “数字-数字-20”中的数字指对应的约束水平的强弱, 如“8-8-20”代表两侧向由2根直径为8 mm的GFRP筋组成的被动约束;“20”代表混凝土设计强度为20 MPa, 其28 d实测强度fc0为25.4 MPa;ρ为约束刚度比, 可根据式(6) 计算得出.同时, 考虑到混凝土材料的离散性, 每组浇筑3个相同的混凝土试块.

|
图 9 双向约束试验装置图 Fig. 9 Sketch of biaxial confinement apparatus |
| 表 4 混凝土试块分组及试验结果 Table 4 Specimens details and test results |
本试验采用的减摩层由2层内抹黄油的0.05 mm厚的原聚四氟乙烯(PTFE)组成[17].三轴试验采用与上述拉伸验相同的试验机和采集系统.采用有效行程30 mm的位移计及应变片采集变形信息.为了模拟静力加载, 加载速度取0.1 mm/s.
对FRP包裹圆形、非圆形截面混凝土柱的试验研究结果表明:混凝土柱都是因FRP布被拉断而丧失承载力[18-19].Lam等[20]分别采用2种FRP材料:GFRP和碳纤维复合材料CFRP, 研究了FRP包裹混凝土圆柱的力学性能, 发现FRP拉伸试验中得到的FRP极限拉伸应变大于FRP包裹圆柱试验中FRP拉断时的应变, GFRP和CFRP包裹圆柱时的拉断应变分别为0.013 8和0.008 7(本次试验以侧向应变达到0.012 0作为混凝土达到极限强度的侧向极限应变).
与FRP布约束混凝土标准圆柱的轴压试验结果类似, 混凝土立方体试块在均匀约束下, 其峰值强度fcu与素混凝土强度fc0的比值(fcu/fc0)随着约束刚度比ρ的增长而增长(见表 4).因此, 通过该试验装置可以对混凝土立方体试块实施双向被动围压试验, 为混凝土在被动约束下的应力应变的研究提供试验基础.
6 结论(1) 不同规格的GFRP筋可以实现不同的约束刚度, 使得该试验装置系统实现应力路径的可变性.带钢套管的GFRP筋对应的折点应变εcr处于0.80%~0.93%, 折点总变形Δcr变化较大, 最小值为2.16 mm, 最大值为3.08 mm;其最小总变形对应的混凝土侧向最大膨胀应变为0.012 0, 与GFRP和CFRP包裹圆柱时对应的拉断应变0.013 8和0.008 7 [20]相近, 该装置可以基本达到FRP布的破坏应变水平, 因此, 本试验装置系统采用的GFRP筋满足模拟FRP约束混凝土柱构件的工程应用要求.同时, GFRP筋在循环加载下的刚度变化偏差小, 在该试验装置系统中可以重复使用.
(2) 通过对GFRP筋侧向围压装置的拉拔试验, 得出了由GFRP筋和围压钢板组合成的侧向装置系统的约束刚度K;同时, 试验验证了该刚度值与GFRP筋弹性模型、钢套管的黏结滑移性能及钢板弹性挠曲相关.在相同规格的GFRP筋下, K值可保持恒定, 确保该试验装置系统的稳定性.
(3) 本试验装置设计的原理清晰简单, 除伺服液压试验机外, 试验装置的主要材料为GFRP筋、钢套筒、钢板、位移计、引伸计, 造价约13 600元, 相比改造传统真三轴试验, 具有较高的经济性, 易被推广使用.
(4) 通过一组混凝土试块试验验证了试验装置系统的可行性.该试验装置系统可以基于主体装置采集到混凝土试块在双向被动围压下三向受压试验过程中的试验数据, 试验效率高, 为后期混凝土在FRP约束下的被动约束试验研究的可行性提供基础.试验装置中采用的GFRP筋可以用其他材料代替, 但这些材料必须满足:1) 是弹性材料, 且在一定范围内重复加载刚度无明显退化;2) 由材料形成的K值及变形极限能代表FRP约束混凝土柱的工程应用范围.
| [1] | RICHART F E, BRANDTZAEG A, BROWN R L.A study of the failure of concrete under combined compressive stresses[R]. University of Illinois EngineeringExperiment Station, 1928. |
| [2] | STEINER D. Study of the behavior of concrete under triaxial compression[J]. Journal of Engineering Mechanics, 2002, 128(2): 156–163. DOI:10.1061/(ASCE)0733-9399(2002)128:2(156) |
| [3] | MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804–1826. DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804) |
| [4] | TENG J G, LIN G, YU T. Analysis-oriented stress-strain model for concrete under combined FRP-steel confinement[J]. Journal of Composites for Construction, 2015, 19(5): 04014084. DOI:10.1061/(ASCE)CC.1943-5614.0000549 |
| [5] | 过镇海. 混凝土的强度和变形:试验基础和本构关系[M]. 北京: 清华大学出版社, 1997. |
| [6] |
熊海贝, 李奔奔, 江佳斐. FRP约束混凝土圆柱应力-应变模型的适用性[J].
浙江大学学报:工学版, 2015, 49(12): 2363–2375.
XIONG Hai-bei, LI Ben-ben, JIANG Jia-fei. Applicability of stress-strain model for FRP-confined concrete cylinders[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(12): 2363–2375. |
| [7] | LIM J C, OZBAKKALOGLU T. Lateral strain-to-axial strain relationship of confined concrete[J]. Journal of Structural Engineering, 2014, 141(5): 04014141. |
| [8] | 江佳斐, 肖平成, 李奔奔. 一种用于三轴试验的被动式约束加载装置: 2014106138566[P]. 2015-02-11. |
| [9] | ZHANG B, BENMOKRANE B, CHENNOUF A. Prediction of tensile capacity of bond anchorages for FRP tendons[J]. Journal of Composites for Construction, 2000, 4(2): 39–47. DOI:10.1061/(ASCE)1090-0268(2000)4:2(39) |
| [10] |
周继凯, 杜钦庆, 吕娇云, 等. 玻璃纤维增强复合材料筋材连接试验研究[J].
玻璃钢/复合材料, 2006(5): 24–27.
ZHOU Ji-kai, DU Qin-qing, LV Jiao-yun. Experimental study of glassfiber reinforce polymer bar joint[J]. Fiber Reinforced Plastics/Composites, 2006(5): 24–27. |
| [11] | 中华人民共和国住房和城乡建设部, 中华人民共和国质量监督检验检疫总局. 纤维增强复合材料建设工程应用技术规范: GB50608-2010. 北京: 中国计划出版社, 2010. |
| [12] | American Society of Testing and Materials International. Standard test method for tensile properties of pultruded glass-fiber-reinforced plastic rod:ASTM D 3916-08. 2008.https://compass.astm.org/EDIT/html_anot.cgi?D3916+08(2016). |
| [13] | 中国人民共和国质量监督检验检疫总局, 中华人民共和国标准化管理委员会. 拉挤玻璃纤维增强塑料杆力学性能试验方法: GBT 13096-2008. 北京: 中国标准出版社, 2008. |
| [14] |
周继凯, 杜钦庆, 陈礼和, 等. GFRP筋拉伸力学性能尺寸效应试验研究[J].
河海大学学报:自然科学版, 2008, 36(2): 242–247.
ZHOU Ji-kai, DU Qin-qing, CHEN Li-he, et al. Experimenal study on size effect in tensile mechanical properties of GFRP rebar[J]. Journal of HohaiUniversity:Natural Sciences, 2008, 36(2): 242–247. |
| [15] |
徐新生, 郑永峰. FRP筋力学性能试验研究及混杂效应分析[J].
建筑材料学报, 2007, 10(6): 705–710.
XU Xin-sheng, ZHENG Yong-feng. Hybrid effectanalysis and experimental study on mechanical properties of the FRP bar[J]. Journal of Building Materials, 2007, 10(6): 705–710. |
| [16] |
李树新, 李贵春. FRP筋性能及在混凝土结构中的应用[J].
河北建筑工程学院学报, 2006, 24(1): 10–12.
LI Shu-xin, LI Gui-chun. Function of FRP steel and its application in the concrete structure[J]. Journal of Hebei Institute of Architectural Engineering, 2006, 24(1): 10–12. |
| [17] | 肖平成, 李奔奔, 江佳斐. 减摩擦垫层对混凝土轴压试验的影响[J]. 材料科学与工程学报, 2015, 33(1): 127–132. |
| [18] | 潘景龙, 王雨光, 来文汇. 混凝土柱截面形状对纤维包裹加固效果的影响[J]. 工业建筑, 2001, 31(6): 17–19. |
| [19] | 吴刚, 吕志涛. 纤维增强复合材料(FRP)约束混凝土矩形柱应力-应变关系的研究[J]. 建筑结构学报, 2004, 25(3): 99–106. |
| [20] | LAM L, TENG J G. Ultimate condition of fiber reinforced polymer-confined concrete[J]. Journal of Composites for Construction, 2004, 8(6): 539–548. DOI:10.1061/(ASCE)1090-0268(2004)8:6(539) |



