2. 浙江大学 宁波理工学院, 浙江 宁波 315100
2. Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China
疲劳与断裂是引起工程结构与构件失效最主要的原因[1].钢筋混凝土结构的疲劳破坏一般是受拉钢筋的脆性断裂[2], 由于破坏突然, 会造成非常严重的后果.很多学者对钢筋混凝土结构的疲劳展开了研究, 但由于现有研究方法的不足, 钢筋混凝土结构的疲劳研究受到了一定程度的制约[3],如:材料的差异导致疲劳寿命离散性较大;常规测量手段很难测量介观水平物理量;疲劳后期应力-应变滞回曲线变化单调;基于S-N曲线预测体系复杂的钢筋混凝土寿命并不理想.因此, 迫切需要一种可以无损监测钢筋混凝土结构疲劳性能并评估其疲劳寿命的方法.
压磁效应的机理如下:在循环荷载作用下, 微观塑性化过程导致材料内部的滑移位错, 从而改变材料的纹理、空隙、内含物及其他瑕疵, 这种变化又会改变材料的磁畴结构, 表现为磁化状态的改变.因此, 通过测量铁磁性构件周围压磁场的演变过程就能了解疲劳损伤过程[4].Jiles等[5-6]建立的Jiles-Atherton模型认为铁磁体的磁化强度由不可逆磁化强度和可逆磁化强度组成, 材料的磁化强度与非滞后磁化强度有关, 外力对磁化的影响是磁化强度不断向非滞后磁化强度靠近的不可逆过程.Guralnick等[7-8]对AISI 1018钢材试件进行疲劳加载并记录压磁场, 发现磁感应强度-应变滞回曲线相比应力-应变滞回曲线能反映更多的疲劳损伤相关信息;压磁信号对材料的疲劳损伤很敏感.Vandenbossche等[9]的低周疲劳试验结果显示,压磁信号的变化过程与应变等力学参量一致, 符合疲劳损伤三阶段规律, 其中第三阶段占疲劳寿命的2%~5%.金伟良等[3]指出了传统钢筋混凝土疲劳研究方法存在的问题, 并提出了基于压磁效应的钢筋混凝土疲劳研究的新思路.利用钢筋的压磁效应研究其疲劳性能, 不需要磁化装置, 适合生产现场、野外条件和普查作业;磁场测量仪器体积小、操作方便, 重复性与可靠性好.因此, 利用压磁效应来评估钢筋的疲劳性能是一种非常有效的无损检测技术.
本文进行4个HRB400钢筋试件的静力试验和17个标准试件的轴向拉伸疲劳试验, 并实时连续测量其压磁信号, 研究压磁信号与材料疲劳性能之间的关系, 为钢筋混凝土结构的疲劳研究提供参考.
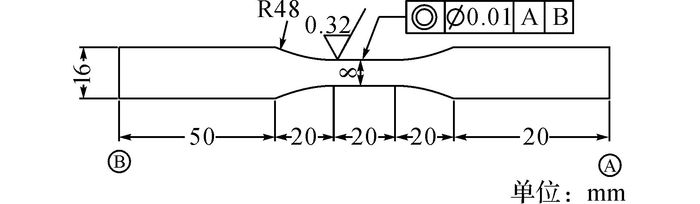
1 钢筋疲劳-压磁试验 1.1 试验设计HRB400钢筋是最常见的建筑用钢筋, 试验试件按照GB/T 15248-2008[10]要求加工, 几何特征如图 1所示;力学性能参数如表 1所示, 表中E为弹性模量, σy为屈服强度, σu为极限强度, δ为伸长率;化学成分如表 2所示.
|
图 1 试件几何特征 Fig. 1 Geometry of specimens |
| 表 1 试件力学性能 Table 1 Mechanical properties of specimens |
| 表 2 试件化学成分 Table 2 Chemical composition of specimens |
使用250 kN电液伺服疲劳试验机对试件进行常幅正弦波加载, 采用应力控制方式, 利用CRIMS引伸计测量应变, 根据应力水平采用2~5 Hz的加载频率.使用2台APS 428D磁通门磁力仪测量试件的磁信号, 选择量程±1 000 mG;使用IMC动态数据采集仪同步采集数据.试件及传感器的安装如图 2所示, 在试件靠近中部的地方放置2个反对称的法向磁探头, 具体位置如图 3所示.探头距试件表面距离为12 mm, 竖直方向偏离试件中线各5 mm, 测得的法向信号分别为Bn1和Bn2(磁感应强度).

|
图 2 试件及传感器安装 Fig. 2 Installation of specimen and sensors |

|
图 3 探头位置及试件TS-F14断裂处 Fig. 3 Position of probes and fracture location of Specimen TS-F14 |
试验主要参数与结果如表 3所示, 其中, 最小应力水平Smin=σmin/σu, 本文所有试件均为0;最大应力水平Smax=σmax/σu;应力比ρ=σmin/σmax=0, 应力幅Δσ=σmax-σmin, Nf为试件疲劳寿命.试件TS-F1在循环加载2×106次后终止试验.
| 表 3 疲劳试验主要参数及结果 Table 3 Main parameters and results of fatigue tests |
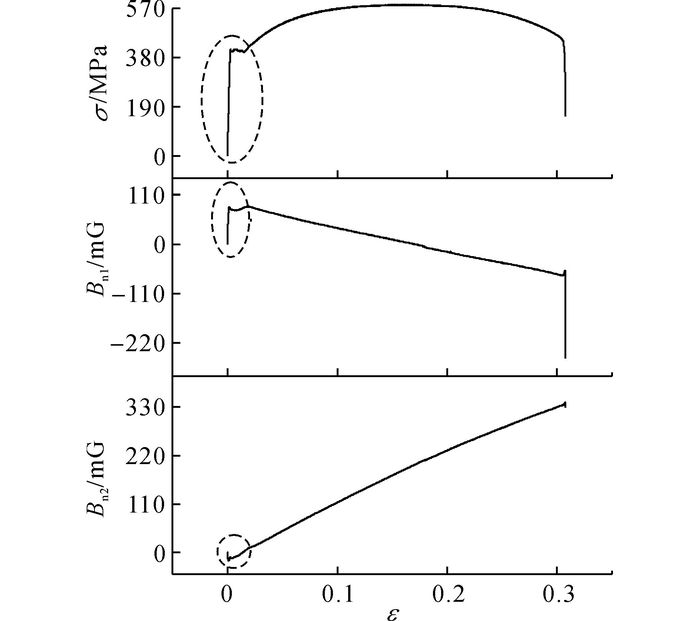
在进行疲劳试验前进行试件S1~S4的静力测试, 如图 4所示为试件S3在静态拉伸过程中的应力σ、磁感应强度B和应变ε的关系, 如图 5所示为试件S3在弹性阶段和屈服阶段的局部放大.由图 5可知, 试件的压磁场分布类似于棒形磁铁, 由于探头反对称布置, 测量结果整体近似对称, 但在弹性阶段和屈服阶段磁信号变化有明显不同, 说明试件不同位置处内部微观结构的差异导致压磁信号在受力过程中的变化有所差别.
|
图 4 试件S3的应力-应变曲线与磁感应强度-应变曲线 Fig. 4 Stress-strain curve and magnetic flux density-strain curve of Specimen S3 |

|
图 5 试件S3在弹性阶段和屈服阶段的应力-应变曲线与磁感应强度-应变曲线局部放大图 Fig. 5 Partial enlarged drawing of stress-strain curve and magnetic flux density-strain curve of Specimen S3 in elastic stage and yielding stage |
从图 4和图 5可知, 磁感应强度-应变曲线和应力-应变曲线有显著区别;在弹性阶段, 应力与应变呈线性关系;但在磁感应强度-应变曲线中, 磁场与应变呈非线性.Bn1在ε=0.001 76时磁场达到极大值82.8 mG (点V1), 此时σ=301.5 MPa, 此后Bn1随着应力增加而减小.在ε=0.001 13时, Bn2出现极小值-18.5 mG (点V2), 此时σ=200.6 MPa;而在ε=0.002 42时, Bn2出现极大值-10.7 mG(点V3), 此时σ=396.5 MPa.在弹性阶段, 磁感应强度-应变曲线比应力-应变曲线更加复杂, 反映了在弹性阶段的拉伸过程中, 试件内部磁畴的转动与(磁)畴壁位移导致磁化状态随之发生改变.
试件进入屈服阶段后, 磁感应强度的变化相比弹性阶段简单, 但对比应力-应变曲线近乎不变的屈服平台, Bn1在极值点之后逐渐减小, Bn2则出现一个极小值-13.4 mG(点V4).随着应变的继续增大, 试件进入强化阶段和颈缩阶段.刚进入强化阶段时, Bn1有所增加, 尔后下降, 试件断裂时Bn1和Bn2均突变.
磁感应强度的变化情况与现有力-磁关系研究结果一致[5-6, 11], 属于铁磁材料的应力磁化过程.在弹性阶段, 磁弹性能迅速累积, 当能量累积到某个阈值后晶体产生滑移, 累积的部分能量得到释放, 磁感应强度Bn1和Bn2均出现极值.根据金属磁记忆理论[12], 应力集中处的法向磁场会出现过零点, 远离此处则基本不变, 因此探头相对初始缺陷的位置将影响测量结果:Bn2附近可能存在初始缺陷, 随着应力的增加, 应力集中现象愈发显著, 导致磁感应强度出现异常, Bn1距初始缺陷较远(>10 mm), 相对位置不同导致结果不同, 如图 5所示.可见, 试件的磁化状态对受力状态很敏感, 不同位置处的磁感应强度变化的不一致反映了试件内部微观结构的差异.
试验发现, 2个法向探头测得的磁信号虽大小不同, 但在弹性阶段总会出现磁信号的极值点, 将出现极值时对应的应力记为σa, 磁信号的极值比为
| $R = \frac{{{\sigma _{\rm{a}}}}}{{{\sigma _{\rm{y}}}}},0 < R < 1.$ | (1) |
静力试件的极值比如表 4所示, 由表 4可知, 由于材料本身的差异, σy和σa均有所波动, 但是极值比R基本保持不变, 4个试件的平均值为0.743, 与Bao等[13]得到的结果类似, 在循环加载过程中, 这个极值点仍会出现.
| 表 4 静力试件的极值比 Table 4 Ratio of extremums of static specimens |
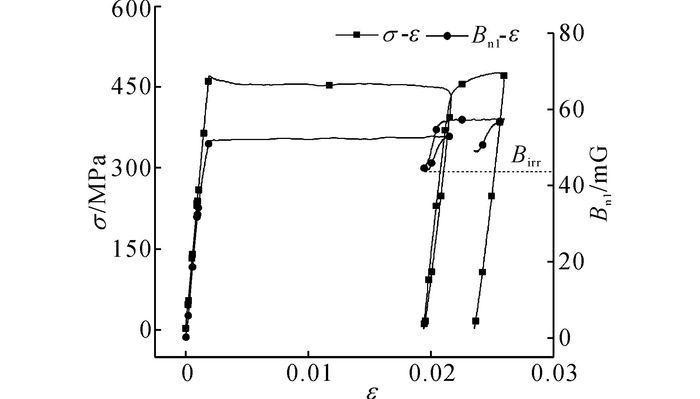
试件TS-F14第1次循环和第2次循环的应力-应变曲线与磁感应强度应变曲线如图 6所示, n为循环次数.对比图 6和图 5可知:由于试验应力从应力水平的均值迅速增加, 导致磁能累积到阈值时, 试件已经进入屈服阶段, 因而在第1、2次循环中, 磁感应强度的极值比R接近于1.由图 6可知, 第1次循环结束后产生了很大的不可逆磁化, 试件TS-F14卸载至0时的法向不可逆磁感应强度Birr=44.6 mG, 相比初始状态增加了44.6 mG;第2次循环结束后Birr=49.1 mG, 增加了4.5 mG.根据接近理论[6], 循环荷载作用下铁磁材料的应力致磁化将逐渐接近无滞后的理想磁化状态, 不可逆磁化增量ΔBirr会逐渐减小, 与本试验的结果相符.
|
图 6 试件TS-F14应力-应变滞回曲线与磁感应强度-应变滞回曲线(n=1, 2) Fig. 6 Stress-strain hysteresis loops and magnetic flux density-strain hysteresisloops of SpecimenTS-F14 (n=1, 2) |
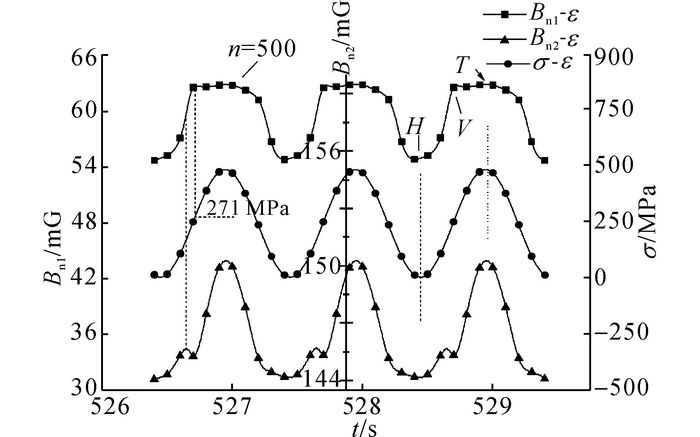
试件TS-F14第500~502次循环Bn(t)和σ(t)的时变曲线如图 7所示.在循环荷载作用下, Bn1出现极大值时, σa=271 MPa, Ra=0.67.点H、T分别为磁感应强度曲线的“头部”、“尾部”, 点V为维拉里反转点, 第500次循环时Bn1在点V先减小后增加, 在点T出现极大值, 当应力为0时,Birr=55.0 mG.在应力集中部位, 高密度的位错积聚形成磁畴边界, 产生漏磁场.由图 3可知, 试件TS-F14的疲劳断裂位置更靠近Bn2;加载阶段Bn2出现的2个极值点, 可能是漏磁场与应力致磁化综合作用的结果.
|
图 7 试件TS-F14磁感应强度时变曲线和应力时变曲线(n=500~502) Fig. 7 Bn time-varying trace and stress time-varying trace of specimen TS-F14 (n=500~502) |
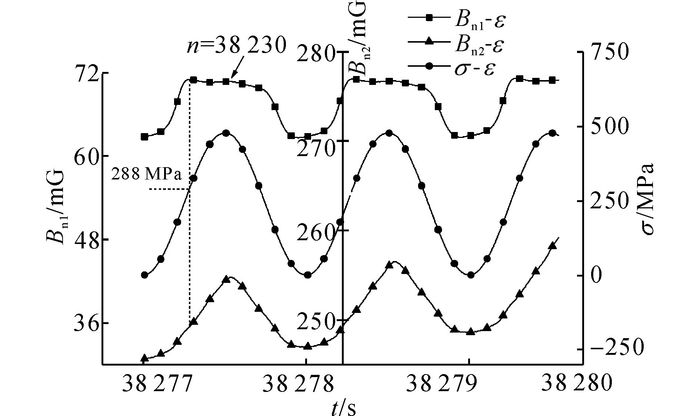
试件TS-F14第38 230循环的Bn(t)和σ(t)时变曲线如图 8所示, 此时试件已接近疲劳破坏, Bn1极值点对应的σa=288 MPa, Ra=0.71, 与第500次循环相比, Bn1在极值点V后持续减小;当σ=0时, Birr=63.0 mG.试件TS-F14接近疲劳破坏时Bn2的2个极值点已经消失;磁感应强度迅速增加, 这是由于疲劳第三阶段的宏观疲劳裂纹已经很大且失稳扩展, 裂纹处的漏磁场显著影响压磁信号, 因此, 此时的压磁信号随循环进程加速畸变.靠近断裂处的Bn2时变曲线变化尤其明显, 说明Bn2能够反映出更多的疲劳损伤相关信息.
|
图 8 试件TS-F14磁感应强度时变曲线和应力时变曲线(n=38 230~38 232) Fig. 8 Bn time-varying trace and stress time-varying trace of Specimen TS-F14 (n=38 230~38 232) |
由图 7~8可知, 当应力控制加载时, 对单个循环来说, 应变时变曲线在整个疲劳损伤过程中除了绝对值有所增大外, 形态上并无明显变化, 磁感应强度时变曲线则变化显著.因为Bn1距断口较远, 偏向于反映试件整体的疲劳损伤状态, 其应力磁化曲线更接近已有研究[7-9, 11-12].Bn2则更能反映出断口处的漏磁场演变过程.Bn1和Bn2的变化均是由材料内部的位错累积、裂缝的生成及发展等疲劳损伤发展导致, 因此, 根据Bn(t)的演变可为试件健康状态的判断提供较为直观的依据, 相比完全是正弦曲线的应变、挠度等物理信号, 压磁信号时变曲线能反映出更多的疲劳损伤信息.
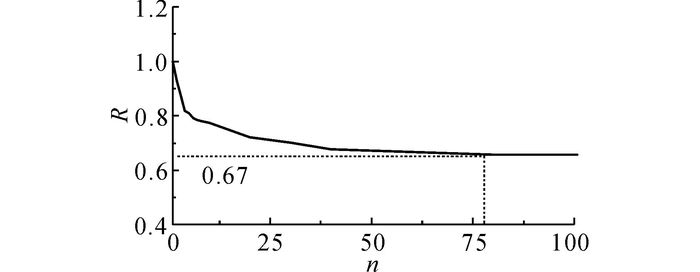
磁场极值比R随循环次数的变化趋势如图 9所示, 经历初始循环后, R从1开始逐渐减小;在约80个循环后, R基本稳定在0.67;在接近疲劳破坏时, R迅速增加, 最后一个循环n=38 248, R=0.75.
|
图 9 试件TS-F14的极值比随循环次数的变化曲线 Fig. 9 Ratio of extremums changing with cycle-index of Specimen TS-F14 |
金属疲劳过程一般可以分为3个阶段:疲劳初始调节阶段、损伤累积阶段和最后破坏阶段[7, 9].一般的疲劳分析都是基于应力-应变滞回曲线, 用以反映结构的变形特征、刚度退化与能量耗散等, 但因形态单调很难反映出试件的裂纹形成、扩展等微观损伤状态.尤其是疲劳后期, 应力-应变滞回曲线的变化仍然单调, 很难揭示其微观的疲劳损伤机理.
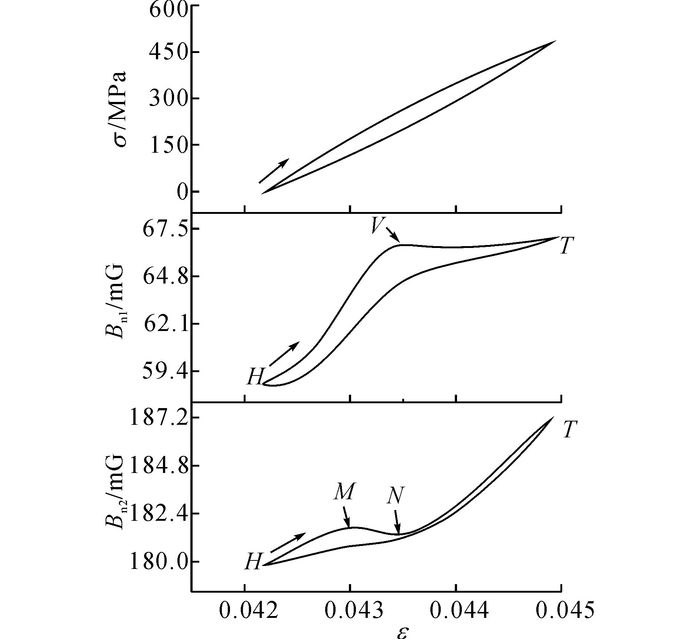
试件TS-F14第20 000次循环的应力-应变滞回曲线与Bn-ε滞回曲线如图 10所示.与静力分析类似, Bn-ε滞回曲线反映了材料内部磁畴结构的改变, 如存在极值点V、M和N等特征, 因此相比应力-应变滞回曲线更能够反映试件在疲劳损伤过程中内部微观结构的变化.
|
图 10 试件TS-F14应力-应变滞回曲线与磁感应强度-应变滞回曲线(n=20 000) Fig. 10 Stress-strain hysteresis loop and magnetic flux density-strain hysteresis loop of SpecimenTS-F14 (n=20 000) |
图 11~12分别是第500, 378 00和38 230~38 231次循环的Bn-ε滞回曲线, 分别处于疲劳的初始损伤累积、裂纹扩展和最后破坏阶段.Bn-ε滞回曲线变化非常显著, 不仅表现为磁感应强度的增加, Bn2-ε滞回曲线的MN段由最开始的下降趋势渐变为持平, 极值点消失.点H、M和N包围的前半段面积也显著减小, 滞回曲线由最开始的饱满的“蝌蚪”状逐渐变成得狭长, 表示试件的耗能能力逐渐降低.

|
图 11 试件TS-F14的磁感应强度-应变滞回曲线 Fig. 11 Magnetic flux density-strain hysteresis loops of Specimen TS-F14 |
|
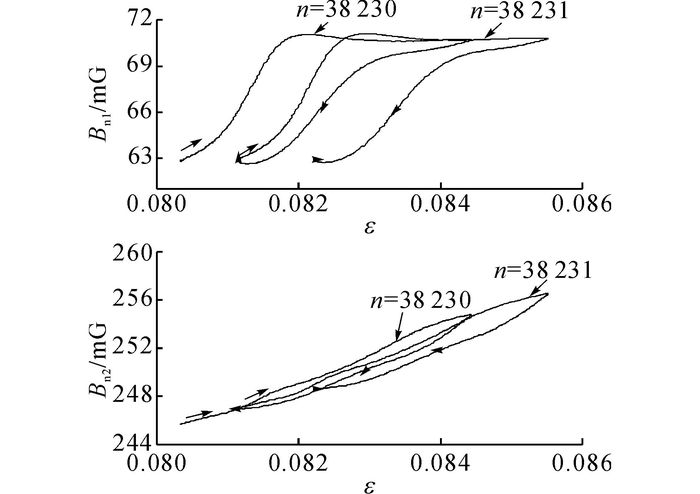
图 12 试件TS-F14失效前的磁感应强度-应变滞回曲线(n=38 230~38 231) Fig. 12 Bnε hysteresis loops approaching fracture of Specimen TS-F14(n=38 230~38 231) |
试件TS-F14失效前的Bn-ε滞回曲线如图 12所示, 可以看到每个加载过程的开始应变都显著增加, 表示构件即将断裂;Bn1-ε曲线不再闭合, Bn2-ε曲线显著畸变;极值点M、N消失;MN段呈直线上升趋势, 最后试件疲劳断裂.
综上所述, 根据极值点M、N的变化可预测试件疲劳失效;比较多个磁探头信号的曲线特征可判断试件失效的大体位置;这些特点可应用于现场无损检测分析.
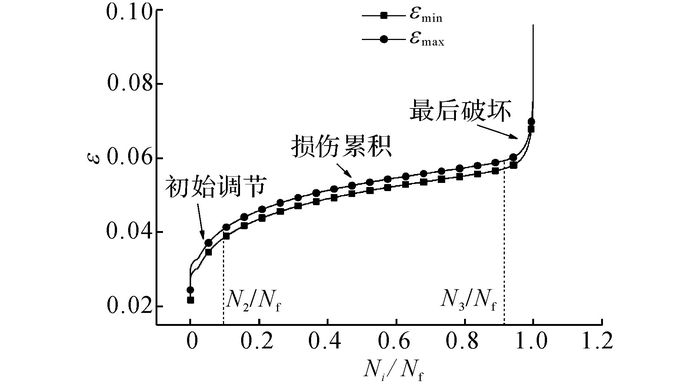
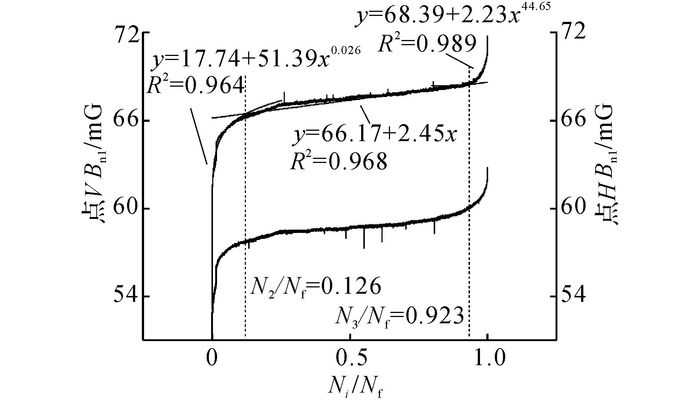
2.4 疲劳三阶段与寿命预测试件TS-F14的最大应变和最小应变的三阶段曲线如图 13所示, 第一和第二阶段过渡点为N2, 第二和第三阶段过渡点为N3, 与已有研究相似, 3个阶段分别占疲劳寿命的13.0%、77.5%、9.5%.试件TS-F14的点H和点V磁感应强度Bn1三阶段曲线如图 14所示(图中,R2为曲线拟合度), 由图可知, 初期的疲劳损伤很小, 相应的漏磁场不会明显影响压磁信号, 特征点V和H的磁感应强度变化符合接近规律, 而在疲劳后期, 宏观裂纹漏磁场导致压磁信号畸变, 基于压磁效应的疲劳研究符合疲劳损伤的三阶段规律;通过曲线拟合可得到钢筋疲劳的各个阶段过渡点(拟合线的交点);试件TS-F14的2个阶段过渡点对应的循环次数与疲劳寿命的比值分别为N2/Nf=12.6%, N3/Nf=92.3%, 与应变的疲劳三阶段所占寿命相差很小.
|
图 13 试件TS-F14的最大应变和最小应变三阶段曲线 Fig. 13 Three stages of maximum strain and minimum strain of Specimen TS-F14 |
|
图 14 试件TS-F14在点H和点V的三阶段曲线 Fig. 14 Three stages of point H and V on Specimen TS-F14 |
虽然相同应力水平下试件的寿命有一定的离散, 不同应力水平下试件的疲劳寿命差别很大, 但疲劳三阶段所占的寿命比基本相同.各试件在点V处的压磁场信号三阶段占疲劳寿命的百分比如表 5所示.试件TS-F1达到2 000 000次时终止试验, 无法计算;其余16个疲劳试件N2/Nf和N3/Nf的平均值分别为10.9%和93.1%.
| 表 5 各试件在点V处的压磁场信号的三阶段占疲劳寿命的百分比 Table 5 Percentage of specimen's three stages marked bypiezomagnetism at point V in fatigue life |
根据在试验过程中确定的过渡点N2和N3, 可大致预测试件剩余疲劳寿命:
| ${n_{{\rm{res}}}} = 9.17{N_2} - {n_{\rm{c}}},{n_{{\rm{res}}}} = 1.07{N_3} - {n_{\rm{c}}}.$ | (2) |
式中:nc为试件已经历的循环次数.
3 结论(1) 与传统应力-应变方法相比, 用压磁场检测铁磁材料内部疲劳损伤的方法更加灵敏, 更能体现内部的疲劳损伤退化过程;利用压磁信号曲线特征点的变化可以进行疲劳失效预警和损伤评估.
(2) 基于压磁效应的HRB400钢筋标准试件的疲劳试验结果表明:在静力加载与循环加载过程中, 压磁信号曲线都存在一个相对稳定的极值比;不同疲劳阶段的压磁滞回曲线存在显著差别;Bn(t)曲线记录了试件的疲劳损伤过程, 根据极值点M、N的变化可预测疲劳失效;比较多个磁探头信号的曲线特征能判断失效的大体位置, 可以发展为无损监测手段.
(3) 利用压磁信号的疲劳三阶段规律可预测试件疲劳寿命, 提出了基于压磁效应的寿命预测方法.
目前, 基于压磁效应的钢筋疲劳研究仍处于试验阶段, 考虑到钢筋混凝土结构的疲劳-压磁问题复较为杂, 试验方法、数据采集与处理、理论基础研究等方面都存在很大的不足, 距离工程应用较远, 还有大量工作需要开展.
| [1] | 陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2002: 1. |
| [2] |
李秀芬, 吴佩刚, 赵光仪. 高强混凝土梁抗弯疲劳性能的试验研究[J].
土木工程学报, 1997, 30(5): 37–42.
LI Xiu-fen, WU Pei-gang, ZHAO Guang-yi. Experimental research on bending fatigue behavior of high-strength concrete beams[J]. China Civil Engineering Journal, 1997, 30(5): 37–42. |
| [3] |
金伟良, 张军, 陈才生, 等. 基于压磁效应的钢筋混凝土疲劳研究新方法[J].
建筑结构学报, 2016, 37(4): 133–142.
JIN Wei-liang, ZHANG Jun, CHEN Cai-sheng, et al. A new method for fatigue study of reinforced concrete structures based on piezomagnetism[J]. Journal of Building Structures, 2016, 37(4): 133–142. |
| [4] | ERBER T, GURALNICKZ S A, DESAIZ R D. Piezomagnetism and fatigue[J]. Journal of Physics D:Applied Physics, 1997, 30(20): 2818–2836. DOI:10.1088/0022-3727/30/20/008 |
| [5] | JILES D C. Theory of the magnetomechanical effect[J]. Journal of Physics D:Applied Physics, 1995, 28(8): 1537–1546. DOI:10.1088/0022-3727/28/8/001 |
| [6] | JILES D C, LI L. A new approach to modeling the magnetomechanical effect[J]. Journal of Applied Physics, 2004, 95(11): 7058–7060. DOI:10.1063/1.1687200 |
| [7] | GURALNICK S A, BAO S, ERBER T. Piezomagnetism and fatigue:Ⅱ[J]. Journal of Physics D:Applied Physics, 2008, 41(11): 1–11. |
| [8] | BAO S, ERBER T, GURALNICK S A, et al. Fatigue, magnetic and mechanical hysteresis[J]. Strain, 2010, 47(4): 372–381. |
| [9] | VANDENBOSSCHE L, DUPR L. Fatigue damageassessment by the continuous examination of the magnetomechanical and mechanical behavior[J]. Journal of Applied Physics, 2009, 105: 07E707. DOI:10.1063/1.3070642 |
| [10] | 中国科学院金属研究所. GB/T15248-2008: 金属材料轴向等幅低循环疲劳试验方法[S]. 北京: 中国标准出版社, 2008. |
| [11] | BIRSS R R, FAUNCE C A, ISAAC E D. Magnetomechanical effects in iron and iron-carbon alloys[J]. Journal of Physics D:Applied Physics, 1971, 4(7): 1040–1048. DOI:10.1088/0022-3727/4/7/322 |
| [12] | DUBOV A A. A study of metal properties using the method of magnetic memory[J]. Metal Science and Heat Treatment, 1997, 39(9): 401–405. DOI:10.1007/BF02469065 |
| [13] | BAO S, FU M, GU Y. Evolution of the piezomagnetic field of ferromagnetic steels subjected to cyclic tensile stress with variable amplitudes[J]. Experimental Mechanics, 2016, 56(6): 1017–1028. DOI:10.1007/s11340-016-0147-0 |



