热声效应是热与声之间相互转换的现象.按能量转换方向的不同, 热声效应可分为2类:1) 热致声, 即热驱动的声振荡, 利用该效应的热机称为热声发动机;2) 声致热, 即声驱动的热量传输, 利用该效应的热机为热声制冷机.行波热声发动机由于工质微团所经历的热声转换热力循环本征可逆[1], 理论热效率高于驻波热声发动机, 是近年来热声研究领域的热点[2-5].
然而, 由于行波热声发动机中通常存在闭合环路, 为Gedeon声直流[6]提供了形成条件.Gedeon声直流是附加于交变流动流场中循环流动于环路结构内的时均质量流, 可造成不利的热损失, 进而给热声发动机系统的热效率带来巨大的负面影响[7-8].Gusev等[9]在绝热边界条件下, 对板叠内的Gedeon声直流进行了理论研究, 指出了直流的方向与声功放大的方向一致, 且直流量的值是影响总能流的主要因素.余国瑶等[10]对一台斯特林热声发动机进行了二维模拟, 研究了Gedeon声直流对压力振幅的影响.邱利民等[11]将红外成像技术引入到热声发动机的研究中, 用于观察在起振与消振的过程中, Gedeon声直流对回热器的温度演变的影响.
行波热声发动机的概念最早由美国的Ceperley[1]于1979年提出.1999年, Backhaus等[2, 7]成功研制出热声斯特林发动机, 相对卡诺效率达到约0.4, 推动了之后行波热声发动机领域研究的快速发展.2010年, 荷兰Kees de Blok等[12]提出了新型四级环路结构行波热声发动机, 通过增加回热器部分的截面积, 有效减小了回热器中的黏性损失, 样机在加热温度为239 ℃时, 相对卡诺效率达到了0.5[13].
本文旨在探索该新晋发展的四级行波热声发动机中Gedeon声直流对于系统性能的影响.基于热声学理论, 针对本实验室搭建的一台四级行波热声发动机的热声核进行了模拟研究, 在给定加热功率以及热声核入口参数的条件下, 研究了不同Gedeon声直流对热声核处的温度分布、体积流速振幅分布、压力振幅分布、压力与速度相位差分布、声功率分布以及总能流率分布的影响, 并且着重针对Gedeon声直流对回热器以及热缓冲管内温度梯度的影响机制进行了分析.在此基础上, 进一步给出了Gedeon声直流对热声发动机热效率影响的定量评估.
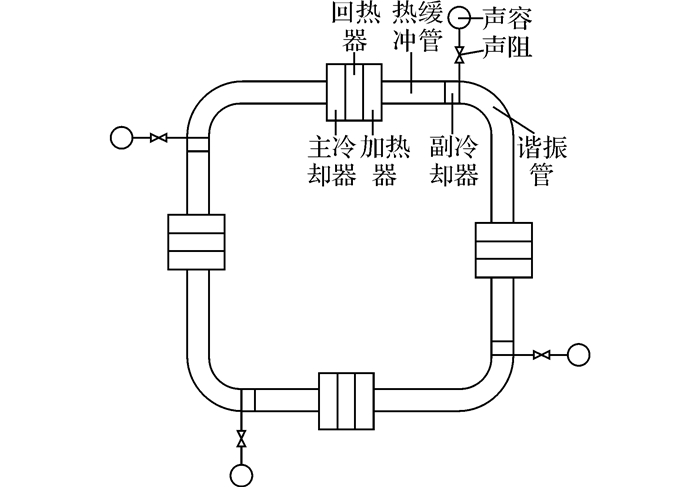
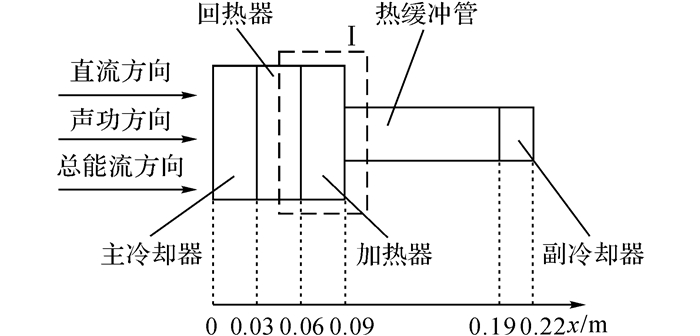
1 物理与数学模型如图 1所示给出了四级行波热声发动机的结构简图.在系统中, 每一级单元的结构完全相同.每一级单元包括了热声核部分、谐振管以及阻容负载.热声核部分主要由主冷却器、回热器、加热器、热缓冲管以及副冷却器组成.由于热致声转换过程发生在热声核中, 鉴于其在热声热机中的重要地位和作用, 考察了Gedeon声直流对热声核部分的影响, 结构见图 2.
|
图 1 四级行波热声发动机结构简图 Fig. 1 Schematic of looped four-stage travelling-wave thermoacoustic engine |
|
图 2 热声核示意图 Fig. 2 Schematic of thermoacoustic core |
本文根据热声学理论, 通过编写程序, 引入Gedeon声直流进行计算, 研究了Gedeon声直流对系统热效率的影响.根据Swift等[14]研究, 考虑Gedeon声直流的影响后, 总能流率为
| $ \begin{array}{l} {H_2} = \frac{1}{2}{\mathop{\rm Re}\nolimits} \left( {{p_1}{{\tilde U}_1}} \right) + \left[ {\frac{1}{2}{\rho _{\rm{m}}}{T_{\rm{m}}}\int {{\mathop{\rm Re}\nolimits} \left( {{s_1}{u_1}} \right){\rm{d}}A} - } \right.\\ \;\;\;\;\;\;\;\;\left. {\left( {{A_{{\rm{gas}}}}\kappa + {A_{\rm{s}}}{\kappa _{\rm{s}}}} \right)\frac{{{\rm{d}}{T_{\rm{m}}}}}{{{\rm{d}}x}} + {m_{2,0}}{c_p}{T_{\rm{m}}}} \right], \end{array} $ | (1) |
式中:p1为压力振幅, U1为体积流速振幅, ρm、Tm、s1、κ分别为工质的平均密度、平均热力学温度、熵流和热导率, u1为速度振幅, Agas为工质的流通面积, As和κs分别为流道固体的截面积与热导率, Re表示取复数的实部, 上标~表示取共轭复数, m2, 0为Gedeon声直流率, cp为比定压热容.式(1) 右边第1项为声功率, 第2项为热流(其包括由熵流携带的热流以及轴向导热), 第3项为Gedeon声直流所携带的能流.可见, m2, 0cpTm表征了Gedeon声直流对于总能流率的影响, 并通过影响总能流率进而影响热声核内的热致声转换性能.
考虑Gedeon声直流后, 针对回热器以及热缓冲管的微元段dx的控制方程如下[15-16]:
回热器:
| $ \begin{array}{l} \frac{{{\rm{d}}{p_1}}}{{{\rm{d}}x}} = - {\rm{i}}\omega {\rho _{\rm{m}}}{u_1}\left[ {1 + \frac{{{{\left( {1 - \phi } \right)}^2}}}{{2\left( {2\phi - 1} \right)}}} \right] - \\ \;\;\;\;\;\;\;\;\;\frac{\mu }{{r_{\rm{h}}^2}}\left[ {\frac{{{c_1}\left( \phi \right)}}{8} + \frac{{{c_2}\left( \phi \right){N_{{\rm{R,1}}}}}}{{3{\rm{\pi }}}}} \right]{u_1}, \end{array} $ | (2) |
| $ \begin{array}{l} \frac{{{\rm{d}}{u_1}}}{{{\rm{d}}x}}= - \frac{{{\rm{i}}\omega \gamma }}{{{\rho _{\rm{m}}}{a^2}}}{p_1} + \beta \frac{{{\rm{d}}{T_m}}}{{{\rm{d}}x}}{u_1} + \\ \;\;\;\;{\rm{i}}\omega \beta \left[ {\frac{{{T_{\rm{m}}}\beta }}{{{\rho _{\rm{m}}}{c_{\rm{p}}}}}\frac{{{\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} + \exp \left( {2{\rm{i}}{\theta _{\rm{p}}}} \right){g_{\rm{v}}}} \right){\varepsilon _{\rm{h}}}}}{{1 + {\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} + \exp \left( {2{\rm{i}}{\theta _{\rm{T}}}} \right){g_{\rm{v}}}} \right){\varepsilon _{\rm{h}}}}}{p_1} - } \right.\\ \;\;\;\;\left. {\frac{1}{{{\rm{i}}\omega }}\frac{{{\rm{d}}{T_m}}}{{{\rm{d}}x}}\frac{{{\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} - {g_{\rm{v}}}} \right){\varepsilon _{\rm{h}}}}}{{1 + {\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} + \exp \left( {2{\rm{i}}{\theta _{\rm{T}}}} \right){g_v}} \right){\varepsilon _{\rm{h}}}}}{u_1}} \right], \end{array} $ | (3) |
| $ \begin{array}{l} \frac{{{\rm{d}}{T_m}}}{{{\rm{d}}x}} = \left\{ { - {\mathop{\rm Re}\nolimits} \left[ {\left( {\frac{{{T_{\rm{m}}}\beta }}{2}\frac{{{\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} + \exp \left( {2{\rm{i}}{\theta _{\rm{p}}}} \right){g_{\rm{v}}}} \right){\varepsilon _{\rm{h}}}}}{{1 + {\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} + \exp \left( {2{\rm{i}}{\theta _{\rm{T}}}} \right){g_{\rm{v}}}} \right){\varepsilon _{\rm{h}}}}} + } \right.} \right.} \right.\\ \left. {\left. {\left. {1 - {T_{\rm{m}}}\beta } \right){p_1}{{\tilde u}_1}{A_{{\rm{gas}}}}} \right] + \left( {{H_2} - {m_{2,0}}{c_p}{T_{\rm{m}}}} \right)} \right\}/\\ \left\{ { - \left( {\frac{{{\rho _{\rm{m}}}{c_p}}}{{2\omega }}{\mathop{\rm Im}\nolimits} \left[ {\frac{{{\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} - {g_{\rm{v}}}} \right){\varepsilon _{\rm{h}}}}}{{1 + {\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} + \exp \left( {2{\rm{i}}{\theta _{\rm{T}}}} \right){g_v}} \right){\varepsilon _{\rm{h}}}}}} \right]{u_1}{{\tilde u}_1}{A_{{\rm{gas}}}} + } \right.} \right.\\ \left. {\left. {{A_{{\rm{gas}}}}\left( {{\kappa _{{\rm{s,eff}}}}\frac{{1 - \phi }}{\phi } + \kappa } \right)} \right)} \right\}, \end{array} $ | (4) |
热缓冲管:
| $ \frac{{{\rm{d}}{p_1}}}{{{\rm{d}}x}} = - \frac{{{\rm{i}}\omega {\rho _{\rm{m}}}}}{{\left( {1 - {f_{\rm{v}}}} \right){A_{{\rm{gas}}}}}}{U_1} $ | (5) |
| $ \begin{array}{l} \frac{{{\rm{d}}{U_1}}}{{{\rm{d}}x}} = - \frac{{{\rm{i}}\omega {A_{{\rm{gas}}}}}}{{{\rho _{\rm{m}}}{a^2}}}\left[ {1 + \frac{{\left( {\gamma - 1} \right){f_{\rm{v}}}}}{{1 + {\varepsilon _{\rm{s}}}}}} \right]{p_1} + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{\beta \left( {{f_{\rm{k}}} - {f_{\rm{v}}}} \right)}}{{\left( {1 - {f_{\rm{v}}}} \right)\left( {1 - \sigma } \right)\left( {1 + {\varepsilon _{\rm{s}}}} \right)}}\frac{{{\rm{d}}{T_{\rm{m}}}}}{{{\rm{d}}x}}{U_1}, \end{array} $ | (6) |
| $ \begin{array}{l} \frac{{{\rm{d}}{T_{\rm{m}}}}}{{{\rm{d}}x}} = \\ \left\{ { - \frac{1}{2}{\mathop{\rm Re}\nolimits} \left[ {{p_1}{{\tilde U}_1}\left( {1 - \frac{{{T_{\rm{m}}}\beta \left( {{f_{\rm{k}}} - {{\tilde f}_{\rm{v}}}} \right)}}{{\left( {1 - {\varepsilon _s}} \right)\left( {1 + \sigma } \right)\left( {1 - {{\tilde f}_{\rm{v}}}} \right)}}} \right)} \right] + } \right.\\ \left. {\left( {{H_2} - {m_{2,0}}{c_p}{T_{\rm{m}}}} \right)} \right\}/\left\{ { - {A_{{\rm{gas}}}}\kappa - {A_{\rm{s}}}{\kappa _{\rm{s}}} - } \right.\\ \left. {\frac{{{\rho _{\rm{m}}}{c_p}{{\left| {{U_1}} \right|}^2}}}{{2\omega {A_{{\rm{gas}}}}\left( {\sigma - 1} \right){{\left| { - {f_{\rm{v}}}} \right|}^2}}}{\mathop{\rm Im}\nolimits} \left[ {{{\tilde f}_{\rm{v}}} + \frac{{\left( {{f_{\rm{k}}} - {{\tilde f}_{\rm{v}}}} \right)\frac{{1 + {\varepsilon _{\rm{s}}}{f_{\rm{v}}}}}{{{f_{\rm{k}}}}}}}{{\left( {1 + {\varepsilon _{\rm{s}}}} \right)\left( {1 + \sigma } \right)}}} \right]} \right\}, \end{array} $ | (7) |
式中:
| $ \begin{array}{l} {c_1}\left( \phi \right) = 1268 - 3545\phi + 2544{\phi ^2},\\ {c_2}\left( \phi \right) = - 2.82 + 10.7\phi - 8.6{\phi ^2}, \end{array} $ |
| $ \begin{array}{l} {N_{{\rm{R}},1}} = 4{u_1}{r_{\rm{h}}}{\rho _m}/\mu ,\\ {\varepsilon _{\rm{s}}} = \phi {\rho _m}{c_p}/\left( {1 - \phi } \right){\rho _{\rm{s}}}{c_{\rm{s}}}, \end{array} $ |
| $ \begin{array}{l} {\varepsilon _{\rm{h}}} = 8{\rm{i}}r_{\rm{h}}^2/b\left( \phi \right){\sigma ^{1/3}}\delta _{\rm{k}}^2,\\ b\left( \phi \right) = 3.91 - 11.29\phi + 9.47{\phi ^2}, \end{array} $ |
| $ \begin{array}{l} {g_{\rm{c}}} = \frac{2}{{\rm{\pi }}}\int_0^{\pi /2} {\frac{{{\rm{d}}z}}{{1 + N_{R,1}^{3/5}{{\cos }^{3/5}}\left( z \right)}},} \\ {g_v} = - \frac{2}{{\rm{\pi }}}\int_0^{\pi /2} {\frac{{{\rm{cos}}\left( {2z} \right){\rm{d}}z}}{{1 + N_{R,1}^{3/5}{{\cos }^{3/5}}\left( z \right)}},} \end{array} $ |
式中:ω为角频率, ϕ为孔隙率, μ为动力黏度, rh为水力半径, γ、β、σ、a、δk分别为工质的比热比、体积膨胀系数、普朗特数、声速和热渗透深度, ρs和cs分别为流道固体的密度与比热容, fv和fk分别为黏滞函数与热函数, κs, eff为有效热导率, θp为压力相位,θT为温度相位, i为虚数符号, Im表示取复数的虚部.此外, 模型假设回热器和热缓冲管外部为绝热边界, 即dH2/dx=0.
2 模型验证美国诺斯阿拉莫斯国家实验室研发的模拟软件DeltaEC, 是目前公认的能对热声发动机以及热声制冷机在小振幅振动的情况下进行较好模拟的软件, 且在2008年改进版本中引入了Gedeon声直流的计算.但DeltaEC是基于给定热端温度进行计算, 而在很多情况下, 给定加热功率的系统效率更受到关注.本文通过编写程序, 开展了在定加热功率的条件下, 不同Gedeon声直流对系统热效率影响的研究.
如图 2所示为所研究的热声核, 主要结构参数见表 1.为了给定一个合理的热声核入口(即图 2中0 m的位置)条件, 利用DeltaEC在无Gedeon声直流的情况下, 对系统进行模拟.负载为阻容负载, 其阻值为1.2×107 (N·s)/m5, 负载声容的体积为450 cm3.以2.5 MPa氦气作为工质, 加热器内工质温度Th=539 K, 而冷却器内工质温度为Tc=298 K.考虑系统的对称性, 取一级单元进行研究.在上述条件下可求得加热功率Pin=760 W, 热声核入口的压力波动幅值为66.59 kPa, 体积流速波动幅值为0.008 3 m3/s, 体积流速相位超前压力波16°, 频率为124 Hz.
| 表 1 四级行波热声发动机的主要参数 Table 1 Main dimensions of four-stage travelling-wave thermoacoustic engine |
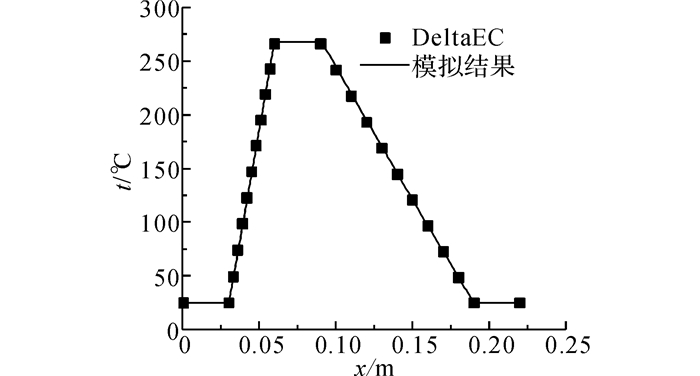
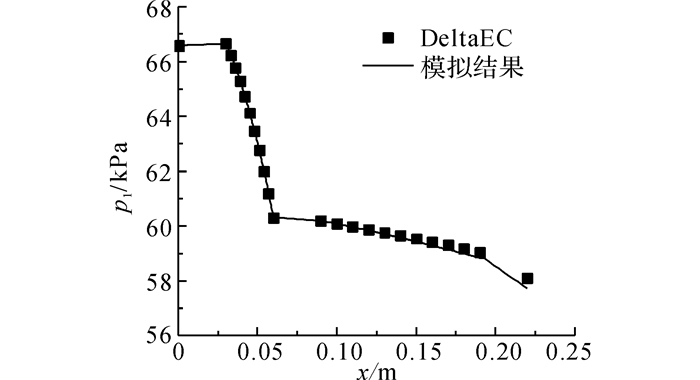
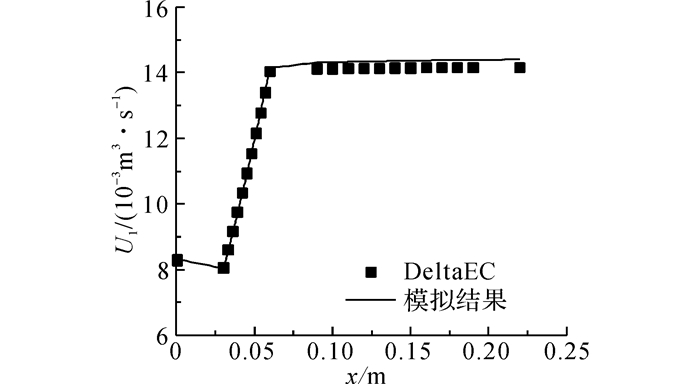
为了验证本文模型计算的合理性, 将上述DeltaEC计算确定的加热功率以及热声核入口参数作为计算条件代入本文的模型进行计算, 并与DeltaEC计算的热声核部分的结果进行了对比.如图 3~5所示给出x=0~0.03 m为主冷却器, x=0.03~0.06 m为回热器, x=0.06~0.09 m为加热器, x=0.09~0.19 m为热缓冲管, x=0.19~0.22 m为副冷却器.图中,t为温度.从图中可见, 模型结果与DeltaEC计算结果吻合, 其中温度的差值最大为1.5 ℃, 压力振幅的计算最大误差为0.56%, 体积流速振幅计算的最大误差为1.6%, 证实了模型计算的合理性.
|
图 3 温度t分布 Fig. 3 Temperature profile |
|
图 4 压力振幅p1分布 Fig. 4 Pressure amplitude profile |
|
图 5 体积流速振幅U1分布 Fig. 5 Volumetric velocity amplitude profile |
针对第2章内的热声核部分, 本文以2.5 MPa的氦气作为工质, 给定单级Pin=760 W.为了更加直观地给出Gedeon声直流对系统性能的影响, 热声核的入口条件给定, 主冷却器和副冷却器的温度为Tc=298 K, 热声核入口的压力波动幅值为66.59 kPa, 体积流速波动幅值为0.008 3 m3/s, 体积流速相位超前压力波16 °, 频率为124 Hz, 计算并分析了Gedeon声直流对于四级行波热声发动机性能的影响.
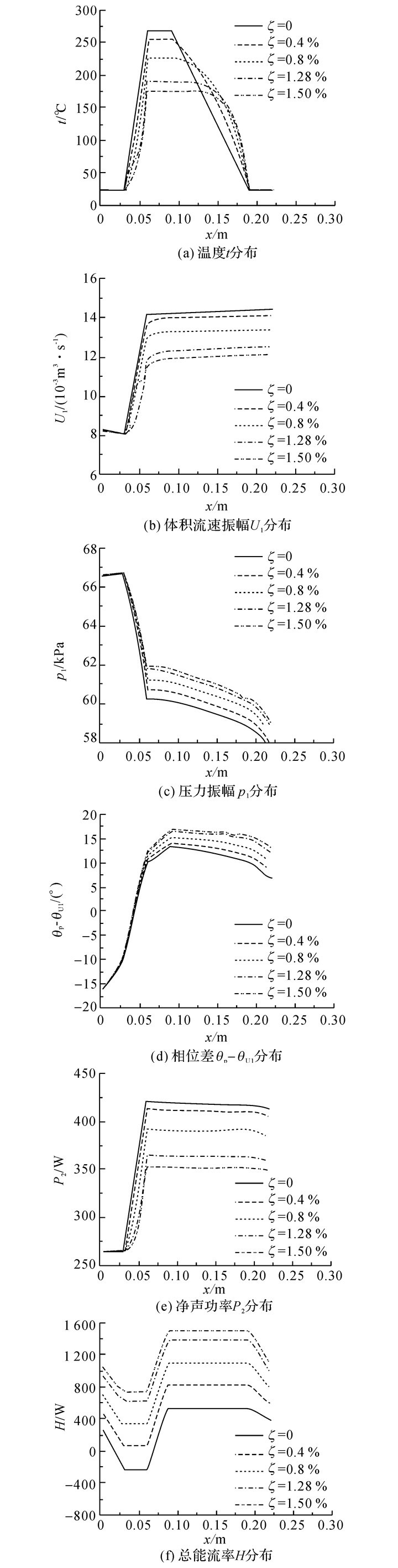
为了便于分析, 将Gedeon声直流量进行无量纲处理, 即定义无量纲Gedeon声直流流率为Gedeon声直流流率与质量流速振幅之比ζ=m2, 0/ρmU1.本文计算了ζ分别为0、0.4%、0.8%、1.28%、1.5%情况下的温度分布、体积流速振幅分布、压力振幅分布、压力与速度相位差分布、声功率分布以及总能流率分布, 见图 6(a)~(f),图中θU1为速度相位.
|
图 6 不同Gedeon声直流条件下的声场分布 Fig. 6 Acoustic field features inside engine with various amount of Gedeon streaming |
由图 6(a)中可见, 随着Gedeon声直流量的增大, 热端的温度降低.Gedeon[6]将Gedeon声直流表达为
| $ {m_{2,0}} = \frac{{{\mathop{\rm Re}\nolimits} \left( {{\rho _1}{{\tilde U}_1}} \right)}}{2} + {\rho _{\rm{m}}}{U_{2,0}} \approx \frac{{{\rho _{\rm{m}}}{P_2}}}{{{p_{\rm{m}}}}} + {\rho _{\rm{m}}}{U_{2,0}}. $ | (8) |
式中:P2为声功流率, pm为平均压力, U2, 0为时均体积流速, U2, 0主要是由非对称部件提供的时均压降驱动.在不考虑U2, 0时, 根据回热器冷端的参数, 可以计算直流量为交变流量的1.28%, 方向为图 2中x轴的正方向.此时, 加热器与主冷却器的温差由241.8 ℃降低到165 ℃, 降低了31.8%.不存在Gedeon声直流时, 回热器的温度分布为近似线性分布, 存在Gedeon声直流后, 回热器的温度明显偏离了线性分布, 回热器冷端部分的温度梯度减小, 随着靠近回热器的热端, 温度梯度逐渐增大.在靠近回热器热端处, 温度梯度甚至可能大于无Gedeon声直流下的温度梯度.
由于回热器内的温度梯度是热声发动机产生热致声转换的根本驱动因素, 热缓冲管内的温度梯度也与热声发动机的热效率相关, 因此在该部分我们重点分析Gedeon声直流对温度梯度的影响机制.根据式(4)、(7) 可知, Gedeon声直流对于温度梯度的影响与当地工质的温度直接相关.为了便于分析, 令式(4) 中各项为
| $ {\rm{RE1}} = {H_2} - {m_{2,0}}{c_p}{T_{\rm{m}}}, $ | (9) |
| $ \begin{array}{l} {\rm{RE2}} = - \frac{1}{2}{\mathop{\rm Re}\nolimits} \left[ {\left( {{T_{\rm{m}}}\beta \frac{{{\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} + \exp \left( {2i{\theta _{\rm{p}}}} \right){g_{\rm{v}}}} \right){\varepsilon _{\rm{h}}}}}{{1 + {\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} + \exp \left( {2i{\theta _{\rm{T}}}} \right){g_{\rm{v}}}} \right){\varepsilon _{\rm{h}}}}} + } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\left. {\left. {1 - {T_{\rm{m}}}\beta } \right){p_1}{{\tilde u}_1}\phi A} \right], \end{array} $ | (10) |
| $ \begin{array}{l} {\rm{RE3}} = - \phi A\left\{ {\frac{{{\rho _{\rm{m}}}{c_{\rm{p}}}}}{{2\omega }}{\mathop{\rm Im}\nolimits} \left[ {\frac{{{\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} - {g_{\rm{v}}}} \right){\varepsilon _{\rm{h}}}}}{{1 + {\varepsilon _{\rm{s}}} + \left( {{g_{\rm{c}}} + \exp \left( {2i{\theta _{\rm{T}}}} \right){g_{\rm{v}}}} \right){\varepsilon _{\rm{h}}}}}} \right]} \right.\\ \;\;\;\;\;\;\;\;\left. {{u_1}{{\tilde u}_1} + \left( {{\kappa _{{\rm{s,eff}}}}\frac{{1 - \phi }}{\phi } + \kappa } \right)} \right\}, \end{array} $ | (11) |
而令式(7) 中的各项为
| $ {\rm{TE1}} = {H_2} - {m_{2,0}}{c_p}{T_{\rm{m}}}, $ | (12) |
| $ {\rm{TE2}} = - {\mathop{\rm Re}\nolimits} \left[ {\frac{{{p_1}{{\tilde U}_1}}}{2}\left( {1 - \frac{{{T_{\rm{m}}}\beta \left( {{f_{\rm{k}}} - {{\tilde f}_{\rm{v}}}} \right)}}{{\left( {1 + {\varepsilon _{\rm{s}}}} \right)\left( {1 + \sigma } \right)\left( {1 - {{\tilde f}_{\rm{v}}}} \right)}}} \right)} \right], $ | (13) |
| $ \begin{array}{l} {\rm{TE3}} = - \left( {\frac{{{\rho _{\rm{m}}}{c_p}{{\left| {{U_1}} \right|}^2}}}{{2\omega {A_{{\rm{gas}}}}\left( {\sigma - 1} \right){{\left| {1 - {f_v}} \right|}^2}}}} \right) \cdot {\mathop{\rm Im}\nolimits} \left[ {{{\tilde f}_v} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{{\left( {{f_{\rm{k}}} - {{\tilde f}_{\rm{v}}}} \right)\frac{{1 + {\varepsilon _{\rm{s}}}{f_{\rm{v}}}}}{{{f_{\rm{k}}}}}}}{{\left( {1 + {\varepsilon _{\rm{s}}}} \right)\left( {1 + \sigma } \right)}}} \right] - {A_{{\rm{gas}}}}\kappa - {A_{\rm{s}}}{\kappa _{\rm{s}}}. \end{array} $ | (14) |
在四级行波热声发动机的声阻抗条件下, 在回热器和热缓冲管内, 式(4) 和(7) 等号右边的分母RE3与TE3始终为负数, 且变化不大;公式(4) 等号右边的分子均为负数, 则可获得正的温度梯度(即沿图 2中x轴正方向温度升高), 且RE2的变化很小, RE1的变化为温度梯度变化的主导因素;对于缓冲管端, 无论是否存在Gedeon声直流, TE1均占主导地位, 且为正数, 使得式(7) 的分子均为正数, 进而导致热缓冲管内温度梯度为负值.因此, 关于Gedeon声直流影响的分析, 关键需要落脚到RE1与TE1这2项.此外, 根据式(1), 图 2所示x轴的正方向为Gedeon声直流的方向, 导致在该方向上回热器和热缓冲管内的总能流率H21和H22均呈现增大趋势, 由于加热器提供的加热功率不变, 二者的差值保持不变.因此, 当出现Gedeon声直流时, 热声系统必须重新协调H21和H22, 使得两者的差值保持不变, 以及在回热器和热缓冲管的冷端工质温度等于25 ℃, 同时在回热器和热缓冲管的热端, 两者温度必须相等的边界条件.同时该协调过程, 还需要顾及上述温度梯度的变化.协调的结果是, H21和H22均增大, 而热端工质温度降低(见图 6(a)), 回热器和热缓冲管内平均温度梯度的绝对值均减小.
首先对回热器内部的情况进行考察, 存在直流后, 回热器内部总能流率H21的值增大, 且在靠近回热器的冷端处, 回热器内工质温度Tm较低, Gedeon声直流引起的能流m2, 0cpTm较小, 因此存在直流后RE1的值相较于无直流的情况增大.回热器内温度梯度为正数且RE3为负数, 存在直流后RE1增大将导致其冷端的温度梯度的绝对值小于无直流的情况.回热器与外界环境绝热, 其内部总能流率H21为常数.存在Gedeon声直流时, 随着x的增大, 回热器内工质温度Tm增大, Gedeon声直流引起的能流m2, 0cpTm增大, 导致RE1明显减小.由于其分子为负数, RE1越小, 其温度梯度绝对值越大, 因此越靠近回热器热端, 温度梯度越大.这是Gedeon声直流使得回热器内温度梯度偏离近似线性分布的原因, 而Gedeon声直流越大, 这种偏离就越显著(见图 6(a)).
热缓冲管中的情况与回热器具有相似性, 而不同之处在于, 热缓冲管内的总能流率H22明显大于回热器内的总能流率H21(两者的差值为加热器提供的加热功率), 导致TE1始终为正数.同样热缓冲管与外界环境绝热, 在热缓冲管内部总能流率H22为常数.因此, 存在Gedeon声直流时, 在热缓冲管的热端部分Tm较大, 导致TE1较小, 而靠近热缓冲管冷端的部分, Tm较小, TE1则较大, 而热缓冲管内的温度梯度为负数, 因此热缓冲管冷端部分负温度梯度的绝对值大于其热端部分.这是Gedeon声直流影响热缓冲管内温度分布(见图 6(a))的机制.
综上所述, 回热器和热缓冲管内RE1与RE2的变化是Gedeon声直流影响其内温度梯度变化(见图 6(a))的主要因素, 且RE1与RE2的变化主要是由于回热器以及热缓冲管内温度的改变造成的, 因此Gedeon声直流对回热器以及热缓冲管内温度分布的影响主要在于其携带的能流改变了回热器以及缓冲管内的温度梯度, 温度分布的变化又进一步导致了Gedeon声直流携带能流的变化, 形成了相互影响的机制.
关于体积流速分布的情况, 图 6(b)显示, 随着直流量的增大, 回热器的体积流速的增益减小, 且变化趋势与回热器温度分布变化相似.根据式(4), 可见Gedeon声直流通过影响温度梯度进而对回热器内的体积流速的放大效应产生影响.无直流时, 回热器部分从冷端到热端的体积流速从0.008 07增大到0.014 16 m3/s, 而Gedeon声直流量为1.28%时, 其体积流速从0.008 07增大到0.012 11 m3/s, 体积流速的增益降低了33.7%, 其值与回热器温度梯度降低的值接近.根据图 6(c)可见, 回热器处的压力振幅沿轴向位置显著降低;存在Gedeon声直流后, 压力振幅的降低幅度减缓.
图 6(d)给出的相位差分布为压力波相对于体积流的相位差.从图中可以看出, 在无Gedeon声直流的情况下, 该相位差从回热器的冷端到热端由-9.99°变化到10.11°, Gedeon声直流1.28%的情况下, 其值由-9.99°变化到12.50°, 相位差为零的位置均出现在靠近回热器轴向的中心附近.可见, Gedeon声直流量对于回热器部分的相位差影响较小.
图 6(e)中给出了不同Gedeon声直流情况下, 声功率沿热声核的轴向分布, 从图中可以看出, 随着Gedeon声直流的增大, 声功率增益明显减小.究其原因, 主要是存在Gedeon声直流后, 回热器靠近冷端部分的温度梯度的减小导致的体积流速放大效应减弱造成的.而温度梯度的变化是Gedeon声直流携带的能流与温度分布相互影响的结果.
图 6(f)给出了总能流率的分布情况.可以看到, 换热器是系统与外界能量交换的部件, 因此总能流率在换热器处呈现显著变化.而回热器和热缓冲管由于与外界环境绝热而保持总能流率不变, 两者内部总能流率之差为加热器处输入系统的加热功率.同时, Gedeon声直流的存在导致总能流率增大.如前所述, 这是存在Gedeon声直流后, 热声系统协调回热器和热缓冲管内的总能流率, 进而同时满足能量守恒和冷热端边界条件的结果.
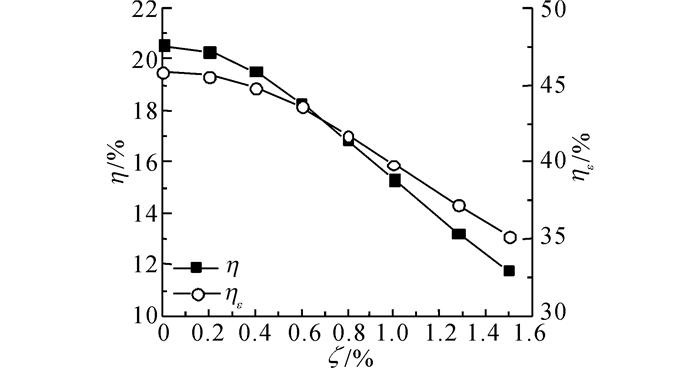
循环于环路中的Gedeon声直流是影响热声发动机热效率的一个至关重要的因素, 图 7定量给出了热效率以及相对卡诺效率随着Gedeon声直流的变化.热效率的定义为η=P0/Pin, P0为回热器产生的净声功率, 即回热器入口与出口产生的声功率之差.相对卡诺效率定义为η=η/(1-Tc/Th).从图 7中可以看出, 随着直流量增大, 热效率迅速降低.当Gedeon声直流量为1.28%时(即无Gedeon声直流抑制手段工况), 热效率从20.1%下降到13.2%, 下降了34.3%;相对卡诺效率从45.8%下降到了37.1%, 下降了19.0%.可见, 在四级环路结构行波热声发动机系统中, 采用适当结构抑制Gedeon声直流, 对于保证系统具有较高的热效率非常重要.
|
图 7 热效率以及相对卡诺效率随Gedeon声直流量的变化 Fig. 7 Dependence of thermal efficiency and relative Carnot efficiency on Gedeon streaming |
此外, 本文的研究是基于给定入口条件, 针对热声核部分的声场进行分析, 以研究Gedeon声直流对于系统性能, 特别是热效率的影响.需要注意的是, 对于实际系统, Gedeon声直流的存在会对整个系统的运行参数产生影响, 即本文给定的所谓入口条件会随直流的改变而发生一定变化.针对整个系统进行模拟, 可以更加准确地考察Gedeon声直流的影响, 我们将在后续工作中进行考虑.
4 结论本文基于热声学理论, 针对四级环路结构行波热声发动机的热声核部分进行了模拟, 以分析Gedeon声直流对该类热声发动机系统性能的影响.首先通过将无Gedeon声直流情况下的模拟结果与DeltaEC的结果进行比较, 验证了模型的合理性.之后, 基于本文的模拟计算结果, 定量分析了存在Gedeon声直流的情况下热声核部分的温度分布、体积流速振幅分布、压力振幅分布、压力与速度相位差分布、声功率分布、总能流率分布以及系统热效率.其中重点对Gedeon声直流对于回热器和热缓冲管内温度分布的影响机制进行了探索, 这是Gedeon声直流影响系统性能的关键.结果表明, 存在Gedeon声直流后, 回热器和热缓冲管内的温度分布明显偏离无直流情况下的近似线性分布, 随着Gedeon声直流量的增大, 回热器内部的温度梯度、体积流速以及声功率增益显著降低, 进而导致系统热效率明显减小, 而Gedeon声直流对压力与体积流速的相位差影响较小.Gedeon声直流携带的能流是影响回热器以及热缓冲管内温度梯度的关键因素, 而温度梯度的改变又进一步影响了Gedeon声直流携带的热量, 形成了相互影响机制.在本文给定条件下, 1.28%的Gedeon声直流量(即无Gedeon声直流抑制手段工况)将导致系统热效率从20.1%下降到13.2%, 下降了34.3%;相对卡诺效率从45.8%下降到37.1%, 下降了19.0%.可见, 在四级环路结构行波热声发动机系统中, 采用适当结构抑制Gedeon声直流, 对于保证系统具有较高的热效率非常重要.
| [1] | CEPERLEY P H. A pistonless Stirling engine—the traveling wave heat engine[J]. Journal of the Acoustical Society of America, 1979, 66(5): 1508–1513. DOI:10.1121/1.383505 |
| [2] | BACKHAUS S, SWIFT G W. A thermoacoustic Stirling heat engine[J]. Nature, 1999, 399: 335–338. DOI:10.1038/20624 |
| [3] | YU G, LUO E, DAI W, et al. An energy-focused thermoacoustic-Stirling heat engine reaching a high pressure ratio above 1.40[J]. Cryogenics, 2007, 47(2): 132–137. DOI:10.1016/j.cryogenics.2006.12.001 |
| [4] | JIN T, MAO C, TANG K, et al. Characteristics study on the oscillation onset and damping of a traveling-wave thermoacoustic prime mover[J]. Journal of Zhejiang University: Science A, 2008, 9(7): 944–949. DOI:10.1631/jzus.A0820061 |
| [5] | TIJANI M E H, SPOELSTRA S. A high performance thermoacoustic engine[J]. Journal of Applied Physics, 2011, 110(9): 093519. DOI:10.1063/1.3658872 |
| [6] | GEDEON D. DC gas flows in Stirling and pulse tube cryocoolers[C]//Cryocoolers 9. New York:Plenum Press, 1997:385-392. http://link.springer.com/chapter/10.1007/978-1-4615-5869-9_45 |
| [7] | BACKHAUS S, SWIFT G W. A Thermoacoustic-stirling heat engine: detailed study[J]. Journal of the Acoustical Society of America, 2000, 107(6): 3148–3166. DOI:10.1121/1.429343 |
| [8] | BIWA T, TASHIRO Y, ISHIGAKI M, et al. Measurements of acoustic streaming in a looped-tube thermoacoustic engine with a jet pump[J]. Journal of Applied Physics, 2007, 101(6): 064914. DOI:10.1063/1.2713360 |
| [9] | GUSEV V, JOB S, BAILLIET H, et al. Acoustic streaming in annular thermoacoustic prime-movers[J]. The Journal of the Acoustical Society of America, 2000, 108(3): 934–945. DOI:10.1121/1.1287023 |
| [10] | YU G Y, LUO E C, DAI W, et al. Study of nonlinear processes of a large experimental thermoacoustic-Stirling heat engine by using computational fluid dynamics[J]. Journal of Applied Physics, 102(7):074901. http://aip.scitation.org/doi/abs/10.1063/1.2784997?journalCode=jap |
| [11] | WANG B, QIU L M, SUN D, et al. Visualization observation of onset and damping behaviors in a traveling-wave thermoacoustic engine by infrared imaging[J]. International Journal of Heat and Mass Transfer, 2011, 54(23): 5070–5076. |
| [12] | WANG C, THUMMES G, HEIDEN C. Control of DC gas flow in a single-stage double-inlet pulse tube cooler[J]. Cryogenics, 1998, 38(8): 843–847. DOI:10.1016/S0011-2275(98)00070-8 |
| [13] | DE BLOK K. Novel 4-Stage Traveling Wave Thermoacoustic Power Generator[C]//In ASME 20103rd Joint US-European Fluids Engineering Summer Meeting collocated with 8th International Conference on Nanochannels, Microchannels, and Minichannels, American Society of Mechanical Engineers. Montreal:[s. n.], 2010:73-79. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1621379 |
| [14] | DE BLOK K. Multi-stage traveling wave thermoacoustics in Practice[C]//19th International Congress on Sound and Vibration. Vilnius:[s. n.], 2012:1-8. |
| [15] | SWIFT G W, GARRETT S L. Thermoacoustics: Aunifying perspective for some engines and refrigerators[J]. Journal of the Acoustical Society of America, 2003, 113(5): 2379–2381. DOI:10.1121/1.1561492 |
| [16] | CLARK J P, WARD W C, SWIFT G W. Design environment for low‐amplitude thermoacoustic energy conversion (DeltaEC)[J]. Journal of the Acoustical Society of America, 2007, 122(5): 3014–3014. |
| [17] | SWIFT GW, WARD WC. Simple harmonic analysis of regenerators[J]. Journal of Thermophysics and Heat Transfer, 1996, 10: 652–662. DOI:10.2514/3.842 |



