随着汽车保有量的爆发式增长, 带来的交通拥堵、环境污染、事故频发成为当前社会亟待解决的问题.发展环境友好且安全舒适的智能电动汽车成为行业发展的共识.将自适应巡航(adaptive cruise control, ACC)系统搭载于电动车不仅可以减少驾驶员操作, 还可以进一步提升纯电动车的经济性.
目前自适应巡航系统在传统发动机车辆上研究较多, 在纯电动车上的研究还比较少.纯电动车将动力源由发动机替换为电机, 同时还引入了一些新技术如再生制动技术, 使得纯电动车的ACC系统控制层算法和执行层执行机构与传统车ACC系统有较大不同, 因此对ACC的控制策略上也有着更大的优化空间.党睿娜等[1]提出了一种兼顾节能与安全的电动车ACC系统, 根据电机效率特性, 对ACC控制策略做出优化, 满足了整车经济性和安全性要求.罗禹贡等[2]考虑内燃机的优化曲线、电动机最佳效率特性、电池最佳效率特性, 提出了混合动力轿车自适应巡航控制系统.
再生制动技术作为新能源汽车的通用技术, 将驱动电机作为发电机, 制动过程中将动能转化为电能提高续驶里程.在城市工况下, 车辆频繁的启动或制动, 在制动过程中所消耗的能量占总消耗能量的50%以上[3], 如何尽可能多地回收这一部分能量对于提高纯电动车整车经济性有着重要的意义.目前对于纯电动车ACC系统加入再生制动技术的研究还比较少.本文将课题组前期对于再生制动技术的研究[4]引入ACC系统, 并设计了基于再生制动优化的ACC系统控制策略.首先对纯电动车再生制动系统特性分析, 并以回收能量作为经济性优化指标, 利用模型预测控制理论建立自适应巡航控制策略, 通过优化ACC系统在车辆减速过程中的制动强度时间历程, 使车辆保证舒适性、安全性、跟随性的前提下尽可能多地回收制动能量.
1 再生制动系统特性分析 1.1 车辆构型目标车辆构型是前轴驱动的纯电动轿车, 如图 1所示.在制动过程中, 电机带动主减速器可以对前轴施加制动力, 由于电机制动力受到电机外特性、电池荷电状态(state of charge, SOC)等因素的影响, 需要机械制动力的协调完成制动.机械制动力通过控制车身电子稳定性控制系统(electronic speed controller, ESC)液压调节单元主动增压实施.
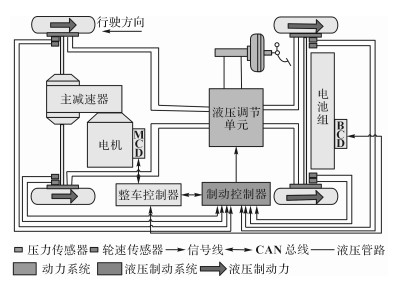
|
图 1 目标车辆构型 Fig. 1 Target vehicle configuration |
制动力分配策略是再生制动系统的核心, 包括前、后轴的制动力分配和电机、液压制动力的分配[5].目的是使再生制动系统满足制动安全性的前提下尽可能多的回收制动能量.传统汽车制动力分配受到制动力法规限制, 遵循一定制动力分配原则, 纯电动汽车的制动力分配同样需要满足一定原则, 同时要尽可能多地回收能量.
联合国欧洲经济委员会汽车法规(ECE)对制动力分配有如图 2所示要求[6], 其中Fbf为前轴制动力, Fbr为后轴制动力, B线限制前轴制动力的最大值, C线限制前轴制动力的最小值.目标车辆为前轴驱动的纯电动轿车构型, 若要提高制动回收能量, 则应分配更多制动力予以前轴电机制动.在大强度制动要求下, 为充分利用地面附着条件防止车轮抱死[7], 电机制动力退出, 仅由液压系统提供制动力.在自适应巡航模式下由于无需考虑制动踏板感觉[8], 为充分回收制动能量, 设计制动力分配策略如图 3所示.
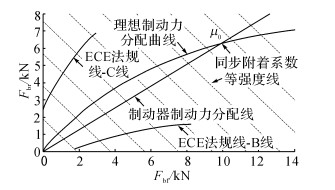
|
图 2 ECE法规中的制动力分配线 Fig. 2 Brake force distribution line in ECE |
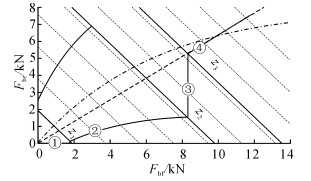
|
图 3 适应巡航模式下制动力分配策略 Fig. 3 Brake force distribution strategy in ACC mode |
在制动强度z<z1时, 法规对前轴制动力下限没有要求, 仅由前轴电机提供制动力;在制动强度z1<z<z2时, 前后轴制动力沿ECE法规下线分配;在z2<z<z3时, 此时制动强度较高, 电机制动力达到最大, 前轴制动力不变, 由后轴增加液压制动力;在z>z3时, 为保证安全性并充分利用地面附着特性, 放弃电机制动, 前后轴制动力沿β线分配.在制动力分配过程中, 若电机制动力不足由液压制动力补偿.制动力分配如式(1) 所示.
| $ \left. \begin{array}{l} {F_{{\rm{bf}}}} = {F_{\rm{b}}},{F_{{\rm{br}}}} = 0,0 < z < {z_1};\\ {F_{{\rm{bf}}}} = {F_{\rm{b}}}\left( {1 - \frac{{\left( {z + 0.04} \right)\left( {{l_1} - z{h_{\rm{g}}}} \right)}}{{0.7zL}}} \right),\\ {F_{{\rm{bf}}}} = {F_{\rm{b}}}\frac{{\left( {z + 0.04} \right)\left( {{l_1} - z{h_{\rm{g}}}} \right)}}{{0.7zL}},{z_1} < z < {z_2};\\ {F_{{\rm{bf}}}} = \frac{{{T_{{\rm{B\_max}}}}{i_{\rm{r}}}}}{{{r_{\rm{w}}}}},{F_{{\rm{br}}}} = {F_{\rm{b}}} - {F_{{\rm{bf}}}},{z_2} < z < {z_3};\\ {F_{{\rm{bf}}}} = {F_{\rm{b}}}\beta ,{F_{{\rm{bf}}}} = {F_{\rm{b}}}\left( {1 - \beta } \right),z > {z_3}. \end{array} \right\} $ | (1) |
式中: Fb为需求总制动力(N);z为制动强度;l1为质心到前轴距离;hg为质心高度(m);L为轴距(m);TBmax为电机最大制动转矩(N·m);ir为主减速器传动比;rw为轮胎滚动半径(m);β为制动器制动力分配系数.
其中边界条件计算如下:
| $ \left. \begin{array}{l} {z_1} = 0.1,\\ {z_2} = \\ \frac{{ - \left( {{l_2} + 0.04{h_{\rm{g}}} + \sqrt {{{\left( {{l_2} - 0.04{h_{\rm{g}}}} \right)}^2} + 2.8{T_{{\rm{Bmax}}}}{i_{\rm{r}}}{h_{\rm{g}}}L/\left( {{r_{\rm{w}}}m} \right)} } \right)}}{{2{h_{\rm{g}}}g}},\\ {z_3} = \\ \left[ {\frac{1}{{2{h_{\rm{g}}}}}\sqrt {l_2^2 + \frac{{4{h_{\rm{g}}}L}}{G}\frac{{{T_{{\rm{Bmax}}}}{i_{\rm{r}}}}}{{{r_{\rm{w}}}}}} - \left( {\frac{{{l_2}}}{{{h_{\rm{g}}}}} + \frac{{{T_{{\rm{Bmax}}}}{i_{\rm{r}}}}}{{{r_{\rm{w}}}}}} \right)} \right] + \frac{{{T_{{\rm{Bmax}}}}{i_{\rm{r}}}}}{{G{r_{\rm{w}}}}}. \end{array} \right\} $ | (2) |
式中:G为整车重量(N), l2为质心到后轴距离(m), m为整车整备质量(kg).
1.3 电机制动力特性影响电机制动力的因素很多.车速、电机效率、电机外特性、电池SOC等因素均会影响电机最大制动力[9].本文仅考虑电机外特性对电机制定力的影响.电机制动力外特性与驱动力外特性相似, 包括恒转矩区和恒功率区.针对于目标车型选用电机, 其外特性可简化为如图 4、式(3) 所示.
| $ {T_{\rm{m}}} = \left\{ \begin{array}{l} \;\;\;\;{T_{{\rm{Bmax}}}},\;\;\;\;\;\;\;\;{n_{\rm{m}}} \le {n_{\rm{b}}};\\ \frac{{9550{P_{{\rm{Bmax}}}}}}{{{n_{\rm{m}}}}},\;\;\;\;{n_{\rm{m}}} > {n_{\rm{b}}}. \end{array} \right. $ | (3) |
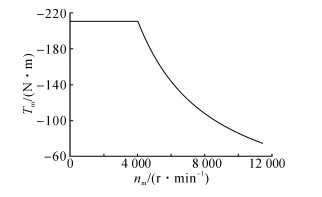
|
图 4 电机外特性 Fig. 4 Motor external characteristic |
式中:nb为电机基速(r/min);PBmax为电机最大制动功率(kW);Tm为电机制动转矩(N·m), nm为电机转速(r/min),
2 面向再生制动优化的自适应巡航控制策略设计的自适应巡航控制策略希望在满足舒适性、安全性的前提下尽可能多的回收制动能量.因此将再生制动算法作为自适应巡航系统的制动控制层算法, 将电机、基于ESC的液压制动系统作为制动执行层的执行机构, 自适应巡航系统整体架构如图 5所示.
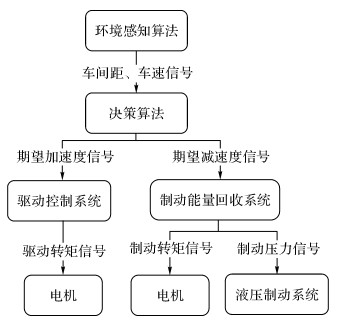
|
图 5 自适应巡航系统架构 Fig. 5 Adaptive cruise control system architecture |
自适应巡航系统的安全车间距涉及到整车安全性、道路利用率和驾驶员可接受度[10].若安全车间距过小, 会让驾驶员产生不安全感, 容易造成碰撞事故.若安全车间距过大, 道路利用率较低, 会出现其他车道车辆插入情况.故算法采用固定时距的车间距算法, 如式(4) 所示.
| $ {d_{{\rm{des}}}}\left( {{v_{\rm{h}}}} \right) = {t_0}{v_{\rm{h}}} + {d_0}. $ | (4) |
式中:ddes为安全车间距(m), vh为自车车速(m/s), t0为时距(s), d0为固定距离(m), 取t0=1, d0=20.
自适应系统要求有较好的跟随性能, 包括对车速的控制和车间距的控制, 其体现在车辆稳定行驶情况下, 车间距误差、车速误差趋近于0.其次要求有较好舒适性, 其体现在车辆尽可能匀速行驶, 避免车辆过大的加减速度对驾驶员产生不适感.此外在制动过程中能尽可能多的回收制动能量.
模型预测控制(model predictive control, MPC)算法基于被控对象的模型, 可以对未来一段时间的系统状态变量和输出进行预测[11].根据预测状态建立优化函数, 利用数值优化的方法求解预测时域内的最优解和相应输出量, 并将优化解的第一个分量作用于系统.模型预测控制具有实时性多目标协调优化的特点, 故本文基于模型预测控制理论设计自适应巡航的决策算法.
2.1 车辆纵向运动模型由于模型预测控制具有实时在线滚动优化的特点, 需要预测模型和优化算法有较高的运算效率, 所以应尽可能简化预测模型.由于电机和液压制动系统响应有一定延迟, 采用一阶惯性环节表示执行机构对期望加速度的响应特性[12], 如式(5) 所示.
| $ {a_{\rm{h}}} = \frac{K}{{{T_{\rm{s}}}s + 1}}{a_{\rm{u}}}. $ | (5) |
式中: ah为自车实际响应加速度、au为系统期望加速度, K为增益,Ts为时间常数,s为传递函数.
根据实车控制数据对系统辨识, 辨识结果取K=1.08, Ts=0.2 s.
将自车行驶距离sh、车辆速度vh、车辆加速度ah作为状态变量xh, 建立状态空间方程:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot x}}}_{\rm{h}}} = \mathit{\boldsymbol{A'}}{x_\mathit{\boldsymbol{h}}} + \mathit{\boldsymbol{B'}}{a_{\rm{u}}}.}\\ {\mathit{\boldsymbol{A'}} = \left[ {\begin{array}{*{20}{c}} 0&1&{{T_{\rm{s}}}}\\ 0&0&1\\ 0&0&{ - 1/{T_{\rm{s}}}} \end{array}} \right],\;\;\;\;\;\;\;\;\mathit{\boldsymbol{B' = }}\left[ \begin{array}{l} 0\\ 0\\ K/{T_{\rm{s}}} \end{array} \right].} \end{array} $ | (6) |
利用式(7) 对状态空间方程离散化处理, 可得式(8):
| $ \mathit{\boldsymbol{A}} = \exp \left( {\mathit{\boldsymbol{A'}}T} \right),\mathit{\boldsymbol{B}} = \left( {\int_0^T {\exp \left( {\mathit{\boldsymbol{A'}}T} \right)} } \right)\mathit{\boldsymbol{B'}}. $ | (7) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_{\rm{h}}}\left( {k + 1\left| k \right.} \right) = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_{\rm{h}}}\left( k \right) + \mathit{\boldsymbol{B}}{a_{\rm{u}}}\left( k \right).}\\ {{\mathit{\boldsymbol{y}}_{\rm{h}}}\left( {k + 1\left| k \right.} \right) = \mathit{\boldsymbol{I}}{\mathit{\boldsymbol{x}}_{\rm{h}}}\left( k \right).} \end{array} $ | (8) |
式中:I为单位矩阵, T为采样周期, yh(k+1|k)为在k时间模型预测k+1时间的系统输出.xh(k+1|k)为在k时间模型预测k+1时间的自车运动状态, 如下式:
| $ \begin{array}{l} {\mathit{\boldsymbol{x}}_{\rm{h}}}\left( {k + 1\left| k \right.} \right) = \\ \;\;\;\;\;\;\;\;{\left[ {{s_{\rm{h}}}\left( {k + 1\left| k \right.} \right),{v_{\rm{h}}}\left( {k + 1\left| k \right.} \right),{a_{\rm{h}}}\left( {k + 1\left| k \right.} \right)} \right]^{\rm{T}}}. \end{array} $ |
为预测前车运动状态xf, 还需建立前车运动的预测模型, 模型假设前车以第k时间的加速度在从k时间开始的预测时域P以匀加速运动.建立状态空间方程:
| $ {\mathit{\boldsymbol{x}}_{\rm{f}}}\left( {k + i\left| k \right.} \right) = {\mathit{\boldsymbol{A}}_{\rm{f}}}{\mathit{\boldsymbol{x}}_{\rm{f}}}\left( {k + i - 1\left| k \right.} \right),\;\;\;\;i = 1 \cdots P. $ | (9) |
式中:
| $ {\mathit{\boldsymbol{A}}_{\rm{f}}} = \left[ {\begin{array}{*{20}{c}} 1&1&{T_{\rm{s}}^2/2}\\ 0&1&{{T_{\rm{s}}}}\\ 0&0&1 \end{array}} \right]. $ |
基于再生制动优化的自适应巡航系统包括4个性能指标的优化.
2.2.1 经济性指标以预测区间内所回收的能量作为经济性指标, 区间内回收能量越多, 经济性指标越好.区间内回收能量大小与电机制动力有关.忽略电池SOC、电池转化效率、电机效率对电机回收能量的影响.根据第1章对再生制动系统特性的分析, 电机制动力主要取决于制动力分配算法和电机外特性.制动力分配算法中前、后轴制动力分配只与制动强度z有关.电机外特性中, 电机最大制动力只与车速有关.在串行协调制动力分配策略下, 前轴制动力尽量使用电机制动, 不足部分由液压制动力补偿.因此可得到电机制动转矩为
| $ {T_{\rm{m}}}\left( {z,{v_{\rm{h}}}} \right) = \min \left( {{T_{{\rm{allo\_bf}}}}\left( z \right),{T_{{\rm{B\_max}}}}\left( {{v_{\rm{h}}}} \right)} \right). $ | (10) |
式中:Tallo_bf(z)为在制动强度z下前轴分配的制动力矩.TB_max(vh)为车速vh下电机能提供的最大制动力矩.
联立式(1)、(3) 和式(10), 得到电机制动力Tm与车速vh, 制动强度z关系如图 6所示.

|
图 6 电机制动转矩与车速, 制动强度关系图 Fig. 6 Relationship map among motor braking torque, vehicle speed and braking strength |
模型预测控制是将预测时域按照采样时间T离散化计算.通过对每个采样时间段所回收能量Em累计求和, 即可得到区间内回收能量.若加速过程, 回收能量取0.采样时间内回收能量如式(11), 关系如图 7所示.
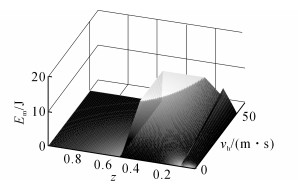
|
图 7 采样时间回收能量与车速, 制动减速度关系图 Fig. 7 Relationship map among regenerative energy in a peried, vehicle speed and braking strength |
| $ \begin{array}{*{20}{c}} {{E_m}\left( {{a_{\rm{h}}}\left( k \right),{v_{\rm{h}}}\left( k \right)} \right) = \frac{{{T_m}\left( {{a_{\rm{h}}}\left( k \right),{v_{\rm{h}}}\left( k \right)} \right)i}}{{{r_{\rm{w}}}}} \times }\\ {\left[ {{v_{\rm{h}}}\left( k \right){T_{\rm{s}}} + \frac{1}{2}{a_{\rm{h}}}\left( k \right)T_{\rm{s}}^2} \right].} \end{array} $ | (11) |
将区间内回收能量作为经济性指标, 如式(12) 所示.
| $ {L_{{\rm{eco}}}} = {w_{\rm{e}}}\sum\limits_{k = 1}^P {{E_{\rm{m}}}\left( {{a_{\rm{h}}}\left( k \right),{v_{\rm{h}}}\left( k \right)} \right)} . $ | (12) |
式中:Leco为经济性指标, we为经济性指标权重.
2.2.2 跟随性指标自适应巡航系统需要稳定跟随前车行驶, 跟随性体现在2个方面, 速度的跟随性和安全车间距离跟随性[13].取速度误差指标Δv(k)、距离误差指标Δd(k), 并将2个指标的平方求和作为跟随性指标, 第k时间的跟随性指标为
| $ {l_t}\left( k \right) = {w_{\Delta {\rm{d}}}}{\left( {\Delta {\rm{d}}\left( k \right)} \right)^2} + {w_{\Delta {\rm{v}}}}{\left( {\Delta v\left( k \right)} \right)^2}. $ | (13) |
式中:Δd(k)=sf(k)-sh(k)-ddes(vh(k)), Δv(k)=vh(k)-vf(k),wΔd和wΔv为距离误差权重和速度误差权重, sf前车行驶位移,sh为自车行驶距离.
预测时域内跟随性指标为
| $ {L_{\rm{t}}}\left( k \right) = \sum\limits_{k = 1}^P {{l_{\rm{t}}}\left( k \right)} . $ | (14) |
安全性体现在车间距要始终保持在安全车间距以外, 避免两车发生碰撞风险, 同时两车之间距离不能过大, 避免旁道车辆插入发生事故.两车车速误差不宜过大.因此约束车间距误差Δd(k)和车速误差Δv(k):
| $ \begin{array}{*{20}{c}} {0 \le \Delta d\left( k \right) \le \Delta {d_{\max }},k = 1 \cdots P.}\\ {\Delta {v_{\min }} \le \Delta v\left( k \right) \le \Delta {v_{\max }},k = 1 \cdots P.} \end{array} $ |
舒适性体现在尽量用较小加速度或减速度调节车速, 避免驾驶员产生不舒适感.定义舒适性指标为
| $ {l_{\rm{a}}}\left( k \right) = {w_{\rm{a}}}{\left( {{a_u}\left( k \right)} \right)^2}. $ | (15) |
式中:wa为舒适性指标权重.约束加速度或减速度变化:
| $ {a_{u\min }} \le {a_u}\left( k \right) \le {a_{u\max }},k = 1 \cdots P. $ |
由2.2节建立的各指标函数和约束条件, 建立优化问题的综合指标方程:
| $ \left. \begin{array}{l} l\left( k \right) = {w_{\rm{e}}}{E_{\rm{m}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{h}}}\left( k \right)} \right) + {\mathit{\boldsymbol{x}}_{\rm{h}}}{\left( k \right)^{\rm{T}}}{\mathit{\boldsymbol{w}}_2}{\mathit{\boldsymbol{x}}_{\rm{h}}}\left( k \right) + \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{w}}_1}{\mathit{\boldsymbol{x}}_{\rm{h}}}\left( k \right) + {w_{\rm{a}}}{a_u}{\left( k \right)^2},\\ L = \sum\limits_{k = 1}^P {l\left( k \right)} . \end{array} \right\} $ | (16) |
式中:w2和w1为二次项和一次项的系数, 计算如下:
| $ \begin{array}{l} {\mathit{\boldsymbol{w}}_2} = \left[ {\begin{array}{*{20}{c}} {{w_{\Delta {\rm{d}}}}}&0&0\\ 0&{{w_{\Delta {\rm{v}}}}}&0\\ 0&0&0 \end{array}} \right],\\ {\mathit{\boldsymbol{w}}_1} = \left[ {\begin{array}{*{20}{c}} { - 2{w_{\Delta {\rm{d}}}}\left( {{s_{\rm{f}}}\left( k \right)} \right),}&{ - {w_{\Delta {\rm{v}}}}{v_{\rm{f}}}\left( k \right),}&0 \end{array}} \right]. \end{array} $ |
对约束整理得
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{\rm{p}}}{\mathit{\boldsymbol{x}}_{\rm{h}}}\left( k \right) \le {\mathit{\boldsymbol{B}}_{\rm{p}}}}\\ {{a_{u\min }} < {a_u}\left( k \right) < {a_{u\max }}.} \end{array} $ | (17) |
式中:
| $ {\mathit{\boldsymbol{A}}_{\rm{p}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ { - 1}&0&0\\ 0&1&0\\ 0&{ - 1}&0 \end{array}} \right],{\mathit{\boldsymbol{B}}_{\rm{p}}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{s_{\rm{f}}}\left( k \right) - {d_{{\rm{des}}}}\left( k \right)}\\ { - {s_{\rm{f}}}\left( k \right) + {d_{{\rm{des}}}}\left( k \right) + \Delta {d_{\max }}}\\ {{v_{\rm{f}}}\left( k \right) + \Delta {v_{\max }}}\\ { - {v_{\rm{f}}}\left( k \right) - \Delta {v_{\min }}} \end{array}} \right]. $ |
最终问题化为式(19) 所描述的优化问题.
| $ \begin{array}{*{20}{c}} {\min L.}\\ {\begin{array}{*{20}{c}} {{\rm{s}}{\rm{.t}}{\rm{.}}}&\begin{array}{l} {\mathit{\boldsymbol{A}}_{\rm{p}}}{\mathit{\boldsymbol{x}}_{\rm{h}}}\left( k \right) \le {\mathit{\boldsymbol{B}}_{\rm{p}}},\\ {a_{u\min }} < {a_u}\left( k \right) < {a_{u\max }};k = 1 \cdots P. \end{array} \end{array}} \end{array} $ | (18) |
由于L中包含区间回收能量函数Em(ah(k), vh(k)), 因此目标方程是一个高度非线性不连续函数, 采用内点法求解该非线性规划问题[14].
3 仿真结果分析将建立的面向再生制动优化的自适应巡航控制策略在Matlab/Simulink下仿真验证.自适应巡航算法参数定义如表 1所示.整车模型采用CarSim模型, 关键参数定义如表 2所示.表中,ρmot, max为电机最大功率,nmot, max为电机最高转速,Tmot, max为电机最大驱动转距.由控制策略计算得到的期望加速度根据车辆纵向动力学模型转化为电机转矩和前、后轴制动压力信号输出至CarSim整车模型.
| 表 1 算法参数设置 Table 1 Algorithm parameter setting |
| 表 2 整车参数设置 Table 2 Vehicle parameter setting |
定义未优化再生制动的MPC自适应巡航算法作为对比算法, 其制动力分配策略、构建方法和参数设置与本文算法相同, 在式(16) 的综合指标方程中忽略经济性指标, 仅对安全性指标和跟随性指标做出优化.
初始状态前车速度10 m/s, 后车速度15 m/s, 两车相距30 m, 前车加速度按照一定轨迹变化, 分别进行有能量回收优化和无能量回收优化MPC自适应巡航算法的仿真对比验证, 仿真结果如图 8~12所示.
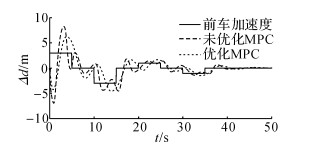
|
图 8 车间距仿真结果 Fig. 8 Simulation result of vehicle spacing |
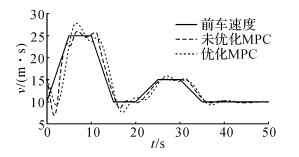
|
图 9 车速仿真结果 Fig. 9 Simulation result of vehicle speed |
|
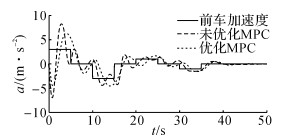
图 10 加速度仿真结果 Fig. 10 Simulation result of vehicle acceleration |
|
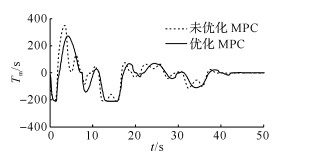
图 11 电机转矩仿真结果 Fig. 11 Simulation result of motor torque |
|
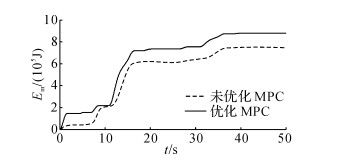
图 12 回收能量仿真结果 Fig. 12 Simulation result of energy recovered |
从仿真结果中可以看出, 2种算法均对前车的车间距、车速跟随性均较好.在开始阶段, 两车车速误差较大、车间距较小, 算法进行了较大幅度的调节, 对前车的跟随性较差, 但随着两车速度的接近, 系统逐渐趋于稳定, 后车实现对前车速度变化的跟随, 但有一定滞后性.当前车进入稳态行驶后, 车间距误差、车速误差最后收敛于0.加速度方面, 未优化MPC算法减速度变化较大, 优化MPC算法减速度变化较小, 其主要由于再生制动系统在中等强度制动下有较好的能量回收效果.
对于再生制动性能的评价, 视亮等[15]曾提出制动能量回收率作为评价指标, 其定义为电机回收的能量与制动过程中总能量的比值.计算如下:
| $ {\eta _{{\rm{reg}}}} = \frac{{\sum\limits_{j = 1}^n {\int_{{t_{{\rm{j}}\_1}}}^{{t_{{\rm{j}}\_2}}} {\frac{{{T_{\rm{m}}}{n_{\rm{m}}}}}{{9.55}}{\rm{d}}t} } }}{{\sum\limits_{j = 1}^n {\frac{1}{2}mv_{{\rm{j}}\_0}^2 - \frac{1}{2}mv_{{\rm{j}}\_{\rm{t}}}^2} }}. $ | (19) |
式中:仿真工况共制动n次, 在第j次制动中, vj_0为制动初始速度(m/s), vj_t为制动结束速度(m/s), tj_1为制动初始时刻(s), tj_2为制动结束时刻(s).
未优化MPC算法仿真工况下能量回收率为32.2%.优化MPC算法仿真工况能量回收率为37.8%.回收能量变化如图 12所示, 未优化算法总回收能量为754.36 kJ;优化算法回收能量890.2 kJ.
4 结语分析了再生制动系统特性, 提出了在自适应巡航模式下的制动力分配策略.分析再生制动的影响因素, 通过制动力分配策略和电机外特性得到制动回收能量与车速、制动强度的关系.基于模型预测控制理论搭建纯电动车自适应巡航系统控制策略, 并将回收制动能量作为经济性指标, 利用内点法求解经济性、跟随性、安全性、舒适性最优的目标方程.
分别基于再生制动优化的ACC算法和未优化的ACC算法在MATLAB/SIMULINK下仿真, 仿真结果2种算法对前车都有较好的跟随性能, 基于再生制动优化的ACC算法相比未优化ACC算法能量回收率提高5.6%.结果表明, 优化算法在满足整车安全性、经济性、舒适性的前提下, 相比未优化算法有着更高的能量回收率.在今后的研究中可以进一步分析电机效率特性, 将纯电动车的驱动和制动过程协调优化以提高自适应巡航系统的经济性.
| [1] |
党睿娜, 李升波, 王建强, 等. 兼顾节能与安全的电动车ACC系统[J].
汽车工程, 2012, 34(5): 379–393.
DANG Rui-na, LI Sheng-bo, WANG Jian-qiang, et al. Adaptive cruise control system of electric vehicles considering both economy and safety[J]. Automotive Engineering, 2012, 34(5): 379–393. |
| [2] |
罗禹贡, 陈涛, 周磊, 等. 奔腾智能混合动力电动轿车自适应巡航控制系统[J].
机械工程学报, 2010, 46(6): 2–7.
LUO Yu-gong, CHEN Tao, ZHOU Lei, et al. Adaptive Cruise control system of besturn intelligent hybrid electric vehicle[J]. Journal Of Mechanical Engineering, 2010, 46(6): 2–7. |
| [3] | WALKER A M, LAMPERTH M U, WILKINS S. On friction braking demand with regenerative braking[R]. London: Imperial College of Science, Technology and Medicine, 2002. |
| [4] |
姚亮. 混合动力轿车再生制动与液压制动协调控制策略研究[D]. 长春: 吉林大学, 2009.
YAO Liang. Study on the integrative control strategy of regenerative braking and hydraulic braking for hybrid electric vehicle[D]. Changchun: Jilin University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10183-2009091689.htm |
| [5] | MUTOH N, AKASHI H. Electric and mechanical brake cooperative control method for FRID EVs under various severe road conditions [C]//IECON 2011-37th Annual Conference on IEEE Industrial Electronics Society. Melbourne: IEEE, 2011: 4570-4576. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6120063 |
| [6] | ECE Regulation No. 13. Uniform Provisions concerning the approval of vehicles of categories M. N and O with regard to braking. [S]. [S. l.]: United Nations Economic Commission for Europe, 2003. |
| [7] | WANG G, XIAO H, ZHANG J, et al. Energy regenerative braking ABS control research on feedback lockup driving-braking integrated system for electric vehicles[J]. Mechanics, 2012, 18(3): 341–346. |
| [8] | DAY A J, HO H P, HUSSAIN K, et al. Brake system simulation to predict brake pedal feel in a passenger car[R]. Bradford City: University of Bradford, 2009. |
| [9] |
卢东斌, 欧阳明高, 谷靖, 等. 电动汽车永磁同步电机最优制动能量回馈控制[J].
中国电机工程学报, 2013, 33(3): 83–91.
LU Dong-bin, OUYANG Ming-gao, GU Jing, et al. Optimal regenerative braking control for permanent magnet synchronous motors in electric vehicles[J]. Proceedings of the CSEE, 2013, 33(3): 83–91. |
| [10] | MIYAJIMA C, NISHIWAKI Y, OZAWA K, et al. Driver modeling based on driving behavior and its evaluation in driver identification[J]. Proceedings of the IEEE, 2007, 95(2): 427–437. DOI:10.1109/JPROC.2006.888405 |
| [11] | SHAKOURI P, ORDYS A, ASKARI M R. Adaptive cruise control with stop&go function using the state-dependent nonlinear model predictive control approach[J]. ISA transactions, 2012, 51(5): 622–631. DOI:10.1016/j.isatra.2012.05.001 |
| [12] |
胡吉. 基于MPC算法的混合动力汽车自适应巡航控制研究[D]. 重庆: 重庆大学, 2015.
HU ji. The research on adaptive cruise control for a hybrid electric vehicle based on mpc algorithm [D]. Chongqing: Chongqing University, 2015. http://d.wanfangdata.com.cn/Thesis/D686513 |
| [13] |
马国成. 车辆自适应巡航跟随控制技术研究[D]. 北京: 北京理工大学, 2014.
MA Guo-cheng. Research on the adaptive cruise control tracking system applied for motor vehicles [D]. Beijing: Beijing Institute of Technology, 2014. paperuri:(3ca57a564b4a0d87cb43ef338a176ce6) |
| [14] | WÄCHTER A, BIEGLER L T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming[J]. Mathematical programming, 2006, 106(1): 25–57. DOI:10.1007/s10107-004-0559-y |
| [15] |
初亮, 蔡健伟, 富子丞, 等. 纯电动汽车制动能量回收评价与试验方法研究[J].
华中科技大学学报:自然科学版, 2014, 42(1): 18–22.
CHU liang, CAI Jian-wei, FU Zi-cheng, et al. Research on brake energy regeneration evaluation and test method of pure electric vehicle[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2014, 42(1): 18–22. |


