近年来, 随着金属复合板在航天航空、石油、化工、轮船等领域的广泛应用, 层状金属复合板的研制、生产与应用越来越引起人们的关注[1-2].矫直作为板形精整与残余应力控制的一道重要工序, 对于高品质板材的生产具有重要意义.辊式矫直工艺以矫直效果良好、生产效率高的特点, 广泛应用于板材的连续生产[3-5].在辊式矫直过程中, 板材与矫直辊的接触点实际上偏离矫直辊正下方而形成一个接触倾角, 此接触倾角会显著影响矫直过程的有效压下量并且具有累积效应, 因此板材矫直过程的精确解析必须考虑接触倾角对矫直过程的影响[6-9].
双金属复合板层间异性材料的结构特征, 使得弯曲特性与单一材料板材存在较大差异, 如应变中性层偏移、弯矩-曲率关系更为复杂、回弹过程的反向屈服等.弯曲特性的差异使得双金属复合板在辊式矫直连续反弯过程中的力学行为显著不同于单一材料板材, 例如当复合板回弹过程中发生反向屈服时, 适用于单一材料板材的矫直区间弹性卸载段、弹性加载段和弹塑性加载段的划分将不再适用与复合板.
本文针对现有矫直理论难以应用于双金属复合板辊式矫直过程的精确解析[6-12], 在双金属复合板截面弯曲特性分析的基础上, 对于弹塑性矫直段采用等分离散曲率再求解离散点坐标的方法, 保证弹塑性段曲率积分值求解得精确与快速, 建立了双金属复合板辊式矫直过程曲率积分解析模型;采用有限元仿真以及与实验数据相比较, 验证了曲率积分模型的正确性, 并对有限元法与曲率积分法矫直过程解析的优劣进行比较;最后运用建立的曲率积分模型对钢-铝复合板辊式矫直过程进行解析, 并与单一材料板材的矫直过程进行对比, 对双金属复合板辊式矫直过程的截面应力分布、弯矩-曲率关系和反向屈服对矫直过程的影响等进行阐述, 为双金属复合板矫直工艺的合理制定提供理论指导.
1 曲率积分的几何模型曲率积分法几何模型的建立过程不涉及截面的力学特征, 因此经典的板材曲率积分的几何关系对于复合板矫直过程同样适用[6-9], 现简要论述如下.
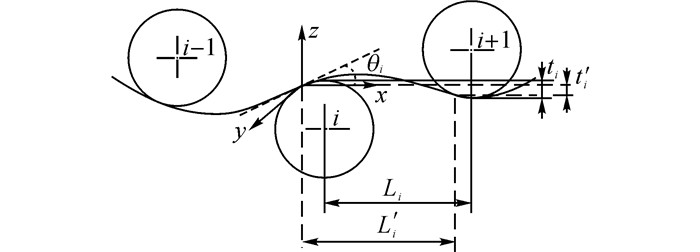
由于板材在矫直过程中厚度基本不发生变化, 因此可以用其几何中性层曲线描述板材矫直过程的板形曲线.矫直过程板材与矫直辊的几何关系如图 1所示.在板材与每个矫直辊接触点处建立坐标系, x轴正向为板材矫直方向.对于板材n辊矫直过程, 将其按每两相邻矫直辊划分为一个矫直区间, 可划分n-1个矫直区间.规定板形曲线下凹时的曲率为正, 上凸时的曲率为负;使板材下凹的弯矩为正, 使板材上凸的弯矩为负.
|
图 1 板材辊式矫直过程示意图 Fig. 1 Plate roller leveling process diagram |
设Ri为第i矫直辊辊径, 由于用板材几何中性层曲线代替板材, 此时用于计算的辊径Ri应是实际矫直辊半径与板厚一半之和.Li为辊距, L′i为相邻接触点沿矫直方向距离;ti为相邻两辊的压下量, t′i为相邻两接触点沿板厚方向距离, 规定板材与i+1辊接触点在i辊接触点上方时, ti与t′i为正, 反之为负;θi为板材与第i矫直辊的接触倾角, θi为锐角, 规定θi位于z轴正半轴时为正, 位于z轴负半轴为负.在小挠度条件下, 矫直区间I(第i矫直辊接触点到第i+1矫直辊接触点的区域)的两辊间实际接触距离L′i和实际压下量t′i满足:
当首辊为上辊时:
| $ \left. {\begin{array}{*{20}{c}} {{{L'}_i} = {L_i} - {R_i}{\theta _i} - {R_{i + 1}}{\theta _{i + 1}},}\\ {{{t'}_i} = {t_i} - {R_i}\theta _i^2/2 - {R_{i + 1}}\theta _{i + 1}^2/2.} \end{array}} \right\} $ | (1) |
式中:Ri+1为第i+1矫直辊辊径,θi+1为板材与第i+1辊的接触倾角.
当首辊为下辊时:
| $ \left. {\begin{array}{*{20}{c}} {{{L'}_i} = {L_i} + {R_i}{\theta _i} + {R_{i + 1}}{\theta _{i + 1}},}\\ {{{t'}_i} = {t_i} + {R_i}\theta _i^2/2 + {R_{i + 1}}\theta _{i + 1}^2/2.} \end{array}} \right\} $ | (2) |
在板材辊式矫直过程中, 矫直区间I内的板材在第i辊接触点处的坐标系下满足:
| $ \left. {\begin{array}{*{20}{c}} {{A_x} = {A_i} + \Delta {A_x},}\\ {{\theta _x} = {\theta _i} + \int_0^x {{A_x}{\rm{d}}x} ,}\\ {{t_x} = \int_0^x {{\theta _x}{\rm{d}}x} .} \end{array}} \right\} $ | (3) |
式中:x∈0, L′
式(3) 中当x=L′i时, 即是板材与第i+1辊接触点处有
| $ \left. {\begin{array}{*{20}{c}} {{\theta _{i + 1}} = {\theta _i} + \int_0^{{{L'}_i}} {{A_x}{\rm{d}}x} ,}\\ {{{t'}_i} = \int_0^{L'} {\left( {{\theta _i} + \int_0^x {{A_x}{\rm{d}}x} } \right){\rm{d}}x} .} \end{array}} \right\} $ | (4) |
式(4) 可转化为
| $ \left. {\begin{array}{*{20}{c}} {{\theta _{i + 1}} = {\theta _i} + \int_0^{{{L'}_i}} {\left( {{A_i} + \Delta {A_x}} \right){\rm{d}}x} ,}\\ {{{t'}_i} = {\theta _i}{{L'}_i} + \int_0^{{{L'}_i}} {\left( {\int_0^x {\left( {{A_i} + \Delta {A_x}} \right){\rm{d}}x} } \right){\rm{d}}x} .} \end{array}} \right\} $ | (5) |
将式(5) 进一步展开为
| $ \left. \begin{array}{l} {\theta _{i + 1}} = {\theta _i} + {A_i}{{L'}_i} + \int_0^{{{L'}_i}} {\Delta {A_x}{\rm{d}}x} ,\\ {{t'}_i} = {\theta _i}{{L'}_i} + {A_i}L_i^{'2}/2 + \int_0^{{{L'}_i}} {\left( {\int_0^x {\Delta {A_x}{\rm{d}}x} } \right){\rm{d}}x} . \end{array} \right\} $ | (6) |
设一重曲率变化量积分值ai与二重曲率变化量积分值bi为
| $ \left. {\begin{array}{*{20}{c}} {{a_i} = \int_0^{{{L'}_i}} {\Delta {A_x}{\rm{d}}x} ,}\\ {{b_i} = \int_0^{{{L'}_i}} {\left( {\int_0^x {\Delta {A_x}{\rm{d}}x} } \right){\rm{d}}x} .} \end{array}} \right\} $ | (7) |
式(6) 可表示为
| $ \left. {\begin{array}{*{20}{c}} {{\theta _{i + 1}} = {\theta _i} + {A_i}{{L'}_i} + {a_i},}\\ {{{t'}_i} = {\theta _i}{{L'}_i} + {A_i}L_i^{'2}/2 + {b_i}.} \end{array}} \right\} $ | (8) |
板材n辊矫直过程可划分n-1个矫直区间, 每个矫直区间可以得到一组式(8).因此对于整个矫直过程可以利用式(8) 建立一个由2(n-1) 个方程构成的方程组.若ai和bi已知, 则方程组中独立的未知量为板材与各辊的接触倾角θi及接触点处板材的曲率Ai, 共2n个.同时对于板材辊式矫直, 首辊的弯曲曲率A1即为板材初始曲率A0, 为已知量;尾辊处的曲率An为倒数第2辊曲率A(n-1)卸载后的曲率, An未知量不独立, 因此独立未知量减少为2(n-1) 个.这样对于2(n-1) 个独立的未知量可以建立2(n-1) 个方程, 方程组存在唯一确定解.由此, 矫直过程的解析问题转化为确定各矫直区间的一重曲率变化量积分值ai与二重曲率变化量积分值bi.
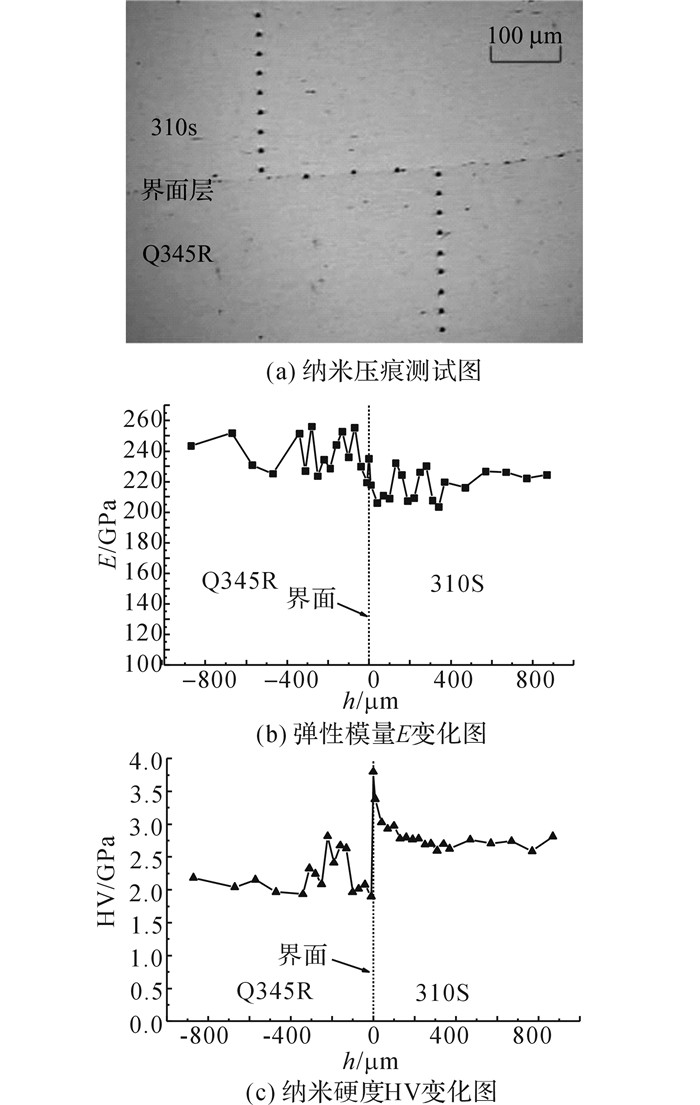
2 曲率积分的力学模型 2.1 双金属复合板弯曲特性分析双金属复合板为2种金属材料组成的分层结构.采用Nano Indenter DCM纳米显微力学探针对热轧Q345/310S不锈钢复合板覆层、基层及界面的力学参数进行测量, 如图 2所示,图中,E为弹性模量,h为与界面的距离,由图中可以看出, 复合板界面处的弹性模量与硬度均大于覆层.实验及相关文献[13]的结果表明对于复合工艺合理的金属复合板, 界面的力学性能往往优于覆层的力学性能, 在加载过程中不会出现分层现象, 且复合板结合界面厚度极薄, 一般为几十微米, 在不产生分层的情况下对宏观力能参数影响极其微小.
|
图 2 不锈钢复合板纳米压痕实验 Fig. 2 Nano-indentation experiment of stainless steel clad plate |
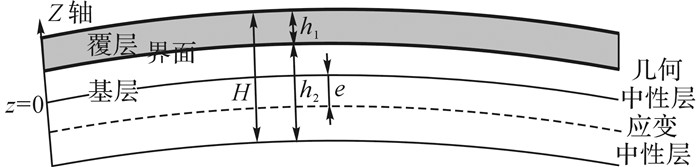
双金属复合板截面如图 3所示, 设复合板的板厚为H, 其中覆层厚度为h1, 基层厚度为h2.设覆层的弹性模量为E1, 屈服极限为σs1, 强化模量为E′1;基层的弹性模量为E2, 屈服极限为σs2, 强化模量为E′2.由于双金属复合板不具有单一材料板材的矩形对称弯曲特性, 弯曲过程中应变中性层与几何中性层不重合, 设偏移量为e, 当应变中性层位于几何中性层之上时e为正值, 反之为负.
|
图 3 复合板截面示意图 Fig. 3 Composite plate section diagram |
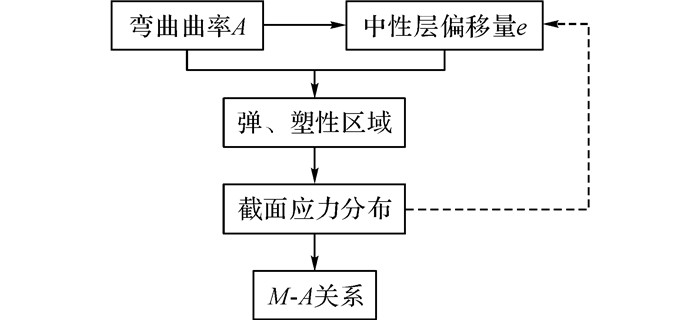
单一材料板材截面简单弯曲的解析思路如下:由于不考虑中性层偏移现象, 根据板材弯曲曲率A确定截面弹性芯高度, 分别计算弹性区域与塑性区域的应力分布, 根据应力分布积分得到弯矩M弯曲曲率A的关系, 即M-A关系.即对于单一材料板材的弯曲过程, 可由弯曲曲率直接推导出截面的力学状态.双金属复合板弯曲过程的解析流程如图 4所示.即对于复合板截面弯曲过程, 首先需要确定复合板在弯曲曲率A时的中性层偏移量e, 根据弯曲曲率与中性层偏移量确定截面的弹、塑性区域, 再确定截面的应力分布, 最后得到弯曲过程的M-A关系.但对于复合板截面弯曲过程, 中性层偏移量需要根据截面的应力来确定.即是截面应力分布的确定需要中性层偏移量, 而中性层偏移量需要根据截面应力分布来计算, 两者之间是耦合关系.所以对于双金属复合板, 弯曲过程截面的力学状态难以通过弯曲曲率直接解析得到.
|
图 4 复合板弯曲解析过程 Fig. 4 Analytical procedure of composite plate bendingprocess |
当弯曲曲率A较小时, 复合板截面不发生塑性变形.此时沿截面高度应变为
| $ \varepsilon = A\left( {z - e} \right). $ | (9) |
式中:z为沿截面高度的坐标, 如图 3所示.
由于此时截面均为弹性区域, 可建立沿截面高度的应力分布与中性层偏移量e关系:
| $ \left. \begin{array}{l} {\sigma _{{\rm{fw}}}} = {E_1}A\left( {z - e} \right),\frac{H}{2} - {h_1} < z \le \frac{H}{2};\\ {\sigma _{{\rm{jw}}}} = {E_2}A\left( {z - e} \right), - \frac{H}{2} \le z \le \frac{H}{2} - {h_1}. \end{array} \right\} $ | (10) |
式中:σfw为覆层的弯曲应力, σjw为基层的弯曲应力.
根据截面应力平衡方程, 此时的截面应力需满足:
| $ \int_{ - \frac{H}{2}}^{\frac{H}{2} - {h_1}} {{E_1}A\left( {z - {e_1}} \right){\rm{d}}z} + \int_{\frac{H}{2} - {h_1}}^{\frac{H}{2}} {{E_2}A\left( {z - {e_1}} \right){\rm{d}}z} = 0. $ | (11) |
式中:e1为截面纯弹性变形时的中性层偏移量.
将式(11) 中积分展开并化简可得截面纯弹性弯曲时的中性层偏移量为
| $ {e_1} = \frac{H}{2} - \frac{{{E_2}{H^2} + \left( {{E_1} - {E_2}} \right)h_1^2}}{{2{E_2}H + 2\left( {{E_1} - {E_2}} \right){h_1}}}. $ | (12) |
将应力与高度坐标的乘积沿截面积分, 可得纯弹性弯曲条件下复合板弯矩M与弯曲曲率A的关系, 如式(13) 所示.为方便后续推导, 用α代替A前面的系数.
| $ \begin{array}{l} M = \int_{ - \frac{H}{2}}^{\frac{H}{2} - {h_1}} {{E_1}A\left( {z - {e_1}} \right)z{\rm{d}}z} + \int_{\frac{H}{2} - {h_1}}^{\frac{H}{2}} {{E_2}A\left( {z - {e_1}} \right)z{\rm{d}}z} = \\ \;\;\;\;\;\;\;\left[ {4\left( {{E_1} - {E_2}} \right)h_1^3 + 6\left( {{e_1} - H} \right)\left( {{E_1} - {E_2}} \right)h_1^2 - } \right.\\ \;\;\;\;\;\;\;\left. {3\left( {2{e_1} - H} \right)\left( {{E_1} - {E_2}} \right){h_1}H + {E_2}{H^3}} \right]\frac{A}{{12}} = \alpha A. \end{array} $ | (13) |
随着弯曲曲率的增大, 复合板截面将发生弹塑性变形.不同于单一材料板材截面自外向内的逐步进入塑性变形, 复合板截面覆层与基层发生塑性变形的顺序和区域与各层材料的力学性能以及弯曲曲率相关, 同时伴随着截面的中性层偏移, 难以通过解析公式直接建立弯曲曲率与截面应力的函数关系.复合板截面弯曲过程部分关系的求解依赖于数值方法.
当截面发生弹塑性弯曲时, 根据小变形平截面假设, 沿截面高度的应变依然满足式(9), 截面弹性区域的应力分布依然满足式(10), 而截面塑性区域的应力为材料的屈服极限与线性强化的应力增量相叠加, 如式(14) 所示, 即对于复合板截面弯曲过程, 当中性层偏移量求得后, 截面的弹、塑性区域与应力分布也随之确定, 再对截面应力沿截面高度积分即能求得截面的弯矩.
| $ \left. \begin{array}{l} {\sigma _{{\rm{fw}}}} = {\sigma _{{\rm{s1}}}} + \left[ {A\left( {z - e} \right) - \frac{{{\sigma _{{\rm{s1}}}}}}{{{E_1}}}} \right]{{E'}_1},\\ {\sigma _{{\rm{jw}}}} = {\sigma _{{\rm{s2}}}} + \left[ {A\left( {z - e} \right) - \frac{{{\sigma _{{\rm{s2}}}}}}{{{E_2}}}} \right]{{E'}_2}. \end{array} \right\} $ | (14) |
复合板截面弹塑性弯曲的数值解析流程如图 5所示, 其具体的求解步骤如下:

|
图 5 复合板弹塑性弯曲解析流程 Fig. 5 Analytical procedure of elastic-plastic bending of composite plate |
1) 截面应力离散.对板材截面连续分布的应力进行离散, 将其等分为m个区段点, 计算分析中用区段点计算应力值σΔj代替区段范围内连续分布的截面应力.
2) 中性层偏移量e的二分法求解.截面弹塑性弯曲曲率为A, 初始e0取为0, 将A、e0代入式(9) 计算沿截面的应变.覆层与基层应变分别小于E1/σs1与E2/σs2的区域, 根据式(10) 计算该区域的截面应力, 覆层与基层应变大于E1/σs1与E2/σs2的区域, 根据式(14) 计算该区域的截面应力.由于此时中性层偏移量取为0, 截面受拉部分与受压部分厚度均为H/2.对截面应力离散并求和, 如式(15) 所示.若σΣ大于0, 表示截面拉应力大于压应力, 根据截面应力平衡原则, 中性层需要向拉应力侧偏移, 取偏移量为拉应力区厚度的一半, 即H/4, 得到一个新的中性层偏移量e1.若截面上半部分受拉, 则取e1为H/4, 若截面下半部分受拉, 则取e1为-H/4;若σΣ小于0, 表示截面拉应力小于压应力, 中性层需要向压应力侧偏移, 同样取偏移量为压应力区厚度的一半, 得到一个新的中性层偏移量e1.再把e1代入公式求取新的截面应力, 进行离散并求和, 继续根据σΣ的正负性对e进行二分法迭代.如此经过n次运算后, en与理论值的相对误差将小于1/2n.
| $ {\sigma _\sum } = \sum\limits_{j = 1}^m {\sigma _\Delta ^j\Delta h} . $ | (15) |
式中:Δh为离散区段的高度, Δh=H/m.
3) 截面弹塑性变形弯矩M的数值求解.求得截面弹塑性变形时的中性层偏移量e后, 将e带入公式求取截面应力, 求解过程如中性层偏移量e的二分法求解部分所述.根据离散的截面应力σΔj求截面弹塑性变形时的弯矩, 如式(16) 所示.
| $ M = \sum\limits_{j = 1}^m {\sigma _\Delta ^j{z_j}\Delta h} . $ | (16) |
式中:zj为离散的区段点沿截面高度的坐标.
2.1.3 截面回弹过程单一材料板材的回弹过程可认为是与加载弯矩等值反向的弯矩在截面上的弹性效应.而双金属复合板由于其截面为非对称结构, 当截面发生弹塑性弯曲变形时, 回弹过程可能会引起截面的反向屈服现象, 当发生反向屈服时, 回弹过程将不再满足弹性效应[14].
首先假设回弹过程不发生反向屈服, 此时回弹过程满足纯弹性效应.当加载弯矩为M, 弹复曲率Af如式(17) 所示, 回弹应力如式(18) 所示.
| $ {A_{\rm{f}}} = - \frac{M}{\alpha }. $ | (17) |
| $ \left. \begin{array}{l} {\sigma _{{\rm{ff}}}} = {E_1}{A_{\rm{f}}}\left( {z - {e_1}} \right),\frac{H}{2} - {h_1} < z \le \frac{H}{2};\\ {\sigma _{{\rm{jf}}}} = {E_2}{A_{\rm{f}}}\left( {z - {e_1}} \right), - \frac{H}{2} < z \le \frac{H}{2} - {h_1}. \end{array} \right\} $ | (18) |
式中:σff为覆层的回弹应力, σjf为基层的回弹应力.
回弹后截面的残余应力为弯曲应力与回弹应力的线性叠加, 如式(19) 所示.
| $ \left. \begin{array}{l} {\sigma _{{\rm{fc}}}} = {\sigma _{{\rm{fw}}}} + {\sigma _{{\rm{ff}}}},\frac{H}{2} - {h_1} < z \le \frac{H}{2};\\ {\sigma _{{\rm{jc}}}} = {\sigma _{{\rm{jw}}}} + {\sigma _{{\rm{jf}}}}, - \frac{H}{2} < z \le \frac{H}{2} - {h_1}. \end{array} \right\} $ | (19) |
式中:σfc为覆层的残余应力, σjc为基层的残余应力.
若回弹过程不发生反向屈服, 则式(19) 中的残余应力需要满足:
| $ \left. \begin{array}{l} \left| {{\sigma _{{\rm{fc}}}}} \right| < {\sigma _{{\rm{s1}}}},\\ \left| {{\sigma _{{\rm{jc}}}}} \right| < {\sigma _{{\rm{s2}}}}. \end{array} \right\} $ | (20) |
当式(20) 中任意一个条件不满足时, 说明截面回弹过程发生了反向屈服.当发生反向屈服时, 回弹过程应看作是与加载弯矩等值反向的弯矩在覆层屈服极限为2σs1、基层屈服极限为2σs2的复合板截面上的弹塑性效应[14].此时,回弹应力的求解过程如截面弹塑性变形解析部分所述, 反向屈服时截面的残余应力同样为弯曲应力与回弹应力的线性叠加.而此时的弹复曲率则需要采用数值方法确定, 具体求解过程如下:
当板材的弯曲曲率为A时, 板材的弹复曲率在0与-A之间, Af0取为(-A+ 0)/2, 根据Af0计算回弹应力与弯矩.若计算得到的弯矩绝对值小于加载弯矩绝对值表示所取弹复量小于理论值, 则取Af1为(Af0-A)/2;若计算得到的弯矩绝对值大于加载弯矩的绝对值, 取Af1为(Af0+0)/2.如此经过n次运算后, Afn与理论值的相对误差小于1/2n.
至此, 复合板任意加卸载曲率A条件下的截面状态可以被完全求解得到.
2.1.4 连续弯曲过程辊式矫直过程中板材截面会经过多次连续的反弯, 前面的弯曲会对后续弯曲产生影响, 即板材辊式矫直过程的多次弯曲是相互影响不独立的过程.
设第i次弯曲截面残余应力为σci, 残留曲率为Aci, 第i+1次的弯曲曲率为Ai+1, 此时截面总的反弯曲率Aw(i+1)为
| $ {A_{{\rm{w}}\left( {i + 1} \right)}} = {A_{i + 1}} - {A_{{\rm{c}}i}}. $ | (21) |
此时中性层偏移量与截面弹、塑性区域求解过程不变, 截面弹性区域弯曲应力求解式(10) 应为式(22)、塑性区域弯曲应力求解式(14) 应为式(23).
| $ \left. \begin{array}{l} {\sigma _{{\rm{fw}}}} = {E_1}A\left( {z - e} \right) + {\sigma _{{\rm{c}}i}},\\ {\sigma _{{\rm{jw}}}} = {E_2}A\left( {z - e} \right) + {\sigma _{{\rm{c}}i}}. \end{array} \right\} $ | (22) |
| $ \left. \begin{array}{l} {\sigma _{{\rm{fw}}}} = {\sigma _{{\rm{s1}}}} + \left[ {A\left( {z - e} \right) - \frac{{{\sigma _{{\rm{s1}}}}}}{{{E_1}}}} \right]{{E'}_1} + {\sigma _{{\rm{c}}i}},\\ {\sigma _{{\rm{jw}}}} = {\sigma _{{\rm{s2}}}} + \left[ {A\left( {z - e} \right) - \frac{{{\sigma _{{\rm{s2}}}}}}{{{E_2}}}} \right]{{E'}_2} + {\sigma _{{\rm{c}}i}}. \end{array} \right\} $ | (23) |
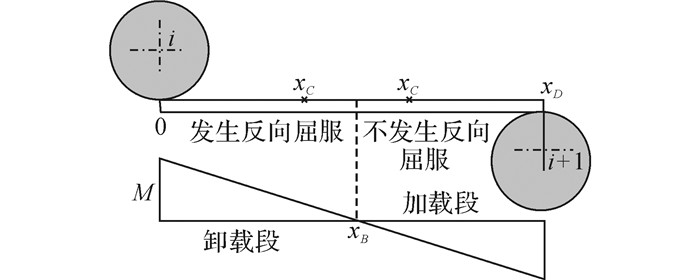
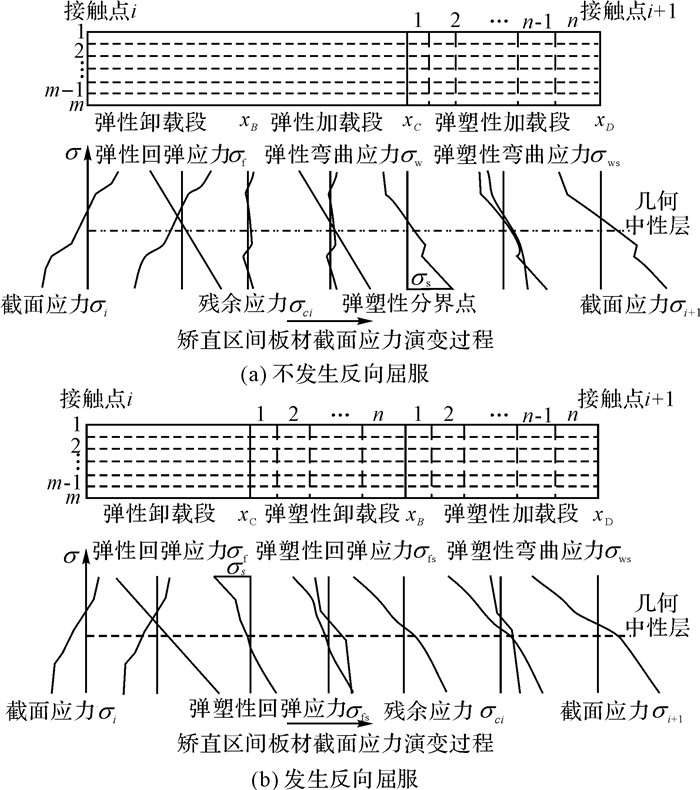
复合板矫直过程中由于反向屈服问题的存在, 使得其在两辊间的加卸载状态也随之发生了变化.板材在矫直区间I内的加卸载状态如图 6所示, 图中xB点为弯矩的加卸载分界点, xC点为板材的弹塑性状态分界点.若板材卸载过程中不发生反向屈服, 则xC点位于加载段, 其中0至xB段为弹性卸载段, xB段至xC段为弹性加载段, xC段至xD段为弹塑性加载段, 与单一材料板材一致.但若板材卸载过程中发生反向屈服, 则板材屈服点xC提前至卸载阶段, 其中0至xC段为弹性卸载段, xC段至xB段为反向屈服诱发的截面弹塑性卸载段, 同时xB段至xD段整体变为弹塑性加载段, 不再存在弹性加载状态.
|
图 6 矫直过程两辊间弯矩分布示意图 Fig. 6 Moment distribution diagram during leveling between two rollers |
根据梁的小变形假设, 受集中载荷的两矫直辊间的弯矩呈线性分布, 因此板材任意截面距离i辊接触点x处的弯矩Mix满足式(24).
| $ {M_{ix}} = {M_i} + \frac{x}{{{{L'}_i}}}\left( {{M_{i + 1}} - {M_i}} \right). $ | (24) |
式中:Mi、Mi+1为板材与第i辊和第i+1辊接触点处的弯矩.
由图 6中分析可知, 矫直区间I内的板材可划分为弹性区间段与弹塑性区间段2种状态(板材未发生弹塑性变形的矫直区间可认为弹塑性段长度为0), 分别对应着不同的曲率变化量积分值的求解方法.
2.2.1 弹性区间段曲率变化量积分值的计算弹性区间段包括弹性加载段和弹性卸载段, 式(13) 中截面弹性弯曲时弯矩M与曲率A关系的微分形式可表示为
| $ {\rm{d}}A = \frac{{{\rm{d}}M}}{\alpha }. $ | (25) |
对式(25) 在[0, x]区间进行积分可得曲率变化量ΔAx满足:
| $ \begin{array}{l} \Delta {A_x} = \int_0^x {{\rm{d}}A{\rm{d}}x} = \int_0^x {\frac{1}{\alpha }{\rm{d}}M{\rm{d}}x} = \frac{1}{\alpha }\left( {{M_{ix}} - {M_i}} \right) = \\ \;\;\;\;\;\;\;\;\; - \frac{x}{{\alpha {{L'}_i}}}\left( {{M_{i + 1}} - {M_i}} \right). \end{array} $ | (26) |
式(26) 满足图 6中[0, xC]弹性区间段的曲率-弯矩关系.因此, 将式(26) 代入式(7) 可得弹性段的一重曲率变化量积分ati和二重曲率变化量积分bti为
| $ \left. {\begin{array}{*{20}{c}} {{a_{{\rm{t}}i}} = \int_0^{{x_C}} {\frac{x}{{\alpha {{L'}_i}}}\left( {{M_{i + 1}} - {M_i}} \right){\rm{d}}x} ,}\\ {{b_{{\rm{t}}i}} = \int_0^{{x_C}} {\int_0^x {\frac{x}{{\alpha {{L'}_i}}}\left( {{M_{i + 1}} - {M_i}} \right)} {\rm{d}}x{\rm{d}}x} .} \end{array}} \right\} $ | (27) |
弹塑性区间段包括弹塑性加载段和弹塑性卸载段.如2.1节所述, 此时截面的弯矩-曲率关系不再满足线弹性关系, 且与前面弯曲加载历史相关, 难以用具体的解析公式表述.因此弹塑性区间段曲率变化量积分值的计算采取离散后的数值方法求解.根据对图 6的分析, 复合板弹塑性段曲率变化量积分的求解需要分2种情况, 弹塑性分界点xC位于加载段和弹塑性分界点xC位于卸载段.
1) 弹塑性分界点位于加载段的情况
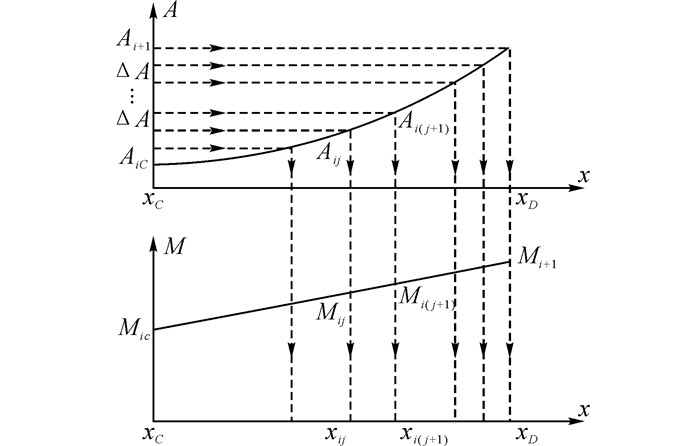
图 6的[xC, xD]弹塑性区间段的曲率变化量积分值asi、bsi如式(28) 所示.弹塑性段的asi、bsi求解过程采取先在xC点与 xD点之间插入一系列离散点, 将弹塑性段按等曲率差值进行离散.根据离散点的弯曲曲率计算该处的弯矩;离散点弯矩求得后根据两辊间弯矩呈线性分布的特征求解离散点在i辊接触点坐标系下沿x轴的坐标.过程如图 7所示, 该离散过程对于曲率变化平缓的区间, 离散点相对稀疏以提高求解速度;而对于曲率变化较大的区间离散点相对密集, 保证求解的精度.这样式(28) 的积分值可由一系列的梯形求和近似得到, 具体求解过程如下.
| $ \left. {\begin{array}{*{20}{c}} {{a_{{\rm{s}}i}} = \int_{{x_C}}^{{x_D}} {\Delta {A_x}{\rm{d}}x} ,}\\ {{b_{{\rm{s}}i}}\int_{{x_C}}^{{x_D}} {\left[ {\int_{{x_D}}^x {\Delta {A_x}{\rm{d}}x} } \right]{\rm{d}}x} .} \end{array}} \right\}. $ | (28) |
|
图 7 矫直区间I内离散点x轴坐标的确定 Fig. 7 Determination of discrete points x coordinate in I leveling range |
对于矫直区间I内的板材, 设弹塑性分界点xC处的曲率为AiC, 板材与i+1辊接触点xD处的曲率为Ai+1.在xC、xD间插入 n-1个点, 将弹塑性区间段按曲率差值等分为n份, j点处的曲率记为Aij.知道j点的弯曲曲率后, 不难求得j点的弯曲应力σw(ij).此时j点截面应力为
| $ {\sigma _{ij}} = {\sigma _{{\rm{c}}i}} + {\sigma _{{\rm{w}}\left( {ij} \right)}}. $ | (29) |
式中:σci为板材经过i辊完全卸载的残余应力.
当j点的截面应力求得后, 采用数值方法求得j点处弯矩Mij.则j点在i辊接触点的坐标系下沿x轴的坐标为
| $ {x_{ij}} = \frac{{{M_{ij}} - {M_i}}}{{{M_{i + 1}} - {M_i}}}{{L'}_i}. $ | (30) |
离散点的曲率与坐标求得后, 弹塑性区间的曲率变化量积分值求解公式如下:
| $ \left. \begin{array}{l} {a_{{\rm{s}}i}} = \sum\limits_{j = 1}^n {\xi \left( {{x_{i\left( {j + 1} \right)}} - {x_{ij}}} \right)} ,\\ {b_{{\rm{s}}i}} = \sum\limits_{k = 1}^{n - 1} {\sum\limits_{j = 1}^k {\frac{\xi }{2}\left( {{x_{i\left( {j + 1} \right)}} - {x_{ij}}} \right)\left( {{x_{i\left( {k + 1} \right)}} - {x_{ik}}} \right)} } + \\ \;\;\;\;\;\sum\limits_{k = 1}^{n - 1} {\sum\limits_{j = 1}^{k + 1} {\frac{\xi }{2}\left( {{x_{i\left( {j + 1} \right)}} - {x_{ij}}} \right)\left( {{x_{i\left( {k + 1} \right)}} - {x_{ik}}} \right)} } . \end{array} \right\} $ | (31) |
式中:ξ=Aij+Ai(j+1)-2Ai/2.
2) 弹塑性分界点位于卸载段的情况
如图 6所示, 当弹塑性分界点xC位于卸载段时, 此时弹塑性段包括弹塑性加载段和弹塑性卸载段.弹塑性加载段的曲率变化量积分值的求法与前一段中的求解方法相同, 而弹塑性卸载段曲率变化量积分值的求解与弹塑性加载段略有不同.同样将弹塑性卸载段按曲率差值等分为n份, j点处的截面应力为
| $ {\sigma _{ij}} = {\sigma _{{\rm{f}}\left( {ij} \right)}} + {\sigma _i}. $ | (32) |
式中:σf(ij)为j点处截面的回弹应力, σi为板材与i辊接触点处的截面应力.
对于弹塑性加载段, 截面应力σij是板材经过i辊完全卸载遗传的残余应力σci与弯曲应力σw(ij)的线性叠加;而弹塑性卸载段截面应力σij是板材在i辊接触点处的截面应力σi与回弹应力σf(ij)的线性叠加, 如图 8所示.
|
图 8 矫直区间I内板材的离散与应力演变过程 Fig. 8 Plate discrete and stress evolution in I leveling range |
首先需判定弹复阶段是否发生了反向屈服, 判定公式如式(20) 所示.若不发生反向屈服, 则xC位于[xB, xD]段, 此时矫直区间I内板材弹塑性分界点xC的曲率AiC在xB 点i辊完全卸载后的残余曲率Aci与i+1辊接触点xD点处的弯曲曲率Ai+1之间.仍然使用二分法进行迭代, 初始AiC0取为(Aci+Ai+1)/2, 计算此时的离散截面应力.若覆层与基层存在任意离散点的应力大于屈服极限说明此时截面已经发生塑性变形, 分界点的曲率应向i辊卸载后的残余曲率Aci接近, AiC1取为(Aci+AiC0)/2;若覆层与基层截面离散点应力均小于屈服极限说明此时截面发生纯弹性变形, 分界点的曲率应在AiC0与Ai+1之间, AiC1取为(Ai+1+ AiC0)/2.如此反复, 直至覆层或基层截面存在一点处的应力与屈服极限的差值小于给定误差η.如此确定弹塑性分界点的曲率AiC后, 计算分界点的弯矩MiC, 根据式(30) 即可确定弹塑性分界点坐标xC.
若发生反向屈服, 则xC位于[0, xB]段, 此时分界点曲率AiC在xB 点i辊完全卸载后的残余曲率Aci与0点i辊接触点处的弯曲曲率Ai之间, 初始AiC0取为(Aci+Ai)/2, 计算此时的离散截面应力.若覆层与基层截面存在任意离散点应力大于屈服极限, AiC1取为(Ai+AiC0)/2, 若截面离散点应力均小于屈服极限, AiC1取为(Aci +AiC0)/2.如此反复, 直至覆层或基层截面存在一点处的应力与屈服极限的差值小于给定误差η.同样当确定弹塑性分界点的曲率后, 计算分界点弯矩再根据式(30) 确定弹塑性分界点坐标xC.本文中η取为0.01 min (σs1, σs2).
矫直区间I内的板材离散过程与应力演变过程如图 8所示.
当弹性段与弹塑性段曲率变化量积分值分别求得后, 式(7) 中的一重曲率变化量积分值和二重曲率变化量积分值可展开为
| $ \left. \begin{array}{l} {a_i} = \int_0^{{x_C}} {\Delta {A_x}{\rm{d}}x} + \int_{{x_C}}^{{x_D}} {\Delta {A_x}{\rm{d}}x} ,\\ {b_i} = \int_0^{{x_C}} {\left( {\int_0^x {\Delta {A_x}{\rm{d}}x} } \right){\rm{d}}x} + \\ \;\;\;\;\;\;\int_{{x_C}}^{{x_D}} {\left( {\int_0^{{x_C}} {\Delta {A_m}{\rm{d}}x} + \int_{{x_C}}^x {\Delta {A_x}{\rm{d}}x} } \right){\rm{d}}x} . \end{array} \right\} $ | (33) |
代入弹性段和弹塑性段的一重和二重曲率变化量积分值, 式(33) 可转化为
| $ \left. \begin{array}{l} {a_i} = {a_{{\rm{t}}i}} + {a_{{\rm{s}}i}},\\ {b_i} = {b_{{\rm{t}}i}} + {b_{{\rm{s}}i}} + \int_{{x_C}}^{{x_D}} {\left( {\int_0^{{x_C}} {\Delta {A_x}{\rm{d}}x} } \right){\rm{d}}x} . \end{array} \right\} $ | (34) |
化简后得一重和二重曲率变化量积分值为
| $ \left. \begin{array}{l} {a_i} = {a_{{\rm{t}}i}} + {a_{{\rm{s}}i}},\\ {b_i} = {b_{{\rm{t}}i}} + {b_{{\rm{s}}i}} + {a_{{\rm{t}}i}}\left( {{{L'}_i} - {x_C}} \right). \end{array} \right\} $ | (35) |
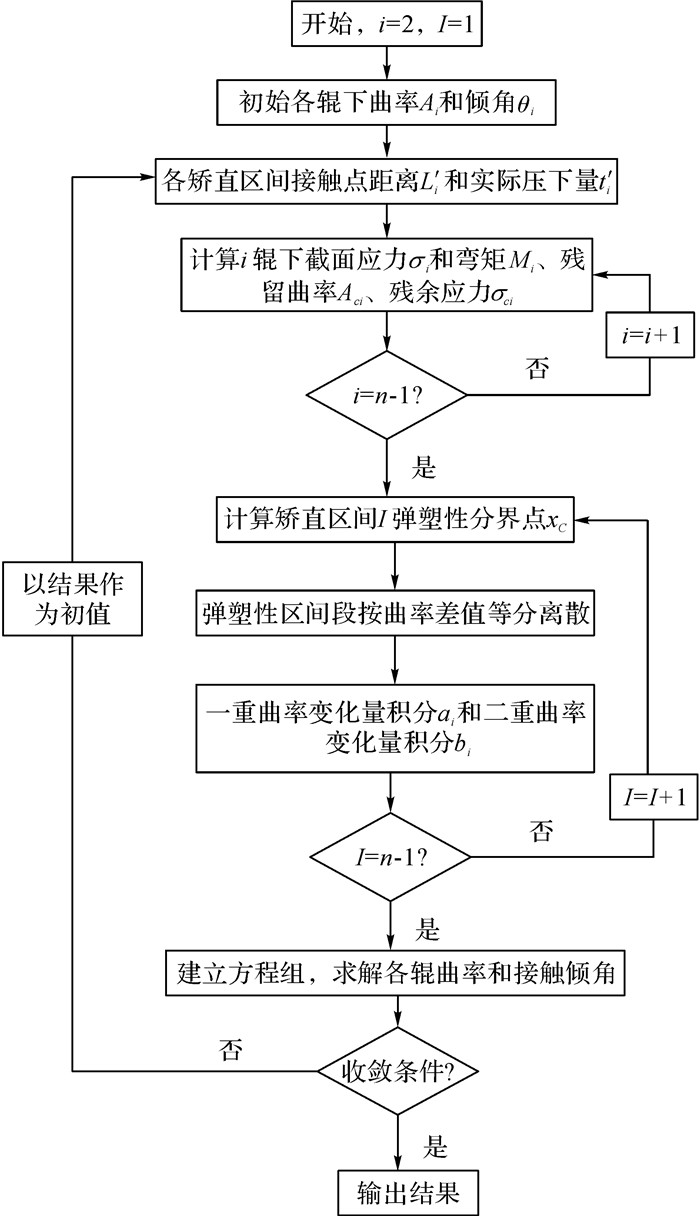
基于第2章分析可得双金属复合板n辊矫直的曲率积分模型整体数值迭代流程如图 9所示, 其中初始的弯曲曲率可根据工程力学方法计算[3], 初始倾角可取为0.
|
图 9 双金属复合板曲率积分模型数值解析流程图 Fig. 9 Bimetal composite plate curvature integration method numerical analysis flow chart |
采用曲率矩阵的内积作为判据[8], 如式(36) 所示:
| $ {{\bar A}_j} = \sqrt {\sum\limits_{i = 1}^n {A_i^2} } . $ | (36) |
当2次迭代所求得矩阵内积的相对误差小于给定精度要求时, 迭代结束, 如式(37) 所示.
| $ \left| {\frac{{{{\bar A}_{j + 1}} - {{\bar A}_j}}}{{{{\bar A}_j}}}} \right| < \zeta . $ | (37) |
运用有限元仿真对曲率积分模型的解析结果进行验证.对钢-铝复合板的辊式矫直过程采用有限元仿真软件ABAQUS进行仿真.钢-铝复合板厚度为30 mm, 其中铝层厚度为5 mm, 碳钢层厚度25 mm.通过拉伸试验, 得到组元材料的力能参数如表 1所示.考虑到组元材料在发生塑性变形后强化较弱, 在允许的误差范围内, 组元材料的材料模型均按理想弹塑性材料考虑, 即相当于覆层与基层的强化模量均为0.
| 表 1 钢-铝复合板材料力学性能参数 Table 1 Material mechanics performance parameters of steel-Al clad plate |
矫直工艺如表 2所示.表中,R为矫正辊辊径,L为矫直辊辊矩,t2为第2辊下压量,t8为第8辊下压量.采用9辊矫直, 其中下排5辊, 上排4辊, 矫直过程上排矫直辊整体倾斜压下.
| 表 2 钢-铝复合板矫直工艺 Table 2 Steel-Al clad plate leveling process parameters |
复合板矫直过程的有限元模型建模过程如下:
1) 钢-铝复合板与矫直辊模型的建立.由于仿真模型研究对象为板材长度方向在矫直过程的变化情况, 故可采用二维模型.钢-铝复合板采用整体建模, 先建立钢-铝复合板几何模型, 将其进行分割为2层, 2层分别赋予钢与铝的材料属性.不考虑矫直辊在矫直过程的变形, 采用离散刚体对矫直辊进行建模, 9辊矫直模型如图 10所示.
|
图 10 钢-铝复合板矫直过程二维仿真模型 Fig. 10 Steel-Al clad plate leveling process two-dimensional simulation model |
2) 接触建立.分别建立铝层表面、钢层表面与复合板的接触, 接触类型为面面接触, 设置钢层表面与矫直辊的滚动摩擦系数为0.15, 铝层表面与矫直辊的滚动摩擦系数为0.17.
3) 分析步设定与边界条件.共创建3个分析步, 第1个分析步中将复合板与下排矫直辊固定, 上排矫直辊向下给定一个微小的压下量, 建立矫直辊与复合板表面的接触;第2个分析步中保持复合板与下排矫直辊固定, 上排矫直辊分别给定不同的压下量;第3个分析步中解除复合板与下排矫直辊的约束, 给定上排矫直辊与下排矫直辊一定的转动量, 依靠摩擦力带动复合板, 进行矫直.
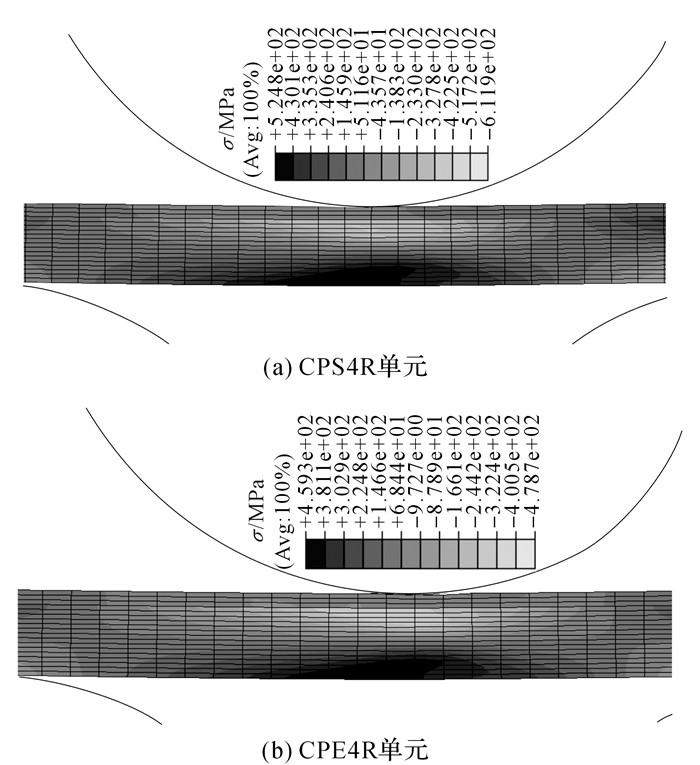
4) 复合板单元选择.分别选取CPS4R单元和CPE4R单元对复合板进行网格划分, 提取矫直过程沿板长方向的正应力σ, 结果如图 11所示.
|
图 11 不同网格单元矫直过程板长方向正应力 Fig. 11 Length direction normal stress of the plate with different grid elements during leveling |
由图 11可以看出CPE4R单元划分的复合板矫直过程的S11绝对值的最大值与基层屈服极限460 MPa接近;而CPS4R单元划分的复合板矫直过程的S11绝对值的最大值达到600 MPa左右, 显然采用CPE4R单元对复合板进行划分更合理.
5) 网格密度确定.采用3种不同的网格密度对模型进行网格划分, 如表 3所示, 工况1复合板共划分1 800个单元, 工况2复合板共划分5 400个单元, 工况3复合板共划分18 000个单元.为减小复合板矫直过程矫直辊与复合板的穿透现象, 设置矫直辊网格大小与复合板单元长度方向尺寸相同.
| 表 3 复合板不同网格密度划分 Table 3 Different mesh density of composite plate |
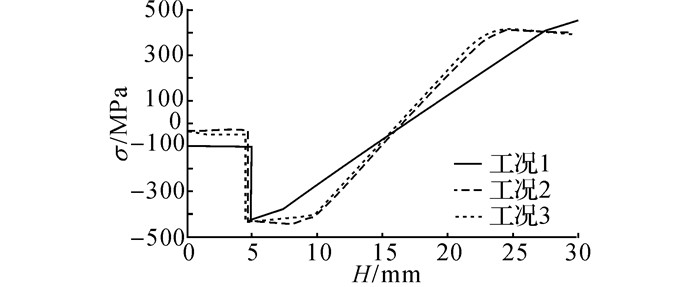
沿截面高度做路径, 提取应力值, 如图 12所示, 由图中可以看出, 工况2与工况3沿截面高度的应力值相差较小, 而工况1与其他2种工况的结果相差较大.工况1的网格密度过大, 工况2的网格密度基本满足计算精度要求, 进一步提高网格密度结果变化不大.3种工况在四核服务器下的运算时间t如表 3所示, 表中Le为板长方向单元尺寸,he为板厚方向单元尺寸,综合运算成本与运算精度, 工况2的网格划分最为合理.
|
图 12 不同网格密度矫直过程板长方向正应力 Fig. 12 Length direction normal stress of plate with different grid density during leveling |
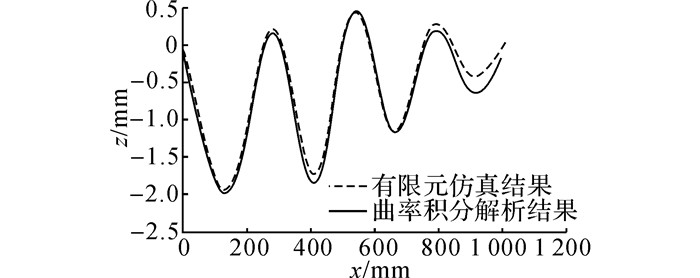
至此, 复合板矫直过程有限元仿真模型建立完成.提取仿真模型矫直过程的中性层曲线并与曲率积分的解析结果相比较, 如图 13所示.由图中可以看出, 2种方法得到的矫直过程中性层曲线的接触点位置基本重合.倒数第2辊处的挠度差值最大, 为0.25 mm, 其余位置的挠度差值均较小, 小于0.15 mm, 2种方法计算得到的矫直过程中性层曲线差别较小.虽然曲率积分法与有限元方法均能对复合板矫直过程进行解析, 但曲率积分法忽略次要因素对矫直过程的影响, 主要关注矫直过程长度方向正应力与长度方向曲率的变化情况, 运算时间远远小于有限元方法, 如上文的算例, 采用有限元获得合理的结果需要100 min, 而采用曲率积分法进行计算仅需要几秒完成, 这使得曲率积分法可用于板材矫直过程控制系统.而曲率积分法不考虑矫直过程类似摩擦与接触应力对复合板表面影响这些问题, 这些问题依赖于其他理论或有限元方法的解决.
|
图 13 有限元法与曲率积分法矫直过程几何中性层曲线比较 Fig. 13 Comparison of geometric neutral layer during leveling of finite element method and curvature integration method |
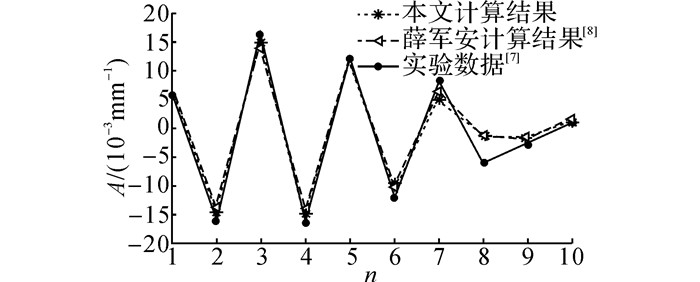
当覆层与基层采用相同的力学参数时, 即能采用本文的曲率积分模型对单一材料板材的辊式矫直过程进行解析.采用曲率积分法, 基于实验条件, 矫直辊数为10, 半径为20 mm, 辊距42 mm, 入、出口压下量分别是1.2和-0.2 mm, 钢板厚度0.8 mm, 屈服应力与弹性模量分别为180和210 GPa, 采用理想弹塑性材料模型, 将本文计算结果与文献[8]计算结果及实验结果进行比较, 如图 14所示.由图中可看出, 除第7、8辊外本文与实验数据[7]矫直过程各辊的反弯曲率相差小于0.001 mm-1, 而本文与薛军文[8]论文计算结果在各辊下差值均较小, 小于0.001 mm-1.
|
图 14 曲率积分法计算结果与实验数据比较 Fig. 14 Comparison of experimental results and numerical results with curvature integration method |
综上, 通过将解析结果与有限元仿真结果与实验数据相对比, 本文的曲率积分法被证明是有效的, 可对复合板矫直过程进行精确的解析.
4 计算结果与分析选取钢-铝复合板的辊式矫直过程作为研究对象, 板材力学性能如表 1所示, 矫直工艺如表 2所示, 板材初始曲率为0.000 14 mm-1.为说明双金属复合板辊式矫直过程与单一材料板材差异, 选取同初始曲率、同厚度、同矫直工艺、材料为基层材料板材的辊式矫直过程作为参照.
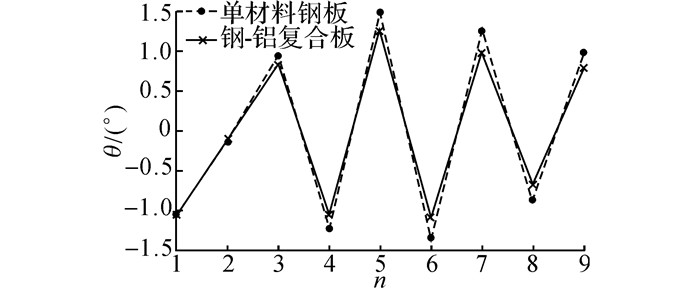
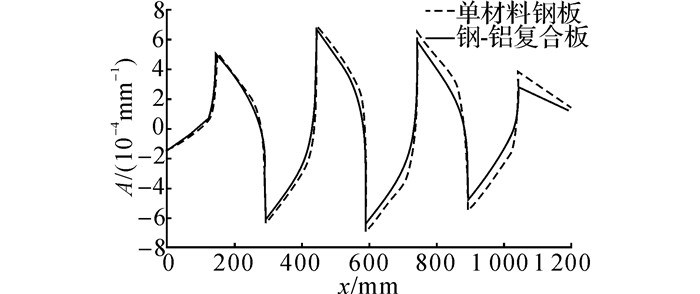
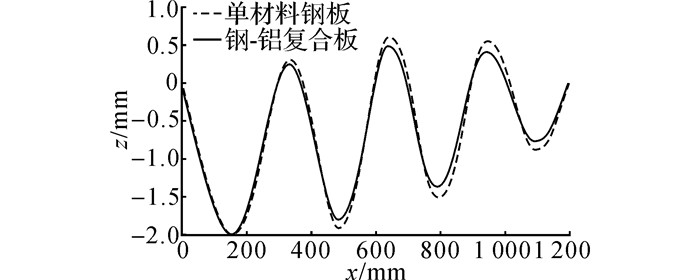
钢-铝复合板与同厚度碳钢板在矫直过程中接触倾角、弯曲曲率和板材曲线的对比如图 15、16、17所示.图 15中首辊接触倾角为负值的原因是由于曲率积分解析过程中, 不考虑板材自重的影响, 板材在矫直过程产生翘曲导致首辊与板材接触点位置落在首辊最高点后方, 表现为滞后接触.图 16中x向起始坐标处对应的曲率即为板材的初始曲率, 终点处对应的曲率即为矫后残留曲率.由图中可以看出, 在相同矫直工艺下, 钢-铝复合板各辊下的接触倾角、弯曲曲率、有效压下量均略小于碳钢板的, 且差值随着弯曲次数的增加呈增大的趋势.
|
图 15 碳钢板与钢-铝复合板矫直过程接触倾角比较 Fig. 15 Contrast of contact angles of carbon steel plate and steel clad aluminum composite plate during leveling |
|
图 16 碳钢板与钢-铝复合板矫直过程曲率分布比较 Fig. 16 Contrast of curvature distribution of carbon steel plate and steel clad aluminum composite plate during leveling |
|
图 17 碳钢板与钢-铝复合板矫直过程中性层曲线比较 Fig. 17 Contrast of neutral layer curves of carbon steel plate and steel clad aluminum composite plate during leveling |
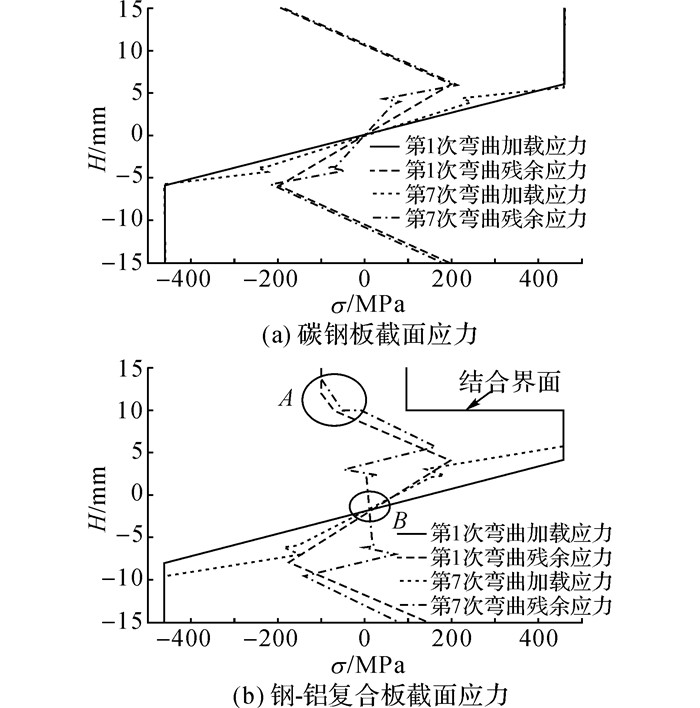
碳钢板和钢-铝复合板矫直过程中第1次和第7次弯曲的截面加载应力和残余应力分别如图 18(a)、(b)所示.由图中可以看出, 钢-铝复合板在弯曲与回弹过程中在结合界面处的应力是不连续的, 同时铝层在回弹后处于反向屈服状态, 如图 18(b)中A区域所示.钢-铝复合板弯曲过程的加载应力和残余应力的中性层在几何中性层下方, 存在明显的中性层偏移现象, 如图 18(b)中B区域所示.图中第7次弯曲的残余应力, 即板材矫直后最终的残余应力.结合图 16可以看出2种板材矫直过程的弯曲曲率差别不大, 但矫后钢-铝复合板碳钢层的残余应力要明显小于碳钢板的残余应力.矫后复合板铝层表面残余应力较大, 这对于复合板的服役性能有不利的影响, 需要后续工艺的处理.
|
图 18 碳钢板与钢-铝复合板矫直过程截面应力 Fig. 18 Section stress of carbon steel plate and steel clad aluminum composite plate during leveling |
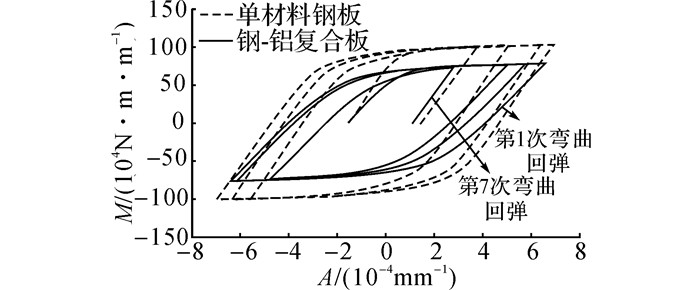
钢-铝复合板和碳钢板矫直过程的M-A关系如图 19所示.从图中可以看出, 随着反弯次数的增加, 钢-铝复合板回弹过程的曲线斜率逐渐增大, 这说明复合板的回弹效应在逐步减弱, 且具有累积效应, 这正是由于钢-铝复合板回弹过程发生了反向屈服.钢-铝复合板矫直过程的弯矩约为碳钢板的2/3, 且M-A曲线斜率要小于碳钢板的, 即是在相同弯矩增量下, 钢-铝复合板经历更大的曲率变化量.从矫直过程的M-A关系来看, 钢-铝复合板更易矫直.
|
图 19 碳钢板与钢-铝复合板矫直过程M-A曲线 Fig. 19 Moment-curvature relationship curves of carbon steel plate and steel clad aluminum composite plate during leveling |
(1) 双金属复合板层间材料力学性能不同, 在弯曲过程中复合板截面应力分布复杂, 同时会出现中性层偏移与反向屈服等现象, 这些造成了双金属复合板辊式矫直过程的力学行为不同于单一材料板材, 如发生反向屈服的板材进行反弯时将没有弹性加载段, 而是经过弹塑性卸载后直接进入弹塑性加载.
(2) 对矫直区间弹性段与弹塑性段采用不同的曲率变化量积分值求解方法, 可以实现对双金属复合板曲率积分模型的求解.对于弹性段, 根据弹性加载的弯矩-曲率关系积分求解曲率变化量积分值;对于弹塑性段, 将其按曲率差值等分离散后求解曲率变化量积分值, 并根据卸载过程是否发生反向屈服将弹塑性段分为2种情况分别讨论.
(3) 通过对复合板矫直过程的有限元仿真并比较矫直过程的中性层曲线能对曲率积分法进行验证, 采用曲率积分法的计算时间远小于有限元方法, 但对矫直过程关键参数如矫直过程应力与曲率的预测精确度较高.
(4) 钢-铝复合板矫直过程的接触倾角与弯曲曲率和相同工艺下基层材料的碳钢板矫直过程差别有限, 但矫直过程的弯矩与矫后残余应力差别较大, 钢-铝复合板矫直过程的弯矩与钢层的残余应力要明显小于碳钢板, 但复合板铝层表面在矫后处于反向屈服状态.复合板的反向屈服现象会减弱板材辊式矫直过程中的回弹效应, 且具有累积效应.
| [1] | WU Chih-Ping, LIU Yan-Cheng. A review of semi-analytical numerical methods for laminated composite and multilayered functionally graded elastic/piezoelectric plates and shells[J]. Composite Structures, 2016, 147: 1–15. DOI:10.1016/j.compstruct.2016.03.031 |
| [2] |
刘环, 郑晓冉. 层状金属复合板制备技术[J].
材料导报:纳米与新材料专辑, 2012, 26(2): 131–134.
LIU Huan, ZHEN Xiao-ran. The manufacturing technique of clad metals sheet[J]. Materials Review: Album of Nanomaterials and New Materials, 2012, 26(2): 131–134. |
| [3] | 崔甫. 矫直原理与矫直机械[M]. 2版. 北京: 冶金工业出版社, 2002: 157-160. |
| [4] | CHEN Wei-hua, LIU Juan, CUI Zhen-shan, et al. A 2.5-dimensional analytical model of cold leveling for plates with transverse wave defects[J]. Journal of Iron & Steel Research International, 2015, 22(8): 664–671. |
| [5] | PHILIPPAUS V, MAILLLARD S. Modern levelers for advanced plate grade[J]. Iron Steel Review, 2009, 52(10): 144. |
| [6] | KADOTA K, MAEDA R. A model of analysis of curvature in leveling process-numeric study of roller leveling process[J]. Journal of Japan Society for Technology of Plasticity, 1993, 34(1): 690–697. |
| [7] | HIGO T, MATSUMOTO H, OGAWA S. Effects of numerical expression of stress-stain curve on curvature of material of roller leveling process[J]. Journal of Japan Society for Technology of Plasticity, 2002, 43(496): 439–443. |
| [8] |
薛军安. 中厚板矫直过程的理论分析及其控制系统[D]. 沈阳: 东北大学, 2009: 34-43.
XUE Jun-an. Theoretical analysis for plate leveling process and its control system[D]. Shenyang: Northeastern University, 2009: 34-43. http://cdmd.cnki.com.cn/article/cdmd-10145-1012300277.htm |
| [9] | LIU Zhi-fang, WANG Yong-qin, YAN Xing-chun. A new model for the plate leveling process based on curvature integration method[J]. International Journal of Mechanical Sciences, 2012, 54: 213–224. DOI:10.1016/j.ijmecsci.2011.10.011 |
| [10] |
管奔, 臧勇, 逄晓男, 等. 矫直过程截面复杂反弯的应力分布与反弯特性解析[J].
中南大学学报:自然科学版, 2012, 43(5): 1740–1745.
GUAN Ben, ZANG Yong, PANG Xiao-nan, et al. Stress distribution and reverse bending behavior of section during roller leveling process[J]. Journal of Central South University: Science and Technology, 2012, 43(5): 1740–1745. |
| [11] |
刘东冶, 何安瑞, 王海滨, 等. 塑性强化材料矫直反弯特性研究[J].
机械工程学报, 2015, 51(8): 76–83.
LIU Dong-ye, HE Rui-an, WANG Hai-bin, et al. Reverse bending research of leveling on plastic hardening material[J]. Journal of Mechanical Engineering, 2015, 51(8): 76–83. |
| [12] | LI CUI, SHI Quan-qiang, LIU Xiang-hua, HU Xian-lei. Residual curvature of longitudinal profile plate roller in leveling process[J]. Journal of Iron and Steel Research, 2013, 20(10): 23–27. DOI:10.1016/S1006-706X(13)60171-5 |
| [13] | SUN Xian-jun, TAO Jie, GUO Xun-zhong. Bonding properties of interface in Fe/Al clad tube prepared by explosive welding[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(10): 2175–2180. DOI:10.1016/S1003-6326(11)60991-6 |
| [14] | 余同希, 章亮炽. 塑性弯曲理论及其应用[M]. 北京科学出版社, 1992: 23-27 |



