齿轮传动广泛应用于工业生产的各个领域, 齿面摩擦激励是齿轮啮合内部激励的重要影响因素, 不仅会加速齿轮的磨损、点蚀和裂纹的萌生[1], 还会影响传动系统的动态特性.接触线长度是影响摩擦激励的主要因素, 对于齿轮尤其是对于斜齿轮而言, 接触线长度变化是一个非常重要的内部激励源[2], 它会影响齿轮副时变啮合刚度、啮合阻尼、摩擦力及摩擦力矩.Lundvall等[3]通过建立一对直齿轮有限元模型, 研究齿面摩擦对齿轮传动特性的影响.研究结果表明:当考虑齿面摩擦后, 输入输出扭矩不再是一个恒定的值, 同时还会引入一个时变的传动误差.由此可见, 对齿轮摩擦激励的研究具有重大的理论意义和工程应用价值.
对于斜齿轮接触线长度计算国内外学者已经做过不少研究工作, 并取得了大量的成果.Smith等[4]阐述了接触线在啮合面内的变化主要是由于齿轮的旋转导致的, 并计算了接触线长度的最大值和最小值.Kiyono等[5]研究结果表明, 随着螺旋角的增大, 接触线条数变多, 即重合度变大, 因此相比直齿轮, 斜齿轮可以有效地控制系统的振动.Chinmaya等[6]将斜齿轮接触区内一个齿的接触线长度变化以分段函数的形式进行表示.李文良等[7]针对Chinmaya在计算时变接触线算法存在计算条件的问题, 推导了适用于不同重合度下啮合面形状和不限制同时参与啮合的接触线条数的通用公式.Jiang等[8]计算了齿轮中心线不平行时的接触线长度.
时变接触线长度将直接影响齿面摩擦力及摩擦力矩大小, 摩擦力及摩擦力矩的计算方法也有学者做过较多的研究.李文良等[9]针对船用斜齿轮, 研究了时变接触线对齿面摩擦力及摩擦力矩的影响.当考虑时变摩擦系数时, Vaishya等[10]通过判断齿面相对滑动速度方向来确定符号函数取值, 确定摩擦力方向.Howard等[11]考虑线性摩擦系数和接触力的变化, 计算了渐开线齿廓齿面的摩擦力.Rao等[12]研究齿面摩擦力与主、从动轮的转动惯量、传动比以及压力角有一定的关联性.王连生等[13]综合考虑齿轮搅油阻力、齿轮润滑油膜与接触齿面之间的摩擦力引起的齿轮阻滞力矩变化对变速箱齿轮敲击振动特性的影响.刘长钊等[14]考虑齿面变摩擦系数计算了斜齿轮副摩擦力及摩擦力矩, 为动力学分析提供了前提条件.
以上文献在未考虑齿轮副制造、装配误差时对斜齿轮接触线长度、摩擦力及摩擦力矩进行了研究.目前, 也有部分学者针对存在几何偏心误差的齿轮进行了动力学特性研究, 马辉等[15-16]通过有限单元法研究了考虑几何偏心的斜齿轮耦合转子系统的振动响应, 但该模型均未考虑摩擦力及摩擦力矩的影响.关于此类齿轮接触线、摩擦激励的研究还鲜有报道, 本文将以一级斜齿轮副为研究对象, 提出考虑几何偏心误差时的斜齿轮副摩擦激励计算方法.通过建立斜齿轮副传动几何模型, 分析偏心误差引起的中心距变化对动态啮合角、传动比及瞬态节圆半径的影响;基于建立的几何模型将各啮合齿对接触线在啮合面内进行分段并叠加计算接触线总长度, 随后, 将各段接触线以瞬态节线为界限分割为2段, 分别计算各段接触线的摩擦力, 以各段接触线中点为摩擦力的作用点, 计算摩擦力矩;以某对斜齿轮为例, 通过数值仿真计算考虑偏心误差时接触线总长度、摩擦力及摩擦力矩, 并与无误差时的结果进行对比.
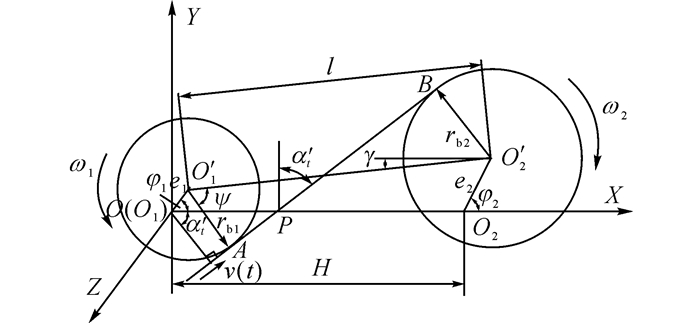
1 考虑偏心误差时斜齿轮副几何模型当存在偏心误差时的一级斜齿轮副几何模型如图 1所示, 绝对坐标系OXYZ原点O位于主动轮旋转中心O1处, O2为从动轮旋转中心, O′1和O′2分别为主动轮和从动轮几何中心, e1和e2分别为主、从动轮偏心量, H为主、从动轮安装中心距, l为实际几何中心距, rb1和rb2为两齿轮基圆半径, ψ为主从动轮几何中心线与啮合线之间夹角的余角, 随时间t变化, φ1和φ2为两齿轮偏心初始位置角, γ为齿轮副方位角, 齿轮副啮合线与基圆相切于点A、B, 啮合线与直线O1O2交于P点, α′t为啮合线与Y轴正向的夹角, 也是偏心齿轮副的动态啮合角.
|
图 1 含偏心误差的斜齿轮副几何模型 Fig. 1 Geometric model of helical gear with geometric eccentricity |
主、从动轮齿数分别为z1、z2, 主动轮逆时针转动, 转速为ω1, 从动轮转速为ω2, 任意时刻t下, O′1和O′2可表示为
| $ \begin{array}{*{20}{c}} {{{O'}_1}\left( {{x_1},{y_1}} \right),{{O'}_2}\left( {{x_2},{y_2}} \right);}\\ {\left. \begin{array}{l} {x_1} = {e_1}\cos \left( {{\varphi _1} + {\omega _1}t} \right),\\ {y_1} = {e_1}\sin \left( {{\varphi _1} + {\omega _1}t} \right),\\ {x_2} = {e_2}\cos \left( {{\varphi _2} - {\omega _2}t} \right) + H,\\ {y_2} = {e_2}\sin \left( {{\varphi _2} - {\omega _2}t} \right). \end{array} \right\}} \end{array} $ | (1) |
实际几何中心距为
| $ l = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} . $ | (2) |
故由几何关系可得角ψ的表达式.
| $ \psi = \arccos \left( {\frac{{a\cos {\alpha _{\rm{t}}}}}{l}} \right). $ | (3) |
式中:a为理论中心距, αt为端面压力角.
齿轮副方位角γ即为几何中心线与水平方向的夹角, 可表示为
| $ \gamma = \arctan \left( {\frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right). $ | (4) |
由图 1中的几何关系可得
| $ {{\alpha '}_{\rm{t}}} = \psi - \gamma . $ | (5) |
动态啮合线AB斜率为
| $ k = \frac{1}{{\tan {{\alpha '}_{\rm{t}}}}}. $ | (6) |
O′1和O′2同时也是主、从动轮基圆圆心, 故两基圆方程可分别表示为
| $ \left. \begin{array}{l} {\left( {x - {x_1}} \right)^2} + {\left( {y - {y_1}} \right)^2} = r_{{\rm{b1}}}^2\\ {\left( {x - {x_2}} \right)^2} + {\left( {y - {y_2}} \right)^2} = r_{{\rm{b2}}}^2 \end{array} \right\}. $ | (7) |
动态啮合线与基圆相切于动点A(x01, y01)和B(x02, y02), 由内公切线性质可得
| $ - \frac{{{x_{01}} - {x_1}}}{{{y_{01}} - {y_1}}} = - \frac{{{x_{02}} - {x_2}}}{{{y_{02}} - {y_2}}} = k. $ | (8) |
联立式(7)、(8) 可得
| $ \begin{array}{l} {x_{01}} = {x_1} + \frac{k}{{\sqrt {{k^2} + 1} }}{r_{{\rm{b1}}}}\\ {y_{01}} = {y_1} - \frac{{{r_{{\rm{b1}}}}}}{{\sqrt {{k^2} + 1} }}\\ {x_{02}} = {x_2} - \frac{k}{{\sqrt {{k^2} + 1} }}{r_{{\rm{b2}}}}\\ {y_{02}} = {y_2} + \frac{{{r_{{\rm{b2}}}}}}{{\sqrt {{k^2} + 1} }}. \end{array} $ | (9) |
动态啮合线与两齿轮回转中心连线交于动点P, 则通过两切点A和B的动态啮合线方程可表示为
| $ \frac{{y - {y_{02}}}}{{x - {x_{02}}}} = \frac{{{y_{02}} - {y_{01}}}}{{{x_{02}} - {x_{01}}}}. $ | (10) |
令y=0即可得P点横坐标为
| $ {x_P} = {x_{02}} - {y_{02}}\frac{{{x_{02}} - {x_{01}}}}{{{y_{02}} - {y_{01}}}}. $ | (11) |
求得偏心齿轮副瞬时传动比i12, 即
| $ {i_{12}} = \frac{{{\omega _1}}}{{{\omega _2}}} = \frac{{H - {x_P}}}{{{x_P}}}. $ | (12) |
当给定输入ω1为恒定值时, 联立式(1)~(12), 可计算随时间t变化的ω2值.
图 1中v(t)为齿轮在任意瞬时t时, 在啮合线方向的速度, 其表达式如下.
| $ v\left( t \right) = {\omega _1}{x_P}\cos \psi . $ | (13) |
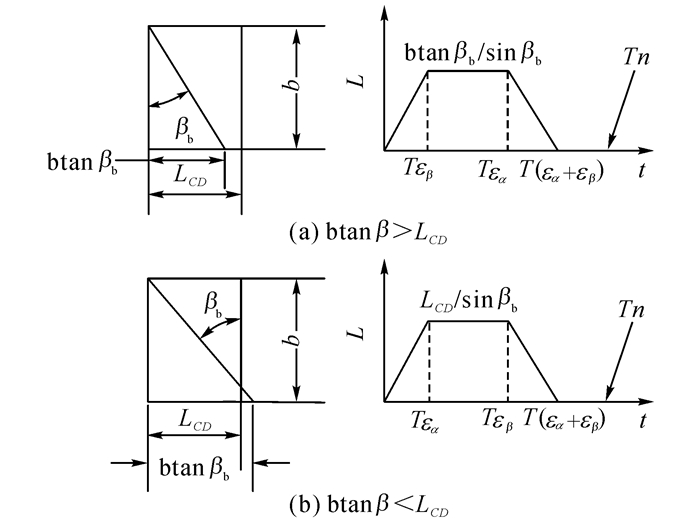
在一个啮合周期内, 理想无误差斜齿轮接触线长度变化示意图如图 2所示.图 2中, b为啮合齿宽, L为动态接触线长度,LCD为齿轮副端面实际啮合线长度.由图 2(a)可知, 当btan βb<LCD时, 端面重合度εα大于轴向重合度εβ;而当btanβb>LCD时, 端面重合度εα将小于轴向重合度εβ, 如图 2(b)所示, 其中βb为基圆螺旋角.T为斜齿轮副的啮合周期, n为大于总重合度的最小整数.
|
图 2 理想无误差斜齿轮单齿接触线长度 Fig. 2 Single-gear contact line length of helical gear without errors |
斜齿轮的端面重合度和轴向重合度分别为
| $ {\varepsilon _\alpha } = \frac{{{L_{CD}}}}{{{P_{\rm{t}}}}},{\varepsilon _\beta } = \frac{{b\tan {\beta _b}}}{{{P_{\rm{t}}}}}. $ | (14) |
式中:Pt为斜齿轮端面法向齿距.
当斜齿轮存在偏心误差时, 由式(2) 可知, 几何中心距l随时间变化而变化.当中心距变大时, 端面重合度变小, 当中心距变小时, 端面重合度变大, 而轴向重合度不发生变化.当主从动轮均存在偏心误差时, 两齿轮几何中心均在变化, 从而导致几何中心距的变化.根据重合度关系可知, 总重合度越大, 接触线长度越长;反之, 接触线长度越短.
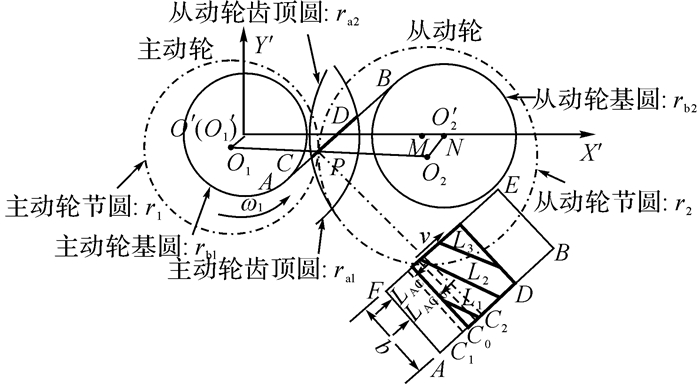
为了便于计算接触线长度的变化, 建立如图 3所示的动坐标系O′X′Y′, 主动轮几何中心O1′固定在动坐标系原点O′上, 从动轮几何中心O2′在X′轴上, 由于几何中心距随时间t在变化, 故O′2在M点和N点之间移动.O1、O2为旋转中心, 主从动轮齿顶圆柱截啮合面可以得到图 3中所示实际啮合面长度CD.将整个啮合面投影至水平面上, 如图中ABEF所示, L1、L2、L3…Ln分别表示各啮合齿对的接触线.
|
图 3 偏心误差斜齿轮动态啮合线及动态接触线 Fig. 3 Dynamic mesh line and contact line of helical gear with geometric eccentricity |
在参考坐标系O′X′Y′下, 主动轮的齿顶圆和基圆圆心位置相对于参考坐标系保持不变, 而从动轮齿顶圆和基圆圆心位置在M点和N点之间变化.此时, C点在其两侧虚线C1和C2之间随从动轮和基圆位置变化而移动, 如图 3所示, C0点为初始位置, 当t=0时, 轮齿刚好啮入, 此时在C0点处的接触线长度为0.虚线C1、C2所在位置为从动轮齿顶圆柱与啮合面交线的极限位置.当几何中心距变大时, 从动轮几何中心往N向移动, C点向C2点移动, 接触线总长度减少;当几何中心距变小时, 从动轮几何中心往M向移动, C点向C1点移动, 接触线总长度增大.图中LAC0表示初始位置时点A、C0的距离, LAC表示任意位置时点A、C的距离.
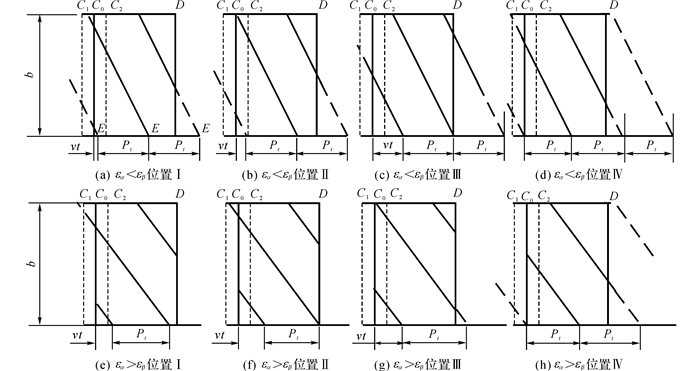
在一个啮合周期内可以将接触线不同的位置分为如图 4所示的4种不同的接触状态, 其中(a)~(d)为端面重合度小于轴向重合度的情况, (e)~(h)为端面重合度大于轴向重合度的情况.由图可知, 单齿接触线长度首先逐渐增大, 而后保持定值不变, 最后逐渐减小至0.
|
图 4 2种不同重合度斜齿轮接触线位置 Fig. 4 Contact lines location of helical gear with two different contact ratios |
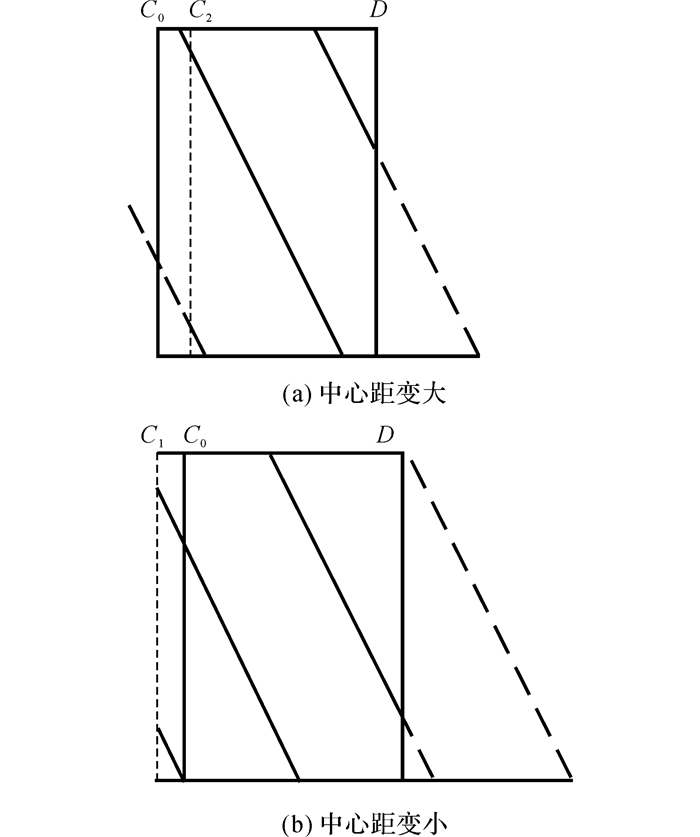
当几何中心距发生变化时, 接触线长度变化示意图如图 5所示.当几何中心距变大时, C0点向C2侧移动, 此时LAC≥LAC0, 重合度变小, 轮齿推迟进入啮合, 如图 5(a)所示;当几何中心距变小时, C0点向C1侧移动, 此时LAC≤LAC0, 重合度变大, 轮齿提前进入啮合, 如图 5(b)所示.
|
图 5 主从动轮中心距变大和变小时接触线长度示意图 Fig. 5 Contact line of pinion change with center distance become large or small |
由于啮合线长度变化具有周期性, 在任意时刻t, 第i对啮合齿接触线下端E点距C点的距离可表示为
将图 4中不同位置的接触线长度以分段函数的形式表示如下:
| $ {L_i} = \left\{ \begin{array}{l} {D_i}/\sin {\beta _b},\\ \min \left( {b\tan {\beta _b},{L_{CD}}} \right)/\sin {\beta _b},\\ \left[ {{L_{CD}} - \left( {{D_i} - b\tan {\beta _b}} \right)} \right]/\sin {\beta _b},\\ 0. \end{array} \right. $ | (15) |
式(15) 各段的取值范围如下:
| $ \left. \begin{array}{l} 0 \le {D_i} < \min \left( {b\tan {\beta _b},{L_{CD}}} \right)\\ \min \left( {b\tan {\beta _b},{L_{CD}}} \right) \le {D_i} < \max \left( {b\tan {\beta _b},{L_{CD}}} \right)\\ \max \left( {b\tan {\beta _b},{L_{CD}}} \right) \le {D_i} < \left( {{L_{CD}} + b\tan {\beta _b}} \right)\\ {D_i} \ge \left( {{L_{CD}} + b\tan {\beta _b}} \right) \end{array} \right\} $ | (16) |
式中:
啮合齿对任意瞬时总接触线长度计算为
| $ L\left( t \right) = \sum\limits_{i = 0}^n {{L_i}\left( t \right)} . $ | (17) |
啮合轮齿在节线两侧滑动方向发生变化, 从而会导致摩擦力在节线两侧发生变化.定义节线右边接触线上的摩擦力方向为正, 左边为负;摩擦力矩以与旋转方向相同为正, 以相反为负.
本文在计算各啮合齿面摩擦力及摩擦力矩时, 将整个齿面的摩擦系数简化为恒定值, 每条接触线以节点为界限分割为2段, 并以各段接触线中点作为摩擦力的作用点, 计算各段接触线的摩擦力及摩擦力矩.实际齿面摩擦系数是时变的, 本文计算时摩擦系数取时变摩擦系数的平均值[8], 同时将接触压力简化为沿接触线均布.简化后摩擦力沿接触线均匀分布, 可视为作用点在各段接触线中点处的集中力, 与计算值相比, 实际的摩擦力在齿顶与齿根处偏小, 在节点附近偏大, 节点处的摩擦力为零, 实际接触压力在节线位置最大, 齿顶齿根处较小.
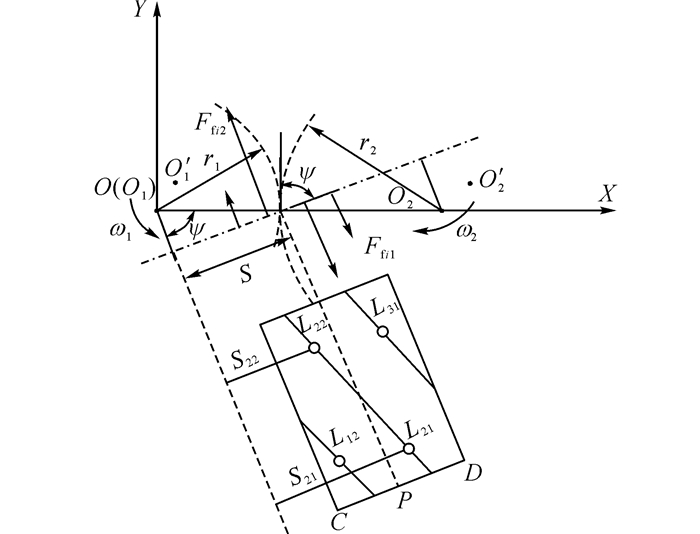
摩擦力方向及摩擦力臂示意图如图 6所示.图中O1、O2为旋转中心, O′1、O′2为几何中心, 坐标系OXY为固定坐标系.本文将齿轮接触线沿接触线长度方向上的压力分布简化为均布的, 各段接触线上的法向力为
| $ {F_{ij}} = \frac{F}{{L\left( t \right)}}{L_{ij}}. $ | (18) |
|
图 6 含偏心误差斜齿轮接触线摩擦力方向和摩擦力臂 Fig. 6 Friction force direction and their corresponding moment arm of helical gear with geometric eccentricity |
式中:Lij为第i对啮合齿的第j段接触线t时刻时的瞬时接触线长度,F为齿轮副总啮合力.
图 6中r1、r2分别为瞬时主从动轮节圆半径, 其中,
| $ {r_1} = {x_P},{r_2} = L - {r_1}. $ | (19) |
故点C和点P及点P和点D的距离LCP和LPD可分别为
| $ \begin{array}{*{20}{c}} {{L_{CP}} = \sqrt {{{\left( {{x_{01}} - {x_P}} \right)}^2} + y_{01}^2} - {L_{{\rm{AC}}}}}\\ {{L_{PD}} = {L_{CD}} - {L_{CP}}.} \end{array} $ | (20) |
则各段接触线摩擦力为
| $ {F_{{\rm{f}}i}} = \mu \frac{F}{{L\left( t \right)}}\left( {{L_{i1}} - {L_{i2}}} \right). $ | (21) |
式中:μ为平均齿面摩擦系数, Li1、Li2如下所示,
| $ \left. \begin{array}{l} {L_{i1}} = 0,{L_{i2}} = {L_i},0 \le {D_i} < {L_{CP}};\\ {L_{i1}} = \left( {{D_i} - {L_{CP}}} \right)/\sin {\beta _b},{L_{i2}} = {L_i} - {L_{i1}},\\ {L_{CP}} \le {D_i} < {L_{CP}} + b\tan {\beta _b};\\ {L_{i1}} = {L_i},{L_{i2}} = 0,\\ {L_{CP}} + b\tan {\beta _b} \le {D_i} < {L_{CD}} + b\tan {\beta _b};\\ {L_{i1}} = 0,{L_{i2}} = 0,\\ {D_i} \le {L_{CD}} + b\tan {\beta _b}. \end{array} \right\} $ | (22) |
总摩擦力为
| $ {F_{\rm{f}}} = \sum\limits_{i = 0}^n {{F_{{\rm{f}}i}}} . $ | (23) |
图中S为线段O1P在啮合线方向的投影, 可表示为
| $ S = {r_1}\sin \psi . $ | (24) |
本文计算摩擦力矩时, 将各段接触线的中点近似为摩擦力的作用点, 即为图 6中接触线上的小圆点.各段接触线摩擦力的摩擦力距为
| $ {T_{{\rm{f}}i}} = {F_{{\rm{f}}i2}}{S_{i2}} - {F_{{\rm{f}}i1}}{S_{i1}}. $ | (25) |
式中:Sij为摩擦力臂, 表达式为
| $ \left. \begin{array}{l} {S_{i1}} = 0,{S_{i2}} = S - {L_{CP}} + \frac{{{L_{i2}}\sin {\beta _b}}}{2},D < {D_i} < {L_{CP}};\\ {S_{i1}} = S + \frac{{{L_{i1}}\sin {\beta _b}}}{2},{S_{i2}} = S + \frac{{{L_{i2}}\sin {\beta _b}}}{2},\\ {L_{CP}} \le {D_i} < {L_{CP}} + b\tan {\beta _b};\\ {S_{i1}} = S + {L_{PD}} - \frac{{{L_{i1}}\sin {\beta _b}}}{2},{S_{i2}} = 0,\\ {L_{CP}} + b\tan {\beta _b} < {D_i} < {L_{CD}} + b\tan {\beta _b};\\ {S_{i1}} = 0,{S_{i2}} = 0,{D_i} \ge {L_{CD}} + b\tan {\beta _b}. \end{array} \right\} $ | (26) |
总摩擦力矩为
| $ {T_{\rm{f}}} = \sum\limits_{i = 0}^n {{T_{{\rm{f}}i}}} . $ | (27) |
针对一对含有偏心误差的斜齿轮进行数值仿真分析, 其具体参数如表 1所示.表中mn为法面模数, αn为法面压力角, β为螺旋角, ω为转速, P为输入功率.斜齿轮角αt和βb与表 1中给出的法面压力角αn, 螺旋角β关系式如下:
| $ tan{\alpha _t} = \tan {\alpha _{\rm{n}}}\sec \beta , $ | (28) |
| $ \sin {\beta _b} = \tan \beta \cos {\alpha _{\rm{t}}}. $ | (29) |
| 表 1 齿轮副详细几何参数及运动参数 Table 1 Specification of helical gear |
采用上述方法, 运用MATLAB编程求解该齿轮副接触线长度、摩擦力及摩擦力矩.
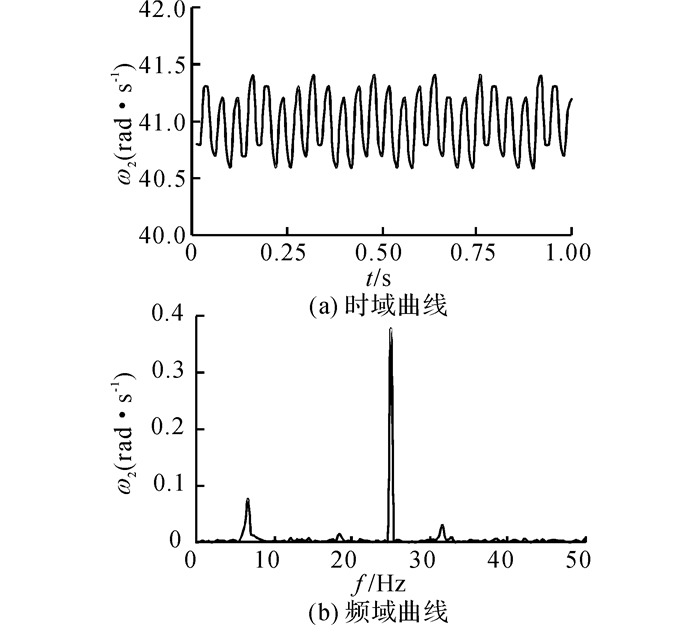
当取偏心量e1=e2=0.2 mm时, 可求解出从动轮转速ω2, 其时域和频域曲线如图 7所示.图中,f为频率从图 7(a)中可知, 当主从动轮均存在偏心误差时, 从动轮转速不再是恒定值, 而是瞬时变化的, 呈现一定的周期性, 其频域主要峰值出现在25 Hz以及6.5 Hz, 分别为输入转频以及输出转频.
|
图 7 从动轮转速时域频域曲线 Fig. 7 Time-domain and frequency-domain of gear speed |
由式(15)~(17) 可计算出存在偏心误差时斜齿轮接触线总长度.
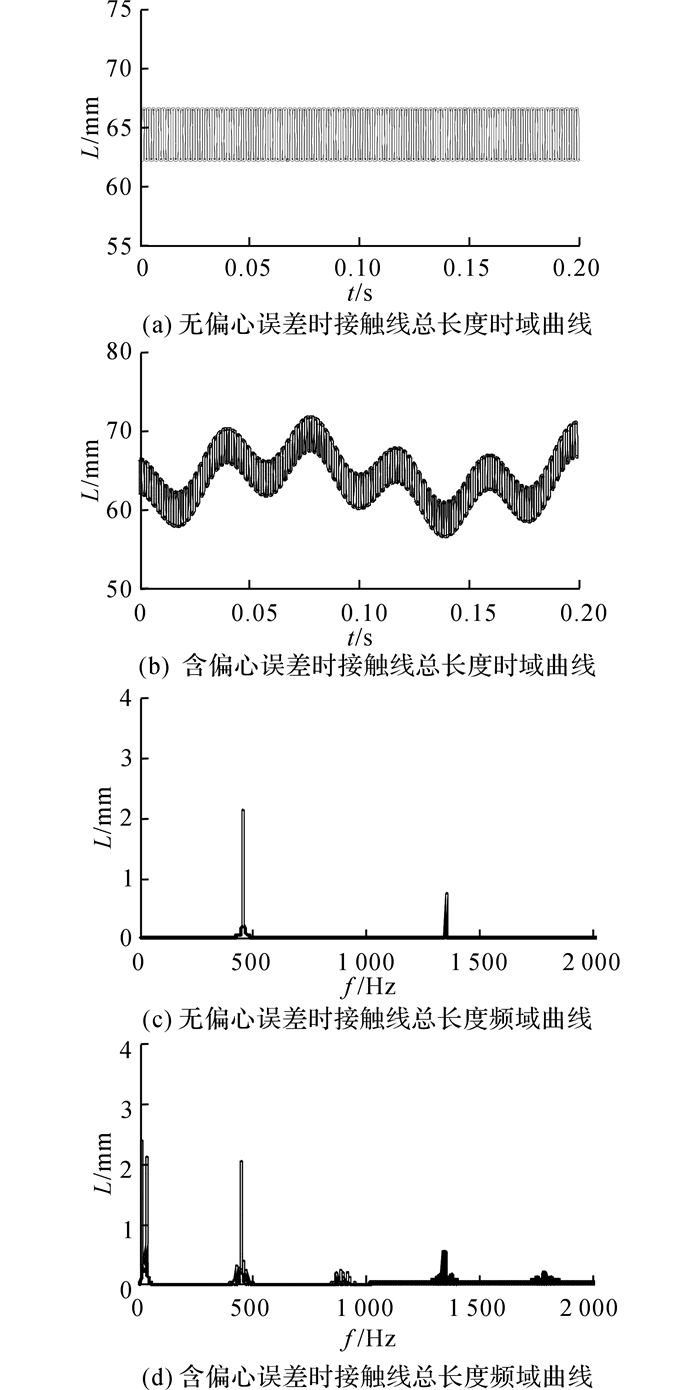
图 8(a)和8(b)给出了不含偏心误差和含偏心误差的斜齿轮副动态接触线总长度时域曲线图, 由图中可知, 两者均表现出一定的周期性, 但不考虑偏心误差时接触线总长度波动明显小于考虑偏心误差时, 其频域曲线表现出更加丰富的周期性, 由图 8(c)和8(d)可看出不含偏心误差的斜齿轮副动态接触线长度频域曲线仅仅在啮合频率450 Hz及其倍频处出现峰值, 而含偏心误差的频域曲线不仅在啮合频率及其倍频处出现峰值, 在主动轮和从动轮转频处(25 Hz和6.4 Hz)也出现峰值, 同时在啮合频率附近还出现了间隔为转频的边频频率, 这些频率的出现均是由齿轮的偏心误差引起的.当齿轮存在偏心误差时, 轮齿啮合过程中齿轮副中心距将发生改变, 接触线长度曲线的频谱图会产生以齿轮啮合频率为载波信号、偏心齿轮所在轴的转频为调制信号的调制现象[17], 出现图 8(d)中的边频带.
|
图 8 动态接触线总长度 Fig. 8 Total length of dynamic contact line |
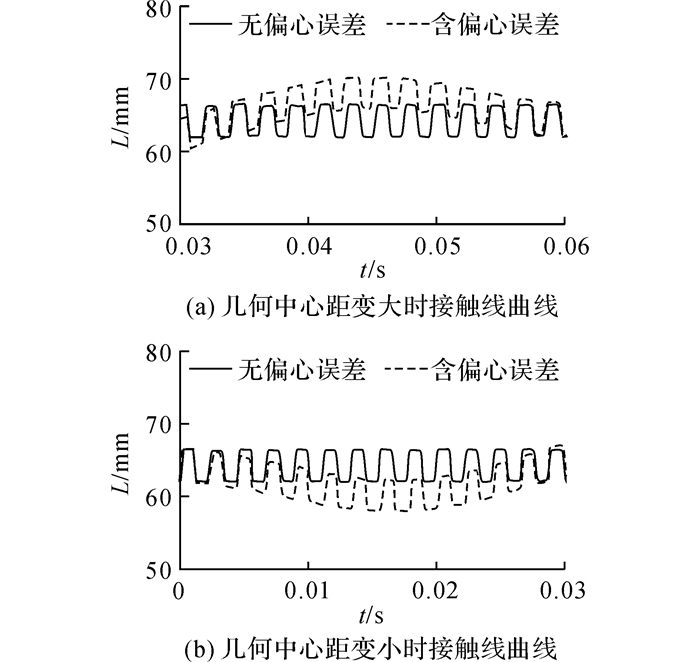
由以上分析可知, 含偏心误差的斜齿轮副几何中心距将发生变化, 从而会导致接触线长度的变化.当主从动轮几何中心距变大时, 齿轮副总重合度变小, 接触线总长度小于不考虑偏心误差时的总接触线长度, 如图 9(a)所示;当主从动轮几何中心距变小时, 齿轮副总重合度变大, 接触线总长度大于不考虑偏心误差时的总接触线长度, 如图 9(b)所示.
|
图 9 不同几何中心距时齿轮副动态接触线总长度 Fig. 9 Total length of dynamic contact line with different center distance |
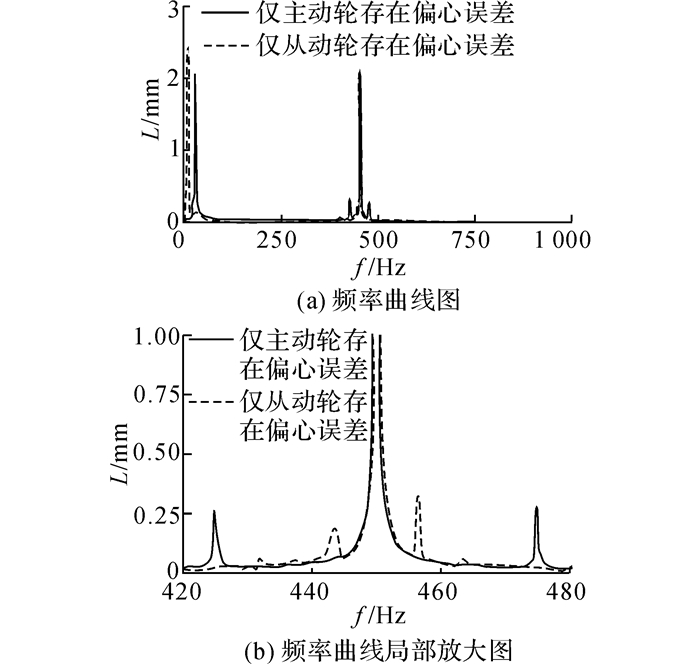
以上分析均是基于主从动轮都考虑偏心误差时的计算, 为了对比分析, 现仅考虑一个齿轮存在偏心误差, 而另外一个齿轮认为是理想无误差齿轮, 其频谱图如图 10所示.
|
图 10 含不同偏心误差时频域曲线对比 Fig. 10 Compare with differences error in pinion or gear |
由图 10(a)及 (b)可知, 无论主动轮还是从动轮出现偏心误差, 动态总接触线长度的频域曲线都会在啮合频率及其各次谐波处以及存在偏心误差齿轮所在轴的转频处出现峰值, 同时在啮合频率及其各次谐波频率两侧也会出现间隔为偏心齿轮所在轴转频的边频带.
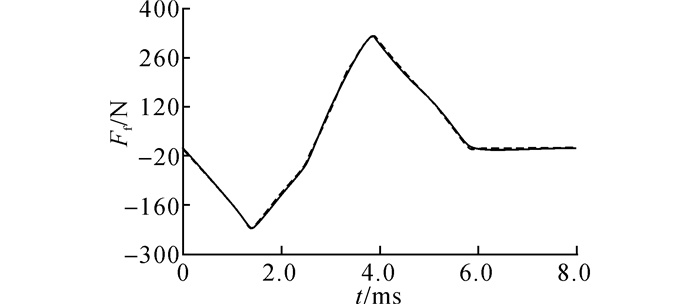
在计算接触线长度后, 根据式(18)~(23) 可计算该齿轮副的动态摩擦力.无误差齿轮单齿摩擦力曲线如图 11所示.由之前的分析可得当考虑齿轮偏心误差后, 齿轮可能推迟进入啮合或者提前进入啮合, 故考虑偏心后单齿摩擦力会比理想状态下略小或者略大, 但基本趋势应相同.由于偏心误差的影响, 每对齿单齿摩擦力并非完全相同, 故本文不一一列出.
|
图 11 无误差单齿摩擦力曲线 Fig. 11 Friction force of single-gear without errors |
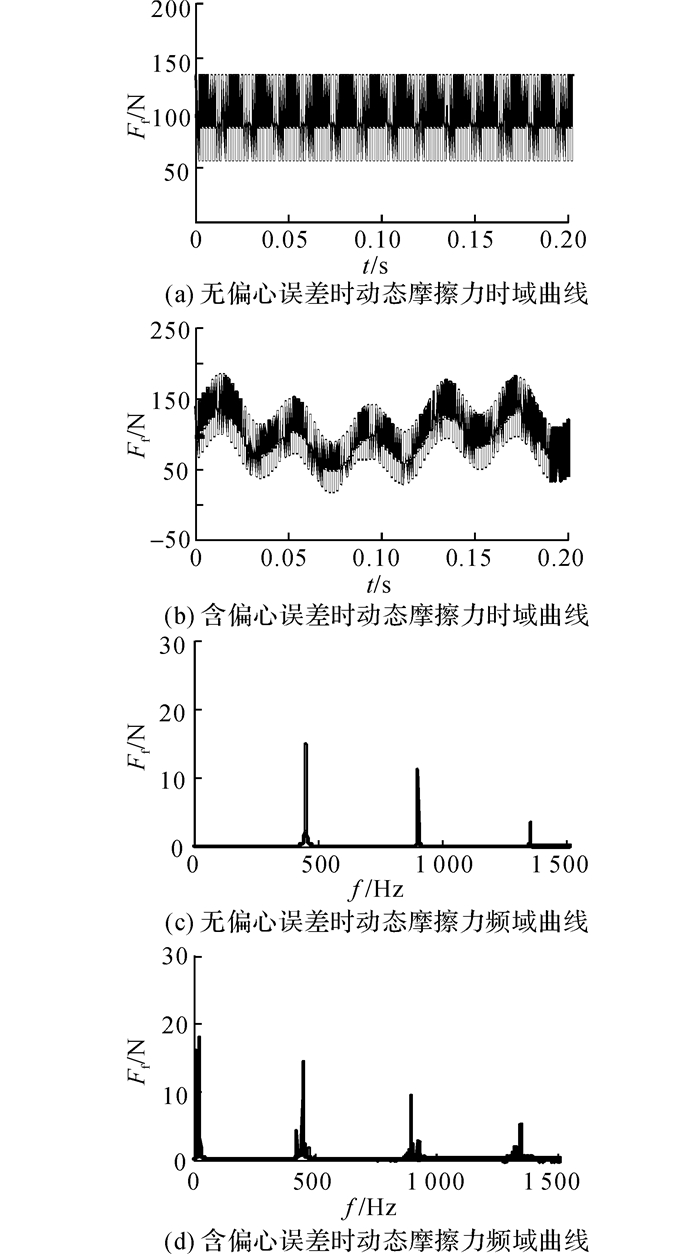
将各瞬时单齿摩擦力进行叠加, 可得总摩擦力.不考虑偏心误差和考虑偏心误差时总摩擦力时域频域曲线分别如图 12所示.由图可知, 考虑偏心误差和无偏心误差时域频域曲线规律与接触线长度规律相似, 当无偏心误差时, 其周期性较为单一, 只体现出啮合频率;而当考虑偏心误差后, 时域曲线周期性变得较为丰富, 从频域曲线可以看出, 不仅在啮合频率处出现峰值, 还在主从动轮的转频处也出现峰值, 同时, 啮合频率附近还出现了转频的边频.
|
图 12 动态摩擦力曲线 Fig. 12 The curve of dynamic friction force |
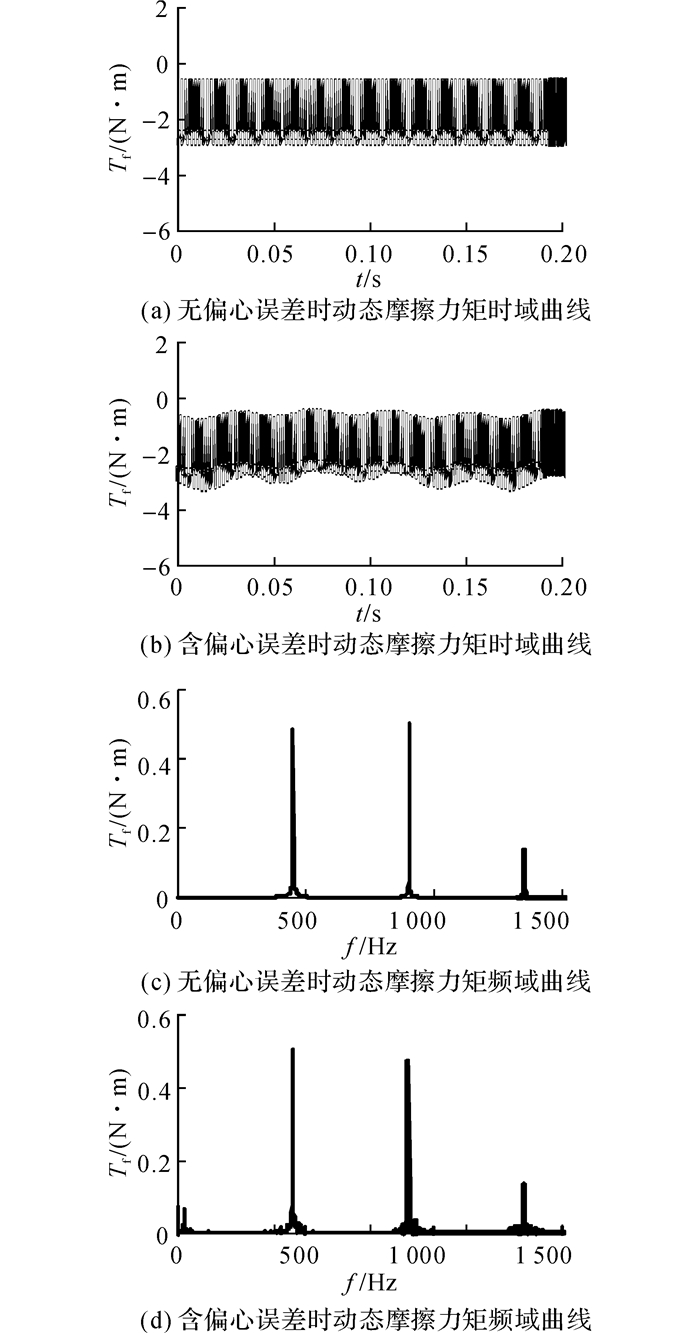
根据式(24)~(27), 分别计算无偏心误差和含偏心误差斜齿轮副摩擦力矩.其时域频域曲线如图 13所示.
|
图 13 动态摩擦力矩曲线 Fig. 13 The curve of dynamic friction torque |
由图可知, 考虑偏心误差前后, 摩擦力矩与摩擦力规律也较为相似.当不存在偏心误差时, 摩擦力矩周期成分单一, 仅在啮合频率处出现峰值;当考虑存在偏心误差时, 时域和频域曲线都变得比较复杂, 不仅在啮合频率及其各次谐波处出现峰值, 在主从动轮转频处也出现峰值, 同时在啮合频率及其各次谐波两侧还出现了边频现象.
5 结论(1) 考虑偏心误差的影响, 建立了斜齿轮副几何模型, 采用几何方法推导了含偏心误差的斜齿轮副动态啮合角、瞬时节圆半径以及瞬时传动比表达式, 并计算了主动轮恒定转速输入时, 从动轮转速变化规律.
(2) 通过将接触线划分为4个不同位置以分段函数形式表示各段接触线长度, 并进行叠加, 得出接触线总长度, 而后将各条接触线以节线为界分为两段, 分别计算各段摩擦力以及总摩擦力, 以各段接触线中点作为摩擦力的作用点计算各接触线摩擦力矩及总摩擦力矩.
(3) 对比分析含偏心误差与不含偏心误差的斜齿轮接触线长度、摩擦力及摩擦力矩的时域频域曲线, 结果表明:含偏心误差的斜齿轮接触线长度、摩擦力及摩擦力矩都比不含偏心误差时更加复杂, 其频域不仅在啮合频率及其倍频处出现峰值, 在输入及输出轴转频处也出现峰值, 同时还在啮合频率及其倍频两侧出现许多间隔为转频的边频, 影响了传动系统的平稳性.
由于在研究偏心误差时的斜齿轮摩擦激励的计算方法时, 对斜齿轮啮合模型进行了一定的简化, 理论计算结果会与实际值会存在一定的差异, 为精确计算含偏心误差斜齿轮的摩擦激励, 齿面摩擦系数、接触压力等都是需要进一步考虑的时变因素.
| [1] | FLASKER J, FAJDIGA G, GLODEZ S, et al. Numerical simulation of surface pitting due to contact loading[J]. International Journal of Fatigue, 2001, 23(7): 599–605. DOI:10.1016/S0142-1123(01)00020-2 |
| [2] | VELEX P, SAINSOT P. An analysis study of tooth friction excitations in errorless spur and helical gears[J]. Mechanism Machine Theory, 2002, 37(7): 641–658. DOI:10.1016/S0094-114X(02)00015-0 |
| [3] | LUNDVALL O, STROMBERG N, KLARBRING A. A flexible multi-body approach for frictional contact in spur gears[J]. Journal of Sound and Vibration, 2004, 278(3): 479–499. DOI:10.1016/j.jsv.2003.10.057 |
| [4] | SMITH J D. Gears and their vibration[M]. New York: Marcel Dekker, 1983. |
| [5] | KUBO A, KIYONO S. Vibrational excitation of cylindrical involute gears due to tooth form error[J]. Bulletin of JSME, 1980, 23(183): 1536–1543. DOI:10.1299/jsme1958.23.1536 |
| [6] | KAR C, MOHANTY A R. An algorithm for determination of time-varying frictional force and torque in a helical gear system[J]. Mechanism and Machine Theory, 2007, 42(4): 482–496. DOI:10.1016/j.mechmachtheory.2006.04.007 |
| [7] |
李文良, 王黎钦, 常山, 等. 斜齿轮时变接触线改进算法及螺旋角对接触线影响[J].
哈尔滨工程大学学报, 2013, 33(12): 1529–1533.
LI Wen-liang, WANG Li-qin, CHANG Shan, et al. The improved algorithm of time-varying contact line and influence on contact line with different helix angles[J]. Journal of Harbin Engineering University, 2013, 33(12): 1529–1533. |
| [8] | JIANG Han-jun, SHAO Yi-min. The influence of mesh misalignment on the dynamic characteristics of helical gears including sliding friction[J]. Journal of Mechanical Science and Technology, 2015, 29(11): 4563–4573. DOI:10.1007/s12206-015-1001-5 |
| [9] |
李文良, 王黎钦, 常山, 等. 船用斜齿轮时变接触线对齿面摩擦力及摩擦扭矩的影响研究[J].
船舶力学, 2013, 17(4): 418–424.
LI Wen-liang, WANG Li-qin, CHANG Shan, et al. Study on the impact of time-varying contact line on tooth surface friction force and friction torque of helical gear[J]. Journal of Ship Mechanics, 2013, 17(4): 418–424. |
| [10] | VAISHYA M, SINGH R. Sliding friction-induced non-linear and parametric effects in gear dynamic[J]. Journal of Sound and Vibration, 2001, 248(4): 671–694. DOI:10.1006/jsvi.2001.3818 |
| [11] | HOWARD I, JIA S. The dynamic modeling of a spur gear in mesh including friction and crack[J]. Mechanical Systems And Signal Processing, 2001, 15(5): 831–853. DOI:10.1006/mssp.2001.1414 |
| [12] | RAO A C. Gear friction coefficients and force[J]. Wear, 1979, 53(1): 87–93. DOI:10.1016/0043-1648(79)90219-9 |
| [13] |
王连生, 郝志勇, 郑康, 等. 考虑齿轮阻滞力矩的变速箱敲击噪声仿真与试验[J].
浙江大学学报:工学版, 2014, 48(5): 911–916.
WANG Lian-sheng, HAO Zhi-yong, ZHENG Kang, et al. Simulation and experiment in transmission gear rattle considering drag torque[J]. Journal of Zhejiang University: Engineering Science, 2014, 48(5): 911–916. |
| [14] |
刘长钊, 秦大同, 廖映华. 考虑齿面变摩擦系数的斜齿轮传动变速过程动力学分析[J].
振动与冲击, 2014, 33(24): 150–157.
LIU Chang-zhao, QIN Da-tong, LIAO Ying-hua. Dynamic model for a parallel-axis helical gears transmission system based on variable friction coefficient between contact teeth[J]. Journal of Vibration and Shock, 2014, 33(24): 150–157. |
| [15] |
马辉, 王奇斌, 黄婧, 等. 考虑几何偏心的斜齿轮耦合转子系统振动响应分析[J].
航空动力学报, 2013, 28(1): 16–24.
MA Hui, WANG Qi-bin, HUANG Jing, et al. Vibration response analysis of gear coupled rotor system considering geometric eccentric effect of helical gears[J]. Journal of Aerospace Power, 2013, 28(1): 16–24. |
| [16] | ZHANG Yi-min, WANG Qi-bin, MA Hui, et al. Dynamic analysis of three-dimensional helical geared rotor system with geometric eccentricity[J]. Journal of Mechanical Science and Technology, 2013, 27(11): 3231–3. DOI:10.1007/s12206-013-0846-8 |
| [17] | 丁康, 李巍华, 朱小勇. 齿轮及齿轮箱故障诊断实用技术[M]. 北京: 机械工业出版社, 2005: 08. |


