浮空器具有垂直起降、无动力悬停, 长时驻空及载荷能力大等优点, 近年来成为空间飞行器研究的热点[1].由于临近空间环境的低密度和飞艇自身低的飞行速度, 利用舵面来控制飞艇姿态角的效率很低, 因此Chen等[2]提出一类更有效的临近空间多螺旋桨组合浮空器模型, 可以满足临近空间飞行工况.
传统飞艇控制研究在建模时, 往往忽略螺旋桨动力学系统.螺旋桨的性能会极大地影响能源分配和续航时间[3].基于Chen等[2]的飞艇模型, 采用的控制方法是线性[4]或非线性[5], 均在飞艇“外循环”系统中直接把螺旋桨推力作为控制系统的输入.
在真实情况下, 螺旋桨推力取决于安装在螺旋桨上电机的扭矩命令信号[6].在同等转速下, 螺旋桨输出推力会随桨盘来流速度的不同而发生改变.同时, 由于来流的不稳定(突风、螺旋桨与艇身的互相干扰、螺旋桨与螺旋桨之间的互相干扰等)、模型误差的存在, 螺旋桨系统存在一定的推力损失.
本文针对高空螺旋桨特性, 建立螺旋桨动力学模型.利用基于非线性状态观测器的反馈控制方法, 分析螺旋桨动力学系统对飞艇“外循环”控制系统性能的影响.
1 飞艇动力学模型 1.1 不考虑螺旋桨系统的动力学模型
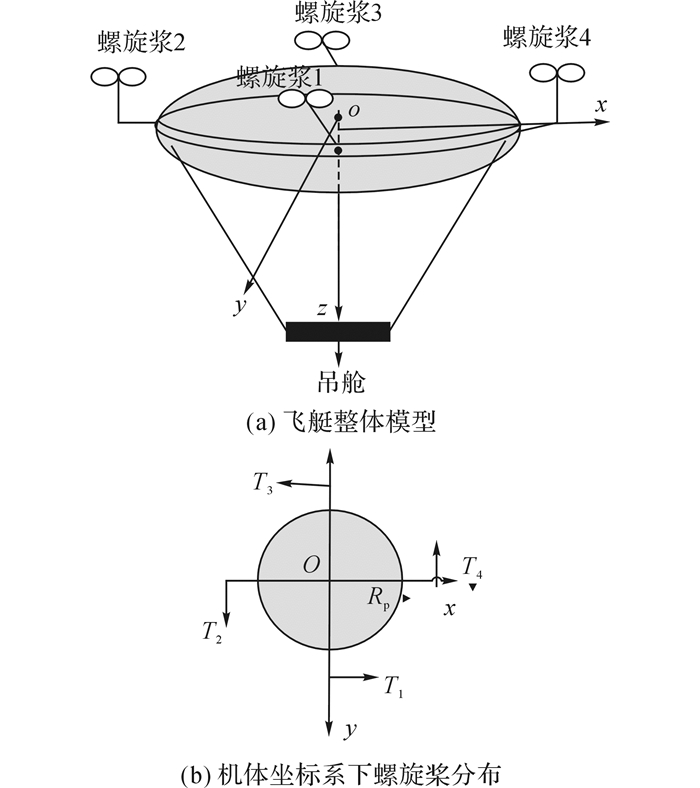
|
图 1 多螺旋桨组合浮空器结构图 Fig. 1 Structure of multi-vectored airship |
根据文献[2]可知, 多螺旋桨组合浮空器动力学方程为
| $ \mathit{\boldsymbol{M}}{\left( {\dot u, \dot v, \dot w, \dot p, \dot q, \dot r} \right)^{\rm{T}}} = {\mathit{\boldsymbol{F}}_{\rm{A}}} + {\mathit{\boldsymbol{F}}_{{\rm{GB}}}} + {\mathit{\boldsymbol{F}}_{\rm{I}}} + {\mathit{\boldsymbol{F}}_{\rm{T}}}. $ | (1) |
式中:M为质量矩阵;u、v、w、p、q、r为飞艇在机体坐标系下的线速度和角速度.式(1) 的右端项对应力和力矩, 包括重力和浮力的合力FGB、空气动力FA、柯氏力FI、螺旋桨矢量推力FT.空气动力FA为
| $ {\mathit{\boldsymbol{F}}_{\rm{A}}} = \left[{\begin{array}{*{20}{c}} {{F_{\rm{a}}} \cdot \cos \mathit{\Omega }}\\ {{F_{\rm{a}}} \cdot \sin \mathit{\Omega }}\\ {{q_\infty } \cdot {C_z} \cdot {S_{{\rm{ref}}}}}\\ {-{M_{\rm{a}}} \cdot \cos \mathit{\Omega }}\\ {{M_{\rm{a}}} \cdot \sin \mathit{\Omega }}\\ 0 \end{array}} \right]. $ | (2) |
式中:Cz为空气法向力;q∞为流体动压;Ω为x轴和空速在水平面内分量之间的夹角;
| $ {F_{\rm{a}}} = {q_\infty } \cdot {C_x} \cdot {S_{{\rm{ref}}}}, $ | (3) |
| $ {M_{\rm{a}}} = {q_\infty } \cdot {C_{{\rm{m}}y}} \cdot {S_{{\rm{ref}}}} \cdot {L_{{\rm{ref}}}}. $ | (4) |
其中Cx、Cmy分别为空气轴向力和力矩系数;Sref=Vol2/3为参考面积, 为457.949 3 m2;Lref=Vol1/3为参考长度, 为21.399 7 m,Vol为飞艇体积.利用计算流体力学(computational fluid dynamics, CFD)方法得到的飞艇气动系数Cx、Cz、Cmy如图 2所示.图中, α为气动迎角.
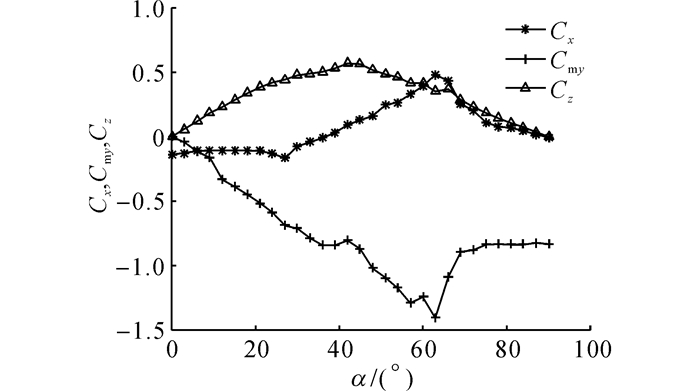
|
图 2 飞艇空气动力系数 Fig. 2 Aerodynamic coefficient for airship |
将FT=[fx, fy, fz, mx, my, mz]T作为飞艇控制输入量.飞艇状态方程为
| $ \left. \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_1} = {\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{x}}_2}, \\ {{\mathit{\boldsymbol{\dot x}}}_2} = {\mathit{\boldsymbol{G}}_2}\left( {\mathit{\boldsymbol{f}} + {\mathit{\boldsymbol{F}}_{\rm{T}}}} \right). \end{array} \right\} $ | (5) |
式中:f=FA+FGB+FI, x1=[x, y, z, φ, θ, ψ]T, x2=[u, v, w, p, q, r]T分别为位置和速度状态向量, 其中θ、ψ、φ分别为俯仰角、偏航角、滚转角, x、y、z为地面位置坐标.
矩阵G1、G2分别如下:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_1} = \left[{\begin{array}{*{20}{c}} {\cos \psi \cos \theta }&{\cos \psi \sin \theta \sin \varphi-sin\psi cos\varphi }&{\cos \psi \sin \theta \cos \varphi + \sin \psi \sin \varphi }&0&0&0\\ {\sin \psi \cos \theta }&{\sin \psi \sin \theta \sin \varphi + \cos \psi \cos \varphi }&{\sin \psi \sin \theta \cos \varphi-\cos \psi \sin \varphi }&0&0&0\\ {-\sin \theta }&{\cos \theta \sin \varphi }&{\cos \theta \cos \varphi }&0&0&0\\ 0&0&0&1&{\sin \varphi \tan \theta }&{\cos \varphi \tan \theta }\\ 0&0&0&0&{\cos \varphi }&{ - \sin \varphi }\\ 0&0&0&0&{\frac{{\sin \varphi }}{{\cos \theta }}}&{\frac{{\cos \varphi }}{{\cos \theta }}} \end{array}} \right], }\\ {{\mathit{\boldsymbol{G}}_2} = {{\left[{\begin{array}{*{20}{c}} {m + {m_{11}}}&0&0&0&{m{x_{\rm{G}}}}&{-m{y_{\rm{G}}}}\\ 0&{m + {m_{22}}}&0&{-m{z_{\rm{G}}}}&0&{m{x_{\rm{G}}}}\\ 0&0&{m + {m_{33}}}&{m{y_{\rm{G}}}}&{-m{x_{\rm{G}}}}&0\\ 0&{ - m{z_{\rm{G}}}}&{m{y_{\rm{G}}}}&{{I_x} + {m_{44}}}&0&0\\ {m{z_{\rm{G}}}}&0&{ - m{x_{\rm{G}}}}&0&{{I_x} + {m_{55}}}&0\\ { - m{y_{\rm{G}}}}&{m{x_{\rm{G}}}}&0&0&0&{{I_x} + {m_{44}}} \end{array}} \right]}^{ -1}}.} \end{array} $ |
式中:(xG, yG, zG)为重心坐标, 为(0 m, 0 m, 3.7 m);飞艇质量m为1 007.325 2 kg;m11~m66为飞艇附加质量, m11为237.437 1 kg, m22为237.437 1 kg, m33为606.857 1 kg, m44为2 012.6 kg, m55为2 012.6 kg, m66为0 kg;飞艇的惯性矩Ix为218 550 kg·m2, Iy为218 550 kg·m2, Iz为139 530 kg·m2.
1.2 飞艇PI控制器设位置控制参考状态量为
| $ {\mathit{\boldsymbol{x}}_{1{\rm{c}}}} = {\left[{{x_{\rm{c}}}, \;\;{y_{\rm{c}}}, \;\;{z_{\rm{c}}}, \;\;{\varphi _{\rm{c}}}, \;\;{\theta _{\rm{c}}}, \;\;{\psi _{\rm{c}}}, } \right]^{\rm{T}}}. $ |
可以获得如下PI控制律[7]:
| $ {{\mathit{\boldsymbol{\dot x}}}_{1{\rm{c}}}} = {\mathit{\boldsymbol{K}}_{\rm{p}}}\left( {{\mathit{\boldsymbol{x}}_{1{\rm{c}}}}-{\mathit{\boldsymbol{x}}_1}} \right) + {\mathit{\boldsymbol{K}}_{\rm{i}}}\int {\left( {{\mathit{\boldsymbol{x}}_{1{\rm{c}}}}-{\mathit{\boldsymbol{x}}_1}} \right){\rm{d}}t} . $ | (6) |
式中:Kp为比例增益向量, Kp=[1, 1, 1, 2.5, 2.5, 2.5]T;Ki为积分增益向量, Ki=[1.5, 1.5, 1.5, 2, 2, 2]T.
x2c=[ur, vr, wr, pr, qr, rr]T为
| $ {\mathit{\boldsymbol{x}}_{2{\rm{c}}}} = \mathit{\boldsymbol{G}}_1^{-1}{{\mathit{\boldsymbol{\dot x}}}_{1{\rm{c}}}}. $ | (7) |
飞艇控制输入量为
| $ {\mathit{\boldsymbol{F}}_{\rm{T}}} = \mathit{\boldsymbol{G}}_2^{-1}{{\mathit{\boldsymbol{\dot x}}}_{2{\rm{c}}}}-\mathit{\boldsymbol{f}}. $ | (8) |
输入推力和扭矩为
| $ {\mathit{\boldsymbol{F}}_{\rm{T}}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{F}}_{{T_{{\rm{HV}}}}}}. $ | (9) |
水平推力和垂直推力FTHV为
| $ {\mathit{\boldsymbol{F}}_{{T_{{\rm{HV}}}}}} = {\mathit{\boldsymbol{B}}^{-1}}{\mathit{\boldsymbol{F}}_{\rm{T}}} = {\mathit{\boldsymbol{B}}^{-1}}\left( {-\mathit{\boldsymbol{f + G}}_2^{ - 1}{{\mathit{\boldsymbol{\dot x}}}_{2{\rm{c}}}}} \right). $ | (10) |
式中:B为间接控制矩阵[7],
| $ \mathit{\boldsymbol{B = }}\left[{\begin{array}{*{20}{c}} 0&1&0&{-1}&0&0&0&0\\ {-1}&0&1&0&0&0&0&0\\ 0&0&0&0&{-1}&{ - 1}&{ - 1}&{ - 1}\\ 0&0&0&0&0&{{R_{\rm{p}}}}&0&{{R_{\rm{p}}}}\\ 0&0&0&0&{{R_{\rm{p}}}}&0&{ - {R_{\rm{p}}}}&0\\ { - {R_{\rm{p}}}}&{ - {R_{\rm{p}}}}&{ - {R_{\rm{p}}}}&{ - {R_{\rm{p}}}}&0&0&0&0 \end{array}} \right]. $ |
其中,Rp为螺旋桨到飞艇体积中心的距离, 为18.5 m.FTHV为水平推力和垂直推力, 可以写成:
| $ {\mathit{\boldsymbol{F}}_{{T_{{\rm{HV}}}}}} = \left[{\begin{array}{*{20}{c}} {{f_{{\rm{1H}}}}}\\ {{f_{{\rm{2H}}}}}\\ {{f_{{\rm{3H}}}}}\\ {{f_{{\rm{4H}}}}}\\ {{f_{{\rm{1V}}}}}\\ {{f_{{\rm{2V}}}}}\\ {{f_{{\rm{3V}}}}}\\ {{f_{{\rm{4V}}}}} \end{array}} \right]. $ |
每个螺旋桨的矢量转角μi(i=1, 2, 3, 4) 可以表示为
| $ {\mu _i} = \arcsin \frac{{{f_{i{\rm{H}}}}}}{{\sqrt {f_{i{\rm{H}}}^2 + f_{i{\rm{V}}}^2} }};i = 1, 2, 3, 4. $ | (11) |
FTHV和实际螺旋桨推力T=[T1, T2, T3, T4]T的关系为
| $ {\mathit{\boldsymbol{F}}_{{T_{{\rm{HV}}}}}} = \left[{\begin{array}{*{20}{c}} {\sin {\mu _1}}&0&0&0\\ 0&{\sin {\mu _2}}&0&0\\ 0&0&{\sin {\mu _3}}&0\\ 0&0&0&{\sin {\mu _4}}\\ {-\cos {\mu _1}}&0&0&0\\ 0&{-\cos {\mu _2}}&0&0\\ 0&0&{-\cos {\mu _3}}&0\\ 0&0&0&{ - \cos {\mu _4}} \end{array}} \right]\mathit{\boldsymbol{T}}. $ | (12) |
根据文献[8]可知, 螺旋桨动力学方程可以写成
| $ 2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}\dot n = {Q_{\rm{m}}}-{Q_{\rm{p}}}-2{\rm{ \mathsf{ π} }}{K_{\rm{n}}}n. $ | (13) |
式中:n为电机转速, 转动惯量Jm为1.89×10-2kg·m2, 线性阻尼系数Kn为0.116 7 kg·m2/s, Qm为电机命令扭矩, Qp为螺旋桨扭矩.Qm和n都是可测的.
螺旋桨进距比J可以表示为
| $ J = \frac{{{u_{\rm{a}}}}}{{nD}}. $ | (14) |
式中:ua为螺旋桨轴向来流速度; n为螺旋桨转速,n≥0;D为螺旋桨直径,D=4 m.如图 3所示为螺旋桨在不同轴向来流速度下的推力Tp曲线.
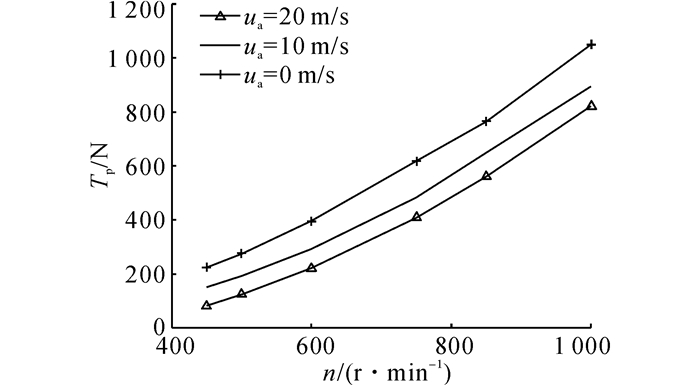
|
图 3 螺旋桨在不同轴向来流速度下的推力曲线 Fig. 3 Thrusts at different axis flow velocity |
螺旋桨输出推力可以表示为
| $ {T_{\rm{p}}} = {G_{{T_{\rm{p}}}}}{n^2} + {\Delta _{\rm{T}}}. $ | (15) |
式中:GTp是大于零的常数, 它可以通过CFD的方法在J=0的时候获得, 本文仿真中GTp为4.01;ΔT为当J>0时所引起的推力损失.
描述推力损失的微分方程可以表示为
| $ {{\dot \Delta }_{\rm{T}}} =-\frac{1}{\tau }{\Delta _{\rm{T}}} + {w_{\rm{d}}}. $ | (16) |
式中:wd表示有界噪声;τ为时间常数, 可以依据飞艇速度和轨迹追踪误差选择[9].
ΔT作为一个随时间变化的状态量, 以一阶状态方程表示.因为螺旋桨桨盘来流速度未知、气流非定常扰动等原因, 得到ΔT的准确模型是非常困难的, 但在估计未知变量的时候经常使用该模型[9].
螺旋桨特性可以由无量纲推力系数KT和扭矩系数KQ表示, 它们通过Tp、Qp、n计算:
| $ {K_{\rm{T}}} = \frac{{{T_{\rm{p}}}}}{{\rho {D^4}{n^2}}}, $ | (17) |
| $ {K_{\rm{Q}}} = \frac{{{Q_{\rm{p}}}}}{{\rho {D^5}{n^2}}}. $ | (18) |
式中:ρ为当地空气密度, 为0.088 9 kg/m3.
KT和KQ是J的一次函数.KT和KQ可以近似为
| $ {K_{\rm{T}}} = {\alpha _1}J + {\alpha _2}, $ | (19) |
| $ {K_{\rm{Q}}} = {\beta _1}J + {\beta _2}. $ | (20) |
式中:α1、α2、β1、β2是4个无量纲常数, 它们可以通过CFD方法得到, 本文中α1为-0.208 2, α2为0.219 8, β1为-0.015 2, β2为0.022 4.如图 4所示为KT、KQ的一次函数拟合.图 4显示推力会随J发生极大的变化.
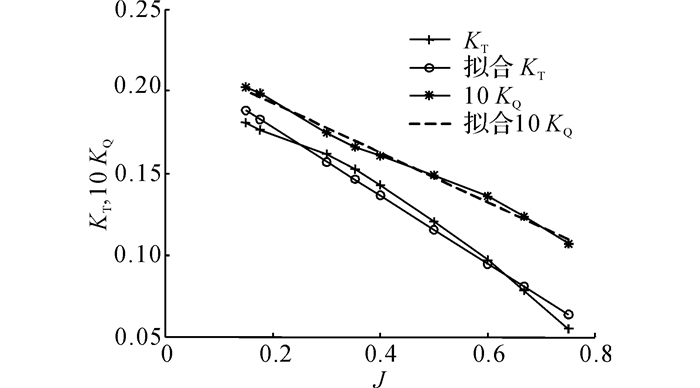
|
图 4 螺旋桨推力和扭矩系数 Fig. 4 Thrust and torque coefficients for propeller |
Smogeli等[10-11]用期望推力和估计进距比
结合式(15)、(17)、(19), 进距比可以表示为
| $ J = \frac{{\frac{{{G_{{T_{\rm{p}}}}}{n^2} + {\Delta _{\rm{T}}}}}{{\rho {D^4}{n^2}}}-{\alpha _2}}}{{{\alpha _1}}}. $ | (21) |
结合式(18)、(20)、(21), 可得
| $ {Q_{\rm{p}}} = {k_1}{n^2} + {k_2}{\Delta _{\rm{T}}}. $ | (22) |
式中:
| $ \begin{array}{*{20}{c}} {{k_1} = D\left[{\frac{{{\beta _1}}}{{{\alpha _1}}}{G_{{T_{\rm{p}}}}}-\left( {\frac{{{\beta _1}{\alpha _2}}}{{{\alpha _1}}}-{\beta _2}} \right)\rho {D^4}} \right], }\\ {{k_2} = \frac{{{\beta _1}}}{{{\alpha _1}}}D.} \end{array} $ |
将式(22) 代入式(13), 结合式(16) 的螺旋桨动力学模型, 可以写成
| $ 2{\rm{\pi }}{J_{\rm{m}}}\dot n = {Q_{\rm{m}}}-{k_1}{n^2}-2{\rm{\pi }}{K_{\rm{n}}}n-{k_2}{\Delta _{\rm{T}}}, $ | (23) |
| $ {{\dot \Delta }_{\rm{T}}} =-\frac{1}{\tau }{\Delta _{\rm{T}}} + {w_{\rm{d}}}. $ | (24) |
系统输出可以表示为
| $ y = n. $ | (25) |
由螺旋桨气动特性可得, k1>0, k2>0, 因此n2∈[0, ∞].
假设非线性增益l和m用来估计推力损失:
| $ \begin{matrix} 2\text{ }\!\!\pi\!\!\text{ }{{J}_{\text{m}}}\dot{\hat{n}}={{Q}_{\text{m}}}-{{k}_{1}}{{{\hat{n}}}^{2}}-2\text{ }\!\!\pi\!\!\text{ }{{K}_{\text{n}}}\hat{n}-\\ {{k}_{2}}{{{\hat{\Delta }}}_{\text{T}}}+l\left( y-\hat{y} \right), \\ \end{matrix} $ | (26) |
| $ {{{\dot{\hat{\Delta }}}}_{\text{T}}}=-\frac{1}{\tau }{{{\hat{\Delta }}}_{\text{T}}}+m\left( y-\hat{y} \right). $ | (27) |
式中:
| $ 2\text{ }\!\!\pi\!\!\text{ }{{J}_{\text{m}}}\dot{\tilde{n}}=-\left( {{k}_{1}}{{n}^{2}}-{{k}_{1}}{{{\hat{n}}}^{2}} \right)-\left( l+2\text{ }\!\!\pi\!\!\text{ }{{K}_{\text{n}}} \right)\tilde{n}-{{k}_{2}}{{{\tilde{\Delta }}}_{\text{T}}}, $ | (28) |
| $ {{{\dot{\tilde{\Delta }}}}_{\text{T}}}=-\frac{1}{\tau }{{{\tilde{\Delta }}}_{\text{T}}}-m\tilde{n}+w. $ | (29) |
当增益l和m满足如下条件时
| $ l >-2{\rm{\pi }}{K_{\rm{n}}}, $ | (30) |
| $ \left| {\frac{{{k_2}l}}{{2{\rm{\pi }}{J_{\rm{m}}}}} + m} \right| < 2\sqrt {\frac{{2{\rm{\pi }}{K_{\rm{n}}} + l}}{{2{\rm{\pi }}\tau {J_{\rm{m}}}}}} . $ | (31) |
观测器系统估计值会收敛到真实值的邻域内, 这是由于观测器误差关于噪声wd是“输入-状态”稳定的[12].在本文仿真中, l取-0.295 9, m取0.97.
证明:考虑Lyapunov函数:
| $ \begin{array}{l} {{\dot V}_{\rm{o}}}\left( {\tilde n, {{\tilde \Delta }_{\rm{T}}}} \right) =-\left( {\frac{{{K_{\rm{n}}}}}{{{J_{\rm{m}}}}}{{\tilde n}^2} + \frac{l}{{2{\rm{\pi }}{J_{\rm{m}}}}}} \right){{\tilde n}^2}-\frac{1}{\tau }\tilde \Delta _{\rm{T}}^2-\\ \;\;\;\left( {\frac{1}{{2{\rm{\pi }}{J_{\rm{m}}}}}{k_2} + m} \right)\tilde n{{\tilde \Delta }_{\rm{T}}} + w{{\tilde \Delta }_{\rm{T}}} - \frac{1}{{2{\rm{\pi }}{J_{\rm{m}}}}}{k_1}\left( {{n^2} - {{\hat n}^2}} \right)\tilde n. \end{array} $ | (32) |
考虑到对于任意n、
| $ \begin{array}{l} {{\dot V}_{\rm{o}}}\left( {\tilde n, {{\tilde \Delta }_{\rm{T}}}} \right) \le-\left( {\frac{{{K_{\rm{n}}}}}{{{J_{\rm{m}}}}}{{\tilde n}^2} + \frac{l}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}}} \right){{\tilde n}^2}-\frac{1}{\tau }\tilde \Delta _{\rm{T}}^2-\\ \;\;\;\;\left( {\frac{1}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}}{k_2} + m} \right)\tilde n{{\tilde \Delta }_{\rm{T}}} + w{{\tilde \Delta }_{\rm{T}}} \le - \mathit{\boldsymbol{\tilde e}}_{\rm{o}}^{\rm{T}}\mathit{\boldsymbol{Q}}{{\mathit{\boldsymbol{\tilde e}}}_{\rm{o}}} + {{\tilde \Delta }_{\rm{T}}}w. \end{array} $ | (33) |
式中:
| $ \mathit{\boldsymbol{Q = }}\left[{\begin{array}{*{20}{c}} {\frac{{2{\rm{ \mathsf{ π} }}{K_{\rm{n}}} + l}}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}}}&{\frac{1}{2}\left( {\frac{{{k_2}l}}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}} + m} \right)}\\ {\frac{1}{2}\left( {\frac{{{k_2}l}}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}} + m} \right)}&{\frac{1}{\tau }} \end{array}} \right]. $ |
为了使Lyapunov函数小于零, 选取Q为负定矩阵.当wd=0时, 观测器误差模型(28) 和(29) 是全局渐进稳定的.当wd≠0时, 式(33) 变成:
| $ \begin{array}{l} {{\dot V}_{\rm{o}}} \le-{\lambda _{\min }}{\lambda _\mathit{\boldsymbol{Q}}}{\left\| {{\mathit{\boldsymbol{e}}_{\rm{o}}}} \right\|^2} + \left| {{{\tilde \Delta }_{\rm{T}}}} \right|\left| {{w_{\rm{d}}}} \right| \le-{\lambda _{\min }}{\lambda _\mathit{\boldsymbol{Q}}}{\left\| {{\mathit{\boldsymbol{e}}_{\rm{o}}}} \right\|^2} + \\ \left\| {{\mathit{\boldsymbol{e}}_{\rm{o}}}} \right\|\left| {{w_{\rm{d}}}} \right| =-\left( {1 - \theta } \right){\lambda _{\min }}{\lambda _\mathit{\boldsymbol{Q}}}{\left\| {{\mathit{\boldsymbol{e}}_{\rm{o}}}} \right\|^2} - \theta {\lambda _{\min }}{\lambda _\mathit{\boldsymbol{Q}}}{\left\| {{\mathit{\boldsymbol{e}}_{\rm{o}}}} \right\|^2} + \\ \left\| {{\mathit{\boldsymbol{e}}_{\rm{o}}}} \right\|\left| {{w_{\rm{d}}}} \right|. \end{array} $ | (34) |
式中:λQ为Q的特征值,0 < θ < 1.对于任何
| $ \left\| {{\mathit{\boldsymbol{e}}_{\rm{o}}}} \right\| \ge \frac{{\left| {{w_{\rm{d}}}} \right|}}{{\theta {\lambda _{\min }}{\lambda _\mathit{\boldsymbol{Q}}}}} = \rho \left( {\left| {{w_{\rm{d}}}} \right|} \right), $ | (35) |
可以导出
| $ \dot V \le-\left( {1-\theta } \right){\lambda _{\min }}{\lambda _\mathit{\boldsymbol{Q}}}{\left\| {{\mathit{\boldsymbol{e}}_{\rm{o}}}} \right\|^2}. $ | (36) |
式中:ρ是线性κ函数, 则系统是关于|wd|“输入-状态”稳定的, 控制误差以ρ(sup t>t0(|wd|))为界.
4 螺旋桨动力学模型控制律设计电机的期望转速为
| $ {{\bar n}_{\rm{d}}} = \sqrt {\frac{{{T_{{\rm{pd}}}}-{{\hat \Delta }_{\rm{T}}}}}{{{G_{{T_{\rm{P}}}}}}}} . $ | (37) |
为了使参考信号nd和
| $ {{\ddot n}_{\rm{d}}} + 2{\omega _{\rm{c}}}\xi {{\dot n}_{\rm{d}}} + \omega _{\rm{c}}^2{n_{\rm{d}}} = \omega _{\rm{c}}^2{{\bar n}_{\rm{d}}}. $ | (38) |
式中:ωc为截止角频率, ωc=40 rad/s;ξ为阻尼系数, ξ=1.
定义追踪误差为e=n-nd, 并且使控制律为
| $ \begin{array}{l} {Q_{\rm{m}}} = {k_1}n\hat n + 2{\rm{\pi }}{K_{\rm{n}}}\hat n + {k_2}{{\hat \Delta }_{\rm{T}}} + \\ \;2{\rm{\pi }}{J_{\rm{m}}}{{\dot n}_{\rm{d}}}-{K_{{\rm{p1}}}}e-{K_{{\rm{p2}}}}{n^2}e. \end{array} $ | (39) |
式中:控制器增益
| $ {K_{{\rm{p1}}}} > \frac{{{\rm{\pi }}K_{\rm{n}}^2}}{{2{J_{\rm{m}}}}} + \frac{{\tau k_2^2}}{{2{\rm{\pi }}{J_{\rm{m}}}}}, {K_{{\rm{p2}}}} > \frac{{k_1^2}}{{8{\rm{\pi }}{J_{\rm{m}}}}}, $ |
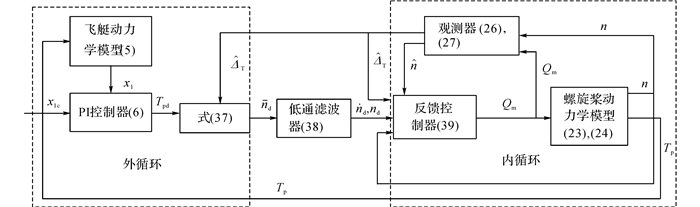
则螺旋桨动力学系统关于wd为“输入-状态”稳定的.在仿真中, Kp1=9.133 6, Kp2=6.172 3.如图 5所示为飞艇系统的框图.
|
图 5 飞艇控制系统框图 Fig. 5 Block diagram of whole control system |
证明:根据式(23) 可知, 追踪误差为
| $ \dot e = \frac{1}{{2{\rm{\pi }}{J_{\rm{m}}}}}\left( {{Q_{\rm{m}}}-{k_1}{n^2}-2{\rm{\pi }}{K_{\rm{n}}}n-{k_2}{\Delta _{\rm{T}}} - 2{\rm{\pi }}{J_{\rm{m}}}{{\dot n}_{\rm{d}}}} \right). $ | (40) |
设Lyapunov函数为:V=e2/2+Vo.对该函数求导:
| $ \begin{array}{l} \dot V \le e\dot e- \frac{{\left( {2{\rm{\pi }}{K_{\rm{n}}} + l} \right)}}{{2{\rm{\pi }}{J_{\rm{m}}}}}{{\tilde n}^2}- \left( {\frac{{{k_2}l}}{{2{\rm{\pi }}{J_{\rm{m}}}}} + m} \right)\tilde n{{\tilde \Delta }_{\rm{T}}}- \frac{1}{\tau }\tilde \Delta _{\rm{T}}^2 + \\ \;\;\;\;{{\tilde \Delta }_{\rm{T}}}{w_{\rm{d}}} \le e\left( {\dot n - {{\dot n}_{\rm{d}}}} \right) - \frac{{\left( {2{\rm{\pi }}{K_{\rm{n}}} + l} \right)}}{{2{\rm{\pi }}{J_{\rm{m}}}}}{{\tilde n}^2} - \\ \;\;\;\;\left( {\frac{{{k_2}l}}{{2{\rm{\pi }}{J_{\rm{m}}}}} + m} \right)\tilde n{{\tilde \Delta }_{\rm{T}}} - \frac{1}{\tau }\tilde \Delta _{\rm{T}}^2 + {{\tilde \Delta }_{\rm{T}}}{w_{\rm{d}}} \le \\ \;\;\;\;e\left[{\frac{1}{{2{\rm{\pi }}{J_{\rm{m}}}}}\left( {{Q_{\rm{m}}}-{k_1}{n^2}-2{\rm{\pi }}{K_{\rm{n}}}n-{k_2}{\Delta _{\rm{T}}}} \right) - {{\dot n}_{\rm{d}}}} \right] -\\ \;\;\;\;\frac{{\left( {2{\rm{\pi }}{K_{\rm{n}}} + l} \right)}}{{2{\rm{\pi }}{J_{\rm{m}}}}}{{\tilde n}^2} -\left( {\frac{{{k_2}l}}{{2{\rm{\pi }}{J_{\rm{m}}}}} + m} \right)\tilde n{{\tilde \Delta }_{\rm{T}}} -\frac{1}{\tau }\tilde \Delta _{\rm{T}}^2 + \tilde \Delta _{\rm{T}}^2{w_{\rm{d}}}. \end{array} $ | (41) |
将式(39) 代入式(41), 可得
| $ \begin{array}{l} \dot V \le \frac{1}{{2{\rm{\pi }}{J_{\rm{m}}}}}\left( {-e{k_1}n\tilde n-2{\rm{\pi }}{K_{\rm{n}}}e\tilde n-{k_2}e{{\tilde \Delta }_{\rm{T}}}} \right) - \\ \;\;\;\;\;\frac{{\left( {2{\rm{\pi }}{K_{\rm{n}}} + l} \right)}}{{2{\rm{\pi }}{J_{\rm{m}}}}}{{\tilde n}^2} - \left( {\frac{{{k_2}l}}{{2{\rm{\pi }}{J_{\rm{m}}}}} + m} \right)\tilde n{{\tilde \Delta }_{\rm{T}}} - \frac{1}{\tau }\tilde \Delta _{\rm{T}}^2 + {{\tilde \Delta }_{\rm{T}}}{w_{\rm{d}}}. \end{array} $ | (42) |
利用如下性质:
| $ -\frac{1}{{2{\rm{\pi }}{J_{\rm{m}}}}}e{k_1}n\tilde n =-{\left( {\frac{{{k_1}}}{{4{\rm{\pi }}{J_{\rm{m}}}}}ne + \tilde n} \right)^2} + \left( {\frac{{k_1^2}}{{16{{\rm{\pi }}^2}J_{\rm{m}}^2}}{n^2}{e^2} + {{\tilde n}^2}} \right), $ | (43) |
| $ -\frac{{{K_{\rm{n}}}}}{{{J_{\rm{m}}}}}e\tilde n =-{\left( {\frac{{{K_{\rm{n}}}}}{{2{J_{\rm{m}}}}}e + \tilde n} \right)^2} + \left( {\frac{{K_{\rm{n}}^2}}{{4J_{\rm{m}}^2}}{e^2} + {{\tilde n}^2}} \right), $ | (44) |
| $ \begin{array}{l} -\frac{{{k_2}e{{\tilde \Delta }_{\rm{T}}}}}{{2{\rm{\pi }}{J_{\rm{m}}}}} =-{\left( {\frac{{\sqrt \tau {k_2}}}{{2{\rm{\pi }}{J_{\rm{m}}}}}e + \frac{1}{{2\sqrt \tau }}{{\tilde \Delta }_{\rm{T}}}} \right)^2} + \\ \;\;\left( {\frac{{\tau k_2^2}}{{4{{\rm{\pi }}^2}J_{\rm{m}}^2}}{e^2} + \frac{1}{{4\tau }}\tilde \Delta _{\rm{T}}^2} \right). \end{array} $ | (45) |
将式(43)~(45) 代入式(42) 的对应项中, 重写式(42), 可得
| $ \begin{array}{l} \dot V \le \left( {\frac{{k_1^2}}{{16{{\rm{ \mathsf{ π} }}^2}J_{\rm{m}}^2}}-\frac{{{K_{{\rm{p}}2}}}}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}}} \right){n^2}{e^2} + \\ \;\;\;\;\left( {\frac{{K_{\rm{n}}^2}}{{4J_{\rm{m}}^2}}-\frac{{{K_{{\rm{p}}1}}}}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}} + \frac{{\tau k_2^2}}{{4{{\rm{ \mathsf{ π} }}^2}J_{\rm{m}}^2}}} \right){\mathit{\boldsymbol{e}}^2} + \mathit{\boldsymbol{e}}_{\rm{o}}^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{e}}_{\rm{o}}} + {{\tilde \Delta }_{\rm{T}}}{w_{\rm{d}}}. \end{array} $ | (46) |
式中:
| $ \mathit{\boldsymbol{P}} = \left[{\begin{array}{*{20}{c}} {\frac{{2{\rm{ \mathsf{ π} }}{K_{\rm{n}}} + l-4{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}}}&{\frac{1}{2}\left( {\frac{{{k_2}l}}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}} + m} \right)}\\ {\frac{1}{2}\left( {\frac{{{k_2}l}}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}} + m} \right)}&{\frac{3}{{4\tau }}} \end{array}} \right]. $ |
若控制器增益和观测器增益同时满足:
| $ \begin{array}{l} {K_{{\rm{p}}1}} > \frac{{{\rm{ \mathsf{ π} }}K_{\rm{n}}^2}}{{2{J_{\rm{m}}}}} + \frac{{\tau k_2^2}}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}}, \\ {K_{{\rm{p}}2}} > \frac{{k_1^2}}{{8{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}}, \\ l > 4{\rm{ \mathsf{ π} }}{J_{\rm{m}}}-2{\rm{ \mathsf{ π} }}{K_{\rm{n}}}, \\ \left| {\frac{{{k_2}l}}{{2{\rm{ \mathsf{ π} }}{J_{\rm{m}}}}} + m} \right| < 2\sqrt {\frac{{3\left( {2{\rm{ \mathsf{ π} }}{K_{\rm{n}}} + l-4{\rm{ \mathsf{ π} }}{J_{\rm{m}}}} \right)}}{{8{\rm{ \mathsf{ π} }}\tau {J_{\rm{m}}}}}}, \end{array} $ |
则当wd=0时, 螺旋桨动力学系统为全局渐进稳定的.当wd≠0时, 系统“输入-状态”稳定的证明方法与证明观测器“输入-状态”稳定的方法相同.
5 浮空器控制仿真验证飞艇追踪期望轨迹所需功率可以表示为
| $ P = 2{\rm{\pi }}\sum\limits_{i = 1}^4 {{Q_{{\rm{p}}i}} \cdot {n_i}} . $ | (47) |
动力系统消耗能量可以表示为
| $ E = \int\limits_0^t {P{\rm{d}}t} . $ | (48) |
传统模型利用螺旋桨在J=0时的特性数据以及不考虑螺旋桨动力学模型设计电机扭矩控制器[13].电机命令扭矩计算如下:
| $ {T_{{\rm{pd}}}} = \sqrt {f_{i{\rm{H}}}^2 + f_{i{\rm{V}}}^2} ;i = 1, 2, 3, 4. $ | (49) |
| $ {Q_{\rm{m}}} = \frac{{D{K_{\rm{Q}}}\left| {_{J = 0}} \right.}}{{{K_{\rm{T}}}\left| {_{J = 0}} \right.}}{T_{{\rm{pd}}}}. $ | (50) |
式中:Tpd为每个螺旋桨的期望推力.
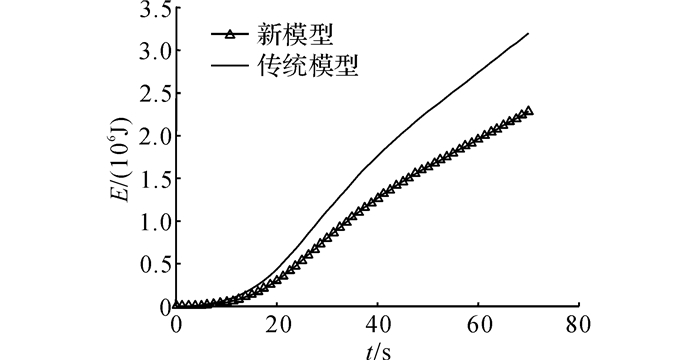
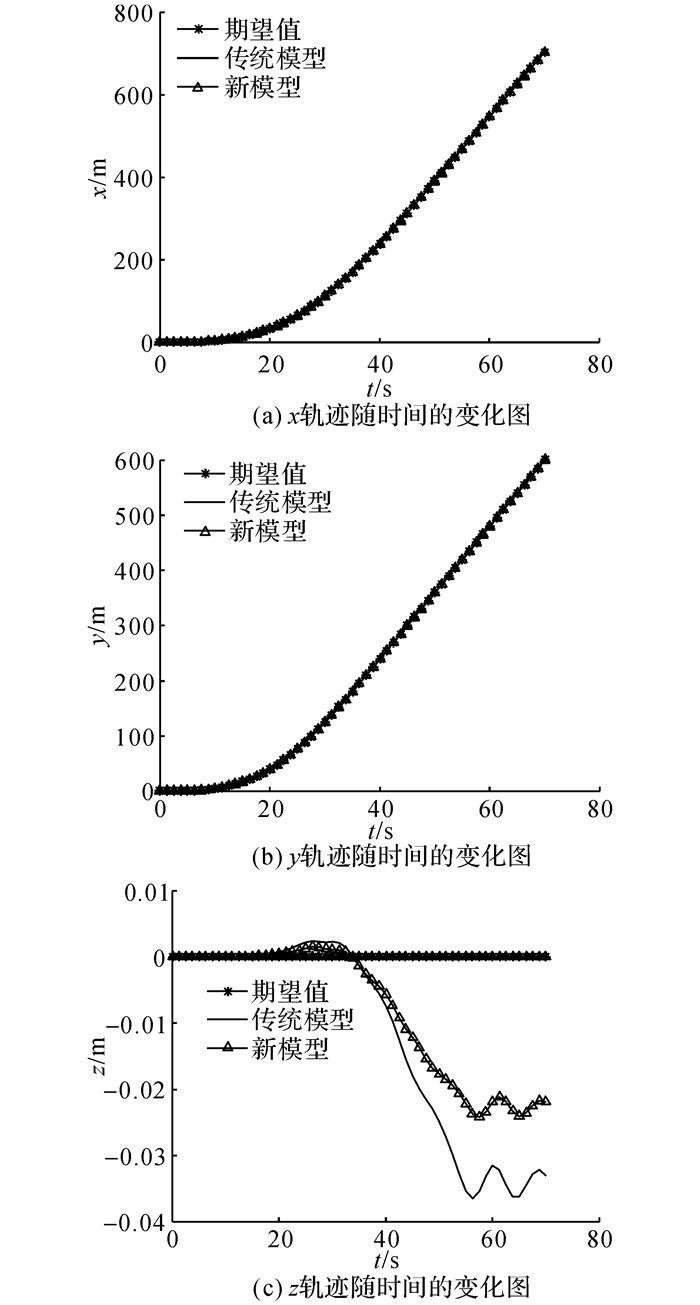
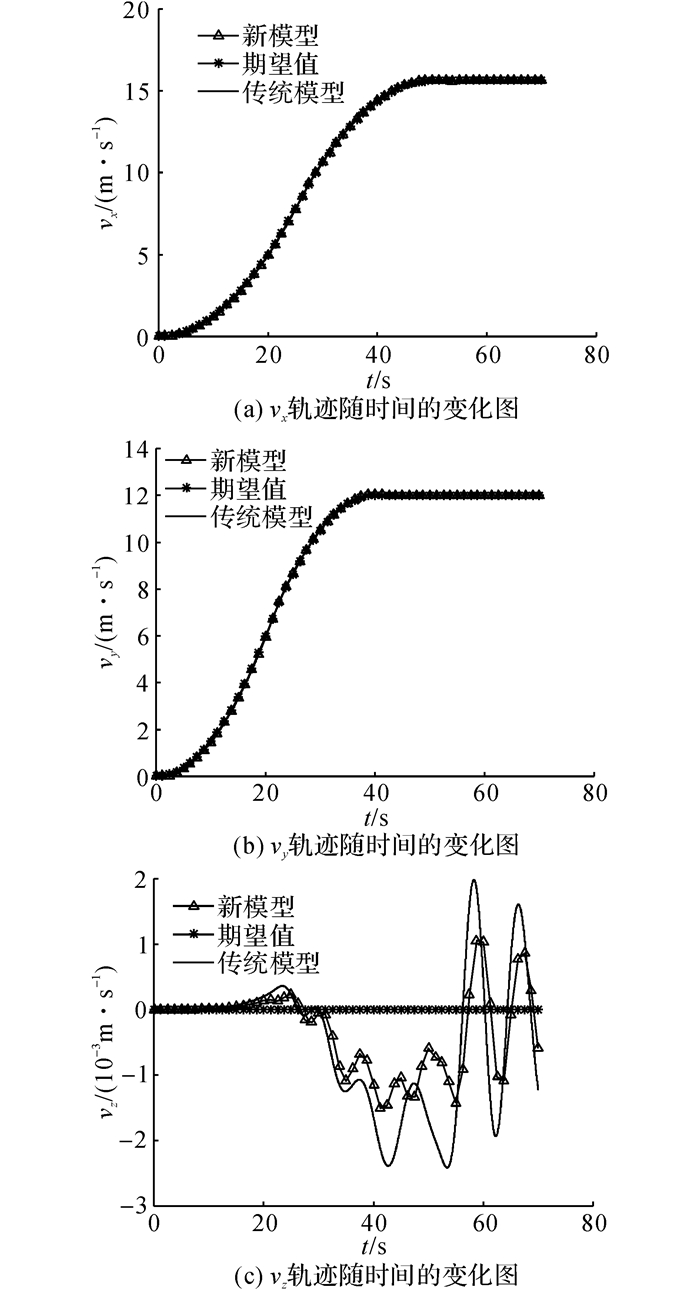
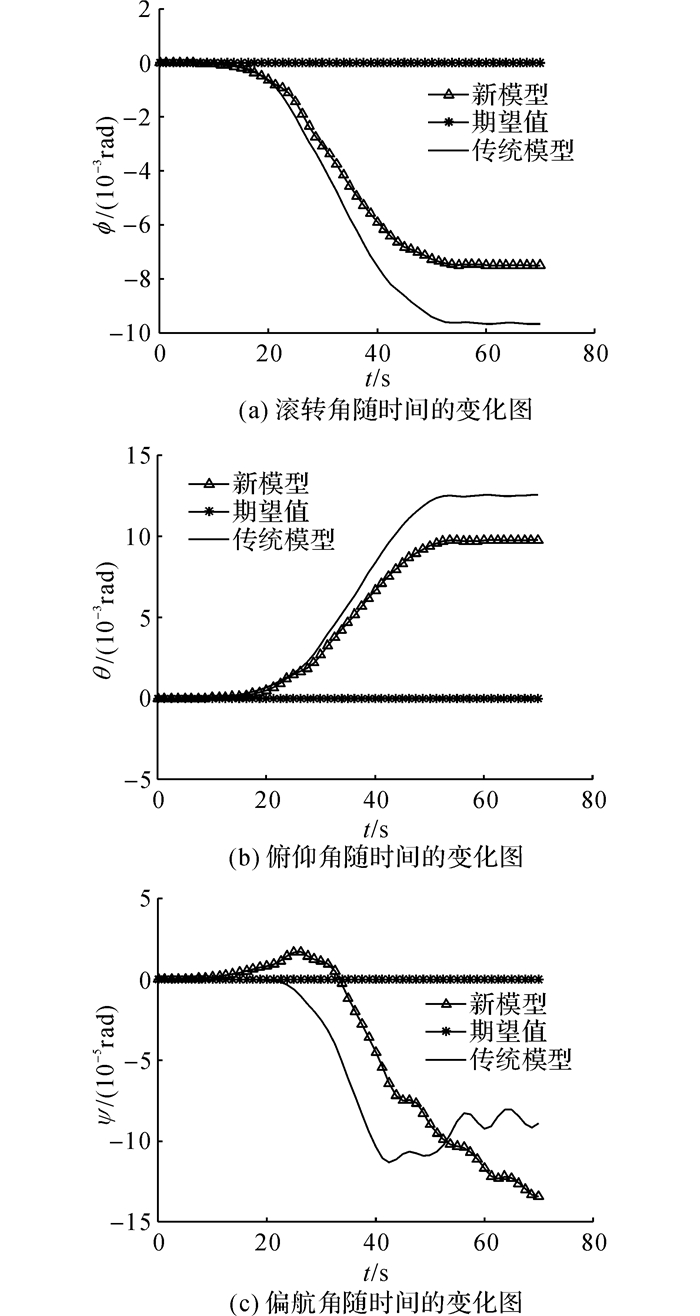
5.1 飞艇“外循环”仿真飞艇动力系统所需功率和能量如图 6、7所示.可以看出, 考虑螺旋桨的动力系统的飞艇模型对飞艇动力系统能源的需求大大降低.如图 8所示,x、y、z为飞艇在地坐标系中的位置分量.如图 9所示, vx、vy、vz为飞艇在地坐标系中的速度分量.如图 8~10所示, 由于“外循环”系统中的PI控制器能够快速地补偿追踪误差, 即使考虑螺旋桨动力学的新模型在追踪期望值时的误差较传统模型更小, 它们都能够跟踪到期望轨迹、速度和姿态角.在仿真中, 通过假定螺旋桨来流速度与飞艇在x和y轴上的速度相等, 从而得到未知的有界噪声, 这样可以通过式(14)、(21)、(24) 得到wd.如图 10所示为有界噪声wd随时间的变化曲线.图中, 幅值为0.4、周期为6 s的正弦信号加在未知的有界噪声上, 来表示螺旋桨桨盘前方非定常来流的影响.

|
图 6 功率随时间的变化图 Fig. 6 Time history of consumed power |
|
图 7 能量随时间的变化图 Fig. 7 Time history of consumed energy |
|
图 8 x、y、z位置轨迹随时间的变化图 Fig. 8 Time history of x, y, z tracking |
|
图 9 vx、vy、vz速度轨迹随时间变化图 Fig. 9 Time history of vx, vy, vz tracking |
|
图 10 姿态角随时间的变化图 Fig. 10 Time history of angle tracking |
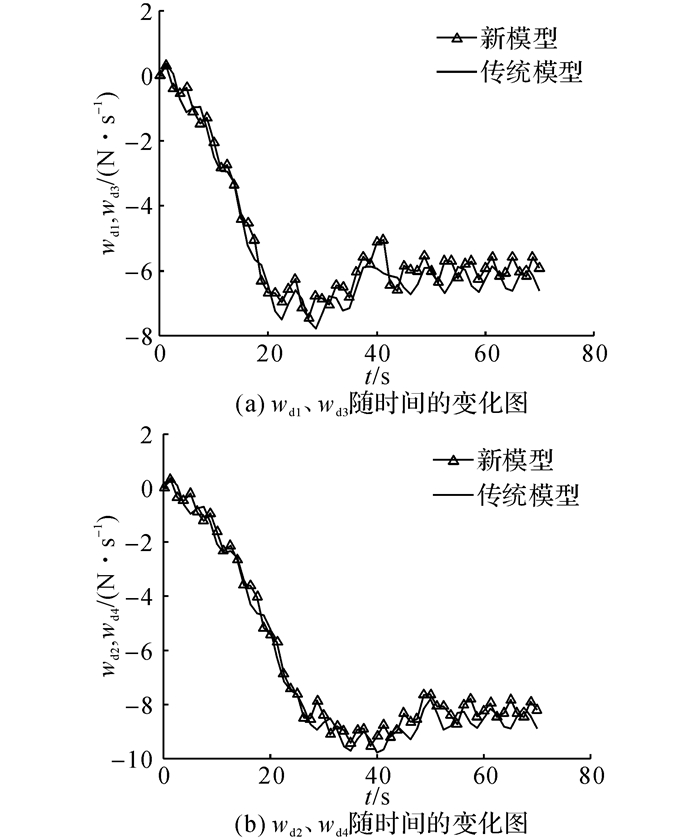
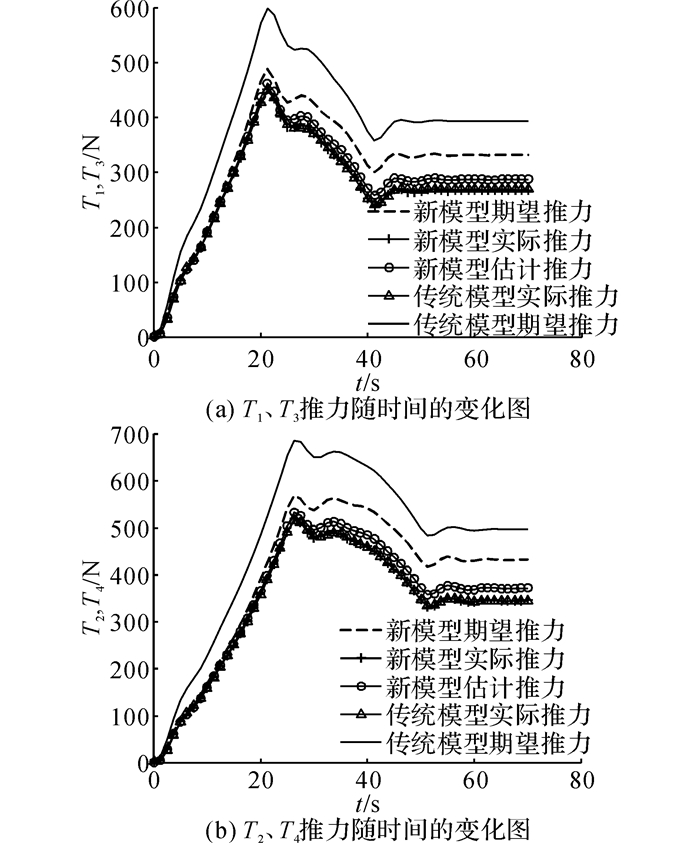
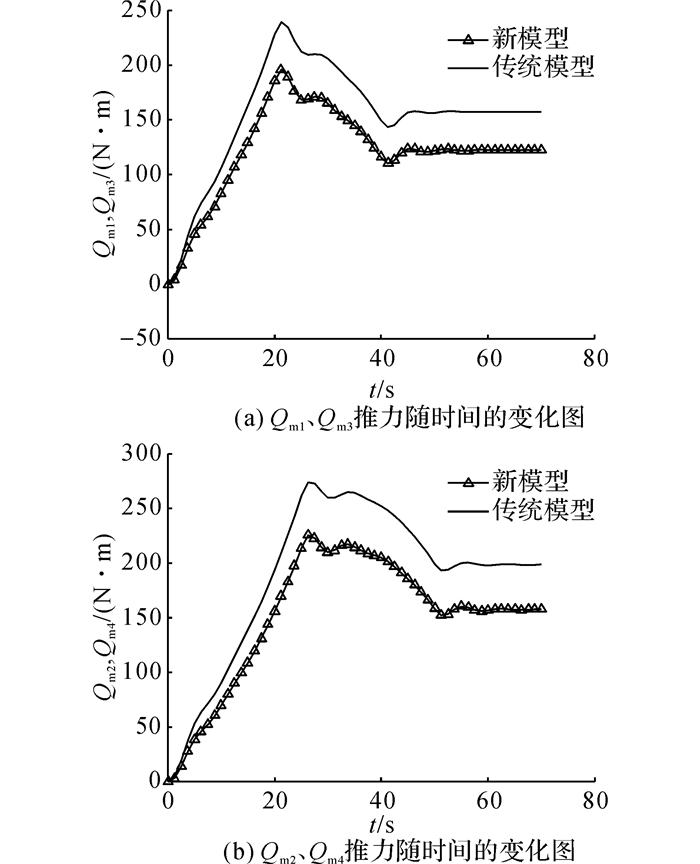
如图 11所示为飞艇传统模型和新模型下噪声wd随时间的变化曲线.如图 12所示为螺旋桨系统期望推力、实际推力和估计推力.可以看出, 反馈控制器能够很好地跟踪期望推力, 同时观测器估计推力和实际推力之间的误差是因为外界噪声wd≠0引起的, 这显示了螺旋桨系统是关于wd“输入-状态”稳定的.如图 13所示为在反馈控制器和传统控制器下的电机命令扭矩, 由于反馈控制器具有对推力损失很好的补偿能力和控制效果, 在非线性反馈控制器下电机所需的命令扭矩较传统控制扭矩小, 这会减小电机命令扭矩饱和问题发生的几率.
|
图 11 噪声随时间的变化图 Fig. 11 Time history of bounded input noise |
|
图 12 期望、实际、估计推力随时间的变化图 Fig. 12 Time history of desired thrusts, actual thrusts and estimated thrusts of propeller system |
|
图 13 电机命令扭矩随时间的变化图 Fig. 13 Time history of command motor torques |
(1) 本文针对飞艇的控制问题, 结合电机螺旋桨动力学模型与飞艇的六自由度动力学模型, 通过直接把电机螺旋桨扭矩信号作为控制系统的输入量, 引入电机-螺旋桨和螺旋线推力损失动力学方程, 使得飞艇模型更加准确, 避免螺旋桨性能变化所导致的控制效果变差甚至失效问题.
(2) 考虑电机螺旋桨动力学模型, 基于非线性状态观测器的反馈控制方法对螺旋桨桨推力损失进行在线估计和追踪期望推力.从理论上证明了观测器和控制器的“输入-状态”稳定性.
(3) 本文提出的方法与传统方法相比, 能够更好地跟踪位置期望值.同时, 可以大大地降低动力系统能源需求和螺旋桨电机命令扭矩, 从而延长飞艇持续巡航时间, 并避免电机由于过早出现饱和而导致的系统不稳定性.
| [1] | ZHENG X, WANG X, CHENG Z, et al. The efficiency analysis of high-altitude propeller based on vortex lattice lifting line theory[J]. The Aeronautical Journal, 2016: 1–22. |
| [2] | CHEN L, ZHOU G, YAN X, et al. Composite control of stratospheric airships with moving masses[J]. Journal of Aircraft, 2012, 49(3): 794–801. DOI:10.2514/1.C031364 |
| [3] | JIAO J, SONG B F, ZHANG Y G, et al. Optimal design and experiment of propellers for high altitude airship[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2017: 0954410017704217. |
| [4] | ZHENG Z W, YAN K Y, YU S X, et al. Path following control for a stratospheric airship with actuator saturation [EB/OL]. 2016-01-21. http://journals.sagepub.com/doi/pdf/10.1177/0142331215625770. |
| [5] | HAN D, WANG X L, CHEN L. Adaptive backstepping control for a multi-vectored thrust stratospheric airship with thrust saturation in wind[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2016, 230(1): 45–59. DOI:10.1177/0954410015586861 |
| [6] | CHEN S, WANG H, SONG B. Modeling and dynamic simulation study of big inertia propulsion system of high altitude airship [C]//2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC). Dengleng, China: IEEE, 2011: 4065-4068. |
| [7] | CHEN L, LIU F, WEN Y, et al. Design and control of a multi-vectored thrust airship[J]. Differences, 2015, 50: 2. |
| [8] | FOSSEN T I, BLANKE M. Nonlinear output feedback control of underwater vehicle propellers using feedback form estimated axial flow velocity[J]. IEEE Journal of Oceanic Engineering, 2000, 25(2): 241–255. DOI:10.1109/48.838987 |
| [9] | PIVANO L, JOHANSEN T A. A four-quadrant thrust estimation scheme for marine propellers: theory and experiments[J]. IEEE Transactions on Control Systems Technology, 2009, 17(1): 215–226. DOI:10.1109/TCST.2008.922602 |
| [10] | SMOGELI O N, SORENSEN A J, FOSSEN T I.Design of a hybrid power/torque thruster controller with thrust loss estimation [C]//Proceeding of IFAC Conference on Control Applications in Marine Systems (CAMS'04). Ancona: Elsevier, 2004. |
| [11] | PIVANO L, JOHANSEN T A, SMOGELI O N, et al. Nonlinear thrust controller for marine propellers in four-quadrant operations [C]//American Control Conference. New York: IEEE, 2007: 900-905. |
| [12] | KHALIL H K, GRIZZLE J W. Nonlinear systems[M]. 3rd ed. New Jersey: Prentice hall, 1996. |
| [13] | SMOGELI O N, RUTH E, SERENSEN A J. Experimental validation of power and torque thruster control [C]//Proceedings of the 2005 IEEE International Symposium on Mediterrean Conference on Control and Automation. Limassol: IEEE, 2005: 1506-1511. |



