空间绳系卫星系统(tethered satellite system, TSS)是指利用柔性系绳将两个或两个以上的卫星连接在一起的空间飞行系统.本文研究一种新型呈Golay-3分布的四星绳系闭合系统, 用于空间光学干涉测量.其中3颗作为集光器部署在空间, 另一颗星为中心星, 用于干涉成像.环绕星与中心星之间由用于传递光路的轻质光纤连接.
绳系卫星编队(tethered satellite formation, TSF)因其广泛的应用前景, 得到了越来越多研究者的关注.余本嵩等[1]对绳卫星系编队动力学和控制作了详细的调查研究.Jin等[2]介绍了系绳动力学模型和绳系系统的动力学模型和控制和相关的地面实验情况;Savaglio等[3]研究小偏心率椭圆轨道上绳系卫星平台的轨道平面内运动;Chapel等[4]考虑系绳系统中的“跳绳”运动, 给出预测该运动形式中的进动和圆化现象的模型;Beletsky等[5]提出双金字塔型编队模型, 当围绕地心指向进行旋转时, 该编队是稳定的;Kalantzis等[6]研究串行式多体绳系编队在三维空间中的动力学;Tragesser[7]研究用于对地观测的旋转三角形绳系构型, 该系统考虑系绳弹性时没有稳定的构型;Tregesser等[8]研究三维双金字塔型构型时, 发现一些特别的构型是稳定的;Kim等[9]提出多种多星体闭环形式的绳系构型;Kumar[10]研究轨道平面内旋转三角形编队的动力学;刘丽丽等[11]研究系绳释放过程中, 在张力限制下的饱和控制器;Williams等[12]研究对地观测绳系编队的动力学, 提出最适合对地观测任务的旋转速度;刘延柱[13]利用高斯最小拘束原理研究释放中的绳系卫星的动力学模型;Yousefian等[14]针对双星绳系系统的防震动问题, 设计最小二乘控制器来减小系绳的震动.Wen等[15]研究三体绳系面内编队回收的控制问题, 提出新型的消耗能量小的回收方案.刘丽丽等[16]基于Gauss伪谱算法设计最优控制器, 利用系绳张力和电流实现三维绳系系统子星轨道转移.Chang等[17]设计基于状态相关黎卡提方程(SDRE)的控制器, 以减小卫星姿态误差.王长青等[18]研究绳系卫星释放过程中卫星姿态运动对系统的影响;Kristiansen等[19]将已有的几种绳系模型在数学形式上进行统一.
本文研究4颗卫星组成的绳系闭合编队系统, 主要工作如下:建立新型的四星闭合系统动力学模型, 推导存在的自旋平衡构型, 分析表明四星闭合系统自旋平衡构型是不稳定的.针对系统自旋难以保持相应构型的特点, 本文设计鲁棒性强的滑模变结构控制器, 采用符号函数和饱和函数设计滑模控制器.仿真结果表明, 该控制器具有较强的鲁棒性, 可以实现系统自旋平衡构型的稳定;分析指出采用软变结构策略的滑模控制器, 能够有效地减小系统抖震, 增强控制的稳定性.
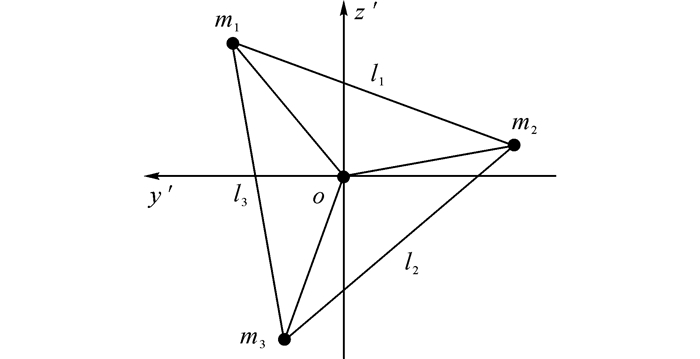
1 四星绳系系统动力学模型 1.1 空间几何关系在几何关系上3个点可以确定一个平面, 将3颗环绕星运行的平面称为构型平面, 这个平面是随时间变化的.环绕星系统的质心与几何中心始终重合, 建立质心的轨道坐标系oxyz, 则构型平面始终穿过原点o, 采用两个独立变量可以确定构型平面.假设构型平面由平面oyz经过以下过程生成:绕x轴转动角α, 绕y轴转动角θ.新的坐标系统为ox′y′z′, 构型平面为oy′z′, 如图 1(a)所示.称ox′y′z′为构型坐标系, 构型平面oy′z′与当地水平面oyz的夹角θ为构型倾角.为了使得构型平面描述具备唯一性, 对构型倾角进行约束, 即θ∈[-90°, 90°];当θ=0°时, α=0°;当θ=90°时, α∈[0, 180°).根据旋转关系可知, 从轨道坐标系oxyz到构型坐标系ox′y′z′的方向余弦矩阵为
| $ \mathit{\boldsymbol{R = }}\left[{\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta \sin \alpha }&{-\sin \theta \cos \alpha }\\ 0&{\cos \alpha }&{\sin \alpha }\\ {\sin \theta }&{-\cos \theta \sin \alpha }&{\cos \theta \cos \alpha } \end{array}} \right]. $ | (1) |

|
图 1 绳系编队系统的几何关系图 Fig. 1 Geometry of triangular tethered satellite formation |
在构型平面oy′z′中, 令m1与m2之间的系绳长为l1, m2与m3之间的系绳长为l2, 系绳向量为l1和l2分别表示从m1到m2、m2到m3的矢径, 从-y′轴顺时针地转到l1和l2的角度分别为ϕ1和ϕ2, 如图 1(b)所示.第j颗环绕星的坐标为(y′j, z′j), 根据几何关系可知,
| $ \left[{\begin{array}{*{20}{c}} {{{y'}_1}}&{{{z'}_1}}\\ {{{y'}_2}}&{{{z'}_2}}\\ {{{y'}_3}}&{{{z'}_3}} \end{array}} \right] = \mathit{\boldsymbol{M}}\left[{\begin{array}{*{20}{c}} {{l_1}\cos {\phi _1}}&{{l_1}\sin {\phi _1}}\\ {{l_2}\cos {\phi _2}}&{{l_2}\sin {\phi _2}} \end{array}} \right]. $ | (2) |
式中:M为与质量分布相关的矩阵,
| $ \mathit{\boldsymbol{M = }}\left[{\begin{array}{*{20}{c}} {{\eta _2} + {\eta _3}}&{{\eta _3}}\\ {-{\eta _1}}&{{\eta _3}}\\ {-{\eta _1}}&{-\left( {{\eta _1} + {\eta _2}} \right)} \end{array}} \right]. $ | (3) |
其中, ηj=mj/(m1+m2+m3).
1.2 动力学方程3颗环绕星相对中心星的动能为
| $ K = \frac{1}{2}\sum\limits_{j = 1}^3 {m\left( {{{\mathit{\boldsymbol{\dot r}}}_j} + \mathit{\boldsymbol{\omega }} \times {\mathit{\boldsymbol{r}}_j}} \right) \cdot \left( {{{\mathit{\boldsymbol{\dot r}}}_j} + \mathit{\boldsymbol{\omega }} \times {\mathit{\boldsymbol{r}}_j}} \right)} . $ | (4) |
式中:ω=[0, 0, ω]T为质心轨道的角速度矢量.式(4) 忽略每颗卫星绕着质心旋转的角速度对卫星瞬时轨道角速度的影响, 原因是在卫星绕着质心旋转的过程中, 其相对于质心的空间位置变化与质心相对于地心空间的变化相比, 可以忽略不计.
3颗环绕星相对于中心星的势能为
| $ U =-\sum\limits_{j = 1}^3 {\left( {\frac{{\mu {m_j}}}{{\left| {{\mathit{\boldsymbol{R}}_0} + {\mathit{\boldsymbol{r}}_j}} \right|}}-\frac{{\mu {m_j}}}{{\left| {{\mathit{\boldsymbol{R}}_0}} \right|}}} \right)} . $ | (5) |
式中:R0为质心轨道矢量, 其方向与卫星旋转坐标系的x轴一致;rj为每颗卫星相对矢量, 则有|rj|
四星系统的相对动能与相对势能差为
| $ V = K-U. $ | (6) |
根据Lagrange方程, 有
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial V}}{{\partial {{\dot q}_j}}}-\frac{{\partial V}}{{\partial {q_j}}} = {Q_{{q_j}}}. $ | (7) |
式中:qj为系统状态, Qqj为广义力.在该系统中, qj∈{l1, l2, ϕ1, ϕ2, α, θ}.将式(6) 代入式(7), 可得系统的动力学方程.构型平面内的动力学方程如下:
| $ \begin{array}{l} \frac{3}{m}{Q_{{l_j}}} = 2{{\ddot l}_i} + {{\ddot l}_j}\cos \left( {{\phi _i}- {\phi _j}} \right) + 2\left( {{{\dot \phi }_j} + b} \right){{\dot l}_j}\sin \left( {{\phi _i}- {\phi _j}} \right)-\\ \left( {a - \ddot \alpha \cos \theta - {{\ddot \phi }_j}} \right){l_j}\sin \left( {{\phi _i} - {\phi _j}} \right) - {\left( {{{\dot \phi }_j} + b} \right)^2}{l_j}\cos \left( {{\phi _i} - {\phi _j}} \right) - 2\left( {{{\dot \phi }_i} + b} \right){{\dot l}_i} + \\ cd\left[{2{l_i}\sin \left( {2{\phi _i}} \right) + {l_j}\sin \left( {{\phi _i} + {\phi _j}} \right)} \right] -\left( {{c^2} + 3{\omega ^2}{{\sin }^2}\theta -{\omega ^2}} \right)\left( {2{l_i}{{\sin }^2}{\phi _i} + {l_j}\sin {\phi _i}\sin {\phi _j}} \right) -\\ \left( {{d^2} - {\omega ^2}} \right)\left( {2{l_i}{{\cos }^2}{\phi _i} + {l_j}\cos {\phi _i}\cos {\phi _j}} \right), \end{array} $ | (8) |
| $ \begin{array}{l} \frac{3}{m}{Q_{{\phi _i}}} = {{\ddot l}_j}{l_i}\sin \left( {{\phi _j}- {\phi _i}} \right) + 2\left( {{{\ddot \phi }_i} + \ddot \alpha \cos \theta } \right)l_i^2 + \left( {{{\ddot \phi }_j} + \ddot \alpha \cos \theta } \right){l_i}{l_j}\cos \left( {{\phi _i} + {\phi _j}} \right)-\\ a{l_i}\left[{2{l_i} + {l_j}\cos \left( {{\phi _i} + {\phi _j}} \right)} \right] + 4\left( {{{\dot \phi }_i} + b} \right){l_i}{{\dot l}_i} + 2\left( {{{\dot \phi }_j} + b} \right){l_i}{{\dot l}_j}\cos \left( {{\phi _i} + {\phi _j}} \right) +\\ \left[{{{\left( {{{\dot \phi }_j} + b} \right)}^2} + {d^2}-{\omega ^2}} \right]{l_i}{l_j}\sin \left( {{\phi _i} + {\phi _j}} \right) + cd{l_i}\left[{2{l_i}\cos \left( {2{\phi _i}} \right) + {l_j}\cos \left( {{\phi _i} + {\phi _j}} \right)} \right] +\\ \left( {{d^2} -{c^2} -3{\omega ^2}{{\sin }^2}\theta } \right)\left( {2{l_i}\sin {\phi _i} + {l_j}\sin {\phi _j}} \right){l_i}\cos {\phi _i}. \end{array} $ | (9) |
式中:(i, j)=(1, 2) 或者(i, j)=(2, 1).由式(8)、(9) 可以看出, 自旋角速度越快, 系绳张力越大, 构型内保持稳定.构型平面外动力学方程如下所示:
| $ \begin{array}{l} \frac{3}{m}{Q_\alpha } = \cos \theta \left[{2\sum\limits_{i = 1}^2 {{{\ddot \phi }_i}l_i^2 + \left( {{{\ddot \phi }_1} + {{\ddot \phi }_2}} \right){l_1}{l_2}\cos \left( {{\phi _1}-{\phi _2}} \right)} } \right] + \left( {{{\ddot l}_1}{l_2} - {l_1}{{\ddot l}_2}} \right)\cos \theta \sin \left( {{\phi _1} - {\phi _2}} \right) + \\ 2\dot \alpha \left[{2\sum\limits_{i = 1}^2 {{l_i}{{\dot l}_i} + \left( {{{\dot l}_1}{l_2}-{l_1}{{\dot l}_2}} \right)\cos \left( {{\phi _1}-{\phi _2}} \right)} } \right] +\\ 2\cos \theta \left[{2\sum\limits_{i = 1}^2 {{{\dot \phi }_i}{l_i}{{\dot l}_i} + \left( {{{\dot \phi }_1}{{\dot l}_1}{l_2}-{{\dot \phi }_2}{l_1}{{\dot l}_2}} \right)\cos \left( {{\phi _1}-{\phi _2}} \right)} } \right] - \\ 2c\sin \theta \left[{\sum\limits_{i = 1}^2 {{l_i}{{\dot l}_i}\sin \left( {2{\phi _1}} \right)}-2\sum\limits_{i = 1}^2 {{{\dot \phi }_i}l_i^2{{\cos }^2}{\phi _i} + {{\dot l}_1}{l_2}\sin {\phi _1}\cos {\phi _2} + {l_1}{{\dot l}_2}\cos {\phi _1}\sin {\phi _2}}-} \right.\\ \left. {\left( {{{\dot \phi }_1}-{{\dot \phi }_2}} \right){l_1}{l_2}\cos {\phi _1}\cos {\phi _2}} \right] -\\ 2d\sin \theta \left[{e-\sum\limits_{i = 1}^2 {{{\dot \phi }_i}l_i^2\sin \left( {2{\phi _i}} \right)-\left( {\sin {\phi _2}-\sin {\phi _1}} \right){l_1}{l_2}} \sum\limits_{i = 1}^2 {{{\dot \phi }_i}\cos {\phi _i}} } \right] - \\ \left[{2\dot \alpha + \cos \theta \left( {{{\dot \phi }_1} + {{\dot \phi }_2}} \right)} \right]\left( {{{\dot \phi }_1} - {{\dot \phi }_2}} \right){l_1}{l_2}\sin \left( {{\phi _1} - {\phi _2}} \right) +\\ \left( {{\omega ^2}\sin 2\alpha + 2\ddot \alpha } \right)\left[{\sum\limits_{i = 1}^2 {l_i^2 + {l_1}{l_2}\cos \left( {{\phi _1}-{\phi _2}} \right)} } \right] + \\ f\left[{\left( {{\omega ^2}{{\cos }^2}\alpha-{c^2}} \right)\cos \theta-\ddot \theta \sin \theta } \right] - g\left[{2\ddot \alpha {{\sin }^2}\theta + {\omega ^2}\sin 2\alpha \left( {1 + {{\cos }^2}\theta } \right) + 4d\dot \theta \cos \theta } \right], \end{array} $ | (10) |
| $ \begin{array}{*{20}{l}} \begin{array}{l} \frac{3}{m}{Q_\theta } = 2d\left( {\sum\limits_{i = 1}^2 {{l_i}{{\dot l}_i}\sin \left( {2{\phi _1}} \right) + {{\dot l}_1}{l_2}\cos {\phi _1}\sin {\phi _2} + {l_1}{{\dot l}_2}\sin {\phi _1}\cos {\phi _2}} + } \right.\\ \left. {2\sum\limits_{i = 1}^2 {{{\dot \phi }_i}l_i^2{{\sin }^2}{\phi _i} + {l_1}{l_2}\sin {\phi _1}\sin {\phi _2}} \sum\limits_{i = 1}^2 {{{\dot \phi }_i}} } \right) + \end{array}\\ {2c\left( {e + \sum\limits_{i = 1}^2 {{{\dot \phi }_i}l_i^2\sin \left( {2{\phi _i}} \right) + {l_1}{l_2}\cos {\phi _1}\sin {\phi _2}} \sum\limits_{i = 1}^2 {{{\dot \phi }_i}} } \right) -\\ f\left[ {\ddot \alpha \sin \theta - \dot \alpha \omega \sin \alpha \cos \theta - \omega b\sin \alpha } \right] + }\\ {g\left[ {2bd - 3{\omega ^2}\sin \left( {2\theta } \right) + 2\left( {\ddot \theta + \dot \alpha \omega \cos \alpha } \right)} \right].} \end{array} $ | (11) |
式中:
| $ \left. \begin{array}{l} a = \dot \theta \left( {\dot \alpha \sin \theta + \omega \cos \alpha \cos \theta } \right)-\dot \alpha \omega \sin \alpha \sin \theta, \\ b = \dot \alpha \cos \theta-\omega \cos \alpha \sin \theta, \\ c = \dot \theta + \omega \sin \alpha, \\ d = \dot \alpha \sin \theta + \omega \cos \alpha \cos \theta, \\ e = 2\sum\limits_{i = 1}^2 {{l_i}{{\dot l}_i}{{\sin }^2}{\phi _i} + \left( {{{\dot l}_1}{l_2} + {l_1}{{\dot l}_2}} \right)\sin {\phi _1}\sin {\phi _2}}, \\ f = \sum\limits_{i = 1}^2 {l_i^2\sin \left( {2{\phi _i}} \right) + {l_1}{l_2}\sin \left( {{\phi _1} + {\phi _2}} \right), } \\ g = \sum\limits_{i = 1}^2 {l_i^2{{\sin }^2}{\phi _i} + {l_1}{l_2}\sin {\phi _1}\sin {\phi _2}.} \end{array} \right\} $ | (12) |
该模型如图 2所示.
|
图 2 绳系编队系统的闭环结构 Fig. 2 Closed loop structure of tethered formationsystem |
利用系绳将卫星连接, 可以在较低成本的前提下有效地抑制构型发散.对于旋转稳定的绳系编队系统, 离心力使得系绳一直处于紧张状态, 使得构型形状能够得到自动维持, 只需对构型平面进行控制.
2 自旋平衡构型分析 2.1 自旋平衡构型基于前文假设可知, 连接中心星与环绕星之间系绳不承担力的作用.自旋平衡构型是在某一恒定自旋角速度下, 形状得到保持且构型平面指向不变的构型.显然, 系绳之间的拉力需要满足uj≥0, 此处uj=3Tj/(mω2L), j=1, 2, 3为无量纲的系绳张力.为了方便, 引入系绳之间的长度比ε和系绳角度差Δϕ如下:
| $ \left. \begin{array}{l} \varepsilon = {\mathit{\Lambda }_2}/{\mathit{\Lambda }_1}, \\ \Delta \phi = {\phi _2}-{\phi _1}. \end{array} \right\} $ | (13) |
定义无量纲时间为τ=ωt, ()′=d/dτ为对无量纲时间的导数.无量纲长度为Λj=lj/L, Γj=rj/L, 其中L为系绳完全展开时的长度.为了描述的唯一性, 对卫星的编号顺序进行限制:编号从小到大的顺序与构型平面法线向量ox′一致, 因此, 角度误差Δϕ≥0.考虑到Λ″1=Λ′1=0, Λ″2=Λ′2=0, α″=α′=0, β″=β′=0, ϕ′1=ϕ′2=ϕ′≠0, 并且需要对任意ϕ1成立, 可得
| $ \left. {\begin{array}{*{20}{c}} {\alpha = {0^ \circ }, {{180}^ \circ }, }\\ {\theta = {{30}^ \circ }} \end{array}} \right\}或\left. {\begin{array}{*{20}{c}} {\varepsilon = 1, }\\ {\Delta \phi = {{120}^ \circ }.} \end{array}} \right\} $ | (14) |
即自旋平衡构型有以下2种情况.
1) 特定平面内空间圆构型如下:自旋角速度为ϕ′=ϕ*, 系绳处于松弛状态, 与自由编队飞行的空间圆队形相同, 构型倾角θ=30°, 构型方位角α=0°或α=180°.
2) 任意平面内的等边三角形构型如下:系绳上的张力大于0, 满足ε=1且Δϕ=120°, 构型角速度ϕ′≥2.58或ϕ′≤-0.58.
为了使系绳能够始终处于紧张状态, 需要有足够大的自旋角速度来克服重力梯度来维持构型形状;对于空间圆编队平面内的自旋构型来说, 构型形状的维持破坏了构型平面本身的稳定性, 需要提供额外的控制力来保持构型平面的稳定性.
2.2 自旋平衡构型稳定性分析考虑系统呈等边三角形分布, 自旋角速度ϕ′满足前面提出的要求, 令状态向量为
| $ \mathit{\boldsymbol{x = }}\left[{\begin{array}{*{20}{c}} \alpha \\ \theta \\ {\alpha '}\\ {\theta '} \end{array}} \right]. $ | (15) |
系统状态方程为
| $ \mathit{\boldsymbol{x' = }}f\left( \mathit{\boldsymbol{x}} \right). $ | (16) |
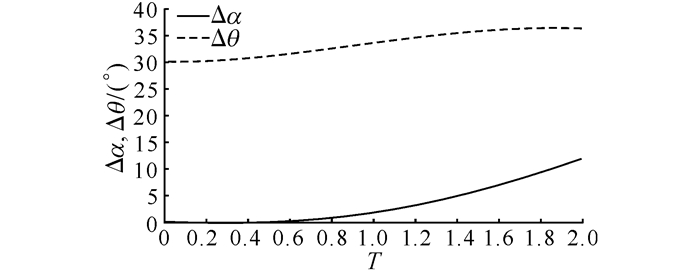
以初始参数α=0°, θ=30°, ϕ′=1.1为例进行仿真, 如图 3所示.图中,T为轨道周期.可以看出, 两个轨道周期内构型方位角偏差为12°, 构型倾角偏差为15.9°.在不施加额外控制力的情形下, 构型参数逐渐发散, 系统不稳定.由于系绳的存在使系统具有强非线性特性, 滑模控制(SMC)具有抗干扰性好、强鲁棒性的特点, 选取滑模控制对系统进行构型保持控制.
|
图 3 构型参数变化 Fig. 3 Change of configuration parameters |
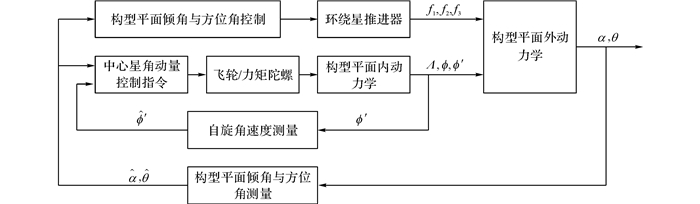
研究的四星星绳系编队系统构型利用自旋保持构型平面内稳定和喷气推进施加主动控制, 保持构型外稳定;对于自旋构型系统, 构型平面外和构型平面内的运动可以认为是解耦的, 控制系统分内、外2个环路, 方框图如图 4所示.
|
图 4 四星绳系闭合系统控制方框图 Fig. 4 Control block diagram of four-body closed tether system |
根据式(10)、(11) 可知, 当自旋速度达到一定值时, 构型平面内能够保持稳定.构型平面外的运动方程为
| $ \left. \begin{array}{l} \left[{\alpha ''\left( {{{\sin }^2}\theta-2} \right) + \theta '\alpha '\sin 2\theta + } \right.\\ 2\left( {\phi '\sin \theta + \cos \alpha {{\cos }^2}\theta } \right)\theta ' + \\ \left. {\left( {2\phi '-\cos \alpha \sin \theta } \right)\sin \alpha \sin \theta } \right] = {\eta _\alpha }\sin \theta, \\ \left[{\theta '' + 2\left( {\phi '\sin \theta + \cos \alpha {{\cos }^2}\theta } \right)\alpha '-} \right.\\ \left( {3 + {{\cos }^2}\alpha-{\alpha ^{'2}}} \right)\cos \theta \sin \theta + \\ \left. {2\phi '\cos \alpha \cos \theta } \right] = {\eta _\theta }. \end{array} \right\} $ | (17) |
式中:
| $ \left. \begin{array}{l} {\eta _\alpha } = \frac{2}{{3\mathit{\Lambda }}}\left[{{f_1}, {f_2}, {f_3}} \right]\mathit{\boldsymbol{M}}\left[{\begin{array}{*{20}{c}} {\cos {\phi _1}}\\ {\cos {\phi _2}} \end{array}} \right], \\ {\eta _\theta } = \frac{2}{{3\mathit{\Lambda }}}\left[{{f_1}, {f_2}, {f_3}} \right]\mathit{\boldsymbol{M}}\left[{\begin{array}{*{20}{c}} {\sin {\phi _1}}\\ {\sin {\phi _2}} \end{array}} \right]. \end{array} \right\} $ | (18) |
其中,
| $ {f_j} = \frac{3}{{m{\omega ^2}L}}{F_j}, $ |
Fj为控制力.中心星与环绕星系统的质心位置重合要求主动控制力的合力为零, 即满足f1+f2+f3=0, 可得
| $ \left[{\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ {{f_3}} \end{array}} \right] = \sqrt 3 \mathit{\Lambda }\left[{\begin{array}{*{20}{c}} {\cos \left( {{\phi _1} + {{30}^ \circ }} \right)}&{\sin \left( {{\phi _1} + {{30}^ \circ }} \right)}\\ {\cos \left( {{\phi _1} + {{150}^ \circ }} \right)}&{\sin \left( {{\phi _1} + {{150}^ \circ }} \right)}\\ {\cos \left( {{\phi _1} + {{270}^ \circ }} \right)}&{\sin \left( {{\phi _1} + {{270}^ \circ }} \right)} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{\eta _\alpha }}\\ {{\eta _\beta }} \end{array}} \right]. $ | (19) |
设计闭环控制律时, 只需选取合适的ηα和ηθ, 即可得到每颗星所需的控制力.
取构型平面参数为αd=0°和θd=30°, 构型自旋角速度ϕ′>1.定义控制误差为Δα=α-αd, Δθ=θ-θd;误差状态向量为
| $ \mathit{\boldsymbol{\hat x' = }}\hat f\left( \mathit{\boldsymbol{x}} \right) + \hat G\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{\hat u}}. $ | (20) |
光滑函数
令r=[Δα, Δθ]T, 有干扰存在时, 系统动力学方程(20) 可以改写成
| $ \mathit{\boldsymbol{r'' = \bar f + \bar g}}\left( {\mathit{\boldsymbol{\hat u}} + {\mathit{\boldsymbol{u}}_{\rm{d}}}} \right). $ | (21) |
式中:ud为干扰力,
| $ \mathit{\boldsymbol{\bar g = }}\left[{\begin{array}{*{20}{c}} {{{\hat G}_{31}}}&{{{\hat G}_{32}}}\\ {{{\hat G}_{41}}}&{{{\hat G}_{42}}} \end{array}} \right]. $ |
假设干扰力有界, 且满足:
| $ \left| {\left[{\mathit{\boldsymbol{\bar g}}{\mathit{\boldsymbol{u}}_{\rm{d}}}} \right]\left( i \right)} \right| \le u_{\rm{d}}^ * \left( i \right);\;\;i = 1, 2. $ | (22) |
选取滑模切换面s为
| $ \mathit{\boldsymbol{s}}\left( \mathit{\boldsymbol{x}} \right) = \left[\varepsilon \right]\mathit{\boldsymbol{r}} + \mathit{\boldsymbol{r'}}. $ | (23) |
式中:[ε]为正对角阵.选取Lyapunov函数为V=sTs/2, 其对无量纲时间τ的导数为
| $ V' = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left[{\mathit{\boldsymbol{\bar f + \bar g}}\left( {\mathit{\boldsymbol{\hat u}} + {\mathit{\boldsymbol{u}}_{\rm{d}}}} \right) + \left[\varepsilon \right]\mathit{\boldsymbol{r'}}} \right]. $ | (24) |
令
| $ \mathit{\boldsymbol{\bar f + \bar g\hat u}} + {\mathit{\boldsymbol{K}}_u}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) + \left[\varepsilon \right]\mathit{\boldsymbol{r' = }}0. $ | (25) |
式中:Ku为对角正定增益矩阵;sgn(s)为s的分量取符号函数sgn(sj)组成的列向量.相应的控制律为
| $ \mathit{\boldsymbol{\hat u}} =- {{\mathit{\boldsymbol{\bar g}}}^{- 1}}\left[{\mathit{\boldsymbol{\bar f + }}\left[\varepsilon \right]\mathit{\boldsymbol{r'}} + {\mathit{\boldsymbol{K}}_u}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right)} \right]. $ | (26) |
为了减小抖振的不利影响, 可以采用饱和函数代替符号函数, 得到最终的控制律为
| $ \mathit{\boldsymbol{\hat u}} =- {{\mathit{\boldsymbol{\bar g}}}^{- 1}}\left[{\mathit{\boldsymbol{\bar f + }}\left[\varepsilon \right]\mathit{\boldsymbol{r'}} + {\mathit{\boldsymbol{K}}_u}{\rm{sat}}\left( {\mathit{\boldsymbol{s}}, \delta } \right)} \right]. $ | (27) |
式中:
| $ {\rm{sat}}\left( {{s_j}, \delta } \right) = \left\{ \begin{array}{l} {s_j}/\delta, \;\;\;\;\;\;\;\left| {{s_j}} \right| < \delta ;\\ {\mathop{\rm sgn}} \left( {{s_j}} \right), \;\;\;\left| {{s_j}} \right| \ge \delta . \end{array} \right. $ | (28) |
为了使得误差收敛较快, 一般取增益kui
| $ \mathit{\boldsymbol{\hat u}} \cong- {{\mathit{\boldsymbol{\bar g}}}^{- 1}}\left[{\left( {{\mathit{\boldsymbol{K}}_u}\left[\varepsilon \right]/\delta } \right)\mathit{\boldsymbol{r + }}\left( {{\mathit{\boldsymbol{K}}_u}/\delta + \left[\varepsilon \right]} \right)\mathit{\boldsymbol{r' + \bar f}}} \right]. $ | (29) |
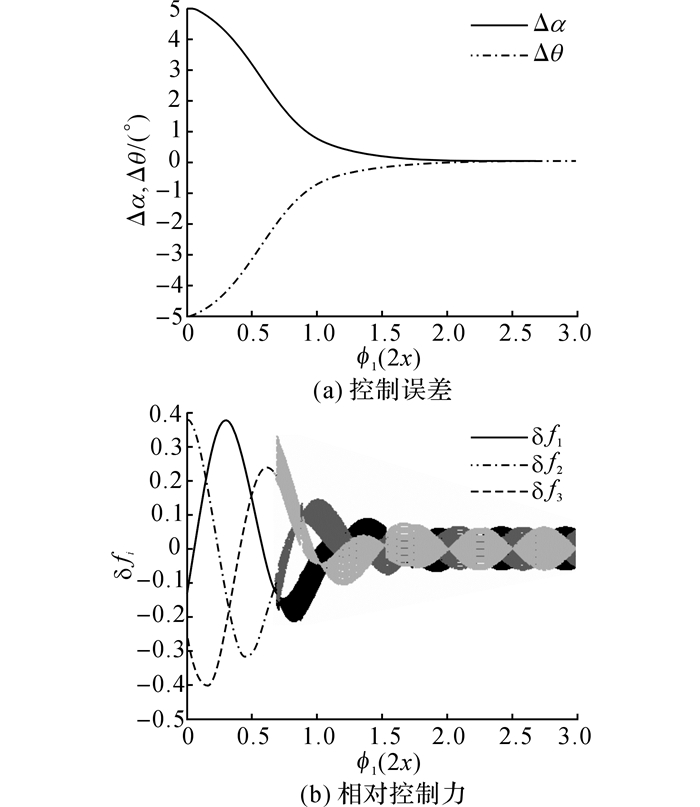
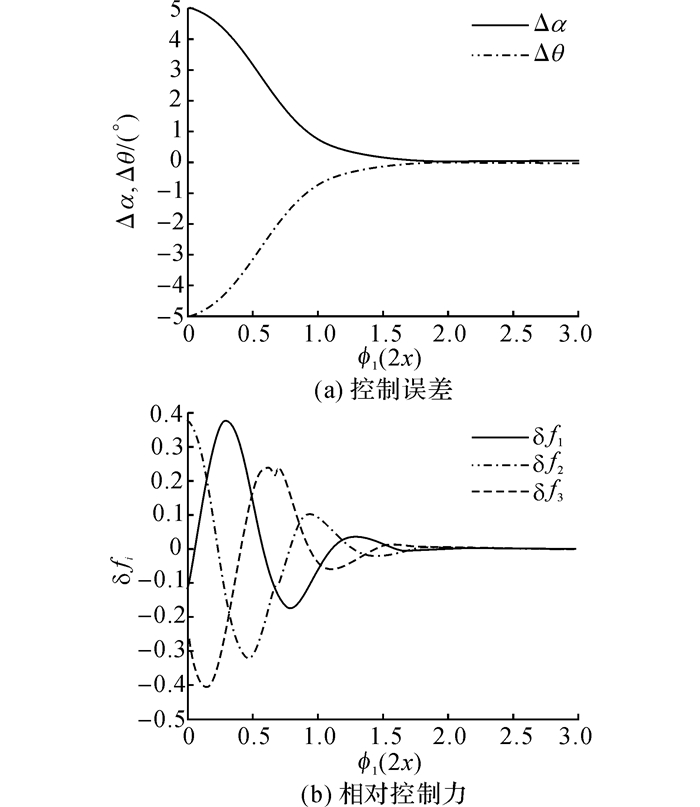
取自旋角速度为ϕ′=1.015, 噪声量级为10-3, 控制参数设置为ε=0.5, Ku=10-2I, δ=10-3.仿真初始误差为Δα0=-5°, Δθ0=5°, 仿真结果如图 5、6所示.图 5采用符号函数的控制策略, 图 6采用饱和函数的软变结构策略.从图 5(a)、6(a)可以看出, 两种滑模变结构控制均能使系统构型状态误差较快地收敛, 使系统自旋平衡构型达到稳定状态;对比图 5(b)、6(b)可知, 采用符号函数时, 相对控制力存在较严重的抖振, 采用饱和函数的软变结构策略可以明显地降低系统相对控制力的抖振, 提高系统稳定性.
|
图 5 滑模控制方法 Fig. 5 Sliding mode control |
|
图 6 滑模控制软变结构方法 Fig. 6 Soft variable structure method of SMC |
本文针对空间四星绳系闭合系统自旋平衡构型的不稳定性, 设计基于滑模变结构的控制器.首先提出新的Golay-3布局的绳系编队系统, 即1颗位于空间圆圆心上的中心星与3颗均匀分布在空间圆上的环绕星模型.分析模型动力学特性, 建立相应的动力学方程, 推导自旋平衡构型.为了消除系统自旋平衡构型的不稳定带来的不利影响, 分别设计基于符号函数和饱和函数的滑模变结构控制器.仿真结果表明, 两种控制器均可以保持系统自旋平衡稳定, 进一步分析表明采用饱和函数的滑模变结构控制器能够大幅度降低系统抖振, 有效增强自旋平衡构型的稳定性, 这一研究结果能够为工程实现提供一定的参考价值.
| [1] |
余本嵩, 文浩, 金栋平. 绳系卫星编队动力学及控制研究进展[J].
动力学与控制学报, 2015, 13(5): 321–328.
YU Ben-song, WEN Hao, JIN Dong-ping. Advances indynamics and control of tethered satellite formations[J]. Journal of Dynamics and Control, 2015, 13(5): 321–328. DOI:10.6052/1672-6553201520150501 |
| [2] | JIN D P, HU H Y. Advances in dynamics and control of tethered satellite systems[J]. Acta Mechanica Sinica, 2008, 24(3): 229–241. DOI:10.1007/s10409-008-0159-9 |
| [3] | SAVAGLIO C, VINH N X. Planar motion of a tethered satellite-platform system in a slightly elliptic orbit [C]//Proceedings of the AAS/AIAA Astrodynamics Conference. San Diego: Univelt, 1992: 2449-2468. |
| [4] | CHAPEL J D, FlANDERS H. Tether dynamics and control results for tethered satellite system's initial flight[J]. NASA STI/Recon Technical Report A, 1993, 95: 327–346. |
| [5] | BELETSKY, VLADIMIR V, LEVIN E M. Dynamics of space tether systems[J]. Advances in the Astronautical Sciences, 1993, 83(1993): 83–96. |
| [6] | KALANTZIS S, MODI V J, PRADHAN S, et al. Order-N formulation and dynamics of multibody tethered systems[J]. Journal of Guidance Control and Dynamics, 1998, 21(2): 277–285. DOI:10.2514/2.4233 |
| [7] | TRAGESSER S G. Formation flying with tethered spacecraft [C]//AIAA/AAS Astrodynamics Specialist Conference.: AIAA/AAS, 2000: 14-17. |
| [8] | TRAGESSER S G, TUNCAY A. Orbital design of earth-oriented tethered satellite formations [C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.: AIAA/AAS, 2002: 51-64. |
| [9] | KIM M, HALL C D. Control of a rotating variable-length tethered system[J]. Journal of Guidance Control and Dynamics, 2012, 27(5): 849–858. |
| [10] | KUMAR K D. Review on dynamics and control of nonelectrodynamic tethered satellite systems[J]. Journal of Spacecraft and Rockets, 2006, 43(4): 705–720. DOI:10.2514/1.5479 |
| [11] |
刘丽丽, 文浩, 金栋平, 等. 三维电动力绳系子卫星轨道转移的最优控制[J].
计算力学学报, 2011, 28(2): 178–182.
LIU Li-li, WEN Hao, JIN Dong-ping, et al. Optimal control of orbit transfer of 3-dimensional electric power rope[J]. Chinese Journal of Computational Mechanics, 2011, 28(2): 178–182. DOI:10.7511/jslx201102004 |
| [12] | WILLIAMS T, MOORE K. Dynamics of tethered satellite formations[J]. Advances in the Astronautical Sciences, 2002, 112: 1219–1235. |
| [13] |
刘延柱. 基于高斯原理的多体系统动力学建模[J].
力学学报, 2014, 46(6): 940–945.
LIU Yan-zhu. Modeling of multibody system dynamics based on Gauss principle[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 940–945. DOI:10.6052/0459-1879-14-143 |
| [14] | YOUSEFIAN P, SALARIEH H. Anti-sway control of tethered satellite systems using attitude control of the main satellite[J]. Acta Astronautica, 2015, 111: 300–307. DOI:10.1016/j.actaastro.2015.02.027 |
| [15] | WEN Hao, ZHU Zheng-hong, JIN Dong-ping, et al. Space tether deployment control with explicit tension constraint and saturation function[J]. Journal of Guidance Control and Dynamics, 2015, 39: 1–6. |
| [16] |
刘丽丽, 文浩, 金栋平, 等. 三体绳系卫星面内编队飞行的回收控制[J].
振动工程学报, 2008, 21(3): 223–227.
LIU Li-li, WEN hao, JIN Dong-ping, et al. Retrieval control of a three-body tethered formation in orbital plane[J]. Journal of Vibration Engineering, 2008, 21(3): 223–227. |
| [17] | CHANG I, PARK S Y, CHOI K H. Nonlinear attitude control of a tether-connected multi-satellite in three-dimensional space[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1950–1968. DOI:10.1109/TAES.2010.5595606 |
| [18] |
王长青, 杜崇刚, 李爱军. 绳系卫星释放阶段的空间姿态非线性稳定控制[J].
西北工业大学学报, 2016, 34(1): 60–66.
WANG Chang-qing, DU Chong-gang, LI Ai-jun. Nonlinear stability control of tethered sub-satellite attitude in deployment[J]. Journal of Northwestern Polytechnical University, 2016, 34(1): 60–66. |
| [19] | KRISTIANSEN K U, PALMER P, ROBERTS M. A unification of models of tethered satellites[J]. SIAM Journal on Applied Dynamical Systems, 2011, 10(3): 1042–1069. DOI:10.1137/090779887 |



