浮空器是指主要依靠大气浮力提供升力的一类飞行器[1].浮空器具有节能、垂直起降和滞空时间长等优点, 将在无人侦查和交通运输等方面发挥重要作用[2].欠驱动浮空器是指控制量的维数小于空间自由度的维数的浮空器.欠驱动特性普遍存在于现实中, 车辆、船舶、飞行器等很多机械装置都是欠驱动的[3].
欠驱动浮空器控制的主要难点是存在系统数学模型的强非线性, 各控制通道间相互耦合, 执行机构存在饱和约束以及系统内部不确定性与外部风场的干扰等问题, 给控制器的设计增加了难度[4].Yamada等[5]设计出一种自适应鲁棒控制器, 保证欠驱动浮空器在受到外界未知扰动和内部不确定的情况下, 系统状态全局收敛和稳定.Zheng等[6]利用制导律和轨迹线性化控制, 分别设计姿态控制环路, 速度控制环路, 控制欠驱动飞艇跟踪目标路径.
自滑模变结构控制(SMC)方法被Emelyanov[7]提出来后, 受到广泛关注.滑模变结构控制被运用在各种欠驱动系统上, 由于欠驱动系统不满足Brockett必要条件[8], 无法用解耦的方法单独设计各通道的控制律.利用滑模变结构控制解决欠驱动问题的主要在于使状态量降维.降维的方式主要为以下两种.
1) 设计虚拟控制, 使虚拟变量的维数等于控制量的维数.将虚拟变量视为控制对象, 利用状态间相互耦合的关系, 分别设计滑模变结构控制律.王岩[9]按照该设计过程, 将反步法与滑模变结构控制相结合, 加入滤波器实现滤波和微分的功能.Wang等[10]提出设计虚拟控制量的方法, 虽然没有用到滑模变结构控制, 但虚拟变量的设计方法值得借鉴.Ashrafiuon等[11-12]通过将跟踪位置误差和转角转变为跟踪速度误差, 实现降维.
2) 直接设计滑模变结构控制器, 利用多个自由度变量设计滑模面, 滑模面的个数等于或大于控制量的个数.刘贤朋等[13-14]介绍了滑模迭代的方法, 将欠驱动部分与可驱动部分通过非线性组合设计成滑模面, 得到滑模变结构控制律.
本文根据受控对象的特点, 按照第一种方法设计合适的控制器, 主要内容如下.1) 给出浮空器的三自由度模型.2) 利用滑模变结构控制设计外环环路, 安排目标指令的过渡过程, 同时计算目标指令的微分信号.3) 设计关于前飞速度的一阶滑模面, 求出推力, 设计关于侧向速度的二阶滑模面, 求出转矩.4) 设计连续滑模变结构控制, 通过调整边界层厚度, 减小滑模变结构控制律抖颤对执行机构的影响.5) 考虑浮空器所受到的复杂扰动影响, 引入自适应方法估计扰动上界, 提高控制器的鲁棒性.6) 通过仿真分析所设计控制器的有效性和鲁棒性.
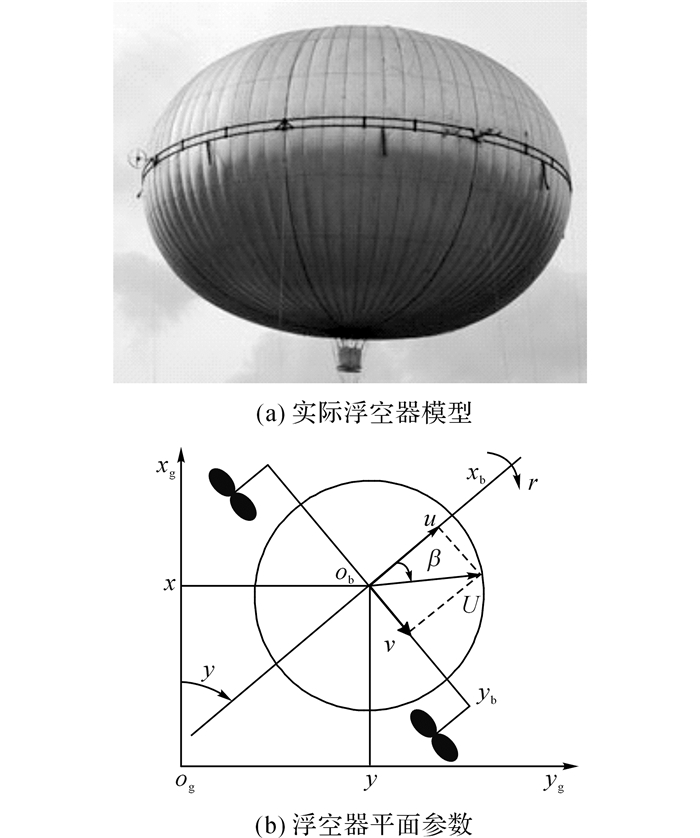
1 浮空器的模型讨论的浮空器是一种由矢量螺旋桨驱动的无尾飞艇, 艇体为欧拉体, 赤道位置两侧对称装有螺旋桨.浮空器只受到两个矢量螺旋桨驱动, 横侧向飞行是无法直接驱动的, 所以该浮空器是欠驱动的.这类浮空器的建模已经有较多的研究[15-18], 本文着重研究浮空器的水平运动特征, 根据张昊等[15-18]给出的六自由度模型, 提取出三自由度模型.如图 1所示为浮空器模型和浮空器的运动参数.浮空器的运动方程如下.
|
图 1 浮空器模型和平面运动参数 Fig. 1 Actual mode of aerostat and underactuated aerostat's horizontal kinematics |
| $ \begin{array}{*{20}{c}} {\left[{\begin{array}{*{20}{c}} {m + {m_{11}}}&0&0&0&0&0\\ 0&{m + {m_{22}}}&0&0&0&0\\ 0&0&{{I_z} + {m_{33}}}&0&0&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {\dot u}\\ {\dot v}\\ {\dot r}\\ {\dot x}\\ {\dot y}\\ {\dot \psi } \end{array}} \right] = }\\ {\left[{\begin{array}{*{20}{c}} {\left( {m + {m_{22}}} \right)vr + {F_{{\rm{A}}x}} + {F_{{\rm{T}}x}} + {\Delta _u}}\\ {-\left( {m + {m_{11}}} \right)ur + {F_{{\rm{A}}y}} + {\Delta _v}}\\ {\left( {{m_{11}}-{m_{22}}} \right)uv + {N_{\rm{a}}} + {N_{\rm{T}}} + {\Delta _r}}\\ {u\cos \psi-v\sin \psi }\\ {u\sin \psi + v\cos \psi }\\ r \end{array}} \right].} \end{array} $ | (1) |
式中:[x, y, ψ]分别为惯性坐标系xgogyg中, 浮空器的位置与偏航角;[u, v, r]为机体坐标系xbobyb中浮空器的速度与角速度;m为浮空器质量;Iz为浮空器沿ozg轴转动惯量, ozg轴为垂直于xgogyg平面, 与ogxg、ogyg轴构成笛卡尔坐标系;[m11, m22, m33]分别为附加质量.式(1) 的前3个公式表示机体坐标系中系统的动力学方程, 后3个公式表示惯性坐标系中的速度、角速度与机体坐标系中的速度、角速度间的变换关系.浮空器还受到气动力和力矩[FAx, FAy, Na], 螺旋桨推力和力矩[FTx, 0, NT]的作用, 该类浮空器在外形方面上下对称与左右对称, 浮心位于其体心.为了研究水平运动的特性, 需要消除垂直面内运动的影响, 假设浮心与重心重合, 重力等于浮力, 垂直方向不受重浮力及力矩作用.Δ=[Δu, Δv, Δr]为系统所受扰动, 系统总扰动可以表示为内部不确定因素与所受风扰的和, Δ=Δinside+Δwind.其中内扰与风扰分别为有界扰动:
| $ \left| {{\Delta _{{\rm{inside}}}}} \right| \le {{\bar \Delta }_{{\rm{inside}}}}, \left| {{\Delta _{{\rm{wind}}}}} \right| \le {{\bar \Delta }_{{\rm{wind}}}}. $ | (2) |
式中:Δinside、Δwind分别为内部不确定因素与外部扰动的上界.总扰动有界, 即|Δ|≤Δ-=Δinside+Δwind.
1.1 浮空器所受气动力浮空器所受气动力为
| $ \left. \begin{array}{l} {F_{{\rm{A}}x}} = {C_x}Q{S_{{\rm{ref}}}}\cos \beta, \\ {F_{{\rm{A}}y}} = {C_x}Q{S_{{\rm{ref}}}}\sin \beta, \\ {N_{\rm{a}}} = {C_{{\rm{m}}z}}Q{S_{{\rm{ref}}}}{l_{{\rm{ref}}}}-{\mathop{\rm sgn}} \left( r \right)k{r^2}. \end{array} \right\} $ | (3) |
式中:Cx、Cy为浮空器产生的气动力系数在ox、oy方向上的分量;Cmz为气动偏航力矩系数;Q为动压, Q=ρU2/2, 其中
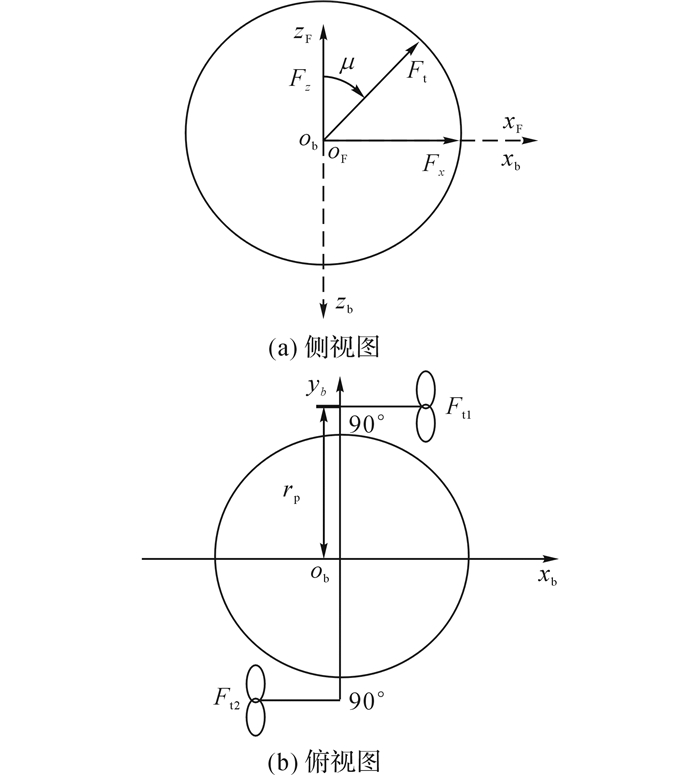
欠驱动浮空器有2个对称分布的矢量螺旋桨, 每个螺旋桨有2个控制自由度, 分别为推力大小和方向.单个螺旋桨提供的推力如图 2所示, 以螺旋桨桨叶中心为原点, 建立局部坐标系, 局部坐标系oxF方向与机体坐标系oxb重合, 局部坐标系ozF方向与机体坐标系ozb方向相反, 螺旋桨提供xbobzb平面内的推力FT.桨叶顺时针旋转产生垂直螺旋桨面的力, 令初始时刻桨面平行于xbobzb平面, 桨叶转动, 产生的力方向为正, 顺时针转动桨面μ, 0 < μ < 2π.
|
图 2 螺旋桨局部坐标系 Fig. 2 Partial coordinate of propellers |
如图 2(a)所示为螺旋桨局部坐标侧视图.图中, 坐标轴xFoFzF为螺旋桨局部坐标系, Ft为螺旋桨输出推力在xFoFzF中的表示, Fx、Fz为Ft沿oFxF、oFzF方向分解:
| $ {F_x} = {F_{\rm{t}}}\sin \mu, {F_z} = {F_{\rm{t}}}\cos \mu . $ | (4) |
如图 2(b)所示为螺旋桨局部坐标侧视图.图中, Ft1、Ft2为两个螺旋桨输出推力.螺旋桨输出的矢量推力对机体浮心产生的推力及力矩为
| $ \left[{\begin{array}{*{20}{c}} {{F_{{\rm{T}}x}}}\\ {{N_{\rm{T}}}} \end{array}} \right] = \mathit{\boldsymbol{R}}\left[{\begin{array}{*{20}{c}} {{F_{{\rm{t1}}}}\sin {\mu _1}}\\ {{F_{{\rm{t2}}}}\sin {\mu _2}}\\ {{F_{{\rm{t1}}}}\cos {\mu _1}}\\ {{F_{{\rm{t2}}}}\cos {\mu _2}} \end{array}} \right], \mathit{\boldsymbol{R = }}\left[{\begin{array}{*{20}{c}} 1&{-1}&0&0\\ {{r_{\rm{p}}}}&{{r_{\rm{p}}}}&0&0 \end{array}} \right]. $ | (5) |
式中:rp为螺旋桨安装轴心与机体浮心的距离, R为控制分配矩阵.由于R不是方阵, 须求广义逆, 采用MATLAB中的pinv(.)命令处理.
2 运动学关系设目标状态量为(xd, yd, ψd, ud, vd, rd), 根据式(1) 的第4、5个公式可知, 目标速度ud、vd与目标速度
| $ \left. \begin{array}{l} {u_{\rm{d}}} = {{\dot x}_{\rm{d}}}\cos \psi + {{\dot y}_{\rm{d}}}\sin \psi, \\ {v_{\rm{d}}} =-{{\dot x}_{\rm{d}}}\sin \psi + {{\dot y}_{\rm{d}}}\cos \psi . \end{array} \right\} $ | (6) |
为了让浮空器实际位置达到目标轨迹, 减少可能出现的位置稳态误差, 根据误差方程xe=x-xd, ye=y-yd, ue=u-ud, ve=v-vd, 将(ue,ve)与(xe,ye)相关联, 重新定义新的目标速度[12]:
| $ \left. \begin{array}{l} {{\tilde u}_{\rm{d}}} = {{\dot x}_{\rm{d}}}\cos \psi + {{\dot y}_{\rm{d}}}\sin \psi-k\left( {{x_{\rm{e}}}\cos \psi + {y_{\rm{e}}}\sin \psi } \right), \\ {{\tilde v}_d} =-{{\dot x}_{\rm{d}}}\sin \psi + {{\dot y}_{\rm{d}}}\cos \psi + k\left( {{x_{\rm{e}}}\sin \psi-{y_{\rm{e}}}\cos \psi } \right). \end{array} \right\} $ | (7) |
式中:参数k为正常数, 目标前飞速度与目标侧向速度由目标轨迹位置与跟踪位置误差共同决定, k决定了跟踪位置误差与目标轨迹位置之间的比例关系.两边同时求微分, 可得
| $ \left. \begin{align} & {{{\dot{\tilde{u}}}}_{\rm{d}}}={{{\ddot{x}}}_{\rm{d}}}\cos \psi +{{{\ddot{y}}}_{\rm{d}}}\sin \psi +{{{\tilde{v}}}_{d}}r-k\left( {{{\dot{x}}}_{\rm{e}}}\cos \psi +{{{\dot{y}}}_{\rm{e}}}\sin \psi \right), \\ & {{{\dot{\tilde{v}}}}_{d}}=-{{{\ddot{x}}}_{\rm{d}}}\sin \psi +{{{\ddot{y}}}_{\rm{d}}}\cos \psi-{{{\tilde{u}}}_{\rm{d}}}r+k\left( {{{\dot{x}}}_{\rm{e}}}\sin \psi-{{{\dot{y}}}_{\rm{e}}}\cos \psi \right). \\ \end{align} \right\} $ | (8) |
根据式(1) 可知,
| $ u = \dot x\cos \psi + \dot y\sin \psi, v =-\dot x\sin \psi + \dot y\cos \psi . $ | (9) |
速度误差方程可以表示为
| $ {{\tilde u}_{\rm{e}}} = u-{{\tilde u}_{\rm{d}}}, {{\tilde v}_{\rm{e}}} = v-{{\tilde v}_{\rm{d}}}. $ | (10) |
根据式(7)、(9)、(10) 可知, 速度误差表示为
| $ \left[{\begin{array}{*{20}{c}} {{{\tilde u}_{\rm{e}}}}\\ {{{\tilde v}_{\rm{e}}}} \end{array}} \right] = \mathit{\boldsymbol{J}}\left[{\begin{array}{*{20}{c}} {{{\dot x}_{\rm{e}}} + k{x_{\rm{e}}}}\\ {{{\dot y}_{\rm{e}}} + k{y_{\rm{e}}}} \end{array}} \right], \mathit{\boldsymbol{J = }}\left[{\begin{array}{*{20}{c}} {\cos \psi }&{\sin \psi }\\ {-\sin \psi }&{\cos \psi } \end{array}} \right]. $ | (11) |
由于矩阵J非奇异,
由式(1) 可知, 角速度与速度耦合, 通过控制
| $ \begin{align} & \left[\begin{matrix} {{{\dot{\tilde{u}}}}_{\rm{e}}} \\ {{{\dot{\tilde{v}}}}_{\rm{e}}} \\ \end{matrix} \right]=\left[\begin{matrix} -r\sin \psi & r\cos \psi \\ -r\cos \psi &-r\sin \psi \\ \end{matrix} \right]\left[\begin{matrix} {{{\dot{x}}}_{\rm{e}}}+k{{x}_{\rm{e}}} \\ {{{\dot{y}}}_{\rm{e}}}+k{{y}_{\rm{e}}} \\ \end{matrix} \right]+ \\ & \ \ \ \ \ \ \ \ \ \ \left[\begin{matrix} \cos \psi & \sin \psi \\ -\sin \psi & \cos \psi \\ \end{matrix} \right]\left[\begin{matrix} {{{\ddot{x}}}_{\rm{e}}}+k{{{\dot{x}}}_{\rm{e}}} \\ {{{\ddot{y}}}_{\rm{e}}}+k{{{\dot{y}}}_{\rm{e}}} \\ \end{matrix} \right]= \\ & \ \ \ \ \ \ \ \ \ \ \left[\begin{matrix} r{{{\tilde{v}}}_{\rm{e}}} \\ -r{{{\tilde{u}}}_{\rm{e}}} \\ \end{matrix} \right]+\left[\begin{matrix} \cos \psi & \sin \psi \\ -\sin \psi & \cos \psi \\ \end{matrix} \right]\left[\begin{matrix} {{{\ddot{x}}}_{\rm{e}}}+k{{{\dot{x}}}_{\rm{e}}} \\ {{{\ddot{y}}}_{\rm{e}}}+k{{{\dot{y}}}_{\rm{e}}} \\ \end{matrix} \right]. \\ \end{align} $ | (12) |
离散滑模变结构控制器设计分为以下2个步骤:首先分别利用速度误差设计滑模面, 设计等效控制保证系统轨迹到达滑模面;然后利用切换函数设计变结构控制, 保证系统状态轨迹在滑模面上运动.
3.1.1 推力设计设计纵向控制律, 得到螺旋桨推力.以速度误差
| $ {S_1} = {\lambda _1}\int_0^t {{{\tilde u}_{\rm{e}}}\left( \tau \right){\rm{d}}\tau + {{\tilde u}_{\rm{e}}}} ;{\lambda _1} > 0, $ | (13) |
两边同时求微分, 可得
| $ {{{\dot{S}}}_{1}}={{\lambda }_{1}}{{{\tilde{u}}}_{\text{e}}}\left( \tau \right)+{{{\dot{\tilde{u}}}}_{\text{e}}}={{\lambda }_{1}}{{{\tilde{u}}}_{\text{e}}}\left( \tau \right)+\dot{u}-{{{\dot{\tilde{u}}}}_{\text{d}}}. $ | (14) |
将式(1) 的第1个公式代入, 有
| $ \begin{align} & {{{\dot{S}}}_{1}}=\frac{1}{m+{{m}_{11}}}\left[{{\lambda }_{1}}\left( m+{{m}_{11}} \right){{{\tilde{u}}}_{\text{e}}}+{{F}_{\text{A}x}}+{{F}_{\text{T}x}}+ \right. \\ & \ \ \ \ \ \ \left. \left( m+{{m}_{22}} \right)vr-\left( m+{{m}_{11}} \right){{{\dot{\tilde{u}}}}_{\text{d}}}+{{\Delta }_{u}} \right]. \\ \end{align} $ | (15) |
等效控制的推力为
| $ \begin{align} & {{F}_{\text{T}x\text{eq}}}=-\left[{{\lambda }_{1}}\left( m+{{m}_{11}} \right){{{\tilde{u}}}_{\text{e}}}+{{F}_{\text{A}x}}+ \right. \\ & \ \ \ \ \ \ \ \ \ \ \left. \left( m+{{m}_{22}} \right)vr-\left( m+{{m}_{11}} \right){{{\dot{\tilde{u}}}}_{\text{d}}} \right]. \\ \end{align} $ | (16) |
等效控制不足以保证系统在遇到干扰和内部不确定情况下系统的跟踪性能, 需要引入变结构控制, 令变结构控制:
| $ \left. \begin{array}{l} {F_{{\rm{T}}x{\rm{vss}}}} =-{K_1}\left( {m + {m_{11}}} \right){\mathop{\rm sgn}} \left( {{S_1}} \right), \\ {F_{{\rm{T}}x}} = {F_{{\rm{T}}x{\rm{eq}}}} + {F_{{\rm{T}}x{\rm{vss}}}}. \end{array} \right\} $ | (17) |
为了验证控制律(17) 能够使ue收敛, 证明过程如下.
证明:选取Lyapunov函数:
| $ {V_1} = \frac{1}{2}\left( {{m_{11}} + m} \right)S_1^2. $ | (18) |
等式两边同求微分:
| $ \begin{align} & {{{\dot{V}}}_{1}}=\left( m+{{m}_{11}} \right){{S}_{1}}{{{\dot{S}}}_{1}}= \\ & \ \ \ \ \ \ \ {{S}_{1}}\left( {{\lambda }_{1}}\left( m+{{m}_{11}} \right){{{\tilde{u}}}_{\text{e}}}+{{F}_{\text{A}x}}+{{F}_{\text{T}x}}+ \right. \\ & \ \ \ \ \ \ \ \left. \left( m+{{m}_{22}} \right)vr-\left( m+{{m}_{11}} \right){{{\dot{\tilde{u}}}}_{\text{d}}}+{{\Delta }_{u}} \right)= \\ & \ \ \ \ \ \ \ -\left( {{K}_{1}}\left( m+{{m}_{11}} \right)\rm{sgn} \left( {{S}_{1}} \right)+{{\Delta }_{u}} \right){{S}_{1}}. \\ \end{align} $ | (19) |
要满足
| $ {K_1} = \frac{{{{\bar \Delta }_u}}}{{\left( {m + {m_{11}}} \right)}} + {\eta _1};{\eta _1} > 0. $ | (20) |
将式(20) 代入式(19), 可得
| $ \begin{array}{l} \dot V =-\left( {{{\bar \Delta }_u}{S_1}{\mathop{\rm sgn}} \left( {{S_1}} \right) + {\Delta _u}{S_1}} \right)-\\ \;\;\;\;\;\;{\eta _1}\left( {m + {m_{11}}} \right){S_1}{\mathop{\rm sgn}} \left( {{S_1}} \right) \le \\ \;\;\;\;\;\;-{\eta _1}\left( {m + {m_{11}}} \right){S_1}{\mathop{\rm sgn}} \left( {{S_1}} \right). \end{array} $ | (21) |
满足Lyapunov稳定性定理, ue收敛到零.
3.1.2 转矩设计设计横向和偏航控制律, 得到转矩.以
| $ {{S}_{2}}={{{\dot{\tilde{v}}}}_{e}}+{{\lambda }_{2}}{{{\tilde{v}}}_{e}}+{{\lambda }_{3}}\int_{0}^{t}{{{{\tilde{v}}}_{e}}\left( \tau \right)\text{d}\tau }. $ | (22) |
式中:λ2、λ3为正常数, 两边同时微分, 可得
| $ {{{\dot{S}}}_{2}}={{{\ddot{\tilde{v}}}}_{e}}+{{\lambda }_{2}}{{{\dot{\tilde{v}}}}_{e}}+{{\lambda }_{3}}{{{\tilde{v}}}_{e}}=\ddot{v}-{{{\ddot{\tilde{v}}}}_{\text{d}}}+{{\lambda }_{2}}\left( \dot{v}-{{{\dot{\tilde{v}}}}_{\text{d}}} \right)+{{\lambda }_{3}}{{{\tilde{v}}}_{\text{e}}}. $ | (23) |
根据式(1), 计算横向速度的二阶微分:
| $ \begin{array}{l} \ddot v =- \frac{{u\frac{{m + {m_{11}}}}{{{I_z} + {m_{33}}}}\left[{\left( {{m_{11}}-{m_{22}}} \right)uv + {N_{\rm{a}}} + {N_{\rm{T}}} + {\Delta _r}} \right]}}{{m + {m_{22}}}} + \\ \;\;\;\;\;\;\;\frac{{{{\dot \Delta }_v}}}{{m + {m_{22}}}} + \mathit{\Pi}, \end{array} $ | (24) |
| $ \mathit{\Pi = }\frac{{\left[{\rho S{C_{Ly}}u-\left( {m + {m_{11}}} \right)r} \right]\dot u + \rho S{C_{Ly}}v\dot v}}{{m + {m_{22}}}}. $ | (25) |
根据式(8) 计算目标横向速度的二阶微分:
| $ \left. \begin{align} & {{{\ddot{\tilde{v}}}}_{\rm{d}}}={{v}_{r}}-{{{\tilde{u}}}_{\rm{d}}}\frac{\left( {{m}_{11}}-{{m}_{22}} \right)uv+{{N}_{a}}+{{N}_{\rm{T}}}+{{\Delta }_{r}}}{{{I}_{z}}+{{m}_{33}}}, \\ & {{v}_{r}}=-2r\left( {{{\ddot{x}}}_{\rm{d}}}\cos \psi +{{{\ddot{y}}}_{\rm{d}}}\sin \psi \right)-{{v}_{\rm{d}}}r-\\ & {{\overset{\ldots }{\mathop{x}}\, }_{\rm{d}}}\sin \psi +{{\overset{\ldots }{\mathop{y}}\, }_{\rm{d}}}\cos \psi +k\left( {{{\ddot{x}}}_{\rm{e}}}\sin \psi-{{{\ddot{y}}}_{\rm{e}}}\cos \psi \right)+ \\ & 2kr\left( {{{\dot{x}}}_{\rm{e}}}\cos \psi +{{{\dot{y}}}_{\rm{e}}}\sin \psi \right). \\ \end{align} \right\} $ | (26) |
令等效控制的力矩为
| $ \left. \begin{align} & {{N}_{\rm{Teq}}}=-{{b}^{-1}}\left[\mathit{\Pi }-{{v}_{r}}+{{\lambda }_{2}}\left( \dot{v}-{{{\dot{\tilde{v}}}}_{\rm{d}}} \right)+{{\lambda }_{3}}{{{\tilde{v}}}_{\rm{e}}} \right]-\\ & \ \ \ \ \ \ \ \ \ \ \ {{N}_{\rm{a}}}-\left( {{m}_{11}}-{{m}_{22}} \right)uv, \\ & b=\frac{{{{\tilde{u}}}_{\rm{d}}}}{{{I}_{z}}+{{m}_{33}}}-u\frac{m+{{m}_{11}}}{\left( m+{{m}_{22}} \right)\left( {{I}_{z}}+{{m}_{33}} \right)}. \\ \end{align} \right\} $ | (27) |
等效控制不足以保证系统在受到扰动情况下的性能, 定义变结构控制:
| $ {{N}_{\text{Tvss}}}=-{{K}_{2}}\left( {{I}_{z}}+{{m}_{33}} \right)\rm{sgn} \left( {{S}_{2}} \right). $ | (28) |
偏航控制力矩为
| $ {{N}_{\text{T}}}={{N}_{\text{Teq}}}+{{N}_{\text{Tvss}}}. $ | (29) |
为了验证控制力矩(29) 能够使偏航角速度与横侧向速度收敛, 证明过程如下.
证明:选取Lyapunov函数:
| $ \left. \begin{array}{l} {V_2} = \frac{1}{2}S_2^2, \\ {{\dot V}_2} = {S_2}{{\dot S}_2} =-{S_2}\left( {b{K_2}\left( {{I_z} + {m_{33}}} \right){\mathop{\rm sgn}} \left( {{S_2}} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {b{\Delta _r} + \frac{1}{{m + {m_{22}}}}{{\dot \Delta }_v}} \right). \end{array} \right\} $ | (30) |
要满足
| $ \left. \begin{array}{l} {K_2} = \left( {b{\Delta _r} + \frac{1}{{m + {m_{22}}}}{{\dot \Delta }_v}} \right){\left[{b\left( {{I_z} + {m_{33}}} \right)} \right]^{ -1}} + {\eta _2}, \\ {\eta _2} > 0, b > 0. \end{array} \right\} $ | (31) |
将式(31) 代入式(30), 可得Lyapunov方程为
| $ \begin{align} & {{{\dot{V}}}_{2}}=-\left[b\left( {{{\bar{\Delta }}}_{r}}\left| {{S}_{2}} \right|+{{\Delta }_{r}}{{S}_{2}} \right)+\frac{1}{m+{{m}_{22}}}\times \right. \\ & \ \ \ \ \ \ \ \ \left. \left( {{{\dot{\bar{\Delta }}}}_{v}}\left| {{S}_{2}} \right|+{{{\dot{\Delta }}}_{v}}{{S}_{2}} \right) \right]-{{\eta }_{2}}b\left( {{I}_{z}}+{{m}_{33}} \right)\left| {{S}_{2}} \right|\le \\ & \ \ \ \ \ \ \ \ -{{\eta }_{2}}b\left( {{I}_{z}}+{{m}_{33}} \right)\left| {{S}_{2}} \right|. \\ \end{align} $ | (32) |
要满足b>0, 则须保证:
| $ \frac{{{{\tilde u}_{\rm{d}}}}}{{{I_z} + {m_{33}}}}-u\frac{{m + {m_{11}}}}{{\left( {m + {m_{22}}} \right)\left( {{I_z} + {m_{33}}} \right)}} > 0. $ | (33) |
只研究浮空器前向飞行状态, 即u>0.为了达到满意的跟踪性能, 稳态前飞速度误差与稳态当前速度的关系为
偏航稳定性得证, ve稳定并趋于零.在执行机构饱和能力范围内, 浮空器可以抵御风扰和内部不确定性的影响.
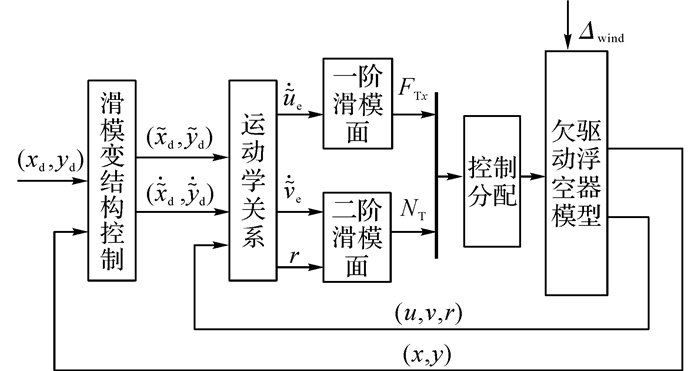
3.2 改进滑模变结构控制器离散滑模变结构控制在保持系统稳定和抵抗干扰方面具有很好的性能, 但是由于控制的不连续性, 离散滑模变结构控制不可避免会产生抖颤.抖颤现象会导致执行机构的反复制动, 严重影响寿命, 甚至会影响系统的稳定性[19].本文提出改进滑模变结构控制, 设计外环控制回路对输入信号进行处理, 内环控制回路运用连续滑模变结构控制, 设计推力和力矩.控制器的结构如图 3所示.
|
图 3 改进滑模变结构控制结构框图 Fig. 3 Structure picture of advanced SMC |
为了根据目标轨迹规划出合理的虚拟轨迹, 设计外环控制回路, 采用滑模变结构控制器.设控制系统如下:
| $ \left. \begin{array}{l} {{\dot x}_1} = {x_2}, \\ {{\dot x}_2} = u. \end{array} \right\} $ | (34) |
式中:x1、x2为虚拟轨迹的状态量.令跟踪误差e=x1-xd, 滑模面设计为
| $ \sigma {\rm{ = }}\dot e + {c_1}e + {c_2}\int_0^t {e{\rm{d}}} \tau . $ | (35) |
对式(35) 求微分, 可得
| $ \begin{array}{l} \dot \sigma = \ddot e + {c_1}\dot e + {c_2}e = \\ \;\;\;\;\;\;\left( {{{\dot x}_2}-{{\ddot x}_{\rm{d}}}} \right) + {c_1}\left( {{{\dot x}_1}-{{\dot x}_{\rm{d}}}} \right) + {c_2}\left( {{x_1}-{x_{\rm{d}}}} \right) = \\ \;\;\;\;\;\;\left( {u - {{\ddot x}_{\rm{d}}}} \right) + {c_1}\left( {{x_2} - {{\dot x}_{\rm{d}}}} \right) + {c_2}\left( {{x_1} - {x_{\rm{d}}}} \right). \end{array} $ | (36) |
令等效控制为
| $ u = {c_1}{{\dot x}_{\rm{d}}}-{c_1}{x_2}-{c_2}{x_1} + {c_2}{x_{\rm{d}}} + {{\ddot x}_{\rm{d}}}. $ | (37) |
假设目标轨迹的指令无干扰, 设计虚拟轨迹无需考虑变结构控制.论证系统(34) 的稳定性如下.
证明:设计Lyapunov方程为
| $ V = \frac{1}{2}{\sigma ^2}. $ | (38) |
对式(38) 微分, 可得
| $ \dot V = \sigma \dot \sigma = 0. $ | (39) |
可知, 在不受扰动的前提下, 等效控制能够保证系统(34) 稳定.
以下列轨迹为例, 目标轨迹为
| $ x = 3t + 200;y = 4t. $ | (40) |
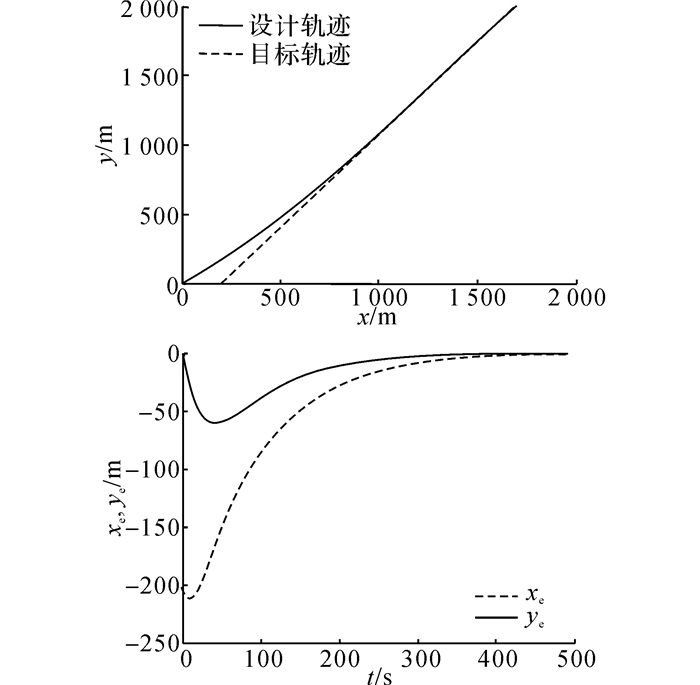
初始点[x(0), y(0)]=[0, 0], x、y轴的控制参数分别为c1x=0.1, c2x=0.001, c1y=0.05, c2y=0.000 5, 设计外环控制.轨迹规划与位置误差如图 4所示.
|
图 4 轨迹规划与位置误差 Fig. 4 Trajectory planning and position errors |
利用滑模变结构控制律(17) 和(29), 对系统控制需要预先知道扰动的上界Δ, 可是这在实际环境中往往很难做到[20].扰动上界估计过大, 将增大控制的抖动, 影响系统的稳定;扰动上界估计过小, 则无法消除扰动的影响.设计自适应滑模变结构控制, 可以在未知扰动的情况下, 实现对扰动的估计和补偿, 同时保证系统的稳定性.
根据式(17)、(29) 设计推力和转矩, 等效控制为式(16)、(27).以推力为例, 变结构控制部分的设计如下:
| $ {F_{{\rm{Tvss}}}} =-{\beta _1}\left( {m + {m_{11}}} \right){\mathop{\rm sgn}} \left( {{S_1}} \right). $ | (41) |
与式(20) 类似, 其中β1为
| $ {\beta _1} = \frac{{{\mathit{\Gamma }_u}}}{{\left( {m + {m_{11}}} \right)}} + {\eta _1};{\eta _1} > 0. $ | (42) |
式中:Γu表示对Δu的估计, 满足条件:
| $ {{\mathit{\dot \Gamma }}_u} = {\alpha _u}\left( {m + {m_{11}}} \right)\left| {{S_1}} \right|. $ | (43) |
其中, αu为正常数.令扰动估计误差为
证明:设计Lyapunov方程为
| $ {{\tilde V}_1} = \frac{1}{2}\left( {m + {m_{11}}} \right)S_1^2 + \frac{1}{{2{\alpha _u}}}\mathit{\tilde \Gamma }_u^2. $ | (44) |
对式(44) 两边微分, 可得
| $ \begin{align} & {{{\dot{\tilde{V}}}}_{1}}=\left( m+{{m}_{11}} \right){{S}_{1}}{{{\dot{S}}}_{1}}+{{{\mathit{\tilde{\Gamma }}}}_{u}}{{{\mathit{\dot{\tilde{\Gamma }}}}}_{u}}/{{\alpha }_{u}}= \\ & \ \ \ \ -{{\eta }_{1}}\left( m+{{m}_{11}} \right){{S}_{1}} \rm{sgn} \left( {{S}_{1}} \right)+\left( {{\Delta }_{u}}{{S}_{1}}-{{{\bar{\Delta }}}_{u}}\left| {{S}_{1}} \right| \right)\le \\ & \ \ \ \ -{{\eta }_{1}}\left( m+{{m}_{11}} \right){{S}_{1}} \rm{sgn} \left( {{S}_{1}} \right)\le 0. \\ \end{align} $ | (45) |
可知, S1与
转矩的设计如下:
| $ {N_{\rm{T}}} = {N_{{\rm{Teq}}}}-{\beta _2}\left( {{I_z} + {m_{33}}} \right){\mathop{\rm sgn}} \left( {{S_2}} \right). $ | (46) |
| $ \left. \begin{array}{l} {\beta _2} = \left( {b{\mathit{\Gamma }_r} + \frac{1}{{m + {m_{22}}}}{\mathit{\Gamma }_v}} \right){\left[{b\left( {{I_z} + {m_{33}}} \right)} \right]^{ -1}} + {\eta _2};\\ {\eta _2} > 0;b > 0, {{\mathit{\dot \Gamma }}_r} = {\alpha _r}b\left| {{S_2}} \right|, {{\mathit{\dot \Gamma }}_v} = {\alpha _v}\left| {{S_2}} \right|/\left( {m + {m_{22}}} \right). \end{array} \right\} $ | (47) |
设计扰动估计误差
证明:设计Lyapunov方程如下:
| $ \left. \begin{align} & {{V}_{2}}=\frac{1}{2}S_{2}^{2}+\frac{1}{2{{\alpha }_{r}}}\mathit{\tilde{\Gamma }}_{r}^{2}+\frac{1}{2{{\alpha }_{v}}}\mathit{\tilde{\Gamma }}_{v}^{2}, \\ & {{{\dot{V}}}_{2}}={{S}_{2}}{{{\dot{S}}}_{2}}+\frac{1}{{{\alpha }_{r}}}{{{\mathit{\tilde{\Gamma }}}}_{r}}{{{\mathit{\dot{\tilde{\Gamma }}}}}_{r}}+\frac{1}{{{\alpha }_{v}}}{{{\mathit{\tilde{\Gamma }}}}_{v}}{{{\mathit{\dot{\tilde{\Gamma }}}}}_{v}}= \\ & \ \ \ \ \ -{{S}_{2}}\left[b{{\beta }_{2}}\left( {{I}_{z}}+{{m}_{33}} \right)\rm{sgn} \left( {{S}_{2}} \right)+b{{\Delta }_{r}}+ \right. \\ & \ \ \ \ \ \left. {{{\dot{\Delta }}}_{v}}/\left( m+{{m}_{22}} \right) \right]+\left( {{\mathit{\Gamma }}_{r}}-{{{\bar{\Delta }}}_{r}} \right)b\left| {{S}_{2}} \right|+ \\ & \ \ \ \ \ \left( {{\mathit{\Gamma }}_{r}}-{{{\bar{\dot{\Delta }}}}_{v}} \right)\left| {{S}_{2}} \right|/\left( m+{{m}_{22}} \right)= \\ & \ \ \ \ \ -\left( b{{{\bar{\Delta }}}_{r}}\left| {{S}_{2}} \right|-b{{\Delta }_{r}}{{S}_{2}} \right)-\left( {{{\bar{\dot{\Delta }}}}_{v}}\left| {{S}_{2}} \right|-{{{\dot{\Delta }}}_{v}}{{S}_{2}} \right)/ \\ & \ \ \ \ \ \left( m+{{m}_{22}} \right)-{{\eta }_{2}}\left( {{I}_{z}}+{{m}_{33}} \right)\left| {{S}_{2}} \right|\le \\ & \ \ \ \ \ -{{\eta }_{2}}\left( {{I}_{z}}+{{m}_{33}} \right)\left| {{S}_{2}} \right|\le 0. \\ \end{align} \right\} $ | (48) |
可知, S2与
由于滑模变结构控制的不连续性会导致执行机构发生抖颤现象, 将不连续的控制函数sgn替换为连续的控制函数sat:
| $ {\rm{sat}}\left( {\frac{S}{\varepsilon }} \right) = \left\{ \begin{array}{l} {\mathop{\rm sgn}} S, \;\;\left| {\frac{S}{\varepsilon }} \right| > 1, \varepsilon > 0;\\ \left| {\frac{S}{\varepsilon }} \right|, \;\;\;\;\;\left| {\frac{S}{\varepsilon }} \right| \le 1, \varepsilon > 0. \end{array} \right. $ | (49) |
式中:ε为边界层厚度.为了保证用饱和函数sat替换sgn后系统稳定性不变, 下面证明替换饱和函数的系统满足Lyapunov稳定性.
证明:用饱和函数sat替换sgn, 式(45) 替换为
| $ \begin{align} & {{{\dot{V}}}_{1}}={{S}_{1}}{{{\dot{S}}}_{1}}+{{{\mathit{\tilde{\Gamma }}}}_{u}}{{{\mathit{\dot{\tilde{\Gamma }}}}}_{u}}/\left[\alpha \left( m+{{m}_{11}} \right) \right]= \\ & \ \ \ \ \ \ -\left( {{\beta }_{1}}\rm{sat}\left( {{S}_{1}}/{{\varepsilon }_{1}} \right)+{{\Delta }_{u}} \right){{S}_{1}}+ \\ & \ \ \ \ \ \ {{{\mathit{\tilde{\Gamma }}}}_{u}}\left( {{{\mathit{\dot{\Gamma }}}}_{u}}-{{{\dot{\bar{\Delta }}}}_{u}} \right)/\left[\alpha \left( m+{{m}_{11}} \right) \right]. \\ \end{align} $ | (50) |
满足
| $ {\beta _1} = \frac{{{\mathit{\Gamma }_u}{\mathop{\rm sgn}} \left( {{S_1}} \right)}}{{\left( {m + {m_{11}}} \right){\rm{sat}}\left( {{S_1}/{\varepsilon _1}} \right)}} + {\eta _1}. $ | (51) |
式中:η1为大于零的常数.当满足|S1/ε1|>1时, 证明与离散滑模变结构控制一样, 系统保持稳定.当|S1/ε1|≤1时, 式(50) 满足:
| $ \begin{array}{l} {{\dot V}_1} =-\left( {{{\bar \Delta }_u}\left| {{S_1}} \right| + {\Delta _u}{S_1}} \right)/\left( {m + {m_{11}}} \right)-{\eta _1}\left| {{S_1}} \right| \le \\ \;\;\;\;\;\;\;-{\eta _1}\left| {{S_1}} \right|. \end{array} $ | (52) |
同理, 式(48) 替换为
| $ \begin{align} & {{{\dot{V}}}_{2}}={{S}_{2}}{{{\dot{S}}}_{2}}+\frac{1}{{{\alpha }_{r}}}{{{\mathit{\tilde{\Gamma }}}}_{r}}{{{\mathit{\dot{\tilde{\Gamma }}}}}_{r}}+\frac{1}{{{\alpha }_{r}}}{{{\mathit{\tilde{\Gamma }}}}_{v}}{{{\mathit{\dot{\tilde{\Gamma }}}}}_{v}}= \\ &-{{S}_{2}}\left( b{{\beta }_{2}}\left( {{I}_{z}}+{{m}_{33}} \right)\rm{sat}\left( {{S}_{2}} \right)+b{{\Delta }_{r}}+\frac{1}{m+{{m}_{22}}}{{{\dot{\Delta }}}_{v}} \right)+ \\ & \left( {{\mathit{\Gamma }}_{r}}-{{{\bar{\Delta }}}_{r}} \right)b\left| {{S}_{2}} \right|+\left( {{\mathit{\Gamma }}_{v}}-{{{\bar{\dot{\Delta }}}}_{v}} \right)\left| {{S}_{2}} \right|/\left( m+{{m}_{22}} \right). \\ \end{align} $ | (53) |
满足
| $ {\beta _2} = \frac{{\left( {b{\mathit{\Gamma }_r} + \frac{1}{{m + {m_{22}}}}{\mathit{\Gamma }_v}} \right){\mathop{\rm sgn}} \left( {{S_2}} \right)}}{{b\left( {{I_z} + {m_{33}}} \right){\rm{sat}}\left( {{S_2}} \right)}} + {\eta _2}. $ | (54) |
式中:η2为大于零的常数.当满足|S2/ε2|>1时, 证明与离散滑模变结构控制一样, 系统保持稳定.当|S2/ε2|≤1时, 满足:
| $ \begin{array}{l} {{\dot V}_2} =-{S_2}\left( {b{\beta _2}\left( {{I_z} + {m_{33}}} \right){S_2}/{\varepsilon _2} + {\Delta _{vr}}} \right) + \\ \;\;\;\;\;\;\;\left( {{\mathit{\Gamma }_{vr}}-{{\bar \Delta }_{vr}}} \right)\left| {{S_2}} \right| = \\ \;\;\;\;\;\;\;-\left( {{{\bar \Delta }_{vr}}\left| {{S_2}} \right| + {\Delta _{vr}}{S_2}} \right) - {\eta _2}b\left( {{I_z} + {m_{33}}} \right)\left| {{S_2}} \right| \le \\ \;\;\;\;\;\;\; - {\eta _2}b\left( {{I_z} + {m_{33}}} \right)\left| {{S_2}} \right| \le 0. \end{array} $ | (55) |
该系统满足Lyapunov稳定性条件, 稳定性不变.
为了防止饱和函数出现非线性饱和情况, 设定|S/ε|≤1, 即两个滑模面满足:
| $ \left. \begin{array}{l} \left| {{\lambda _1}\int_0^t {{u_{\rm{e}}}\left( \tau \right){\rm{d}}\tau + {u_{\rm{e}}}} } \right| \le {\varepsilon _1}, \\ \left| {{{\dot v}_{\rm{e}}} + {\lambda _2}{v_{\rm{e}}} + {\lambda _3}\int_0^t {{u_{\rm{e}}}\left( \tau \right){\rm{d}}\tau } } \right| \le {\varepsilon _2}. \end{array} \right\} $ | (56) |
以上海交通大学所做的欧拉体形浮空器为对象.仿真所需的浮空器结构参数如表 1所示.
| 表 1 仿真所需的浮空器结构参数 Table 1 Parameters of aerostat for simulation |
以式(40) 为目标轨迹, 初始状态为
| $ \left. \begin{array}{l} x\left( 0 \right) = 0, y\left( 0 \right) = 0, \psi \left( 0 \right) = 0, \\ u\left( 0 \right) = 0, v\left( 0 \right) = 0, r\left( 0 \right) = 0. \end{array} \right\} $ | (57) |
控制器参数为
| $ \left. \begin{array}{l} k = 0.05, {\lambda _1} = 0.001, r_1^1 = 0.01, r_2^1 = 0.01, {\lambda _2} = 2, \\ {\lambda _3} = 0.5, {\alpha _u} = 0.0001, {\alpha _v} = 0.000001, {\alpha _r} = 0.0001. \end{array} \right\} $ | (58) |
在浮空器可抗风能力范围内, 假设浮空器受到的风流扰动为
| $ {\Delta _{{\rm{win}}{{\rm{d}}_x}}} = \sin t;{\Delta _{{\rm{win}}{{\rm{d}}_y}}} = \cos t. $ | (59) |
沿着惯性坐标正方向, 风的方向为正, 反之为负.在有风流扰动的影响下, 浮空器机体坐标系中的速度表示为
| $ \left[{\begin{array}{*{20}{c}} {{u_w}}\\ {{v_w}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\cos \psi }&{-\sin \psi }\\ {\sin \psi }&{\cos \psi } \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{\Delta _{{\rm{win}}{{\rm{d}}_x}}}}\\ {{\Delta _{{\rm{win}}{{\rm{d}}_y}}}} \end{array}} \right]. $ | (60) |
浮空器所受动压为
| $ \tilde Q = \frac{1}{2}\rho \left[{{{\left( {u + {u_w}} \right)}^2} + {{\left( {v + {v_w}} \right)}^2}} \right]. $ | (61) |
将式(61) 代入式(3), 可得浮空器在受到风扰时的气动力和力矩.可知, 风流对浮空器的影响体现在气动力上, 即
| $ {\Delta _{{\rm{wind}}}} = \left[{{{\tilde F}_{{\rm{a}}x}}, {{\tilde F}_{{\rm{a}}y}}, {{\tilde N}_{\rm{a}}}} \right]. $ | (62) |
离散滑模变结构控制, 扰动上界估计为
| $ \bar \Delta = \left[{50, 50, 70} \right]. $ |
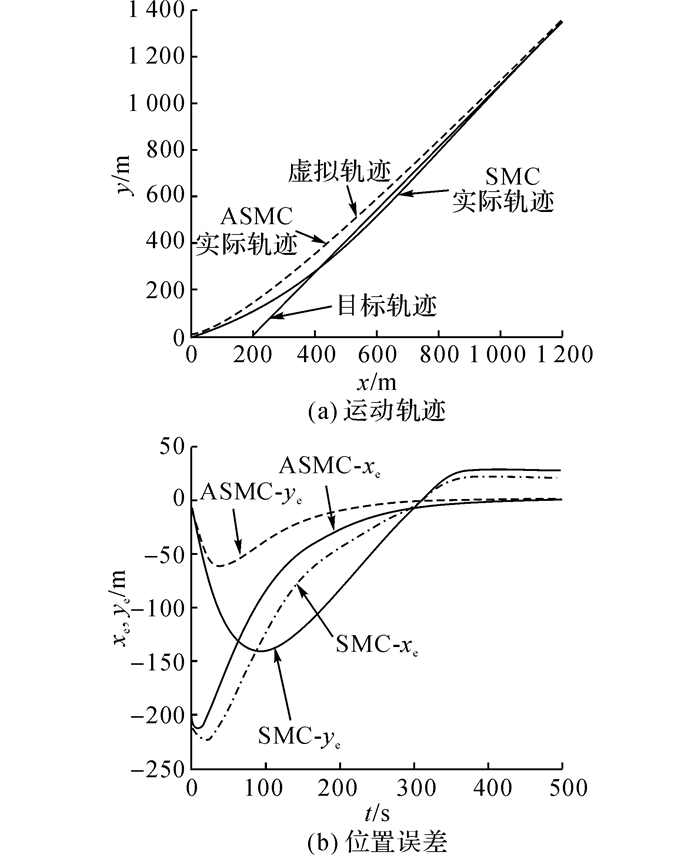
分别运用离散滑模变结构控制(SMC)与改进滑模变结构控制(ASMC)设计控制器, 浮空器运动轨迹如图 5(a)所示.采用ASMC控制方法, 则浮空器实际路径与外环控制回路规划的轨迹重合, 且最终趋于目标轨迹.跟踪位置误差如图 5(b)所示, 浮空器位置误差平滑减小, 最终在零附近稳定.采用SMC控制方法得到的系统实际轨迹与目标轨迹的偏差较大.
|
图 5 浮空器运动轨迹和位置误差 Fig. 5 Trajectory of aerostat and position errors |
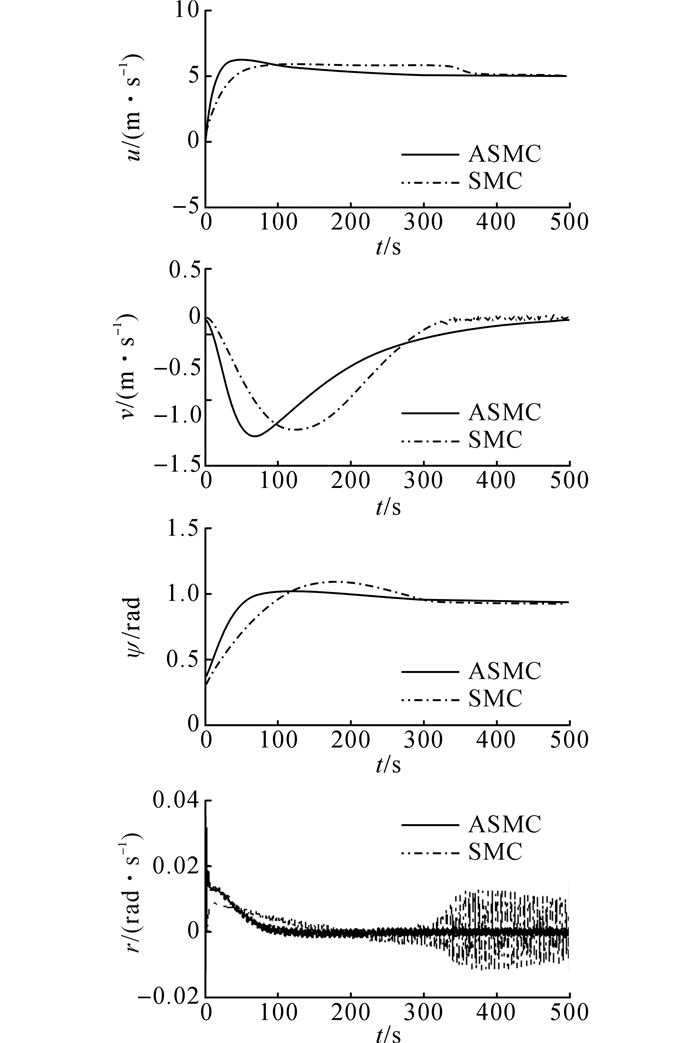
如图 6所示为浮空器机体坐标系的各状态量变化.改进滑模变结构(ASMC)控制器, 各状态量稳定, 角速度变化缓慢趋于零.由于存在扰动作用, 角速度存在抖颤.虽然离散滑模变结构(SMC)控制器的系统状态量趋于常值, 但是状态量抖动较大.
|
图 6 浮空器速度和偏航角与角速度变化 Fig. 6 Velocity, yaw and it's angular speed of aerostat |
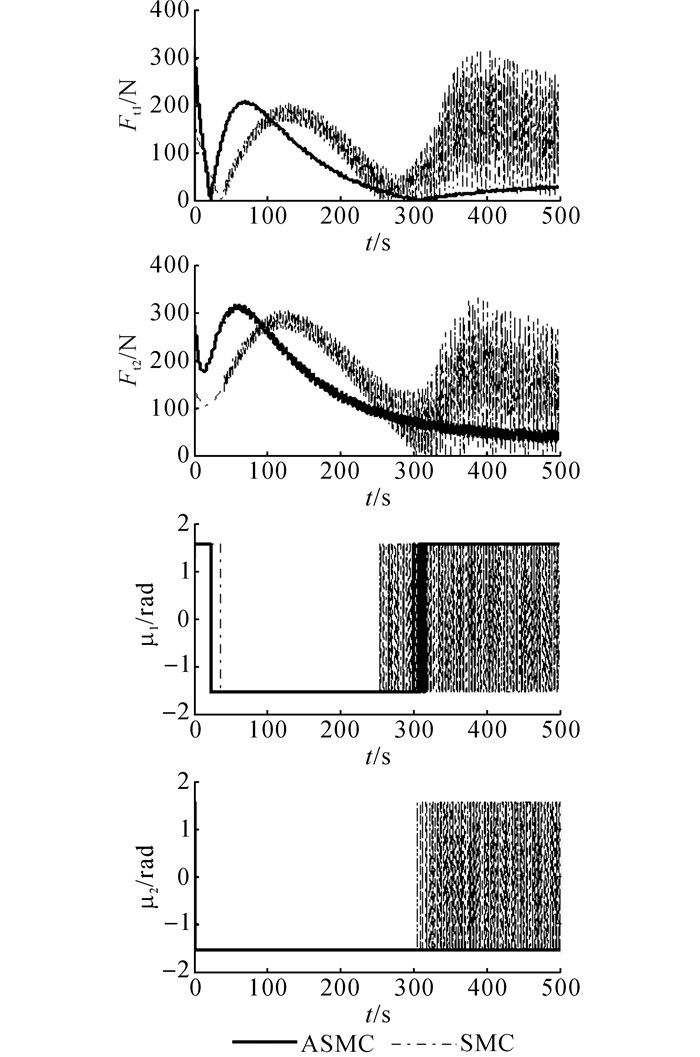
执行机构的推力与转角如图 7所示.采用改进滑模变结构控制器, 则执行机构输出未出现饱和, 抖颤较小, 螺旋桨制动较少.利用离散滑模变结构控制, 则螺旋桨频繁操作, 力的大小有较大抖动, 且推力达到饱和, 转角快速偏转.
|
图 7 执行机构的推力与转角变化 Fig. 7 Variation of actuators' force and angle |
如图 5~7所示, 所设计的滑模变结构控制器相对于离散滑模变结构控制器控制的有饱和约束和受扰动影响的欠驱动浮空器完成直线轨迹跟踪任务较好, 浮空器受扰动的影响较小, 鲁棒性较强.
5 结语本文建立欠驱动浮空器的三自由度模型, 设计内外环控制回路, 进行直线轨迹跟踪.解决了欠驱动浮空器模型的复杂非线性与状态量耦合、模型内部不确定与外部扰动、执行机构饱和、执行机构抖颤问题.将所设计的控制器与离散滑模变结构控制进行比较, 仿真显示了所设计控制器的有效性.
| [1] | CHEN L, ZHANG H, DUAN D P. Control system design of a multivectored thrust stratospheric airship[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2013, 228(11): 2045–2054. |
| [2] | LIESK T. Integral backstepping control of an unmanned, unstable, fin-less airship [C]//AIAA Guidance, Navigation, and Control Conference. Toronto: [s. n.], 2010. |
| [3] |
丁凤. 几类欠驱动机器人系统的滑模控制与应用[D]. 武汉: 华中科技大学, 2013.
DING Feng. Sliding mode control and application for underactuated robot systems [D]. Wuhan: Huazhong University of Science and Technology, 2013. |
| [4] | HUANG J, DING F, WANG Y. Sliding mode control with nonlinear disturbance observer for a class of underactuated system [C]//2013 32nd Chinese Control Conference (CCC). [S. l.]: IEEE, 2013: 541-546. |
| [5] | YAMADA M, TAKI Y, KATAYAMA A, et al. Robust global stabilization and disturbance rejection of an underactuated nonholonomic airship [C]//IEEE International Conference on Control Applications. Singapore: IEEE: 2007: 886-891. |
| [6] | ZHENG Z, HUO W. Planar path following control for stratospheric airship[J]. IET Control Theory and Applications, 2013, 7(2): 185–201. DOI:10.1049/iet-cta.2011.0462 |
| [7] | EMELYANOV S V. Variable structure control systems: synthesis of scalar and vector systems by state and output feedback[J]. Computational Mathematics and Modeling, 2010, 21(3): 253–274. DOI:10.1007/s10598-010-9069-3 |
| [8] | BROCKETT R W. Asymptotic stability and feedback stabilization[J]. Differential Geometric Control Theory, 1983, 27(1): 181–191. |
| [9] |
王岩. 欠驱动船舶运动的非线性鲁棒控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
WANG Yan. Research on nonlinear robust control of underactuated surface vessels motion [D]. Harbin: Harbin Engineering University, 2013. |
| [10] | WANG W, HUANG J. Globally adaptive path tracking control of underactuated ships [C]//2013 25th Chinese Control and Decision Conference (CCDC). Guiyang: IEEE, 2013: 595-600. |
| [11] | ASHRAFIUON H, MUSKE K R, MCNINCH L C, et al. Sliding-mode tracking control of surface vessels[J]. IEEE Transactions on Industrial Electronics, 2008, 55(11): 4004–4012. DOI:10.1109/TIE.2008.2005933 |
| [12] | YU R, ZHU Q, XIA G, et al. Sliding mode tracking control of an underactuated surface vessel[J]. IET Control Theory and Applications, 2012, 6(3): 461–466. DOI:10.1049/iet-cta.2011.0176 |
| [13] |
刘贤朋, 卜仁祥, 刘勇. 基于动态滑模的欠驱动船舶航迹跟踪控制[J].
大连海事大学学报, 2014(2): 5–9.
LIU Xian-peng, BU Ren-xiang, LIU Yong. Path following for underactuated ships based on dynamic sliding mode control[J]. Journal of Dalian Maritime University, 2014(2): 5–9. |
| [14] | LI R, LI T, BU R, et al. Active disturbance rejection with sliding mode control based course and path following for underactuated ships[J]. Mathematical Problems in Engineering, 2013, 2013(1): 1–9. |
| [15] |
张昊. 多螺旋桨组合浮空器非线性PID和多胞LPV鲁棒控制器设计[D]. 上海: 上海交通大学, 2014.
ZHANG Hao. Controller design of multi-propeller airship by using nonlinear PID and polytropic LPV robust approaches [D]. Shanghai: Shanghai Jiaotong University, 2014. |
| [16] | HAN D, WANG X, CHEN L, et al. Command-filtered backstepping control for a multi-vectored thrust stratospheric airship[J]. Transactions of the Institute of Measurement and Control, 2016, 38(1): 93–104. DOI:10.1177/0142331214568237 |
| [17] |
张昊, 陈丽. 多螺旋桨组合浮空器LPV鲁棒变增益H∞控制[J].
计算机仿真, 2014, 31(5): 72–77.
ZHANG Hao, CHEN Li. Robust variable gaincontrol for multi-propeller aerostat based on LPV H∞[J]. Computer Simulation, 2014, 31(5): 72–77. |
| [18] | CHEN L, DUAN D P, SUN D S. Design of a multi-vectored thrust aerostat with a reconfigurable control system[J]. Aerospace Science and Technology, 2016, 2016(53): 95–102. |
| [19] | FENG Y, HAN F, YU X. Chattering free full-order sliding-mode control[J]. Automatica, 2014, 50(4): 1310–1314. DOI:10.1016/j.automatica.2014.01.004 |
| [20] | CONG B L, CHEN Z, LIU X D. On adaptive sliding mode control without switching gain overestimation[J]. International Journal of Robust and Nonlinear Control, 2014, 24(3): 515–531. DOI:10.1002/rnc.v24.3 |



