2. 中国航发商用航空发动机有限责任公司, 上海 200241;
3. 中航工业金城南京机电液压工程研究中心, 江苏 南京 211106
2. AECC Commercial Aircraft Engine Limited Company, Shanghai 200241, China;
3. AVIC Nanjing Engineering Institute of Aircraft Systems, Nanjing 211106, China
作动器是飞机液压系统的重要执行部件, 可靠性直接影响飞机安全, 作动器的许多故障都是由往复密封失效引起的[1-2].O形密封作为典型的动静密封结构, 因其结构简单、性能优良, 在航空作动器中广泛使用.在密封失效机理方面, 国外学者很早就开始对其开展研究.Green等[3]考虑橡胶超弹性, 利用经验公式计算不同压缩率静密封的接触宽度与接触压力, 说明用平面应变假设密封截面的解法可行;Gawliski[4]分别求解干摩擦与存在润滑条件下的静密封、旋转密封和往复密封摩擦力, 并通过试验测试磨损效果, 发现磨损与接触压力、杆粗糙特性等各个因素有关;Schmidt等[5]提出基于Archard法, 通过ABAQUS动网格二次开发功能求解O形圈磨损量的方法.国内, 有很多学者对密封进行研究:胡殿印等[6]对固体火箭发动机上O形圈建立有限元轴对称模型, 探讨O形圈的应力分布规律;吴琼[7]对液压作动器密封磨粒磨损进行分析, 并对密封寿命进行预测;欧阳小平等[8-10]针对VL结构密封性能进行分析, 认为接触压力决定磨损特性.
目前, 密封仿真分析的对象主要以接触压力和内部应力为主, 没有从橡胶材料失效的角度进行深入分析.本文以传统O形密封为研究对象, 针对橡胶材料分析表面磨损机理和疲劳失效机理, 提出基于断裂力学的材料疲劳失效理论来预测密封寿命.对HBZ 4-1995标准中压缩率与拉伸率的相关要求进行失效分析, 计算密封疲劳寿命, 通过标准对提出的方法进行验证.
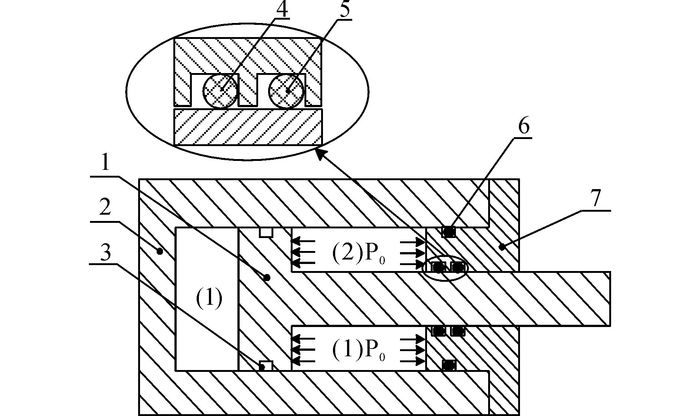
1 密封材料失效理论如图 1所示, 航空液压作动器存在往复动密封和静密封, 其中动密封安装在活塞沟槽处和衬套沟槽处, 分别为活塞密封和杆密封.作动器动作为入行程, 流体压力为p0.由于往复密封面间存在频繁相互滑动和表面磨损现象, 作动器中的往复密封更容易失效, 本文针对杆密封进行研究.作动器往复密封失效包括密封表面磨损失效和材料疲劳失效.
|
1-活塞;2-缸体;3-活塞密封;4-一级杆密封;5-二级杆密封;6-静密封;7-端盖与衬套 图 1 航空液压作动器简图 Fig. 1 Sketch of aircraft hydraulic cylinder |
在实际工作中, 密封与作动杆的接触面间无法保持全流体润滑, 相互滑动中存在摩擦与磨损.由于航空作动器作动杆的粗糙度低, 且对油液清洁度要求高, 因此疲劳磨损和摩擦磨损占主要地位[11].疲劳磨损是长时间周期性摩擦造成的一种低强度磨损.在可靠性要求高的航空作动器内, 这种磨损不可忽视.
假设如下:刚性面表面是理想正弦形波纹, 微凸体均匀分布;橡胶磨损体积与变形体积成正比, 磨损层厚度与微凸体压入深度以及表面粗糙度效应成正比;应力幅值与一个微凸体承受的平均法向载荷成正比, 疲劳磨损的耐磨性可由下式[12]表示:
| $\frac{\beta }{f} = K\sigma _0^t{E^{2\left( {1 - t} \right)/3}}{\left( {\frac{{{N_{\rm{f}}}}}{A}} \right)^{\left( {1 - t} \right)/3}}{\left( {\frac{\lambda }{R}} \right)^{\left( {5 - 2t} \right)/3}}.$ | (1) |
式中:β为耐磨性系数, f为摩擦系数, K为常数, σ0为抗拉强度, E为弹性模量, t为动态疲劳特性指数, Nf为法向载荷, A为实际接触面积, λ为橡胶表面的平均波纹长度, R为微凸体的曲率半径, Nf/A为接触压力.考虑进摩擦表面的粗糙度, 橡胶磨损快慢可用下式表示:
| $I = k{\left( {\frac{{fE}}{{{\sigma _0}}}} \right)^t}{\left( {\frac{{{N_{\rm{f}}}}}{E}} \right)^{1 + t\gamma }}.$ | (2) |
式中:I为磨损速率, k为常数, γ为粗糙度.由式(2) 可知, 磨损速率与载荷呈单调关系.接触面所受的载荷越大, 橡胶磨损越快[12].
根据特征撕裂能的概念[13-14]以及对橡胶在刚性物体表面上滚动时损失的功所进行的一系列研究结果, 获得耐磨性系数为
| $\beta = \frac{T}{\delta } + \omega + 0.9 \times \frac{{N_{\rm{f}}^{4/3}\left( {1 - e} \right)\left( {\varepsilon + 1} \right)}}{{\delta b{{\left( {Erb} \right)}^{1/3}}}}$ | (3) |
式中:T为橡胶的特征撕裂能, δ为橡胶卷曲状碎屑的厚度, b为橡胶卷曲状碎屑的宽度, r为橡胶卷曲状碎屑的半径, ω为单位伸长能的平均值, e为橡胶弹性, ε为伸长率.由式(3) 可知, 在橡胶确定的情况下, 摩擦磨损的耐磨性仅与载荷相关:载荷越大, 磨损越厉害.
1.2 密封材料疲劳失效除了密封面间的磨损失效, 工作中还存在由于周期性载荷造成材料内部疲劳引起的疲劳破坏.橡胶材料的疲劳理论主要有以下2种:一是基于S-N曲线, 二是基于断裂力学.
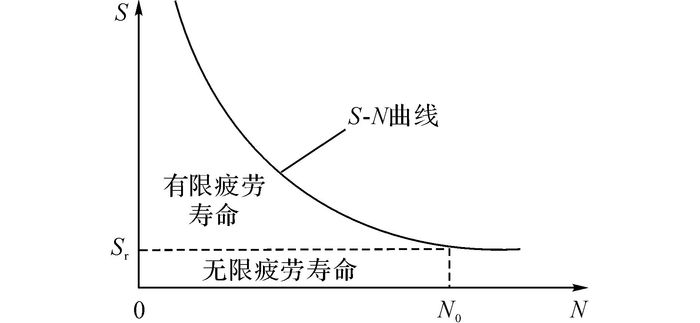
1.2.1 基于S-N曲线方法S-N曲线是描述周期性变化特定应力或应变下的材料寿命[15].其中S为应力σ或应变ε; N为材料疲劳寿命, 在往复密封中表示往复循环次数.这是一种基于唯象理论的方法, 需要基于大量实验, 获得多个应力或应变下材料的疲劳寿命;然后进行拟合, 制成疲劳曲线, 如图 2所示.图中, N为循环次数, S为损伤参量.当寿命超过N0时, 可以认为材料疲劳寿命无限, 即S<Sr时, N→∞, 其中Sr为疲劳极限[16].
|
图 2 S-N曲线 Fig. 2 Curve of S-N |
由于S-N曲线基于大量实验, 无法根据材料参数直接获得, 采用基于断裂力学方法预测寿命.
1.2.2 基于断裂力学方法基于断裂力学的橡胶密封疲劳理论认为, 橡胶材料疲劳失效的主要原因是橡胶内部产生撕裂(断裂), 因此利用断裂力学预测橡胶疲劳寿命成为重要的研究手段[17].
橡胶的断裂原因存在以下2个:1) 橡胶裂纹的萌生;2) 橡胶裂纹的扩展.后者是假设橡胶内部由于工艺问题天生存在缺陷, 以微小裂纹的形式存在, 更符合现实[9], 因此是主要的研究方向.
将能量释放率作为密封橡胶材料的疲劳损伤参量.橡胶撕裂过程如下:当外界产生的应力与应变产生的能量大于材料断裂所需能量时, 在裂纹开口处撕裂, 释放一定能量抵消产生的能量而得到缓冲, 再次提供能量以后开始进行下一次撕裂.往复密封的每一次作动循环都将产生一定能量而造成裂纹扩展, 得到在每个循环周期内的裂纹扩展量, 该扩展量由裂变能决定[18-19].裂纹扩展率可以表示为撕裂能的函数:
| $\frac{{{\rm{d}}a}}{{{\rm{d}}N}} = B{T^\beta }.$ | (4) |
式中:a为裂纹长度, B、β为材料常数, T为单个循环中的最大撕裂能.
用单边切口拉伸来描述密封的撕裂形式, 对于满足式(4) 的SENT形式裂纹扩展率, 可以表示为
| $\frac{{{\rm{d}}a}}{{{\rm{d}}N}} = B{\left( {\frac{{2{\rm{\pi }}}}{{\sqrt \lambda }}{w_0}a} \right)^\beta }.$ | (5) |
式中:a0为裂纹初始长度;λ为伸长比, λ=1+ε; w0为应变能密度, 是ε的函数:
| ${w_0} = \int_0^{{\varepsilon _0}} {\sigma \left( \varepsilon \right){\rm{d}}\varepsilon } .$ | (6) |
对式(5) 积分可得材料由原始裂纹尺寸a0扩展到长度a时所需的循环周期数:
| $\begin{array}{l} N = \int_{{a_0}}^a {{B^{ - 1}}{T^{ - \beta }}{\rm{d}}a{\rm{ = }}} \\ \quad \quad \frac{1}{{B\left( {\beta - 1} \right){{\left( {\frac{{2{\rm{\pi }}}}{{\sqrt \lambda }}{w_0}} \right)}^\beta }}}\left( {\frac{1}{{a_0^{\beta - 1}}} - \frac{1}{{{a^{\beta - 1}}}}} \right). \end{array}$ | (7) |
当橡胶发生断裂时, a宏观可见, a0约为20 μm[20], 因此有
| $N = \frac{1}{{B\left( {\beta - 1} \right){{\left( {\frac{{2{\rm{\pi }}}}{{\sqrt \lambda }}{w_0}} \right)}^\beta }}}\frac{1}{{a_0^{\beta - 1}}}.$ | (8) |
由式(7) 可知, 密封橡胶的寿命与橡胶参数、初始裂纹长度以及橡胶裂纹处的应变有关.在橡胶材料固定的情况下, 橡胶的寿命只与橡胶的应变有关:应变越大, 寿命越短.假设橡胶初始裂纹在内部均匀分布, 寿命取决于最大应变.
航空标准认为压缩率和拉伸率直接表征作动杆、O形圈和沟槽间的配合关系, 影响密封结构表面的接触压力状态和内部应力分布情况, 对密封失效和寿命的影响极大, 是保证密封效果的重要因素, 因此将O形圈的压缩率和拉伸率作为仿真目标, 利用基于断裂力学的方法计算疲劳寿命.
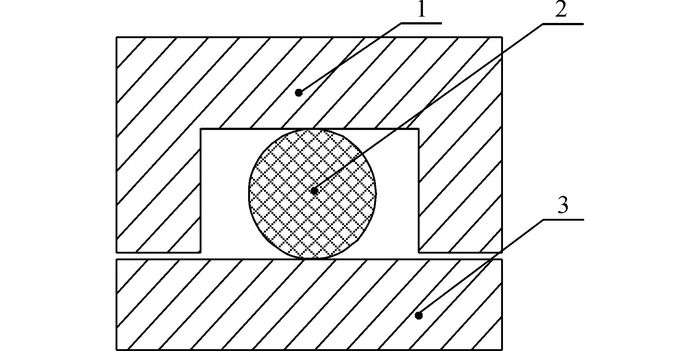
2 O形密封结构及建模O形密封沟槽尺寸来自AS4716标准, 密封圈尺寸按照HBZ 4-1995标准, 结构见图 3.该密封结构可以承受28 MPa流体压力.
|
1-衬套;2-O形圈;3-作动杆 图 3 O形密封几何模型结构 Fig. 3 O-ring seal geometry configuration |
O性密封材料为丁腈橡胶, 使用Mooney-Rillin超弹性体模型来描述丁腈橡胶力学性能.该模型对于形变率很小的密封圈适用, 二参数简化模型[21]为
| $U = {C_{10}}\left( {{{\bar I}_1} - 3} \right) - {C_{01}}\left( {{{\bar I}_2} - 3} \right) + D{\left( {{J^{{\rm{el}}}} - 1} \right)^2}.$ | (9) |
式中:U为应变能;
衬套与活塞杆材料为不锈钢, E=200 GPa, 泊松比ν=0.28.
选取PLANE183轴对称单元作为ANSYS仿真模型的平面单元, CONTA169作为接触单元, TARGE172作为目标单元.为了更好地描述不规则边界形状, 网格采用三角形6节点单元, 主密封副摩擦系数f=0.1, 副密封副摩擦系数f=0.2.计算过程分为以下2步.1) 压缩密封件完成安装:固定作动杆, 衬套向下移动;2) 加流体压力, 流体压力为28 MPa.
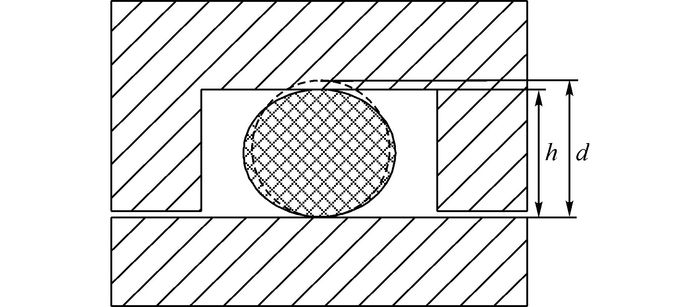
3 压缩率对O形密封失效影响压缩率Y是密封安装截面压缩量与自然状态下截面高度之比, 如图 4所示, 公式如下:
|
图 4 压缩率的定义 Fig. 4 Definition of compression ratio |
| $Y = \frac{{d - h}}{d} \times 100\% .$ | (10) |
式中:d为O形圈自由状态下的截面直径, h为O形圈槽底与被密封表面的距离.利用衬套与作动杆间隙来控制密封压缩率, 研究不同压缩率对O形密封性能的影响规律.设置压缩率分别为Y=8%、12%(标准)、16%(标准)、20%.
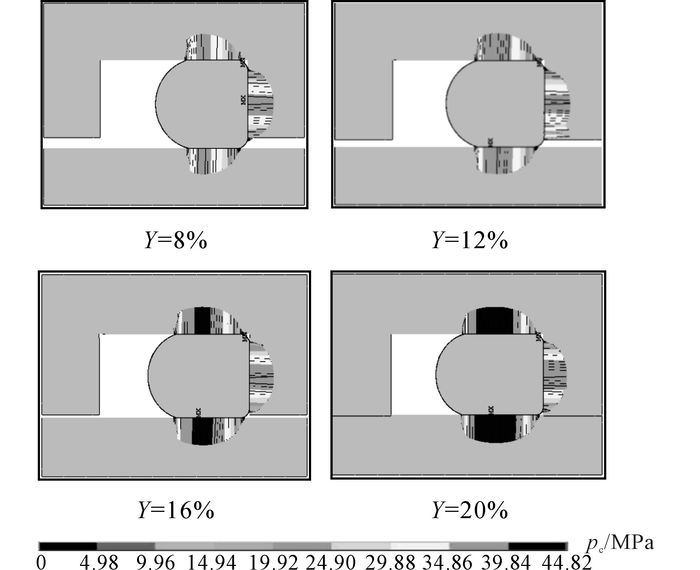
3.1 压缩率对O形密封磨损失效的影响对Y=8%、12%、16%、20% 4种压缩率进行仿真, 如图 5所示为不同压缩率下的O形密封接触压力pc云图对比.由于Y=20%时的接触压力最大, 以该色标为基准.
|
图 5 不同压缩率下O形密封接触压力云图 Fig. 5 Contact pressure contours of O-ring seal under different compression ratios |
通过仿真结果可知, 施加流体压力28 MPa后, 密封面接触压力最大值达到34.78、37.71、41.23、44.82 MPa.随着压缩率的增加, 最大接触压力上升, 从而磨损加快.根据式(1)~(3) 可以求得磨损速率, 进而根据要求确定磨损寿命.
3.2 压缩率对O形密封内部疲劳失效的影响分别对密封内部应力与应变进行仿真, 应力pm分布云图如图 6所示.图中, 色标以Y=20%为基准.由图 6可知, 压缩率增大, 最大应力先下降后上升, 且在标准压缩率范围内的应力较小.

|
图 6 不同压缩率下O形密封MISES应力云图 Fig. 6 MISES stress contours of O-ring seal underdifferent compression ratios |
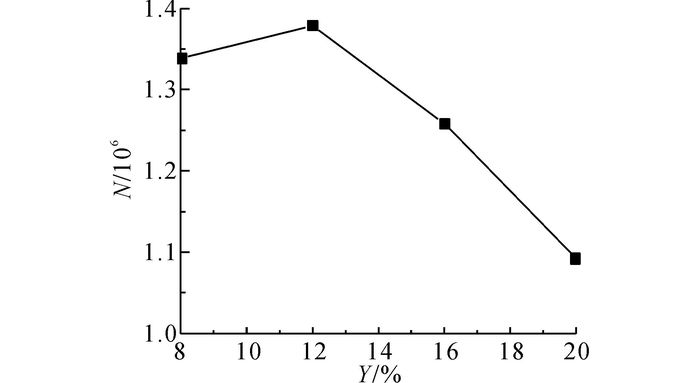
以应力为疲劳损失参量.通过仿真获得压缩率Y=8%、12%、16%和20%的密封最大MISES应力分别为16.02、15.51、17.13和19.98 MPa, 应变分别为0.355 3、0.347 5、0.379 3和0.434 1.根据式(7) 可以预测4种压缩率的寿命, 其中应变能密度w0通过式(6) 利用拟合求得, 得到的寿命变化如图 7所示.
|
图 7 不同压缩率下O形密封疲劳寿命 Fig. 7 Fatigue life of O-ring seal under different compression ratios |
从图 7可知, 在12%压缩率之后, 疲劳寿命开始下降.密封效果与疲劳寿命同时达到要求, 才能保证航空作动器正常工作.当压缩率增加时, 接触压力直线上升, 疲劳寿命先上升后下降, 因此标准中内部动密封压缩率选择12%~17%是合适的, 同时可以说明仿真结果与标准吻合很好.
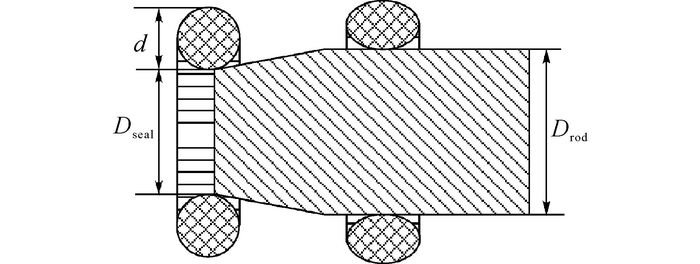
4 拉伸率对O形密封失效影响在密封圈使用过程中, 为了保证配合间隙, 防止O形圈在预装载时发生扭曲等变形, 自由状态下, 密封圈内径较作动杆直径较小, 故在装配中, 密封圈会有一定的拉伸量.如图 8所示.拉伸率α可按下式计算:
|
图 8 拉伸率定义 Fig. 8 Definition of tensile ratio |
| $\alpha = \frac{{{D_{{\rm{rod}}}} + d}}{{{D_{{\rm{seal}}}} + d}}.$ | (11) |
式中:Drod为作动杆直径, Dseal为密封圈内径.
拉伸率是沿轴向计算, 由于ANSYS轴对称模型的计算特点, 二维模型不能满足要求, 此处采用三维模型.
为了节约计算时间, 在不影响结果的前提下, 截取密封轴向30%作为仿真对象.衬套、作动杆以及O形密封都选择SOLID225固体单元, 材料与3章相同, 将不锈钢接触单元设置为TARGE170, 丁腈橡胶设置为CONTA174.在副密封面间, 摩擦因数f=0.2, 主密封面间摩擦因数f=0.1.本文压缩率为16%.
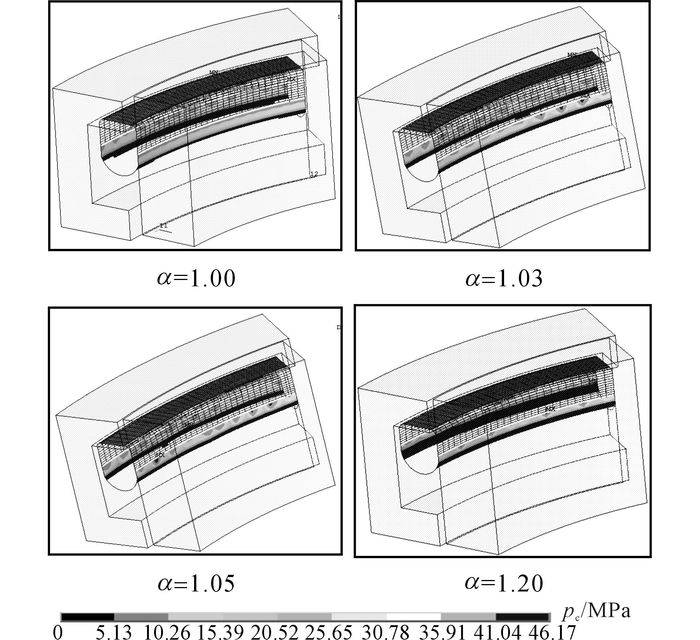
4.1 拉伸率对O形密封磨损失效的影响对α=1、1.03、1.05、1.2四种拉伸率进行仿真, 如图 9所示为不同拉伸率下的O形密封接触压力云图对比.图中, α=1.05时接触压力最大, 因此以该色标为基准.
|
图 9 不同拉伸率下O形密封接触压力云图 Fig. 9 Contact pressure contours of O-ring seal under different tensile ratios |
通过仿真结果可知, 不同拉伸率主密封面的最大接触压力分别为40.51、43.81、46.19和42.73 MPa.在所选的几个拉伸率中, 标准内(α=1.03、1.05) 的密封接触压力最大, 密封效果最好, 但相应磨损较快.
4.2 拉伸率对O形密封内部疲劳失效的影响分别对密封内部应力与应变进行仿真, 应力pm分布云图如图 10所示.图中, 色标以α=1.2为基准.由图 10可知, 拉伸率增大, 最大应力越大.

|
图 10 不同拉伸率下O形密封MISES应力云图 Fig. 10 MISES stress contours of O-ring seal under different tensile ratios |
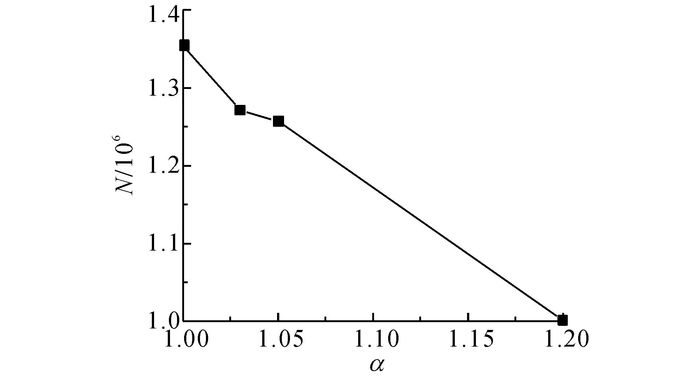
在ANSYS中获得α=1、1.03、1.05和1.2的密封最大MISES应力分别为13.95、14.94、15.13和19.38 MPa, 应变分别为0.321 2、0.324 3、0.325 7和0.333 5.由此得到不同拉伸率下的疲劳寿命, 如图 11所示.
|
图 11 不同拉伸率下O形密封疲劳寿命 Fig. 11 Fatigue life of O-ring seal under different tensile ratios |
由图 11可知, 随着拉伸率的增加, 密封疲劳寿命下降, 且几乎是线性下降, 所以拉伸率应尽量小, 以保证密封寿命.为了保证密封效果和密封寿命, 应综合考虑接触压力和疲劳寿命.标准中的拉伸率(α=1.03、1.05) 满足要求, 说明仿真结果与标准吻合很好.
5 结论(1) 针对密封的不同压缩率与拉伸率, 通过仿真分析得到的结论与航空标准基本符合, 因此可以采用仿真与少量试验结合的方法对相关标准进行制定.
(2) 提出基于断裂力学方法结合仿真分析计算航空液压密封疲劳寿命, 认为基于断裂力学法得到的结果与标准中给出的推荐值一致.该方法比基于试验制定的S-N曲线方便实用, 可以取代S-N曲线法更快地获得数据.
(3) 为了保证密封效果与使用寿命, 应保证压缩率和拉伸率在适当范围内, 太大或太小的参数都无法保证最优的密封性能.
| [1] |
刘志新. 某型号伺服作动器健康状况综合评判与寿命预测研究[D]. 哈尔滨: 哈尔滨工业大学, 2011: 12-15.
LIU Zhi-xin. Research on the state of health compregensive evaluation and the life prediction of a certain servo actuator [D]. Harbin: Harbin Institute of Technology, 2011: 12-15. |
| [2] | 欧阳小平, 杨华勇, 郭生荣, 等. 现代飞机液压技术[M]. 杭州: 浙江大学出版社, 2016: 261-270. |
| [3] | GREEN I, ENGLISH C. Stresses and deformation of compressed elastomeric O-ring seals [C]//14th International Conference on Fluid Sealing. Firenze:, 1994: 6-8. |
| [4] | GAWLISKI M. Friction and wear of elastomer seals[J]. Archives of Civil and Mechanical Engineering, 2007, 7(4): 57–67. DOI:10.1016/S1644-9665(12)60225-8 |
| [5] | SCHMIDT T, ANDRE M, POLL G. A transient 2D-finite-element approach for the simulation of mixed lubrication effects of reciprocating hydraulic rod seals[J]. Tribology International, 2010, 43(10): 1775–1785. DOI:10.1016/j.triboint.2009.11.012 |
| [6] |
胡殿印, 王荣桥, 任全彬, 等. 橡胶O形圈密封结构的有限元分析[J].
北京航空航天大学学报, 2005, 31(2): 255–260.
HU Dian-yin, WANG Rong-qiao, REN Quan-bin, et al. The finite element analysis of rubber O-ring seal structure[J]. Beijing University of Aeronautics and Astronautics, 2005, 31(2): 255–260. |
| [7] |
吴琼. 液压作动器的密封磨粒磨损及寿命预测若干问题研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 30-43.
WU Qiong. An investigation on some issues of sealing abrasive wear and life prediction of certain type aircraft actuator [D]. Harbin: Harbin Institute of Technology, 2013: 30-43. |
| [8] |
欧阳小平, 薛志全, 彭超, 等. 航空作动器的VL密封特性分析[J].
浙江大学学报:工学版, 2015, 49(9): 1755–1761.
OUYANG Xiao-ping, XUE Zhi-quan, PENG Chao, et al. Performance analysis on VL seal in aircraft cylinder[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(9): 1755–1761. |
| [9] |
欧阳小平, 薛志全, 彭超, 等. 于混合润滑理论的航空作动器密封性能分析[J].
北京航空航天大学学报, 2016, 42(2): 251–257.
OUYANG Xiao-ping, XUE Zhi-quan, PENG Chao, et al. Analysis on aircraft cylinder seal property based on mixed lubrication theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(2): 251–257. |
| [10] |
薛志全. 航空液压作动器往复密封机理分析[D]. 杭州: 浙江大学, 2016: 2-32.
XUE Zhi-quan. Analysis of the mechanism of the reciprocating seal in the aircraft hydraulic cylinder [D]. Hangzhou: Zhejiang University, 2016: 2-32. |
| [11] | 张嗣伟. 橡胶磨损原理[M]. 北京: 石油工业出版社, 1998: 1-9. |
| [12] | KRAGELSKII I V, NEPOMNVASCHCHII E F. Fatigue wear under elastic contact conditions[J]. Wear, 1965, 8(4): 303–319. DOI:10.1016/0043-1648(65)90005-0 |
| [13] | RIVLIN R S, THOMAS A G. Rupture of rubber, part Ⅰ: characteristic energy for tearing[J]. Journal of Polymer Science, 1953, 10(3): 291–318. DOI:10.1002/pol.1953.120100303 |
| [14] | GREENSMITH H W. Rupture of rubber, Ⅳ. tear properties of vulcanizates containing carbon black[J]. Journal of Polymer Science, 1957, 21(98): 175–187. |
| [15] | 刘鸿文. 材料力学[M]. 5版. 北京: 高等教育出版社, 2011: 343-350. |
| [16] |
赵永翔, 高庆, 王金诺. 估计三种常用应力-寿命模型概率设计S-N曲线的统一方法[J].
核动力工程, 2001, 22(01): 42–52.
ZHAO Yong-xiang, GAO Qing, WANG Jin-nuo. Unified approach for estimating the probabilistic designS-N curves of three commonly used fatigue stress-life models[J]. Nuclear Power Engineering, 2001, 22(01): 42–52. DOI:10.3969/j.issn.0258-0926.2001.01.010 |
| [17] |
董作见, 吴晓, 王忠, 等. 基于断裂力学的O形密封圈疲劳性能研究[J].
润滑与密封, 2014, 39(11): 59–62.
DONG Zuo-jian, WU Xiao, WANG Zhong, et al. Research on fatigue performance of O-ring based on fracture mechanics[J]. Lubrication Engineering, 2014, 39(11): 59–62. |
| [18] | GENT A N, LINDLEY P B, THOMAS A G. Cut growth and fatigue of rubbers. Ⅰ. the relationship between cut growth and fatigue[J]. Journal of Applied Polymer Science, 1964, 8(1): 455–466. DOI:10.1002/app.1964.070080129 |
| [19] | 郦正能. 应用断裂力学[M]. 北京: 北京航空航天大学出版社, 2012: 26-32. |
| [20] |
丁智平, 陈吉平, 宋传江, 等. 橡胶弹性减振元件疲劳裂纹扩展寿命分析[J].
机械工程学报, 2010, 46(22): 58–64.
DING Zhi-ping, CHEN Ji-ping, SONG Chuan-jiang, et al. Analysis of fatigue crack growth life for rubber vibration damper[J]. Journal of Mechanical Engineering, 2010, 46(22): 58–64. |
| [21] | TRELOAR L R G. The physics of rubber elasticity[M]. New York: Oxford University Press, 1975: 80-101. |


