层间结构是桥面铺装结构的重要组成部分^[1-2], 也是铺装结构的薄弱区域和病害多发区.在车辆水平荷载的作用下, 各层间结构、尤其对于材料性质存在巨大差异的混凝土调平层和沥青铺装层层间结构, 由于变形协调性差的原因, 往往使层间结构提前破坏并成为桥面铺装推移、拥包等病害的直接诱因^[3-7], 层间寿命已成为制约铺装结构整体寿命的重要影响因素^[8].桥面铺装作为桥梁工程和道路工程的交叉领域, 目前尚未形成完善的铺装结构设计理论和设计方法^[9], 尤其对于调平层和沥青铺装层层间结构, 工程设计人员大多仅仅依靠经验, 选用调平层表面处理措施和防水黏结层材料.

本文采用有限元方法, 对桥面铺装结构的受力特点进行分析.根据混凝土调平层与沥青铺装层层间所受正应力与水平向切应力所呈现出的特殊关系, 提出铺装结构层间极限剪切边界的概念, 针对轮载、铺装层厚度等影响因素进行层间极限剪切边界的敏感性分析.对采用铣刨、拉毛层间处治措施以及原状界面的组合结构, 分别开展有竖向压力作用下的层间剪切试验, 将不同界面抗剪强度回归方程与层间极限剪切边界方程建立联系, 为桥面铺装层间结构设计提供依据.

选取铜黄高速(铜川—黄陵)沮河特大连续刚构桥为研究对象, 连续刚构桥中跨跨中为桥面铺装的关键截面^[10], 为此选取中跨跨中直线段13 m长梁段进行桥面铺装层间结构受力分析, 梁段高度为3.50~3.54 m.为了简化计算模型, 在此不考虑铺装结构横坡.模型边界条件设置如下：两侧端部仅限制竖直方向位移, 各结构层层间设置为完全连续.根据圣维南原理可知, 铺装结构仅在距模型两端边界处一定范围内受边界条件的影响, 因此模型中间部位的计算结果可以反映铺装结构的真实受力状况.由于不同部位所需的计算精度不同, 网格划分的尺寸不同, 梁体结构划分较粗、而铺装层划分较细, 同时在荷载作用区域进行了局部网格细化处理.

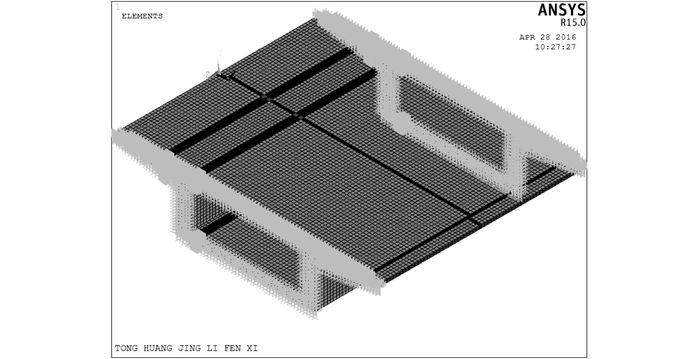
如无特殊说明, 计算均采用《公路桥涵通用设计规范》(JTG D60-2015) 中规定的公路一级荷载140 kN.通过比利时轮压与轴载经验公式^[11]确定的接地压强为0.85 MPa, 采用0.188 m×0.188 m的正方形均布荷载加载, 荷载中心距为0.32 m, 加载时不考虑车辆离心力的作用, 荷载作用在横向最不利受力位置^[12], 计算模型如图 1所示.

图 1

图 1 桥面铺装计算模型 Fig. 1 Calculation model of bridge deck pavement

计算时, 首先采用铜黄高速桥面铺装典型结构进行受力分析, 主梁梁体为C50预应力混凝土, 调平层为C40配筋混凝土, 沥青面层材料分别采用SBS改性沥青SMA-13和AC-20C型纤维沥青混合料.模型各部所用材料单元和参数如表 1所示.

表 1

表 1 模型不同结构材料所用单元及参数取值 Table 1 Elements and parameters of different structural materials 结构材料 厚度/cm 模量/MPa 泊松比 单元类型 沥青上面层 4 1 200 0.3 Solid185 沥青下面层 6 1 400 0.3 Solid185 混凝土调平层 10 32 500 0.166 7 Solid185 主梁 - 34 500 0.166 7 Solid185

表 1 模型不同结构材料所用单元及参数取值 Table 1 Elements and parameters of different structural materials

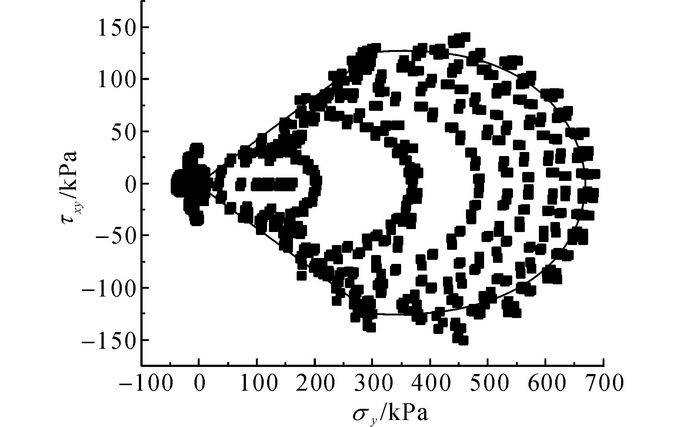
选择桥面铺装层间结构受剪最不利状态作为本文的研究对象, 荷载水平力系数取为0.5^[11].考虑到路面结构层间剪切强度与其受到的竖向压力有关, 以沥青铺装层与混凝土调平层层间节点所受到的竖向正应力σ_y为X轴, 横桥向水平切应力τ_xy、纵桥向水平切应力τ_yz以及层间合成水平切应力τ_S为Y轴, 分别绘制散点分布图.如图 2~4所示, 为了更清楚地展现散点分布的特点, 近似绘出了散点群的外轮廓线.

图 2

图 2 层间各节点所受正应力与横向切应力分布图 Fig. 2 Compressive stress and transverse shear stress distribution of all nodes between layers

图 3

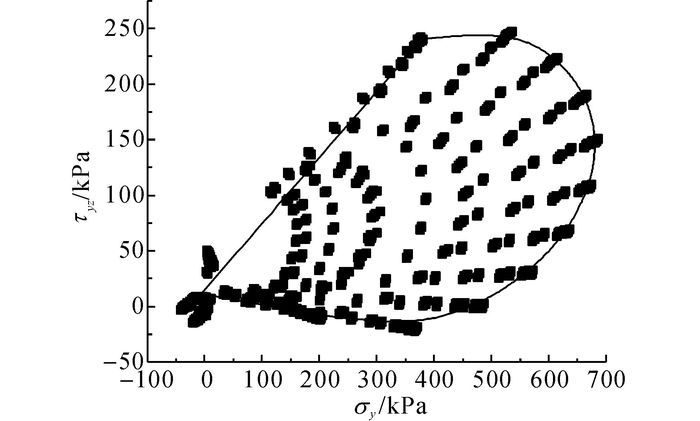
图 3 层间各节点所受正应力与纵向切应力分布图 Fig. 3 Compressive stress and longitudinal shear stress distribution of all nodes between layers

图 4

图 4 层间各节点所受正应力与层间合成水平切应力分布图 Fig. 4 Compressive stress and interlayer synthetic shear stress distribution of all nodes between layers

由图 2~4可知, 层间节点所受竖向正应力与横、纵向以及合成水平切应力均在一定范围内呈现出有规律的分布特点, 其中纵向切应力、合成切应力与正应力的分布规律相似.已有研究成果表明, 沥青铺装层与混凝土调平层层间抗剪强度随正压力呈线性规律变化^[3].在正应力相同的条件下, 所受切应力越小的节点的剪切安全系数越高, 相反, 所受切应力越大, 即切应力越接近层间抗剪强度的节点越容易产生剪切破坏.在层间所有节点中, 所受正应力和水平切应力在坐标系中近似位于通过(0, 0) 点的“直线”型外轮廓线上的节点是最易首先发生剪切破坏的节点.将图 4中的“直线”型外轮廓线定义为桥面铺装层间极限剪切边界, 即在车辆水平荷载作用下, 桥面铺装层间结构最易发生剪切破坏的节点所受到的正应力和层间切应力所呈现的特殊对应关系.在层间极限剪切边界方程一定的情况下, 拟合方程的斜率越大、截距越大, 则铺装结构层间极限剪切边界对应位置发生层间剪切破坏的可能性越大.采用方程的斜率和截距来表征对应节点的层间受剪状态.在进行桥面铺装结构设计时, 只需控制层间极限剪切边界上节点的受剪状况, 即可保证调平层与沥青铺装层层间处于受剪安全状态.

为了找到层间极限剪切边界上的节点在桥面铺装层间结构中所处的位置, 在正方形均布荷载内部及周围取10条路径, 如图 5所示.

图 5

图 5 路径分布 Fig. 5 Paths distribution

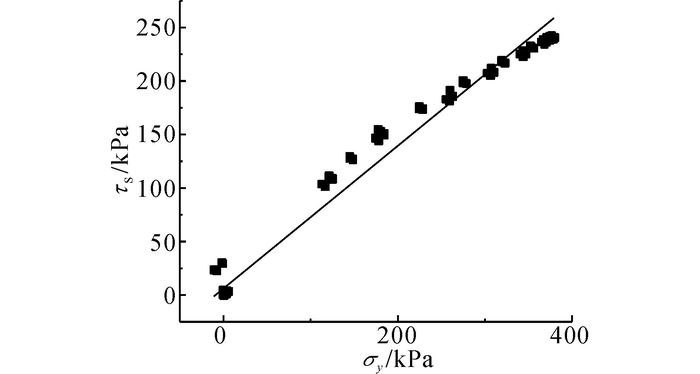
分别提取各条路径上节点的正应力, 计算对应的合成水平切应力, 绘制τ_S-σ_y散点分布图.对散点进行拟合, 与合成水平切应力层间极限剪切边界进行对比分析, 最终发现路径3上节点的τ_S-σ_y散点分布图具有显著的线性分布特征.拟合直线具有很高的拟合度, 且与图 4中的“直线型”外轮廓线, 即层间极限剪切边界基本重合, 因此路径3上节点是层间结构最易发生层间剪切破坏的节点组合, 路径3上节点τ_S-σ_y散点分布图及拟合直线如图 6所示.

图 6

图 6 层间极限剪切边界 Fig. 6 Interlayer shearing limited boundary

取0.7~1.2 MPa 6个接地压强等级开展层间极限剪切边界分析, 水平力系数统一取0.5^[11], 层间极限剪切边界拟合直线方程设为y=a+bx, 拟合直线特征参数如表 2所示.

表 2

表 2 不同荷载等级层间极限剪切边界方程特征参数 Table 2 Characteristic parameters of interlayer shearing limited boundary equation under different load conditions 特征参数 参数值 0.7 MPa 0.8 MPa 0.9 MPa 1.0 MPa 1.1 MPa 1.2 MPa a 5.041 0 5.760 9 6.480 1 7.201 0 7.920 7 8.640 4 b 0.664 9 0.664 9 0.665 0 0.665 0 0.665 0 0.665 0 R2 0.983 9 0.983 9 0.983 9 0.983 9 0.983 9 0.983 9 xmax/kPa 312.63 357.29 401.94 446.59 491.24 535.89 ymax/kPa 212.91 243.32 273.77 304.18 334.60 365.01

表 2 不同荷载等级层间极限剪切边界方程特征参数 Table 2 Characteristic parameters of interlayer shearing limited boundary equation under different load conditions

由表 2的计算、拟合结果可知, 当水平力系数为0.5时, 不同接地压强等级下桥面铺装层间极限剪切边界方程的斜率基本维持不变, 方程截距随着接地压强的增加而增加, 1.2 MPa较0.7 MPa条件下增加了71%, 但由于截距本身数值较小, 因此对铺装结构层间剪切状态的影响是极其有限的；虽然方程本身变化不大, 但随着接地压强的增加, 层间节点受到的最大正应力和相应的最大切应力不断增加.

为了进一步分析水平力系数对层间极限剪切边界的影响, 接地压强统一取为0.85 MPa, 水平力系数取0~0.5^[11]6个等级, 不同水平力系数拟合直线的特征参数如表 3所示.

表 3

表 3 不同水平力系数层间极限剪切边界方程特征参数 Table 3 Characteristic parameters of interlayer shearing limited boundary equation under different transverse force coefficients conditions 特征参数 参数值 0 0.1 MPa 0.2 MPa 0.3 MPa 0.4 MPa 0.5 MPa a 4.118 1 4.552 2 4.971 4 5.372 6 5.755 5 6.120 7 b 0.457 3 0.508 0 0.553 5 0.594 4 0.631 4 0.665 0 R2 0.975 6 0.978 4 0.980 3 0.981 8 0.982 9 0.983 9

表 3 不同水平力系数层间极限剪切边界方程特征参数 Table 3 Characteristic parameters of interlayer shearing limited boundary equation under different transverse force coefficients conditions

由表 3的计算、拟合结果可知, 在相同的接地压强条件下, 随着水平力系数的不断增大, 层间极限剪切边界方程的斜率和截距均近似呈线性增加.当水平力系数由0增加到0.5时, 斜率增幅为45%, 截距增幅为49%, 虽然截距增幅稍大, 但由于本身数值较小, 对边界方程和层间节点的受剪状态影响是非常有限的；相反, 虽然斜率增幅相对较小, 但对层间极限剪切边界所对应节点的受剪状态影响是非常显著的, 以受到正应力为400 kPa的层间节点为例, 水平力系数为0.5时由拟合方程确定的对应的切应力为272.1 kPa, 较水平力系数为0条件下的187.0 kPa增加了46%.

综上所述, 单纯接地压强不是影响桥面铺装层间极限剪切边界的关键因素；相反, 水平力系数是影响铺装结构层间极限剪切边界的关键因素, 水平力系数越大, 边界方程斜率越大, 层间节点发生剪切破坏的可能性越大.

为了确定各层厚度对桥面铺装层间极限剪切边界的影响, 首先保持沥青铺装下层厚度为6 cm, 上层厚度依次取4~6 cm 3个等级；同时, 保持沥青铺装上层厚度为4 cm, 下层厚度依次取4~8 cm 5个等级, 边界方程特征参数如表 4所示.表中, H_U为沥青上面层厚度, H_D为沥青下面层厚度.

表 4

表 4 不同厚度层间极限剪切边界方程特征参数 Table 4 Characteristic parameters of interlayer shearing limited boundary equation under different thickness conditions 特征参数 参数值 参数值 HU=4 cm HU=5 cm HU=6 cm HD=4 cm HD=5 cm HD=6 cm HD=7 cm HD=8 cm a 6.120 7 5.712 8 5.267 6 6.577 1 6.446 2 6.120 7 5.720 2 5.264 2 b 0.665 0 0.639 3 0.616 2 0.727 4 0.699 5 0.665 0 0.641 1 0.613 5 R2 0.983 9 0.983 4 0.983 2 0.986 4 0.985 0 0.983 9 0.983 4 0.983 1

表 4 不同厚度层间极限剪切边界方程特征参数 Table 4 Characteristic parameters of interlayer shearing limited boundary equation under different thickness conditions

由表 4可知, 当沥青铺装下层厚度不变时, 随着沥青铺装上层厚度的增加, 边界方程斜率近似呈线性降低, 当H_U=6 cm时, 方程斜率为0.616 2, 较H_U=4 cm时的0.665 0降低了7.3%.与改变沥青铺装上层的影响规律相似, 边界方程斜率随沥青铺装下层厚度的增加而近似呈线性降低；当H_D=8 cm时, 方程斜率为0.613 5, 较H_D=4 cm时的0.727 4降低了15.7%, 4~6 cm范围内由增加单位厚度而带来的方程斜率降幅略大于6~8 cm范围内的降幅.

综上所述, 增加沥青铺装上、下层厚度均可以降低桥面铺装发生层间剪切破坏的概率, 在沥青铺装总厚度一定的情况下, 增加沥青铺装上层或增加沥青下层所带来的效果相差不大.

为了进一步确定混凝土调平层厚度对层间极限剪切边界的影响, 保持沥青铺装层4 cm+6 cm厚度组合不变, 调平层厚度依次取6~10 cm 5个等级, 边界方程特征参数如表 5所示.

表 5

表 5 不同调平层厚度层间极限剪切边界方程特征参数 Table 5 Characteristic parameters of interlayer shearing limited boundary equation under different thickness of concrete leveling layer conditions 特征参数 参数值 6 cm 7 cm 8 cm 9 cm 10 cm a 6.184 1 6.025 4 6.066 6 6.097 6 6.120 7 b 0.659 4 0.654 8 0.658 4 0.661 8 0.665 0 R2 0.983 6 0.984 2 0.984 1 0.984 0 0.983 9

表 5 不同调平层厚度层间极限剪切边界方程特征参数 Table 5 Characteristic parameters of interlayer shearing limited boundary equation under different thickness of concrete leveling layer conditions

由表 5可知, 在保持两层沥青铺装层厚度不变的情况下, 随着混凝土调平层厚度的减小, 边界方程斜率呈先减小后增加的趋势变化, 当调平层厚度为7 cm时达到最小, 但总体变化幅度非常微小, 不足1.5%.由此表明, 改变调平层厚度对于改善桥面铺装层间结构的剪切状态作用不大.

成型C40水泥混凝土板分别在混凝土板表面进行铣刨、拉毛处理, 保持构造深度分别为1.2 mm和0.7 mm；在养护完成后, 分别喷洒最佳用量^[3]的SBS改性沥青并撒布碎石作为防水黏结层材料^[13]；最后摊铺纤维沥青混合料作为沥青铺装下层材料、并碾压成型, 养护后钻芯得到直径和高度均为10 cm的圆柱体剪切试验用试件.

在25 ℃条件下开展有正压力存在条件下的层间剪切试验, 剪切速率统一取为5 mm/min, 采用夹具分别对上、下结构层施加水平力, 以保证试件破坏位置位于结构层层间, 试件层间抗剪强度τ_max随正压力的变化情况如图 7所示.根据摩尔—库伦理论对试验结果进行回归分析, 分别得到铣刨、拉毛和原状界面抗剪强度回归方程, 如表 6所示.

图 7

图 7 层间抗剪强度随正压力变化情况 Fig. 7 Variation of shear strength between layers with positive pressure

表 6

表 6 抗剪强度回归方程 Table 6 Regression equations of shear strength 层间处治措施 回归方程 铣刨界面 τmax=tan 34.8°σy+246.8(R2=0.995 36) 拉毛界面 τmax=tan 22.6°σy+210.4(R2=0.984 94) 原状界面 τmax=tan 10.7°σy+185.8(R2=0.927 41)

表 6 抗剪强度回归方程 Table 6 Regression equations of shear strength

由图 7和表 6的试验、拟合结果可知, 铣刨、拉毛和原状界面3种界面型式层间黏聚力分别为246.8、210.4和185.8 kPa, 内摩擦角分别为34.8°、22.6°和10.7°, 说明铣刨层间界面形式具有更大的层间黏聚力和内摩擦角, 因此铣刨层间处治措施的组合结构具有优良的层间抗剪切性能.

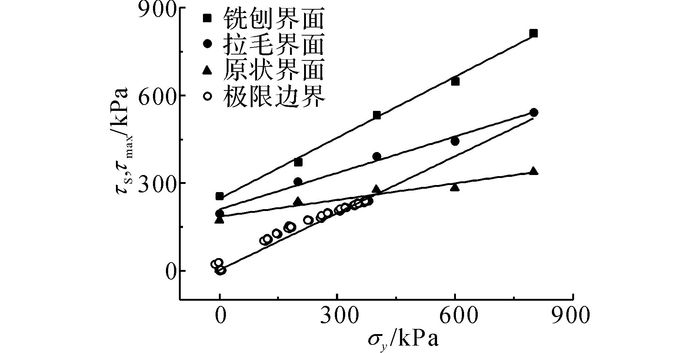
为了将室内试验与力学分析结果建立联系, 绘制抗剪强度回归方程和桥面铺装层间极限剪切边界方程, 如图 8所示.铺装结构采用提到的典型铺装结构, 车辆接地压强取0.85 MPa, 水平力系数为0.5.

图 8

图 8 抗剪强度回归线与极限边界的关系 Fig. 8 Relationship between shear strength regression line and limited boundary

由图 8可知, 极限边界方程的斜率远大于原状界面组合结构抗剪强度回归方程的斜率, 处于铣刨界面与拉毛界面之间.对于铺装整体结构, 在不考虑沥青混合料本身受剪破坏的情况下, 在0.85 MPa接地压强作用下, 混凝土调平层与沥青铺装层层间极限剪切边界附近节点最大正应力仅能达到400 kPa, 但此时足以使原状界面铺装结构处于临界剪切破坏状态.调平层表面不采取特殊处治措施而仅保持为原状界面会严重降低铺装结构的抗剪能力.

对于拉毛层间处治措施, 在不考虑沥青混合料本身受剪破坏的情况下, 在0.85 MPa接地压强作用下, 铺装结构处于剪切安全状态.随着车辆接地压强的不断增大, 虽然极限边界方程斜率基本维持不变, 但层间节点所受正应力会不断增加, 因此, 铺装结构层间抗剪安全系数不断降低, 当层间正应力达到800 kPa时, 铺装结构处于临界剪切破坏状态.

对于铣刨层间处治措施, 在不考虑沥青混合料本身受剪破坏的情况下, 抗剪强度方程斜率大于极限边界方程斜率, 因此层间剪切安全系数不会因为由于车辆接地压强增加而导致的层间正应力的增加而降低, 铺装结构始终处于剪切安全状态.综上所述, 在上文所述的典型铺装结构条件下, 铣刨层间处治措施可以保证桥面铺装沥青铺装层与混凝土调平层层间处于剪切安全状态.

(1) 根据桥面铺装混凝土调平层与沥青铺装层层间正应力与水平向切应力所呈现出的特殊关系, 提出铺装结构层间极限剪切边界的概念, 并通过计算、拟合求出特定条件下的极限边界方程.

(2) 在不考虑沥青混合料本身受剪破坏的情况下, 接地压强对桥面铺装层间极限剪切边界方程的影响微小, 水平力系数是铺装结构层间极限剪切边界的关键影响因素.水平力系数越大, 边界方程斜率越大, 层间节点发生剪切破坏的可能性越大.

(3) 增加沥青铺装上、下层厚度均可以降低桥面铺装发生层间剪切破坏的概率, 且增加相同厚度的上层或下层厚度对铺装结构层间剪切状态的改善效果是相似的, 调平层厚度对层间剪切状态的影响较小.

(4) 铣刨层间处治措施下组合结构抗剪强度回归方程斜率大于极限边界方程斜率, 因此在典型铺装结构条件下, 铣刨层间处治措施可以保证桥面铺装沥青铺装层与调平层层间处于剪切安全状态.

本文采用ANSYS有限元计算软件, 在对桥面铺装混凝土调平层与沥青铺装层层间结构受力分析的基础上, 提出桥面铺装层间极限剪切边界的概念.与室内剪切试验建立联系, 分析铺装结构层间剪切状态.限于计算量的原因, 模型各结构层层间接触状态均设置为完全连续, 建议后续研究考虑调平层与沥青铺装层的真实接触状态, 考虑匝道处桥面铺装层间结构受力状态, 进一步对桥面铺装层间极限剪切边界进行研究, 同时考虑沥青混合料本身的受剪状态, 为桥面铺装结构设计方法的完善提供参考.