不同的右转车流信号控制方式会极大地影响直右共用车道的通行能力.常见的右转交通信号控制方式包括红灯右转与右转滞后放行两类.我国各城市道路交叉口内过街行人及非机动车数量众多, 使得非机动车与右转机动车的相互干扰和冲突不可忽视[1].右转车辆受到非机动车的影响最明显.直行绿灯启亮后, 在直行红灯期间排队等待的非机动车以饱和流率通过冲突区, 此时非机动车严重影响右转机动车驶离交叉口;当直行红灯期间累积到达的非机动车全部通过冲突区后, 后续到达的非机动车密度明显减小, 此时非机动车对右转机动车的干扰影响减弱[2].
右转滞后放行是采用信号控制分离非机动车和右转机动车冲突的一种信号控制方式, 该信号控制方式使得直行绿灯启亮后的一段时间内不允许右转, 这段时间称为滞后放行时间.设置右转滞后放行时间可以使得直行的行人和非机动车在直行绿灯启亮初期无冲突地通过交叉口, 有效地减少右转车流与行人、非机动车的冲突, 从而提高交叉口的运行效率与安全性.红灯右转是指在直行的信号灯为红灯显示时允许右转的信号控制方式.该控制方式能够有效地减少右转车辆的延误和油耗, 因此城市道路交叉口越来越多地使用红灯右转信号控制方式[3].
有关信号控制影响下的直右共用车道通行能力的研究较缺乏.美国道路通行能力手册Transportation Research Board. Highway capacity manual: 2010. Washington DC: Transportation Research Board, 2010.(highway capacity manual, HCM)仅考虑不受交通信号影响下右转车比例对共用车道通行能力的影响.Akcelik[4]粗略估计了短车道的影响, 但模型仅考虑了转向比例.Tian等[5]考虑短车道车辆排队造成阻挡的影响, 提出计算右转短车道通行能力的概率模型, 并指出信号交叉口右转短车道通行能力与短车道长度、转向比例和周期时长密切相关.Wu[6-7]提出考虑交叉口内可容纳车辆数的单条直右共用车道通行能力计算模型.He等[8]根据进口道不同车流的转向比例、短车道几何特征及信号周期, 提出考虑短车道排队阻塞情况下的信号交叉口进口道通行能力计算模型.
黄迪等[9]以右转机动车穿越相邻车道直行自行车行为为例, 建立机动车穿越自行车的行为决策模型.梁春岩等[10]分析右转机动车通过交叉口的延误时间, 并建立机非冲突交叉口右转机动车行程时间模型.宗二凯等[11]分析直右共用车道的交通流运行特性, 提出直右共用车道通行能力计算模型.赖元文等[12]考虑短右转车道长度、行人和自行车到达规律、右转车辆到达规律等交通流特性, 建立短右转车道影响下的直行车道通行能力分析模型.杨晓光等[13]通过对各国大量道路通行能力研究文献的分析, 重点综述了信号控制交叉口通行能力的成果.
综上所述, 信号交叉口右转车道通行能力的研究主要聚焦于右转短车道通行能力的研究, 已有研究没有考虑右转车流信号控制对直右共用车道通行能力的影响.不同于以往研究中直右共用车道的阻塞情况, 红灯右转和右转滞后放行信号控制条件下的直右共用车道通行能力计算更加复杂, 不仅需要考虑车辆转向比例引起的阻挡, 更要考虑不同的交通信号控制方式对共用车道通行能力的影响.本文在考虑红灯右转和右转滞后放行信号控制条件的基础上, 重新估算直右共用车道的通行能力.
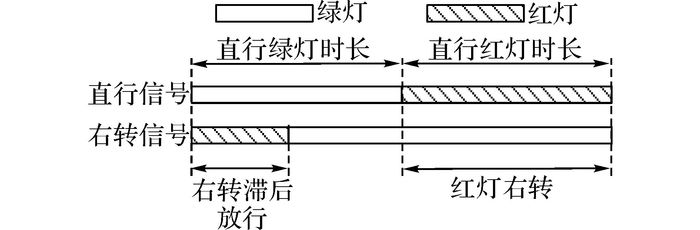
1 直右共用车道阻挡情况分析直右共用车道上到达的车辆既有直行车,又有右转车, 因此, 在红灯右转和右转滞后放行信号的控制条件下, 直行车流和右转车流均可能引起共用车道的阻挡.一旦发生阻挡, 则后续到达的车辆需要与引起阻挡的车辆共同在停车线后排队等待, 直到引起阻挡的车辆通过交叉口, 后续车辆才能开始放行.右转滞后放行信号的控制示意图如图 1所示.
|
图 1 右转滞后放行示意图 Fig. 1 Illustration of lag time of right-turn |
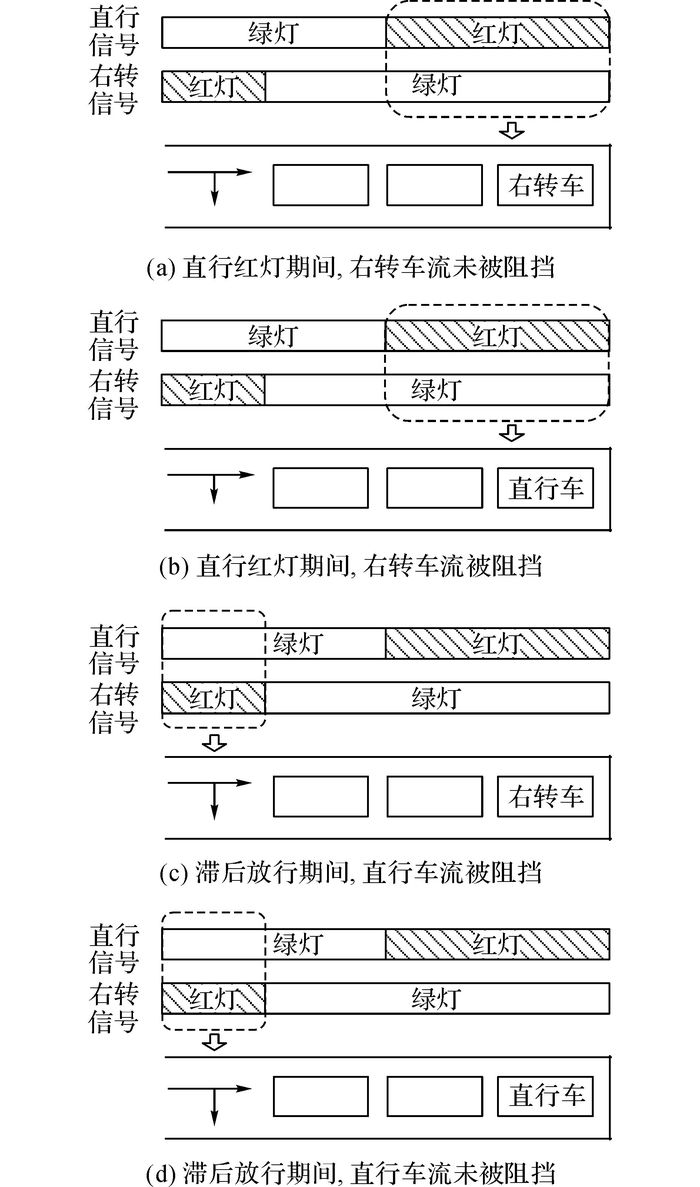
直右共用车道车辆受阻挡情况如图 2所示.
|
图 2 直右共用车道车辆受阻挡情况 Fig. 2 Situations of blockage on shared right-turn lane |
直右共用车道上存在2种可能发生阻挡的情况, 即直行红灯期间右转车辆的放行被直行车辆的到达阻挡, 以及右转滞后放行期间直行车辆的放行被右转车辆的到达阻挡.若直行红灯期间直右共用车道上通过停车线的车辆均为右转车辆, 且右转滞后放行期间直右共用车道上通过停车线的车辆均为直行车辆, 则直右共用车道上的车辆该周期不发生阻挡情况.
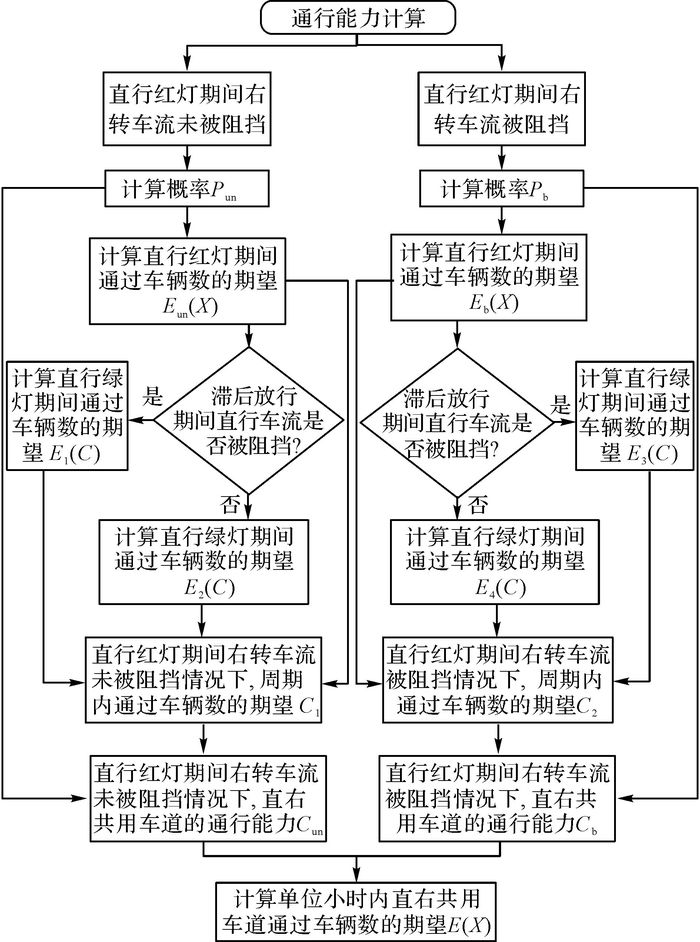
2 通行能力计算模型混合车流到达直右共用车道停车线会发生4种情况:直行红灯期间右转车流未被阻挡、直行红灯期间右转车流被阻挡、滞后放行期间直行车流未被阻挡和滞后放行期间直行车流被阻挡.通过计算上述4种情况发生的概率及通过车辆数的期望, 将4种情况的期望累加得到周期通过车辆数的期望, 最后将周期通过车辆数的期望扩展至单位小时内通过车辆数的期望, 得到红灯右转和右转滞后放行交通信号控制方式影响下的直右共用车道通行能力.该模型的计算思路如图 3所示.
|
图 3 通行能力模型计算示意图 Fig. 3 Illustration of calculating capacity model |
假设在直行车流绿灯后期及直行车流红灯期间, 非机动车流量较小, 出口道满足车辆运行要求, 右转车流不受该方向行人、非机动车以及对向其他机动车的影响, 即在右转机动车能够通行的时间段内, 右转机动车能够以饱和流率释放.
2.1 直行红灯期间, 右转车流未被阻挡情况直行红灯期间能够通过停车线的车辆均为右转车辆.此时, 需要确定未发生阻挡情况下通过车辆数的上限值, 即该模型的研究范围.该上限值可以表述如下:
| $ M = {\mathop{\rm int}} \left( {\frac{r}{h}} \right) + 1. $ | (1) |
式中:M为直行红灯期间直右共用车道上通过交叉口的最大右转车辆数的期望,r为直行红灯时长,h为混合车流的平均车头时距.M的小数部分意味着直行红灯末尾时, 右转车辆的车头已通过停车线, 但车身没有完全通过停车线, 此时认为该车能够通过交叉口, 即对M向上取整.M辆车均为右转车的概率可以表述为
| $ {P_{{\rm{un}}}} = {p^M}. $ | (2) |
式中:Pun为直行红灯期间右转车流未被阻挡的概率;p为直右共用车道上的右转比例, 则直行比例为1-p.
在直行红灯期间右转车流未被阻挡的情况下, 直右共用车道上能够通过交叉口的最大车辆数的期望为
| $ {E_{{\rm{un}}}}\left( X \right) = M{P_{{\rm{un}}}}. $ | (3) |
直行绿灯启亮初期的滞后放行时间内, 直行车辆的放行可能被右转车辆的到达阻挡.若滞后放行时间内无右转车辆到达停车线, 则直行绿灯期间无阻挡发生.在滞后放行时间内, 直右共用车道上能够通过交叉口的直行车辆数的期望为
| $ N = {\mathop{\rm int}} \left( {B/\bar h} \right) + 1. $ | (4) |
式中:N为滞后放行时间内, 直右共用车道上能够通过交叉口的最大车辆数的期望;B为右转滞后放行绿灯时间.同样地, 对N向上取整.
直行绿灯启亮后, 若第一辆右转车在滞后放行时间内到达停车线, 则直右共用车道上发生阻挡, 发生阻挡前连续到达停车线的直行车辆数可能为0,1,…,N-1.假设第一辆右转车之前有n辆连续到达停车线的直行车辆, 则该n辆直行车可以在滞后放行时间内通过交叉口.第一辆右转车之前有n辆直行车的概率及第一辆右转车在滞后放行时间内被阻挡的概率为
| $ f\left( n \right) = p{\left( {1 - p} \right)^n}, $ | (5) |
| $ {P_1} = \sum\limits_{n = 0}^{N - 1} {f\left( n \right)} = 1 - {\left( {1 - p} \right)^N}. $ | (6) |
式中:f (n)为第一辆右转车之前有n辆直行车的概率, P1为第一辆右转车在滞后放行时间内被阻挡的概率.右转车辆引起的阻挡会造成直行绿灯期间车辆排队二次启动, 使直行相位有效绿灯时间缩短了一个启动损失时长.二次启动后, 能够通过交叉口的车辆数根据混合车流的平均车头时距h计算.直行绿灯期间可以通过交叉口的车辆数的期望为
| $ {C_1}\left( n \right) = n + \left( {g - B - L} \right)/\bar h. $ | (7) |
式中:C1(n)为在直行绿灯期间可以通过交叉口的车辆数期望, g为直行相位有效绿灯时间, L为启动损失时间.在该情况下, 直行绿灯期间能够通过交叉口的车辆数的期望为
| $ {E_1}\left( C \right) = \sum\limits_{n = 0}^{N - 1} {f\left( n \right){C_1}\left( n \right)} . $ | (8) |
式中:E1(C)为在直行红灯期间右转车流未被阻挡、滞后放行期间直行车流被阻挡情况下, 直行绿灯期间能够通过交叉口的车辆数的期望.
2.1.2 滞后放行期间, 直行车流未被阻挡情况若通过停车线的前N辆车均为直行车, 即第一辆右转车到达停车线位于N辆直行车之后, 则滞后放行期间直行车流不会被阻挡.第一辆右转车未被阻挡的概率为
| $ {P_2} = {\left( {1 - p} \right)^N}. $ | (9) |
式中:P2为滞后放行期间直行车流未被阻挡的概率.右转车辆引起阻挡的概率受边界条件的约束.
| $ {P_1} + {P_2} = 1. $ | (10) |
直行绿灯期间通过车辆数的期望为
| $ {E_2}\left( C \right) = {P_2}g/\bar h. $ | (11) |
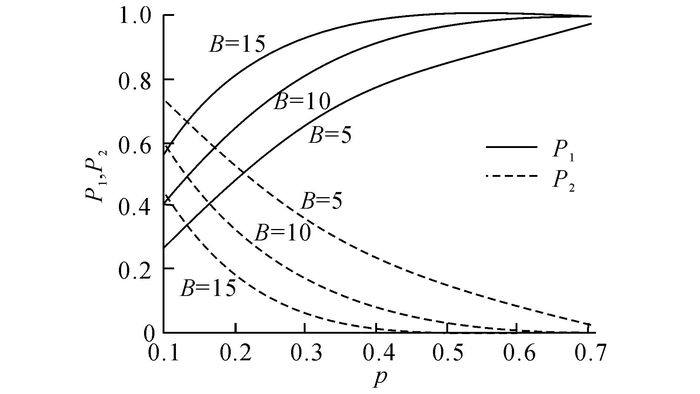
式中:E2(C)为在直行红灯期间右转车流未被阻挡、滞后放行期间直行车流未被阻挡的情况下, 直行绿灯期间能够通过交叉口车辆数的期望.右转车辆引起阻挡的概率如图 4所示.
|
图 4 右转车辆引起阻挡的概率 Fig. 4 Probability of blockage caused by right-turnvehicles |
由E1(C)、E2(C), 可得直行绿灯期间通过车辆数的期望:
| $ {E_1}\left( X \right) = {E_1}\left( C \right) + {E_2}\left( C \right). $ | (12) |
式中:E1(X)为在直行红灯期间右转车流未被阻挡情况下, 直行绿灯期间通过车辆数的期望.直右共用车道周期通过车辆数的期望为
| $ {C_1} = {E_1}\left( X \right) + {E_{{\rm{un}}}}\left( X \right). $ | (13) |
式中:C1为在直行红灯期间右转车流未被阻挡的情况下, 直右共用车道周期通过车辆数的期望.直右共用车道的通行能力为
| $ {C_{{\rm{un}}}} = m{C_1}. $ | (14) |
式中:Cun为在直行红灯期间右转车流未被阻挡的情况下, 直右共用车道的通行能力;m为信号交叉口单位小时内的周期数.
2.2 直行红灯期间, 右转车流被阻挡情况若直行红灯期间右转车流被阻挡, 则直右共用车道上的车辆均在停车线后排队等待, 直至直行绿灯启亮, 引起阻挡的直行车辆通过交叉口后, 后续车辆才可继续放行.
假设该阻挡发生前已有x(0≤x≤M-1) 辆右转车通过停车线.在该情况下, 有且仅有x辆右转车在直行红灯期间通过停车线的概率为
| $ f\left( x \right) = \left( {1 - p} \right){p^x}. $ | (15) |
式中:f (x)为有且仅有x辆右转车在直行红灯期间通过停车线的概率.x取不同值, 意味着不同的阻挡情况.如x=1, 可以表述为发生阻挡前有且仅有1辆右转车能够通过停车线, 即直行红灯期间停车线后的第一辆车为右转车, 停车线后的第二辆车为引起阻挡的直行车.直行红灯期间右转车流被阻挡情况对应的通过车辆数的期望为
| $ {E_{\rm{b}}}\left( C \right) = xf\left( x \right). $ | (16) |
式中:Eb(C)为直行红灯期间, 右转车流被阻挡情况下通过车辆数的期望.发生阻挡前, 能够通过停车线的右转车辆数x共有M种情况, 即0, 1, …, M-1.在直行红灯期间, 右转车流被阻挡的概率为
| $ {P_{\rm{b}}} = \sum\limits_{x = 0}^{M - 1} {f\left( x \right)} . $ | (17) |
式中:Pb为直行红灯期间右转车流被阻挡的概率.引起该阻挡概率受边界条件的约束.
| $ {P_{{\rm{un}}}} + {P_{\rm{b}}} = 1. $ | (18) |
此时, 直行红灯期间通过车辆数的期望为
| $ {E_{\rm{b}}}\left( X \right) = \sum\limits_{x = 0}^{M - 1} {{E_{\rm{b}}}\left( C \right)} . $ | (19) |
式中:Eb(X)为在直行红灯期间右转车流被阻挡的情况下, 直行红灯期间通过车辆数的期望.
2.2.1 滞后放行期间, 直行车流被阻挡情况右转车流被阻挡后, 直右共用车道停车线后排队的第一辆车定为直行车, 因此右转滞后放行时间内至少能够通过一辆车.在第一辆车通过后的滞后放行时间内, 直右共用车道上通过交叉口的最大车辆数的期望为N-1.在第一辆右转车到达停车线之前, 能够连续到达停车线的直行车辆数可能为0, 1, …, N-2.此时, 式(4)、(5)、(7) 仍适用.直行绿灯期间通过车辆数的期望为
| $ {E_{\rm{3}}}\left( C \right) = \sum\limits_{n = 0}^{N - 2} {f\left( n \right){C_1}\left( n \right) + 1} . $ | (20) |
式中:E3(C)为在直行红灯期间右转车流被阻挡, 滞后放行期间直行车流被阻挡情况下, 直行绿灯期间通过车辆数的期望.第一辆右转车被阻挡的概率为
| $ {P_3} = \sum\limits_{n = 0}^{N - 2} {f\left( n \right)} = 1 - {\left( {1 - p} \right)^{N - 1}}. $ | (21) |
式中:P3为在直行红灯期间右转车流被阻挡, 滞后放行期间直行车流被阻挡的情况下, 第一辆右转车被阻挡的概率.
2.2.2 滞后放行期间, 直行车流未被阻挡情况在滞后放行期间未发生阻挡的情况下, 第一辆右转车未被阻挡的概率为
| $ {P_4} = 1 - {P_3} = {\left( {1 - p} \right)^{N - 1}}. $ | (22) |
式中:P4为在直行红灯期间右转车流被阻挡, 滞后放行期间直行车流未被阻挡情况下, 第一辆右转车未被阻挡的概率.直行绿灯期间通过车辆数的期望为
| $ {E_{\rm{4}}}\left( C \right) = {P_4}g/\bar h. $ | (23) |
式中:E4(C)为在直行红灯期间右转车流被阻挡, 滞后放行期间直行车流未被阻挡的情况下, 直行绿灯期间通过车辆数的期望.
2.2.3 期望通行能力由E3(C)及E4(C), 可得直行绿灯期间通过车辆数的期望:
| $ {E_2}\left( X \right) = {E_3}\left( C \right) + {E_4}\left( C \right). $ | (24) |
式中:E2(X)为在直行红灯期间右转车流被阻挡情况下, 直行绿灯期间通过车辆数的期望.由E2(X)及Eb(X), 可得直右共用车道周期通过车辆数的期望:
| $ {C_2} = {E_2}\left( X \right) + {E_{\rm{b}}}\left( X \right). $ | (25) |
式中:C2为在直行红灯期间右转车流被阻挡情况下, 直右共用车道周期通过车辆数的期望.直右共用车道通行能力的期望为
| $ {C_{\rm{b}}} = m{C_2}. $ | (26) |
式中:Cb为在直行红灯期间右转车流被阻挡的情况下, 直右共用车道的通行能力.
2.3 最终通行能力由Cun、Pun、Cb及Pb, 可得直右共用车道的最终通行能力:
| $ E\left( X \right) = {C_{{\rm{un}}}}{P_{{\rm{un}}}} + {C_{\rm{b}}}{P_{\rm{b}}}. $ | (27) |
式中:E(X)为考虑红灯右转和右转滞后放行的直右共用车道通行能力.
3 模型分析下面通过数值计算分析不同信号配时参数下的直右共用车道通行能力的变化趋势.直右共用车道的信号控制的基本参数取值如下:直行相位绿信比取0.4;g分别为20、30、40 s;L取2 s;h取2.0 s(VISSIM仿真1 h所有车头时距的平均值).
以g=20 s为例, 在直行红灯期间右转车流被阻挡的情况下, E2(X)和Eb(X)的关系如图 5所示.可以看出, 在直行红灯期间右转车流被阻挡情况下, 直行绿灯期间能够通过交叉口车辆数的期望E2(X)随着转向比例的增加而减小;当转向比例相同时, E2(X)随着B的增大而减小.在直行红灯期间, Eb(X)仅受转向比例的影响, Eb(X)随着转向比例的增加而增大;在不同的B下, 两者的变化幅度不一致, 这会导致直行红灯期间右转车流被阻挡情况下的直右共用车道周期通过车辆数的期望C2在不同的滞后放行时间下的变化趋势不同.当转向比例较小时, Eb(X)增幅明显小于E2(X)减幅;当转向比例较大时, Eb(X)增幅大于E2(X)减幅.当滞后放行时间B取3或4时, C2不随着p单调递减(具体数值见表 1);当B取其他值时, C2随着p单调递减.

|
图 5 红灯右转被阻挡时的通过车辆数 Fig. 5 Numbers of passing vehicles when right-turn movement being blocked during red |
| 表 1 C2的异常变化趋势 Table 1 Tendency of C2 when B=3 and B=4 |
在直行红灯期间右转车流被阻挡的情况下, Cb的整体趋势如图 6所示.

|
图 6 红灯右转被阻挡时通行能力的期望 Fig. 6 Expecting capacity when right-turn movement being blocked during red |
从图 6可以看出, 当红灯右转被阻挡时, 直右共用车道通行能力的期望随着滞后放行时间的增大而减小;当滞后放行时间一定时, 转向比例越大, 期望通行能力越小.当滞后放行时间较小时, 转向比例的变化对期望通行能力的影响不大, 随着滞后放行时间的增大, 转向比例对期望通行能力的影响加剧.这主要是因右转车在直行绿灯初始时刻对直行车流的阻挡概率增加造成的.上述模型的计算结果符合实际情况.
在不同直行绿灯时间(相同直行绿信比)的情况下, 考虑红灯右转和右转滞后放行的直右共用车道通行能力模型计算结果如图 7所示.

|
图 7 直右共用车道期望通行能力模型计算结果 Fig. 7 Expected capacity of model calculation values on shared right -turn lane |
如图 7所示, 当转向比例相同时, 直行绿灯时间越小, 直右共用车道的期望通行能力随着滞后放行时间的增大而减小的趋势越明显.随着有效绿灯时间的增加(绿信比不变), 直右共用车道的期望通行能力随着增加.这主要是由于滞后放行时间占整个有效绿灯时间的比例减少, 进而减少了右转车辆在绿灯初期对直行车的阻挡概率.在设置直右共用车道时, 适当地增加信号周期及对应直行相位的绿灯时间, 能够有效地提高共用车道的通行能力.
4 仿真验证在实际环境中, 很难通过设置不同的信号配时参数来验证模型的有效性, 实际交叉口的渠化形式、转向比例及信号配时方案是固定的, 不能随意调整参数, 因此通过实际数据计算进行验证是不可行的.对于转向比例、直行绿灯时间和滞后放行时间影响下的通行能力, 只能通过仿真进行验证.通过对杭州市实际交叉口渠化形式及信号配时参数进行调查及筛选, 作为仿真时的参数输入, 采用VISSIM仿真软件输出结果与理论模型计算结果进行对比分析, 验证理论模型的精确性.在交通仿真过程中, 通过改变不同的信号配时参数, 可以对比分析不同滞后放行时间、不同绿信比、不同有效绿灯时间等多种情景下的仿真值和模型计算值.
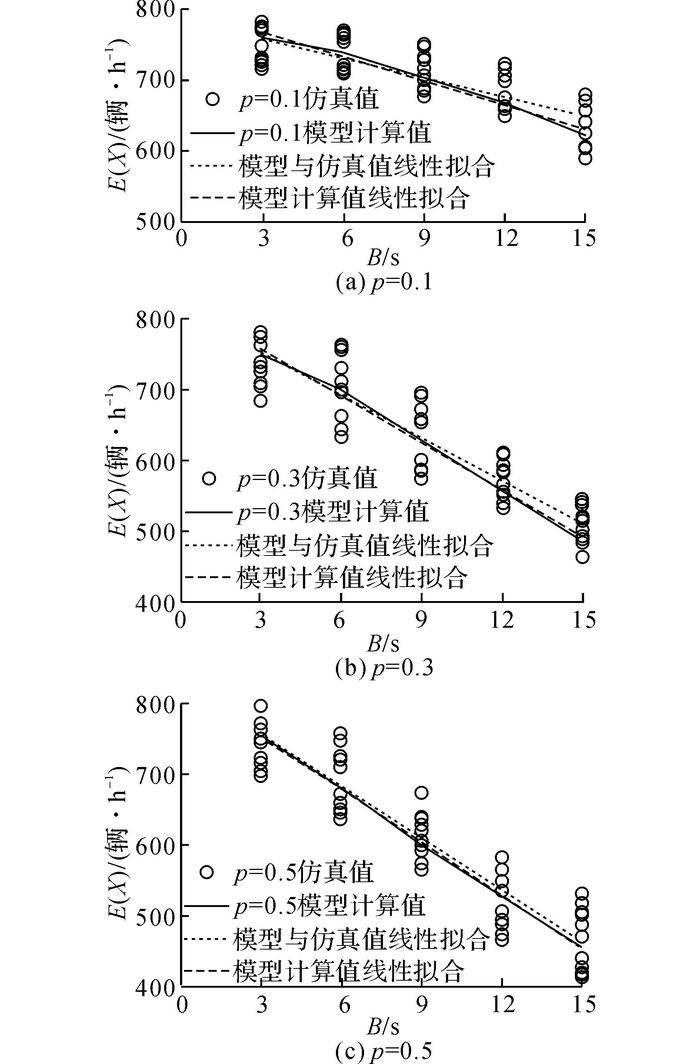
在实际的仿真过程中, 由于仿真前900 s车辆未完全进入路网, 因此统计900 s与3 600 s之间的通过车辆数, 并扩展至小时通过车辆数.直右共用车道的交通需求设置为1 600辆/h, 绿信比为0.4, 确保直右共用车道一直处于饱和状态.在仿真过程中, 相关参数取默认值, 同时不考虑行人及非机动车对右转车辆的干扰.通过设置10组不同的随机数, 得到考虑红灯右转和右转滞后放行的直右共用车道通行能力仿真结果.将仿真结果与理论模型计算值进行对比, 以g取30 s为例, 对模型计算值进行线性拟合.对模型计算值与10组仿真结果(共11组通行能力)进行拟合, 如图 8所示.当g取20和40 s时, 能够获得相同的趋势.
|
图 8 通行能力模型计算值和仿真值对比(g=30 s) Fig. 8 Comparisons of capacity model calculation and simulation values (g=30 s) |
当g取30 s时, 对模型计算值的线性拟合以及对模型与仿真值的线性拟合相应的拟合参数, 如表 2~4所示.
| 表 2 模型计算值线性拟合参数 Table 2 Linear fitting parameters of model calculation values |
| 表 3 模型计算值与仿真值线性拟合参数 Table 3 Linear fitting parameters of model calculation values with ten simulation values |
| 表 4 模型与仿真值线性拟合的标准误差 Table 4 Standard errors of model calculation values with simulation values |
模型计算结果与仿真值的绝对误差ea及相对误差er如图 9所示.可以看出, 模型计算结果与仿真值的绝对误差及相对误差波动范围较小, 始终保持在较低范围内.

|
图 9 模型计算结果与仿真值的误差(g=30 s) Fig. 9 Error values of model calculation values and simulation values (g=30 s) |
仿真与拟合结果表明, 该模型计算值与仿真值的平均绝对误差为6.29, 平均相对误差为1.16%, 且总体趋势一致.整体来说, 直右共用车道的通行能力随着滞后放行时间的增加而减小.当直行绿灯时间相同时, 转向比例越大, 线性拟合的斜率越小, 期望通行能力下降速度越快.当直行绿灯时间与滞后放行时间相同时, 转向比例越大, 直右共用车道通行能力越小.直右共用车道的通行能力随着有效绿灯时间的增加而增加(绿信比不变).由此可见, 仿真结果与模型分析结果一致.
5 结语信号交叉口直右共用车道通行能力已有研究较少考虑交通信号控制方式及参数对车道通行能力的影响.本文同时考虑两种右转车辆信号控制方式, 在分析红灯右转和右转滞后放行信号控制情况下的信号交叉口直右共用车道阻挡情况基础上, 应用概率论相关方法, 提出考虑红灯右转和右转滞后放行的直右共用车道通行能力计算模型, 并通过VISSIM仿真软件对理论模型结果进行验证.结果表明, 理论模型具有较高的估计精度, 能够为信号交叉口通行能力分析、交通信号参数优化提供理论依据.本文仅考虑一条直右共用车道在红灯右转和右转滞后放行信号控制方式下的通行能力, 未考虑相邻直行车道数量影响下直行车辆对共用车道选择行为及通行能力变化的影响, 这将在后续研究中进行深入分析.
| [1] |
杨晓光, 蒲文静, 龙亮. 基于交通冲突分析的交叉口机动车信号灯设置[J].
同济大学学报:自然科学版, 2005, 33(12): 1596–1599.
YANG Xiao-guang, PU Wen-jing, LONG Liang. Traffic signal warrant study based on traffic conflict analysis for uncontrolled intersections[J]. Journal of Tongji University: Natural Science, 2005, 33(12): 1596–1599. |
| [2] |
刘红元, 钱大琳, 李珊珊. 信号交叉口机非冲突临界流量研究[J].
交通信息与安全, 2010, 28(4): 77–80.
LIU Hong-yuan, QIAN Da-lin, LI Shan-shan. Critical flow of conflict between motor vehicles and non-motor vehicles at signalized intersection[J]. Traffic Information and Security, 2010, 28(4): 77–80. |
| [3] | QURESHI M A. A delay model for exclusive right-turn lanes at signalized intersections with uniform arrivals and right turns on red [D]. Knoxville: University of Tennessee, 2000: 1-3. |
| [4] | AKCELIK R. Lane-by-lane modeling of unequal lane use and flares at roundabouts and signalized intersections: the SIDRA solution[J]. Traffic Engineering and Control, 1997(38): 388–399. |
| [5] | TIAN Z, WU N. Probabilistic model for signalized intersection capacity with a short right-turn lane[J]. Journal of Transportation Engineering, 2006, 132(3): 205–212. DOI:10.1061/(ASCE)0733-947X(2006)132:3(205) |
| [6] | WU N. Total approach capacity at signalized intersections with shared and short lanes: generalized model based on a simulation study[J]. TransportationResearch Record, 2007, 2027(2027): 19–26. |
| [7] | WU N. Modelling blockage probability and capacity of shared lanes at signalized intersections[J]. Procedia-Social and Behavioral Sciences, 2011, 16(16): 481–491. |
| [8] | HE D H, PENG Z R. Probabilistic-based capacity model at signalized intersection approach with left-turn short lane [C]//Transportation Research Board 93rd Annual Meeting.: TRB, 2014: 5-6. |
| [9] |
黄迪, 钱大琳, 赵春龙. 平交口右转机动车穿越直行自行车行为研究[J].
北京交通大学学报, 2006, 30(3): 23–26.
HUANG Di, QIAN Da-lin, ZHAO Chun-long. Study on behavior of right-turning motor crossing through bicycles at grade intersection[J]. Journal of Beijing Jiaotong University, 2006, 30(3): 23–26. |
| [10] |
梁春岩, 王春光, 沈占, 等. 机非混行交叉口右转机动车行程时间计算方法[J].
吉林大学学报:工学版, 2007, 37(5): 1053–1057.
LIANG Chun-yan, WANG Chun-guang, SHEN Zhan, et al. Calculation method of travel time of right-turn vehicle at motor-and-non motor-vehicle mixed traffic intersection[J]. Journal of Jilin University: Engineering and Technology Edition, 2007, 37(5): 1053–1057. |
| [11] |
宗二凯, 邵长桥. 信号交叉口直右共用车道通行能力研究[J].
交通运输系统工程与信息, 2011, 11(6): 62–67.
ZONG Er-kai, SHAO Chang-qiao. Capacity research on shared through-right turn lanes at signalized intersections[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(6): 62–67. |
| [12] |
赖元文, 荣建, 刘小明. 短右转车道影响下的信号交叉口的直行通行能力[J].
公路交通科技, 2013, 30(3): 131–135.
LAI Yuan-wen, RONG Jian, LIU Xiao-ming. Through capacity of signalized intersection influenced by short right turn lane[J]. Journal of Highway and Transportation Research and Development, 2013, 30(3): 131–135. |
| [13] |
杨晓光, 赵靖, 马万经. 信号控制交叉口通行能力计算方法研究综述[J].
中国公路学报, 2014, 27(5): 148–157.
YANG Xiao-guang, ZHAO Jing, MA Wan-jing. Review on calculation method for signalized intersection capacity[J]. China Journal of Highway and Transport, 2014, 27(5): 148–157. |



