2. 吉林大学 吉林省道路交通重点实验室, 吉林 长春 130022;
3. 青岛理工大学 汽车与交通学院, 山东 青岛 266520
2. Jilin Province Key Laboratory of Road Traffic, Jilin University, Changchun 130022, China;
3. College of Automobile and Transportation, Qingdao Technological University, Qingdao 266520, China
交通事件是交通运输系统中的一个重要问题.据统计, 美国60%的城市快速路和超过一半的高速公路拥堵是由交通事件造成的[1].在我国上海, 交通事件引起的快速路交通拥堵占总拥堵的50%~75%[2].目前, 已经提出了许多卓有成效的事件自动检测(automatic incident detection, AID)算法.其中, 基于交通流参数的AID算法最常用.这类AID算法适用于具有连续交通流的道路, 例如高速公路和城市快速路.对于间断交通流的道路, 没有较通用的AID算法, 例如Ghosh等[3]提出针对信号控制主干路的定制AID算法.本文主要关注基于交通流参数的AID算法.早期AID算法原理相对简单, 虽然实用性较好, 但检测效果难以满足要求.自上世纪90年代, 出现了许多先进的AID算法, 例如神经网络[4-5]、SVM [6-7]和决策树[2, 8].这些方法属于机器学习的范畴, 把交通事件检测看作二分类(事件和非事件)问题, 通过学习事件上、下游交通流参数数据, 自动生成检测规则, 有效挖掘数据的隐含信息.基于机器学习的AID算法更有前景.近年来, Wang等[9]提出基于时间序列方法和机器学习方法的组合AID算法, 使用时间序列方法预测正常状态下的交通流参数, 并将预测的交通流参数、实测交通流参数和两者之间的差值作为SVM的输入, 通过SVM判断是否发生交通事件.Xiao等[10]提出集成多个多核函数SVM的AID算法, Liu等[11]提出集成多个朴素贝叶斯分类器的AID算法.实证分析表明, 集成多个分类器的AID算法具有更好的鲁棒性.目前的研究主要集中在已有算法的组合和集成, 没有考虑将较新的机器学习算法应用于交通事件检测.极限学习机[12](extreme learning machine, ELM)是一种新型的单层前馈神经网络学习算法.ELM随机选择输入权值而不需要调整, 并通过Moore-Penrose广义逆矩阵计算输出权值.ELM训练速度更快, 泛化能力更强, 避免陷入局部极小.为了减少确定隐层神经元数和随机分配权重所消耗的时间, Huang等[13]使用核矩阵代替ELM隐层特征映射, 得到核极限学习机(kernel extreme learning machine, KELM).在多个领域, KELM的性能优于SVM[14].此外, 现有算法通常以原始交通流参数为输入变量[5-6, 8, 10-11], 忽略特征变量集的构建和重要特征变量的选择.在机器学习分类方面, 选择重要特征变量, 去除冗余特征变量, 能够有效地提高分类正确率[15].
本文提出基于变量选择和KELM的AID算法.首先, 使用基本交通流参数及其组合, 构建较全面的初始变量集, 通过随机森林-递归特征消除(random forest-recursive feature elimination, RF-RFE)方法[16]选出重要变量.然后, 使用重要变量数据训练KELM, 并通过万有引力搜索算法(gravitational search algorithm, GSA)[17]优化模型参数.最后, 基于Ⅰ-880高速公路的交通事件数据, 测试分析模型性能.
1 平衡数据集在实际中, 交通事件样本数远少于非事件样本数, 两类样本的数量是不平衡的;因此, 交通事件检测可以看作不平衡数据的二分类问题.若直接使用不平衡数据训练模型或算法, 则将导致少数类样本的误分类率远高于多数类样本.因为只要把多数类样本正确分类, 就能获得较高的分类正确率.少数类的分类正确率更加重要, 直接决定交通事件的检测效果.
目前, 处理不平衡数据分类问题的方法主要有以下两种:1) 通过重采样(包括多数类样本的欠采样和少数类样本的过采样)重构数据集, 使其达到平衡;2) 在不改变原始样本数据集的前提下, 改进模型或算法, 使其适用于不平衡数据集.两种方法各有优点, 相比而言, 第一种方法的使用更加简便, 应用范围更广.合成少数过采样技术(synthetic minorityover-sampling technique, SMOTE)是一种常用的过采样技术, 并衍生出许多改进形式[18].SMOTE的基本原理是通过k近邻方法, 寻找距离每一个少数类样本最近的k个少数类样本;然后在少数类样本和k个最近邻少数类样本的连线上随机线性插值, 生成k个新样本, 并将生成的k个新样本归为少数类样本.SMOTE能够生成原始样本中不存在的新样本, 因此在一定程度上避免了分类算法的过拟合.选用标准SMOTE平衡交通事件检测样本, 具体的实现步骤如下.
1) 对于事件样本集中的每一个样本xi, 以欧式距离作为度量标准, 搜索事件样本集中距离该样本最近的k个样本.
2) 根据非事件样本数和事件样本数的比值确定采样倍率N, 从每个事件样本xi的k个最近邻样本中随机选取N个样本, 记为xij.
3) 根据式(1), 在随机选取的最近邻样本xij和事件样本xi之间随机线性插值, 构造新的事件样本.
| $ {x^{{\rm{new}}}} = {x_i} + {\rm{rand}}\left( {0,1} \right) \times \left( {{x_{ij}} - {x_i}} \right). $ | (1) |
式中:rand (0, 1) 表示属于区间[0, 1]的一个随机数.
4) 将新产生的事件样本与原始样本集合并, 得到一个相对平衡的训练样本集.
2 初始变量集构建交通事件引起交通流参数的显著变化是设计AID算法的基本依据.事件地点上游和下游交通流参数的变化趋势分别如图 1、2所示.图中,Q为流量, Occ为占有率,v为速度.在正常状态下, 交通流参数(流量、速度和占有率)的变化相对平稳.当发生交通事件时, 事件地点的上游流量和速度快速下降, 占有率快速上升;随之, 下游流量和占有率下降, 速度上升.当交通事件结束后, 交通流参数恢复了相对平稳的状态.
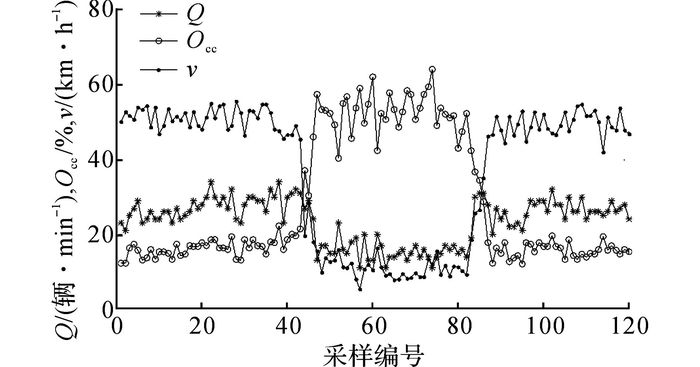
|
图 1 上游检测器的交通流参数变化趋势 Fig. 1 Trend of traffic parameters of upstream detector |
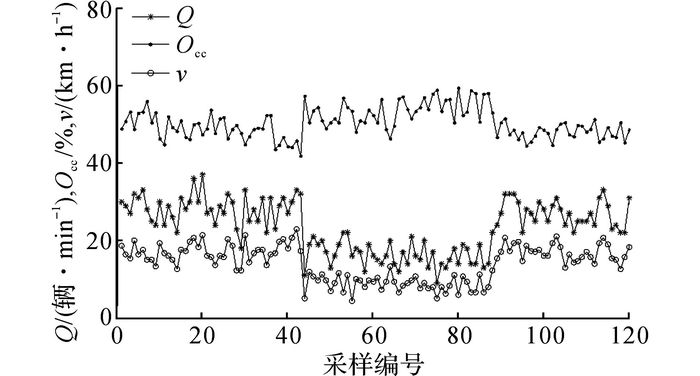
|
图 2 下游检测器的交通流参数变化趋势 Fig. 2 Trend of traffic parameters of downstream detector |
正常状态下的交通流参数可以作为事件检测的基准, 因而需要预测正常状态下的交通流参数, 例如SND算法.此外, 事件地点上、下游交通流参数的组合有明显变化.例如California算法采用上、下游占有率的差值.本文以上、下游交通流参数的实测值、预测值及其组合, 构建较全面的初始变量集.初始变量集包含5个部分:1) 上游检测器的实测交通流参数;2) 下游检测器的实测交通流参数;3) 上游检测器实测交通流参数和预测参数的差值;4) 下游检测器实测交通流参数和预测参数的差值;5) 上、下游相邻检测器实测交通流参数的差值.所构建的初始变量集如表 1所示.其中, 采用移动平均法求得交通流参数的预测值, 使用相邻的前4个数据预测第5个数据.
| 表 1 交通事件检测初始变量集 Table 1 Initial variables set of traffic incident detection |
采用RF-RFE算法从交通事件检测初始变量中选择重要变量, 不仅能够降低输入数据的维数, 而且能够提高分类的正确率.
3.1 随机森林和变量重要性分析随机森林是Breiman[19]提出的一种多棵决策树集成学习算法.随机森林不仅能够用于分类和回归, 而且可以度量变量重要性(variable importance, VI).基于随机森林的变量重要性度量方法有多种, 其中基于OOB数据分类正确率的变量重要性度量方法是最常用的一种, 基本思想如下:依次对OOB数据中的每个变量添加随机噪声干扰, 通过所有决策树的OOB数据分类正确率下降的平均值决定该变量的重要性.算法的主要步骤如下.
1) 生成随机森林.
a) 采用Bootstrap抽样技术, 从K个原始训练样本中随机地、有放回地抽取K′个样本.使用所抽取的样本数据构建一棵决策树hk(k=1, 2, …, p), 没有选中的K-K′个样本构成袋外数据Kkoob.
b) 在决策树的每个节点处抽取交通事件检测初始变量集的mtry(mtry<15) 个变量, 分别计算每个变量蕴含的信息量, 从mtry个变量中选择一个分类能力最佳的变量进行节点分裂.
c) 每棵树都自然生长, 不进行剪枝.
d) 重复步骤a)~c)共计p次, 生成含有p棵决策树的随机森林f={s1, s2, …, sp}.
2) 对于随机森林中的每一棵决策树sk, 使用袋外数据Lkoob进行分类, 并统计交通事件样本的分类正确率Rk.
3) 训练集的每个初始变量记作λl(l=1, 2, …, 15), 依次将袋外数据Lkoob的λl添加随机噪声干扰, 所得新的袋外数据记作
4) 根据式(2) 计算变量λl的重要度.
| $ {V_{\rm{I}}} = \frac{1}{p}\sum\limits_{i = 1}^p {\left( {{R_k} - {{\hat R}_k}} \right)} . $ | (2) |
递归特征消除(recursive feature elimination, RFE)是一种基于特征变量排序的变量选择方法[20].RF-RFE算法采用随机森林分析变量重要性, 并根据变量重要性排序, 进而通过RFE方法选择重要变量.RF-RFE算法的流程如图 3所示.首先基于初始变量训练集数据, 使用随机森林计算变量重要性并排序;然后每次删除重要性最小的变量, 并使用剩余变量重新测试随机森林的分类正确率.这样逐次迭代, 计算每次分类的正确率, 直到所有特征变量序列搜索完毕.最终得到所有变量的重要度排序和随机森林, 对应不同变量个数的分类正确率.

|
图 3 RF-RFE算法流程图 Fig. 3 Flowchart of RF-RFE |
KELM是ELM的一种改进形式, 因此先介绍ELM, 然后引出KELM.ELM作为一种广义单层前馈神经网络, 输出为
| $ \begin{array}{l} {f_L}\left( x \right) = \\ \sum\limits_{i = 1}^L {{\beta _i}{h_i}\left( {{x_j}} \right)} = \sum\limits_{i = 1}^L {{\beta _i}{g_i}\left( {{\mathit{\boldsymbol{w}}_i} \cdot {\mathit{\boldsymbol{x}}_j} + {b_i}} \right)} = h\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{\beta }}. \end{array} $ | (3) |
式中:j=1, …, N, wi∈Rn为第i个节点(神经元)在隐层和输入层之间的权值向量, bi为第i个隐层节点的偏置, βi∈R为第i个隐层节点和输出节点之间的权重.fL(x)为前馈神经网络的输出, wi·xj为wi和xj的内积.在网络学习前, 需要随机确定学习参数wi和bi.
如果具有L个隐层节点的单层前馈网络能够近似N个样本且误差为零, 那么存在βi、wi和bi, 使得
| $ \sum\limits_{i = 1}^L {{\beta _i}g\left( {{\mathit{\boldsymbol{w}}_i} \cdot {\mathit{\boldsymbol{x}}_j} + {b_i}} \right)} = {\mathit{\boldsymbol{t}}_j};j = 1,2, \cdots ,N. $ | (4) |
式(4) 可以简写为Hβ=T.其中,
| $ \mathit{\boldsymbol{H = }}\left( {\begin{array}{*{20}{c}} {h\left( {{\mathit{\boldsymbol{x}}_1}} \right)}\\ \vdots \\ {h\left( {{\mathit{\boldsymbol{x}}_N}} \right)} \end{array}} \right) = {\left[ {\begin{array}{*{20}{c}} {h\left( {{\mathit{\boldsymbol{w}}_1},{b_1},{\mathit{\boldsymbol{x}}_1}} \right)}& \cdots &{h\left( {{\mathit{\boldsymbol{w}}_L},{\mathit{\boldsymbol{b}}_L},{\mathit{\boldsymbol{x}}_1}} \right)}\\ \vdots &{}& \vdots \\ {h\left( {{\mathit{\boldsymbol{w}}_1},{b_1},{\mathit{\boldsymbol{x}}_N}} \right)}& \cdots &{h\left( {{\mathit{\boldsymbol{w}}_L},{b_L},{\mathit{\boldsymbol{x}}_N}} \right)} \end{array}} \right]_{N \times L}}, $ | (5) |
| $ \mathit{\boldsymbol{\beta = }}\left[ {\mathit{\boldsymbol{\beta }}_1^{\rm{T}},\;\;\; \cdots ,\;\;\;\mathit{\boldsymbol{\beta }}_L^{\rm{T}}} \right]_{L \times r}^{\rm{T}}, $ | (6) |
| $ \mathit{\boldsymbol{T = }}\left[ {\mathit{\boldsymbol{t}}_1^{\rm{T}},\;\;\; \cdots ,\;\;\;\mathit{\boldsymbol{t}}_N^{\rm{T}}} \right]_{N \times r}^{\rm{T}}. $ | (7) |
H为神经网络的隐层矩阵, H的第i列表示当输入为x1, x2, …, xN时, 第i个隐层神经元的输出.H的第j行表示当输入为xj时, 隐层的输出向量.一种计算Moore-Penrose广义逆矩阵的方法是正交投影法:
| $ {\mathit{\boldsymbol{H}}^\dagger } = {\mathit{\boldsymbol{H}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{H}}^{\rm{T}}}} \right)^{ - 1}}. $ | (8) |
根据岭回归理论, 将HHT对角线增加一个正数, 使得最终的解方案更加稳定, 泛化能力更好, 可得
| $ f\left( \mathit{\boldsymbol{x}} \right) = h\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{\beta = }}h\left( \mathit{\boldsymbol{x}} \right){\mathit{\boldsymbol{H}}^{\rm{T}}}{\left( {\frac{\mathit{\boldsymbol{I}}}{C}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{H}}^{\rm{T}}}} \right)^{ - 1}}\mathit{\boldsymbol{T}}. $ | (9) |
式中:I为单位矩阵, C为惩罚系数.若隐层特征映射函数h(x)是未知的[13], 则根据式(10) 将一个核矩阵用于ELM.
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{{\rm{ELM}}}} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{H}}^{\rm{T}}}:{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{{\rm{EL}}{{\rm{M}}_{i,j}}}} = h\left( {{\mathit{\boldsymbol{x}}_i}} \right) \cdot h\left( {{\mathit{\boldsymbol{x}}_j}} \right) = K\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j}} \right). $ | (10) |
式中:K(xi, xj)为核函数.ELM分类器的输出可以简写为
| $ f\left( \mathit{\boldsymbol{x}} \right) = {\left[ {\begin{array}{*{20}{c}} {K\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_1}} \right)}\\ \vdots \\ {K\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_N}} \right)} \end{array}} \right]^{\rm{T}}}{\left( {\frac{\mathit{\boldsymbol{I}}}{C} + {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{{\rm{ELM}}}}} \right)^{ - 1}}\mathit{\boldsymbol{T}}. $ | (11) |
由于核函数在ELM中的应用, 这种新型学习算法称为KELM.在KELM中, 不需要考虑隐层特征函数h(x)、权重向量wi、偏置bi以及隐层节点数L.相反地, KELM只考虑核函数K(xi, xj)和训练样本.许多核函数可以用于KELM, 例如线性核函数、多项式核函数和RBF核函数.选用RBF核函数K(u, v)=exp (-||u-v||2/(2σ2)).使用RBF核函数的KELM包括2个重要参数:惩罚参数C和核参数σ.C用于权衡拟最小拟合误差和输入权重的最小范数, σ定义了从输入空间到一些高维空间的非线性映射.
4.2 引力搜索算法(GSA)GSA给出一个智能体集合, 能够根据牛顿万有引力定律来寻找最优解方案.将这些智能体看作物体, 它们之间相互吸引.由于力的作用, 所有物体都会像较重的物体移动.假设在n维空间中存在D个智能体, 那么第i个智能体的位置可以定义为
| $ {O_i} = \left( {o_i^1, \cdots ,o_i^d, \cdots ,o_i^n} \right);i = 1,2, \cdots ,D. $ | (12) |
式中:oid为在第d维空间的第i个智能体.GSA的主要步骤如下.
1) 初始化每个智能体的速度和位置.
2) 评价每个智能体的适应度.
3) 根据式(13) 更新引力常数G(t).
| $ G\left( t \right) = {G_0} \times \exp \left( { - \alpha /T} \right). $ | (13) |
式中:G0为初始引力常数, α为衰减系数(任意常数), T为最大迭代次数.
4) 根据下式计算每个智能体的引力(惯性)质量:
| $ \left. \begin{array}{l} {m_i}\left( t \right) = \frac{{{\rm{fi}}{{\rm{t}}_i}\left( t \right) - {\rm{worst}}\left( t \right)}}{{{\rm{best}}\left( t \right) - {\rm{worst}}\left( t \right)}},\\ {M_i}\left( t \right) = \frac{{{m_i}\left( t \right)}}{{\sum\nolimits_{j = 1}^D {{m_j}\left( t \right)} }}. \end{array} \right\} $ | (14) |
式中:Mi(t)和fiti(t)分别为智能体i在t时刻的质量和适应度, worst(t)和best(t)分别为智能体的最差和最佳适应度.
5) 根据下式所示的万有引力定律, 求得智能体的合力:
| $ F_{ij}^d\left( t \right) = G\left( t \right)\frac{{{M_i}\left( t \right) \cdot {M_j}\left( t \right)}}{{{R_{ij}}\left( t \right) + \varepsilon }} \cdot \left( {o_i^d\left( t \right) - o_j^d\left( t \right)} \right). $ | (15) |
式中:Fijd(t)为在d维空间的智能体i和在t时刻的智能体j之间的引力;Mi(t)和Mj(t)分别为智能体i和智能体j的被动引力质量;ε为一个很小的常数, 用来避免分母为零;oid(t)为在d维空间中智能体i的位置;ojd(t)为智能体j在t时刻的位置;Rij(t)=oi(t), oj(t)2为智能体i和智能体j之间的欧氏距离.
6) 计算智能体的加速度.在d维空间中, t时刻的加速度aid(t)可以表示为
| $ a_j^d\left( t \right) = \frac{{\sum\nolimits_{i = 1,j \ne 1}^N {{\rm{rand}} \cdot F_{ij}^d\left( t \right)} }}{{{M_i}\left( t \right)}}. $ | (16) |
式中:rand为属于区间[0, 1]的随机数.
7) 根据下式更新智能体的速度和位置:
| $ \mu _i^d\left( {t + 1} \right) = {\rm{rand}} \cdot \mu _i^d\left( t \right) + a_i^d\left( t \right), $ | (17) |
| $ o_i^d\left( {t + 1} \right) = o_i^d\left( t \right) + o_i^d\left( {t + 1} \right). $ | (18) |
8) 若满足停止条件, 则输出解方案.否则, 转到步骤2).
4.3 AID算法流程基于变量选择和KELM的AID算法流程如图 4所示.由图 4可知, AID算法包括以下2个部分:1) 重要变量的选择;2) 模型训练和参数优化.算法的具体步骤如下.
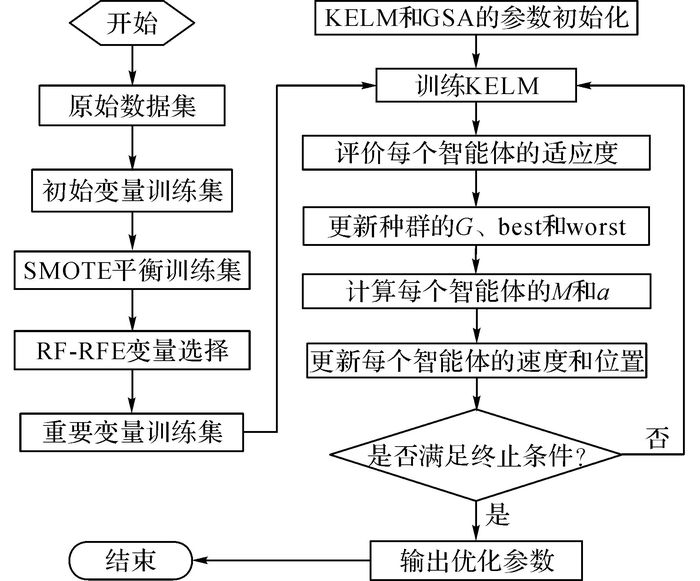
|
图 4 AID算法流程图 Fig. 4 Flowchart of AID algorithm |
1) 采用SMOTE平衡数据集中的事件样本和非事件样本.
2) 使用RF-RFE算法选择重要变量.
a) 使用初始变量构建训练集.训练集包括多个训练样本.训练集的输入为
| $ {\rm{Input}} = \left[ {{\lambda _{i,j}}} \right] = \left[ {\begin{array}{*{20}{c}} {{\lambda _{1,1}}}&{{\lambda _{2,1}}}& \cdots &{{\lambda _{15,1}}}\\ {{\lambda _{1,2}}}&{{\lambda _{2,2}}}& \cdots &{{\lambda _{15,2}}}\\ \vdots & \vdots &{}& \vdots \\ {{\lambda _{1,m}}}&{{\lambda _{2,m}}}& \cdots &{{\lambda _{15,m}}} \end{array}} \right]. $ |
训练集的输出为
| $ {\rm{Output}}= \left[ {{y_j}} \right] = \left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}}\\ \vdots \\ {{y_m}} \end{array}} \right]. $ |
式中:m为训练样本总数, λi, j为第j个输入样本的第i个变量.第i个变量的具体内容见表 1.yj∈{-1, 1}表示第j个输入样本所对应交通事件的判别标签, -1表示有交通事件, 1表示无交通事件.
b) 使用RF评价15个初始变量的重要度, 并记录训练集的分类正确率.
c) 删除重要度最小的变量, 使用剩余变量构建新的训练集;重新评价剩余变量的重要度, 并记录训练集的分类正确率.
d) 重复步骤c), 直至搜索完毕全部变量, 即仅仅剩余重要度最大的1个变量.
经过步骤2), 可得15个初始变量的重要度排序以及每个训练集的分类正确率.获得最高分类正确率的训练集所对应的输入变量, 即为重要变量.
3) 训练KELM并采用GSA优化参数.
a) 初始化KELM参数和GSA参数.
b) 使用重要变量构建训练集来训练KELM, 计算和评价每个智能体的适应度.
c) 更新种群的G(t)、best(t)和worst(t).
d) 计算每个智能体的Mi(t)和oid(t).
e) 更新每个智能体的位置和速度.
f) 判断是否满足终止条件.如果满足终止条件, 转到步骤g);否则转到步骤b), 直到满足条件.
g) 输入KELM的最优参数.
5 实例分析 5.1 实验数据及预处理实验数据来源于美国著名的Ⅰ-880高速公路交通事件数据库.Ⅰ-880高速公路路段长度为9.2英里, 车道数为3~5, 其中包括一些高占有率车道.在北向车道和南向车道, 分别设有18个和17个环形线圈检测站(详细信息参见文献[21]).该数据库完整记录了采样时段内的环形线圈采集的交通流量、速度和占有率数据(采样间隔为30 s)以及事件发生的位置和起止时间等信息.该数据库广泛应用于AID算法的验证和评价.数据库包括45个交通事件(共计4 136组样本).随机选取23个交通事件数据用于训练, 剩余22个交通事件数据用于测试.由于非事件数据量过于庞大, 通常随机无放回地抽取非事件样本用于构建训练集和测试集.为了较大程度地保留非事件样本的信息, 将训练集和测试集的事件样本比例都设置为20%, 训练集和测试集组成如表 2所示.
| 表 2 训练集和测试集的样本组成 Table 2 Composition of training set and test set sample |
为了使两类样本相对平衡, 采用SMOTE增加训练集中的交通事件样本.SMOTE具体参数设置如下:邻近样本点个数为5, 过采样倍率为300%.平衡后的训练集中两类样本数均为8 144个.为了消除不同量纲的影响, 提升训练速度和分类效果, 将数据归一化到区间[0, 1].归一化公式为
| $ {y_i} = \frac{{{x_i} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}. $ | (19) |
式中:xi为原始数据, yi为归一化数据, xmax为原始数据最大值, xmin为原始数据最小值.
5.2 变量选择使用RF-RFE算法评价交通事件检测初始变量的重要度, 并从中选择重要变量.需要确定的参数包括随机特征变量个数和决策数的数量.根据文献[19]的建议可知, 随机特征变量个数mtry为特征变量总数的平方根, 此处mtry取4;决策数的数量设置为1 000.所得的初始变量按照重要度降序排列为:{15, 12, 9, 13, 10, 6, 7, 14, 11, 3, 8, 4, 2, 5, 1}.每次删除重要度排序在最后一位的特征变量, 重新计算分类正确率.分类正确率Ac随变量个数Nv的变化曲线如图 5所示.当变量个数为15时, 即为初始变量集.随着不重要变量的删除, 分类正确率大致呈上升趋势.因为删除不重要变量能够减小冗余信息对算法的影响.当变量个数为6时, 得到最高分类正确率;然后随着变量数的减少, 分类正确率逐渐下降.这是因为删除了重要性较大的变量.选择重要性最大的前6个变量(上、下游相邻检测器实测占有率的差值, 下游检测器实测占有率与预测占有率的差值, 上游检测器实测占有率与预测占有率的差值, 上、下游相邻检测器实测流量的差值, 下游检测器实测流量与预测流量的差值, 下游检测器的实测占有率)作为交通事件检测的重要变量.使用重要变量构建训练集, 训练集输入矩阵为
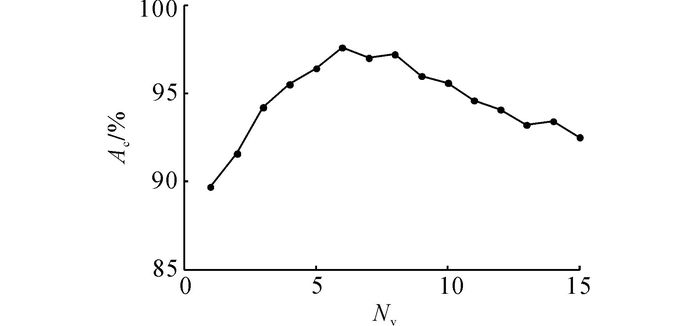
|
图 5 分类正确率与变量个数之间的关系 Fig. 5 Relationship of classification accuracy and variables number |
| $ \left[ {\begin{array}{*{20}{c}} {{\lambda _{15,1}}}&{{\lambda _{12,1}}}&{{\lambda _{9,1}}}&{{\lambda _{13,1}}}&{{\lambda _{10,1}}}&{{\lambda _{6,1}}}\\ {{\lambda _{15,2}}}&{{\lambda _{12,2}}}&{{\lambda _{9,2}}}&{{\lambda _{13,2}}}&{{\lambda _{10,2}}}&{{\lambda _{6,2}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{\lambda _{15,16,288}}}&{{\lambda _{12,16,288}}}&{{\lambda _{9,16,288}}}&{{\lambda _{13,16,288}}}&{{\lambda _{10,16,288}}}&{{\lambda _{6,16,288}}} \end{array}} \right]. $ |
其中, 每个行向量表示一个训练样本, 共计16 288个;每个列向量表示一个重要变量.前8 144个输入样本所对应的输出为-1, 表示有交通事件;后8 144个输入样本所对应的输出为1, 表示无交通事件.
5.3 算法参数优化采用重要变量构建的训练集训练KELM, 使用GSA优化KELM参数.将分类正确率作为适应度函数(目标函数).GSA具体参数设置如下:种群数量为20, 初始引力常数G0=100, 衰减率α=10, 最大迭代次数Tmax=100, 惩罚参数C∈[0.1, 1 000], 核参数σ∈[0.01, 100].
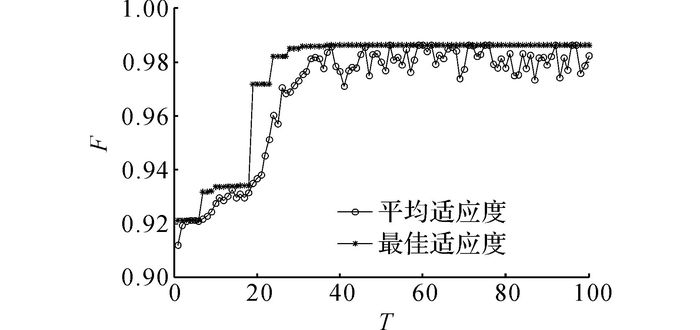
在训练过程中, 使用K折交叉验证避免过拟合和欠拟合.将训练集随机分为K个不相交的子集, K-1个子集用于训练, 使用余下的一个子集用于验证.如此重复K次, 直到所有子集都作为一次验证集.将K次验证结果的平均值作为评价指标.本文采用的是5折交叉验证.如图 6所示为适应度F曲线.图中,T为迭代次数.可知, 最佳适应度随着迭代的增加逐渐上升.平均适应度在波动中上升.当迭代次数为76时, 最佳适应度和平均适应度均为0.986 5, 所对应的参数组合为:C=10.34, σ=0.22.
|
图 6 适应度曲线 Fig. 6 Fitness curves |
为了更好地分析KELM的检测性能, 选择反向传播神经网络(back propagation neural network, BPNN)和SVM作为对比算法.BPNN和SVM用于交通事件检测的详细步骤分别见文献[5]和[7].采用单隐层的BPNN, 并使用GSA算法优化初始权值和阈值.SVM采用RBF核函数, 核函数参数和惩罚系数使用GSA优化.
AID算法性能的评价指标包括交通事件检测率(detection rate, DR)、误报率(fa1se alarm rate, FAR)和平均检测时间(mean time to detection, MTTD).DR表示在特定的时间段内, 检出的事件数量占实际事件数的百分比.FAR表示在特定时间段内, 误报事件数占所有决策次数的百分比.MTTD表示检测到事件发生时刻与事件实际发生时刻差值的算术平均值.DR和FAR用于衡量AID算法的检测性能, MTTD用于描述AID算法的检测效率.DR、FAR和MTTD 3个指标彼此相关, 相互依赖.若获得较高的DR, 则必定导致较高的FAR;在降低FAR的同时, 必然会降低DR.相似地, 若获得较短的MTTD, 则FAR相对较高.当评价一种新的AID算法时, 通常需要权衡这3个指标.
分别使用初始变量和重要变量构建训练集, 测试这3种算法的性能, 结果如表 3所示.可知, 与使用初始变量的AID算法相比, 使用重要变量AID算法在DR、FAR和MTTD 3个指标方面都得到了提升, 具有更高的DR, 更低的FAR和更短的MTTD.其中, KELM的性能优于BPNN和SVM.
| 表 3 KELM、BPNN和SVM的检测效果 Table 3 Performance of KELM, BPNN and SVM |
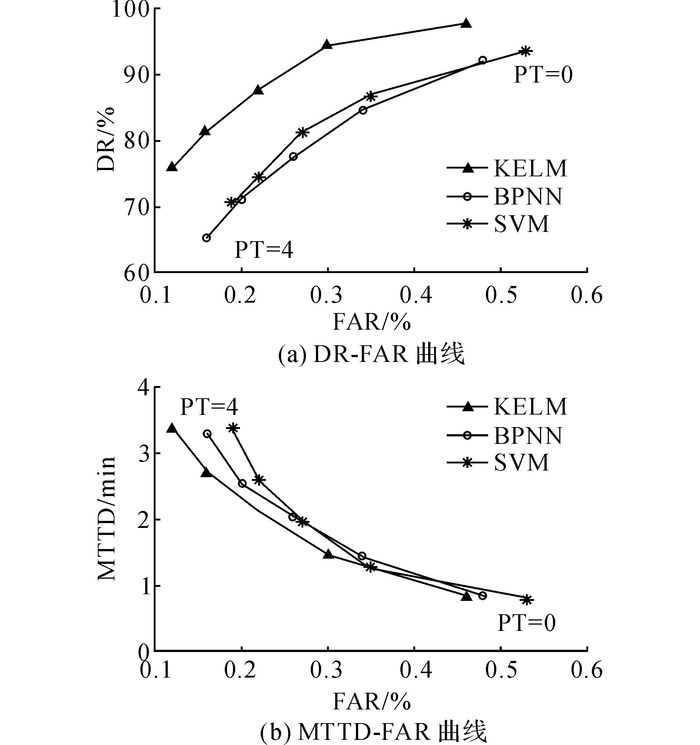
持续性检验(persistence test, PT)是降低FAR的有效方式[8].持续性检验是指连续n个间隔检测到交通事件, 最终判定交通事件的发生.当没有持续性检验时, PT=0.MTTD随着持续性检验次数的增加而变长, DR随着持续性检验次数的增加而降低.PT在一定程度上影响了检测效果和检测效率.当PT=0~4时, 3种算法的性能曲线如图 7所示.如图 7(a)所示为DR-FAR曲线, 如图 7(b)所示为MTTD-FAR曲线.如表 3所示为PT=0时, 3个指标的取值, 对应FAR的最大值.由图 7(a)可以看出, KELM的DR-FAR曲线更靠近左上角, 说明KELM的性能更好, 即在相同DR的条件下, FAR更低;在相同FAR的条件下, DR更高.对于每一算法的DR-FAR曲线, 当PT=1时, FAR下降幅度较大, DR下降较小.当PT次数继续增加时, FAR的下降逐渐缓慢, DR的下降逐渐加快.从图 7(b)可知, KELM的MTTD-FAR曲线更靠近左下角, 说明KELM的性能更好, 即在相同FAR的条件下, MTTD更短;在相同MTTD的条件下, FAR更低.对于每一算法的MTTD-FAR曲线, 当PT=1时, 虽然在一定程度上增大MTTD, 但是FAR的下降幅度较大.随着PT次数的增加, FAR的下降速度变得缓慢, MTTD的增大速度加快.综上所述, KELM的检测性能由于BPNN和SVM, PT=1能够较好地权衡DR、FAR和MTTD 3个指标.
|
图 7 KELM、BPNN和SVM的性能曲线 Fig. 7 Performance curves of KELM, BPNN and SVM |
(1) 采用RF-RFE算法能够有效地选择交通事件检测的重要变量, 不仅降低了AID算法的输入维数, 而且以重要变量为输入的AID算法具有更好的性能.
(2) KELM算法性能优于BPNN和SVM.
(3) 当持续性检测次数为1时, 能够较好地权衡DR、FAR和MTTD 3个指标.
为了得到更具有普遍性的结论, 在未来研究中需要将该AID算法用于其他交通事件数据集, 并从理论上分析和论证KELM用于交通事件检测的优越性.此外, 如何构建更加全面的交通事件检测初始变量集有待进一步的探讨.
| [1] | LINDLEY J A. Urban freeway congestion: quantification of the problem and effectiveness of potential solutions[J]. ITE Journal, 1987, 57(1): 27–32. |
| [2] |
姬杨蓓蓓, 张小宁, 孙立军. 基于贝叶斯决策树的交通事件持续时间预测[J].
同济大学学报:自然科学版, 2008, 36(3): 319–324.
JIYANG Bei-bei, ZHANG Xiao-ning, SUN Li-jun. Incident duration prediction grounded on Bayesian decision method based tree algorithm[J]. Journal of Tongji University: Natural Science, 2008, 36(3): 319–324. |
| [3] | GHOSH B, SMITH D P. Customization of automatic incident detection algorithms for signalized urban arterials[J]. Journal of Intelligent Transportation Systems, 2014, 18(4): 426–441. DOI:10.1080/15472450.2013.806843 |
| [4] | KARIM A, ADELI H. Comparison of fuzzy-waveletradial basis function neural network freeway incidentdetection model with California algorithm[J]. Journal of Transportation Engineering, 2002, 128(1): 21–30. DOI:10.1061/(ASCE)0733-947X(2002)128:1(21) |
| [5] | SRINIVASAN D, JIN X, CHEU R L. Evaluation ofadaptive neural network models for freeway incidentdetection[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(1): 1–11. DOI:10.1109/TITS.2004.825084 |
| [6] |
陈维荣, 关佩, 邹月娴. 基于SVM的交通事件检测技术[J].
西南交通大学学报, 2011, 46(1): 63–67.
CHEN Wei-rong, GUAN Pei, ZOU Yue-xian. Automatic incident detection technology based on SVM[J]. Jounal of Southwest Jiaotong University, 2011, 46(1): 63–67. |
| [7] | YUAN F, CHEU R L. Incident detection using support vector machines[J]. Transportation Research Part C:Emerging Technologies, 2003, 11(3): 309–328. |
| [8] | CHEN S, WANG W. Decision tree learning for freeway automatic incident detection[J]. Expert Systems with Applications, 2009, 36(2): 4101–4105. DOI:10.1016/j.eswa.2008.03.012 |
| [9] | WANG J, LI X, LIAO S S, et al. A hybrid approach for automatic incident detection[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(3): 1176–1185. DOI:10.1109/TITS.2013.2255594 |
| [10] | XIAO J, GAO X, KONG Q J, et al. More robust and better: a multiple kernel support vector machine ensemble approach for traffic incident detection[J]. Journal of Advanced Transportation, 2014, 48(7): 858–875. DOI:10.1002/atr.v48.7 |
| [11] | LIU Q, LU J, CHEN S, et al. Multiple Naïve bayes classifiers ensemble for traffic incident detection[J]. Mathematical Problems in Engineering, 2014, 2014: 1–16. |
| [12] | HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70(1): 489–501. |
| [13] | HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2012, 42(2): 513–529. DOI:10.1109/TSMCB.2011.2168604 |
| [14] | PAL M, MAXWELL A E, WARNER T A. Kernel-based extreme learning machine for remote-sensing image classification[J]. Remote Sensing Letters, 2013, 4(9): 853–862. DOI:10.1080/2150704X.2013.805279 |
| [15] | XIE W, LI Y, MA Y. Breast mass classification in digital mammography based on extreme learning machine[J]. Neurocomputing, 2016, 173(3): 930–941. |
| [16] | GRANITTO P M, FURLANELLO C, BIASIOLI F, et al. Recursive feature elimination with random forest for PTR-MS analysis of agroindustrial products[J]. Chemometrics and Intelligent Laboratory Systems, 2006, 83(2): 83–90. DOI:10.1016/j.chemolab.2006.01.007 |
| [17] | RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA: a gravitational search algorithm[J]. Information sciences, 2009, 179(13): 2232–2248. DOI:10.1016/j.ins.2009.03.004 |
| [18] |
楼晓俊, 孙雨轩, 刘海涛. 聚类边界过采样不平衡数据分类方法[J].
浙江大学学报:工学版, 2013, 47(6): 944–950.
LOU Xiao-jun, SUN Yu-xuan, LIU Hai-tao. Clustering boundary over-sampling classification method for imbalanced data sets[J]. Journal of Zhejiang University: Engineering Science, 2013, 47(6): 944–950. |
| [19] | BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5–32. DOI:10.1023/A:1010933404324 |
| [20] | GUYON I, WESTON J, BARNHILL S, et al. Gene selection for cancer classification using support vector machines[J]. Machine Learning, 2002, 46(1/3): 389–422. DOI:10.1023/A:1012487302797 |
| [21] | TENG H, QI Y. Application of wavelet technique to freeway incident detection[J]. Transportation Research Part C: Emerging Technologies, 2003, 11(3): 289–308. |



