2. 浙江警察学院 交通管理工程系, 浙江 杭州 310053;
3. 吉林大学 交通学院, 吉林 长春 130022
2. Department of Traffic Management Engineering, Zhejiang Police College, Hangzhou 310053, China;
3. College of Transportation, Jilin University, Changchun 130022, China
电动自行车(electric bicycle, EB)作为一种便捷、低廉、灵活、环保的绿色出行方式, 近年来在我国许多城市呈现迅猛发展态势.据统计, 全国电动自行车保有量已从2004年底的1 000万辆迅速增长到2013年底的2亿辆[1].由于电动自行车运行速度远大于普通自行车, 两种不同速度的交通流在同一断面交织运行, 也带来了一系列突出的交通效率、交通管理及交通安全等方面的问题[2-4].我国现行《电动自行车通用技术条件》(GB17761-1999) 规定, 电动自行车设计最高速度不大于20 km/h.然而, 实际调查结果表明, 电动自行车运行速度往往为20~35 km/h, 普遍存在超过限速的情况.由于我国对电动自行车的管理是按照非机动车进行管理, 其与普通自行车共用自行车道, 两种不同速度车流的混合运行带来了严重的交通安全隐患与运行效率问题[5].
速度分布模型是开展道路行程时间预测、服务水平分析的重要基础, 国内外对于机动车交通流速度的研究取得了重要的研究成果[6].Dey等[7]提出速度分布曲线模型, 用以拟合快速车辆与慢速车辆混合运行情况下的速度数据.Cherry[8]通过2006年在上海和昆明的抽样调查表明:上海电动自行车与普通自行车的自由流速度约为18.2和13.0 km/h, 昆明为17.9和12.8 km/h.Lin等[9]调查了昆明自行车专用车道的速度特性.统计结果表明, 电动自行车的速度为21.86 km/h, 比普通自行车快47.6%.从上述研究可以看出, 针对电动自行车的研究主要侧重速度的基本特性分析, 缺乏对速度分布模型及其特性的研究.
本文通过采集杭州市部分典型道路混合自行车速度数据, 定量分析速度特性.考虑车辆构成类型、骑行人特性等特征, 建立混合自行车速度的高斯混合模型, 采用最大期望算法对模型参数进行估计.通过拟合优度显著性检验的方法, 确定高斯混合分布的最优成分数, 为混合自行车交通流速度特性分析、自行车道服务水平分析、限速临界值确定提供理论依据.
1 数据采集与分析 1.1 交通调查由于杭州市具有较高的电动自行车出行比例以及相对完善的自行车道路系统, 选取杭州市区主干道4条典型的机非隔离非机动车道进行数据采集.采用视频摄像调查的方法, 自动记录自行车通过两个断面的时刻, 并计算得到车辆速度数据;通过后期人工视频调查方法, 获取车辆类型、年龄、性别等特征参数.调查路段的相关情况及混合自行车交通流的基本特点, 如表 1所示.表中, l为车道宽度, n为观测的自行车样本量,q为流量.
| 表 1 原始调查数据样本的基本特性 Table 1 Basic characteristics of filed survey samples |
将车辆类型分为普通自行车、轻便电动自行车(bicycle-style e-bike, BSEB)和摩托化电动自行车(scooter-style e-bike, SSEB)三类;性别分为男性和女性两类;年龄分为青年(小于40岁)、中年(40至60岁)和老年(大于60岁)三类.4条路段总结获取了11 303辆自行车的速度样本数据, 其中两类电动自行车占比为63.3%.在所有样本数据中, 男性骑行人占比为68.4%, 青年骑行人占比为71.0%.
1.2 统计特性表 2给出不同类型自行车速度样本的基本统计特性参数.表中,vmax、vmin分别为n辆自行车速度的最大值和最小值,vm为速度中值,v和sv分别为n辆自行车的样本均值和标准差, v85为85%分位数,γ、β分别为偏度和峰度.其中, 偏度(skewness)和峰度(kurtosis)是两个重要的描述样本概率密度函数特性的指标.偏度和峰度的计算公式如下:
| $\gamma = \frac{{\sum\limits_{i = 1}^n {{{\left( {{v_i} - \bar v} \right)}^3}} }}{{\left( {n - 1} \right)s_v^3}},$ | (1) |
| $\beta = \frac{{\sum\limits_{i = 1}^n {{{\left( {{v_i} - \bar v} \right)}^4}} }}{{\left( {n - 1} \right)s_v^4}}.$ | (2) |
式中:vi为第i辆自行车的速度.从表 2可以得到如下结论.
| 表 2 不同类型自行车速度的基本统计结果 Table 2 Statistical results of speed data for different bicycle type |
1) 4个路段的普通自行车平均速度分别为10.83、11.82、15.70及14.87 km/h, 远低于电动自行车的平均速度, 两类电动自行车的速度没有显著差异.由于电动自行车由电力驱动, 外形尺寸差异不会导致运行速度存在很大的差异.混合自行车运行速度的结论与先前的研究结果[3, 9-10]一致.
2) 前两个路段的平均速度(12.42和13.92 km/h)明显小于后两个路段(18.68和17.67 km/h).这是由于前两个路段车道较窄且流量较大, 部分时间会出现短暂的接近饱和状态, 平均速度较低.后两个路段由于车道较宽、流量较小, 交通状态基本维持在自由流状态.上述交通状态的不同会导致混合自行车交通流速度分布概率密度函数的差异.
3) 85%分位速度经常被用于确定道路的自由流速度.从表 2可以看出, 电动自行车85%分位速度明显高于普通自行车.4个路段所有车辆的85%分位速度分别为18.00、21.43、23.26以及24.52 km/h.随着车道宽度的增加, 车辆之间的侧向干扰会随之减少, 因而自由流速度随之增加.后两个路段电动自行车的自由流速度都超过25 km/h, 超过规范20 km/h的限速值, 表明电动自行车超速现象较普遍.
4) 从偏度数据来看, 前两个路段所有类型车辆的偏度都大于零, 说明速度概率密度函数存在较明显的右偏现象.造成这种现象的主要原因是这两个路段的流量相对较大, 大部分车辆形成较稳定的车流, 速度差异性不大.部分高速行驶的电动自行车形成了右偏的长尾分布.后两个路段的偏度特性不同, 偏度较小且存在左偏特性.这主要是源于大部分车辆都处于自由流运行状态, 只有部分普通自行车的运行速度较低, 从而形成了左偏的长尾特性.
5) 从峰度数据来看, 与机动车速度数据具有正态分布的特性不同, 不同地点及车辆类型的自行车速度数据都存在较明显的峰度特征.这是由于与机动车相比, 自行车具有更加明显的集群性.速度离散程度较低, 概率密度函数会比正态分布具有更大的峰度, 形成“尖峰”特征.
2 速度分布模型 2.1 基本假设对于自行车骑行人来说, 速度受到骑行人特性(性别、年龄、性格、驾驶经验等)、车辆类型(普通自行车、电动自行车等)、道路特性(路面情况、隔离情况、道路线形等)以及环境因素(交通状况、天气情况等)的影响[11-13].对于特定条件下的速度分析来说, 道路特性以及环境因素等影响可以忽略不计, 自行车速度的选择主要受到交通状态(流量)、骑行人特性(性别、年龄)以及车辆类型(普通自行车、轻便电动自行车和摩托化电动自行车)的影响.本文主要针对这三种类影响因素进行分析建模.可以假设不同影响因素的组合导致了骑行人选择不同的速度, 即不同影响因素决定了速度来自于不同的亚类.假设存在M种不同的影响因素组合, 那么某一辆自行车速度来自于其中的某种亚类.由于受到不同因素的影响, 不同亚类概率密度函数的参数不同.假设不同亚类自行车速度样本都服从相同的分布函数(如正态分布、对数正态分布等), 分布函数的参数(均值、方差等)随着不同影响因素的变化而变化.
2.2 高斯混合模型通过上述假设可知, 混合自行车速度样本构成了多元概率分布模型.采用高斯混合模型(Gaussian mixture model, GMM)来拟合混合自行车速度样本数据.具有M种亚类的高斯混合模型可以采用下式[14-16]表达:
| $P\left\{ {{v_k}\left| {\left( {{w_i},{u_i},\sigma _i^2} \right)} \right.} \right\} = \sum\limits_{i = 1}^M {{w_i}g\left( {{v_k}\left| {{u_i},\sigma _i^2} \right.} \right)} .$ | (3) |
式中:vk为第k辆自行车的观测速度;wi (i =1, …, M)为第i亚类分布的权重系数, 表示第i类自行车速度样本占总样本的比例, 须满足
| $g\left( {{v_k}\left| {{u_i},{\sigma _i}} \right.} \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _i}}}\exp \left\{ { - \frac{1}{{2\sigma _i^2}}{{\left( {{v_k} - {u_i}} \right)}^2}} \right\}.$ | (4) |
其中, μi和σi分别为第i亚类正态分布的均值与标准差.
高斯混合模型中存在很多变量, 选择不同的模型结构(类型数量与模型参数), 会得到不同的速度分布模型.其中, 权重系数是高斯混合模型的核心, 是进行模型参数估计与样本类型识别的关键.
2.3 参数估计对于某一特定路段的自行车速度样本数据, 在确定GMM模型的亚类数量M后, 模型参数估计的核心是得到GMM参数合集
| $\log \prod\limits_{k = 1}^N {p\left( {{v_k}\left| \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right.} \right)} = \sum\limits_{k = 1}^N {\log p} \left( {{v_k}\left| \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right.} \right).$ | (5) |
由于GMM参数在式(5) 中都是隐性表达的, 无法通过直接求导得到最大值.应用EM算法估计的具体步骤如下.
1) 通过K均值聚类算法初始化GMM参数
2) E步骤.针对第k个非机动车速度样本vk, 它属于第i个亚类的概率为
| $\gamma \left( {k,i} \right) = \frac{{{w_i}g\left( {{v_k}\left| {{u_i},{\sigma _i}} \right.} \right)}}{{\sum\limits_{j = 1}^M {{w_i}g\left( {{v_k}\left| {{u_j},{\sigma _j}} \right.} \right)} }}.$ | (6) |
3) M步骤.对式(6) 求导, 得到最大似然估计对应的均值和方差:
| ${u_i} = \frac{1}{N}\sum\limits_{k = 1}^N {\gamma \left( {k,i} \right)} {v_k},$ | (7) |
| $\sigma _i^2 = \frac{1}{{{N_i}}}\sum\limits_{k = 1}^N {\gamma \left( {k,i} \right)} {\left( {{v_k} - {u_i}} \right)^2}.$ | (8) |
式中:
| ${w_i} = \frac{{{N_i}}}{N}.$ | (9) |
4) 通过预设最小误差, 判断似然函数是否收敛.若收敛, 则停止迭代, 得到最终的估计结果;否则, 返回2) 重新进行迭代计算.
3 结果与讨论 3.1 估计结果由于无法直接确定适合混合自行车速度分布的亚类数, 假设GMM分别具有2~6种亚类, 并对这5种情况采用EM算法分别进行模型参数估计.不同亚类下, 4条路段的模型参数估计结果如表 3所示.
| 表 3 亚类数为2~6的GMM参数估计结果 Table 3 Estimation results of parameters for GMM under component numbers 2-6 |
4个路段样本数据的经验概率密度函数与一元至六元GMM分布下的概率密度pp函数如图 1所示.可以看出, 路段1和2的速度数据具有明显的双峰现象, 路段3和4的速度数据接近正态分布.同时, 多元GMM分布能够好地描述混合自行车速度样本所具有的多峰及偏态特性.
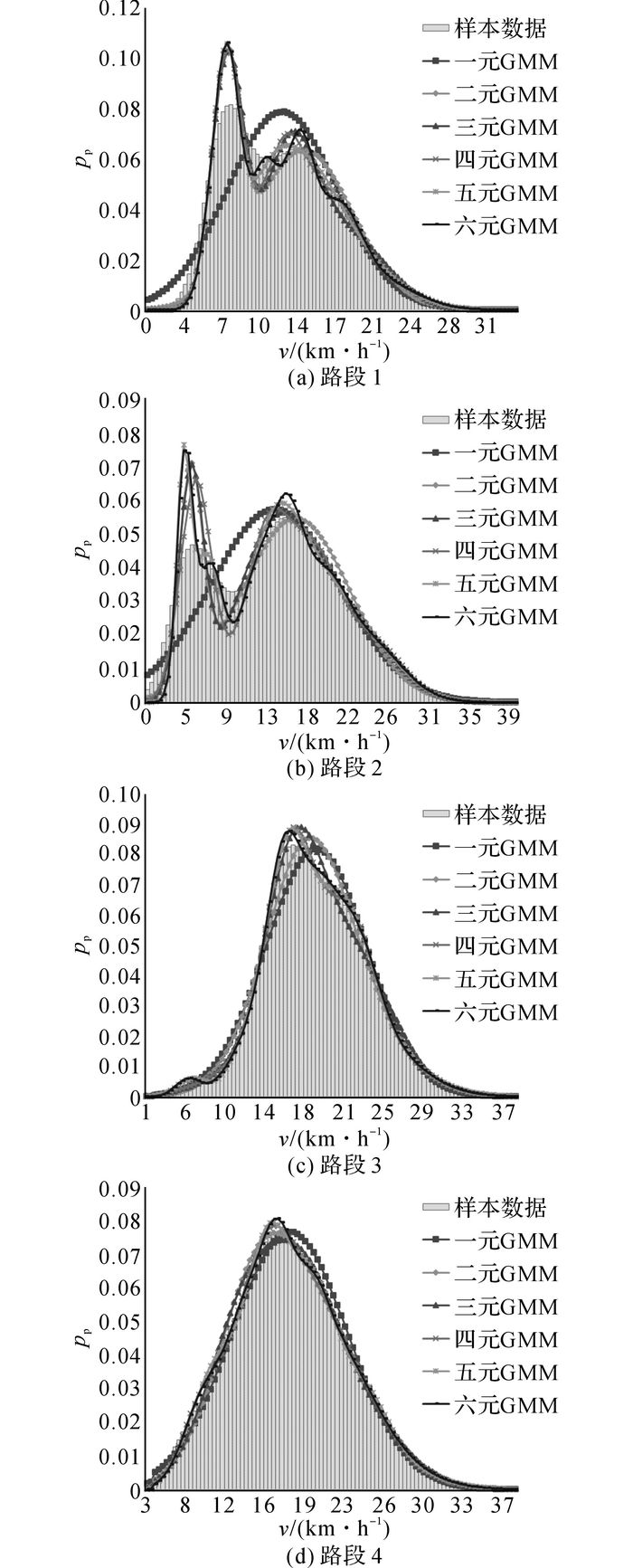
|
图 1 观测值与多元GMM的概率密度函数 Fig. 1 Probability functions of observations and multi-component GMMs |
为了进一步确定GMM的亚类数, 分别对样本数据的经验分布与估计的GMM分布进行Kolmogorov-Smirnov(K-S)拟合优度检验.K-S检验是基于累积分布函数, 检验速度样本的经验分布是否服从M类的GMM分布.K-S检验的H值以及p值结果如表 4所示.表中,tCPU为CPU时间,ni为迭代次数, L为似然估计值.可以看出, 在0.05显著性水平下, 路段1和2的速度样本数据服从五元及六元GMM分布;路段3和4的速度样本数据服从三元及四元GMM分布.若按照0.1的显著性水平进行假设检验, 则路段1~4分别服从六元、五元、三元及三元GMM分布.p越大, 拟合的GMM分布与速度样本经验分布之间越没有显著性的差异, 即拟合得到的混合自行车速度GMM分布越接近实际样本数据的经验分布.可以利用p确定GMM分布的最优亚类数量.
| 表 4 EM算法性能与K-S检验结果 Table 4 Performances of EM algorithm and results of K-S test |
由于路段1和2存在多种交通状态、交通状态、自行车类型以及驾驶员特性等多种因素综合作用, 导致速度分布特性异常复杂, 需要更多亚类才能很好地拟合自行车速度样本数据.对于路段3和4而言, 由于交通状态基本都处于自由流状态下, 交通状态对速度的影响几乎可以忽略, 仅自行车类型以及驾驶员特性因素会对速度分布产生影响.这种情况下得到的最优亚类数量为3类.在各自最优亚类数量的情况下, 4个路段速度数据的各亚类概率密度与总体概率密度函数如图 2所示.
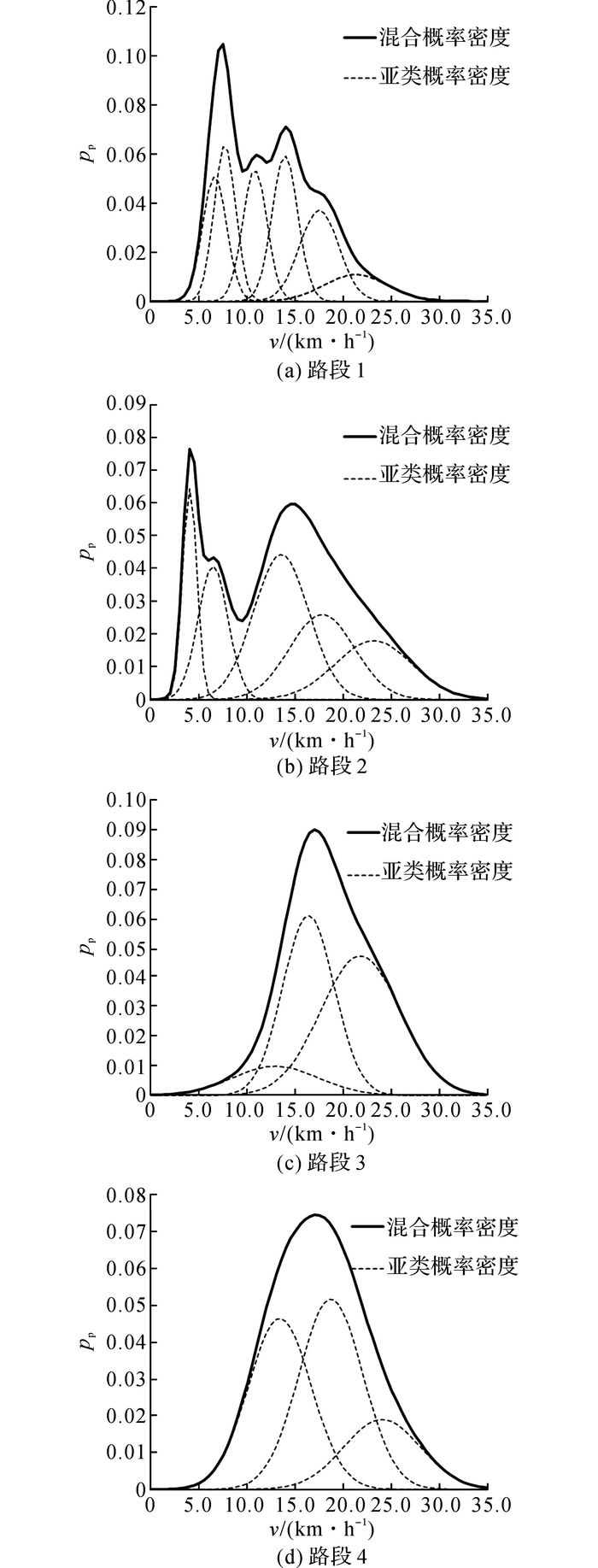
|
图 2 不同路段拟合的混合分布 Fig. 2 Fitted mixture distributions for different segments |
由于交通状态、骑行人特性以及车辆类型这三类因素对自行车速度的影响是非常复杂的, 很难定量确定哪种影响因素导致速度样本属于某种亚类.只能定性地通过不同影响因素速度样本的t检验结果来区分速度均值是否存在显著性的差异, 以此作为区分不同亚类的基本依据[2, 4].
3.3 模型应用在得到估计的最优拟合GMM分布后, 可以应用该分布模型分析不同限速阈值下的自行车分布情况.在限速值vlim下, 第i亚类中超速自行车比例的计算公式为
| ${p_i}\left( {{v_{\lim }}} \right) = 1 - F\left( {{v_{\lim }}\left| {{u_i},{\sigma _i}} \right.} \right).$ | (10) |
式中:vlim为确定的限速阈值;pi(vlim)为第i亚类在限速阈值vlim下超过限速值的自行车比例;F为正态分布的累积概率密度函数.
表 5给出在限速阈值为20、25及30 km/h的条件下,4个路段不同亚类中超速车辆的比例.可以看出, 当限速阈值为20 km/h时, 4个路段最高车速亚类中, 超速自行车比例分别占65.5%、78.4%、66.8%及84.3%, 大部分自行车速度处于超速范围.随着限速阈值的增加, 超速自行车比例大大降低.采用混合分布模型估算超速自行车比例, 分析不同亚类自行车超速的特性, 以此作为确定临界限速阈值的基本依据.
| 表 5 超速自行车比例分析 Table 5 Percentages of bicycles over speed limit |
速度分布模型是开展通行能力分析、服务水平确定以及行程时间估计的重要前提与基础.针对混合自行车交通流而言, 由于受到交通状态、车辆类型、集群行为以及骑行人特性等诸多因素的影响, 速度分布特性与机动车相比更加复杂.本文在收集大量混合自行车交通速度数据的基础上, 分析自行车交通流速度样本的相关统计参数.通过对多种影响因素的归类, 构建基于高斯混合模型的速度分布函数, 采用EM算法对模型参数进行最大似然估计.通过K-S拟合优度检验, 确定GMM分布的最佳亚类数目.结果表明, 由于自行车受到多种因素的影响, 针对多种交通状态下的自行车速度数据, 需要更多亚类的GMM分布进行拟合;在自由流状态下, 三元GMM分布可以很好地拟合速度样本数据.通过对GMM的应用, 进一步分析不同限速阈值下自行车的超速特性, 为不同类型自行车限速管理提供了依据.
上述研究将为丰富和发展自行车交通流理论, 为自行车道的规划设计与管理提供科学依据.在后续研究中, 需要进一步探索GMM中不同亚类的数目、权重系数、模型参数与自行车类型、骑行人特性等因素之间的关系, 构建两者之间的定量关系模型.
| [1] | 新华网. 电动自行车数量破2亿, "新国标"将出台[EB/OL]. 2013-10-20. http://news.xinhuanet.com/fortune/2013-10/20/c_125566241.htm. |
| [2] | JIN S, QU X, ZHOU D, et al. Estimating cycleway capacity and bicycle equivalent unit for electric bicycles[J]. Transportation Research Part A, 2015, 77: 22–248. |
| [3] | QU X, YANG Y, LIU Z, et al. Potential crash risks of expressway on-ramps and off-ramps: a case study in Beijing, China[J]. Safety Science, 2014, 70: 58–62. DOI:10.1016/j.ssci.2014.04.016 |
| [4] | XU C, YANG Y, JIN S, et al. Potential risk and its influencing factors for separated bicycle paths[J]. Accident Analysis and Prevention, 2016, 87: 59–67. DOI:10.1016/j.aap.2015.11.014 |
| [5] |
周旦, 马晓龙, 金盛, 等. 混合非机动车交通流超车次率影响因素模型[J].
浙江大学学报:工学版, 2015, 49(9): 1672–1678.
ZHOU Dan, MA Xiao-long, JIN Sheng, et al. Modeling influencing factors of vehicle passing rate in mixed bicycle traffic flow[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(9): 1672–1678. |
| [6] | ALLEN D P, ROUPHALL N, HUMMER J E, et al. Operational analysis of uninterrupted bicycle facilities[J]. Transportation Research Record, 1998, 1636: 29–36. DOI:10.3141/1636-05 |
| [7] | DEY P P, CHANDRA S, GANGOPADHAYA S. Speed distribution curves under mixed traffic conditions[J]. Journal of Transportation Engineering, 2006, 132(6): 475–481. DOI:10.1061/(ASCE)0733-947X(2006)132:6(475) |
| [8] | CHERRY C R. Electric two-wheelers in China: analysis of environmental, safety, and mobility impacts [R]. Berkeley: University of California, 2007: 101. |
| [9] | LIN S, HE M, TAN Y, et al. Comparison study on operating speeds of electric bicycles and bicycles: experience from field investigation in Kunming, China[J]. Transportation Research Record, 2008, 2048: 52–59. DOI:10.3141/2048-07 |
| [10] | LI Z, WANG W, LIU P, et al. Modeling bicycle passing maneuvers on multilane separated bicycle paths[J]. Journal of Transportation Engineering, 2013, 139(1): 57–64. DOI:10.1061/(ASCE)TE.1943-5436.0000480 |
| [11] | DU W, YANG J, POWIS B, et al. Understanding on-road practices of electric bike riders: an observational study in a developed city of China[J]. Accident Analysis and Prevention, 2013, 59: 319–326. DOI:10.1016/j.aap.2013.06.011 |
| [12] | DOZZA M, WERNEKE J. Introducing naturalistic cycling data: what factors influence bicyclists' safety in the real world?[J]. Transportation Research Part F, 2014, 24: 83–91. DOI:10.1016/j.trf.2014.04.001 |
| [13] | SCHEPERS J P, FISHMAN E, DEN HERTOG, et al. The safety of electrically assisted bicycles compared to classic bicycles[J]. Accident Analysis and Prevention, 2014, 73: 174–180. DOI:10.1016/j.aap.2014.09.010 |
| [14] | JIN S, QU X, WANG D. Assessment of expressway traffic safety using Gaussian mixture model based on time to collision[J]. International Journal of Computational Intelligence Systems, 2011, 4(6): 1122–1130. DOI:10.1080/18756891.2011.9727860 |
| [15] | JIN S, WANG D, XU C, et al. Short-term traffic safety forecasting using Gaussian mixture model and Kalman filter[J]. Journal of Zhejiang University: Science A, 2013, 14(4): 231–243. DOI:10.1631/jzus.A1200218 |
| [16] | PARK B J, ZHANG Y, LORD D. Bayesian mixture modeling approach to account for heterogeneityin speed data[J]. Transportation Research Part B, 2010, 44(5): 662–673. DOI:10.1016/j.trb.2010.02.004 |



