2. 江西理工大学 建筑与测绘工程学院, 江西 赣州 341000;
3. 江西省环境岩土与工程灾害控制重点实验室, 江西 赣州 341000
2. School of Architectural and Surveying and Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
3. Environmental Ground and Disaster Control Key Laboratory of Jiangxi Province, Ganzhou 341000, China
红黏土为碳酸盐岩在热带、亚热带湿热气候条件下经过物理、化学分化和红土化作用形成的一种褐红、棕红等颜色的黏性土体, 广泛分布于我国南方云贵高原、四川东部、两湖两广等地区, 具有高含水率、高塑性、低渗透性、低强度等特点, 导致修建于红黏土地基上的高速公路、铁路、机场跑道等交通设施在服役期间产生过大的沉降[1-4].为了揭示交通荷载作用下红黏土地基的长期变形规律, 准确预测运营沉降, 降低维护用费, 诸多学者对包含红黏土在内的软黏土在交通荷载作用下的长期变形特性进行试验研究[5-11].
陈颖平等[5]对重塑样和原状样进行循环三轴试验, 研究无静偏应力和有静偏应力软黏土在不排水循环荷载作用下的累积变形特性;蔡袁强等[6]通过不排水循环三轴试验, 分别研究单、双向激振下各向同性和各向异性固结的杭州软黏土的动力特性;张勇等[7]通过饱和重塑软黏土室内不排水动三轴试验, 研究循环荷载作用下饱和重塑软黏土的累积塑性应变发展形态.以上研究具有较大的工程意义, 揭示了软黏土的长期动力特性, 但循环三轴试验都是在不排水条件下进行的, 而实际路基在长期交通荷载下存在一定程度的排水, 或者称为部分排水.目前, 针对部分排水条件下软黏土长期动力特性的研究较少.
Akira等[8]对淤泥土开展一系列部分排水条件下的循环三轴试验, 基于试验结果提出不同固结压力下的淤泥土变形模型;丁智等[9]研究排水条件对杭州饱和软黏土长期动力特性的影响, 得出在相同的振动情况下排水振动的应变比不排水时的应变大;王军等[10]对温州原状饱和软黏土, 在不排水和排水条件下开展连续循环加载和分阶段循环加载试验, 分析循环荷载作用及一定时间的停振对土体动力特性的影响;郭林等[11]对温州原状饱和软黏土进行不同循环应力比下的不排水和部分排水大周数循环三轴试验, 表明部分排水条件下软黏土试样的动力特性表现出很大的不同.以上试验在一定程度上揭示了部分排水条件下软黏土的长期动力特性, 但由于试验组数有限, 没有系统阐述部分排水条件下软黏土的长期力学特性, 缺少不同应力路径下部分排水条件黏土试样的循环特性试验研究, 鲜有针对天然红黏土试样在部分排水条件下的动力试验研究.
本文采用GDS动力测试系统, 对赣南地区原状红黏土开展部分排水条件下的长期动力试验, 研究部分排水条件下红黏土的孔压累积和模量变化情况.重点分析循环应力比、平均初始固结压力和初始固结应力比对红黏土累积变形的影响, 提出考虑循环应力比、平均初始固结压力、初始固结应力比和循环次数的累积应变模型.
1 试验土样及方案 1.1 试验仪器采用英国GDS公司研发的动三轴测试系统, 如图 1所示.仪器主要由轴向激振器、围压控制器、轴向力与位移传感器、孔压及围压传感器、反压器、信号调节装置及动态控制系统组成.仪器通过压力室底座施加轴向力和轴向变形, 控制压力室液体进出施加围压, 测得反压器液体体积的变化量计算排水试验中试验的体应变.仪器精度较高, 其中轴向位移精度为7%, 轴力精度为0.2 N, 围压和孔压传感器精度为1 kPa, 反压体积精度为1 mm3, 能够精准地控制施加的压力, 确保试验结果准确可靠.

|
图 1 GDS三轴仪器示意图 Fig. 1 Schematic view of test apparatus |
试验所用红黏土试样取自江西理工大学应用科学院后天然路基层, 场地条件如图 2所示, 地下水位深度为1.5 m, 取样深度为2.0~2.5 m.采用薄壁取样法, 尽量减少对原状土的扰动.取完样后, 立即对薄壁管两端进行密封, 储存在实验室的恒温恒湿箱内以备试验使用.在试验前, 通过标准土力学试验测得试验所用原状红黏土的基本物理力学指标如下:相对密度Gs=2.67~2.70, 天然水质量分数wn(水)=26.5%~27.8%, 液限wL=35.2%, 塑性指数Ip=18.2%, 初始孔隙比e0=0.78, 饱和度Sr=90.1%~94.5%, 前期固结压力pc=45 kPa.

|
图 2 路基层地质剖面图 Fig. 2 Geologic profile of subgrade layers |
首先采用专用切样器, 将原状土样切成尺寸为直径为50 mm、高100 mm的试验试样, 然后将试样装入GDS三轴压力室进行反压饱和.分三阶段逐级施加300 kPa反压、310 kPa围压, 保持10 kPa有效压力, 饱和24 h后采用B检测检验土样的饱和程度, 试验的孔压系数B值大于0.98, 则认为土样达到饱和要求.最后施加设定的围压进行等压固结, 当孔隙水压力消散到等于反压时, 认为土样固结完成.对于不同的初始固结应力比(K0固结)试验, 在初始10 kPa有效压力的基础上, 以0.1 kPa/min的速率增加竖向应力, 使试样的应力达到设定固结应力比后, 在应力路径控制模块中, 以同等的相对速率施加围压和竖向力进行K0固结, 使试样最终达到设定的初始固结应力比.当试样的应变发展速率可以降到0.001%/h以下时, 认为试样固结完成.
1.4 加载方案在试样固结完成后, 对试验施加设定的循环应力进行相应试验研究.试验的参数如下:初始偏应力为q0, 初始平均应力为p′0, 初始固结应力比为η, 动应力幅值为σ1ampl, 竖向循环应力比为ζ, 分别定义为
| $ {q_0} = {{\sigma '}_1} - {{\sigma '}_3}, $ | (1) |
| $ {{p'}_0} = \left( {{{\sigma '}_1} - 2{{\sigma '}_3}} \right)/3, $ | (2) |
| $ \eta = {q_0}/{{p'}_0}, $ | (3) |
| $ \sigma _1^{{\rm{ampl}}} = \sigma _1^{'\max } - \sigma _1^{'\min }, $ | (4) |
| $ \zeta = \sigma _1^{{\rm{ampl}}}/{{p'}_0}. $ | (5) |
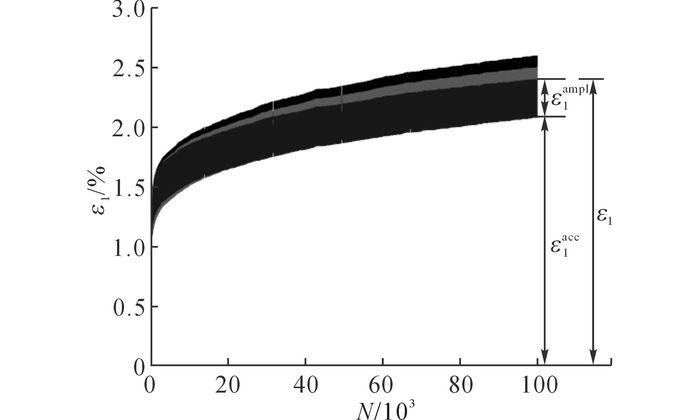
此外, 在循环荷载试验中, 竖向应变ε1由竖向累积应变ε1acc和应变幅值ε1ampl组成:
| $ {\varepsilon _1} = \varepsilon _1^{{\rm{acc}}} + \varepsilon _1^{{\rm{ampl}}}. $ | (6) |
对应的回弹模量定义如下:
| $ {M_{\rm{r}}} = \sigma _1^{{\rm{ampl}}}/\varepsilon _1^{{\rm{ampl}}}. $ | (7) |
三轴试验分为A、B、C、D共4组, 具体试验方案如表 1所示.A组为3个相同应力状态下的重复性试验, 确保试验的有效性和数据的可靠性.B为8个不同循环应力比(包含A组其中1个)在相同初始固结压力下的循环荷载试验, 研究循环应力比对红黏土累积变形的影响.C组为4个不同初始固结压力(包含B组其中1个)在相同循环应力比下的循环荷载试验, 研究初始固结压力对红黏土累积变形的影响.D组为4个(包含B组其中1个)不同初始固结应力比在相同循环应力比下的循环荷载试验, 研究不同初始固结应力比对红黏土累积变形的影响.所有试验采用轴力控制模式, 加载频率为1 Hz, 加载波形为半正弦波, 循环次数为100 000次.所有试验在排水条件下开展, 由于黏土的低渗透性导致排水不畅孔压累积, 称为部分排水条件试验.将试样顶部与反压器相连形成排水通道, 孔压在底部测得.试验中, 忽略由于红黏土渗透性较低而产生的不均匀孔压和变形, 假定试样底部孔压为单元体实际有效孔隙水压力, 假定试样平均应变为单元体实际应变.
| 表 1 不同循环应力路径加载方案 Table 1 Summary of test programs |
由于原状土的不确定性以及取样和运输过程中对土的扰动, 试验试样的力学特性存在一定的离散性.为了检验试验的有效性, 确保试验数据真实可靠, 在试验起初开展3个重复性试验.从所取原状土样中随机挑选3个土块进行制样, 采用同样的制样方法, 施加大于先期固结压力的围压进行固结;然后在同样的应力条件(p′0=100 kPa, ζ=0.16, η=0) 下进行动力加载, 测得3个试样轴向应变随循环加载次数的发展规律, 如图 3所示.可以看出, 3个试样的竖向变形具有较高的可重复性, 相对误差约为8%, 由下式计算得到:
|
图 3 重复性试验结果 Fig. 3 Repetability test results |
| $ \Delta = \left( {\varepsilon _{\max }^{{\rm{acc}}} - \varepsilon _{\min }^{{\rm{acc}}}} \right)/\varepsilon _{{\rm{av}}}^{{\rm{acc}}} \times 100. $ | (8) |
式中:εmaxacc、εminacc、εavacc分别为3个重复性试验中的最大、最小、平均累积应变, Δ为相对误差.相对误差远小于后续试验中所分析因素的影响值, 则试验误差在可接受范围内, 本文所得的试验结果真实有效.
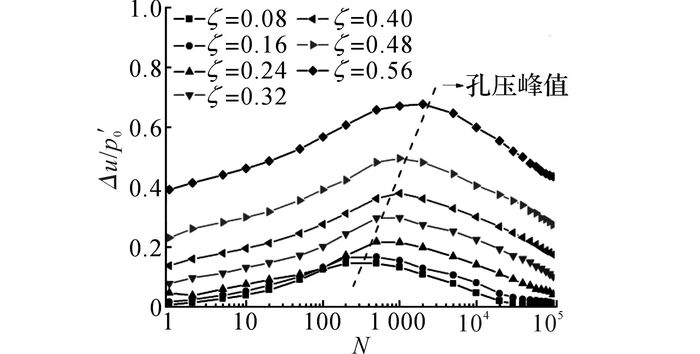
2.2 不同循环应力比如图 4所示为在p′0=100 kPa, η=0的条件下,B组试验中归一化超孔压Δu/p′0随交通荷载循环次数的发展规律.可以看出, 对于各循环应力比的部分排水试验, 在施加动荷载初期, 由于红黏土渗透性低, 排水滞后, 孔压存在一定程度的累积, 并逐渐增大, 达到峰值.随着循环次数的不断增大, 孔隙水逐渐排出, 孔压呈现降低趋势.试验初期孔压随着循环应力比的增大而增大, 孔压峰值对应的循环次数随着循环应力比的增大而增加.对于较大的循环应力比试验, 在试验结束时, 存在较大的残余孔压, 随着循环应力的减小, 残余孔压依次减小, 对于较小的循环应力比试验(ζ=0.08和ζ=0.16), 超孔压可完全消散, 残余孔压为0.
|
图 4 不同循环应力比下归一化孔压随循环次数的发展曲线 Fig. 4 Normalized pore water pressure accumulations versus number of cycles under different cycle stress ratios |
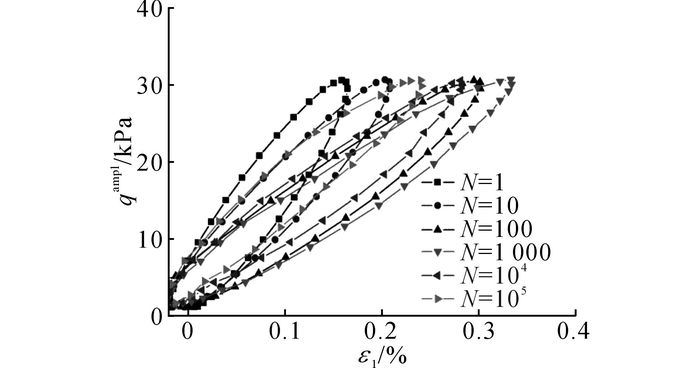
如图 5所示, p′0=100 kPa, ζ=0.16, η=0,以B2为例, 绘制了循环次数N=10、100、1 000、10 000、100 000时的滞回曲线图.不同循环次数下的滞回圈都从原点开始, 省略各圈对应的竖向累积应变, 对比分析不同循环次数下滞回圈的形状变化.可以看出, 在部分排水条件下, 随着循环次数的增加, 每循环荷载产生的回弹应变逐渐增加, 滞回圈逐渐变长;随着循环次数的继续增加, 每循环荷载产生的回弹应变开始减小, 滞回圈逐渐缩短.这与孔压的发展趋势相对应, 在试验初期, 孔压不断积累, 有效应力逐渐降低, 每循环荷载对应的回弹变形增加.随着孔压的消散, 有效应力的增加, 试样强度逐渐增加, 每循环荷载对应的回弹变形相对减少.
|
图 5 不同循环次数下的滞回圈曲线 Fig. 5 Hysteresis loops at certain loading cycles |
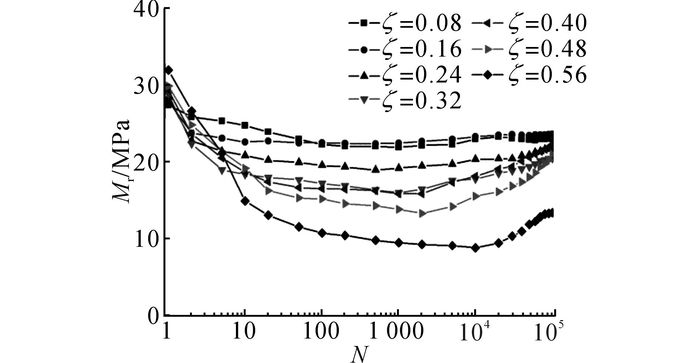
为了进一步反映红黏土在部分排水条件下的回弹特性, 如图 6所示为在p′0=100 kPa, η=0的条件下,不同循环应力比试验的回弹模量随循环次数的变化规律.可以看出, 对于所有的循环应力比试验, 由于孔压的积累, 回弹模量在试验初期都出现了较大的衰减, 随着孔压的消散, 回弹模量都逐渐增加.此外, 可以看出, 高循环应力比试验的初始回弹模量较大, 但由于初期较高的超孔压力, 回弹模量迅速降低, 高循环应力比试验的回弹模量低于低循环应力比的回弹模量.随着循环次数的增大, 孔压消散, 不同循环应力比试样的回弹模量表现不同.对于较大的循环应力比, 例如ζ=0.56和ζ=0.48, 由于前期孔压累积较大, 消散较慢, 循环应力比越大, 回弹模量越小;对于中间的循环应力比, 随着超孔压的逐渐消散, 相对较大环应力比试验的回弹模量增速较大, 逐渐接近并高于相对较小循环应力比试验的回弹模量, 例如ζ=0.4对应的回弹模量在试验结束前已大于ζ=0.32和ζ=0.24对应的回弹模量;对于较小的循环应力比而言, 尽管产生了较大的超孔压, 但超孔压的影响小于循环应力比的影响, 相对较大循环应力比试验的回弹模量迅速超过相对较小循环应力比试验, 例如ζ=0.16, 当循环次数N>100时, 回弹模量大于ζ=0.08对应的回弹模量.
|
图 6 不同循环应力比下回弹模量随循环次数的发展曲线 Fig. 6 Rebound modulus versus number of cycles under different cycle stress ratios |
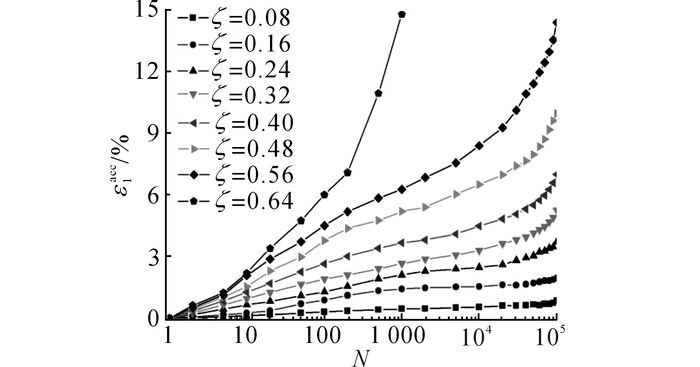
如图 7所示为在p′0=100 kPa, η=0的条件下,不同循环应力比试验的竖向累积变形随循环次数的变化规律.总体来说, 竖向累积变形随着循环应力比的增大而增大.Werkmeister等[12]根据土体长期累积变形率随循环次数的发展规律, 将土体长期变形行为分为3类:塑性安定(plastic shakedown)、塑性蠕变(plastic creep)、增量破坏(incremental collapse).本文仅考虑试样的竖向变形, 认为累积应变率为单位循环次数试样竖向累积变形的增量.当循环应力较小(ζ<0.16) 时, 累积应变率随着循环次数的增加而逐渐减少, 趋近于0;竖向累积应变逐渐趋于稳定, 则土体处于塑性安定行为范畴;当循环应力较大(0.16<ζ<0.56) 时, 累积应变率随着循环次数的增加而逐渐减少至恒定的较小值, 累积应变以较小的速率继续发展, 则土体处于塑性蠕变行为范畴;随着循环应力比的继续增大(ζ>0.56), 累积应变率始终保持较大值, 累积应变在较小的循环次数下迅速发展直至破坏, 则土体处于增量破坏行为范畴.根据实验结果, 可以选取ζ=0.16为该试验条件下的塑性安定界限, ζ=0.56为该试验条件下的塑性蠕变界限.
|
图 7 不同循环应力比下竖向累积变形随循环次数的发展曲线 Fig. 7 Axial strain accumulations versus number of cycles under different cycle stress ratios |
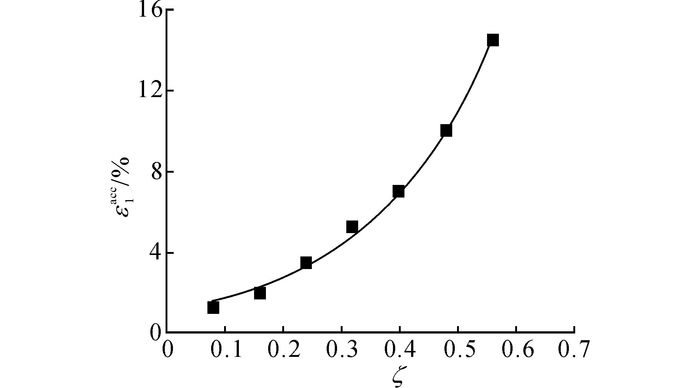
为了更直观地反映循环应力比对红黏土竖向累积变形的影响, 如图 8所示为在N=105,p′0=100 kPa, η=0的条件下,试验结束时, 即N=105时竖向累积应变随循环应力比的发展规律.可以看出, 随着循环应力比的增加, 累积应变明显增大, 变化速率随循环应力比的增加而增大.
|
图 8 循环105次时竖向累积变形随循环应力比的发展曲线 Fig. 8 Axial strain accumulations versus cycle stress ratios when 105 cycles |
采用指数函数来描述循环应力比对竖向累积变形的影响, 函数的具体形式如下:
| $ \varepsilon _1^{{\rm{acc}}}\left( \zeta \right) = a\exp \left( {b\zeta } \right). $ | (9) |
式中:a、b为试验参数, 由拟合可得, a=1.116, b=4.575, 拟合度R2=0.996, 表明指数函数能够很好地反映竖向累积变形随循环应力比的变化规律.
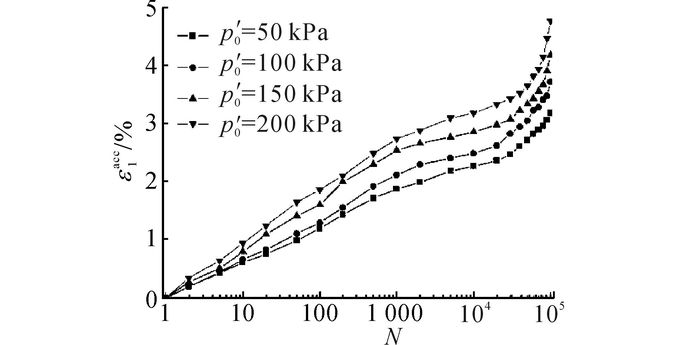
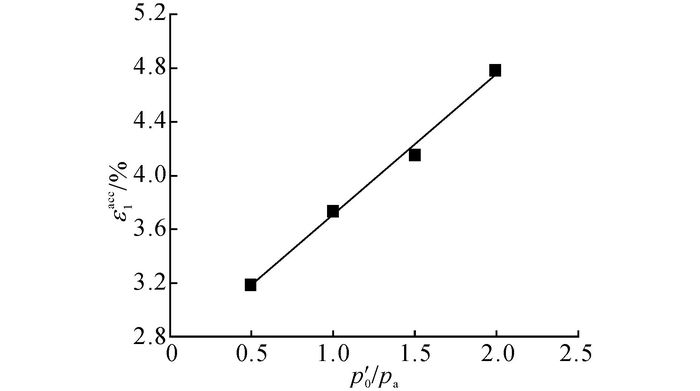
2.3 不同平均初始固结压力为了反映不同平均初始固结压力对红黏土累积变形的影响, 如图 9所示为当ζ=0.24, η=0时,不同平均初始固结压力下红黏土竖向累积变形随循环次数的发展曲线.图中, C组4个试验都施加相同的ζ=0.24, 以保证试验结果的可比性.可以看出, 4个试验的竖向累积变形随循环次数的发展都呈现出类似的规律.对于相同的循环应力比, 随着平均初始固结压力的增加, 竖向累积变形增大.为了进一步说明平均初始固结压力对累积变形的影响, 如图 10所示为当N=105时,竖向累积应变随归一化平均初始固结应力p′0/pa的发展规律.图中, pa为大气压力, 本文取pa=100 kPa.从图 10可以看出, 红黏土竖向累积变形与归一化平均初始应力存在较好的线性关系.
|
图 9 不同平均初始固结压力下竖向累积变形随循环次数的发展曲线 Fig. 9 Axial strain accumulations versus number ofcycles under different averageinitial consolidation pressures |
|
图 10 循环105次时竖向累积变形随平均初始固结压力的发展曲线 Fig. 10 Axial strain accumulations versus average initial consolidation pressures when 105 cycles |
采用线性函数来描述归一化平均初始固结压力对竖向累积变形的影响, 函数具体形式如下:
| $ \varepsilon _1^{{\rm{acc}}}\left( {{{p'}_0}} \right) = c\left( {{{p'}_0}/{p_{\rm{a}}}} \right) + d. $ | (10) |
式中:c、d为试验参数.由拟合得到, c=1.044, d=2.656, 拟合度R2=0.997, 表明线性函数能够很好地反映竖向累积变形随归一化平均初始固结压力的变化规律.
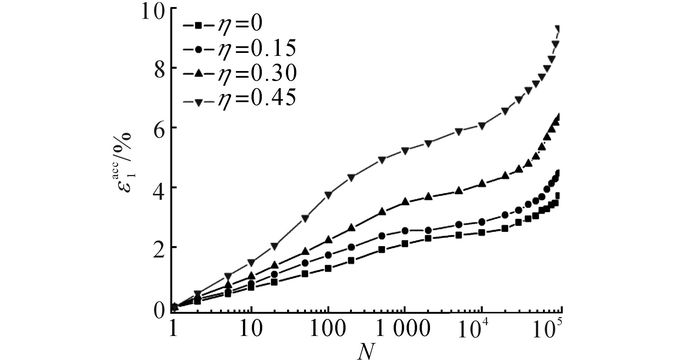
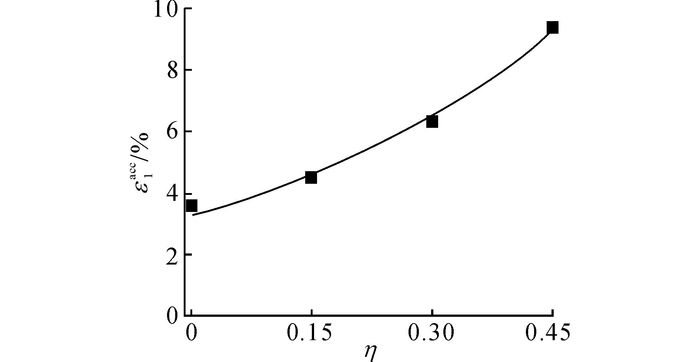
2.4 不同初始固结应力比如图 11所示为不同初始固结应力比下红黏土竖向累积变形随循环次数的变化规律.图中, D组4个不同初始固结应力比试验都在同样的初始平均固结应力和循环应力比下开展, 即p′0=100 kPa, ζ=0.24, 以保证试验结果的可比性.可以看出, 随着初始固结应力比的增加, 竖向累积变形明显增大.为了进一步说明初始固结应力比对累积变形的影响, 如图 12所示为当p′0=100 kPa, ζ=24,N=105时竖向累积应变随初始固结应力比的发展规律.可以看出, 红黏土竖向累积变形随着初始固结应力比的增加而明显增大, 变化速率随初始固结应力比的增加而逐渐增大.
|
图 11 不同初始初始固结应力比下竖向累积变形随循环次数的发展曲线 Fig. 11 Axial strain accumulations versus number of cycles under different initial consolidation stress ratios |
|
图 12 循环105次时竖向累积变形随初始固结应力比的发展曲线 Fig. 12 Axial strain accumulations versus initial consolidation stress ratios when 105 cycles |
采用指数函数来描述循环应力比对竖向累积变形的影响, 函数具体形式如下:
| $ \varepsilon _1^{{\rm{acc}}}\left( \eta \right) = m\exp \left( {n\eta } \right). $ | (11) |
式中:m、n为试验参数.由拟合得到, m=3.272, n=2.300, 拟合度R2=0.989, 表明指数函数能够很好地反映竖向累积变形随初始固结应力比的变化规律.
2.5 累积应变模型基于不同循环应力比、不同平均初始固结压力、不同初始固结应力比的试验结果, 提出考虑循环应力比、平均初始固结压力、初始固结应力比和循环次数的竖向累积变形模型, 具体表达式如下:
| $ \varepsilon _1^{{\rm{acc}}} = k\varepsilon _1^{{\rm{acc}}}\left( \zeta \right)\varepsilon _1^{{\rm{acc}}}\left( {{{p'}_0}} \right)\varepsilon _1^{{\rm{acc}}}\left( \eta \right)\varepsilon _1^{{\rm{acc}}}\left( N \right). $ | (12) |
式中:ε1acc(N)为考虑循环次数对累积变形的影响函数;k为试验参数, 包含其他因素对红黏土累积变形的影响.将ε1acc(ζ)、ε1acc(p′0)、ε1acc(η)的具体表达式(9)~(11) 代入式(12), 可得
| $ \varepsilon _1^{{\rm{acc}}} = \varepsilon _{1{\rm{ref}}}^{{\rm{acc}}}\exp \left( {b\zeta + n\eta } \right)\left( {c\left( {{{p'}_0}/{p_{\rm{a}}}} \right) + d} \right)\varepsilon _1^{{\rm{acc}}}\left( N \right). $ | (13) |
式中:ε1refacc=ack为常数, 表示参考累积应变.
对竖向累积应变进行循环应力比、平均初始固结压力和初始固结应力比的归一化, 可得
| $ \varepsilon _1^{{\rm{acc}}}/\left[ {\exp \left( {b\zeta + n\eta } \right)\left( {c\left( {{{p'}_0}/{p_{\rm{a}}}} \right) + d} \right)} \right]\varepsilon _{1{\rm{ref}}}^{{\rm{acc}}}\varepsilon _1^{{\rm{acc}}}\left( N \right). $ | (14) |
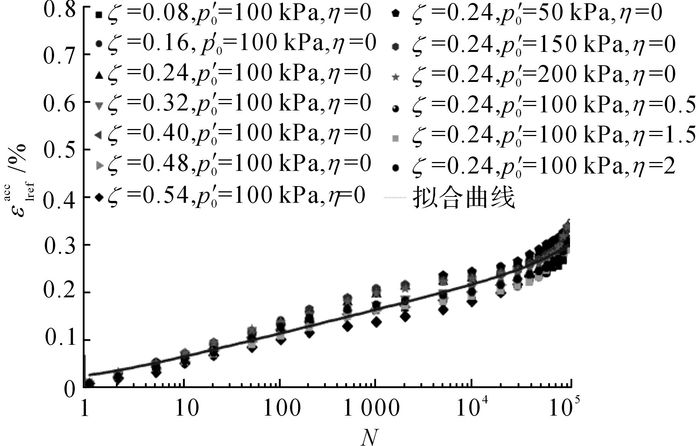
如图 13所示为B、C、D 3组全部试验归一化的竖向累积应变随循环次数的发展规律.可以看出, 通过循环应力比、平均初始固结压力和初始固结应力比影响函数归一化后的竖向累积变形能够很好地重叠在一起, 表明上述模型能够很好地反映不同应力条件对红黏土竖向累积变形的影响, 证明了提出的累积应变模型的正确性.
|
图 13 归一化的竖向累积变形随循环次数的发展曲线 Fig. 13 Normalized axial strain accumulations versus number of cycles for four test series |
采用对数函数来描述循环次数比对竖向累积变形的影响.函数的具体形式如下:
| $ \varepsilon _{1{\rm{ref}}}^{{\rm{acc}}}\varepsilon _1^{{\rm{acc}}}\left( N \right) = h\ln \left( {1 + jN} \right) + lN. $ | (15) |
式中:h、j、l为试验参数.由拟合可得, h = 0.029, j = 2.300, l = 3.515×10-7, 拟合度R2=0.957, 表明对数函数能够很好地反映竖向累积变形随循环次数的变化规律.将式(15) 代入式(13), 可得红黏土部分排水条件下竖向累积应变模型的完整表达式:
| $ \begin{array}{l} \varepsilon _1^{{\rm{acc}}} = \exp \left( {b\zeta + n\eta } \right)\left[ {c\left( {{{p'}_0}/{p_{\rm{a}}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\left. d \right]\left[ {h\ln \left( {1 + jN} \right) + lN} \right]. \end{array} $ | (16) |
模型参数如表 2所示.
| 表 2 竖向累积应变模型参数 Table 2 Axial strain accumulation model parameters |
(1) 对于部分排水条件下的红黏土循环荷载试验, 在施加循环荷载初期, 孔压迅速累积并达到峰值;随着循环次数的增大, 孔压逐渐降低, 在低循环应力比下可最终消散.
(2) 在循环荷载作用初期, 由于孔压累积, 红黏土回弹模量迅速降低达到最小值;随着循环次数的增大, 超孔压降低, 回弹模量逐渐恢复.高循环应力比试验的回弹模量在试验后期随着孔压的降低, 逐渐高于低循环应力比的回弹模量.
(3) 部分排水条件下红黏土的竖向累积变形分别随循环应力比、平均初始固结压力、初始固结应力比、循环次数的增大而增大.试验结束时的最终累积变形与循环应力比呈指数增长关系, 与平均初始固结压力呈线性增长关系, 与固结应力比呈指数增长关系;与循环次数呈对数增长关系.
(4) 建立考虑循环应力比、平均初始固结压力、初始固结应力比和循环次数的累积变形模型, 能够准确地预测不同动应力状态下红黏土的竖向累积变形.
| [1] | 工程地质手册编委会. 工程地质手册[M]. 北京: 中国建筑工业出版社, 2007: 55-61. |
| [2] |
康景文, 甘鹰, 张仕忠, 等. 昆明新机场红黏土冲压地基处理实验研究[J].
岩土工程学报, 2010, 32(supple.2): 496–500.
KANG Jing-wen, GAN Ying, ZHANG Shi-zhong, et al. Original stamping foundation treatment of red clay of new airport in Kunming[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(supple.2): 496–500. |
| [3] |
黄质宏, 朱立军, 廖义玲, 等. 不同应力路径下红粘土的力学特性[J].
岩石力学与工程学报, 2004, 23(15): 2599–2603.
HUANG Zhi-hong, ZHU Li-jun, LIAO Yi-ling, et al. Mechanical properties of red clay under different stress paths[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(15): 2599–2603. DOI:10.3321/j.issn:1000-6915.2004.15.022 |
| [4] |
李剑, 陈善雄, 姜领发, 等. 应力历史对重塑红黏土动力特性影响的试验研究[J].
岩土工程学报, 2014, 36(9): 1657–1665.
LI Jian, CHEN Shan-xiong, JIANG Ling-fa, et al. Experimental study on influence of stress history on dynamic properties of remolded red clay[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(9): 1657–1665. DOI:10.11779/CJGE201409012 |
| [5] |
陈颖平, 黄博, 陈云敏. 循环荷载作用下软黏土不排水累积变形特性[J].
岩土工程学报, 2008, 30(5): 764–768.
CHEN Ying-ping, HUANG Bo, CHEN Yun-min. Deformation and strength of structure soft clay under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 764–768. |
| [6] |
蔡袁强, 王军, 海钧. 双向激振循环荷载作用下饱和软黏土强度和变形特性研究[J].
岩石力学与工程学报, 2008, 27(3): 495–504.
CAI Yuan-qiang, WANG Jun, HAI Jun. Study of strength and deformation behaviors of soft clay under bidirectional exciting cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 495–504. |
| [7] |
张勇, 孔令伟, 郭爱国, 等. 循环荷载下饱和软黏土的累积塑性应变试验研究[J].
岩土力学, 2009, 30(6): 1542–1548.
ZHANG Yong, KONG Ling-wei, GUO Ai-guo, et al. Cumulative plastic strain of saturated soft clay under cyclic loading[J]. Rock and Soil Mechanics, 2009, 30(6): 1542–1548. |
| [8] | AKIRA S, LAWALENNA S, NORIHIKO M. Partially drained cyclic behavior and its application to the settlement of a low embankment road on silty-clay[J]. Soils and Foundations, 2003, 43(1): 33–46. DOI:10.3208/sandf.43.33 |
| [9] |
丁智, 张涛, 魏新江, 等. 排水条件对不同固结度软黏土动力特性影响试验研究[J].
岩土工程学报, 2015, 37(5): 893–899.
DING Zhi, ZHANG Tao, WEI Xin-jiang, et al. Experimental study on effect of different drainage conditions on dynamic characteristics of soft clay under different degrees of consolidation[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(5): 893–899. DOI:10.11779/CJGE201505015 |
| [10] |
王军, 蔡袁强, 郭林, 等. 分阶段循环加载条件下温州饱和软黏土孔压和应变发展规律[J].
岩土工程学报, 2012, 34(7): 1349–1354.
WANG Jun, CAI Yuan-qiang, GUO Lin, et al. Pore pressure and strain development of Wenzhou saturated soft soil under cyclic loading by stages[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(7): 1349–1354. |
| [11] |
郭林, 蔡袁强, 王军. 长期循环荷载作用下排水条件对饱和软黏土动力特性影响[J].
岩土力学, 2013, 34(supple.2): 94–99.
GUO Lin, CAI Yuan-qiang, WANG Jun. Influence of drainage condition on dynamic cyclic behavior of saturated soft clay under long-term cyclic loading[J]. Rock and Soil Mechanics, 2013, 34(supple.2): 94–99. |
| [12] | WERKMEISTER S, DAWSON A, WELLNER F. Permanent deformation behavior of granular materials and the shakedown concept[J]. Transportation Research Record, 2001, 1757(1): 75–81. |



